A Control Engineering Framework for Quadrotors: An Application for

the Crazyﬂie 2.X

Rafael Socas

, Raquel Dormido

, Mar

ıa Guinaldo

and Sebasti

an Dormido

Department of Computer Science and Automatic Control, Universidad Nacional de Educaci

on a Distancia (UNED),

28040 Madrid, Spain

Keywords:

Non-linear Systems, Autonomous Robots, Control Laboratories, Crazyﬂie 2.X, Control Education.

Abstract:

In this work, a new framework to develop and investigate new control algorithms in quadrotors is presented.

The proposed system includes two main elements: 1) a simulation laboratory and 2) a real environment based

on the Crazyﬂie 2.X quadcopter. Both elements offer all the necessary tools to design and implement a wide

variety of controllers in the real system. The phases to carry out the controller’s designs and how to apply

them to the real quadrotor are explained in detail. A practical application to check the proposed framework

and some additional experiments have been investigated in depth. The simulation and experimental results

corroborate the validity of the proposed framework.

1 INTRODUCTION

In recent years, the industry and the scientiﬁc com-

munity are showing a growing interest in robotics.

Robots are becoming more and more prevalent in in-

dustries such as manufacturing, medical, space, au-

tomotive, etc. They have a crucial role in danger-

ous, routine or high accuracy tasks. The use of aerial

robots is increasing rapidly in both scientiﬁc and com-

mercial ﬁelds. In fact, it has been one of the areas

where the researchers have focused their efforts. The

quadrotor architecture has been chosen in many re-

search groups for its low dimension, simple mecha-

nisms and good manoeuvrability. However, control-

ling a quadrotor is not easy because of the coupled

dynamics and its commonly under-actuated design

conﬁguration (Mahony et al., 2012). In addition, the

quadrotor presents a highly non-linear dynamics and

several uncertainties during its missions (Lee et al.,

2013). These facts make ﬂight control an interesting

research area.

A large number of techniques are propossed in

the literature: one of the most used techniques is the

PID control strategy. This control method has a good

performance in this kind of problems and the con-

trol laws can be implemented in a simple way (Zhou

https://orcid.org/0000-0001-6496-3007

https://orcid.org/0000-0003-1175-5065

https://orcid.org/0000-0002-7043-6673

https://orcid.org/0000-0002-2405-8771

et al., 2017). The Linear Quadratic Regulator (LQR)

provides optimal feedback gains to enable the stabil-

ity and the high performance of the closed-loop sys-

tem (Zhang et al., 2016). The Lyapunov techniques

guarantee, under certain conditions, the asymptoti-

cal stability of the quadrotor (Safaei and Mahyuddin,

2016). When there are parametric uncertainties or it

is difﬁcult to model the dynamic of the system, the

adaptive control methods provide a good performance

(Andrievsky et al., 2005). Backstepping control tech-

niques guarantee the stability of the quadrotor, but a

lot of computation is required (Fan et al., 2017). If the

dynamic feedback control is used, it allows to trans-

form the dynamic of the quadrotor into a linear system

and the ﬂy movements can be decoupled (Taniguchi

et al., 2014). In environments where GPS (Global Po-

sitioning Systems) signal is not available, the visual

feedback control techniques are the most popular so-

lutions (Shirai et al., 2017). Other techniques such

as fuzzy logic (Wahyunggoro et al., 2016) or neural

networks (Emran and Najjaran, 2017) are being lately

used to solve these control problems.

From the research and control point of view to-

day many researchers focus on designing new con-

trol strategies that use quadrotors platforms. What-

ever control technique is used, its validation is usu-

ally performed through simulations, since perform-

ing experiments over real platform requires much ef-

fort. Moreover, most of the developed platforms may

be difﬁcult to replicate and not be directly available

Socas, R., Dormido, R., Guinaldo, M. and Dormido, S.

A Control Engineering Framework for Quadrotors: An Application for the Crazyﬂie 2.X.

DOI: 10.5220/0010482003590366

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 359-366

ISBN: 978-989-758-522-7

359

to other research groups. Recently, a nano quadro-

tor low-cost platform has been developed (Giernacki

et al., 2017). Crazyﬂie is an open-source and open-

hardware project which is supported by a very active

community where the software and the projects are

accessible and many applications for developing are

available.

In this paper, a new framework that provides great

ﬂexibility for investigating and developing new con-

trol techniques for quadrotors, and more speciﬁcally

for Crazyﬂie 2.X, is presented. Our proposal includes

methodologies and tools to validate the control tasks,

in such a way that the presentation of real results will

be an enhancement to the theoretical contributions.

Using the framework all the stages of development,

from the design of the controllers to the ﬁnal adjust-

ment in a real environment can be carried out. In con-

trast to other works such as (Giernacki et al., 2017),

the aim of this paper is to provide a step by step guide

to have the platform ready so that researchers, engi-

neers and students can easily develop and test new

control algorithms for Crazyﬂie 2.X and, if desired,

add new layers on the top of the developed tools eas-

ily.

The paper is organized as follows. Section 2

includes an overview of the Crazyﬂie 2.X platform

(Giernacki et al., 2017). In section 3, the control

scheme of the system is shown. The new control en-

gineering framework is described in section 4. In sec-

tion 5, a practical application is investigated including

simulation and experimental results. Finally, the con-

clusions and future work are discussed.

2 OVERVIEW OF THE DYNAMIC

MODEL OF THE QUADROTOR

To deﬁne the dynamic model of the Crazyﬂie 2.X,

some hypothesis have been taken into account: the

aircraft is a rigid body with a constant mass and the

geometry and the propulsion are symmetrical. This

vehicle has six degree of freedom: the position of the

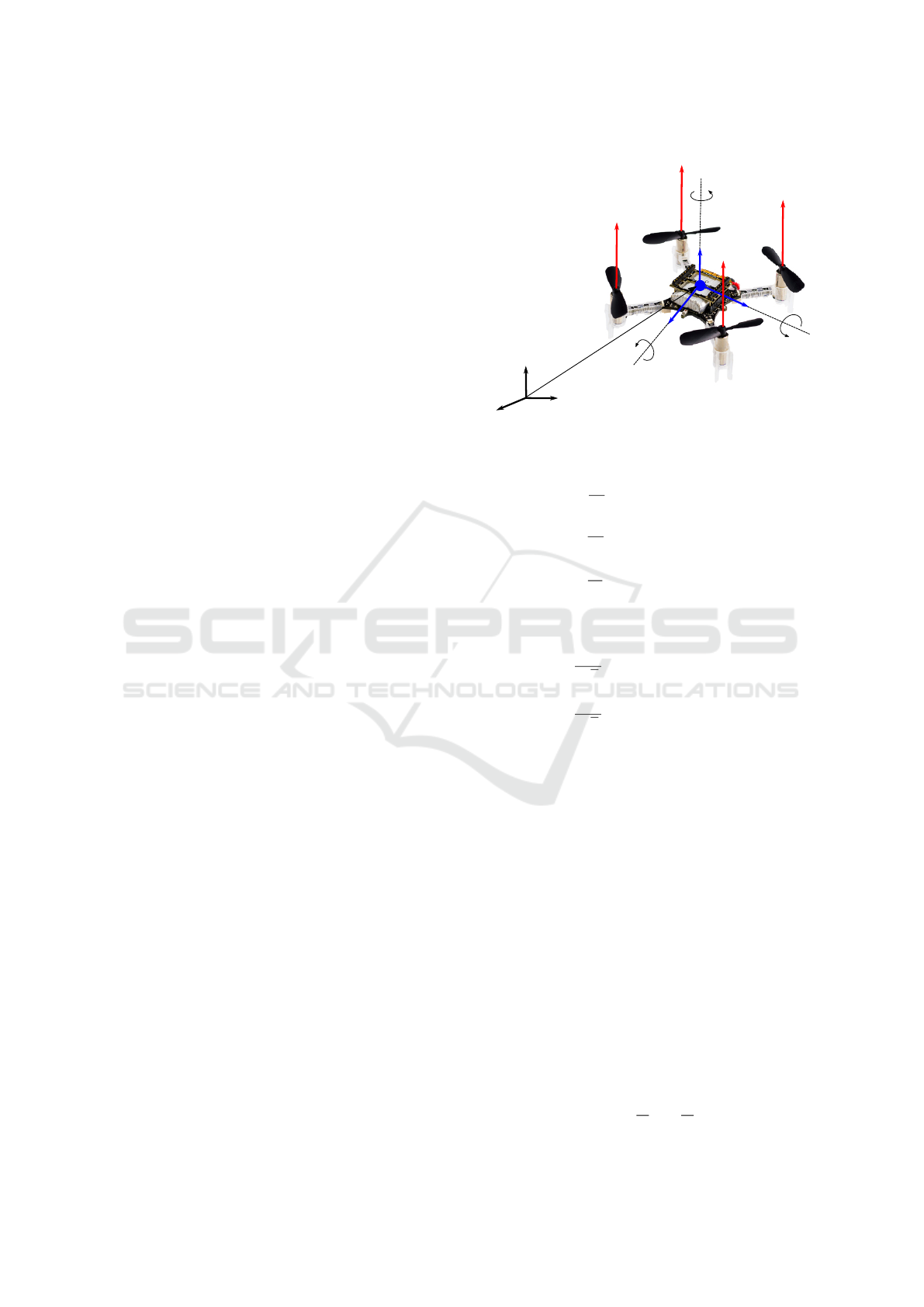
CG (Center of Gravity) of the aircraft with respect to

the inertial frame (P

= {x, y, z}) and the orientation

of the quadrotor which is described by the Euler an-

gles (Φ = {φ, θ, ψ}). These angles, the roll φ, the

pitch θ and the yaw ψ represent the rotation of the

body frame with respect to the inertial frame. The po-

sition and the orientation of the drone are depicted in

Figure 1.

The state of the system can be obtained taking

into account the mechanical classical laws of motion.

The angular speeds of the body frame (p, q, r) are de-

scribed by (1)-(3),

Figure 1: Position P

= {x, y, z} and orientation Φ =

{φ, θ, ψ} of the quadrotor.

˙p =

(qr (I

−I

) + M

) (1)

˙q =

(rp (I

−I

) + M

) (2)

˙p =

(pq(I

−I

) + M

) (3)

where M

, M

and M

are the momentums deﬁned by

(4)-(6)

√



−Ω

+ Ω



(4)

√



−Ω

+ Ω

−Ω



(5)

= C



−Ω

+ Ω

−Ω



(6)

where d denotes the distance from the CG to the cen-

ter of each motor, C

is the thrust coefﬁcient that rep-

resents the upward force generated by each propeller

where F

= C

Ω

(Ω

is the angular speed of each

propeller) and C

the aerodynamic drag coefﬁcient,

see Figure 1. In these equations the angular accel-

erations have been neglected because they tend to be

small compared to the other terms. On the other hand,

the gyroscopic moments have also been neglected due

to the inertia moments of the motors tends to be small

(Sabatino, 2015). The terms I

, I

and I

denote the

inertia moments about its three axes. Based on the hy-

pothesis that the body of the quadcopter is symmetri-

cal around all its axes, all crossed terms (I

, I

, etc.)

can be considered equal to zero. Then, the Euler an-

gles can be obtained by the integration of the equation

(7)













1 S

0 C

−S













(7)

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

360

where S

denotes sin(i), C

represents cos(i) and T

means tan(i) with i = {φ, θ, ψ}. And, the position of

the CG of the quadrotor with respect the inertial frame

is obtained by the integration of (8)-(10)

¨x =



+ S



(8)

¨y =



−C



(9)

¨z =





−g (10)

where F

∑

, m is the total mass of the aircraft

and g the acceleration of gravity (9.81 m/s

). In (Luis

and Ny, 2016) more details of the dynamic model of

the Crazyﬂie 2.X are presented. Finally, in (F

orster,

2015) an exhaustive work has been done to identify

the main parameters of Crazyﬂie 2.X.

On the other hand, linearisation is useful to design

a control system using linear classical design tech-

niques. It also allows to analyse the system character-

istics such as system stability, disturbance rejection,

and reference tracking. Considering the Crazyﬂie 2.X

as it was analysed in (Luis and Ny, 2016), the trim

point is F

= mg = 4C

Ω

, it means that the drone is

hovering at constant altitude. Taking into account this

assumption, the equilibrium propeller speed is

Ω

(11)

Once the linear model is obtained the ﬂight modes

can be decoupled. In this case, four models can be ob-

tained: vertical, directional, lateral and longitudinal.

3 QUADROTOR’S CONTROL

SCHEME

The control architecture for the Crazyﬂie 2.X or for

similar quadrotors is depicted in Figure 2 (Landry

et al., 2015). It is divided in two groups: the on-

board controllers inside the drone and the off-board

controllers that are implemented in external systems

such as a PC. The communication between these two

groups, the on-board and the off-board controllers, is

made by a radio interface of 2.4 GHz. There is a mo-

dem in the drone side and the crazyradio PA in the

PC side. Over this radio link, the Sensor Information

SI = (z, φ, θ, ψ, p, q, r) and the Control Commands

CC = (Ω, φ

, θ

, r

) are interchanged. In this archi-

tecture, the input Ω in the control mixer denotes the

thrust. This kind of robots needs high frequency con-

trol to get a stable ﬂight. For this reason, the on-board

controllers are required. In this architecture, the rate

controller works with 500 Hz and the attitude con-

troller with 250 Hz. The set of on-board controllers

is composed by the control mixer, the rate controller

and the attitude controller, these controllers are im-

plemented in the ﬁrmware of the drone Crazyﬂie 2.X.

The rate controller and the attitude controller are

implemented by discrete-time PID controller (12)

= K

+ K

∑

n=1

+ K

−e

k−1

] (12)

where u

is the control signal, e

the error signal

and K

, K

and K

are the controller’s gains. In the

ﬁrmware of the Crazyﬂie 2.X the gains for the rate

and for the attitude controllers are deﬁned.

The Control Commands CC are used to set the

references for the on-board controllers. On the other

hand, the Sensor Information SI can be obtained with

a maximum frequency of 100 Hz. This is the main

reason why the rate and the attitude controllers can-

not be implemented outside the drone. Finally, in the

off-board controllers, the altitude, x-y position (if ad-

ditional sensors are included to get the x and y coor-

dinates) and yaw position controllers can be imple-

mented using the SI and the CC.

4 THE NEW CONTROL

ENGINEERING FRAMEWORK

The framework proposed in this work is based on

the control architecture of the Crazyﬂie 2.X. This

framework will help to develop quadrotor control

techniques (see Figure 3). With methodologies and

tools included in it, the researchers and students will

be able to investigate and develop new control tech-

niques applied to these types of aircrafts. This new

framework offers the necessary tools to undertake all

the stages of development, from the design of the con-

trollers to the ﬁnal adjustment in the real environment.

The proposed framework is composed of two main

elements: 1) a simulation laboratory based on Mat-

lab/Simulink tools and 2) The instructions to setup

a real-world environment testing area based on the

drone Crazyﬂie 2.X with its hardware and software

components.

4.1 Simulation Laboratory

In the simulation laboratory (Figure 3a)) two mod-

els of the Crazyﬂie 2.X are available: the linear and

the non-linear model, both elements have been imple-

mented as Simulink blocks. The output is the Sensor

Information SI = (z, φ, θ, ψ, p, q, r). The input of the

A Control Engineering Framework for Quadrotors: An Application for the Crazyﬂie 2.X

361

(p,q,r)

CC=(Ω,ϕ

,θ

)

SI=(z,ϕ,θ,ψ,p,q,r)

Motors

Acelerometer

Gyro

Flow deck

Loco

Sensors

Actuators

Sensor

Fusion

(ϕ,θ,ψ)

(z)

Control

Mixer

Rate

Controller

A�itude

Controller

(Δϕ,Δθ,Δψ)

(p,q,r)

)

(Ω)

(ϕ,θ)

(ϕ

,θ

)

Input

Output

PWM

f=500Hz

f=250Hz

2.4 GHz

Oﬀ-board Controllers

Drone Crazyﬂie 2.X

Modem

Crazyradio PA

On-board Controllers

Figure 2: Control architecture of the Crazyﬂie 2.X.

Crazyﬂie 2.X

Crazyradio PA

Model of the Crazyﬂie 2.X

Python - API cﬂib

On-board

Controllers

Linear Model

Non-Linear Model

Oﬀ-board

Controllers

Modem

Firmware

Actuators

Sensors

PWM

,ψ

)

references

Oﬀ-board Controllers

Figure 3: Control engineering framework. a) Simulation

laboratory in Matlab

T M

/Simulink

T M

, b) real environment

based on the Crazyﬂie 2.X.

model should be the moments M

, M

and the

force F

, but for practical reasons, it is better to use

the motor signals PWM

. To use these inputs in the

models, the following relationship between the vari-

ables PWM

and Ω

is used (Luis and Ny, 2016):

Ω

= 0.2685PWM

+ 4070.3 (13)

The input of the on-board controllers is the Control

Commands CC = (Ω, φ

, θ

, r

). Finally, some off-

board controllers have been deﬁned in the system,

these controllers will be described later in the prac-

tical application.

4.2 Real Environment

The real environment is composed by a PC with the

Crazyradio PA and the drone Crazyﬂie 2.X including

the hardware ﬂow deck (Figure 3b). The Crazyra-

dio PA is connected to the PC and it allows the ra-

dio interface to communicate the PC with the drone.

In the PC the off-board controllers are implemented

in python scripts based on the API cﬂib. Using this

API a set of commands are available to interact with

the drone, some of them for getting the sensor infor-

mation (logging functionality) and others for sending

control commands to the drone. Although python is

an interpreted language, the real-time is guaranteed

because the sample rate in the radio interface is rela-

tively low.

To get the sensor information SI the logging func-

tionality of the Crazyﬂie 2.0 has been used. This fea-

ture allows to read the sensor information with max-

imum frequency of 100 Hz (sampling time=0.01s).

Using the API cﬂib, this task can be implemented in a

simple way. Using this methodology to read the sen-

sor information, the noise in these devices can be eas-

ily estimated. After calibrating the sensors, the noise

in the sensors can be modelled by a normal distribu-

tion N(µ, σ), where µ is the mean and σ the standard

deviation. In this system µ ≈ 0 and σ is presented

in Table 1. In order to get more realistic results in

the simulation laboratory, these models of the noise

will be included in the experiments. To send a control

command CC to the drone the API cﬂib provides the

command cf.commander.send setpoint(roll, pitch,

yawrate, thrust) where roll=φ

and pitch=θ

in de-

grees, yawrate=r

in degrees/s and thrust=Ω a value

between 0 and 65,535. With this command is very

easy to build many control schemes. For example,

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

362

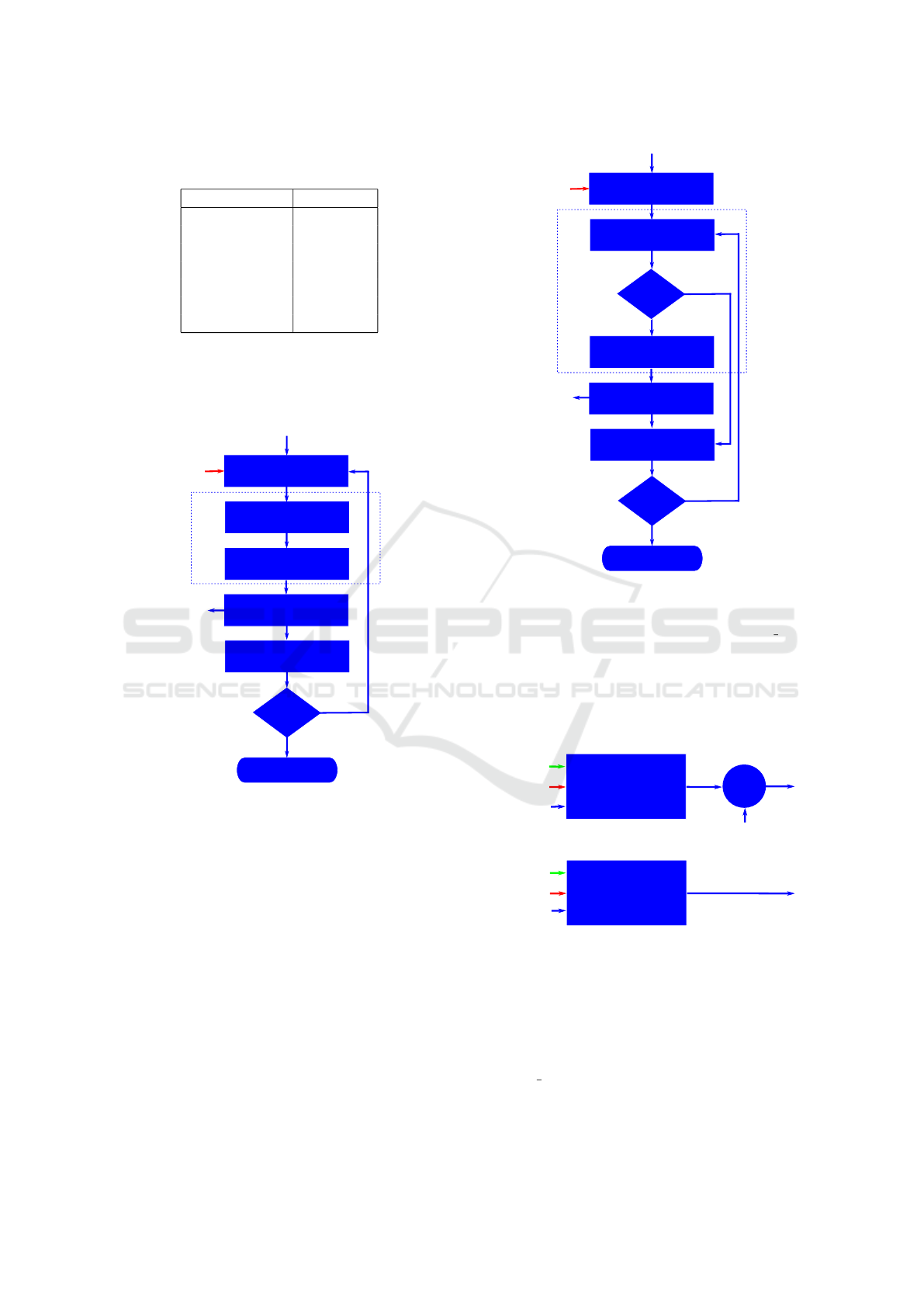
Table 1: Standard deviations (σ) for the noise model of the

sensors.

Model variable σ

z 0.00132 m

φ 0.119

θ 0.180

ψ 0.149

p 0.795

q 0.752

r 0.695

to deﬁne a PID controller, the algorithm presented

in Figure 4 can be used. On the other hand, if an

event-based PID controller (

Aarz

en, 1999) is needed

the structure in Figure 5 can be implemented. There

Stop

sleep(sampling_time)

Condition?

Yes

Exit

SI=(z,ϕ,θ,ψ,p,q,r)

TX Control Commands

RX Sensor Information

CC=(Ω,ϕ

,θ

)

e=references-SI

CC=PID(e,K

)

Controller

Figure 4: Algorithm for the periodic PID. The error signal

e is obtained from the desired setpoint signals references

and the SI. In this scheme, PID() denotes a PID controller

whose parameters are the error signal e and K

, K

which mean the proportional, integral and derivative terms.

is a wide variety of control techniques that can be used

and investigated in depth both in the simulation envi-

ronment and in the real system.

5 PRACTICAL APPLICATIONS

AND EXPERIMENTAL

RESULTS

To check the functionality and the uses cases of the

presented framework some experiments have been

proposed. To investigate the control design capabil-

Stop

sleep(sampling_time)

Condition?

Yes

Exit

SI=(z,ϕ,θ,ψ,p,q,r)

TX Control Commands

RX Sensor Information

CC=(Ω,ϕ

,θ

)

e=references-SI

CC=PID(e,K

)

abs(e)>

Yes

Controller

Event_Th?

Figure 5: Algorithm for the event-based PID. This structure

has similar blocks that the PID controller but includes an

addition element called event detector (ED). The ED checks

if the error signal e crosses the event threshold Event Th.

ities of the framework, in this experiment, two au-

topilots have been developed in the off-board con-

trollers. The ﬁrst autopilot AP1 is an altitude (z) con-

troller and the second one AP2 is a directional (ψ)

controller (see Figure 6). These autopilots have been

PID

Periodic & Event

Event_Th

PID

Periodic & Event

Event_Th

Figure 6: The proposed autopilots. a) AP1: altitude con-

troller, b) AP2: directional controller.

developed by classical periodic PID controllers and

by event-based PID controllers. In this way, these

two control schemes can be compared. These con-

trollers can work in both modes: periodic PID or

event-based PID. On the one hand, when the parame-

ter Event T h=0, the system works in a periodic mode.

On the other hand, when this parameter is higher than

zero it works as an event-based controller. The ob-

A Control Engineering Framework for Quadrotors: An Application for the Crazyﬂie 2.X

363

jective of the altitude controller (Figure 6 a)) is the

tracking of the reference signal z

. The output Ω that

is set to the on-board controller, it is composed of the

output of the PID, Ω

, and the equilibrium signal Ω

The directional controller (Figure 6 b)) uses the refer-

ence signal ψ

and the sensor information ψ to calcu-

late the reference signal r

for the on-board controller.

In this application, the reference signals φ

and θ

are

set to zero because these autopilots allow the hovering

of the drone.

To design these controllers, the Matlab Control

System Toolbox has been used. With these tools,

the controller’s gains have been obtained, at the same

time, to check the event-based implementation the

thresholds Event T h has been set. In (Socas et al.,

2015) some methodologies to set event-based con-

trollers have been presented, using these methods the

event-based controller can be set in a simple way. In

Table 2 the parameters of the designed off-board con-

trollers are shown.

Table 2: Parameters of the off-board controllers.

Parameter Altitude Directional

9,500 40

0 10

45,000 25

Event T h 0.008 m 5

In the simulation laboratory the linear and the non-

linear model of the Crazyﬂie 2.X have been analysed

considering the previous controllers. Once it has been

checked that the results of both models are similar,

only the non-linear model of the drone has been con-

sidered in this work because it is the most realistic

one. The experiments last 15s and the two reference

signals have been modiﬁed. The altitude reference z

is set to 0.4 m at t = 0s and at t = 5s the yaw ref-

erence ψ

has a slope of 15

/s until it reaches 90

t = 11s. In these experiments, the models of noise

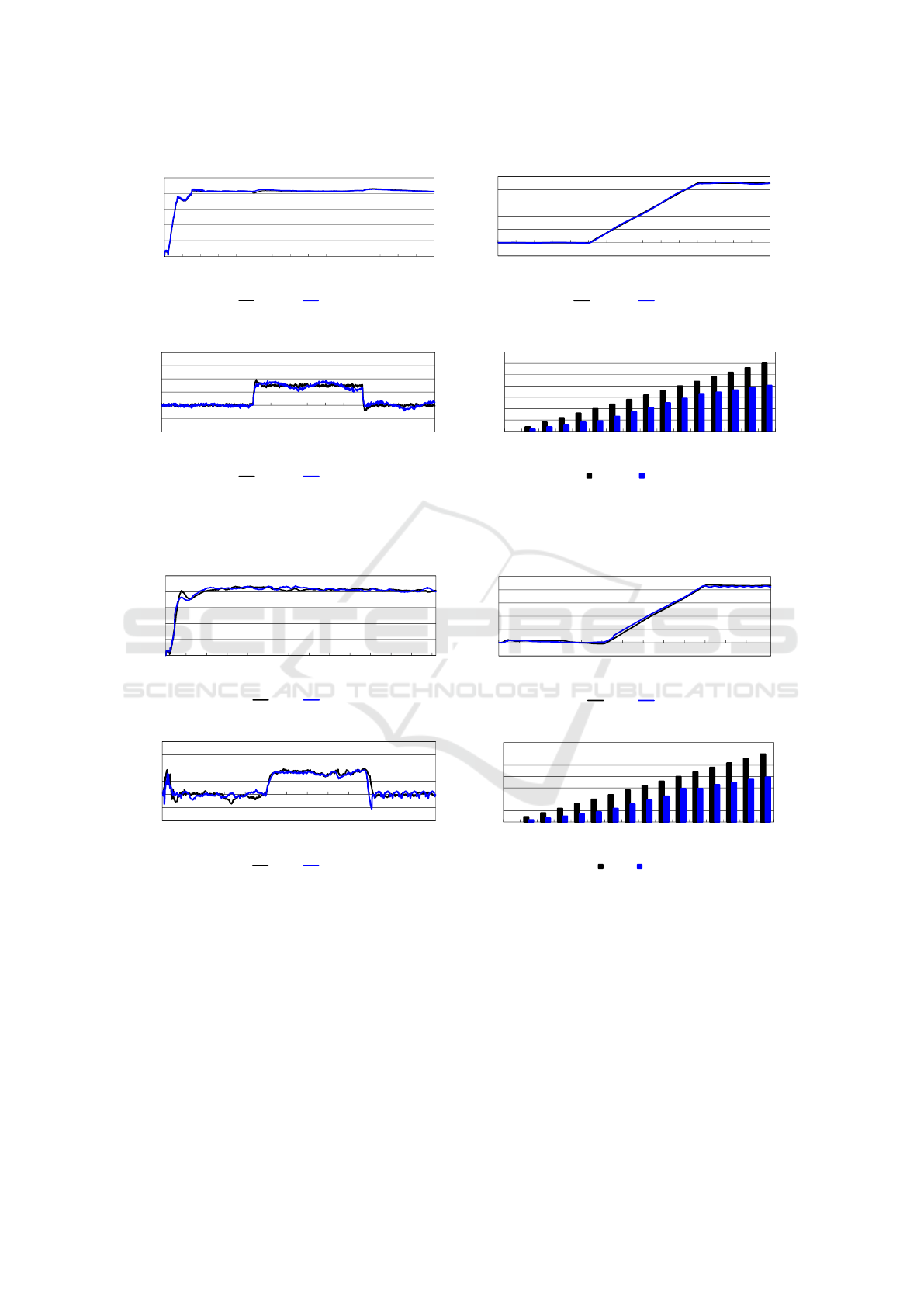
presented in Table 1 are also included. The simu-

lation results are depicted in Figure 7. In these ﬁg-

ures the results for the periodic controller and for the

event-based controller are presented. The designed

controllers have similar behaviour and present a good

tracking of the reference signals, according to Figure

7 a) and b). The main difference between the periodic

and the event-based schemes is the activity of the con-

trollers. In these experiments, the periodic controllers

take around 3,000 control actions but the event-based

implementation only needs 67% of the control actions

than the periodic system (see Figure 7 d)).

In view of these simulation results, the Crazyﬂie

2.X can be operated safely in the real environment.

Once satisfactory results have been achieved in the

simulation setup, the next step is to check the be-

haviour of these controllers in the real environment.

The results obtained in these experiments are shown

in the Figure 8. In this case, both controllers have

a stable response and present a good tracking of the

reference signals (see Figure 8 a) and b)). In the real

environment the controllers have to compensate the

disturbances that occur during takeoff, the turbulence

produced by the drone in the air and the noise in the

sensors. These effects are clearly observed in the vari-

able r in Figure 8 c), and also to a lesser extent in

the variables z and ψ (see Figure 8). In the simula-

tion models, only the noise of the sensors has been

considered. This is a good approach because the real

event-based solution and the simulation model gener-

ate the same number of events (see Figure 7 d) and

Figure 8 d)).

To evaluate the performance of these controllers

and also to compare the event-based controllers with

respect to periodic classical approaches, the perfor-

mances indexes introduced in (S

anchez et al., 2009)

can be used. In this work, the IAE Integral Absolute

Error and the N

ratio of events have been consid-

ered. Taking into account the results of the experi-

ments, the performance indexes for these controllers

are presented in Table 3.

Table 3: Performance indexes for the altitude and direc-

tional controllers.

Altitude Controller IAE(m) N

(%)

Periodic PID 38.34 100

Event PID 39.52 73

Directional Controller IAE(

/100) N

(%)

Periodic PID 28.44 100

Event PID 36.80 59

In these experiments, if the periodic PID con-

troller is considered as the reference, the event-based

altitude controller presents better results than the

event-based directional controller. In this case, the

IAE is 39.52 vs. 38.34 for the altitude (3% higher) and

36.80 vs. 28.44 (29% higher). Moreover, regarding

the ratio of events N

the altitude controller reaches a

value of 73% while the directional controller obtains

59%. Thus the directional controller shows better re-

sults than the altitude controller. The results illustrate

that the accuracy of the altitude controller is better

than the directional controller. However if the activity

is taken into account, the directional controller has a

better behaviour than the altitude controller (59% vs.

73% respectively).

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

364

-20

100

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

t(s)

ψ(˚)

Periodic NL Event NL

-20

-10

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

t(s)

r(˚/s)

Periodic NL Event NL

500

1,000

1,500

2,000

2,500

3,000

3,500

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

t(s)

Accumulated samples vs. events

Periodic NL Event NL

0,00

0,10

0,20

0,30

0,40

0,50

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

t(s)

z(m)

Periodic NL Event NL

Figure 7: Simulation results for the non-linear model. Black line represents the response for the periodic controller and blue

line for the event-based implementation. a) Altitude z, b) yaw ψ, c) yaw rate r and d) accumulated samples vs. accumulated

events.

0.00

0.10

0.20

0.30

0.40

0.50

0 1 2 3 4 5 7 8 9 10 11 12 14 15

t(s)

z(m)

Periodic Event

-20

100

0 1 2 3 4 5 7 8 9 10 11 12 14 15

t(s)

ψ(˚)

Periodic Event

500

1,000

1,500

2,000

2,500

3,000

3,500

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

t(s)

Accumulated samples vs. events

Periodic Event

-20

-10

0 1 2 3 4 5 7 8 9 10 11 12 14 15

t(s)

r(˚/s)

Periodic Event

Figure 8: Experimental results. a) Altitude z, b) yaw ψ, c) yaw rate r and d) accumulated samples vs. accumulated events.

Black line represents the response for the periodic controller and blue line for the event-based implementation.

6 CONCLUSIONS

A new framework for quadrotor control engineering

has been proposed. The two main elements, the simu-

lation laboratory and the real environment offer to en-

gineers and researchers all the tools needed to develop

control applications on drone platforms. In this work,

the solution has been particularized for the Crazyﬂie

2.X, but it can be applied to other quadrotors in a sim-

ple way. All elements in the framework have been

described in detail and the guidelines to develop con-

trol applications for the Crazyﬂie 2.X have been ex-

plained in depth. A practical application to test this

new proposal has been investigated. In this case, two

autopilots have been designed and analysed in this

framework using periodic PID and event-based PID.

The simulation and experimental results show that it

is very simple to design these controllers using this

A Control Engineering Framework for Quadrotors: An Application for the Crazyﬂie 2.X

365

approach. Finally, some performance indexes have

been introduced to validate the response of the de-

signed controllers.

ACKNOWLEDGEMENTS

This work was supported in part by the Spanish

Ministry of Economy and Competitiveness under

the Project CICYT RTI2018-094665-B-I00 and the

Project CICYT DPI2017-84259-C2-2-R. Also, the

Project GID2016-6 supported by UNED.

REFERENCES

Aarz

en, K.-E. (1999). A simple event-based pid controller.

IFAC Proceedings Volumes, 32(2):8687–8692.

Andrievsky, B., Fradkov, A., and Peaucelle, D. (2005).

Adaptive control experiments for laas” helicopter”

benchmark. In 2005 International Conference on

Physics and Control, PhysCon 2005, pages 760–765.

Emran, B. J. and Najjaran, H. (2017). Adaptive neural net-

work control of quadrotor system under the presence

of actuator constraints. In 2017 IEEE International

Conference on Systems, Man, and Cybernetics (SMC),

pages 2619–2624. IEEE.

Fan, Y., Cao, Y., and Li, T. (2017). Adaptive integral back-

stepping control for trajectory tracking of a quadro-

tor. In 2017 4th International Conference on Informa-

tion, Cybernetics and Computational Social Systems

(ICCSS), pages 619–624. IEEE.

orster, J. (2015). System identiﬁcation of the crazyﬂie 2.0

nano quadrocopter. B.S. thesis, ETH Zurich.

Giernacki, W., Skwierczy

nski, M., Witwicki, W., Wro

nski,

P., and Kozierski, P. (2017). Crazyﬂie 2.0 quadrotor as

a platform for research and education in robotics and

control engineering. In 2017 22nd International Con-

ference on Methods and Models in Automation and

Robotics (MMAR), pages 37–42. IEEE.

Landry, B. et al. (2015). Planning and control for quadro-

tor ﬂight through cluttered environments. PhD thesis,

Massachusetts Institute of Technology.

Lee, B.-Y., Lee, H.-I., and Tahk, M.-J. (2013). Analysis of

adaptive control using on-line neural networks for a

quadrotor uav. In 2013 13th International Conference

on Control, Automation and Systems (ICCAS 2013),

pages 1840–1844. IEEE.

Luis, C. and Ny, J. L. (2016). Design of a trajectory track-

ing controller for a nanoquadcopter. arXiv preprint

arXiv:1608.05786.

Mahony, R., Kumar, V., and Corke, P. (2012). Multirotor

aerial vehicles: Modeling, estimation, and control of

quadrotor. IEEE Robotics and Automation magazine,

19(3):20–32.

Sabatino, F. (2015). Quadrotor control: modeling, nonlin-

ear control design, and simulation. Ms thesis, KTH

Royal Institute of Technology, Stockholm, Sweden.

Safaei, A. and Mahyuddin, M. N. (2016). Lyapunov-based

nonlinear controller for quadrotor position and atti-

tude tracking with ga optimization. In 2016 IEEE

Industrial Electronics and Applications Conference

(IEACon), pages 342–347. IEEE.

anchez, J., Guarnes, M., Dormido, S., and Visioli, A.

(2009). Comparative study of event-based control

strategies: An experimental approach on a simple

tank. In 2009 European Control Conference (ECC),

pages 1973–1978. IEEE.

Shirai, J., Yamaguchi, T., and Takaba, K. (2017). Remote

visual servo tracking control of drone taking account

of time delays. In 2017 56th Annual Conference of the

Society of Instrument and Control Engineers of Japan

(SICE), pages 1589–1594. IEEE.

Socas, R., Dormido, S., and Dormido, R. (2015). Event-

based control strategy for the guidance of the

aerosonde uav. In 2015 European Conference on Mo-

bile Robots (ECMR), pages 1–6. IEEE.

Taniguchi, T., Eciolaza, L., and Sugeno, M. (2014).

Quadrotor control using dynamic feedback lineariza-

tion based on piecewise bilinear models. In 2014

IEEE Symposium on Computational Intelligence in

Control and Automation (CICA), pages 1–7. IEEE.

Wahyunggoro, O., Cahyadi, A. I., et al. (2016). Trajec-

tory and altitude controls for autonomous hover of a

quadrotor based on fuzzy algorithm. In 2016 8th Inter-

national Conference on Information Technology and

Electrical Engineering (ICITEE), pages 1–6. IEEE.

Zhang, K., Chen, J., Chang, Y., and Shi, Y. (2016). Ekf-

based lqr tracking control of a quadrotor helicopter

subject to uncertainties. In IECON 2016-42nd Annual

Conference of the IEEE Industrial Electronics Society,

pages 5426–5431. IEEE.

Zhou, J., Deng, R., Shi, Z., and Zhong, Y. (2017). Robust

cascade pid attitude control of quadrotor helicopters

subject to wind disturbance. In 2017 36th Chinese

Control Conference (CCC), pages 6558–6563. IEEE.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

366