
Resolving Confusion of Unknowns in Autonomous Vehicles: Types and
Perspectives
Kaushik Madala and Hyunsook Do
Department of Computer Science and Engineering, University of North Texas, Denton, U.S.A.
Keywords:
Safety Of The Intended Functionality (SOTIF), ISO 21448, UL 4600, Machine Learning Safety, Autonomous
Vehicle Safety, SAE Level 5 of Driving Automation.
Abstract:
Autonomous vehicles are susceptible to unknowns. In particular, vehicles with SAE level 5 of driving au-
tomation, which need to operate in complex operational design domain (ODD) conditions, have a very high
chance to face unknowns. While the industrial standards ISO 21448 and UL 4600 hint at analyzing unknowns
from the analysts and engineers’ perspective, the unknowns from different perspectives such as a autonomous
vehicle or a machine learning model within an autonomous vehicle can differ from those perceived by en-
gineers and analysts. In this paper, we discuss the different types of unknowns considering three different
perspectives: analysts and engineers, autonomous vehicles, and machine learning (ML) models. We also clar-
ify the often confused concepts of unknown knowns and unknowns unknowns for each perspective. Using a
running example, we show how considering unknowns from different perspectives will aid in designing a safe
autonomous vehicle.
1 INTRODUCTION
Autonomous vehicles have gained great attention in
recent years. The eventual goal of autonomous ve-
hicles is to reach driving automation of SAE level
5 (Committee et al., 2018), where the vehicles shall be
able to operate autonomously and safely at any loca-
tion without human feedback/intervention. Operating
anywhere requires engineers of the autonomous vehi-
cles to consider a complex operational design domain
(ODD) (BSI/PAS, 2020). This requires engineers to
explicitly consider the various environmental factors
(e.g., snow, rain), road infrastructural elements (e.g.,
traffic signs, road arrow markings), road types (e.g.,
freeway, straight road), and other road users (e.g.,
skateboarders, pedestrians). Note that every element
of ODD can have various attributes.
For example, a pedestrian can have attributes such
as race, gender, type of clothing, and color of cloth-
ing. Considering all the possible values of these at-
tributes and analyzing their effect on safety of a sys-
tem can be challenging. Further, it is possible to over-
look some of the elements or attributes and to have
certain ODD elements that are not widely known as
these elements are specific to a few locations. This
makes autonomous vehicles susceptible to unknown
scenarios and situations (Hejase et al., 2020) - both
unknown knowns and unknown unknowns (Pickard
et al., 2010). These unknowns can compromise the
safety of the vehicles. Hence, autonomous vehicles
must be designed taking unknowns into account. In
this paper, we simply refer unknown scenarios and
situations as unknowns.
Finding unknowns can be challenging because un-
knowns are highly perspective dependent. The indus-
trial autonomy safety standards ISO 21448 (ISO/PAS,
2019) and UL 4600 (ANSI/UL, 2020) stress the need
for analyzing unknowns and reducing the hazards
that can be caused by the unknowns. Both the stan-
dards mostly refer to unknowns from the viewpoint
of the engineers and analysts who design and analyze
the safety of the system, respectively. However, un-
knowns can also be considered from the perspective
of autonomous vehicles and machine learning models
used in those autonomous vehicles.
For example, let us consider a traffic sign detec-
tion machine learning model in an autonomous vehi-
cle. If the traffic sign detection model is identifying
traffic signs correctly in one frame but not the subse-
quent frame, then the causes for such behavior can be
unknowns to the engineers and analysts. This can be
due to one of the following reasons: 1) the engineers
and analysts might not be familiar with the factors
affecting the traffic sign detection model’s inference,
and 2) the run-time occurrence of such behaviors by
646
Madala, K. and Do, H.
Resolving Confusion of Unknowns in Autonomous Vehicles: Types and Perspectives.
DOI: 10.5220/0010482106460653
In Proceedings of the 7th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2021), pages 646-653
ISBN: 978-989-758-513-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the traffic sign detection model might not have been
exposed to engineers and analysts. On the other hand,
if the machine learning model is not trained to detect
pedestrians, then pedestrians are unknowns to the traf-
fic sign detection model. However, this does not im-
ply pedestrians are unknowns to the autonomous ve-
hicle as it can have another machine learning model
which can detect pedestrians. In this example, we
can observe that identifying unknowns of a machine
learning model helps us to understand what additional
machine learning models we will need to ensure that
we can identify objects that are part of ODD and
can compromise safety. Exposing unknowns to au-
tonomous vehicles will aid in making better design
decisions. Similarly, exposing unknowns to engineers
and analysts helps to make better safety solutions,
gather better data, and revise ODD. These observa-
tions lead to our central research question: “Should
we consider unknowns from different perspectives
to ensure safety of an autonomous vehicle?”. We
address this central research question by answering
the following research questions:
RQ1. What are unknowns from the perspective of
machine learning models, autonomous vehicles, and
engineers and analysts, respectively?
RQ2. What are similarities and dissimilarities
among the unknowns from the three perspectives?
In this paper, we address these research questions
by comparing the unknowns from each perspective
with others using a running example. We discuss
unknowns and their sub-categories (i.e., unknown
knowns and unknown unknowns) from the perspec-
tives of engineers and analysts, autonomous vehi-
cles, and machine learning models in an autonomous
vehicles. We discuss similarities and dissimilari-
ties among the unknowns from the three perspectives
and provide the details on how sub-categories of un-
knowns from one perspective can relate and differ to
sub-categories of unknowns from other perspectives.
The rest of the paper is organized as follows. Sec-
tion 2 discusses about the classification of knowns and
unknowns. Section 3 details about the importance of
unknowns with respect to ISO 21448 and UL 4600.
Section 4 discusses the types of unknowns with re-
spect to the three perspectives mentioned earlier with
an example. Section 5 provides insights and observa-
tions, and we finally conclude in Section 6.
2 KNOWNS AND UNKNOWNS
We can classify knowns and unknowns based on the
knowledge possessed by an intelligent agent/person
(or a group of intelligent agents/persons) such as an
engineer, analyst, autonomous system or organiza-
tion. We can consider a set U which represents an
entire universal knowledge. Considering each intelli-
gent agent, we can divide U into two subsets: a set K
denoting the knowledge possessed by the agent and
a set N denoting the rest of universal knowledge not
possessed by the agent. We can represent this mathe-
matically in Equation 1, where K ⊂ U and N ⊂ U.
U = K ∪ N (1)
We can further divide a set K into subsets. There
are many classifications of K proposed by the existing
literature (Smith, 2001; McCormick, 1997; De Jong
and Ferguson-Hessler, 1996) (e.g., explicit and tacit
knowledge (Smith, 2001); factual, procedural, con-
ceptual and meta-cognitive knowledge (McCormick,
1997)). In this paper, to focus on knowns and un-
knowns, we classify K into following subsets: 1) a set
D representing the direct knowledge, i.e., knowledge
which an intelligent agent can comprehend and/or an-
alyze easily after seeing an object, action or event,
and 2) a set I representing the indirect knowledge, i.e.,
knowledge inferred using the knowledge from D. We
can represent the relation between K, D, and I using
Equation 2.
K = D ∪ I (2)
To understand the relation between sets D and I,
let us consider ‘P (D)’ which is the power set of D
and a set V = {valid, invalid}. We can define a set
I as shown in Equation 3, where f(x) is a function
which provides the inference that can be generated
based on input x, g(f(x)) is a function which tells if
the inference output given from f(x) is a valid or in-
valid inference. Each element in I must have a map-
ping to only one of the elements in V, i.e., the intelli-
gent agent shall be able to derive valid or invalid in-
ferences from D. We mentioned element ‘x’ belongs
to P (D) because I cannot exist without D, i.e., with-
out the knowledge from a set D, we cannot infer the
corresponding knowledge in I.
I = { f (x) | x ∈ P (D) and g( f (x)) ∈ V } (3)
Based on the knowledge possessed and informa-
tion recognized by an intelligent agent, we can clas-
sify the knowns and unknowns similar to ones clas-
sified by the existing literature (Pickard et al., 2010;
Collins and Cruickshank, 2014; Jensen et al., 2017)
as shown in Figure 1. We also illustrate the relation
between these classifications and sets U, K, N, D and I
in Figure 2. The figure shows four widely recognized
classifications as follows.
Resolving Confusion of Unknowns in Autonomous Vehicles: Types and Perspectives
647
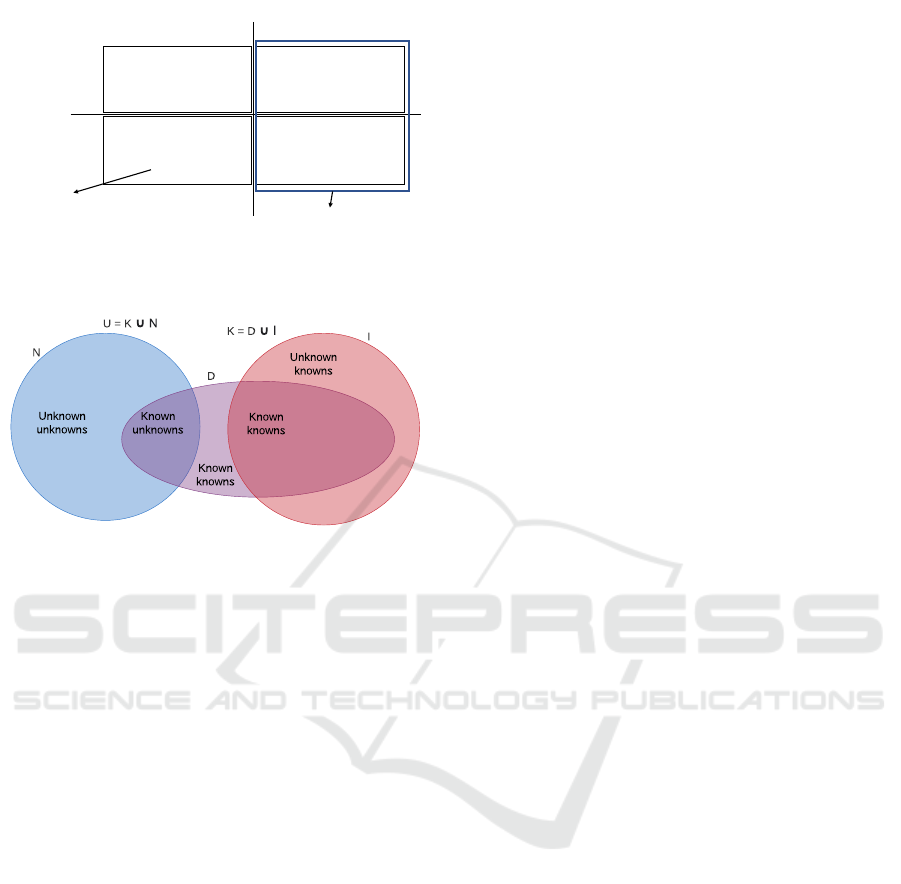
Known knowns Unknown knowns
Known unknowns Unknown unknowns
Within the
knowledge
of intelligent
agent
Outside the
knowledge
of intelligent
agent
Identified by the
intelligent agent
Not identified by the
intelligent agent
Need knowledge from intelligent
agents who have a different expertise
Unknowns
Figure 1: Classification of knowns and unknowns for an
intelligent agent.
Known
knowns
Known
unknowns
Unknown
unknowns
Known
knowns
Unknown
knowns
N
D
I
K = D ? I
U = K ? N
Figure 2: Venn diagram showing the different types of
knowns and unknowns and their relation with sets U, K, N,
D and I.
1. Known Knowns: These refer to the concepts and
information that are present within the scope of
the knowledge possessed by an intelligent agent.
In the knowledge classification, we discussed
prior, known knowns are a subset of the set K. An
example of known known is the object correctly
recognized by an individual agent.
2. Known Unknowns: These refer to the concepts
and information that are identified by an intelli-
gent agent but not within the scope of their knowl-
edge. For an intelligent agent to identify a concept
or information that is out of scope their knowl-
edge, the agent should have a basic knowledge
about the existence of the concepts, but does not
need to have expertise enough to make observa-
tions or inferences from it. Known unknowns are
sets which have few elements in the set D and no
elements in the set I. Since only few elements in
D help us in recognizing the unknown concepts,
the knowledge that can be inferred from these el-
ements is mostly part of the set N as we will need
more knowledge to make a meaningful inference.
An example of known unknown is a runtime mon-
itor identifying that the machine learning model is
uncertain of its input (Weiss and Tonella, 2021).
3. Unknown Knowns: These refer to concepts and
information which are within the scope of knowl-
edge possessed by an intelligent agent but are not
identified. Unknown knowns mostly belong to the
set I as they mostly represent the overlooked in-
formation by an intelligent agent either due to the
insufficient analysis, a lack of awareness about
presuppositions we have, a lack of proper infer-
ence, or due to the effect from mental factors such
as stress, anxiety, and others. An example of un-
known known is the misprediction of an object by
a machine learning model which was recognized
in the previous frame. In this case, the model
knows the object and has knowledge to identify
it, but was unable to identify it. An unknown
known when exposed and analyzed will change
into a known known.
4. Unknown Unknowns: These are concepts and
information which are not in the scope of knowl-
edge of an intelligent agent and not identified by
the agent. For the misprediction example we used
for unknown known, the cause that resulted in a
misprediction of an object, which was correctly
recognized in the previous frame, can be an un-
known unknown to engineers until the frame is
exposed and analyzed. All unknown unknowns
belong to the set N. When exposed, unknown
unknowns change mostly into known unknowns.
However, with sufficient knowledge and exper-
tise (potentially with the help from other experts),
unknown unknowns when exposed can change to
known knowns.
Related Work. To date many researchers (Pickard
et al., 2010; Collins and Cruickshank, 2014; Jensen
et al., 2017) have discussed the need for finding
unknowns and proposed approaches to identify or
expose unknowns. The application domains for
such approaches mostly include biomedical applica-
tions (Collins and Cruickshank, 2014; Hoskisson and
Seipke, 2020), software security (Al-Zewairi et al.,
2020; Rashid et al., 2016), system design (Jensen
et al., 2017), complex systems (Pickard et al., 2010),
and autonomous vehicles (Wong et al., 2020; He-
jase et al., 2020; Zhu et al., 2020). For example,
Zhu et al. (Zhu et al., 2020) proposed a weakly-
hard paradigm framework to model as well as mit-
igate time-based uncertainties for autonomous soft-
ware. Even though all these current approaches dis-
cuss identification of unknowns or their mitigations,
they do not consider different perspectives, which are
the main concerns when we identify unknowns and
understand reasons why such consideration is impor-
tant.
In the next sections, we will discuss why we need
to perform unknown analysis for autonomous vehi-
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
648

Known hazardous
scenarios
(Area 2)
Known and not
hazardous scenarios
(Area 1)
Unknown hazardous
scenarios
(Area 3)
Unknown and not
hazardous scenarios
(Area 4)
Known
Unknown
Hazardous
Not Hazardous
Figure 3: Scenario categories described in ISO 21448 stan-
dard.
cles and different perspectives we need to consider for
performing such an analysis.
3 INDUSTRIAL STANDARDS AND
UNKNOWNS
Industrial standards for safety of autonomy such as
ISO 21448 (ISO/PAS, 2019) and UL 4600 (ANSI/UL,
2020) stress the need for analyzing unknowns to re-
duce the risks for autonomous vehicles. As au-
tonomous vehicles with SAE level 5 of driving au-
tomation operate in a complex and changing ODD, it
is possible to overlook some characteristics of ODD,
which might be uncovered over time or when an un-
safe situation is exposed.
ISO 21448 (ISO/PAS, 2019) is an industrial stan-
dard that details steps to analyze the safety of the in-
tended functionality (SOTIF) of autonomous vehicles
and thereby achieve compliance with respect to SO-
TIF. The standard focuses on identifying the gaps in
nominal requirements and in reducing the safety is-
sues for a system when exposed to unknown condi-
tions. The standard illustrates a four quadrant struc-
ture for scenario categories as shown in Figure 3. We
can observe that the categories are based on whether
the scenarios are known or unknown and if they are
hazardous or not. Each quadrant in Figure 3 repre-
sents a category and the corresponding area number
that is assigned. For example, Area 1 implies scenar-
ios which are known and non-hazardous. The goal of
SOTIF is to increase Area 1 and reduce Areas 2 and
3. This illustrates the importance the ISO 21448 has
given in need for analyzingunknown scenarios and
proposing mechanisms to ensure autonomous vehi-
cles operate safely in such scenarios.
Similarly, UL 4600 (ANSI/UL, 2020) which de-
tails a process of creating a safety case for au-
tonomous vehicles also stresses the need for consid-
ering unknowns as a part of assuring safety of an au-
tonomous vehicle. The standard mentions unknowns
when discussing the safety case and arguments, au-
tonomy function and support, dependability, lifecycle
concerns, metrics and safety performance indicators,
and assessment. The standard suggests to use feed-
back loops to keep track of unknowns. By doing so,
we can accumulate knowledge of unknowns overtime
and thus change design as needed. Hence, we can
conclude analyzing unknowns for autonomous vehi-
cles plays a vital role in assuring its safety for its op-
eration in a complex ODD.
Note that it is not possible to identify all un-
knowns, and it might be very difficult to replicate
some of the unknowns that are exposed in the real
world. Hence, the standards focus more on proving
that the occurrence of unknowns is rare and that we
have mechanisms to accumulate the knowledge of un-
knowns over time as they occur. In addition to these
standards, there is a functional safety standard ISO
26262 (ISO, 2018) for automotive, which deals only
with malfunctions of electrical and electronic systems
used in the vehicles but not unknowns.
4 UNKNOWN TYPES AND
DIFFERENT PERSPECTIVES
Although both ISO 21448 and UL 4600 stress the
need for analyzing unknowns, the focus of these stan-
dards is often interpreted as analyzing unknowns from
the engineers and analysts’ perspective. This inter-
pretation comes from the assumption that unknowns
perceived by engineers and analysts are not different
from the ones by autonomous vehicles or machine
learning models’ perspective. However, this is not al-
ways true. Machine learning algorithms, which are
intended for effective generalization based on data on
which they are trained, could produce correct out-
puts for instances that might be unknowns to engi-
neers and analysts. Hence, it is possible for unknowns
to differ from different perspectives such as machine
learning models used in autonomous vehicles, au-
tonomous vehicles (i.e., vehicle-level unknowns), and
engineers and analysts. This leads to our central re-
search question stated in Section 1: Should we con-
sider unknowns from different perspectives to en-
sure safety of an autonomous vehicle?
To answer our central research question, we
specifically investigate the following two research
questions:
RQ1. What are unknowns from the perspective of
machine learning models, autonomous vehicles, and
engineers and analysts, respectively?
RQ2. What are similarities and dissimilarities
Resolving Confusion of Unknowns in Autonomous Vehicles: Types and Perspectives
649

among the unknowns from these three perspectives?
After finding answers from these two research ques-
tions, we will conclude by answering our central
question.
Running Example: To better illustrate unknowns from
different perspectives, let us consider a running exam-
ple of a level 5 autonomous vehicle which has cam-
eras and a LIDAR and travels in city roads that have
high density of pedestrians. Let us also assume that
the pedestrians are multicultural and diverse in nature.
4.1 RQ1: Unknowns from the Three
Perspectives
4.1.1 Unknowns with Respect to Machine
Learning Models
Machine learning models play a vital role for per-
ception and motion planning in autonomous vehicles.
Tasks for which machine learning models are used
include road object detection (Ashraf et al., 2016),
pedestrian detection (Yang et al., 2020), traffic sign
detection (Ayachi et al., 2020), unknown object de-
tection (Wong et al., 2020) and trajectory estima-
tion (Rozumnyi et al., 2020). The results of a ma-
chine learning model are highly dependent on its data,
algorithm, and the training process followed. An un-
known with respect to a machine learning algorithm
is something which it cannot identify or detect. A ma-
chine learning model is susceptible to both unknown
knowns and unknown unknowns.
Unknown Knowns for Machine Learning Models:
Unknowns knowns for a machine learning model im-
plies that the predictions regarding an object or an ac-
tion are correct for the previous inputs or subsequent
inputs, but are not correct for the current input. To
better understand unknown knowns, let us consider
the running example in which the autonomous vehi-
cle detects pedestrians on city roads. If we assume
the vehicle relies on cameras for pedestrian detection,
then the input to the machine learning model that de-
tects pedestrians will be a sequence of frames. If a
pedestrian is identified in one frame but not identi-
fied in the subsequent frame, then we can refer to the
latter case as an unknown known with respect to the
machine learning model. This is because the machine
learning model has knowledge to identify the pedes-
trian, but it might not always be able to correctly infer
it.
Unknown Unknowns for Machine Learning Mod-
els: A machine learning model cannot detect or per-
form something that is never trained for. For exam-
ple, if the training data of pedestrians for our running
example is missing data on pedestrians belonging to
a certain race and/or gender or pedestrians wearing
a certain type of clothing, then the model might not
be able to identify such pedestrians because it never
knows such pedestrians would exist in the first place.
Such instances for which machine models are never
trained for are considered as unknown unknowns for
machine learning models.
4.1.2 Unknowns with Respect to Autonomous
Vehicles
When we consider unknowns with respect to au-
tonomous vehicles, we refer to situations or events
that an autonomous vehicle might not be familiar with
or might have misinterpreted the situations or events
as something else. Unknowns with respect to an au-
tonomous vehicle are highly dependent on the archi-
tecture and the nature of sensor fusion. Similar to
machine learning models, an autonomous vehicle also
has a possibility of facing unknown knowns and un-
known unknowns.
Unknown Knowns for Autonomous Vehicles: An
autonomous vehicle takes a decision based on infor-
mation it gathers from different sensors. If the au-
tonomous vehicle’s algorithm prioritizes one sensor
over the other and the least prioritized sensor (not the
highly prioritized one) provides correct information
for a potential collision, then we can refer to such
a situation as unknown knowns to autonomous ve-
hicles. In our running example, if we consider the
autonomous vehicle to have cameras and a LIDAR,
and the cameras are prioritized over a LIDAR, then
a pedestrian not detected by the machine models in
the cameras but correctly detected by a LIDAR might
be ignored by the vehicle. In this situation, the vehicle
has the knowledge of the presence of a pedestrian, but
the priority of sensors in the algorithm made it to ig-
nore the pedestrian detected by the LIDAR. Since the
motion planner takes action based on the output from
camera models, the occurrence of the pedestrian will
be an unknown known to the autonomous vehicle.
Unknown Unknowns for Autonomous Vehicles:
An autonomous vehicle can face situations or ODD
conditions which it never faced before. Such situa-
tions and ODD conditions, which autonomous vehi-
cles are completely unfamiliar with and either can-
not process the corresponding information or ignore
them, are considered as unknown unknowns to au-
tonomous vehicles. For example, let us assume the
autonomous vehicle is never trained to operate it in
snowy weather due to the low probability of snow in
that region. If such a vehicle faces an unexpected
snowfall in the region of its operation, then it is an
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
650

unknown unknown condition with respect to the au-
tonomous vehicle.
4.1.3 Unknowns with Respect to Engineers and
Analysts
Since level 5 autonomous vehicles need to be able
to travel everywhere without human intervention, the
engineers and analysts of the autonomous vehicle will
need to consider complex ODD conditions. How-
ever, it is not possible for the engineers and ana-
lysts to know all possible conditions that occur in the
world and the ones which might affect the behavior
of the autonomous vehicle. Hence, there might be
some aspects that are overlooked or unknown to engi-
neers and analysts. While considering engineers and
analysts from diverse backgrounds and experiences
across various regions can reduce the total number of
unknowns, it is possible that we can have new poten-
tial unknowns. Also, as environments change, new
unknowns can occur over time, which the engineers
and analysts might not be familiar with unless such
conditions or situations are exposed to them. This can
result in a lack of consideration of such scenarios or
situations while verifying the system as well as a lack
of presence of such environments in simulation tools.
Similar to machine learning models and autonomous
vehicles, there can be unknown knowns and unknown
unknowns with respect to engineers and analysts of
an autonomous vehicle.
Unknown Knowns for Engineers and Analysts:
It is possible for engineers and analysts to over-
look some aspects when designing an intelligent au-
tonomous vehicle. The reason behind overlooking the
aspects can be intentional (e.g., to reduce complex-
ity/scope) or unintentional. We refer to such aspects
as unknown knowns. For our running example, if the
engineers and analysts did not consider pedestrians’
race when training the pedestrian detection machine
learning model or analyzing the model, and the model
did not predict people of a certain race properly, then
it is an unknown known to the engineers and analysts.
The engineers despite having knowledge of different
races of people could have assumed that the machine
learning model will be effective in identifying pedes-
trians of all races, thereby making the missing pre-
dictions of pedestrians belonging to a specific race as
unknown knowns to engineers and analysts.
Unknown Unknowns for Engineers and Analysts:
The unknown unknowns for engineers and analysts
can occur mostly either due to a lack of knowledge
about some ODD elements and conditions or due to
a lack of appropriate understanding/analysis of ma-
chine learning models used in autonomous vehicles.
For example, in our running example, if a pedestrian
wore a reflective costume which resulted in a col-
lision, such an occurrence can be an unknown un-
known to the engineers and analysts. This is because
the engineers and analysts have never seen such an
occurrence before and hence did not take into ac-
count pedestrians with reflective costumes when de-
signing the autonomous vehicle. Another example
of unknown unknowns for engineers and analysts is
the root causes for the non-deterministic behavior of
a machine learning model, which identified an object
in one frame but did not identify the same object in
the subsequent frame for multiple inputs. This im-
plies the machine learning model has knowledge to
recognize the object, but the engineers and analysts
do not know why it produces the correct output for
one frame and the incorrect one for the other despite
having knowledge about recognizing objects.
As mentioned earlier, once exposed unknown
unknowns translate to known unknowns or known
knowns depending on knowledge gained by the en-
gineers and analysts.
4.2 RQ2: Comparing the Unknowns
from Different Perspectives
So far, we have discussed unknowns with respect to
machine learning models, autonomous vehicles, and
engineers and analysts. However, are all these un-
knowns same or different? If they are different, how
do they differ from each other? We shall now com-
pare these unknowns from different perspectives.
An unknown for a machine learning model in an
autonomous vehicle need not to be unknown to other
machine learning models or algorithms that rely on a
sensor different from the sensor being used by the cur-
rent machine learning model. This implies unknowns
of a machine learning model and unknowns of an au-
tonomous vehicle are not necessarily the same. The
unknowns of one machine learning model can be
knowns to other machine learning models or can be
exposed using sensors that are different from the in-
put sensor to the machine learning model. The causes
of unknown knowns for a machine learning model can
be unknown unknowns to engineers and analysts. For
example, if a machine learning model is able to de-
tect an object in the previous frame but not the current
frame, then we consider it to be an unknown known
for the machine learning model. However, the en-
gineers and analysts might not be familiar with such
behavior of the machine learning model until it is ex-
posed to them. Hence, it becomes unknown unknown
for engineers and analysts.
Any ODD elements which are not considered by
Resolving Confusion of Unknowns in Autonomous Vehicles: Types and Perspectives
651

engineers and analysts because they do not know
about their occurrence in the location considered are
unknown unknowns, and remain unknown unknowns
with respect to both an autonomous vehicle and ma-
chine learning model. This is because if the engi-
neers and analysts do not know about the existence
of an ODD element or condition in the first place,
the corresponding design criterion might never have
been taken into account. With respect to unknowns
for an autonomous vehicle, however, they are not nec-
essarily the same as unknowns for engineers and an-
alysts. This is because the machine learning mod-
els used in autonomous vehicles are meant to support
generalization to some extent. The process of gener-
alization involves a machine learning model provid-
ing the expected output for an input which it has not
been trained on or validated on. Hence, it is possible
for machine learning models to work for some cases,
even if they are not part of training data. Hence, un-
knowns for the autonomous vehicles need not to be
the same as unknowns for engineers and analysts.
From the analysis of RQ1 and RQ2, we can con-
clude that,in the case of level 5 autonomous vehicles,
unknowns for engineers and analysts, unknowns for
autonomous vehicles, and unknowns for a machine
learning model used in the autonomous vehicle are
not necessarily the same.
5 DISCUSSION
Our comparison among the unknowns considering
three different perspectives (autonomous vehicles,
machine learning models within autonomous vehi-
cles, and engineers and analysts) has shown that the
unknowns perceived by these different perspectives
can differ. This difference among these perspectives
tells us the need to analyze unknowns considering
all three, rather than following the typical practices,
which tend to focus on unknowns identified by the
engineers and analysts. If we use algorithms that
are robust and not stochastic in the autonomous ve-
hicle software, the unknowns identified from the au-
tonomous vehicle’s perspective will be the same as
ones from the engineers and analysts’ perspective.
However, all autonomous vehicle heavily rely on ma-
chine learning models which are stochastic and not
very robust in nature. Hence, for the central research
question which aims to clarify if we need to consider
unknowns from different perspectives to ensure safety
of the autonomous vehicle, we can conclude that we
will need to consider unknowns from all three differ-
ent perspectives.
We believe that by exposing unknowns from the
three perspectives, we can design the system better to
handle unknown circumstances, as well as make the
probability of facing unknown situations extremely
rare. Further, by analyzing unknowns for machine
learning models, we can understand if we need to add
examples with certain elements into data and retrain
a machine learning model or if we need to use other
machine learning models and other sensor modalities
to ensure safe operation of the system. Analyzing un-
knowns from the three perspectives also help the sim-
ulation engineers in enhancing existing simulation en-
vironments as well as building environments for eval-
uating new scenarios and situations.
6 CONCLUSION
In this research, we discussed how unknowns in an
autonomous vehicle can be considered from differ-
ent perspectives and their differences. In this paper,
we focused on level 5 autonomous vehicles without
considering vehicle-to-everything (V2X) connectiv-
ity (Hobert et al., 2015). We also used only a small
running example as a proof of concept for the pro-
posed idea. As a part of future work, we plan to ana-
lyze unknowns comprehensively by considering V2X
communication. We also plan to conduct an extensive
analysis to better understand how unknowns differ for
the three different perspectives and how identifying
them will play a major role in assuring safety of the
system, even when operating in a complex ODD.
ACKNOWLEDGEMENTS
We would like to thank kVA by UL for their feedback
on the topic.
REFERENCES
Al-Zewairi, M., Almajali, S., and Ayyash, M. (2020). Un-
known security attack detection using shallow and
deep ann classifiers. Electronics, 9(12):2006.
ANSI/UL (2020). 4600. Standard for Evaluation of Au-
tonomous Products.
Ashraf, K., Wu, B., Iandola, F. N., Moskewicz, M. W.,
and Keutzer, K. (2016). Shallow networks for
high-accuracy road object-detection. arXiv preprint
arXiv:1606.01561.
Ayachi, R., Afif, M., Said, Y., and Atri, M. (2020). Traf-
fic signs detection for real-world application of an ad-
vanced driving assisting system using deep learning.
Neural Processing Letters, 51(1):837–851.
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
652

BSI/PAS (2020). 1883:2020. Operational Design Do-
main (ODD) taxonomy for an automated driving sys-
tem (ADS) – Specification.
Collins, R. A. and Cruickshank, R. H. (2014). Known
knowns, known unknowns, unknown unknowns and
unknown knowns in dna barcoding: a comment on
dowton et al. Systematic biology, 63(6):1005–1009.
Committee, S. O.-R. A. V. S. et al. (2018). Taxonomy and
definitions for terms related to driving automation sys-
tems for on-road motor vehicles. SAE Standard J,
3016.
De Jong, T. and Ferguson-Hessler, M. G. (1996). Types
and qualities of knowledge. Educational psychologist,
31(2):105–113.
Hejase, M., Barbier, M., Ozguner, U., Ibanez-Guzman, J.,
and Acarman, T. (2020). A validation methodology
for the minimization of unknown unknowns in au-
tonomous vehicle systems. In 2020 IEEE Intelligent
Vehicles Symposium (IV), pages 114–119. IEEE.
Hobert, L., Festag, A., Llatser, I., Altomare, L., Visintainer,
F., and Kovacs, A. (2015). Enhancements of v2x
communication in support of cooperative autonomous
driving. IEEE communications magazine, 53(12):64–
70.
Hoskisson, P. A. and Seipke, R. F. (2020). Cryptic or
silent? the known unknowns, unknown knowns, and
unknown unknowns of secondary metabolism. mBio,
11(5).
ISO (2018). 26262. Road Vehicles – Functional Safety.
ISO/PAS (2019). 21448. Road vehicles - Safety of the in-
tended functionality.
Jensen, M. B., Elverum, C. W., and Steinert, M. (2017).
Eliciting unknown unknowns with prototypes: Intro-
ducing prototrials and prototrial-driven cultures. De-
sign Studies, 49:1–31.
McCormick, R. (1997). Conceptual and procedural knowl-
edge. International journal of technology and design
education, 7(1-2):141–159.
Pickard, A. C., Nolan, A. J., and Beasley, R. (2010). 8.3.
1 certainty, risk and gambling in the development of
complex systems. In INCOSE International Sympo-
sium, volume 20, pages 1051–1061. Wiley Online Li-
brary.
Rashid, A., Naqvi, S. A. A., Ramdhany, R., Edwards, M.,
Chitchyan, R., and Babar, M. A. (2016). Discovering
”unknown known” security requirements. In Proceed-
ings of the 38th International Conference on Software
Engineering, ICSE ’16, page 866–876, New York,
NY, USA. Association for Computing Machinery.
Rozumnyi, D., Matas, J., Sroubek, F., Pollefeys, M., and
Oswald, M. R. (2020). Fmodetect: Robust detection
and trajectory estimation of fast moving objects. arXiv
preprint arXiv:2012.08216.
Smith, E. A. (2001). The role of tacit and explicit knowl-
edge in the workplace. Journal of knowledge Man-
agement.
Weiss, M. and Tonella, P. (2021). Fail-safe execution of
deep learning based systems through uncertainty mon-
itoring. In 2021 IEEE 14th International Confer-
ence on Software Testing, Validation and Verification
(ICST). IEEE.
Wong, K., Wang, S., Ren, M., Liang, M., and Urtasun,
R. (2020). Identifying unknown instances for au-
tonomous driving. In Conference on Robot Learning,
pages 384–393. PMLR.
Yang, P., Zhang, G., Wang, L., Xu, L., Deng, Q., and Yang,
M.-H. (2020). A part-aware multi-scale fully convolu-
tional network for pedestrian detection. IEEE Trans-
actions on Intelligent Transportation Systems.
Zhu, Q., Li, W., Kim, H., Xiang, Y., Wardega, K., Wang, Z.,
Wang, Y., Liang, H., Huang, C., Fan, J., et al. (2020).
Know the unknowns: addressing disturbances and un-
certainties in autonomous systems. In Proceedings of
the 39th International Conference on Computer-Aided
Design, pages 1–9.
Resolving Confusion of Unknowns in Autonomous Vehicles: Types and Perspectives
653
