
Explainable Federated Learning for Taxi Travel Time Prediction
Jelena Fiosina
a
Institute of Informatics, Clausthal Technical University, Julius-Albert Str. 4, D-38678, Clausthal-Zellerfeld, Germany
Keywords:
FCD Trajectories, Traffic, Travel Time Prediction, Federated Learning, Explainability.
Abstract:
Transportation data are geographically scattered across different places, detectors, companies, or organisations
and cannot be easily integrated under data privacy and related regulations. The federated learning approach
helps process these data in a distributed manner, considering privacy concerns. The federated learning archi-
tecture is based mainly on deep learning, which is often more accurate than other machine learning models.
However, deep-learning-based models are intransparent unexplainable black-box models, which should be
explained for both users and developers. Despite the fact that extensive studies have been carried out on
investigation of various model explanation methods, not enough solutions for explaining federated models
exist. We propose an explainable horizontal federated learning approach, which enables processing of the dis-
tributed data while adhering to their privacy, and investigate how state-of-the-art model explanation methods
can explain it. We demonstrate this approach for predicting travel time on real-world floating car data from
Brunswick, Germany. The proposed approach is general and can be applied for processing data in a federated
manner for other prediction and classification tasks.
1 INTRODUCTION
Most real-world data are geographically scattered
across different places, companies, or organisations,
and, unfortunately, cannot be easily integrated under
data privacy and related regulations. This is especially
topical for the transportation domain, in which ubiq-
uitous traffic sensors and Internet of Things create a
world-wide network of interconnected uniquely ad-
dressable cooperating objects, which enable exchange
and sharing of information. With the increase in the
amount of traffic, a large number of available decen-
tralised data is available.
Fuelled by a large amount of data collected in
various domains and the high available computing
power analytical procedures and statistical models for
data interpretation and processing rely on methods
of artificial intelligence (AI). In recent years, a large
progress of AI has been achieved. These data-driven
methods replace complex analytical procedures by
multiple calculations. They are easily applicable and,
in most cases, more accurate considering their ma-
chine learning (ML) ancestry. The accuracy and inter-
pretability are two dominant features present in suc-
cessful predictive models. However, more accurate
black-box models are not sufficiently explainable and
a
https://orcid.org/0000-0002-4438-7580
transparent. This feature of AI-driven systems com-
plicates the user acceptance and can be troublesome
even for model developers.
Therefore, the contemporary AI technologies
should be capable of processing these data in a de-
centralised manner, according to the data privacy reg-
ulations. Moreover, the algorithms should be maxi-
mally transparent, which makes the decision-making
process user-centric.
Federated learning is a distributed ML approach,
which enables model training on a large corpus of de-
centralised data (Konecn
´
y et al., 2016). It has three
major advantages: 1) it does not need to transmit the
original data to the cloud, 2) the computational load
is distributed among the participants, and 3) it as-
sumes synchronisation of the distributed models with
a server for more accurate models. The main assump-
tion is that the federated model should be parametric
(e. g., deep learning) because the algorithm synchro-
nises the models by synchronising the parameters. A
known limitation of deep learning is that neural net-
works inside it are unexplainable black-box models.
Numerous model-agnostic and model-specific (e.g.,
Integrated gradients, DeepLIFT) methods for expla-
nation of black-box models are available (Kraus et al.,
2020). Distributed versions of these methods exist,
which allow them to be executed on various processes
670
Fiosina, J.
Explainable Federated Learning for Taxi Travel Time Prediction.
DOI: 10.5220/0010485606700677
In Proceedings of the 7th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2021), pages 670-677
ISBN: 978-989-758-513-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

on graphics processing units (GPUs)
1
. However, to
the best of our knowledge, studies on the explanation
of geographically distributed federated deep learning
models are lacking.
The mentioned challenges are topical in the trans-
portation domain, in which the generation and pro-
cessing of big data are necessary. We propose
a privacy-preserving explainable federated model,
which achieves a comparable accuracy to that of the
centralised approach on the considered real-world
dataset. We predict the Brunswick taxi travel time
based on floating car data trajectories obtained from
different taxi service providers, which should remain
private. The proposed model makes predictions for
the stated problem and allows a joint learning pro-
cess over different users, processing the data stored
in each of them without exchanging their raw data,
but only parameters, as well as providing joint expla-
nations about variable importance.
We address several research questions. 1) Which
is the most accurate ML prediction method for the
given data in a centralised manner? We identify the
best hyper-parameters for each method. 2) Under
which conditions federated learning is effective? We
distribute the dataset among various providers, and
analyse after which point the distributed and non-
synchronised models lose their accuracy and feder-
ated learning is beneficial. We define an optimal syn-
chronisation plan for parameter exchange, identifying
the hyper-parameters and frequency of parameter ex-
change that is acceptable and beneficial. 3) Do exist-
ing black-box explanation methods successfully ex-
plain federated learning models? We investigate how
the state-of-the-art explainability methods can explain
federated models.
The rest of the paper is organised as follows. Sec-
tion 2 describes the state-of-the-art. Section 3 de-
scribes the proposed explainable federated deep learn-
ing concept and parameter synchronisation mech-
anisms. Section 4 introduces the available data,
presents the experimental setup, and provides insights
into the data preprocessing step. Section 5 presents
the model validation and experimental results.
2 STATE OF THE ART
2.1 Distributed Data Analysis
The large amount of contemporary generated data
in the transportation domain requires application of
state-of-the-art methods of distributed/decentralised
1
https://captum.ai/
data analyses as well as investigation of novel ap-
proaches capable of processing distributed data often
with data privacy requirements.
When data centralisation is available, accurate
prediction models can be developed, which address
the big data challenge through smart ‘artificial’ par-
titioning and parallelisation of data and computation
within a cloud-based architecture or powerful super
computers (Fiosina and Fiosins, 2017).
Often, data should be physically and logically dis-
tributed without transmission of big information vol-
umes, without the need to store, manage, and pro-
cess massive datasets in one location. This approach
enables a data analysis with smaller datasets. How-
ever, scaling it up requires novel methods to effi-
ciently support the coordinated creation and main-
tenance of decentralised data models. Specific de-
centralised architectures (e.g., multi-agent systems
(MAS)) should be implemented to support the de-
centralised data analysis, which requires a coordi-
nated suite of decentralised data models, including
parameter/data exchange protocols and synchronisa-
tion mechanisms among the decentralised data mod-
els (Fiosina et al., 2013a).
The MAS based representation of transportation
networks helps overcome the limitations of cen-
tralised data analyses, which will enable autonomous
vehicles to make better and safer routing decisions
(Dotoli et al., 2017). Various cloud-based architec-
tures for intelligent transportation systems were pro-
posed (Khair et al., 2021). A cloud-based architec-
ture, which focuses on decentralised big transporta-
tion data analyses was presented in (Fiosina et al.,
2013a).
Travel-time is an important parameter of trans-
portation networks, which accurate prediction helps
to reduce delays and transport delivery costs, im-
proves reliability through better selection of routes
and increases the service quality of commercial deliv-
ery by bringing goods within the required time win-
dow (Ciskowski et al., 2018). A centralised deep
learning based approach to the estimation of travel-
time for ride-sharing problem was discussed in (Al-
Abbasi et al., 2019).
Often proper travel time forecasting model needs
a pre-processing such as data filtering and ag-
gregation. Travel-time aggregation models (non-
parametric, semi-parametric) for decentralized data
clustering and corresponding coordination and pa-
rameter exchange algorithms were researched in
(Fiosina et al., 2013b). Travel-time estimation and
forecasting using decentralized multivariate linear
and kernel-density regression with corresponding pa-
rameter/data exchange was proposed in (Fiosina et al.,
Explainable Federated Learning for Taxi Travel Time Prediction
671

2013a).
Initial requirements and ideas for methods of de-
centralised data analysis development in the trans-
portation domain operating with big data flows have
been identified (Fiosina et al., 2013b). The impact
of incorporating decentralised data analysis methods
into MAS-based applications taking into account in-
dividual user routing preferences has been assessed
(Fiosina and Fiosins, 2014).
2.2 Federated Learning
Federated learning (Konecn
´
y et al., 2016) was pro-
posed by Google and continues the research line
of distributed data analyses, which focuses mainly
on development of privacy-preserved ML models for
physically distributed data. When the isolated dataset
used by each company cannot create an accurate
model, the mechanism of federated learning enables
access to more data and better training of models.
Federated learning enables different devices to collab-
oratively learn a shared prediction model while main-
taining all training data on the device, without the
need to store the data in the cloud. The main differ-
ence between federated learning and distributed learn-
ing is attributed to the assumptions on the properties
of the local datasets, as distributed learning originally
aims to parallelise the computing power, whereas fed-
erated learning originally aims to train on heteroge-
neous datasets (Konecn
´
y et al., 2016). This approach
may use a central server that orchestrates the different
steps of the algorithm and acts as a reference clock
or they may be peer-to-peer, where no such central
server exists. In this study, we use a central server
for this aggregation, while local nodes perform local
training (Yang et al., 2019).
The general principle consists of training local
models on local data samples and exchanging param-
eters (e.g., the weights of a deep neural network) be-
tween these local models at some frequency to gener-
ate a global model (Bonawitz et al., 2019). To ensure
a good task performance of a final central ML learn-
ing model, federated learning relies on an iterative
process broken down to an atomic set of client–server
interactions referred to as federated learning round
(Yang et al., 2019). Each round of this process con-
sists of transmitting the current global model state to
participating nodes, training local models on these lo-
cal nodes to produce a set of potential model updates
at each node, and aggregating and processing these
local updates into a single global update and applying
it to the global model.
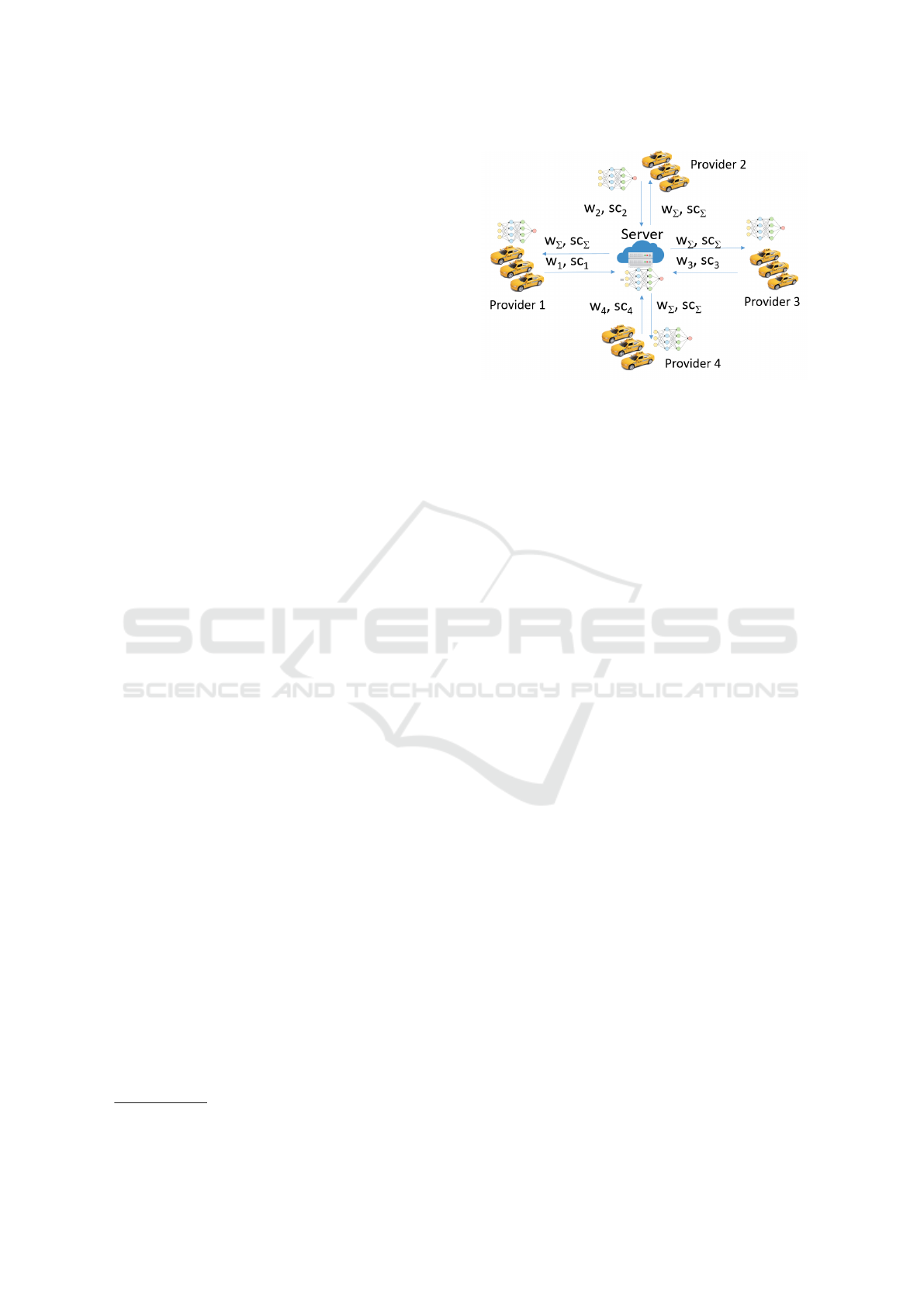
We consider N data owners {F
i
}
N
i=1
, who wish to
train an ML model by consolidating their respective
Figure 1: Architecture of horizontal federated learning.
data {D
i
}
N
i=1
. A centralised approach uses all data
together D = ∪
N
i=1
D
i
to train a model M
Σ
. A feder-
ated system is a learning process in which the data
owners collaboratively train a model M
FD
, where any
data owner F
i
does not expose its data D
i
to others.
In addition, the accuracy of M
FD
, denoted as V
FD
,
should be very close to the performance of M
Σ
, V
Σ
(Yang et al., 2019). Each row of the matrix D
i
repre-
sents a sample, while each column represents a fea-
ture. Some datasets may also contain label data. The
feature X , label Y , and sample Ids I constitute the
complete training dataset (I, X, Y ). The feature and
sample space of the data parties may not be identi-
cal. We classify federated learning into horizontal,
vertical, and federated transfer learning based on the
data distribution among various parties. In horizontal
or sample-based federated learning data sets share the
same feature space but different in samples. In verti-
cal or feature-based federated learning data sets share
the same sample ID space but differ in feature space.
In federated transfer learning data sets differ in both
sample and feature space, having small intersections.
In this study, we develop a joint privacy-
preserving model of travel time forecasting of differ-
ent service providers based on the horizontal feder-
ated learning architecture. The training process of
such a system is independent on specific ML algo-
rithms. All participants share the final model parame-
ters (Figure 1).
2.3 Explainable AI
Conventional ML methods, such as linear regression,
decision trees, and support vector machine, are inter-
pretable in nature. Typically, highly accurate complex
deep learning-based black-box models are favoured
over less accurate but more interpretable conventional
ML models. Extensive studies have been carried out
in the past few years to design techniques to make AI
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
672
methods more explainable, interpretable, and trans-
parent to developers and users (Molnar, 2020). Join-
ing such methods in hybrid systems (e.g., ensem-
bling) further increases their explainability and ob-
tained accuracy, (Holzinger, 2018). AI for explain-
ing decisions in MAS was discussed in (Kraus et al.,
2020).
Model-agnostic and model-specific explanation
methods have been reported (Molnar, 2020). Model-
agnostic methods, such as LIME, Sharpley Values,
are implementable for each model. However, they re-
quire a large number of computations and often are
not applicable for big datasets used in deep learn-
ing (Molnar, 2020). Sharpley values method was
implemented in (Wang, 2019) to interpret a vertical
federated learning model. Model-specific methods
are more suitable for deep learning, which focus on
only one type of model and are more computationally
effective (Molnar, 2020), e.g., Integrated Gradients
(Sundararajan et al., 2017), and DeepLIFT (Shriku-
mar et al., 2017), (Ancona et al., 2018). These meth-
ods have an additive nature, which enables comput-
ing them in a distributed manner across processors,
machines, or GPUs. For example, the explainabil-
ity scores can be calculated on the participants’ local
data, and then accumulated at the server together
2
.
In this study, we focus on integrated gradients,
which represent the integral of gradients with respect
to inputs along the path from given baseline to input.
3 EXPLAINABLE FEDERATED
LEARNING
We propose a federated model explaining strategy and
illustrate it on a travel time prediction problem. Our
aim is to describe the application of state-of-the-art
explainability methods to federated learning, while
maintaining data privacy. We apply the federated
learning architecture and explainability methods to
the focal problem and consider what information and
how often should be exchanged. Moreover, the ap-
plication of each explainability method to a concrete
task only produces baseline results because the result
interpretation is specific to the particular task or ap-
plication at hand (Fiosina et al., 2019).
Let N participants {F
i
}
N
i=1
own datasets {D
i
}
N
i=1
as previously defined. For the federated learning
process, each participant F
i
divides its dataset D
i
=
D
T R
i
∪ D
T E
i
into training set D
T R
i
and test set D
T E
i
.
We train the models on D
T R
i
and calculate attribution
scores on D
T E
i
. {M
i
}
N
i=1
are the participants’ local
2
https://captum.ai/
Figure 2: Explainable federated learning architecture.
models, while M
FD
is the federated model. As we
consider learning on batches, M
<epoch,batch>
i
is the lo-
cal model of the participant F
i
for the current epoch
and batch of data, while M
<epoch,batch>
FD
is the cur-
rent federated model. w
epoch,batch
i
are the current pa-
rameters of the model M
<epoch,batch>
i
: w
epoch,batch
i
=
w(M
<epoch,batch>
i
). The training process is described
in Algorithm 1. Note, that the synchronisation should
not appear each batch, so a logical variable synchro-
nisation supervises this process. FedAverage() is a
parameter synchronisation procedure at server side,
which, in the simplest case, is an average value, cal-
culated for each parameter over all local models. We
start the variable explanation process when the fed-
erated training process is finished and a copy of the
common federated model M
<localF D>
i
of each F
i
is lo-
cally available. The scoring algorithm is one of the
explainability methods mentioned above.
4 EXPERIMENTAL SETUP
We predict the Brunswick taxi travel time based on
floating car data (FCD) trajectories obtained from two
different taxi service providers. The data were avail-
able for the period of January 2014 - January 2015.
Each raw data item contains: car identifier, time mo-
ment, geographical point and status (free, drives to
client, drives with client, etc.). The data were received
approximately every 40 s. We consider the map of
Brunswick and surrounding as a box with coordinates
in the latitude range of 51.87
◦
−52.62
◦
and longitude
range of 10.07
◦
− 11.05
◦
(Figure 3).
To evaluate whether the travel times depend on
weather conditions, we used corresponding histori-
cal data about rains, wind, temperature, atmospheric
pressure, etc. However, good-quality weather data for
the given region were available only until the end of
Explainable Federated Learning for Taxi Travel Time Prediction
673

Algorithm 1: Explainable federated learning train-
ing process.
Result: Trained M
FD
model
Define initial w
i
for M
i
, epoch=1 ;
while The loss function does not converge do
foreach batch of data do
foreach F
i
in parallel do
Train(M
<epoch,batch>
i
, D
T R,batch
i
);
if synchronisation then
F
i
sends w
<epoch,batch>
i
to the
server;
if synchronisation then
Server averages the parameters and
broadcasts them: w
<epoch,batch>
FD
=
FedAverage(w
<epoch,batch>
i
);
foreach F
i
in parallel do
F
i
receives updated parameters
from the server and updates its
model:
M
<epoch,batch>
i
= M
<epoch,batch>
FD
;
epoch = epoch + 1
Training process is over. Last obtained
M
<epoch,batch>
FD
is the final model: M
<localF D>
i
of each F
i
;
foreach participant F
i
in parallel do
foreach instance j of D
T E
i
dataset do
Calculates attribution scores: sc
i, j
=
ScoringAlgorithm(M
<localF D>
i
,D
T E
i, j
);
F
i
calculates its average scores and sends the
result to the server: sc
i∗
=
∑
j
sc
i, j
|D
T E
i
|
;
Server aggregates the participant scores and
broadcasts the result: sc
FD
=
∑
i
sc
i∗
˙
|D
T E
i
|
|∪
i
D
T E
i
|
;
foreach participant F
i
in parallel do
Each F
i
updates its attribution scores:
sc
i∗
= sc
FD
;
September 2014, so that we reduced our trajectory
dataset accordingly.
We developed a multi-step data pre-processing
pipeline. We constructed a script to transform the data
into trajectories according to time points, locations,
and car identifier. The raw trajectories were then anal-
ysed to determine their correctness. We split trajecto-
ries with long stay periods into shorter trips. Round
trips with the same source and destination were sepa-
rated into two trips. Some noisy unrealistic data with
probably incorrect global positioning system (GPS)
signals, with incorrect status, or unrealistic average
speeds (less than 13 km or more than 100 km), were
also removed. After this cleaning, the number of tra-
jectories was 542066.
Figure 3: Road network of Brunswick and surrounding
We then connected the trajectories with the open
street map and obtained a routable graph. Addition-
ally, we divided the map into different size grids (e.g.,
200m×200m) to determine whether this aggregation
can improve our forecasts. Therefore, we knew to
which zone the start and end points of each trip be-
long. Moreover, we found the nearest road graph
node to the source and destination of each trip and
calculated the shortest-path distance. To improve the
prediction model and filter the noisy data, we calcu-
lated the distance between the start and end points of
each trip according to the FCD trajectory. If the dis-
tances of the shortest path trajectory and FCD trajec-
tory were considerably different, we analysed the trip
more closely and divided it into a couple of more re-
alistic trips, excluding false GPS signal places.
We stored the raw data, trip data, weather data,
and graph data obtained from open street map (roads
and nodes) in the PostgreSQL database.
For visual presentation of trips, their sources and
destinations as well as graph representation of roads
network of Brunswick we used QGIS
3
(Figure 3).
We predicted the travel time using different methods
(Table 1) and found the corresponding best hyper-
parameters by the grid search.
The forecasting was based on the following fac-
tors: coordinates of the start zone and end zone (200m
× 200m), FCD distance, transformed (with sine and
cosine) weekday and hour, as well as temperature, air
pressure, and rain. We forecasted the travel time in
seconds. We divided the dataset into training (80%)
and test (20%) sets. The dataset was normalised with
MinMax Scaler before the application of the above
methods. We used the mean squared error (MSE)
as an efficiency criterion and 5-fold cross validation
for model comparison. The accuracy with an MSE of
.0010 corresponds to 5 min, while that with an MSE
of .0018 to 7.5 min. We used Python programming
language, PyTorch for deep learning models, PySyft
library
4
for the federated learning (Ryffel et al., 2018)
3
https://www.qgis.org/
4
https://pysyft.readthedocs.io/
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
674

Table 1: Optimal model hyper-parameters.
Model Hyper-parameters
Regression
Linear (no);
Ridge (α = 0.09);
Lasso (α = 1e − 9)
XGBoost
colsample bytree = 0.7;
learning rate = 0.12;
max depth = 9, α = 15;
n estimators = 570
Random forest
num trees=100;
max depth and min samples leaf
are not restricted
Deep learn.
fully conn. percentron
with 2 hidden layers,
number of neurons: 64-100
Re-Lu act. function;
0.2 dropout between hidden layers;
optimiser SGD;
MSE loss function;
NN batchsize=128, epochs=800;
learning rate=0.02
Federated learn.
synchronisation each 2nd batch,
NN batch size is proportional to
the size of each provider’s dataset,
the sum of all provider’s
NN batch size= 128.
and captum
5
library to interpret the models.
5 EXPERIMENTS
5.1 Alternative Predictors
We identified the best ML prediction model (Table
2). For a single data provider (centralised approach),
the best results were obtained by the XGBoost and
random forest methods (.00097 and .0010). Conven-
tional regression methods such as linear, Lasso and
Ridge regressions provided the same inaccurate re-
sults. Deep learning exhibited a slightly lower perfor-
mance than those of the best models. The application
of federated deep learning was impossible because of
a single data owner.
Our next task was to determine under which con-
ditions federated deep learning was effective. De-
spite the fact that XGBoost and random forest meth-
ods provided the most accurate results for the cen-
tralised approach, federated learning could be imple-
mented only on parametric models like deep learn-
ing. Unfortunately it was unknown, which data be-
longed to which provider. Thus we randomly dis-
tributed the data among the providers and this led to
the assumption of identically distributed and equally
5
https://captum.ai/
Table 2: MSE of travel time prediction with different ML
methods.
Model Number of data providers
1 4 8 16 32
Linear,
.0019 .0019 .0019 .0020 .0020
Lasso,
Ridge
regression
XGBoost .00097 .0011 .0012 .0012 .0013
Random
.0010 .0011 .0012 .0012 .0013
forest
Deep
.0011 .0012 .0013 .0014 .0015
learning
Federated
— .0011 .0011 .0011 .0011deep
learning
sized local datasets, which in federated learning is of-
ten not true. Then, we executed various ML models
locally on each provider without synchronisation. Fi-
nally, we analysed after which point the distributed
nonsynchronised models lose their accuracy and fed-
erated learning outperformed other locally executed
ML methods.
The next columns of Table 2 show the MSE of
travel time prediction on distributed data. The average
accuracy of all models except federated deep learning
was reduced. The federated approach led to the same
result as that of the centralised deep learning. There-
fore, the accuracy of the federated model was compa-
rable to those of XGBoost and random forest. Start-
ing at eight data providers, federated learning became
beneficial because it does not lose its accuracy. With
more data providers, the benefits of federated learn-
ing became more evident. The MSE of the federated
model’s prediction remained constant, 0.0011.
Another important parameter that influences the
accuracy of the federated model is the batch size. In
our centralised deep learning model, the optimal so-
lution was obtained with batch size = 128 or smaller.
The experiments show that with the increase in the
batch size, the computing speed increases, but the ac-
curacy of the model decreases. This implies that, to
obtain the same accuracy by federated learning, we
have to distribute the batches proportionally among
the providers. Accordingly, with eight data providers,
with equally sized datasets, the batch size will be
128/8 = 16.
5.2 Synchronisation of Models
We investigated the effect of the synchronisation fre-
quency on the accuracy of the federated model. The
accuracy decreased with the step-wise decrease in the
synchronisation frequency (Table 3); we aimed to in-
vestigate this tendency. With synchronisation per-
Explainable Federated Learning for Taxi Travel Time Prediction
675

formed in each batch or even each second batch, the
accuracy remained the same as that of the centralised
approach. The accuracy decreased with a rarer syn-
chronisation.
Table 3: MSE of travel time prediction for different syn-
chronisation frequencies.
Synchronisation each n-th batch Av.
for eight providers MSE
1, 2 .0011
3, 4 .0012
5 .0013
5.3 Explaining of the Federated Model
In this section, we compare the results of variable
importances for local, federated and centralised ap-
proaches. We have chosen Integrated gradients ex-
plainability method as an explainability scoring algo-
rithm because of its simplicity and speed. Moreover
the baseline in this algorithm was taken equal to the
average value of each feature.
Figure 4 contains variable importance calculated
with the federated model for each of eight data
providers locally using their test data. Despite the fact
that the main tendency in variable importance by all of
eight providers remains the same, the locally obtained
results differ from the importance scores, calculated
with all test data. This may lead to inaccurate ex-
plainability by some local providers, especially with
small testset sizes. The proposed importance scores
averaging mechanism (Algorithm 1) allows to avoid
this inaccuracy without transmitting the local testsets.
0
0.005
0.01
0.015
0.02
0.025
0 1
2 3
4 5
6 7
distance
cos/sin
hour
cos/sin
weekday
temp
rain
Data Providers
wind
lon
lat
lon
start zone
end zone
lat
Figure 4: Explainability of individual models.
Figure 5 presents variable importances calculated
for centralised and federated learning approaches us-
ing aggregated test datasets (centralised) or aggrega-
tion of scores (federated), which led to the same re-
sults. We observe that without raw data transfer our
approach allows more accurate calculation of variable
importance than one each provider can obtain using
only its local test set.
Our next task is to investigate, which parameters
0
0.005
0.01
0.015
0.02
0.025
Federated
Centralised
distance
start zone
lon
lat
cos/sin
hour
end zone
sin/cos
weekday
temp
rain
wind
lon
lat
Figure 5: Explainability of federated vs centralised ap-
proach.
have the biggest influence on the results. According
to Figures 4 and 5 the most important variable for all
the models was FCD distance, which was expected.
The next important variables were zones’ coordinates,
sine and cosine of the traveling hour and day of the
week. The division of the map into zones improved
the predictions. However, despite of our expectations,
almost all weather parameters do not significantly in-
fluence the predictions.
6 CONCLUSION
We analysed Brunswick taxi FCD data trajectories for
travel time prediction with different prediction meth-
ods. We identified that XGBoost was the best predic-
tion model for the centralised approach, which pre-
dicted the corresponding travel-time with an MSE of
0.00097. In the case of distributed data providers,
starting at eight providers with equal distributions of
data sources, the federated approach outperformed
XGBoost and random forest methods if they were
executed locally by each data provider. Upon the
synchronisation executed on each second batch, the
corresponding federated deep learning model did not
lose its accuracy compared to the centralised model.
We proposed an approach to explain the horizontal
federated learning model with explainability meth-
ods without transferring raw data to the central server.
This enabled more accurate determination of the most
important prediction variables of the federated model.
We illustrated the considered approach on a travel
time prediction problem using a horizontal federated
learning architecture. For calculation simplicity in
our experiments all providers’ local datasets were of
the same size and the data were identically distributed
in all datasets, which is often not true in real-world
problems. We are planning to consider not equally
sized and not identically distributed datasets in our
future experiments. We assume that the participants
VEHITS 2021 - 7th International Conference on Vehicle Technology and Intelligent Transport Systems
676

with smaller datasets will have more benefits from the
accurate prediction model. A particularly beneficial
case could be if we suppose that each taxi’s dataset
is confidential and should be processed locally (self-
interested ride providers) as in (Ramanan et al., 2020).
Despite the fact, that the proposed explainable
federated approach does not depend on the explain-
ability method, only one explainability method (Inte-
grated gradients) was analysed. We plan to compare
different explainability methods and their combina-
tions as our future work. We believe that this ap-
proach could be successfully implemented for more
complex prediction and classification tasks with more
complex deep learning and federated learning archi-
tectures. For example, we aim to implement explain-
able federated learning for traffic demand forecasting
models.
ACKNOWLEDGEMENTS
The research was funded by the Lower Saxony Min-
istry of Science and Culture under grant number
ZN3493 within the Lower Saxony “Vorab“ of the
Volkswagen Foundation and supported by the Center
for Digital Innovations (ZDIN).
REFERENCES
Al-Abbasi, A. O., Ghosh, A., and Aggarwal, V. (2019).
Deeppool: Distributed model-free algorithm for ride-
sharing using deep reinforcement learning. IEEE
Transactions on ITSs, 20(12):4714–4727.
Ancona, M., Ceolini, E.,
¨
Oztireli, C., and Gross, M. (2018).
Towards better understanding of gradient-based attri-
bution methods for deep neural networks. In In Proc.
of 6th Int. Conf. on Learning Representations, ICLR.
Bonawitz, K., Eichner, H., Grieskamp, W., Huba, D., Inger-
man, A., Ivanov, V., Kiddon, C., Konecn
´
y, J., Maz-
zocchi, S., McMahan, H. B., Overveldt, T. V., Petrou,
D., Ramage, D., and Roselander, J. (2019). Towards
federated learning at scale: System design. CoRR,
abs/1902.01046.
Ciskowski, P., Drzewinski, G., Bazan, M., and Janiczek, T.
(2018). Estimation of travel time in the city using neu-
ral networks trained with simulated urban traffic data.
In DepCoS-RELCOMEX 2018, volume 761 of Ad-
vances in Intelligent Systems and Computing, pages
121–134. Springer.
Dotoli, M., Zgaya, H., Russo, C., and Hammadi, S. (2017).
A multi-agent advanced traveler information system
for optimal trip planning in a co-modal framework.
IEEE Transactions on Intelligent Transportation Sys-
tems, 18(9):2397–2412.
Fiosina, J. and Fiosins, M. (2014). Resampling based mod-
elling of individual routing preferences in a distributed
traffic network. Int. Journal of AI, 12(1):79–103.
Fiosina, J. and Fiosins, M. (2017). Distributed nonpara-
metric and semiparametric regression on spark for big
data forecasting. Applied Comp. Int. and Soft Com-
puting, 2017:13.
Fiosina, J., Fiosins, M., and Bonn, S. (2019). Explainable
deep learning for augmentation of sRNA expression
profiles. Journal of Computational Biology. (to ap-
pear).
Fiosina, J., Fiosins, M., and M
¨
uller, J. (2013a). Big data
processing and mining for next generation intelligent
transportation systems. Jurnal Teknologi, 63(3).
Fiosina, J., Fiosins, M., and M
¨
uller, J. (2013b). Decen-
tralised cooperative agent-based clustering in intelli-
gent traffic clouds. In Proc. of 11th German Conf. on
MAS Technologies, volume 8076 of LNAI, pages 59–
72. Springer.
Holzinger, A. (2018). Explainable AI (ex-AI). Informatik
Spektrum, 41:138–143.
Khair, Y., Dennai, A., and Elmir, Y. (2021). A survey on
cloud-based intelligent transportation system, icaires
2020. In AI and Renewables Towards an Energy Tran-
sition, volume 174 of LNNS. Springer.
Konecn
´
y, J., McMahan, H. B., Ramage, D., and Richt
´
arik,
P. (2016). Federated optimization: Distributed ma-
chine learning for on-device intelligence. CoRR,
abs/1610.02527.
Kraus, S., Azaria, A., Fiosina, J., Greve, M., Hazon, N.,
Kolbe, L., Lembcke, T., M
¨
uller, J., Schleibaum, S.,
and Vollrath, M. (2020). AI for explaining decisions in
multi-agent environment. In AAAI-2020. AAAI Press.
Molnar, C. (2020). Interpretable Machine Learning. A
Guide for Making Black Box Models Explainable.
Lulu.com.
Ramanan, P., Nakayama, K., and Sharma, R. (2020). Baffle:
Blockchain based aggregator free federated learning.
CoRR, abs/1909.07452.
Ryffel, T., Trask, A., Dahl, M., Wagner, B., Mancuso, J.,
Rueckert, D., and Passerat-Palmbach, J. (2018). A
generic framework for privacy preserving deep learn-
ing. CoRR, abs/1811.04017.
Shrikumar, A., Greenside, P., and Kundaje, A. (2017).
Learning important features through propagating ac-
tivation differences. In Proc. of ML Research, vol-
ume 70, pages 3145–3153, Int. Convention Centre,
Sydney, Australia. PMLR.
Sundararajan, M., Taly, A., and Yan, Q. (2017). Ax-
iomatic attribution for deep networks. In Proc. of the
34th Int. Conf. on ML, volume 70 of ICML’17, page
3319–3328. JMLR.org.
Wang, G. (2019). Interpret federated learning with shapley
values. CoRR, abs/1905.04519.
Yang, Q., Liu, Y., Chen, T., and Tong, Y. (2019). Federated
machine learning: Concept and applications. ACM
Trans. Intell. Syst. Technol., 10(2).
Explainable Federated Learning for Taxi Travel Time Prediction
677
