Image Copy-Move Forgery Detection using Color Features and
Hierarchical Feature Point Matching
Yi-Lin Tsai and Jin-Jang Leou
Department of Computer Science and Information Engineering, National Chung Cheng University,
Chiayi 621, Taiwan
Keywords: Copy-Move Forgery Detection, Hierarchical Feature Point Matching, Color Feature, Iterative Forgery
Localization.
Abstract: In this study, an image copy-move forgery detection approach using color features and hierarchical feature
point matching is proposed. The proposed approach contains three main stages, namely, pre-processing and
feature extraction, hierarchical feature point matching, and iterative forgery localization and post-processing.
In the proposed approach, Gaussian-blurred images and difference of Gaussians (DoG) images are constructed.
Hierarchical feature point matching is employed to find matched feature point pairs, in which two matching
strategies, namely, group matching via scale clustering and group matching via overlapped gray level
clustering, are used. Based on the experimental results obtained in this study, the performance of the proposed
approach is better than those of three comparison approaches.
1 INTRODUCTION
Copy-move forgery, a common type of forged images,
copies and pastes one or more regions onto the same
image (Cozzolino, Poggi, and Verdoliva, 2015). Some
image processing operations, such as transpose,
rotation, scaling, and JPEG compression, will make
images more convincing. To deal with copy-move
forgery detection (CMFD), many CMFD approaches
have been proposed, which can be roughly divided
into three categories: block-based, feature point-
based, and deep neural network based.
Cozzolino, Poggi, and Verdoliva (2015) used
circular harmonic transform (CHT) to extract image
block features. A fast approximate nearest-neighbor
search approach (called patch match) is used to deal
with invariant features efficiently. Fadl and Semary
(2017) proposed a block-based CMFD approach using
Fourier transform for feature extraction. Bi, Pun, and
Yuan (2016) proposed a CMFD approach using
hierarchical feature matching and multi-level dense
descriptor (MLDD).
Amerini, et al. (2011) proposed a feature point-
based CMFD approach using scale invariant feature
transform (SIFT) (Lowe, 2004) for feature point
extraction. Amerini, et al. (2013) developed a CMFD
approach based on J-linkage, which can effectively
solve the problem of geometric transformation. Pun,
Yuan, and Bi (2015) proposed a CMFD approach
using feature point matching and adaptive
oversegmentation. Warif, et al. (2017) proposed a
CMFD approach using symmetry-based SIFT feature
point matching. Silva, et al. (2015) presented a CMFD
approach using multi-scale analysis and voting
processes. Jin and Wan (2017) proposed an improved
SIFT-based CMFD approach. Li and Zhou (2019)
developed a CMFD approach using hierarchical
feature point matching. Huang and Ciou (2019)
proposed a CMFD approach using superpixel
segmentation, Helmert transformation, and SIFT
feature point extraction (Lowe, 2004). Chen, Yang,
and Lyu (2020) proposed an efficient CMFD approach
via clustering SIFT keypoints and searching the
similar neighborhoods to locate tampered regions.
Zhong and Pun (2020) proposed a CMFD scheme
using a Dense-InceptionNet. Dense-InceptionNet is
an end-to-end multi-dimensional dense-feature
connection deep neural network (DNN), which
consists of pyramid feature extractor, feature
correlation matching, and hierarchical post-processing
modules. Zhu, et al. (2020) proposed a CMFD
approach using an end-to-end neural network based on
adaptive attention and residual refinement network
(AR-Net). Islam, Long, Basharat, and Hoogs (2020)
proposed a generative adversarial network with a
Tsai, Y. and Leou, J.
Image Copy-Move Forgery Detection using Color Features and Hierarchical Feature Point Matching.
DOI: 10.5220/0010492301530159
In Proceedings of the Inter national Conference on Image Processing and Vision Engineering (IMPROVE 2021), pages 153-159
ISBN: 978-989-758-511-1
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
153

dual-order attention model to detect and locate copy-
move forgeries. In this study, an image copy-move
forgery detection approach using color features and
hierarchical feature point matching is proposed.
This paper is organized as follows. The proposed
image copy-move forgery detection approach is
described in Section 2. Experimental results are
addressed in Section 3, followed by concluding
remarks.
2 PROPOSED APPROACH
2.1 System Architecture
As shown in Figure 1, in this study, an image copy-
move forgery detection approach using color features
and hierarchical feature point matching is proposed.
The proposed approach contains three main stages,
namely, pre-processing and feature extraction,
hierarchical feature point matching, and iterative
forgery localization and post-processing.
Figure 1: Framework of the proposed approach.
2.2 Pre-processing and Feature
Extraction
Let 𝐴

(
𝑥,𝑦
)
, 1≤𝑥≤𝑀, 1≤𝑦≤𝑁, be the input
RGB color image with size 𝑀×𝑁. The input color
image will be converted from RGB color space to HSI
color space and the intensity component image (I) is
enhanced by histogram equalization, which is
converted from HSI color space back to RGB color
space, denoted as 𝐴

(
𝑥,𝑦
)
,1≤𝑥≤𝑀, 1≤𝑦≤
𝑁. To extract enough feature points, in this study,
𝐴

(
𝑥,𝑦
)
is enlarged by 2×2 linear interpolation,
denoted as 𝐸

(
𝑥,𝑦
)
, 1≤𝑥≤2𝑀, 1≤𝑦≤2𝑁.
Then, image 𝐸

(
𝑥,𝑦
)
is converted into gray-level
image 𝐸

(
𝑥,𝑦
)
, 1≤𝑥≤2𝑀, 1≤𝑦≤2𝑁, which
is convolved with Gaussian filters of different scales.
Gaussian-blurred image 𝐿
(
𝑥,𝑦,𝑚

𝜎
)
,1≤𝑥≤2𝑀,
1≤𝑦≤2𝑁, is computed as
𝐿
(
𝑥,𝑦,𝑚

𝜎
)
=𝐺
(
𝑥,𝑦,𝑚

𝜎
)
⨂𝐸

(
𝑥,𝑦
)
,
𝛼=0,1,…,4,
(1)
where 𝐺
(
𝑥,𝑦,𝑚

𝜎
)
denotes the Gaussian kernel, 𝑚
is a constant (here, 𝑚=
√
2
), ⨂ denotes the
convolution operator, and 𝜎 denotes a prior
smoothing value (here, 𝜎=1.6). Difference of
Gaussians (DoG) image 𝐷𝑥,𝑦,𝑚

𝜎,1 ≤ 𝑥≤
2𝑀,1≤𝑦≤2𝑁, is computed as
𝐷

𝑥,𝑦,𝑚

𝜎

=𝐿

𝑥,𝑦,𝑚

𝜎

−𝐿

𝑥,𝑦,𝑚

𝜎

,
𝛽=0,1,2,3.
(2)
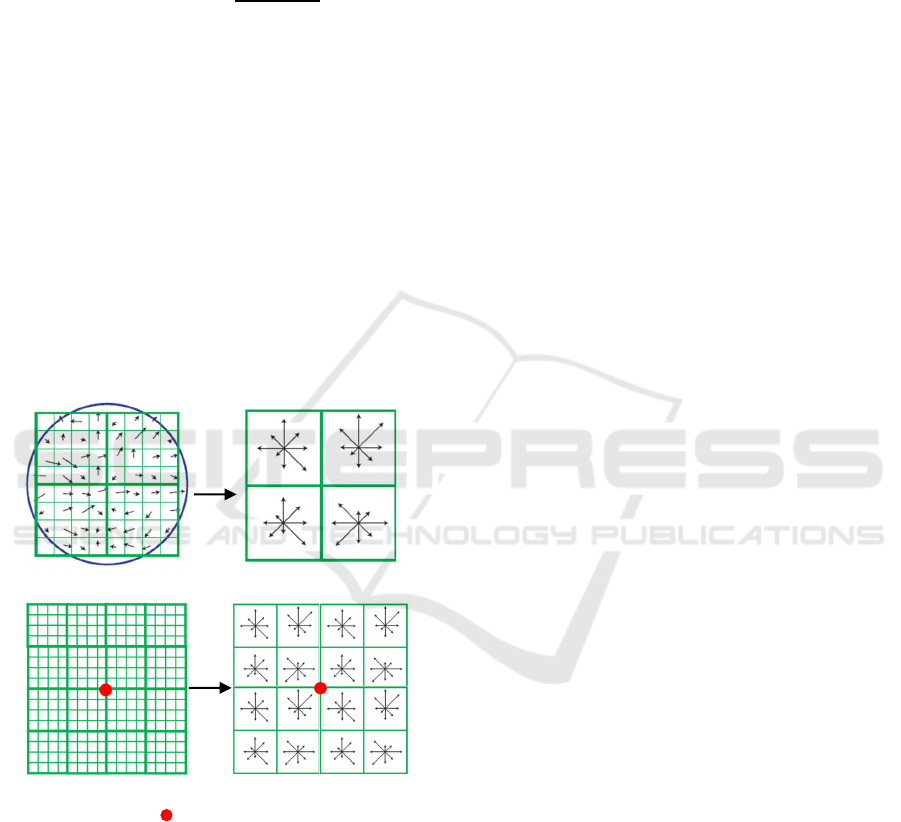
As multiple octaves shown in Figure 2 (Lowe,
2004), each octave contains five Gaussian-blurred
images and four DoG images. The first scale value of
the i-th octave is 𝑚
()
𝜎. The first octave size is
2𝑀×2𝑁, the second octave size with down-sampling
is 𝑀×𝑁, …, etc.
Within an octave, to detect the local maxima and
minima of 𝐷𝑥,𝑦,𝑚

𝜎, if the value of a pixel larger
(or smaller) than those of its 8 neighbors in the same
image and those of 2×9 neighbors in the two
neithboring DoG images with different scales, this
pixel is detected as a feature point. Note that the first
and last DoG images in each octave do not have
feature points.
Figure 2: Illustrated schematic diagram of Gaussian-blurred
images and DoG images (Lowe, 2004).
Second, using edge and contrast thresholds, all
candidate feature points will be refined so that
unstable extrema in SIFT feature points can be filtered
out. The extrema value is computed as
𝐷𝐹

=𝐷+
1
2

𝜕𝐷
𝜕𝐹


𝐹

,
(3)
𝐹

=−
𝜕

𝐷
𝜕
𝐹


×
𝜕𝐷
𝜕
𝐹
,
(4)
IMPROVE 2021 - International Conference on Image Processing and Vision Engineering
154

where 𝐹=(𝑥,𝑦,𝜎)

and 𝑇 is a transpose. All
extrema with
|
𝐷
(
𝑥
)|
being less than 𝑍

(set to 0.1) are
discarded.
Third, to achieve rotational invariance, a gradient
magnitude 𝜇𝑥,𝑦,𝑚

𝜎 and a guiding direction
𝜃𝑥,𝑦,𝑚

𝜎 defined as
𝜇𝑥,𝑦,𝑚

𝜎 =

𝑑

𝟐
+𝑑

𝟐
,
(5)
𝜃𝑥,𝑦,𝑚

𝜎 =tan

(𝑑

/𝑑

),
(6)
𝑑

=𝐷𝑥+1, 𝑦, 𝑚

𝜎−𝐷𝑥−1,𝑦,𝑚

𝜎, (7)
𝑑

=𝐷𝑥,𝑦+1,𝑚

𝜎−𝐷𝑥,𝑦−1,𝑚

𝜎,
(8)
are allocated to each subsisted feature point. A generic
SIFT feature point 𝑃

can be described as a four-
dimensional vector, i.e.,
𝑷
𝒌
=
(
𝒙
𝒌
,𝒚
𝒌
,𝒎
𝒔
𝝈,𝜽
𝒌
)
, 𝒌=𝟏, 𝟐, …,𝒏,
(9)
where (𝑥

,𝑦

) denotes feature point coordinate, 𝑛
denotes the total number of feature points, and 𝑚

𝜎
and 𝜃

denote the scale and guiding direction of 𝑃

,
reprectively.
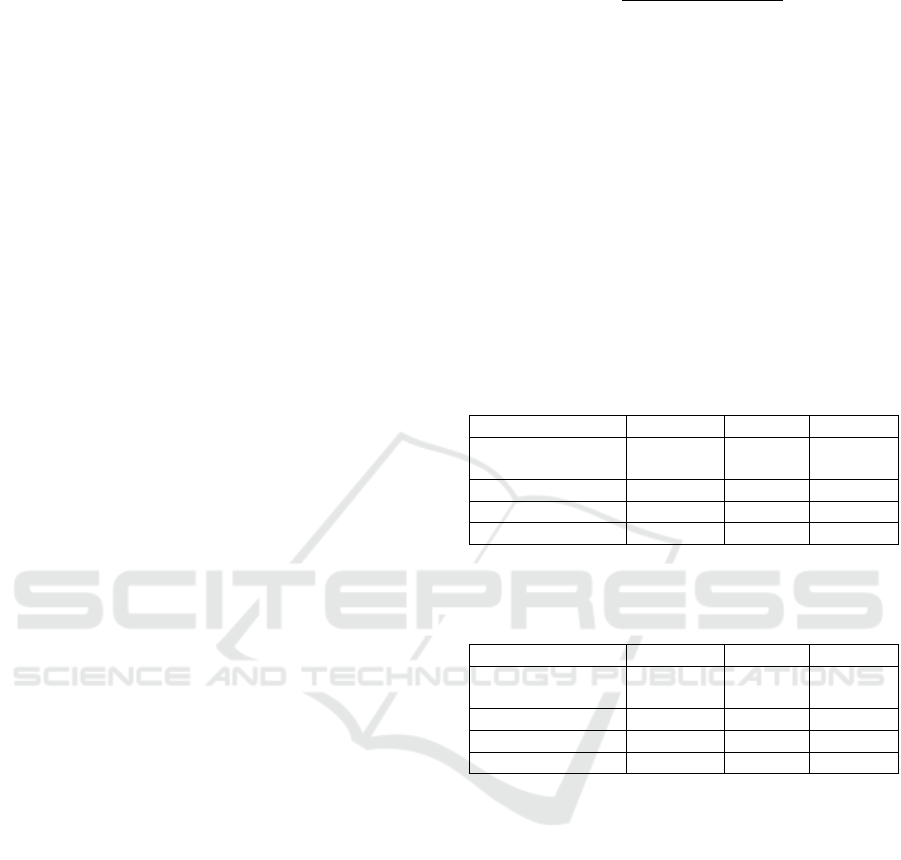
(a) (b)
(c) (d)
Feature point
Figure 3: Schematic diagram of feature point descriptor
(Lowe, 2004): (a) gradient magnitudes and guiding
directions in a 8×8 region around a central feature point, (b)
a 2×2 descriptor, (c) a 16×16 region around a central feature
point, (d) a 128-dimensional descriptor.
As shown in Figure 3, an eight-direction histogram
is formed from gradient magnitudes and guiding
directions of feature points within a 4×4 region,
which has 8 quantized histogram entries covering 360
°
with the length of each arrow denoting its gradient
magnitude. In a 16×16 region around a central
feature point, 16 eight-direction histograms are
generated, resulting in 128-dimensional (16 × 8) row
vector descriptors 𝜔

=𝜔
,
, 𝜔
,
,…,𝜔
,
, 𝑘=
1, 2, ..., 𝑛. For 𝑃

, let 𝐸𝐷

,𝑘=1,2,...,𝑛−1
denote the Euclidean distances between descriptor 𝜔

and other (𝑛−1) descriptors. Let ratio R be defined as
𝑹=𝑬𝑫
𝟏
/𝑬𝑫
𝟐
,
(10)
where 𝐸𝐷

and 𝐸𝐷

denote the smallest and second-
smallest Euclidean distances, respectively. If ratio 𝑅
is less than threshold 𝑍

(𝑍

=0.6), feature point 𝑃

having the smallest Euclidean distance 𝐸𝐷

is a
matching feature point of 𝑃

. 𝑃

, 𝑘=1,2,...,𝑛
having a matching feature point as well as its matching
feature point, i.e., a matching feature point pair, will
be kept; otherwise, it is discarded.
2.3 Hierarchical Feature Point
Matching
In this study, a modified version of hierarchical
feature point matching (Li and Zhou, 2019) is
employed, in which two matching strategies, namely,
group matching via scale clustering and group
matching via overlapped gray level clustering, are
used.
Because Gaussian-blurred images are grouped by
octave, feature points detected in different scales will
be clustered closely, which can be separately
processed. In this study, matching procedures are
performed separately in each single high-resolution
octave and jointly in multiple low-resolution octaves.
Note that feature points in high-resolution octaves are
much sparse than feature points in low-resolution
octaves. In addition, feature points in low-resolution
octaves having higher recognition capabilities can
strongly resist large-scale resizing attack.
Based on the scale values, remaining feature points
are divided into three categories: 𝐶

=
{
𝑃

|
𝛾

≤
𝑚

𝜎<𝛾

}
, 𝐶

=
{
𝑃

|
𝛾

≤𝑚

𝜎<𝛾

}
, 𝐶

=
{
𝑃

|
𝑚

𝜎≥𝛾

}
, where 𝛾

denotes the scale value of
the second DoG image in the i-th octave. Note that 𝐶

contains the first octave, 𝐶

contains the second
octave, and 𝐶

contains the other octaves. Feature
point matching schemes are performed separately on
𝐶

,𝐶

, and 𝐶

.
Because any feature point 𝑃

and its matching
feature point 𝑃

have similiar pixel values, feature
points in cluster 𝐶

, 𝑖=1,2,3, can divided into several
overlapped ranges by pixel (gray) values. In this study,
the range [0, 1, …, 255] of pixel (gray) values is
split into 𝑈 overlapped ranges,
Image Copy-Move Forgery Detection using Color Features and Hierarchical Feature Point Matching
155

𝑈=
255 − 𝑐

𝑐

−𝑐

+1,
(11)
where 𝑐

denotes a range size and 𝑐

denotes an
overlapped size (𝑐

>𝑐

). Let
𝐶
,
=
{
𝑃

|
𝑎

≤𝐺

(
𝑃

)
<𝑏

,𝑃

∈𝐶

}
,
𝑗
=1,2,…,𝑈,
(12)
𝑎

=
(
𝑗
−1
)
×
(
𝑐

−𝑐

)
,
(13)
𝑏

=𝑚𝑖𝑛(𝑎

+𝑐

, 255),
(14)
where 𝐺

(𝑃

) denotes the average gray value of 9
pixels in a 3×3 region centered at 𝑃

. Then, feature
point matching schemes are performed separately in
𝐶
,
, 𝑖=1,2,3, 𝑗=1,2,…,𝑈. Let
𝑄=

𝑄
,
, 𝑖∈
{
1, 2,3
}
,
𝑗
=1, 2, …,𝑈, (15)
where 𝑄
,
denotes the set containing the matched
feature point pairs of 𝐶
,
.
2.4 Iterative Forgery Localization and
Post-processing
For feature point-based copy-move forgery detection,
we face two problems. First, when multiple
replications are performed, the homography is usually
not unique and the number of repeated areas is
uncertain. Second, all matched feature point pairs
usually have no matching orders, and the original and
forged points are usually not distinguished by feature
point matching. In this study, a modified version of
iterative localization (Li and Zhou, 2019) without
segmentation and clustering processes is employed,
which contains four steps: elimination of isolated
matched feature point pairs, estimation of local
homography, homography verification and inlier
selection, and forgery localization using color
information and scale.
Because copy-move forgery is usually performed
in a continuous shape, isolated matched feature point
pairs can be detected. For each matched feature point
pair
(
𝑃

,𝑃


)
∈𝑄, if 𝑁

and 𝑁


denote the numbers
of neighboring matched feature points for 𝑃

and 𝑃


with distances being smaller than a threshold 𝑍

(here,
𝑍

=100), the matched feature point pair
(
𝑃

,𝑃


)
will be discarded if max
{
𝑁

,𝑁


}
<2. If ℳ denotes
the set containing the remaining matched feature point
pairs ∈𝑄, in this study, a portion of matched pairs for
two consecutive local regions will be used to appraise
an affine matrix. First, a matched feature point pair
(
𝑃

,𝑃


)
∈ℳ is randomly selected, then all the
neighboring matched feature points closed to 𝑃

and
𝑃


are recorded as 𝐸

and 𝐸


, respectively, i.e.,
𝐸

=𝑃

∀𝑃

∈
ℳ
,𝐸𝐷𝑃

,𝑃

<𝑍

,
(16)
𝐸


=𝑃

∀𝑃

∈
ℳ
,𝐸𝐷𝑃

,𝑃


<𝑍

,
(17)
where 𝑍

denotes a hyper-parameter (𝑍

=100) and
𝐸𝐷(∙) returns the Euclidean distance. Let ℳ

denote
the set containing all the matched feature point pairs
close to
(
𝑃

,𝑃


)
∈ℳ. Then, RANSAC algorithm
(Gonzalez and Woods, 2018) is employed to estimate
homography 𝐻

between the correspondences of
matched feature point pairs in ℳ

.
To delete incorrect homography estimations, a
homography verification and inlier selection approach
using guiding direction 𝜃

obtained in SIFT feature
point extraction is employed. The guiding direction
difference 𝜃


−𝜃

should be consistent with the
estimated affine homography 𝐻

for each proper
matched feature point pair
(
𝑃

,𝑃


)
. The matched
feature point pair
(
𝑃

,𝑃


)
should be discarded, if
𝑔
(
𝑃

,𝑃


,𝐻

)
=
|
𝜃


−𝜃

−𝜃

|
≤𝑍

,
(18)
where 𝜃

is the estimated rotation calculated from 𝐻

and 𝑍

denotes a threshold (here, 𝑍

=15). Let ℳ


denotes the set containing the remaining matched
feature point pairs in ℳ

after RANSAC homography
verification. A matched feature point pair 𝑃

(
𝑥

,𝑦

)
and 𝑃


(
𝑥


,𝑦


)
, will be related by

𝑥


𝑦


1
≈𝐻


𝑥

𝑦

1
.
(19)
Using guiding information, set ℳ

is defined as
ℳ

=
{
〈
𝑃

,𝑃


〉|‖
𝐻

𝑃

−𝑃


‖


<𝜖,𝑔
(
𝑃

,𝑃


,𝐻

)
≤𝑍

}
.
(20)
The improved homography 𝐻


is defined as
𝐻


=argmin



𝐻


𝑃

−𝑃





〈


,


〉
.
(21)
In this study, a dense field forgery location
algorithm (Li and Zhou, 2019) is employed. For each
feature point in ℳ

, local circular dubious field is
defined as
𝑟

=𝜏𝜎

,
(22)
where 𝜏 denotes a paremeter (here, 𝜏=16). Two
dubious regions 𝑆 and 𝑆

are established for matched
feature point pairs in ℳ

. Dubious regions are refined
IMPROVE 2021 - International Conference on Image Processing and Vision Engineering
156

by color information, and each feature point in 𝑆 is
defined as
𝑃
∗
=𝐻


𝑃

,𝑃

∈𝑆.
(23)
In Equation (23), if the color vectors of 𝑃

and 𝑃
∗
are close, they might be copy-move feature points, i.e.,
𝑃

is the original feature point and 𝑃
∗
is a copy-move
forgery feature point. Let 𝒬

be the set containing all
the matched feature points in 𝑆, i.e.,
𝒬

={𝑃

,𝑃
∗
|
max(|𝑅
(
𝑃

)
−𝑅
(
𝑃
∗
)







|,
𝐺
(
𝑃

)
−𝐺
(
𝑃
∗
)







,𝐵
(
𝑃

)
−𝐵
(
𝑃
∗
)







)<𝑍

},
𝑃

∈𝑆,
(24)
𝑊
(
𝑃
∗
)








=𝑊(𝑃

)/𝑉


∈𝜴(

)
, 𝑊∈
{
𝑅,𝐺,𝐵
}
,
(25)
where 𝑅(𝑃

), 𝐺
(
𝑃

)
, and 𝐵(𝑃

) denote the RGB
values of feature point 𝑃

,𝑉 denotes a normalization
factor, Ω(𝑃

) denotes a 3×3 patch centered at 𝑃

,
and 𝑍

denotes a parameter (here, 𝑍

=10).
On the other hand, each point in 𝑆

is defined as
𝑃
∗

=𝐻



𝑃


,𝑃


∈𝑆

.
(26)
Similarly, let 𝒬

be the set containing all the
matched feature points in 𝑆

. If a feature point
belonging to 𝒬

∪𝒬

, this feature point will be
marked as forgery feature point 𝐴

(𝑥,𝑦). The
above procedure is iterated (here, 15 iterations) to find
all the forgery feature points. Then, all the forgery
feature points are grouped as forgery regions. To make
forgery regions more accurately, morphological close
operator is used to obtain the final forgery regions
𝐴

(𝑥,𝑦) in the image.
3 EXPERIMENTAL RESULTS
The proposed approach has been implemented on an
Intel Core i7-7700K 4.20 GHz CPU with 32GB main
memory for Windows 10 64-bit platform using
MATLAB 9.4 (R2018a). To evaluate the
effectiveness of the comparison and proposed
approaches, FAU dataset (Christlein, et al., 2012) and
CMH1 dataset (Silva, et al., 2015) are employed. FAU
dataset consists of 48 high-resolution uncompressed
PNG color images, whereas CMH1 consists of 23
copy-move forged images.
In this study, based on the final detected forgery
region map and the ground truth map 𝐺𝑇, 𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛
and 𝑟𝑒𝑐𝑎𝑙𝑙 are employed as two performance metrics.
Additionally, based on 𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 and 𝑟𝑒𝑐𝑎𝑙𝑙, 𝑓

score computed as
𝑓

=2×
𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 × 𝑟𝑒𝑐𝑎𝑙𝑙
𝑝
𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 + 𝑟𝑒𝑐𝑎𝑙𝑙
, (27)
is employed as the third performance metric.
To evaluate the performance of the proposed
approach, three comparison approaches, namely,
Amerini, et al. (2013), Pun, et al. (2015), and Li, et al.
(2019) are employed. The final detected forgery
region maps of three comparison approaches and the
proposed approach for two images of FAU dataset are
shown in Figures 4 and 5. In terms of average
𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛, 𝑟𝑒𝑐𝑎𝑙𝑙, and 𝑓

score, performance
comparisons of the three comparison approaches and
the proposed approach for FAU and CMH1 datasets
are listed in Tables 1 and 2, respectively.
Table 1: In terms of average 𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛, 𝑟𝑒𝑐𝑎𝑙𝑙, and 𝑓
1
score, performance comparisons of three comparison
approaches and the proposed approach on FAU dataset.
Approaches
𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 𝑟𝑒𝑐𝑎𝑙𝑙
𝑓

score
Amerini, et al.
(2013)
0.359 0.887 0.455
Pun, et al.
(
2015
)
0.966 0.655 0.753
Li, et al.
(
2019
)
0.921 0.773 0.842
Pro
p
ose
d
0.938 0.815 0.859
Table 2: In terms of 𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛, 𝑟𝑒𝑐𝑎𝑙𝑙, and 𝑓
1
score,
performance comparisons of three comparison approaches
and the proposed approach on CMH1 dataset.
Approaches
𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 𝑟𝑒𝑐𝑎𝑙𝑙
𝑓

score
Amerini, et al.
(2013)
0.942 0.935 0.940
Pun, et al. (2015) 0.929 0.920 0.924
Li, et al.
(
2019
)
0.985 0.960 0.972
Pro
p
ose
d
0.978 0.972 0.975
Based on the experimental results listed in Tables
1 and 2, the proposed approach has good balances
between precision and recall as well as larger 𝑓

scores, as compared with three comparison
approaches. Based on the experimental results shown
in Figures 4 and 5, the final detected forgery region
maps of the proposed approach are better than those
of three comparison approaches.
Image Copy-Move Forgery Detection using Color Features and Hierarchical Feature Point Matching
157

(
a
)
(
b
)
(
c
)
(
d
)
(e) (f)
Figure 4: Final detected forgery region maps of
“red_tower_copy” in FAU dataset: (a) original image; (b)
ground truth, (c)-(f) the detected forgery region maps by
Amerini, et al.’s approach (2013), Pun, et al.’s approach
(2015), Li, et al.’s approach (2019), and the proposed
approach.
(
a
)
(
b
)
(
c
)
(
d
)
(e) (f)
Figure 5: Final detected forgery region maps of
“noise_pattern_copy” in FAU dataset: (a) original image;
(b) ground truth, (c)-(f) the detected forgery region maps by
Amerini, et al.’s approach (2013), Pun, et al.’s approach
(2015), Li, et al.’s approach (2019), and the proposed
approach.
4 CONCLUDING REMARKS
In this study, an image copy-move forgery detection
approach using color features and hierarchical feature
point matching is proposed. Based on the
experimental results obtained in this study, the
performance of the proposed approach is better than
those of three comparison approaches.
ACKNOWLEDGMENTS
This work was supported in part by Ministry of
Science and Technology, Taiwan, ROC under Grants
MOST 108-2221-E-194-049 and MOST 109-2221-E-
194-042.
REFERENCES
Amerini, I., Ballan, L., Caldelli, R., Del Bimbo, A., and
Serra, G., 2011. A SIFT-based forensic method for
copy-move attack detection and transformation
recovery. In IEEE Trans. on Information Forensics and
Security, 6(3), 1099-1110.
Amerini, I., et al., 2013. Copy-move forgery detection and
localization by means of robust clustering with J-
linkage. Signal Processing: Image Communication,
28(6), 659-669.
Bi, X., Pun, C. M., and Yuan, X. C., 2016. Multi-level dense
descriptor and hierarchical feature matching for copy-
move forgery detection. Information Sciences, 345, 226-
242.
Chen, H., Yang, X., and Lyu, Y., 2020. Copy-move forgery
detection based on keypoints clustering and similar
neighborhood search algorithm. IEEE Access, 8, 36863-
36875.
Christlein, V., et al., 2012. An evaluation of popular copy-
move forgery detection approaches. IEEE Trans. on
Information Forensics and Security, 7(6), 1841-1854.
Cozzolino, D., Poggi, G., and Verdoliva, L., 2015. Efficient
dense-field copy–move forgery detection. IEEE Trans.
on Information Forensics and Security, 10(11), 2284-
2297.
Fadl, S. M. and Semary, N. A., 2017. Robust copy-move
forgery revealing in digital images using polar
coordinate system. Neurocomputing, 265, 57-65.
Gonzalez, R. C. and Woods, R. E., 2018. In Digital Image
Processing, Prentice Hall. Upper Saddle River, NJ, 4
th
edition.
Huang, H. Y. and Ciou, A. J., 2019. Copy-move forgery
detection for image forensics using the superpixel
segmentation and the Helmert transformation.
EURASIP Journal on Image and Video Processing, 1,
1-16.
Islam, A., Long, C., Basharat, A., and Hoogs, A., 2020.
DOA-GAN: dual-order attentive generative adversarial
IMPROVE 2021 - International Conference on Image Processing and Vision Engineering
158

network for image copy-move forgery detection and
localization. In IEEE/CVF Conf. on Computer Vision
and Pattern Recognition (CVPR), 4675-4684.
Jin, G. and Wan, X., 2017. An improved method for SIFT-
based copy move forgery detection using non-maximum
value suppression and optimized J-linkage. Signal
Processing: Image Communication, 57, 113-125.
Li, Y. and Zhou, J., 2019. Fast and effective image copy-
move forgery detection via hierarchical feature point
matching. IEEE Trans. on Information Forensics and
Security, 14(5), 1307-1322.
Lin, X., et al., 2016. SIFT keypoint removal and injection
via convex relaxation. IEEE Trans. on Information
Forensics and Security, 11(8), 1722-1735.
Lowe, D. G., 2004. Distinctive image features from scale-
invariant keypoints. Int. Journal of Computer Vision,
60(2), 91-110.
Pun, C., Yuan, X., and Bi, X., 2015. Image forgery detection
using adaptive oversegmentation and feature point
matching. IEEE Trans. on Information Forensics and
Security, 10(8), 1705-1716.
Silva, E., et al., 2015. Going deeper into copy move forgery
detection: exploring image telltales via multi-scale
analysis and voting processes. Journal of Visual
Communication and Image Representation, 29, 16-32.
Warif, N. B. A., et al., 2017. SIFT-symmetry: a robust
detection method for copy-move forgery with reflection
attack. Journal of Visual Communication and Image
Representation, 46, 219-232.
Zhong, J. L. and Pun, C. M., 2020. An end-to-end Dense-
InceptionNet for image copy-move forgery detection.
IEEE Trans. on Information Forensics and Security, 15,
2134-2146.
Zhu, Y., et al., 2020. AR-Net: adaptive attention and
residual refinement network for copy-move forgery
detection. IEEE Trans. on Industrial Informatics,
16(10), 6714-6723.
Image Copy-Move Forgery Detection using Color Features and Hierarchical Feature Point Matching
159