
A Study of Higher Order Volume Scattering in a Layer of Discrete
Random Scatterers
Muhamad Jalaluddin Jamri
a
, Syabeela Syahali
b
and Dina Naqiba Nur Ezzaty Abd Wahid
c
Faculty of Engineering and Technology, Multimedia University, Melaka, Malaysia
Keywords: Remote Sensing, Volume Scattering, Backscattering Coefficient, Discrete Random Scatterers, Radiative
Transfer Equation.
Abstract: Remote sensing has been widely used as an earth observation technique to study the polar region. Volume
scattering process is one of the scattering processes that occur in a layer of discrete random scatterers in
remote sensing. In certain layer, volume scattering is significant and important to determine the value of
backscattering coefficient. Previous study modelled the volume scattering only for first and second order. In
this paper, a third order volume backscattering coefficient formulation is derived and added into the theoretical
modelling of volume scattering, and its backscattering coefficient is analysed for different types of layer
configuration embedded with discrete random scatterers. The condition of which the third order volume
scattering may be important is studied. Results show that, third order volume scattering activity is significant
when the scatterers in the layer are larger and with higher permittivity in both lower and higher incident angles,
for all the frequency range studied.
1 INTRODUCTION
In recent years, there has been a lot of interest in the
use of microwave remote sensing (Boerner, Mott, &
Luneburg, 1997;Guo, Jia, & Paull, 2017;Xiong &
Shi, 2017) for a layer of discrete random scatterers
such as sea ice (Syahali & Ewe, 2013), snow (Syahali
& Ewe, 2016) and oil palm (Toh, Ewe, Tey, & Tay,
2019). It is interesting and important to model and
calculate the interaction of the electromagnetic wave
with the medium, as the backscattering returns from
the medium will be recorded and processed. Hence, it
is important to model the scattering process as
accurately as possible, and reliable to be used in
certain conditions. In modelling the scattering process
in an electrically dense medium where the average
separation between the scatterer is comparable to the
wavelength (Ewe & Chuah, 1998a), there are three
types of scattering involved, which are surface
scattering, surface-volume scattering and volume
scattering (Syahali & Ewe, 2013, 2016). For volume
scattering, the scattering terms included to calculate
the backscattering coefficient was up to the second
a
https://orcid.org/0000-0003-2273-3232
b
https://orcid.org/0000-0002-6847-8591
c
https://orcid.org/0000-0002-6982-8549
order volume backscattering (Ewe, Chuah, & Fung,
1998b), which limits the scatterers involved in the
mechanism to only two scatterers. However, for
certain medium where volume scattering activity may
be dominating, higher order volume scattering may
be significant, therefore, more term needs to be
derived and added in the formulation.
Radiative transfer theory (Chandrasekhar, 1960;
Tsang, Kubacsi, & Kong, 1981) had been identified
as the form of electromagnetic radiation between
medium. Therefore, theoretical model for an
electrically dense medium based on the radiative
transfer theory was developed to calculate and study
the scattering mechanisms. The dense medium was
constructed as a layer randomly embedded with
distributed spherical scatterers in a homogenous
medium and based on (Mao-yan, Jun, Jian, & Hai-
long, 2007) the spherical scatterer is modelled as a
Mie scatterer. The parameters such as frequency,
scatterer radius, permittivity of the scatterer and
incident angle are some of the factors that determine
the volume backscattering from these scatterers.
Jamri, M., Syahali, S. and Wahid, D.
A Study of Higher Order Volume Scattering in a Layer of Discrete Random Scatterers.
DOI: 10.5220/0010494101770183
In Proceedings of the 7th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2021), pages 177-183
ISBN: 978-989-758-503-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
177

In this paper, a third order volume backscattering
coefficient formulation is derived from the Radiative
Transfer Theory equation by using the iterative
method (Tsang et al, 1981;Karam, Fung, Lang, &
Chauhan, 1992) and inspection of its backscattering
coefficient is done for layers with different scatterer
permittivity and size, and using different frequency
and incident angle of the wave. The performance of
backscattering coefficient mainly depends on these
parameters and the condition of which the third order
volume scattering is significant and may contribute to
the total backscattering coefficient values are
analysed and discussed before the research is
concluded. This research is important to determine
the condition which the higher order volume
scattering may be important and should be included
in theoretical modelling, as reference for researchers
working in this area.
2 METHODOLOGY
2.1 Model Configuration
Figure 1 shows a cross section of the layer used in
theoretical modelling (Ewe & Chuah, 1997). The layer
is modelled as a discretely inhomogeneous medium of
depth d (in m), in which randomly distributed spherical
scatterers are embedded in a homogenous medium.
This layer is bounded on top and bottom by irregular
surface boundaries. Above the layer is air, and below
is a homogeneous half space.
Figure 1: Cross section of the layer.
The Radiative Transfer Equation from
(Chandrasekhar, 1960) characterizes the propagation
and scattering of specific intensity inside a medium
and is given by
d IP IK
dz
Id
cos
e
(1)
where
is the Stokes vector,
e
K
is the extinction
matrix, and
P
is the phase matrix of the medium
(Tsang, Kong, & Shin, 1985).
The phase matrix
P
is associated with the first
two Stokes’ parameters of the scatterers and is given
in (2).
'
and
'
in this equation are the polar and
azimuth angle before scattering, while
and
are
the polar and azimuth angle after scattering.
n
2
||
is the Dense Medium Phase Correction Factor
(Chuah, Tjuatja, Fung, & Bredow, 1996) and
S
is the
Stokes’ matrix for Mie scatterers with close spacing
amplitude correction (Fung & Eom, 1985).
n
2
||
is the correction factor that needs to be included into
the phase matrix to take into account the coherent
effect of the scattering of the closely spaced scatterers
in an electrically dense medium.
hhhv
vhvv
n
PP
PP
SP
2
||)',';,(
(2)
In (Ewe et al, 1998b), this radiative transfer
equation was solved up to second order solutions.
Zeroth order solutions characterize the scattering
process without any scatterer involved whereas first
and second order solutions characterize the scattering
process involving one and two scatterers. Through
this iterative solution, many scattering terms were
derived and calculated. The scattered intensity I is
related with the backscattering coefficient, by this
formula
iq
sps
pq
I
I
cos4
(3)
2.2 Theoretical Modelling
After solving (1) iteratively, the third order solution
is given by
,,0(),,(),(
),,0(
2
)(sec
212
3
SedSR
I
dK
e
(4)
where I
3
+
is the upward intensity, R the reflectivity
matrix, d the depth of the layer, K
e
the volume
extinction coefficient, and S
2
-
and S
2
+
are the
downward and upward scattered intensities.
The second term of (4) describes upward scattered
intensity from the third scatterer. One of the scattering
GISTAM 2021 - 7th International Conference on Geographical Information Systems Theory, Applications and Management
178

mechanisms which can be derived from this term is
illustrated in Figure 2, where the incident intensity is
being transmitted from outer layer to inner layer of
the medium through the upper boundary and hits the
first scatterer. Then, the scattered downward intensity
hits the second scatterer and scattered upward before
hitting the third scatterer. Finally, it is scattered into
upward direction of angle
s1
.
In this study, the derived volume backscattering
term from the third order solution depicted in Figure
2 is shown in (5) through (6) and describes the
intensity being scattered by three scatterers. The
arguments in the left hand side of the equation
describes the upward and downward directions of the
intensity throughout the scattering process, starting
from the right to left.
i
iisspqs
pq
I
I
downdownupup
),;,(cos4
),,,(
3
3
(5)
)secsec)(sec(
)()(
)sec)(sec(
)(1
sec''secsec
)()()(
);,(
),;,(),;,(
sinsecsinsec
sec)()(cos4
'
1
'
1
'
1
'
1
'
1
'
1
''
1,1
''''
1
''''''
2
''
11
,,
3
2
0
2
0
2
0
2
0
''''''''''''
1,1101,01
etsepet
spt
sepet
sp
eteuieq
tiqu
ii
ss
hvthvu
siisss
KKK
LL
KK
L
KKK
LLL
P
PP
dddd
TT
(6)
where
s1
and
i1
are the scattered angle and
incident angle, respectively, in the random layer
through the Snell’s Law while
s
and
i
are the
angles outside the layer.
''
and
'
are the scattered
angles in the layer during the scattering processes
with the scatterer. p and q are the scattered
polarization and incident polarization, respectively
Figure 2: Scattering mechanisms from the term of Equation
6.
while u and t are the polarization during the scattering
processes in the layer.
I
i
is the incident intensity while T
10
and T
01
are the
transmittivity from top boundary into the layer, and
from layer into the top boundary, respectively. P is
the phase matrix of the medium, and K
e
is the volume
extinction coefficient. L with positive and negative
superscripts describe the attenuation of upward and
downward intensities, respectively, and is given by
dK
u
eu
eL
sec
)(
(7)
After all, only
),,0(
2
S
from (4) is taken into
account due to the dominant impact for volume
scattering process.
3 RESULT AND DISCUSSION
Theoretical analysis is done by applying the third
order volume backscattered coefficient solution to a
layer of discrete random scatterers. Based on (Fung &
Eom, 1985) and (Chuah, Tjuatja, Fung, & Bredow,
1997), any layer containing spherical scatterers
treated as an inhomogeneous medium. In performing
the third order volume backscattering calculation,
volume backscattering terms is calculated by the
model simulation written in FORTRAN software.
This is useful to examine in detail each backscattering
mechanism in the media. The model is programmed
to allow the inputs of various physical parameters so
that it gives flexibility in simulating the model for
different parameters, such as frequency, permittivity
of the scatterers, incident angle of the wave and
scatterer radius.
The input parameters used are based on (Syahali
& Ewe, 2016) and listed in Table 1. The third order
volume scattering is calculated for different
polarization and different input parameters, over a
range of frequency from 4 GHz to 14 GHz. The effect
A Study of Higher Order Volume Scattering in a Layer of Discrete Random Scatterers
179
of permittivity, incident angle and scatterer radius on
the contribution of third order volume scattering is
investigated. This is done by varying the permittivity,
incident angle and scatterer radius of the
inhomogeneous medium.
Table 1: Model parameters used in theoretical analysis.
Parameter Estimated Values
Incident angle 10°
Scatterer Radius/mm 0.5
Volume fraction/% 30
Effective relative
permittivity of top layer
(1.0, 0.0)
Relative permittivity of
sphere
(2, 0.001)
Background relative
permittivity
(1.0, 0.0)
Lower half-space
permittivity
(5.0, 0.0)
Thickness of layer/m 0.5
Top surface rms height
and correlation
length/cm
0.14, 0.7
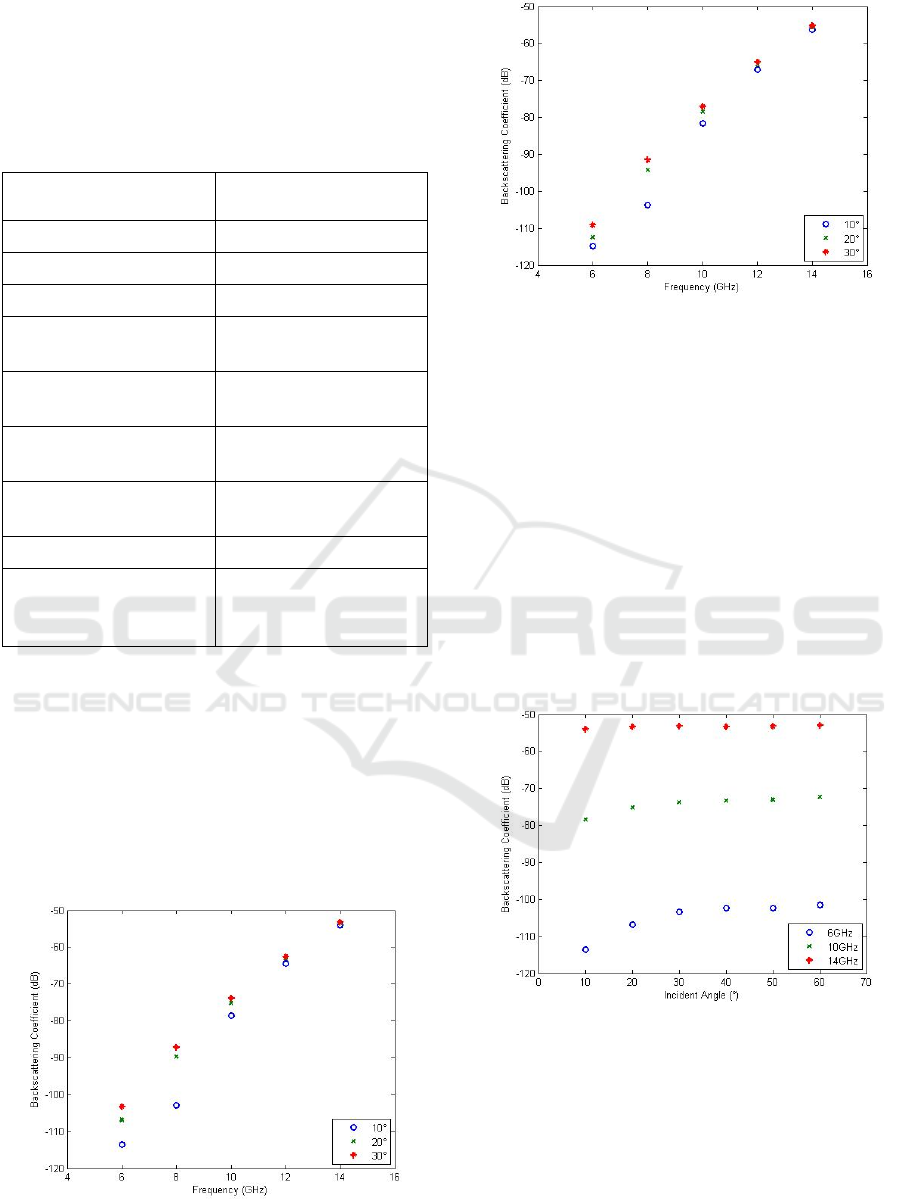
To investigate the effect for different incident
angles, the incident angle is first varied from 10° to
20° and 30°. The third order volume backscattering
return is observed against frequency for co-polarized
(VV) and cross polarized (VH) wave return. The
pattern shows that the third order volume
backscattering coefficient is increasing along with the
frequency. This is because the albedo increases as
frequency increases (Fung, 1994;Fung & Chen,
2010).
Figure 3: Third order volume scattering coefficient (VV
polarization) against frequency for various incident angle.
Figure 4: Third order volume scattering coefficient (VH
polarization) against frequency for various incident angle.
It can also be seen that the third order volume
backscattering coefficient increases when the
incident angle is increased. To study this effect in
more detail, Figure 5 shows the plot of third order
volume backscattering coefficient (VV polarization)
against incident angle for various frequency. It can be
observed that the increment of the backscattering
coefficient with incident angle mainly occurs at low
frequency. The reason may be due to longer
wavelength responding more with change in incident
angles because of its ability to penetrate deeper into
the layer. This suggests that higher order volume
scattering is more significant when the wave used is
of higher frequency.
Figure 5: Third order volume scattering coefficient (VV
polarization) against incident angle for various frequency.
Next, for permittivity of the scatterer, the real part
is varied from 2 to 3 and 4 while the imaginary part
remains constant. Then, the third order volume
backscattering return for each input permittivity is
plotted for co-polarized (VV) and cross polarized
(VH) return over the frequency of 4 GHz to 14 GHz
in Figure 6 and 7. For co-polarized (VV) and cross
GISTAM 2021 - 7th International Conference on Geographical Information Systems Theory, Applications and Management
180
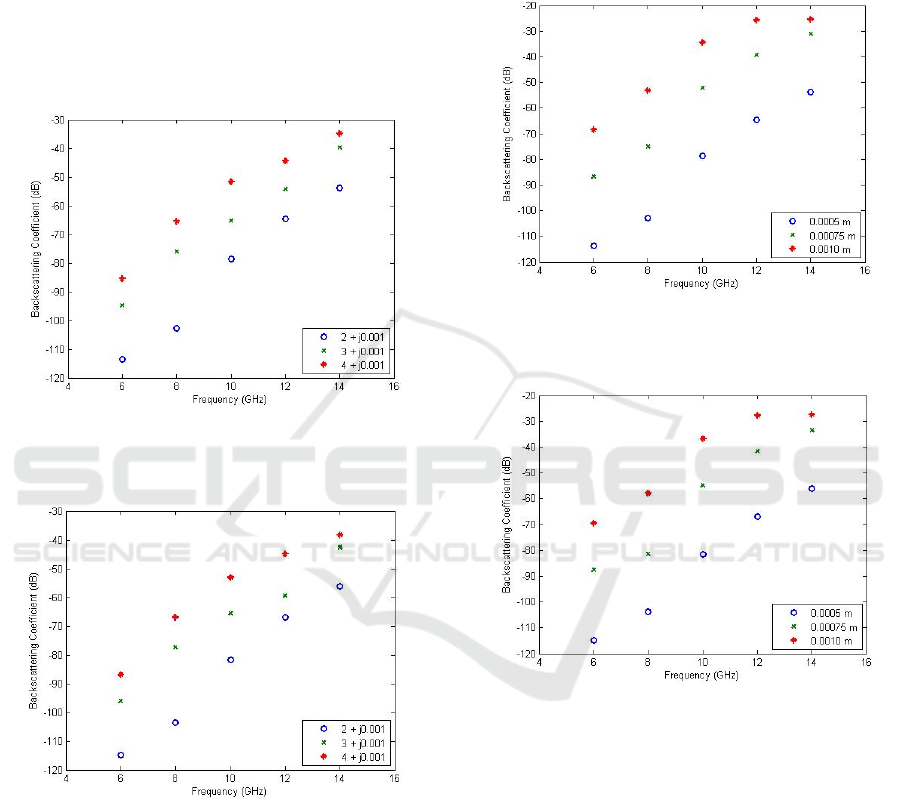
polarized (VH) return, the pattern shows that third
order volume backscattering coefficient is increasing
along with the frequency for all the permittivity
values used. It can also be seen that the third order
volume backscattering coefficient increases when the
permittivity is increased in this range of frequency.
Higher permittivity increases the visibility of the
scatterers in the medium and this may have increased
the volume scattering activity. This shows that the
third order volume scattering is significant in the area
where the scatterers have high permittivity values.
Figure 6: Third order volume scattering coefficient (VV
polarization) against frequency for various permittivity of
scatterers.
Figure 7: Third order volume scattering coefficient (VH
polarization) against frequency for various permittivity of
scatterers.
In Figure 8 and 9, variation of the size of the
discrete random scatterers is shown for co-polarized
(VV) and cross polarized (VH), where the value for
the radius is varied from 0.5 mm to 0.75 mm and 1.0
mm for backscattering return over frequency 4 GHz
to 14 GHz. Results show that larger particles cause
greater backscattering return in like and cross
polarization. As with the permittivity, the improved
scatterer’s visibility due to larger size may have
improved the third order volume backscattering
coefficient, suggesting the importance of higher order
volume scattering in the medium filled with large
scatterers. It can also be seen for both polarized return
that the third order volume backscattering is increasing
with frequency for all the scatterer radius used.
Figure 8: Third order volume scattering coefficient (VV
polarization) against frequency for various radius of
scatterers.
Figure 9: Third order volume scattering coefficient (VH
polarization) against frequency for various radius of
scatterers.
Lastly, to further analyse the contribution of
higher order volume scattering, analysis is done on
the backscattering coefficient of different orders of
volume scattering in a larger frequency range. Figure
10 shows the plot of volume backscattering
coefficient (VV polarization) against frequency for
first, second and third order volume scattering. It
shows that after 15 GHz, volume scattering is
dominated by first and second order scattering.
Therefore, higher order volume scattering is not
significant at this frequency range, to determine the
value of backscattering coefficient, because the third
order backscattering coefficient started to disappear
at high frequency.
A Study of Higher Order Volume Scattering in a Layer of Discrete Random Scatterers
181
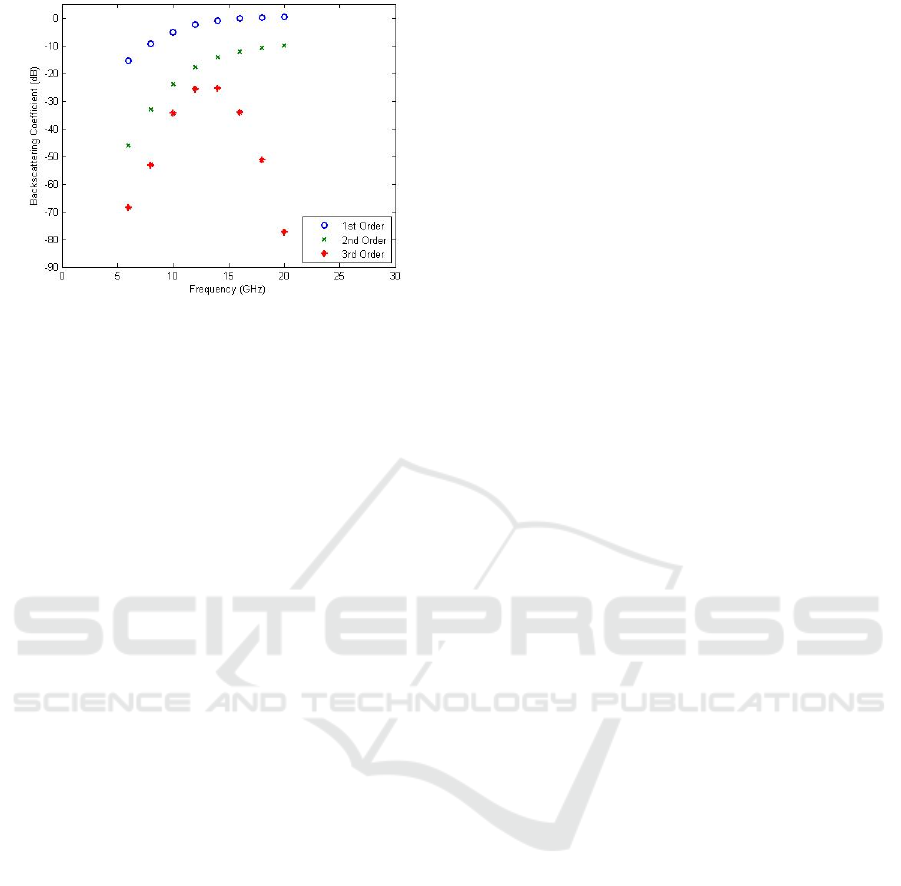
Figure 10: Volume scattering coefficient (VV polarization)
against frequency for different order backscattering
coefficient.
4 CONCLUSIONS
In this paper, third order volume scattering is derived
and presented. Theoretical analysis shows that there
is an increase in the pattern of the third order volume
backscattering coefficient as the frequency of the
wave used gets higher, and when the radius and
permittivity of scatterers in the layer are larger. This
suggests that higher order volume scattering is
significant and should be considered in developing
theoretical modelling in these areas. However, further
study in higher frequency range shows that after 15
GHz, volume scattering is dominated by first and
second order volume scattering, indicating that higher
order volume scattering is no more significant at very
high frequency range. In future, this model may be
further improved by considering more third order
volume scattering terms and by incorporating
numerical solution model in the phase matrix
calculation (Lum, Ewe, & Jiang, 2015;Lum, Fu, Ewe,
Jiang, & Chuah, 2017a;Lum, Fu, Ewe, & Jiang,
2017b;Syahali, Ewe, Vetharatnam, Jiang, &
Kumaresan, 2020).
REFERENCES
Boerner, W. , Mott, H., & Luneburg, E. (1997). Polarimetry
in remote sensing: basic and applied concepts.
IGARSS'97. 1997 IEEE International Geoscience and
Remote Sensing Symposium Proceedings. Remote
Sensing - A Scientific Vision for Sustainable
Development, 3, pp. 1401-1403 vol.3.
Chandrasekhar, S. (1950). 1960, Radiative Transfer. Dever,
New York.
Chuah, H. T., Tjuatja, S., Fung, A. K., & Bredow, J. W.
(1996). A phase matrix for a dense discrete random
medium: Evaluation of volume scattering coefficient.
IEEE Transactions on Geoscience and Remote Sensing,
34(5), 1137-1143.
Chuah, H. T., Tjuatja, S., Fung, A. K., & Bredow, J. W.
(1997). Radar backscatter from a dense discrete random
medium. IEEE transactions on geoscience and remote
sensing, 35(4), 892-900.
Ewe, H. T., & Chuah, H. T. (1997, August). A study of
dense medium effect using a simple backscattering
model. In IGARSS'97. 1997 IEEE International
Geoscience and Remote Sensing Symposium
Proceedings. Remote Sensing-A Scientific Vision for
Sustainable Development (Vol. 3, pp. 1427-1429).
IEEE.
Ewe, H. T., & Chuah, H. T. (1998a, July). An analysis of
the scattering of discrete scatterers in an electrically
dense medium. In IGARSS'98. Sensing and Managing
the Environment. 1998 IEEE International Geoscience
and Remote Sensing. Symposium Proceedings.(Cat. No.
98CH36174) (Vol. 5, pp. 2378-2380). IEEE.
Ewe, H. T., Chuah, H. T., & Fung, A. K. (1998b). A
backscatter model for a dense discrete medium:
Analysis and numerical results. Remote Sensing of
Environment, 65(2), 195-203.
Fu, X., Jiang, L. J., & Ewe, H. T. (2016). A novel relaxed
hierarchical equivalent source algorithm (RHESA) for
electromagnetic scattering analysis of dielectric
objects. Journal of Electromagnetic Waves and
Applications, 30(12), 1631-1642.
Fung, A. K. (1994). Microwave scattering and emission
models and their applications. Norwood, MA: Artech
House, 1994.
Fung, A. K., & Eom, H. J. (1985). A study of backscattering
and emission from closely packed inhomogeneous
media. IEEE transactions on geoscience and remote
sensing, (5), 761-767.
Fung, A. K. & Chen, K. S. (2010). Microwave scattering
and emission models for users. Artech house.
Guo, Y., Jia, X., & Paull, D. (2017). Sequential classifier
training for rice mapping with multitemporal remote
sensing imagery. ISPRS Annals of the Photogrammetry,
Remote Sensing and Spatial Information Sciences, 4,
161.
Karam, M. A., Fung, A. K., Lang, R. H., & Chauhan, N. S.
(1992). A microwave scattering model for layered
vegetation. IEEE Transactions on Geoscience and
Remote Sensing
, 30(4), 767-784.
Lum, C. F., Ewe, H. T., Xin, F., Jiang, L. J., & Chuah, H.
T. (2017a, July). An analysis of scattering from snow
with relaxed hierachical equivalent source algorithm. In
2017 IEEE International Geoscience and Remote
Sensing Symposium (IGARSS) (pp. 1434-1437). IEEE.
Lum, C. F., Ewe, H. T., & Jiang, L. J. (2015, December). A
study of single scattering of scatterer at various
orientation angles with equivalence principle
algorithm. In 2015 10th International Conference on
Information, Communications and Signal Processing
(ICICS) (pp. 1-4). IEEE.
GISTAM 2021 - 7th International Conference on Geographical Information Systems Theory, Applications and Management
182

Lum, C. F., Fu, X., Ewe, H. T., & Jiang, L. J. (2017b). A
study of scattering from snow embedded with non-
spherical shapes of scatterers with Relaxed Hierarchical
Equivalent Source Algorithm (RHESA). Progress In
Electromagnetics Research, 61, 51-60.
Mao-yan, W., Jun, X., Jian, W., & Hai-long, L. (2007,
October). Mie Series Study on Electromagnetic
Scattering of Metallic Sphere Covered by Double-
negative Metamaterials. In 2007 International
Symposium on Electromagnetic Compatibility (pp. 482-
485). IEEE.
Syahali, S., & Ewe, H. T. (2013). Remote sensing
backscattering model for sea ice: Theoretical modelling
and analysis. Advances in Polar Science, 24(4), 258-
264.
Syahali, S., & Ewe, H. T. (2016). Backscattering analysis
for snow remote sensing model with higher order of
surface-volume scattering. Progress In
Electromagnetics Research, 48, 25-36.
Syahali, S., Ewe, H. T., Vetharatnam, G., Jiang, L. J., &
Kumaresan, H. A. (2020). Backscattering Analysis of
Cylinder Shaped Scatterer in Vegetation Medium:
Comparison Between Theories. Journal of Engineering
Technology and Applied Physics, 2(1), 15-18..
Toh, C. M., Ewe, H. T., Tey, S. H., & Tay, Y. H. (2019). A
study on oil palm remote sensing at l-band with dense
medium microwave backscattering model. IEEE
Transactions on Geoscience and Remote Sensing,
57(10), 8037-8047.
Tsang, L., Kong, J. A., & Shin, R. T. (1985). Theory of
microwave remote sensing(Book). Research supported
by the Schlumberger-Doll Research Center, NSF,
NASA, Navy, et al. New York, Wiley-Interscience, 1985,
627 p.
Tsang, L., Kubacsi, M. C., & Kong, J. A. (1981). Radiative
transfer theory for active remote sensing of a layer of
small ellipsoidal scatterers. Radio Science, 16(03), 321-
329.
Xiong, C., & Shi, J. (2017, July). A new snow light
scattering model and its application in snow parameter
retrieval from satellite remote sensing. In 2017 IEEE
International Geoscience and Remote Sensing
Symposium (IGARSS) (pp. 1473-1476). IEEE.
A Study of Higher Order Volume Scattering in a Layer of Discrete Random Scatterers
183
