Preventive Model-based Veriﬁcation and Repairing for SDN Requests

∗

Igor Burdonov

, Alexandre Kossachev

, Nina Yevtushenko

1,2

Jorge L

opez

3,4

, Natalia Kushik

and Djamal Zeghlache

Ivannikov Institute for System Programming of the Russian Academy of Sciences, Moscow, Russia

National Research University Higher School of Economics, Moscow, Russia

ecom SudParis, Institut Polytechnique de Paris, Palaiseau, France

Airbus Defence and Space, Issy-Les-Moulineaux, France

Keywords:

Software Deﬁned Networking, Systems Engineering, Veriﬁcation, Repairing, Graph Paths.

Abstract:

Software Deﬁned Networking (SDN) devices (e.g., switches) route trafﬁc according to the conﬁgured ﬂow

rules, and thus a set of virtual paths gets implemented in the data plane. We propose a novel preventive ap-

proach for verifying that no misconﬁgurations (e.g., inﬁnite loops), can occur given the requested set of paths.

Such veriﬁcation is essential since when conﬁguring a set of data paths, other not requested and undesired

paths (including loops) may be unintentionally conﬁgured. We show that for some cases the requested set of

paths cannot be implemented without adding such undesired behavior, i.e., only a superset of the requested

set can be implemented. We present a veriﬁcation technique for detecting such issues of potential misconﬁg-

urations and estimate the complexity of the proposed method. Finally, we propose a technique for debugging

and repairing a set of paths in such a way that the corrected set does not induce undesired paths into the data

plane, if the latter is possible.

1 INTRODUCTION

Traditional networks have currently evolved largely

due to the incorporation of software engineering ap-

proaches. One of the technologies that contributes

to this evolution is the Software Deﬁned Network-

ing (SDN) paradigm, that allows implementing var-

ious data paths employing common resources. When

using SDN technology, the network entities are man-

aged through the controller that works independently

of the network equipment and is ‘responsible’ for in-

stalling the necessary rules to the forwarding devices

(e.g., switches) (Sezer et al., 2013). As a result,

SDN provides agile controllability and observability

by separating the control and data planes. SDN is a

new technology entering novel domains (for exam-

ple, the IoT domain) (Mohammed et al., 2020) with

novel applications actively being developed. To guar-

antee the requested network is conﬁgured correctly,

SDN components and compositions need to be thor-

oughly tested and veriﬁed. For example, one can be

interested in verifying the absence of loops and packet

This work was partly supported by the Ministry of Sci-

ence and Higher Education of Russian Federation (grant

number 075-15-2020-788).

loss, or the security and access control issues. Such

data plane veriﬁcation has been largely investigated,

especially in the past decade.

Related Work. Recent works devoted to veriﬁ-

cation and testing of an SDN data plane and related

data paths can be intuitively split into several groups.

The ﬁrst group focuses on the application of for-

mal veriﬁcation and model checking approaches to

data plane veriﬁcation or forwarding devices in isola-

tion; in this case, classical networks (not necessarily

SDN) with related access control, security and other

network properties are considered. Correspondingly,

these techniques mostly differ in the underlying for-

malism utilized for describing the speciﬁed behavior

and related properties. Boolean functions and their

satisﬁability, symbolic model checking / execution

and SMT solving (Mai et al., 2011), (Canini et al.,

2012), (Dobrescu and Argyraki, 2013) as well as al-

gebra of sets (Boufkhad et al., 2016) have been con-

sidered for checking for example, reachability issues,

absence of loops, etc. The problem can also be solved

via corresponding static analysis when the network

device is implemented in the programming language

(for example, P4) (Stoenescu et al., 2018).

Approaches of the second group tend to focus on

Burdonov, I., Kossachev, A., Yevtushenko, N., López, J., Kushik, N. and Zeghlache, D.

Preventive Model-based Veriﬁcation and Repairing for SDN Requests.

DOI: 10.5220/0010494504210428

In Proceedings of the 16th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2021), pages 421-428

ISBN: 978-989-758-508-1

421

active testing of a data plane via corresponding trafﬁc

generation and monitoring of the forwarding behav-

ior of switches of interest (Zeng et al., 2012), (Fayaz

et al., 2016), (David et al., 2014). In automatic trafﬁc

generation, the packets / ﬂows to be sent through the

switches are generated at hosts in an active mode such

that speciﬁc network failures can be captured when

monitoring the data plane.

The third group of techniques relies on model

based testing. Existing model based testing tech-

niques either consider a given SDN component, such

as for example an SDN enabled switch (Yao et al.,

2014) or an SDN framework as a whole can be tested

(Berriri et al., 2018), (Yevtushenko et al., 2018).

Contribution. The existing approaches often rely

on a current network conﬁguration, i.e., the rules have

been already pushed to the switches while in this pa-

per, we propose a novel preventive model-based ap-

proach for verifying programmable network proper-

ties. Indeed, given the set of paths to be implemented

on the data plane for connecting appropriate hosts, if

this set is not consistent or can lead to potential loops

then its implementation should be avoided (the soft-

ware should not be reconﬁgured as per the request).

Let P be a set of paths which should be implemented

on the data plane for packets of a given trafﬁc type.

The set P should be ‘inspected’ before its actual im-

plementation, checking whether it is possible to pre-

cisely implement the set P on the data plane or there

will be additional (unintended) paths implemented?

In the latter case, it can happen that there are imple-

mented paths which are not edge simple and thus, a

loop for packets of a given trafﬁc type can occur. In

this paper, we show that given a trafﬁc type which

is deﬁned by the packet headers (packets with the

same trafﬁc type follow the same data paths) and a set

of (requested) paths P, the implementation of P can

induce new paths appearing on the data plane, and

moreover, if all the paths of P are edge simple (no

loops should occur) it does not guarantee the absence

of potential cycles on the data plane. We establish

the criterion for the absence of those that relies on the

property of the set P to be arc closed (Section 3). This

criterion and the preventive veriﬁcation method on its

basis form the main contributions of the paper. Ex-

perimental results built over well-known SDN com-

ponents (the Onos controller and Open vSwitches)

conﬁrm the necessity of such preventive veriﬁcation;

otherwise, in the implemented network, the packets

generated at a certain host can go into inﬁnite loops,

i.e., can simply ﬂood the network. These results can

be used when developing any SDN application or

when engineering SDN controllers, in order to im-

plement safe SDN controllers. Another contribution

of the paper is a technique for an automatic debug-

ging and repairing of a set P of paths that did not pass

the veriﬁcation in such a way, that the resulting set

of paths becomes arc closed (and thus safe to imple-

ment). For both, veriﬁcation and debugging / repair-

ing approaches, their related complexity is discussed.

This paper is a short version and thus, it omits sev-

eral fundamental and experimental details, the inter-

ested reader can refer to of (Burdonov et al., 2019).

The structure of the paper is as follows. Section

2 presents the necessary background. Section 3 dis-

cusses the possibility of inducing undesired paths on

the data plane that can cause, for example, inﬁnite cy-

cles. The proposed preventive veriﬁcation approach

for the set of paths P, together with the criterion for

the absence of undesired links and the related com-

plexity analysis is presented in Section 4. Automatic

debugging and repairing of the set of paths for which

the veriﬁcation failed, is proposed in Section 5. Sec-

tion 6 concludes the paper.

2 PRELIMINARIES

SDN is a networking paradigm that consists in sep-

arating the control and data plane layers (OpenNet-

workingFoundation, 2012); this paradigm relies in

software components: controller, forwarding devices,

and applications. With a centralized SDN controller,

SDN applications can reconﬁgure the SDN data plane

(the forwarding devices). SDN-enabled forwarding

devices steer the incoming network packets based on

so-called ﬂow rules installed (through the controller)

by the SDN applications. A ﬂow rule consists of three

main (functional) parts: a packet matching part, an

action part and a location / priority part. The match-

ing part describes the values which a received network

packet should have for a given rule to be applied. The

action part states the required operations to perform

to the matched network packets, while the location /

priority part controls the hierarchy of the rules using

tables and priorities. We focus on the resulting im-

plemented data paths (produced by the rules installed

at the forwarding devices); more precisely, we focus

on the analysis of such data paths and the potentially

unintended additional data paths resulting from a con-

ﬁguration.

The SDN resource topology (data plane) or re-

source network connectivity topology (RNCT) is rep-

resented as an undirected graph G = (V, E) where

E ⊆ {{a, b}|a ∈ V & b ∈ V } without multiple edges

and loops. The set V = H ∪ S, H ∩ S =

0, of nodes

represents network devices such as hosts (the set H)

and switches (the set S). Edges of the graph (the set

ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering

422

E) represent connections (links) between two nodes

in G and each link can transmit packets in both di-

rections. Correspondingly, we write (a, b) if a packet

is transmitted from a to b and (b, a) when it is trans-

mitted from b to a. We reasonably assume that each

host is connected exactly with one switch and that G

is connected; otherwise, each (connected) component

can be treated as a separate network.

Data paths

are sets of paths which carry pack-

ets, i.e., those paths can have appropriate parameters

according to which the packets are then forwarded;

in other words, each packet belongs to an appropri-

ate trafﬁc type. When a forwarding rule is installed

on an SDN-enabled switch, a data link from and to

other node (-s) adjacent to the switch is created, i.e.,

a packet accepted from adjacent nodes is forwarded

to a (corresponding) set of ports that are connected to

appropriate ports of other nodes.

A host can generate packets that are forwarded to

a single switch connected with this host. A switch

can only forward packets; moreover, we assume that

a switch does not modify the packet header, i.e.,

the packet’s trafﬁc type and payload are not changed

through the network. A switch can forward a packet

to several ports, and the set of ports depends on the

trafﬁc type as well as on the input port from which

it arrives. Every node a of the graph G (a host or a

switch) has a set of ports which can be input as well as

output and each such port corresponds to some edge

at the node a and vice versa, each edge at the node a

is associated with a corresponding port. Thus, there is

one-to-one correspondence between edges at the node

a and the set of its ports, i.e., there is one-to-one cor-

respondence between the set of ports of a and the set

of neighbor nodes of a, since G has no multiple edges

nor node (self) loops. Therefore, without loss of gen-

erality, we can use a neighbor node instead of the port

number.

A path is a sequence of neighboring nodes of G,

i.e., a path is a sequence

of nodes such that there is

an edge between neighboring sequence nodes. A path

π = x

· . . . · x

starts at the node x

, is ﬁnished at the

node x

, has length n − 1, and passes via an arc (x

i+1

) for i ∈ {1, . .. , n − 1}. The path is edge simple

if it passes via each arc at most one time; the path is

node simple if all its nodes are pairwise different. A

path is complete if its head and tail nodes are hosts

and there are no hosts as intermediate nodes.

An SDN application conﬁgures sets of paths

(through the controller) which should transport cor-

responding packets, i.e., those paths can have ap-

propriate parameters (which deﬁne their trafﬁc type)

They are directed, differently from the topology itself.

We use ‘·’ for denoting the sequence concatenation.

according to which the packets are then forwarded

(OpenNetworkingFoundation, 2015). The ﬂow rules

of a switch can be written as a mapping of input ports

into subsets of output ports. If the subset of output

ports is empty then the switch will ‘drop’ a packet

that arrived at a corresponding input port.

We assume that an SDN application conﬁgures the

switch tables in such a way that each rule determines

the set of output ports depending on the trafﬁc type

and an input port. As G has no multiple edges it

implies that a rule determines the set of neighboring

nodes where a packet has to be forwarded. We also

assume that all the switches have in their tables only

the information sent by the controller, i.e., no default

rules or external interfaces are considered. For the

sake of simplicity and in fact, without loss of general-

ity for our purpose, we assume that all the rules have

the same priority. For packets belonging to the same

trafﬁc type, we can consider every rule as a triple (a,

s, b) ∈ V × S ×V where a and b are neighbors of s.

This rule says that getting a packet with the corre-

sponding trafﬁc type from neighbor a, switch s should

send it to the neighbor b. If there are several rules

which differ only in the neighbor b, then switch s per-

forms cloning, i.e., the incoming packet is transmitted

to several neighbors. The set of rules of all switches

is called conﬁguration (for the given trafﬁc type).

3 IMPLEMENTING THE GIVEN

SET OF COMPLETE PATHS

The set of complete paths that should be implemented

on the data plane is based on a user request or prede-

ﬁned conﬁguration (by a given application). Corre-

spondingly, before setting a switch conﬁguration ac-

cording to a set of paths, it would be useful to verify

whether a given set of paths can be eventually imple-

mented. Note that hereafter we assume that the re-

quested set of paths P does not contradict the RNCT

G. A trivial check that P forms a sub-graph of G can

be performed beforehand, if necessary.

When implementing a set of paths P, three options

are possible. 1) P can be implemented as it is and in

this case, the edge simplicity should be veriﬁed for

the set P. 2) P cannot be implemented without im-

plementing unintended paths, i.e., a superset of P is

implemented. In this case, the condition of the edge

simplicity should be checked for this superset. If the

minimal superset of P that can exist on the data plane

has cycling paths, then the set P cannot be imple-

mented (packet loops may ﬂood the network) in the

given data plane. 3) P cannot be implemented but the

minimal superset of P that can be implemented satis-

Preventive Model-based Veriﬁcation and Repairing for SDN Requests

423

ﬁes the edge simplicity property. We further discuss

how given a set P of paths, a corresponding switch

conﬁguration is speciﬁed and given a switch conﬁgu-

ration, which paths are induced by this conﬁguration.

Complete paths induce switch rules. When im-

plementing rules for a complete path (for the given

trafﬁc type) α · a · b · c · β where a, b, c ∈ V, α, β ∈ V

∗

we need a rule (a, b, c), i.e., a switch b once getting a

packet belonging to this trafﬁc type from the neighbor

a has to send it to the neighbor c. Formally, the set P

of paths induces the set P↓ of rules:

∀a ∈ V, b ∈ S, c ∈ V, α ∈ V

∗

, β ∈ V

∗

α · a · b · c · β ∈ P implies that there is a rule (a, b,

c) ∈ P↓.

Switch rules induce paths. The rule (a, b, c) in-

duces a path a · b · c of length 2. If there is a path

α · x · y and there is a rule (x, y, z) then there is a path

α·x·y·z. Formally, a switch conﬁguration P↓ induces

the set of complete paths, written P↓↑:

∀b

∈ V

, b

), (b

, b

), . . . , (b

n−1

, b

, a

) ∈ P ↓

where a

and a

are the only hosts, there is a path

· b

. . . · b

n−1

· b

· a

in P↓↑.

By deﬁnition, the set P↓↑ has only complete paths

and the following statement holds.

Proposition 1. Given a switch b, for each rule (a, b,

c) ∈ P↓ of this switch, there is a path α · a · b · c · β ∈

P↓↑ for some α and β.

We now establish the conditions when two paths

α· x ·y · β and α

·x ·y ·β

in the set P↓↑ induce another

two paths in this set.

Proposition 2. Given a switch conﬁguration P↓, P↓

induces the set of complete paths P↓↑ with the follow-

ing features:

∀α, α

, β, β

∈ V

∗

α · x · y · β ∈ P↓↑ & α

· x · y · β

∈ P↓↑ =⇒ α · x ·

y · β

∈ P↓↑.

According to Proposition 2, the set of data paths

on the data plane induced by the given set P is exactly

P↓↑, and in fact, it is the actual set of paths that gets

implemented when requesting to implement the set P.

The set P of complete paths is closed with respect

to a given arc (x, y) if for each two paths α · x · y · β

and α

· x · y ·β

of the set P which have a common arc

(x, y), paths α · x · y · β

and α

· x · y · β are also in P.

The set P of paths is arc closed if P is closed w.r.t.

each arc over the set E. Given a set P of complete

paths, the arc closure of P is the smallest arc closed

set of complete paths that contains P. According to

the deﬁnition of an arc closed set and Proposition 2,

the following statement can be established.

Proposition 3. Given a set P of complete paths, the

set P↓↑ is the arc closure of P.

Corollary 1. The set P↓↑ coincides with P if and only

if P is arc closed.

The above corollary establishes necessary and suf-

ﬁcient conditions for the precise implementation of

set P on the data plane (without additional ‘undesired’

paths).

Corollary 2. If P has only edge simple paths and is

arc closed then P↓↑ has only edge simple paths.

If P is not arc closed then P cannot be imple-

mented on the data plane up to the equality relation.

Moreover, sometimes P cannot be implemented on

the data plane at all as its arc closure has some cy-

cling paths. Figure 1 shows an example when the set

P has two edge simple paths α and β from initial host

to the ﬁnal host h

(left of the ﬁgure), the set of

rules induced by this set is shown at the bottom and

an induced path γ of the set P↓↑ is illustrated at the

right. The path is not edge simple, and this example

illustrates that cycles can occur even when paths of

the set P are edge simple.

Similar to P, all the paths of the set P↓↑ are com-

plete paths. However, if P↓↑ is a proper superset of P

then we have to check whether all the paths of the set

P↓↑ are edge simple. If it is the case then the set P can

be implemented on the data plane up to the set P↓↑

(i.e., with additional unspeciﬁed paths from P↓↑ \P).

If it is not the case then the set P should be modiﬁed

and this issue is discussed in Section 5.

From a practical point of view, perhaps the most

interesting application is when some set P↓↑ of paths

is already implemented on the data plane and a new

request arrives; either a request A to add new paths

(P∪A) or a request R to remove paths (P\R) to / from

the original set. In this case, the same check should

be performed on ((P∪ A)\R)↓↑ before implementing

/ removing paths, guaranteeing the implementability

of the augmented set of paths. Algorithm 1 sum-

marizes the necessary veriﬁcation steps (Section 4)

and returns the corresponding verdict about the im-

plementability of a given set of paths.

Practical / Experimental Motivation. In order to

verify if our (fundamental) ﬁndings can occur in real

SDN framework implementations, an experimental

evaluation was performed. Experiments were carried

in a virtual machine running GNU/Linux CentOS 7.6

with 8 vCPUs and 16GB of RAM. The Onos (Berde

et al., 2014) SDN controller (version 4.2.8) was in-

stalled via a Docker (Merkel, 2014) container. To em-

ulate the SDN data plane, the Containernet (Peuster

et al., 2018) was also installed through a Docker con-

tainer.

The paths shown in Figure 1 were conﬁgured in-

dependently and successful communication from h

ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering

424

Paths to be

implemented:

An induced

path:

P ={α = h

· s

· h

, β = h

· s

· h

}

P↓={(h

, s

), (s

, s

), (s

, s

), (s

, s

), (s

, s

), (s

, s

, h

, s

), (s

, s

), (s

, s

), (s

, s

), (s

, s

), (s

, s

, h

)}

γ =h

· s

· . . . · s

· s

· h

∈ P↓↑

Figure 1: Induced (cyclic) paths’ occurrence.

to h

was discovered, i.e., there was no problem while

conﬁguring both paths independently. When both

paths were conﬁgured simultaneously, the loop was

effectively produced. A single packet sent from h

to h

produced inﬁnitely many of them. In Figure 2,

we show the packet dump (using the well-known util-

ity tcpdump) as seen by h

. Note that, the packet

sent is an ICMP echo request (using the ping utility),

and the sequence ID is always 1, as the single packet

gets copied inﬁnitely many times. When continuously

sending the packets the network rapidly degraded un-

til the whole infrastructure became unusable. These

experiments conﬁrm the importance of our ﬁndings.

Indeed, it is important to provide SDN frameworks

with veriﬁcation tools before rules are pushed to the

switches. One of the procedures for such veriﬁcation

is given in Algorithm 1.

4 CHECKING THE ARC

CLOSURE

In this section, we propose an algorithm for checking

if a given set of paths P induces unintended paths, i.e.,

a superset of P is implemented (when P is intended);

likewise, we discuss how to detect potential cycles

induced by the implementation of P. Algorithm 1

shows the veriﬁcation steps necessary to check the arc

closure of a given set of paths. Note that the algo-

rithm always terminates due to the ﬁnite calculations

in nested loops, independently if P↓↑ contains a path

with a loop or not.

Proposition 4. Algorithm 1 returns the verdict True

if and only if P is arc closed.

Consider the example in Figure 1; the graph D(P)

is shown in Figure 3. By direct inspection one can as-

sure that there is a cycle (s

, s

), (s

, s

), (s

, s

), (s

) in the graph and thus, the number of paths from

the vertex source to the vertex sink is inﬁnite, and

therefore, the set P is not arc closed.

Algorithm 1: Verifying if the set of paths P is arc closed.

Input : A set P of edge simple complete paths

Output: A verdict whether the set P is arc closed

Derive a subset Q = {q

, . . . , q

} of P that contains

all the paths of length greater than two; we

denote as k

the length of a path q

j ∈ {1, . . . , k};

Derive a graph D(P) =< D, E > for the set Q

where the vertices of D(P) are pairs of vertices of

the paths in Q;

D = {source, sink}; E =

j = 0;

while j < k do

j + +; D = D ∪ {(q

(1), q

(2)), (q

+ 1))};

E = E ∪ {(source, (q

(1), q

(2)), (q

+ 1)), sink)};

m = 2;

while m < k

+ 1 do

D = D ∪ {(q

(m), q

(m + 1))};

E = E ∪ {((q

(m − 1), q

(m)), (q

(m),

(m + 1)))};

m + +;

if the number of paths in D(P) from source to sink

is greater than k then

return False;

return True;

Proposition 5. The complexity of checking the ab-

sence of cycles for a given set of paths P is O(L +

|V |

) where |V | is the number of nodes in G and L is

the sum of the lengths of the paths in P.

The complexity of constructing the graph D(P) is

O(L) where L is the sum of the lengths of the paths

from P. In order to check for (inﬁnite) loops, the ab-

sence of oriented cycles in the graph D(P) needs to

be checked, which is done through a topological sort

(e.g., using depth ﬁrst search (DFS) (Cormen et al.,

2009)). DFS-algorithm can also be used for comput-

ing the number of paths from the source to the sink

Preventive Model-based Veriﬁcation and Repairing for SDN Requests

425

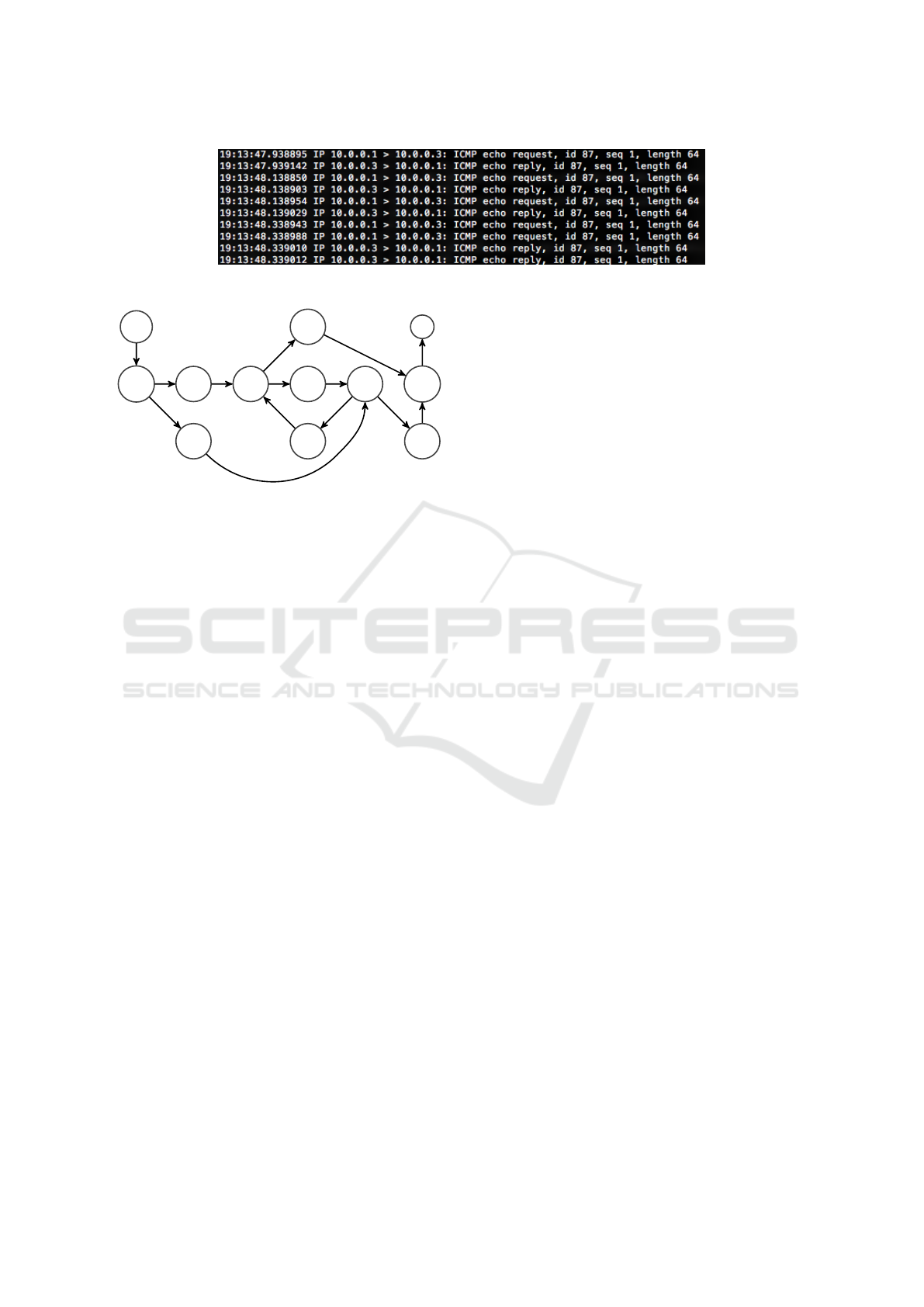
Figure 2: Packet capture showing an inﬁnite loop in the experimental infrastructure.

source

, s

)

, s

)

, s

)

, s

)

, s

)

, s

)

, s

)

, s

)

, h

)

sink

, s

)

Figure 3: Graph D(P) for verifying the set of paths P.

node when there are no cycles. The running time of

the depth ﬁrst search algorithm on the graph D(P) is

evaluated as O (m), where m is the number of arcs of

the graph D(P), m ≤ |V |

5 DEBUGGING AND REPAIRING

A SET OF PATHS

We discuss some possibilities of correcting / modi-

fying the set of paths P whenever this set is not arc

closed. One ﬁrst needs to identify the reason, i.e., a

subset of paths that destroy the corresponding prop-

erty, and the set of paths P should be either augmented

with new paths or on the contrary, certain paths should

be deleted from the set P. In both ways, the result-

ing subset becomes arc closed and thus, can be im-

plemented on the data plane without any additional

links. We refer to this process as automatic P debug-

ging and repairing. Such repairing process can have

various objectives, such as for example: minimization

of the number of paths to be excluded / included from

/ to P, maximization of a host to host connectivity in

the resulting set of paths, minimization of the num-

ber of changes in the paths of the set, minimization of

virtual links on the data plane, etc. We furthermore

discuss some of the possibilities listed above and pro-

pose various debugging and repairing strategies.

For the following subsections, we use the follow-

ing notations. Given a set P of complete paths, let

P = {p

, . . . , p

}, i.e., k = |P|, and k

= |p

| − 1, i.e.,

is the length of p

for all i ∈ {1, . . . , k}.

5.1 Minimizing the Set of Paths to be

Excluded / Included from / to P

The problems we address in this subsection are the

following: how to delete / add a minimal number of

paths from / to the set P, such that the resulting subset

/ superset becomes arc closed.

We say that two different paths p

and p

of P are

incompatible if there exists a common arc, i.e., there

exist u ∈ {1, . . . , k

− 1} and v ∈ {1, . . . , k

− 1} such

that p

(u) = p

(v) & p

(u + 1) = p

(v + 1) while a

path p

(1) · . . . · p

(u) · p

(v + 1) · . . . · p

+ 1) or a

path p

(1) · . . . · p

(v) · p

(u + 1) · . . . · p

+ 1) is not

in P. In this case, one can also say that p

and p

are

incompatible w.r.t. the common arc (a, b) = (p

(u),

(u + 1)). If p

and p

of P are not incompatible,

then they are compatible.

The problem of deleting a minimal number of

paths can be reduced to the well known maximum in-

dependent set problem. For that matter, we propose

to derive an undirected graph G(P) in the following

way: the nodes of the graph correspond to the paths

of the set P. There is an arc between p

and p

, i 6= j,

in the graph G(P) if the paths p

and p

are incom-

patible. Given an undirected graph G(P), a subset of

nodes which are not pairwise connected is an inde-

pendent subset of nodes.

Proposition 6. An independent subset of nodes of

graph G(P) is an arc closed set.

Corollary 3. A subset of P is arc closed if and only if

it is an independent subset of the graph G(P).

Therefore, the problem of minimizing the set of

paths to be excluded from P is reduced to the deriva-

tion of a maximal independent subset of nodes in

G(P). Note that this problem is known to be NP-hard,

and thus the repairing approach can be more complex

than that one presented for the veriﬁcation itself (Sec-

tion 4).

As an example, consider again the paths of the set

P in Figure 1. Note that the paths from P possess the

necessary feature, i.e., they have a common arc (s

) with the above property and the set P has no path

·s

·h

. Therefore, the

corresponding vertices in G(P) are connected, i.e., P

ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering

426

is not arc closed and only the singletons {α} or {β}

are arc closed.

For deriving a minimal superset of P that is arc

closed, the graph D(P) derived in the previous section

can be used. If the graph returned by Algorithm 1 has

no cycles then the set of all paths from the source node

to the sink node is the smallest superset of P that is arc

closed.

Proposition 7. 1. If all the paths from the source

node to the sink node in D(P) are edge simple then

the set of all paths is the smallest superset of P that is

arc closed. 2. If there is a path from the source node

to the sink node in D(P) that is not edge simple then

there is no ﬁnite superset of P that is arc closed.

Note that in case 2, it is not possible to add paths

to the given set P; the set P can be only reduced as it is

discussed at the beginning of the subsection. Indeed,

it is exactly the case for the set P in Figure 1.

5.2 Minimizing the Number of Arc

Changes in the Set P

Consider a set P of edge simple complete paths that is

not arc closed, the question arises: can the paths of the

set be minimally corrected (w.r.t. the number of arcs)

in order to get an arc closed set preserving the head

and tail hosts of each path? We propose a simple way

for modifying a single edge or a sub-path of a path

using edges of the RNCT graph G which were not

utilized in the paths of P (the set N in Algorithm 2).

Proposition 8. Given a set P of edge-simple complete

paths, if Algorithm 2 returns a set Q = {p

, p

, . . . ,

} then this set is arc closed and for each j ∈ {1,

. . . , k}, the head and tail vertices of p

coincide with

those of p

Note that the set of repaired paths returned by

Algorithm 2 has only edge simple paths and is arc

closed, since every time only unused links are utilized

for the replacement. In this paper, we consider only

simple heuristics for repairing a path and the result

signiﬁcantly depends on the order of the paths in P.

Additional research is needed to propose more rig-

orous conditions for repairing a set of initial paths.

Those conditions can be related to the link load dis-

tribution and thus, could re-direct some packets, for

example, for trafﬁc optimization.

As an example, consider again the paths in Fig-

ure 1, assuming that each pair of switches is con-

nected in the RNCT G. These paths have a common

arc (s

, s

) that can be replaced by a path s

· s

After this modiﬁcation the paths have a common arc

, s

) that can be replaced by a path s

·s

. Thus,

Algorithm 2: Repairing via modifying an edge or a

sub-path preserving the head and tail hosts of the path.

Input : A set P of edge-simple complete paths

that is not arc closed, a non-empty set N

of edges between switches of the RNCT

graph G which are not used in the paths

of the set P

Output: A verdict False if paths cannot be

modiﬁed, or a modiﬁed arc closed set P

where the head and tail vertices of each

modiﬁed path p

coincide with those of

the initial path p

of P

Q = {p

};

j = 2;

while j ≤ |P| do

= p

;

l = 1;

while l ≤ |Q| do

p = q

;

if paths p and p

are incompatible w.r.t. P

then

if N =

0 then

return False;

else

while the paths p and p

are

incompatible w.r.t. the common

arc (s

, s

) do

if the paths p and p

have a

common sub-path

· α · s

· s

· β · s

and

, s

) is in N then

Derive p

by replacing a

sub-path

· α · s

· s

· β · s

in p

by a sub-path s

· s

;

Delete (s

, s

) from the

set N;

else if there is a switch s

such that

, s

), (s

, s

) ∈ N then

Derive p

by replacing a

sub-path s

· s

in p by

a sub-path s

· s

;

Delete (s

, s

) and

, s

) from the set N;

else

return False;

l + +;

Add p

to the set Q;

j + +;

return an arc closed set Q = {p

, p

, . . . , p

}

we obtain an arc closed set of paths P

= {h

· s

· h

, h

· s

· h

Preventive Model-based Veriﬁcation and Repairing for SDN Requests

427

6 CONCLUSION

In this paper, we discussed implementability issues

for a given set of paths on an SDN data plane. We

showed that for a ﬁxed trafﬁc type, whenever the re-

quested set contains only edge simple paths, more

(unintended) paths can still be implemented on the

data plane, and some of those can create cycles, i.e.,

inﬁnite packet loops, and we established the neces-

sary and sufﬁcient conditions for a set of requested

paths to be implemented without any undesired con-

nections. Our preventive veriﬁcation approach is use-

ful for guaranteeing that new (requested) and pre-

existing paths form valid conﬁgurations. The esti-

mated (polynomial w.r.t. the total paths’ length) com-

plexity of the proposed approach makes possible its

applicability for large scale virtual networks. For a

set of paths that cannot be implemented directly on

the data plane, we proposed debugging and repairing

approaches for correcting the initial request, such that

the resulting set becomes arc closed. As future work,

we plan to extend the proposed approaches abstract-

ing from a given trafﬁc type as well as considering

other kinds of speciﬁcations for user requests.

REFERENCES

Berde, P., Gerola, M., Hart, J., Higuchi, Y., Kobayashi, M.,

Koide, T., Lantz, B., O’Connor, B., Radoslavov, P.,

Snow, W., et al. (2014). Onos: towards an open, dis-

tributed sdn os. In Proceedings of the third workshop

on Hot topics in software deﬁned networking, pages

1–6. ACM.

Berriri, A., L

opez, J., Kushik, N., Yevtushenko, N., and

Zeghlache, D. (2018). Towards model based testing

for software deﬁned networks. In Proceedings of the

13th International Conference on Evaluation of Novel

Approaches to Software Engineering ENASE, pages

440–446.

Boufkhad, Y., De La Paz, R., Linguaglossa, L., Mathieu, F.,

Perino, D., and Viennot, L. (2016). Forwarding tables

veriﬁcation through representative header sets. arXiv

preprint arXiv:1601.07002.

Burdonov, I. B., Kossachev, A., Yevtushenko, N., L

opez, J.,

Kushik, N., and Zeghlache, D. (2019). Verifying SDN

data path requests. CoRR, abs/1906.03101.

Canini, M., Venzano, D., Pere

ıni, P., Kosti

c, D., and Rex-

ford, J. (2012). A NICE way to test openﬂow applica-

tions. In Presented as part of the 9th USENIX Sympo-

sium on Networked Systems Design and Implementa-

tion (NSDI 12), pages 127–140.

Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C.

(2009). Introduction to algorithms. MIT press.

David, L., Stefano, V., and Olivier, B. (2014). Towards

test-driven software deﬁned networking. In 2014

IEEE Network Operations and Management Sympo-

sium, pages 1–9.

Dobrescu, M. and Argyraki, K. (2013). Toward a veriﬁ-

able software dataplane. In Proceedings of the Twelfth

ACM Workshop on Hot Topics in Networks, page 18.

ACM.

Fayaz, S. K., Yu, T., Tobioka, Y., Chaki, S., and Sekar,

V. (2016). BUZZ: Testing context-dependent poli-

cies in stateful networks. In 13th USENIX Sympo-

sium on Networked Systems Design and Implementa-

tion (NSDI 16), pages 275–289.

Mai, H., Khurshid, A., Agarwal, R., Caesar, M., Godfrey, P.,

and King, S. T. (2011). Debugging the data plane with

anteater. ACM SIGCOMM Computer Communication

Review, 41(4):290–301.

Merkel, D. (2014). Docker: lightweight linux containers for

consistent development and deployment. Linux jour-

nal, 2014(239):2.

Mohammed, A. H., Khaleefah, R. M., k. Hussein, M., and

Amjad Abdulateef, I. (2020). A review software de-

ﬁned networking for internet of things. In 2020 In-

ternational Congress on Human-Computer Interac-

tion, Optimization and Robotic Applications (HORA),

pages 1–8.

OpenNetworkingFoundation (2012). Software-deﬁned net-

working: The new norm for networks. ONF White

Paper.

OpenNetworkingFoundation (2015). Openﬂow switch

speciﬁcation version 1.5. 0. ONF Speciﬁcation.

Peuster, M., Kampmeyer, J., and Karl, H. (2018). Con-

tainernet 2.0: A rapid prototyping platform for hybrid

service function chains. In 2018 4th IEEE Conference

on Network Softwarization and Workshops (NetSoft),

pages 335–337. IEEE.

Sezer, S., Scott-Hayward, S., Chouhan, P. K., Fraser, B.,

Lake, D., Finnegan, J., Viljoen, N., Miller, M., and

Rao, N. (2013). Are we ready for sdn? implementa-

tion challenges for software-deﬁned networks. IEEE

Communications Magazine, 51(7):36–43.

Stoenescu, R., Dumitrescu, D., Popovici, M., Negreanu, L.,

and Raiciu, C. (2018). Debugging P4 programs with

vera. In Proceedings of the 2018 Conference of the

ACM Special Interest Group on Data Communication

SIGCOMM, pages 518–532.

Yao, J., Wang, Z., Yin, X., Shiyz, X., and Wu, J. (2014).

Formal modeling and systematic black-box testing of

sdn data plane. In The IEEE 22nd International Con-

ference on Network Protocols (ICNP), pages 179–

190.

Yevtushenko, N., Burdonov, I. B., Kossachev, A., L

opez, J.,

Kushik, N., and Zeghlache, D. (2018). Test derivation

for the software deﬁned networking platforms: Novel

fault models and test completeness. In 2018 IEEE

East-West Design & Test Symposium EWDTS, pages

1–6.

Zeng, H., Kazemian, P., Varghese, G., and McKeown, N.

(2012). Automatic test packet generation. In Proceed-

ings of the 8th international conference on Emerging

networking experiments and technologies, pages 241–

252. ACM.

ENASE 2021 - 16th International Conference on Evaluation of Novel Approaches to Software Engineering

428