Edge and Corner Detection in Unorganized Point Clouds for Robotic

Pick and Place Applications

Mohit Vohra

, Ravi Prakash

and Laxmidhar Behera

1,2

Department of Electrical Engineering, IIT Kanpur, India

TCS Innovation Labs, Noida, India

Keywords:

Edge Extraction, Unorganized Point Cloud, Autonomous Grasping.

Abstract:

In this paper, we propose a novel edge and corner detection algorithm for an unorganized point cloud. Our edge

detection method classiﬁes a query point as an edge point by evaluating the distribution of local neighboring

points around the query point. The proposed technique has been tested on generic items such as dragons,

bunnies, and coffee cups from the Stanford 3D scanning repository. The proposed technique can be directly

applied to real and unprocessed point cloud data of random clutter of objects. To demonstrate the proposed

technique’s efﬁcacy, we compare it to the other solutions for 3D edge extractions in an unorganized point

cloud data. We observed that the proposed method could handle the raw and noisy data with little variations

in parameters compared to other methods. We also extend the algorithm to estimate the 6D pose of known

objects in the presence of dense clutter while handling multiple instances of the object. The overall approach

is tested for a warehouse application, where an actual UR5 robot manipulator is used for robotic pick and place

operations in an autonomous mode.

1 INTRODUCTION

Over the past decade, the construction industry has

struggled to improve its productivity, while the manu-

facturing industry has experienced a dramatic produc-

tivity increase (Changali et al., 2015) (Vohra et al.,

2019) (Pharswan et al., 2019). A possible reason

is the lack of advanced automation in construction

(Asadi and Han, 2018). However, recently various in-

dustries have shown their interest in construction au-

tomation due to the following beneﬁts, i.e., the con-

struction work will be continuous, and as a result, the

construction period will decrease, which will provide

tremendous economic beneﬁts. Additionally, con-

struction automation improves worker’s safety and

enhances the quality of work. The most crucial part of

the construction is to build a wall and to develop a sys-

tem for such a task; the system should be able to es-

timate the brick pose in the clutter of bricks, grasp it,

and place it in a given pattern. Recently, a New York-

based company, namely "Construction Robotics", has

developed a bricklaying robot called SAM100 (semi-

automated mason) (Parkes, 2019), which makes a

wall six times faster than a human. The SAM100 re-

quires a systematic stack of bricks at regular intervals,

making this system semi-autonomous, as the name

suggests.

Similarly, in the warehouse industry, the task of

unloading goods from trucks or containers is crucial.

With the development of technology, various solu-

tions have been proposed to incorporate automation

in unloading goods (Doliotis et al., 2016) (Stoyanov

et al., 2016). One of the main challenges in the au-

tomation of the above work is that the system has to

deal with a stack of objects, which can come in ran-

dom conﬁgurations, as shown in Fig. 1. For devel-

oping a system for such a task, the system must esti-

mate the pose of the cartons in a clutter, grasp it, and

arrange it in the appropriate stack for further process-

ing.

In this paper, we focus on estimating the pose of

the objects (carton or brick) in clutter, as shown in

Fig. 1. We assume that all the objects present in the

clutter have the same dimensions, which is very com-

mon in warehouse industries (clutter of cartons all

having the same dimensions) and construction sites

(clutter of bricks). Traditionally, Object pose is es-

timated by matching the 2D object features (Lowe,

2004) (Collet et al., 2011) or 3D object features (Drost

et al., 2010) (Hinterstoisser et al., 2016) between ob-

ject model points and view points. Recently, CNN

based solutions have shown excellent results for 6D

Vohra, M., Prakash, R. and Behera, L.

Edge and Corner Detection in Unorganized Point Clouds for Robotic Pick and Place Applications.

DOI: 10.5220/0010501202450253

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 245-253

ISBN: 978-989-758-522-7

245

Figure 1: Cartons Clutter (Image Courtesy: Internet).

pose estimation, which exempts us from using hand-

crafted features. For example, (Xiang et al., 2017)

(Tekin et al., 2018) can estimate the pose of the ob-

jects directly from raw images. Similarly, (Qi et al.,

2017)(Zhou and Tuzel, 2018) can directly process the

raw point cloud data and predict the pose of the ob-

jects. While all the above methods have shown excel-

lent results, they cannot be used directly for our work.

• Since the objects are textureless. Therefore the

number of features will be less, making the feature

matching methods less reliable. Furthermore, due

to the presence of multiple instances of the object,

it can be challenging to select features that corre-

spond to a single object.

• The performance of CNN-based algorithms relies

on extensive training on large datasets. However,

due to the large variety of objects in the warehouse

industry (various sizes and colors), it is challeng-

ing to train CNN for all types of objects.

Therefore, we aim to develop a method that re-

quires fewer features and can easily be deployed for

objects with different dimensions.

The main idea of our approach is that if we can

determine at least three corner points of the cartons,

then this information is sufﬁcient to estimate its pose.

So the ﬁrst step is to extract sharp features like edges

and boundaries in point cloud data. In the case of

edge detection in unstructured 3D point clouds, tradi-

tional methods reconstruct a surface to create a mesh

(Kazhdan and Hoppe, 2013) or a graph (Demarsin

et al., 2007) to analyze the neighborhood of each

point. However, reconstruction tends to wash away

sharp edges, and graph-based methods are computa-

tionally expensive. In (Bazazian et al., 2015), the au-

thor performs fast computation of edges by construct-

ing covariance matrices from local neighbors, but the

author has demonstrated for synthetic data. In (Ni

et al., 2016), the authors locate edge points by ﬁt-

ting planes to local neighborhood points. Further a

discriminative learning based approach (Hackel et al.,

2016) is applied to unstructured point clouds. The au-

thors train a random forest-based binary classiﬁer on

a set of features that learn to classify points into edge

vs. non-edge points. One drawback of their method

is poor performance on unseen data.

In this paper, we present a simple method to ex-

tract edges in real unstructured point cloud data. In

this approach, we assign a score to each point based

on its local neighborhood distribution. Based on the

score, we classify a point as an edge (or boundary)

point or a non-edge point. From the edge points, we

ﬁnd the line equation, the length of the 3D edges, and

the corner points, which are intersections of two or

more edges. For each corner point, the correspond-

ing points in the local object frame are calculated to

estimate the object’s 6D pose. Our approach’s main

advantage is that it can be easily applied to other ob-

jects with known dimensions.

The remainder of this paper is organised as fol-

lows. Proposed 3D edge extraction is presented in

Section II. In Section III corner points are found us-

ing those edges. Pose estimation using edges and cor-

ners are presented in Section IV. In Section V, ex-

perimental results for robotic manipulation using a

6-DOF robot manipulator and their qualitative com-

parison with the state-of-the-art is done. This paper is

ﬁnally concluded in Section VI.

2 EDGE POINTS EXTRACTION

In this section, we will explain the method for extract-

ing the edge points. Input to the algorithm is raw point

cloud data P , user-deﬁned radius r

, and threshold

value t

. The output of the algorithm is point cloud E

which contains the edge points. To decide if a given

query point p

∈ P is an edge point or not, we calcu-

late R (p

), which is deﬁned as a set of all points in-

side a sphere, centered at point p

with radius r

. For

an unorganized point cloud, this is achieved through

a k-dimensional (K-d) tree. We call each point in set

R (p

) as a neighboring point of p

, and it can be rep-

resented as R (p

) =



, n

, . . . , n



. For each query

point p

and neighboring point n

we calculate the di-

rectional vector as

d(p

, n

) = n

− p

(1)

d(p

, n

) =

d(p

, n

)



d(p

, n

)



(2)

Then we calculate the resultant directional vector

R(p

) as sum of all directional vector and normalize

R(p

) =

∑

j=1

d(p

, n

R(p

) =

R(p

)

R(p

)

(3)

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

246

We assign a score s(p

) to each query point p

as an average of the dot product between

R(p

) and

d(p

, n

) for all neighboring points.

s(p

) =

∑

j=1

R(p

) ·

d(p

, n

)

(4)

If s(p

) exceeds some threshold t

, p

is considered

an edge point, otherwise not. We have tested the algo-

rithm on standard data set from Stanford 3D Scanning

Repository

and (Lai et al., 2014), with point cloud

models of various objects such as bowls, cups, cereal

boxes, coffee mugs, soda cans, bunnies, and dragons.

We have also applied our algorithm to a clutter of ran-

dom objects to extract edges, shown in Fig. 2.

(a) Coffee mug (b) bunny

Figure 2: Edge cloud.

3 ESTIMATING THE LENGTH OF

EDGES

Once we have found all the edge points, our next

step is to ﬁnd the line equation of edges, length of

edges, and corner points. In general, the equation of

a line is represented by two entities, a point through

which line passes and a unit directional vector from

that point. However, in our case, we represent the line

with two extreme points. The advantage of the above

representation is that we can estimate the length of the

edge by calculating the distance between two extreme

points. The intersecting point between two edges can

be found by calculating the distance between the ex-

tremities of edges.

3.1 Reference Index and Line Equation

To ﬁnd the line equation, we apply the RANSAC

method on the edge point cloud E . The output of

the RANSAC method is L and I , where L represents

the equation of a line in standard form i.e., a point

http://graphics.stanford.edu/data/3Dscanrep/

and a directional vector, and I represent the set of

inliers. To ﬁnd two extremities of line L, we have

to make sure that two extremities should represent

the same edge because, in a cluttered environment, I

could have points that belong to different objects. So

for this task, we will ﬁnd the reference point p

. We

deﬁne a point p

∈ I , which has the maximum num-

ber of neighbors in I , and r is the reference index of

in I . The maximum number of neighbors property

ensures that p

is not at the extreme ends, and from

we will ﬁnd the two extreme points, which is ex-

plained in the next section. Following are the steps to

estimate the reference index r

• Use RANSAC on E for estimating the line equa-

tion L and set of inliers I .

• We deﬁne R (p

) as set of all inlier points inside a

sphere, centered at point p

, where p

∈ I

• we deﬁne r = argmax

size(R (p

))

3.2 Finding Extremities

In this section, we will explain the procedure to ﬁnd

the extreme points e

and e

in a set of points I

for a reference point p

. To test if a query point

∈ I is an extreme point or not, we ﬁnd a set of

inliers R (p

), with radius r

and represent the set as

R (p

) =



, n

, . . . , n



. For each query point p

we calculate the directional vector from a query point

to the reference point d

= p

− p

, and a local di-

rectional vector from the query point to the neighbor

points d

= n

− p

, where n

∈ R (p

). Now to de-

cide if the query point is an extreme point or not, we

compute the dot product between d

and d

for all

neighboring points. If any of the dot product value is

negative, then p

is not an extreme point; otherwise,

it is. We repeat the procedure for all p

and select the

extreme points which have the smallest distance from

. Implementation of the above procedure is given

in Algorithm 1.

3.3 Get All Edges

To ﬁnd all the lines in the edges point cloud E, we re-

cursively apply the above algorithms, and the points

corresponding to the line will be removed from E to

obtain the new line equation. The following is a se-

quence of steps to extract all the lines.

• Let P be the raw Point cloud data, r

be the radius

and t

be the threshold value to extract the edges

point cloud E.

• Apply RANSAC on E to get reference index r and

set of inliers I .

Edge and Corner Detection in Unorganized Point Clouds for Robotic Pick and Place Applications

247

Algorithm 1: Get extreme points.

Require: r, I

Ensure: e

, e

 extreme points

1: for i = 0 → size(I ) and i 6= r do

2: ﬁnd R (p

)

3: d

= p

− p

5: for j = 0 → size(R (p

)) do

6: d

= n

− p

8: v =

9: if v < 0 then  p

is not an extreme point

10: break

11: end if

12: end for

13: if v > 0 then  p

can be an extreme point

14: p

→ points  save point

15:

→ directions  save direction

16:

→ distances  save distance

17: end if

18: end for

19: e

→ mindis(distances)

20: e

is ﬁrst minima opposite to e

 using saved

• Extract two extreme points e

and e

• Store e

and e

in an array A and remove all the

points between e

and e

from E.

• repeat the steps 2 − 4.

4 POSE ESTIMATION

4.1 Club Edges of Same Cube

Algorithm 2: Get edges of same cube.

Require: A, a

Ensure: C  all edges of a cube

1: l

= A(a)

2: while not traverse all edges do

3: l

∈ A − l

4: if l

⊥ l

and l

∩ l

6= φ then

5: l

, l

→ C  save l

, l

in C

6: A 6≡ l

 remove l

from A

7: l

= l

 replace l

with l

8: end if

9: end while

Once we have all the edges in A, our next step is

to club the edges of the same cube. Let a be an edge

number, and the corresponding edge is l

= A(a). If

represents one edge of a cube, then we need to ﬁnd

all other edges of the same cube. To ﬁnd other edges,

we consider the property that l

must be orthogonal to

, i.e., l

⊥ l

, and intersect with each other at a point,

i.e., l

∩l

6= φ. If l

satisﬁes the above conditions, we

store l

and l

in an array and replace l

with l

. We re-

peat the above steps until we cover all the edges. The

process is described in Algorithm 2. Once we have all

the edges representing the same cube, we compute the

corner points, which are intersections of two or more

edges. These corner points are calculated in the cam-

era frame, and by estimating the corresponding points

in the local object frame, we can estimate the object’s

pose.

(a) Local Brick frame (b) Pose using b, h

Figure 3: Local brick frame and assumptions.

4.2 Corresponding points and Pose

Estimation

4.2.1 Local Frame and Assumptions

Let l, b, h represent the length, breadth, and height of

the cube, and we deﬁne a local frame with the origin

at the centroid of the cube, and x-axis, y-axis, and z-

axis pointing along the length, breadth, and height of

the cube respectively, shown in Fig. 3.

For estimating the pose, we need a minimum

of two orthogonal edges. Although two orthogonal

edges can give two poses, we will assume that the

third axis corresponding to the remaining edge will

point to camera origin. So this assumption ﬁlter out

the one solution, and we will get a unique pose from

two edges shown in Fig. 3.

4.2.2 Corner Points and Directional Vector

Let two edges are l

, l

, and from these edges, we

will calculate three corner points, p

, p

, where

is the intersecting point of two lines, p

is another

extreme of l

and p

is another extreme of l

. We also

deﬁne four unit directional vector d

, d

, t, and d as

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

248

− p

, d

− p

, t =

−p

(5)

d = d

× d

, d =

(6)

Vector d

represents the unit directional vector

corresponding to edge l

, d

represents the unit direc-

tional vector corresponding to edge l

and t represents

the unit directional vector from p

to camera origin.

Vector d is a unit directional vector orthogonal to d

and d

4.2.3 Direction Assignment and Corresponding

Points

Once we have the corner points, our next step is

to ﬁnd their corresponding points in the local object

frame. For estimating the corresponding points, it is

important to verify if the d

( or d

) is representing the

+x(y,z) or -x(y,z) wrt local object frame. Further, we

have to assign the direction to d

and d

in such a way

that third remaining axis of the brick should point to-

wards the camera frame.

We explain direction assignment with an example.

Let

= l and

= b. Since remaining edge is the

height edge so corresponding axis i.e. z-axis of local

frame must point towards the camera frame which is

shown in Fig. 4. From the two edges we compute the

corner points and directional vectors. For visualiza-

tion, we represent l

in red color because l

must have

a direction of either ˆx or − ˆx in local frame. Similarly

we represent l

in green color because l

must have a

direction of either ˆy or − ˆy in local frame. Directional

vector and corner points are represented in black color

(Fig. 4). Let us assume that d

has a direction of ˆx and

has a direction of ˆy in local frame. To verify our

assumption, we compute d which represents the di-

rectional vector along the third axis (z-axis) and val-

idate our assumptions by computing the dot product

between d and t.

As shown in Fig. 4, for the ﬁrst brick our direction

assumptions are correct because dot product between

d and t is positive and corresponding points are given

in Table 1.

For second brick, our direction assumptions are

incorrect because dot product between d and t is neg-

ative, which means either d

has a direction of − ˆx or

has a direction of −ˆy. One can conclude from sec-

ond brick (Fig. 4), that d

with a direction of ˆx and d

with a direction of − ˆy is the valid solution and corre-

sponding points are given in Table1.

If we consider the other solution i.e. − ˆx for d

and ˆy for d

, then as shown in third brick, local cube

frame rotates by an angle 180 about z-axis, and since

the cube is symmetric, so both solutions will project

the same model.

Table 1: Correspondences.

Corner points Brick 1 Brick 2

−

, −

−

, −

−

, −

Figure 4: Direction assignment and corresponding points.

4.2.4 Pose Reﬁnement

Using three correspondences, we compute the pose

of the cube. To further reﬁne the pose, we need more

correspondences. From Algorithm 2 we get C which

represents all edges of same cube and intersection

of edges will give the corner points. From the ini-

tial pose calculated from three correspondences, we

will ﬁnd the correspondence between the other corner

points in camera frame and in local frame by calcu-

lating the distance between corner points and the pre-

dicted corner points from the initial pose. Pair of cor-

ner point and predicted corner point with minimum

distance will form a correspondence pair. Thus more

correspondences will give more accurate pose.

5 EXPERIMENTAL RESULTS

AND DISCUSSION

5.1 Experimental Setup

Our robot platform setup is shown in Fig. 5. It

consists of a UR5 robot manipulator with its con-

troller box (internal computer) and a host PC (external

computer). The UR5 robot manipulator is a 6-DoF

robot arm designed to work safely alongside humans.

The low-level robot controller is a program running

on UR5’s internal computer, broadcasting robot arm

data, receiving and interpreting the commands, and

controlling the arm accordingly. There are several

options for communicating with the robot low-level

controller, for example, teach pendant or opening a

TCP socket (C++/Python) on a host computer. Our

vision hardware consists of an RGB-D Microsoft

Edge and Corner Detection in Unorganized Point Clouds for Robotic Pick and Place Applications

249

(a) Setup (b) Visual Processing (c) Grasp (d) Retrieve (e) Place

Figure 5: Experimental setup and execution steps during robotic manipulation.

Kinect sensor mounted on top of the workspace. Point

cloud processing is done in the PCL library, and ROS

drivers are used for communication between the sen-

sor and the manipulator. A suction gripper is mounted

at the end effector of the manipulator.

5.2 Motion Control Module

The perception module passes the 6D pose of the ob-

ject to the main motion control node running on the

host PC. The main controller then interacts with low

level Robot Controller to execute the motion. A pick

and place operation for an object consists of four ac-

tions: i) approach the object, ii) grasp, iii) retrieve

and iv) place the object. The overall trajectory has

ﬁve way-points: an initial-point (I), a mid-point (M),

a goal-point (G), a retrieval point (R), and a ﬁnal des-

tination point (F). A ﬁnal path is generated which

passes through all of the above points.

i) Approach: This part of the trajectory connects

I and M. The point I is obtained by forward kine-

matics on current joint state of the robot and M is an

intermediate point deﬁned by M = G + d ˆz, where G

is the goal-point provided by the pose-estimation pro-

cess and ˆz is the unit vector in vertical up direction at

G. The value of d is selected subjectively after several

pick-place trial runs.

ii) Grasp: As the robot’s end effector reaches M,

the end-effector align according to the brick pose.

This section of the trajectory is executed between M

and G with directed straight line trajectory of the end

effector.

iii) Retrieve: Retrieval is the process of bringing

the grasped object out of the clutter. This is executed

from G to R. The retrieval path is traversed vertically

up straight line trajectory. R is given by R = G + h ˆz,

where G is the goal-point and ˆz is the unit vector in

vertical up direction at G. The value of h is selected

to ensure the clearance of the lifted object from the

clutter.

iii) Place: Placing is the process of dropping the

grasped object at the destination place. This is exe-

cuted from R to F. Fig. 5 shows the execution steps

during robotic manipulation.

5.3 Experimental Validation

We explore two experimental settings: when bricks

are presented to the robot in isolation and when bricks

are presented in a dense cluttered scenario as shown

in Fig. 7 and Fig. 8 respectively.

5.3.1 Objects Present in the Isolation

In the ﬁrst experiment we measure the dimension of

bricks and place the bricks separately in front of the

3D sensor.

Edge Points: For extracting edges, we perform sev-

eral experiments for selecting the optimum value of

and t

. We initiate with r

= 0.005m and increment

it with a step size of 0.001m. We record the compu-

tation time at each r

(Table 2). Based on quality of

edges (Fig. 6) and computation time we select the r

Based on several trials we found that for extracting

edge points, r

= 0.02m and t

= 0.35 are the optimal

values.

Table 2: Computation time (sec) at various r

= 0.010 r

= 0.015 r

= 0.020 r

= 0.025 r

= 0.030

0.66538 1.29415 2.13939 3.16722 4.40235

Lines and Corner Points: For ﬁnding the equation of

lines we apply RANSAC method with threshold value

of 0.01m and for ﬁnding the corner point, we compute

the distance between two extremities of edges and if

distance is < 0.01m, then corner point is the average

of two extreme points. With these parameters, we ﬁnd

the edges and corner points which is shown in Fig. 7

and computation time for each step is shown in Table

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

250

(a) r

= 0.01 (b) r

= 0.015 (c) r

= 0.025 (d) r

= 0.030

Figure 6: Effect of r

at t

= 0.35.

(a) Raw point cloud (b) Edges Point (c) All Edges (d) Model Fitting

Figure 7: Isolated bricks experiment.

(a) Input (b) Edges points (c) All Edges (d) Model Fitting

Figure 8: Clutter bricks experiment.

Table 3: Computation time (sec) at each step.

Edges Point All edges Model Fitting Total Time

Exp 1 2.13939 2.0854 0.07573 4.36192

Exp 2 2.13056 5.26684 0.21726 7.61466

5.3.2 Clutter of Bricks

In the second experiment we place the brick in clut-

ter as shown in Fig. 8. For edge points and lines,

we use the same parameter values which were used in

experiment 1. Result of each step is shown in Fig. 8

and computation time for each step is shown in Table

3. With each successful grasp of the brick, computa-

tion time will decreases, because the number of points

which needs to be processed will decrease. Above ex-

periment is performed on a system with an i7 proces-

sor having a clock speed of 3.5GHz and 8GB RAM.

5.4 Performance on Different Objects

As mentioned earlier, our method can be easily ap-

plied for the other objects with known dimensions.

Hence we tested our algorithm on two different ob-

jects with different dimensions. Fig. 9 shows the

output of our method on two different objects (only

dimensions are known in advance). A single pose has

Figure 9: Pose predictions for different objects.

been visualized in Fig. 9 to avoid a mess in the im-

ages. From Fig. 9, we can claim that our method can

easily be deployed for other objects.

5.5 Performance Analysis

To demonstrate the efﬁcacy of our proposed edge ex-

traction method from unorganized point cloud, we

compare the results from the method (Bazazian et al.,

2015) for edge extraction. Their method estimates the

sharp features by analysing the eigenvalues of the co-

variance matrix which is deﬁned by each point's k-

Edge and Corner Detection in Unorganized Point Clouds for Robotic Pick and Place Applications

251

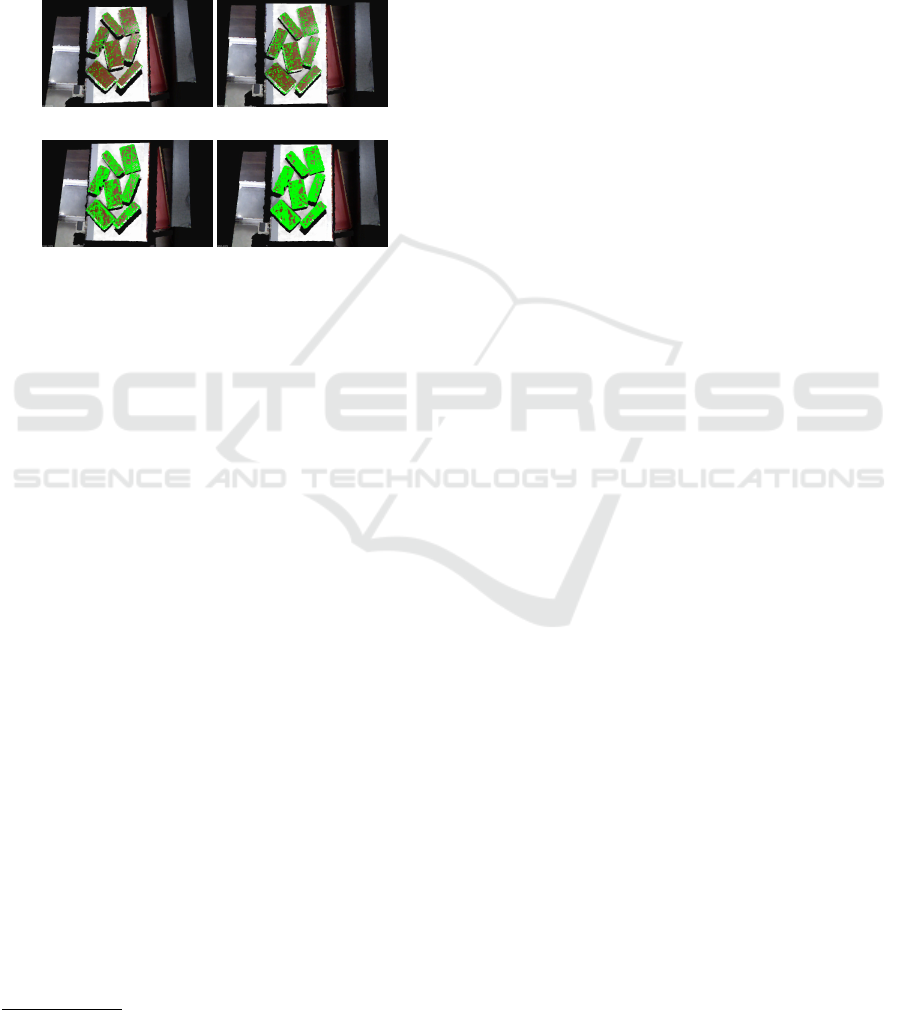
nearest neighbors. We apply their method

on raw

point cloud data with k vary from 4 to 30 as shown in

Fig. 10. The results of the method (Bazazian et al.,

2015) is unsatisfactory on the same data set where our

method perform very well. It is because of the inher-

ent noise in the sensor, points on a ﬂat surface has

large variations. Thus all eigenvalues of the covari-

ance matrix will be large, hence predicts the sharp

edges even at the ﬂat surface.

(a) k = 4 (b) k = 5

Figure 10: Edges from covariance matrix based method.

6 CONCLUSION

Novel edge and corner detection algorithm for un-

organized point clouds was proposed and tested on

generic objects like a coffee mug, dragon, bunny, and

clutter of random objects. The algorithm is used for

6D pose estimation of known objects in clutter for

robotic pick and place applications. The proposed

technique is tested on two warehouse scenarios, when

objects are placed distinctly and when objects are

placed in a dense clutter. Results of each scenario

is reported in the paper along with the computation

time at each step. To demonstrate the efﬁcacy of the

edge extraction technique, we compared it with the

covariance matrix based solution for 3D edge extrac-

tions from unorganized point cloud in a real scenario

and report better performance. The overall approach

is tested in a warehouse application where a real UR5

robot manipulator is used for robotic pick and place

operations.

REFERENCES

Asadi, K. and Han, K. (2018). Real-time image-to-bim reg-

istration using perspective alignment for automated

construction monitoring. In Construction Research

Congress, volume 2018, pages 388–397.

https://github.com/denabazazian/

Bazazian, D., Casas, J. R., and Ruiz-Hidalgo, J. (2015).

Fast and robust edge extraction in unorganized point

clouds. In 2015 International Conference on Digi-

tal Image Computing: Techniques and Applications

(DICTA), pages 1–8. IEEE.

Changali, S., Mohammad, A., and van Nieuwland, M.

(2015). The construction productivity imperative.

How to build megaprojects better.„McKinsey Quar-

terly.

Collet, A., Martinez, M., and Srinivasa, S. S. (2011). The

moped framework: Object recognition and pose esti-

mation for manipulation. The International Journal of

Robotics Research, 30(10):1284–1306.

Demarsin, K., Vanderstraeten, D., Volodine, T., and Roose,

D. (2007). Detection of closed sharp edges in point

clouds using normal estimation and graph theory.

Computer-Aided Design, 39(4):276–283.

Doliotis, P., McMurrough, C. D., Criswell, A., Middleton,

M. B., and Rajan, S. T. (2016). A 3d perception-based

robotic manipulation system for automated truck un-

loading. In 2016 IEEE International Conference on

Automation Science and Engineering (CASE), pages

262–267. IEEE.

Drost, B., Ulrich, M., Navab, N., and Ilic, S. (2010). Model

globally, match locally: Efﬁcient and robust 3d ob-

ject recognition. In 2010 IEEE computer society con-

ference on computer vision and pattern recognition,

pages 998–1005. Ieee.

Hackel, T., Wegner, J. D., and Schindler, K. (2016). Con-

tour detection in unstructured 3d point clouds. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pattern Recognition, pages 1610–1618.

Hinterstoisser, S., Lepetit, V., Rajkumar, N., and Konolige,

K. (2016). Going further with point pair features. In

European conference on computer vision, pages 834–

848. Springer.

Kazhdan, M. and Hoppe, H. (2013). Screened poisson sur-

face reconstruction. ACM Transactions on Graphics

(ToG), 32(3):29.

Lai, K., Bo, L., and Fox, D. (2014). Unsupervised fea-

ture learning for 3d scene labeling. In 2014 IEEE In-

ternational Conference on Robotics and Automation

(ICRA), pages 3050–3057. IEEE.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International journal of computer

vision, 60(2):91–110.

Ni, H., Lin, X., Ning, X., and Zhang, J. (2016). Edge de-

tection and feature line tracing in 3d-point clouds by

analyzing geometric properties of neighborhoods. Re-

mote Sensing, 8(9):710.

Parkes, S. (2019). Automated brick laying system and

method of use thereof. US Patent App. 16/047,143.

Pharswan, S. V., Vohra, M., Kumar, A., and Behera, L.

(2019). Domain-independent unsupervised detec-

tion of grasp regions to grasp novel objects. In

2019 IEEE/RSJ International Conference on Intel-

ligent Robots and Systems (IROS), pages 640–645.

IEEE.

Qi, C. R., Su, H., Mo, K., and Guibas, L. J. (2017). Pointnet:

Deep learning on point sets for 3d classiﬁcation and

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

252

segmentation. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, pages

652–660.

Stoyanov, T., Vaskevicius, N., Mueller, C. A., Fromm, T.,

Krug, R., Tincani, V., Mojtahedzadeh, R., Kunaschk,

S., Ernits, R. M., Canelhas, D. R., et al. (2016). No

more heavy lifting: Robotic solutions to the container

unloading problem. IEEE Robotics & Automation

Magazine, 23(4):94–106.

Tekin, B., Sinha, S. N., and Fua, P. (2018). Real-time seam-

less single shot 6d object pose prediction. In Proceed-

ings of the IEEE Conference on Computer Vision and

Pattern Recognition, pages 292–301.

Vohra, M., Prakash, R., and Behera, L. (2019). Real-time

grasp pose estimation for novel objects in densely

cluttered environment. In 2019 28th IEEE Interna-

tional Conference on Robot and Human Interactive

Communication (RO-MAN), pages 1–6. IEEE.

Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2017).

Posecnn: A convolutional neural network for 6d ob-

ject pose estimation in cluttered scenes. arXiv preprint

arXiv:1711.00199.

Zhou, Y. and Tuzel, O. (2018). Voxelnet: End-to-end learn-

ing for point cloud based 3d object detection. In Pro-

ceedings of the IEEE Conference on Computer Vision

and Pattern Recognition, pages 4490–4499.

Edge and Corner Detection in Unorganized Point Clouds for Robotic Pick and Place Applications

253