
Revisiting Johann Bernoulli's Method for the Brachistochrone
Problem
Ido Braun and Joseph Z. Ben-Asher
Faculty of Aerospace Engineering, Technion, Haifa, 32000, Israel
Keywords: Johann Bernoulli, Brachistochrone, Snell’s Law, Fermat's Principle, Minimum Time.
Abstract: This paper reviews Johann Bernoulli's solution to the Brachistochrone problem, using an analogy to the
movement of light and Fermat's principle of least time. Bernoulli's method is later used to derive solutions to
some generalizations of the Brachistochrone problem. The problems solved using Bernoulli's method are the
classical flat gravity Brachistochrone, spherical gravity outside the earth, and spherical gravity inside the earth
('gravity train').
1 INTRODUCTION
The Brachistochrone problem, meaning in Greek
"shortest time, is the question regarding what is the
shape of the path to slide a point mass between two
arbitrary points with a height difference in the
shortest time possible, while considering only the
action of a constant gravitational force applied on it.
Its formulation is considered as the birth of optimal
control theory. Johann Bernoulli proposed to solve
the problem using an analogy to light (de Icaza,
1993). According to Fermat's principle of least time,
light will manage to find the optimal course in order
to travel between two points at the shortest possible
time. When the points lie in different mediums the
light would refract and change its direction when
passing between the mediums in order to maintain
this principle. The relation between the light
velocities in each medium, and the direction of the
light movement is expressed through Snell's law.
When used in spherical coordinates, Snell's law can
also be generalized.
At a later date, the problem was solved again
using a different approach, with variational calculus
(Grasmair, 2010). This method's purpose is to find the
optimal solution by minimizing the cost function of
the traveling time, and by this to find the route which
would provide the shortest time of travel between the
points. Both Bernoulli's method, and calculus of
variations provided the same solution. In this paper,
several generalizations of the Brachistochrone are
analysed with Bernoulli's method, and are validated
using the calculus of variations method.
The first generalization considered is for a giant
Brachistochrone outside earth, where the gravity
varies with the radius, and the position relative to the
earth's center. The problem was solved both by
Bernoulli's method (Parnovsky,1998), and with
calculus of variations (Mitchell, 2006). To this end,
the derivation of Snell’s law inside a sphere is
provided (this derivation has not been found by the
authors in the literature.) Additionally, the problem is
solved inside the earth for a solution of a 'gravity
train'. This problem has been solved in the past using
Calculus of Variations (Vanderbei, 2013). To the best
of our knowledge, a solution based on Bernoulli's
method has not been published yet. This paper
provides this solution and obtains an equivalent
result.
Thus, the main contributions of this paper are
threefold: i. A tutorial revisit of known solutions by
the Bernoulli’s method; ii. A detailed derivation of
Snell’s law in a sphere; iii. A new solution based on
the Bernoulli’s method.
2 CLASSIC
BRACHISTOCHRONE
Bernoulli used an analogy between the motion of the
point mass on the surface, and a motion of a light
beam between infinitely many varying mediums
(Fig. 1).
Braun, I. and Ben-Asher, J.
Revisiting Johann Bernoulli’s Method for the Brachistochrone Problem.
DOI: 10.5220/0010503501070114
In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 107-114
ISBN: 978-989-758-522-7
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
107
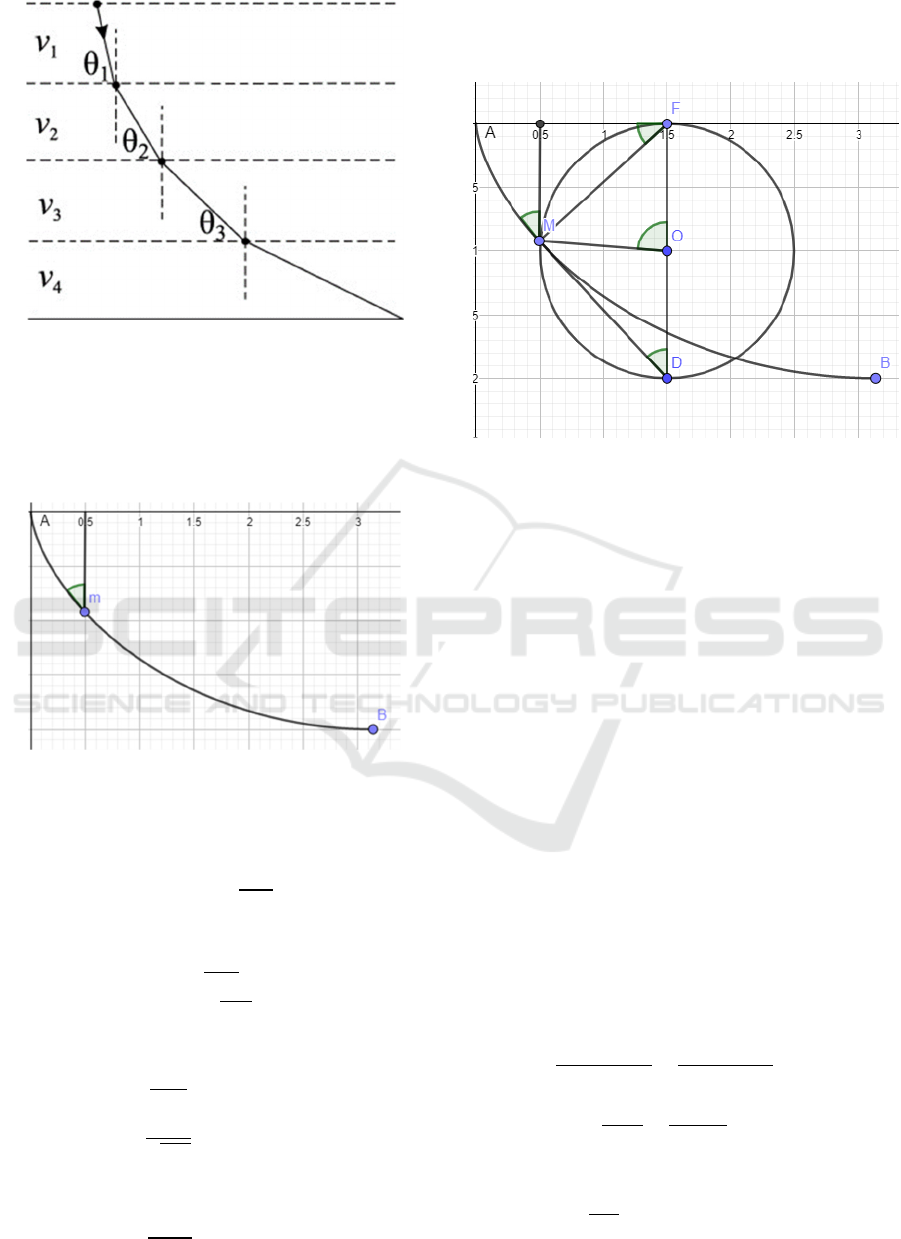
Figure 1: Light's movement through varying mediums.
Assume a point mass travels from point A to point
B using only the gravitational force. Set a Cartesian
coordinate system such that A is located at (0,0), and
B at known (L,H) beneath point A. θ is the angle
between the tangent to the surface and y axis (Fig. 2).
Figure 2: Mass course of movement.
Since the only force applied on the mass is
gravity, the total energy is conserved.
𝐸=𝑉+𝑇=−𝑚𝑔𝑦+
𝑚𝑣
2
=𝑐𝑜𝑛𝑠𝑡
(1)
𝐸
=0
(2)
−𝑚𝑔𝑦 +
𝑚𝑣
2
=0
(3)
⇒𝑣=
2𝑔𝑦
(4)
From Snell's law (see Appendix B):
sin𝜃
𝑣
=𝑐𝑜𝑛𝑠𝑡
(5)
sin𝜃
2𝑔𝑦
=𝑐𝑜𝑛𝑠𝑡
(6)
Squaring both sides and adding g to the constant:
sin
θ
y
=const
(7)
This relation represents the differential equation
of a cycloid. To show how, a geometric proof is
provided (Levi, 2015). Consider the sketch in Fig. 3.
Figure 3: Geometric proof for Brachistochrone.
Since the cycloid is created from a rolling circle with
a radius R, at any given time F is the instant center of
rotation of the circle, so every point on the circle
rotates around F at that moment and performs a
circular motion around that point. M moves in a
circular motion with respect to F at any given time, so
it's velocity is perpendicular to the line MF. The
velocity vector is in the same plane as the surface the
mass slides on, so the tangent line of the surface at
any given moment is perpendicular to MF. Continue
the tangent on a straight line until it reaches the circle
on point D, such that ∢FMD=90°. A circumferential
angle that equals 90° lies on the diameter, so FD is
the diameter of the circle. Define the angle ∢FDM=θ.
θ is a circumferential angle, so the central angle that
lies on the same arc, ∢FOM=2θ. θ is also the angle of
the mass because they are parallel angles. The angle
between a chord in the circle to the tangent of the
circle is the same as the circumferential angle that lies
on this chord from the other side, thus:
∢FDM= ∢MFA=
θ
(8)
Using the law of sines:
𝑀𝐹
sin
(
∢FDM
)
=
𝐷𝐹
sin
(
∢FMD
)
(9)
𝑀𝐹
s
in
𝜃
=
2𝑅
s
in
90
°
(10)
⇒𝑀𝐹=2𝑅sin𝜃 (11)
𝑦
𝑀𝐹
=sin
(
∢MFA
)
(12)
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
108

𝑦
2𝑅 sin𝜃
=sin𝜃
(13)
sin
𝜃
𝑦
=
1
2𝑅
=𝑐𝑜𝑛𝑠𝑡
(14)
Thus Eq. (7) was verified. This equation
represents the cycloid equation (see Appendix A):
𝑥=𝑅
(
2𝜃− sin2𝜃
)
𝑦=𝑅(1 − cos2𝜃)
(15)
Where θ is the angle between the tangent to the
surface and y axis, and is half the angle of the circle's
rotation. R is the radius of the circle:
𝑅=
𝐻
2
(16)
3 SOLVING THE
BRACHISTOCHRONE
PROBLEM FOR EXTERNAL
SPHERICAL EARTH
Assume a spherical earth with a gravitational field:
𝑔
=−
𝑀
⊕
𝐺
𝑟
𝑟
̂
(17)
The center of the earth in ECI coordinates is at
𝑟
=
0 0 0
. It is required to find the course from
point 𝐴
(
𝑥
,𝑦
,𝑧
)
to point 𝐵
(
𝑥
,𝑦
,𝑧
)
) which a
point mass would travel at the shortest time while
applied only a gravitational force directed to 𝑟
.
r
≥r
(18)
Since the earth is assumed to be a perfect sphere, and
the gravity is assumed to be only dependent on ▁r,
there exists a coordinate system where A, and B both
lie on the same plane. So using polar coordinates:
𝐴
(
𝑟
,𝜃
)
,𝐵
(
𝑟
,𝜃
)
(19)
The path of shortest time must satisfy Snell's law in a
sphere (Parnovsky,1998) - see Appendix C:
𝑟sin𝜙
𝑣
(
𝑟
)
=𝑐𝑜𝑛𝑠𝑡
(20)
ϕ is the angle between the tangent to the surface
and the radius vector. It was seen from energy
conservation that v satisfies:
𝑣=
2𝐺𝑀
1
𝑟
−
1
𝑟
(21)
Therefore:
rsinϕ
2GM
1
r
−
1
r
=const
(22)
⇒
r
r
r
−r
sinϕ=const
(23)
In order to find the optimal path, it is required to
identify the relation between ϕ, and θ.
sin𝜙=
𝑟𝑑𝜃
𝑑𝑙
(24)
𝑟
𝑟
𝑟
−𝑟
𝑟𝑑𝜃
𝑑𝑙
=𝑐𝑜𝑛𝑠𝑡=
√
𝑐
(25)
Squaring both sides yields:
𝑟
𝑟
𝑟
−𝑟
𝑟
𝑑𝜃
=𝑐𝑑𝑙
=𝑐
𝑑𝑟
+𝑟
𝑑𝜃
(26)
⟹
𝑑𝜃
𝑑𝑟
=𝜃
(
𝑟
)
=
𝑐
(
𝑟
−𝑟
)
𝑟
𝑟
−𝑐𝑟
(
𝑟
−𝑟
)
(27)
Thus
𝜃
(
𝑟
)
=±
𝑐
(
𝑟
−𝑟
)
𝑟
𝑟
−𝑐𝑟
(
𝑟
−𝑟
)
𝑑𝑟 (28)
The initial and terminal conditions:
𝜃
(
𝑟
)
=𝜃
,𝜃
(
𝑟
)
=𝜃
(29)
The expression obtained via Bernoulli's method
(Parnovsky, 1998) is equivalent to the variational
calculus solution (Mitchell, 2006). Fig. 4 presents
representative trajectories using (28).
Figure 4: External spherical earth Brachistochrone.
Revisiting Johann Bernoulli’s Method for the Brachistochrone Problem
109

4 SOLVING THE
BRACHISTOCHRONE
PROBLEM FOR INTERNAL
SPHERICAL EARTH
Assume a spherical earth with an internal
gravitational field (Levi, 2015):
𝑔
=−
𝐺𝑀
𝑅
𝑟𝑟̂
(30)
The gravitational potential is derived to be:
𝑉
(
𝑟
)
=
𝐺𝑀𝑚
2𝑅
𝑟
𝑅
−3 (31)
The kinetic energy of a point mass during its course:
𝐸=𝑇+𝑉=
1
2
𝑚𝑣
+
𝐺𝑀𝑚
2𝑅
𝑟
𝑅
−3
=𝑐𝑜𝑛𝑠𝑡
(32)
At point A the mass starts the movement:
𝐸
=𝑉
=
𝐺𝑀𝑚
2𝑅
𝑟
𝑅
−3
(33)
1
2
𝑚𝑣
+
𝐺𝑀𝑚
2𝑅
𝑟
𝑅
−3
=
𝐺𝑀𝑚
2𝑅
𝑟
𝑅
−3
(34)
1
2
𝑚𝑣
=
𝐺𝑀𝑚
2𝑅
(
𝑟
−𝑟
)
(35)
⟹𝑣=
𝐺𝑀
𝑅
(
𝑟
−𝑟
)
(36)
The path of shortest time must satisfy (13):
𝑟sin𝜙
𝑣
(
𝑟
)
=𝑐𝑜𝑛𝑠𝑡
(37)
ϕ is the angle between the tangent to the surface and
the radius vector. It was seen from energy
conservation that v satisfies:
𝑣=
𝐺𝑀
𝑅
(
𝑟
−𝑟
)
(38)
Therefore:
𝑟sin𝜙
𝐺𝑀
𝑅
(
𝑟
−𝑟
)
=𝑐𝑜𝑛𝑠𝑡
(39)
𝑟sin𝜙
𝑟
−𝑟
=𝑐𝑜𝑛𝑠𝑡
(40)
The relation between 𝜙 and 𝜃:
sin𝜙=
𝑟𝑑𝜃
𝑑𝑙
(41)
𝑟
𝑟𝑑𝜃
𝑑𝑙
𝑟
−𝑟
=𝑐𝑜𝑛𝑠𝑡
(42)
Squaring both sides yields:
𝑟
𝑟
−𝑟
𝑑𝜃
𝑑𝑙
=𝑐=𝑐𝑜𝑛𝑠𝑡
(43)
𝑟
𝑟
−𝑟
𝑑𝜃
=𝑐𝑑𝑙
=𝑐
(
𝑑𝑟
+𝑟
𝑑𝜃
)
(44)
Thus
𝑟
(
𝜃
)
=
𝑑𝑟
𝑑𝜃
=
𝑟
𝑐
(
𝑟
−𝑟
)
−𝑟
(45)
The same expression has been obtained from both
Calculus of Variations (Vanderbei, 2013), and from
Bernoulli's method. Fig. 5 presents representative
trajectories using (45).
Figure 5: Internal spherical earth Brachistochrone 'Gravity
Train'.
5 CONCLUSIONS
The paper presented and discussed the
Brachistochrone problem, defined by Johan Bernoulli
in 1696. The Brachistochrone problem was solved
using Bernoulli's method of analogy to light.
Additionally, the problem was generalized using
several realistic influences and their effect on the
Brachistochrone curve was derived and analysed. The
Brachistochrone problem was solved for round earth
solutions via Bernoulli's method. It has been shown
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
110

that both methods, Calculus of Variations and
Bernoulli's provide the same solution.
REFERENCES
de Icaza Herrera, Miguel (1993), "Galileo, Bernoulli,
Leibniz and Newton around the brachistochrone
problem." Revista Mexicana de Física 40.3: 459-475.
Grasmair Marcus (2010), Basics of Calculus of Variations,
Norwegian University of Science and Technology.
Parnovsky, A. S. (1998), "Some generalisations of
brachistochrone problem." Acta Physica Polonica-
Series A General Physics 93.145: 55-64.
Mitchell, David R. (2006). "Brachistochrone of a Spherical
Uniform Mass Distribution," arXiv preprint math-
ph/0611055
Vanderbei, Robert J. (2013), "The Subterranean
Brachistochrone," https://economics.princeton.edu/
working-papers/the-subterranean-brachistochrone/.
Levi, Mark (2015), Quick! Find a Solution to the
Brachistochrone Problem, Pennsylvania State
University, SIAM NEW, July/August 2015.
APPENDICES
Appendix A - The path of a Cycloid:
In order to present the derivations of the
Brachistochrone solutions it is first required to define
the shape of the solution path, the Cycloid. Given a
circle with radius 𝑅, rolling on a straight line on the x
axis (Figs. 6-7). It is desired to form the equations of
the path of a given point on the circle, initially located
at 𝐴
(
0,0
)
.
Figure 6: Point on circle before movement.
During the rolling of the circle, point 𝐴 moves around
the center 𝑂. Define 𝜃 as the angle between the
segment 𝑂𝐴, and the initial segment when 𝐴
(
0,0
)
.
The length of 𝑂𝐴 is R as it is the radius of the circle.
The center 𝑂 position changes with respect to 𝜃 as
the circle performs a pure roll by the following
equations:
𝑥
=𝜃𝑅, 𝑦
=𝑅=𝑐𝑜𝑛𝑠𝑡
(46)
Figure 7: Point on circle after movement.
Using trigonometric relations, it is evident that:
𝑥
=𝑥
−𝑅𝑠𝑖𝑛
(
𝜃
)
=𝜃𝑅−𝑅𝑠𝑖𝑛
(
𝜃
)
(47)
𝑦
=𝑅 − 𝑅𝑐𝑜𝑠
(
𝜃
)
(48)
Therefore, the equations of a cycloid are:
𝑥=𝑅
(
𝜃−sin𝜃
)
𝑦=𝑅(1−cos𝜃)
(49)
Fig. 8 presents the shape of a Cycloid.
Figure 8: Shape of a cycloid.
Appendix B - Snell's law derivation (Fig. 9):
Snell's law states that when a beam of light travels
between one medium to another it will deflect
according to the following relation:
𝑛
sin𝜃
=𝑛
sin𝜃
(50)
Where 𝜃 is the angle between the beam of light and
the perpendicular to the medium transition line, and
𝑛 is the refractive index - the ratio between the speed
of light in vacuum and the speed of light in the given
medium.
𝑛=
𝑐
𝑣
(51)
Snell's law is the implementation of Fermat's principle,
which at the time was an empirical law claiming that
light would find the path to travel between two given
Revisiting Johann Bernoulli’s Method for the Brachistochrone Problem
111
points at the minimal time. (At later dates, with a better
understanding of the nature of light Fermat's principle
was proven using Maxwell's equations of
electromagnetism, and by the wave-particle duality
using quantum mechanics.) Given points 𝐴, and 𝐵
which lie in different mediums 𝑛
, and 𝑛
accordingly.
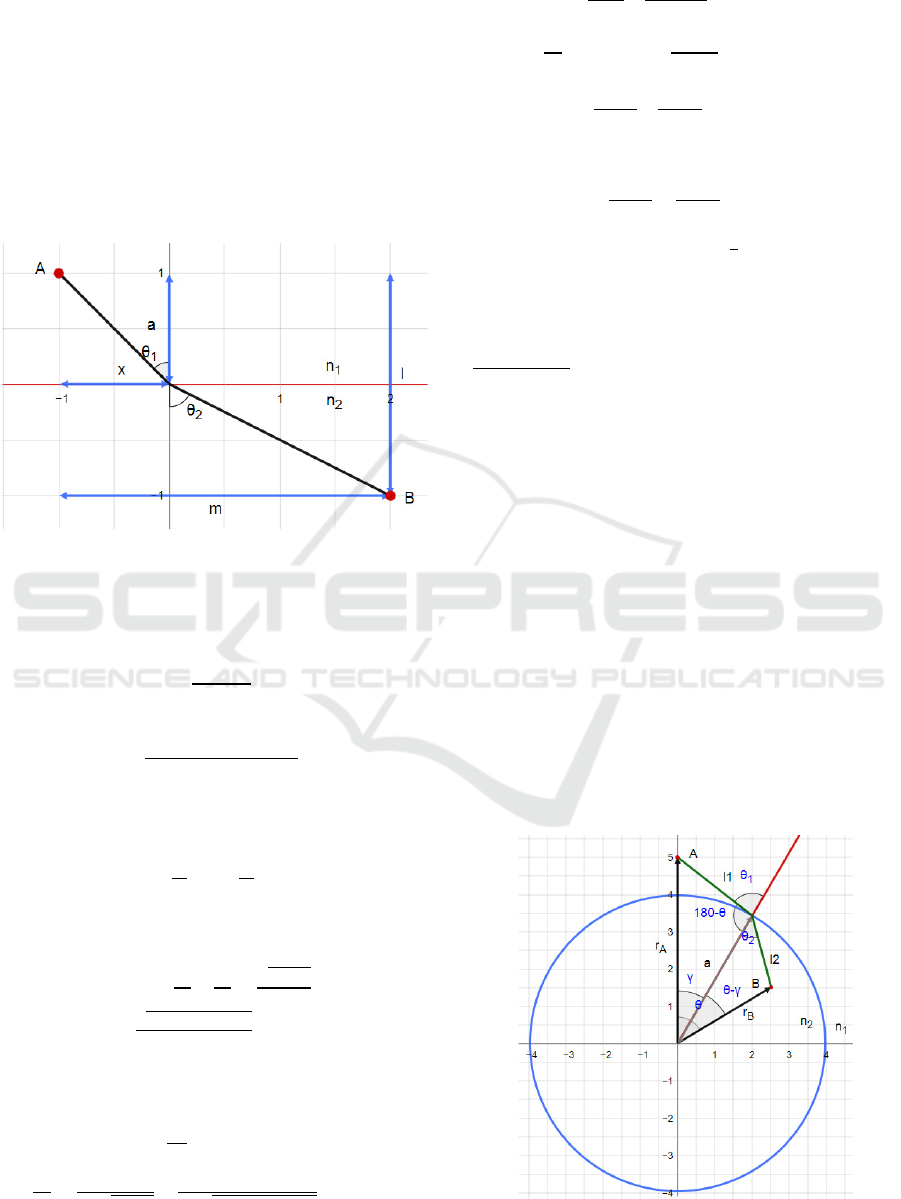
Define the horizontal length 𝑚 between 𝐴, and 𝐵, and
the vertical length 𝑙. The length between 𝐴 and the
medium transition line is 𝑎. Mark 𝑥 as the horizontal
length between 𝐴 and the point of transition between
the mediums, which is unknown.
Figure 9: Refraction of light between mediums.
The velocity in the mediums 𝑛
, and 𝑛
, are 𝑣
, and
𝑣
accordingly.
The distance between 𝐴, and the point of transition:
𝑑
=
𝑥
+𝑎
(52)
The distance between 𝐵, and the point of transition:
𝑑
=
(
𝑙−𝑎
)
+
(
𝑚−𝑥
)
(53)
Since the light velocity is constant in each medium,
the time of travel is:
𝑡
=
, 𝑡
=
(54)
Thus, the total time of travel between 𝐴, and 𝐵 is:
𝑡=𝑡
+𝑡
=
+
=
+
(
)
(
)
(55)
Using Fermat's principle, we wish to minimize the
time as function of 𝑥:
𝑑𝑡
𝑑𝑥
=0
(56)
=
−
(
)
(
)
(
)
=0
(57)
𝑥
𝑣
𝑑
−
(
𝑚−𝑥
)
𝑣
𝑑
=0
(58)
𝑥
𝑑
=sin𝜃
,
𝑚−𝑥
𝑑
=sin𝜃
(59)
sin𝜃
𝑣
−
sin𝜃
𝑣
=0
(60)
Snell's law has been obtained:
sin𝜃
𝑣
=
sin𝜃
𝑣
(61)
By applying the relation 𝑛=
the better-known
equation is obtained:
𝑛
sin𝜃
=𝑛
sin𝜃
(62)
Appendix C – Spherical Snell's law derivation:
Using Fermat's principle of minimum time, it is
desired to compute Snell's law where the refractive
index changes radially on an axis-symmetric sphere,
so in polar coordinates:
𝑛=
𝑓
(
𝑟
)
(63)
Given two mediums, one outside a sphere with radius
𝑟=𝑎, and the second inside the sphere. The
refractive index is therefore:
𝑛
(
𝑟
)
=
𝑛
,𝑟>𝑎
𝑛
,𝑟<𝑎
(64)
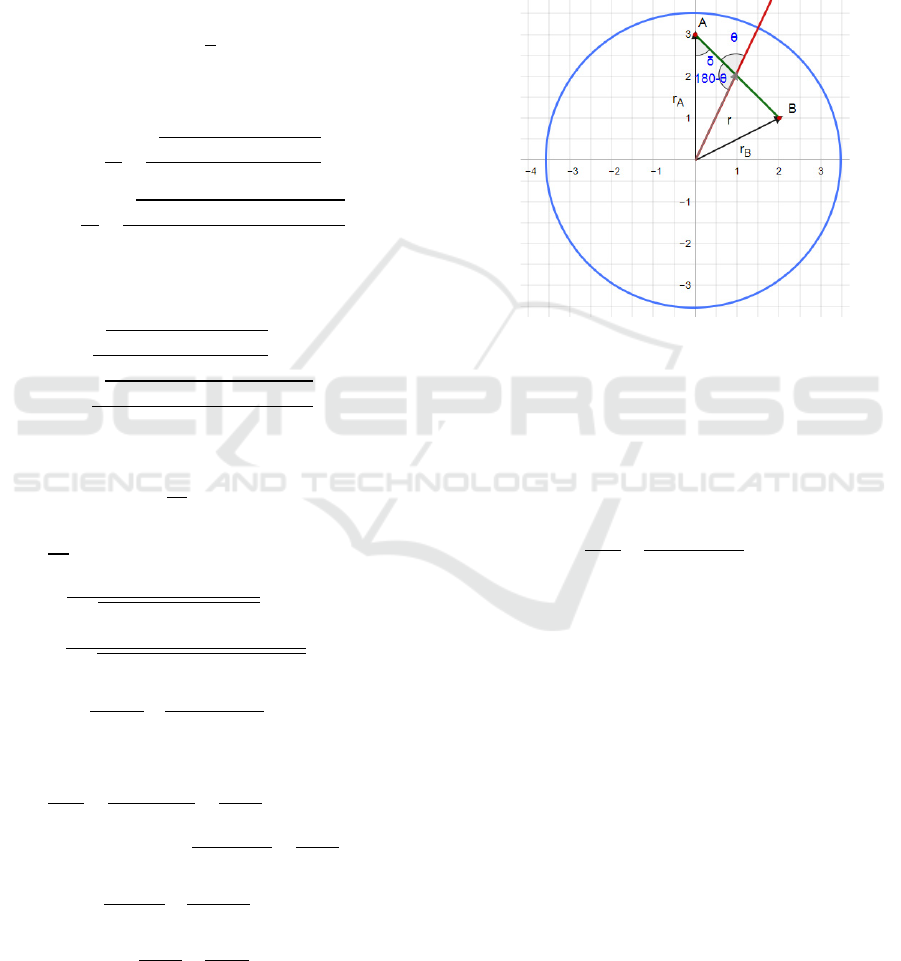
Choosing two arbitrary points: A is outside the
sphere, and B is inside the sphere (Fig. 10).
𝑟
(
𝜃
)
=𝑟
,𝑟
(
𝜃
)
=𝑟
,𝜃=𝜃
−𝜃
(65)
It is required to find the point at which the light would
choose to pass from 𝑛
to 𝑛
in order to travel from
point 𝐴 to point 𝐵 at the minimum possible time.
Figure 10: Refraction of light between spherical mediums.
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
112
The light would travel from point A to the sphere
intersection point an angular distance of 𝛾, the linear
distance traveled over this angle is obtained via the
cosine theorem:
𝑙
=𝑎
+𝑟
−2𝑎𝑟
cos𝛾
(66)
Similarly, for the distance from the intersection to 𝐵:
𝑙
=𝑎
+𝑟
−2𝑎𝑟
cos
(
𝜃−𝛾
)
(67)
The light travels in a given medium at a velocity of:
𝑣=
𝑐
𝑛
(68)
Where 𝑐 is the speed of light in vacuum. The time that
takes the light to cover the distances:
𝑡
=
𝑙
𝑣
=
𝑎
+𝑟
−2𝑎𝑟
cos𝛾
𝑣
(69)
𝑡
=
𝑙
𝑣
=
𝑎
+𝑟
−2𝑎𝑟
cos
(
𝜃−𝛾
)
𝑣
(70)
The total time of travel:
𝑡=𝑡
+𝑡
=
𝑎
+𝑟
−2𝑎𝑟
cos𝛾
𝑣
+
𝑎
+𝑟
−2𝑎𝑟
cos
(
𝜃−𝛾
)
𝑣
(71)
Applying Fermat's principle of minimum time:
𝑑𝑡
𝑑𝛾
=0
(72)
𝑑𝑡
𝑑𝛾
=
𝑎𝑟
sin𝛾
𝑣
𝑎
+𝑟
−2𝑎𝑟
cos𝛾
−
𝑎𝑟
sin
(
𝜃−𝛾
)
𝑣
𝑎
+𝑟
−2𝑎𝑟
cos
(
𝜃−𝛾
)
=0
(73)
𝑟
sin𝛾
𝑣
𝑙
−
𝑟
sin
(
𝜃−𝛾
)
𝑣
𝑙
=0
(74)
Using the sine theorem:
𝑙
sin𝛾
=
𝑟
sin
(
𝜋−𝜃
)
=
𝑟
sin𝜃
,
𝑙
sin
(
𝜃−𝛾
)
=
𝑟
sin𝜃
(75)
𝑟
sin𝜃
𝑣
𝑟
−
𝑟
sin𝜃
𝑣
𝑟
=0
(76)
sin𝜃
𝑣
=
sin𝜃
𝑣
(77)
⟹𝑛
sin𝜃
=𝑛
sin𝜃
(78)
This result is the same as the law derived in linear
coordinates (82). Assume homogenous spherical
medium (Fig. 11), the velocity inside the sphere is
constant:
𝑣
(
𝑟
)
=𝑐𝑜𝑛𝑠𝑡
(79)
Since there is no refraction were 𝑛=𝑐𝑜𝑛𝑠𝑡 the
fastest route would be a straight line, and that is the
path in which the light travels.
Figure 11: Movement of light inside spherical medium.
The angle between the trajectory of the light and the
initial radius vector 𝑟
is constant.
𝛿=𝑐𝑜𝑛𝑠𝑡
(80)
Using the sine theorem for every 𝑟,𝜃
(
𝑟
)
throughout
the course between points 𝐴, and 𝐵:
sin𝛿
𝑟
=
sin
(
180 − 𝜃
)
𝑟
(81)
𝑟sin𝜃=𝑟
sin𝛿=𝑐𝑜𝑛𝑠𝑡
(82)
Since 𝑛
(
𝑟
)
is constant as long as the movement is a
straight line:
𝑛
(
𝑟
)
∙𝑟sin𝜃=𝑐𝑜𝑛𝑠𝑡
(83)
Assuming there is a medium change between points
𝐴, and 𝐵:
During the movement of the light through 𝑙
, and
through 𝑙
there is no medium change, so it has been
showed that the equation holds for these parts of the
course. At the point of the refraction it was proven
that Snell's law applies:
𝑛
sin𝜃
=𝑛
sin𝜃
(84)
Since the radius is the same on that point it can be
multiplied on both sides of the equation:
𝑛
𝑎∙sin𝜃
=𝑛
𝑎∙sin𝜃
(85)
Revisiting Johann Bernoulli’s Method for the Brachistochrone Problem
113

Since the equation is true on the refraction points, and
also between refractions, it applies throughout all of
the movement between points 𝐴, and 𝐵. So, overall:
𝑛
(
𝑟
)
∙𝑟sin𝜃=𝑐𝑜𝑛𝑠𝑡
(86)
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
114
