An Upcycling Tokenization Method for Credit Card Numbers

Cyrius Nugier

1 a

, Diane Leblanc-Albarel

2 b

, Agathe Blaise

3,4 c

, Simon Masson

3,5 d

Paul Huynh

5 e

and Yris Brice Wandji Piugie

6,7 f

LAAS-CNRS, Université de Toulouse, Toulouse, France

CNRS, IRISA, INSA de Rennes, Rennes, France

Thales, Gennevilliers, France

Sorbonne Université, Paris, France

Université de Lorraine, INRIA, Loria, CNRS, Nancy, France

FIME EMEA, Caen, France

Normandie Université, UNICAEN, ENSICAEN, CNRS, GREYC, 14000 Caen, France

Keywords:

Token Service Provider, Credit Card Numbers.

Abstract:

Internet users are increasingly concerned about their privacy and are looking for ways to protect their data.

Additionally, they may rightly fear that companies extract information about them from their online behavior.

The so-called tokenization process allows for the use of trusted third-party managed temporary identities,

from which no personal data about the user can be inferred. We consider in this paper tokenization systems

allowing a customer to hide their credit card number from a webshop. We present here a method for managing

tokens in RAM using a table. We refer to our approach as upcycling as it allows for regenerating used tokens

by maintaining a table of currently valid tokens. We compare our approach to existing ones and analyze its

security. Contrary to the main existing system (Voltage), our table does not increase in size nor slow down

over time. The approach we propose satisﬁes the common speciﬁcations of the domain. It is validated by

measurements from an implementation. By reaching 70 thousand tries per timeframe, we almost exhaust the

possibilities of the “8-digit model” for properly dimensioned systems.

1 INTRODUCTION

Internet users leave digital ﬁngerprints behind them,

even behind a pseudonym. All this data can be stud-

ied in order to infer information about the users and

their behaviors. This is notably done on the largest

e-commerce platforms and social networks. More

speciﬁcally, buying patterns of consumers are ex-

tremely valuable to companies, as they help them un-

derstand their market. In addition, the storing of on-

line payment data is not secure and there is always

a risk of a data leak. Last years have witnessed nu-

merous episodes of credit cards thefts online, like

https://orcid.org/0000-0003-1276-0296

https://orcid.org/0000-0001-5979-8457

https://orcid.org/0000-0002-9598-8482

https://orcid.org/0000-0001-8778-2575

https://orcid.org/0000-0002-6965-3427

https://orcid.org/0000-0002-6258-6073

the Davinci breach (Krebs, Brian, 2019) in February

2019 (2.15 M stolen credit cards), the Bigbadaboom-

II (Thales group, 2018) in March 2018 where compro-

mised details were released by the FIN7 threat group,

and the Bigbadaboom-III (Sussman, 2020) in January

2020 (30 M stolen credit cards), to name only a few. It

is therefore natural for customers to worry about their

card number being leaked and to expect the damage

to be mitigated in case of leakage.

According to (Whatman, 2020), there were 2.8

billion credit cards worldwide in 2019, and the num-

ber of credit card transactions in 2017 was estimated

to 41 billion in the US. Also, according to the Cen-

sus Bureau of the Department of Commerce (U.S.

Department of Commerce, 2020), the estimate of

U.S. retail e-commerce sales for the second quarter

of 2020 was $211.5 billion, an increase of 31.8 per-

cent (±1.2%) from the ﬁrst quarter of 2020. In total,

the estimated e-commerce sales represent 17% of all

sales.

Nugier, C., Leblanc-Albarel, D., Blaise, A., Masson, S., Huynh, P. and Piugie, Y.

An Upcycling Tokenization Method for Credit Card Numbers.

DOI: 10.5220/0010508600150025

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 15-25

ISBN: 978-989-758-524-1

The ability to use multiple fake but veriﬁable

credit card numbers over time and to limit their spend-

ing capacity allows for the protection of the cus-

tomer’s identity and data. However, assigning these

new bank identities called “tokens” to customers in

an efﬁcient and secure way is still a challenge.

Our Contributions. In this paper, we study CCNs

tokenization systems. We take a look at existing ap-

proaches to create a tokenization system and then pro-

pose one that avoids their main issues while still com-

plying with the domain speciﬁcations. We refer to our

approach as upcycling since it allows for regenerating

used tokens by maintaining a table of currently valid

tokens, thus eliminating the need to create new tables

over time and slowing down calculations. To satisfy

auditability requirements, transactional data will be

stored in an external database. We propose a proof

of concept implementation and study its memory and

time performances.

Organization of the Paper. Section 2 introduces

the background of tokenization systems for CCNs.

Section 3 contains related works on the domain. Sec-

tion 4 presents our approach and the different algo-

rithms composing it. We study the compliance with

the speciﬁcations and the impact of different param-

eters on our system. Section 5 gives experimentation

and benchmark results of our proof-of-concept imple-

mentation. The TSP source code used for the tests

and evaluation is available on git as supplementary

material (Albarel., 2021) Section 6 draws conclusions

from our work.

2 BACKGROUND

In this section we introduce the domain of tokeniza-

tion systems for credit card numbers.

2.1 Credit Card Numbers

Credit card numbers (CCNs), or primary account num-

bers (PANs), consist of a maximum of 19 digits that

identify the card issuer and the cardholder. As de-

picted in Figure 1, they are composed up of three main

elements, in accordance with ISO/IEC 7812-1 (Inter-

national Organization for Standardization, 2017):

1. The issuer identiﬁcation number (INN), which

corresponds to the leading 8 numerical digits.

2. The individual account number (IAN), which can

be of variable length – between 1 and 10 digits.

3. A check digit (CD) computed from all the pre-

ceding digits of the PAN using the Luhn algo-

rithm (Luhn, 1960).

The individual account number is usually 7-digit long,

which amounts to a total of 16 digits in a PAN.

INN IAN CD

Figure 1: Credit Card Numbers format.

As for the payment token, it is possible to adopt a

structure that slightly deviates from the conventional

format (Payment Card Industry, 2015). For instance,

the ﬁrst four digits can be used to identify the card

issuer; the last four digits are ﬁxed and can be used for

integrity or error detection purposes in the token (such

as a checksum); the remaining 8 “open” digits in the

middle identify the token. In the remaining sections

of the paper, this format – shown in Figure 2 – will be

considered.

TSP ITN ﬁxed

Figure 2: Possible token format.

At the back of a physical card, three additional digits

form the Card Veriﬁcation Value (CVV). Their pur-

pose is to guarantee the physical possession of the

card and therefore, they have no use in a digital appli-

cation like tokens. Moreover, according to PCI com-

pliance rules, the CVV should never be stored except

by the card issuer (Payment Card Industry, 2020).

2.2 Tokenization

Nowadays, in order to increase the security of online

transactions, many payment systems use to provide

users with a temporary identity. This reduces trace-

ability, limits the possible inferences and risks of data

leakage.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

CCN

Token request

Data retrieval

Token emission

Payment attempt

Payment request

Detokenization

Payment

Time-sensitive op

Customer

TSP

Merchant site

Card issuer

#TOK

Figure 3: A Standard Tokenization System.

A common approach is tokenization: this process re-

places an existing payment card number with a sub-

stitute value called token, that is issued by a trusted

third-party, called a Token Service Provider (TSP),

that serves as a proxy masking the user’s real iden-

tity. A token is then used during a payment transac-

tion, allowing one to proceed with the payment with-

out exposing actual bank details. The Token Service

Provider associates the original card number with the

tokens and stores all sensible data securely.

More precisely, the TSP manages the entire life-

cycle of tokens. The typical scenario in this context is

depicted in Figure 3:

1. Token Request. The customer requests a token

from the TSP.

2. Query. The TSP queries all data needed for the

creation of the token (usually from the card issuer

or customer).

3. Tokenization. The TSP creates a token from the

Credit Card Number and sends it to the customer.

4. Purchase. The customer purchases an item or ser-

vice from an online shop and transmits the token

number instead of their Credit Card Number.

5. Payment Request. The merchant site returns the

token to the TSP and claims the payment.

6. Detokenization. The TSP converts the token back

to the correct Credit Card Number and transmits

the payment request to the card issuer

7. Payment. The card issuer satisﬁes the payment

request from the merchant site.

The main role of the TSP is the role of the token

vault: establishing a correspondence between the to-

ken and the Credit Card Number. The TSP can en-

dorse additional responsibilities like domain manage-

ment (giving additional security by limiting the to-

kens to speciﬁc channels or retail domains) and au-

thentication (ensuring during the detokenization pro-

cess that the token has been legitimately used by the

correct client). For this, it can verify the identity of

the users, by asking them to claim their identity with

a password, through multi-factor authentication, or

with a cryptographic signature, e.g., the ECDSA stan-

dard (Johnson et al., 2001).

Card issuers can endorse the role of TSP, allowing

full control of the tokenization process. Otherwise,

card issuers may use a third-party TSP and integrate

it with their payment systems.

2.3 Speciﬁcations

The speciﬁcations for the tokenization systems are

listed hereafter. They ensure that the goals of protec-

tion of the customer are met without loss of quality of

service.

1. Unicity. Each token should be attributed to at

most one user at any given time.

2. Expiry. A token has a maximum number of uses, a

maximum spending amount and/or an expiry date.

3. Formatting. The format of the token should be

identical to CCNs.

4. Distribution. The distribution of the tokens’ open

digits should be uniform.

5. Unlinkability. Tokens should not be linkable to

one another, or to a user.

6. Timeframe. Tokenization and Detokenization

computation times should not exceed a given

timeframe value denoted T f . In this paper, we

consider T f to be 100 ms as a constraint from card

issuers so the TSP slowdown is not too noticeable

from the customer point of view.

7. Unforgeability. An adversary should be unable to

forge a valid token and obtain payment.

An Upcycling Tokenization Method for Credit Card Numbers

8. Reusability. The space of all tokens’ open digits

being smaller than the expected number of token

requests, the same open digits should be able to

be issued several times.

9. Auditability. This depends on the legislation the

TSP is submitted to. It varies from one country to

another. We consider that the time and data for all

tokenizations and all detokenizations (succeeded

or failed) should be stored for 5 years.

10. Security. Any storage of data should be as secure

as possible as long as all previous speciﬁcations

are validated.

11. Limited Storage Space. Any data storage used

should be small enough to not create additional

costs for TSPs, as long as all previous speciﬁca-

tions are validated.

3 RELATED WORK

In this section, we present the related work on format-

preserving encryption (FPE) and static pre-computed

tables. We position our contribution with respect to

the described related work.

The authors in (Díaz-Santiago et al., 2014) for-

mally deﬁne tokenization systems and identify three

different systems that solve the problem of tokeniza-

tion both securely and efﬁciently. The ﬁrst one uses

format-preserving encryption (FPE), while the lat-

ter two systems rely on off-the-shelf cryptographic

primitives using ordinary block ciphers, stream ci-

phers supporting initialization vectors, and physical

random number generators. The difference between

both relies on whether pairs of token and PAN are

stored in the card-vault in the encrypted form or not.

The authors also give several security notions and

provably secure constructions. However, they do not

consider adaptive constructions, and unlike (Cachin

et al., 2017), they do not address updatable tokens.

The authors also refer to the “Voltage Security” so-

lution (Voltage Security, 2012) as the only solution

at this time to the tokenization problem with known

cryptographic guarantees, using static pre-computed

tables.

As a matter of fact, most existing solutions are

static and do not provide key updatability, i.e., they

do not regularly update the cryptographic keys, while

maintaining the tokens’ consistency, which could lead

to security issues. Therefore, in most practical de-

ployments, cryptographic keys must be re-keyed pe-

riodically to ensure continued security. (Cachin et al.,

2017) constructs two tokenization models for updat-

able tokenization with key evolution, in which a key

exposure does not disclose relations among tokenized

data in the past, and where the updates to the tok-

enized data set can be made by an untrusted entity and

preserve the consistency of the data. The authors for-

mally deﬁne the security requirements that guarantee

unlinkability among different tokens generated from

a same user.

3.1 Format-preserving Encryption

One common option for the generation of tokens is

the use of Format-preserving Encryption (FPE) (Bel-

lare et al., 2009). FPE can be seen as a key-indexed

pseudorandom permutation of the set of all values of

correct format, called domain. The keyspace can be

much greater than the domain (should have crypto-

graphically big enough size).

FPE has gradually emerged as a useful tool in ap-

plied cryptography in recent years. The initial mo-

tivation for its use came from the encryption issues

raised by companies looking for speciﬁc data formats.

For instance, encrypting distinct and unpredictable

16-digit credit card numbers with traditional block ci-

phers would expand the data and change its format,

which would require modiﬁcations of the applications

or databases at huge expense (Liu et al., 2010).

The goal of FPE is to avoid the need for a database

to link a token to a CCN. The natural use of FPE is to

encrypt the individual account digits (and the check-

sum digit) as the 8 open digits of the token. The vali-

dation of the token is then done by decryption of the 8

open digits of the token to retrieve a card number that

is then transmitted to the bank for payment. If the to-

ken given by the merchant to the TSP is incorrect, the

corresponding bank account would be invalid.

For now, the domain size remains out of reach of

known attacks on small domains, as it is big enough.

For example, in (Hoang et al., 2018), attacks are pro-

vided on domains up to 8 bits. Following the attacks

discovered in (Durak and Vaudenay, 2017), the Na-

tional Institute of Standards and Technology (NIST)

recommends using domains of at least one million el-

ements (NIST, 2020). With one hundred million do-

mains, the CCNs FPE systems are still out of reach for

now, but this should be a concern for a long-lasting

system.

The ﬁrst limitation found in the use of FPE is that

the map from users to the 8 open digits is not bijec-

tive, since two banks with different ﬁxed digits can

issue the same open digits to two different users, e.g.,

John Doe, client ID 1234 5678 at BankA and Michel

Dupont, client ID 1234 5678 at BankB. Such a sce-

nario would imply that the tokens generated by these

users would always be the same. These two users can-

SECRYPT 2021 - 18th International Conference on Security and Cryptography

not have tokens issued with the same key. Another

possibility is to have an injective map from card is-

suers to TSP that would avoid this type of conﬂict,

i.e., having a single TSP per card issuer.

Assuming that the indexing secret keys are

changed regularly, two different card numbers with

two different keys can yield the same token. In this

case, in the veriﬁcation phase, it would be impos-

sible to differentiate the two tokens (see Speciﬁca-

tion 1 of Section 2.3) except with the inclusion of ad-

ditional identiﬁcation information that would need to

be stored. Additionally, the pairs (token, secret key)

would anyway be kept in a database in order to know

which key needs to be used to decipher a given token.

Storing these pairs and identiﬁcation data defeats the

advantage of using FPE instead of having a static pre-

computed table (knowingly reducing storage space).

Besides, if we keep the same secret key across

time, it opens the possibility for attackers to trace a

token number, since it is permanently linked to the

card number. This would not comply with Speciﬁca-

tion 5 of Section 2.3.

To summarize, the use of FPE would either cre-

ate collisions or require a database. In the latter case,

it just creates an overhead that can be avoided with

a classical table/database. In conclusion, our system

will not use FPE.

3.2 Static Pre-computed Tables

We call static pre-computed tables those which con-

tains all possible token values computed in advance.

Voltage Security proposed a way to generate and

use tokens (Voltage Security, 2012) in 2012, accord-

ing to the Payment Card Industry Data Security Stan-

dards (PCI DSS) requirements (Payment Card Indus-

try, 2020), which include for example the need to in-

stall and maintain a ﬁrewall conﬁguration to protect

cardholder data, to protect the stored data, to encrypt

every transmission of cardholder data across public

networks, etc.

During tokenization, a token is randomly asso-

ciated with the card number. With a good random

number generator and good management of the ta-

ble where the tokens are stored, this solution is com-

pletely in accordance with the PCI DSS and allows for

a quick tokenization process. During the detokeniza-

tion phase, it simply checks if the token exists in the

table and, in that case, the associated bank account is

returned.

However, the Voltage approach leaves some

doubts about the security of the table, which is kept

in plain text. More importantly, no mechanism avoids

the saturation of the table. This could be a problem if

the maximum number of 10

tokens is reached. For

certain this technique allows for a tokenization that

is fast on average, but problems arise whenever the

number of tokens increases. What Voltage proposes

to tackle this issue is to create a new table when the

previous one is saturated. However, this mechanism

increases the detokenization times since multiple ta-

bles have to be searched to ﬁnd the correct bank ac-

count. Additionally, this creates the need for more

data storage space.

The main design consideration of our contribution

was to remove the increase of storage and computa-

tions over time. Although (Cachin et al., 2017) does

a ﬁrst step by providing encryption and key updata-

bility, it does not allow for table cleaning and token

reusability. Up to our knowledge, we are the ﬁrst to

provide all of these features. Our proposition allows

one to have a dynamic table that is more portable.

Moreover, we propose a method that regularly cleans

the table, considering an expiry time for tokens and

a maximum number of uses. This way, our system

allows reusing the tokens that are no longer in use in

order to ensure the sustainability of our system over a

long time.

4 OUR UPCYCLING

TOKENIZATION METHOD

In this section, we introduce our upcycling tokeniza-

tion method. We discuss how to properly chose pa-

rameters and introduce the composing functions of

our system.

4.1 System Overview

Our approach is a modiﬁcation of Voltage’s static pre-

computed table that integrates a cleaning mechanism.

Thanks to this mechanism, it is not necessary to create

an additional table every time the previous one starts

to be too full. Additionally, we encrypt the table for

more security, and we include a mechanism for updat-

ing encryption keys, as well as a mechanism to detect

accidental modiﬁcations in the table. We include an

extra database for audit purposes.

This construction has been built on the supposi-

tion that the storage of all cryptographic secrets (keys,

initialization values) is proper and secure. Also, we

assume the randomness generators to be cryptograph-

ically strong.

The basis of our approach is the creation of a table

in RAM indexed by the token numbers, which there-

fore consists of n

max

rows, where n

max

is the num-

ber of possible tokens, i.e., 10

in the 8-digit model.

An Upcycling Tokenization Method for Credit Card Numbers

To retrieve data from a token to complete a payment,

there is just to retrieve the data contained in the row of

the table corresponding to the token. A row is there-

fore composed of:

• The credit card number CN, stored on 64 bits to

include the 16 CCNs digits

• A timestamp expiry = current time + lifespan,

which is expressed in seconds and thus stored over

32 bits, or expressed with a larger range or higher

precision and stored over 64 bits. It indicates the

expiry date of the token.

• A counter num_uses of the remaining uses of the

token. An 8-bit integer is enough for the predicted

use of the tokens since increasing the number of

uses of the same token increases its traceability.

If num_uses = 1 for all tokens, this ﬁeld can be

removed.

• A counter credit of the remaining possible spend-

ing with this token. This ﬁeld is also optional.

• If the tokenization scheme includes an authenti-

cation mechanism, all the required data should be

stored in the row, e.g., password, veriﬁcation keys,

email address, or phone number for multi-factor

authentication.

• The random number rand used to generate the to-

ken (32 bits) can also be stored, it allows for the

veriﬁcation of the row during the Clean_table op-

eration.

We propose the functions Tokenization and Deto-

kenization to create and use tokens, and also a

Clean_table function veriﬁes the contents of the table

and removes decayed tokens.

Ideally, the table should be created contiguous in

memory so that the access to the n

element could be

done by calculating the offset from the ﬁrst element.

This way, tokens are perfectly indexed by their value.

This allows keeping a constant access time for lookup

while keeping a minimal database space (Speciﬁca-

tion 6). For security purposes, it is also recommended

that the database should be encrypted via a secret key.

Note that according to the volume of data to store

for authentication the table size can vary. However, a

good computer could have it entirely in RAM without

the use of non-volatile memory.

The number of uses given for a token and its lifes-

pan should be very carefully chosen according to the

expected rate of use of tokens. For example, imagine

an e-commerce scenario, we can say that tokens have

a 10-minute lifespan, since most transactions that are

longer than this become invalid for security reasons.

If the tokens have only one use, every consumer

that fails to complete the transaction leaves an unused

token in the table. If they have more than one, it is

increasingly probable that at least one will never be

used in a transaction and leave a token in the table.

The expiry of the tokens allows to detect them and

remove them periodically.

The best parameters would be to choose the min-

imal numUses and li f espan values that validate the

design constraints on the system. The cleaning of the

table (Clean_table) should be executed periodically,

e.g., once a day or week or month, according to the

expected number of tokens that will not be used dur-

ing their lifespan, the period should be high enough

to ensure there is always room to create new tokens.

All the actions done in the table and every call to

our functions can be stored with a timestamp in a per-

manent external encrypted database to comply with

auditability requirements. According to the legisla-

tion applied on the TSP, some ﬁelds are expected to

be stored or not. The legislation may require the data

to be stored for a given amount of time and deleted af-

terward. Since this is classical database management,

we will just present when our system adds data into

the database.

4.2 Description of the Functions

The three following functions enable one to complete

the whole tokenization and detokenization process, as

well as the maintenance of the table. Hereafter fol-

lows a detailed description of each process.

4.2.1 Tokenization

The tokenization process consists in generating a to-

ken tok from a card number CN. It also implies stor-

ing the data concerning the user in order to proceed

with subsequent detokenizations.

The algorithm Tokenization(Tab, CN, num_uses,

credit expiry, auth, sk) takes as input the table Tab,

the credit card number of the user CN, the maximum

number of uses of the token num_uses, a timestamp

expiry, and any extra information auth that would be

useful to retrieve at the time of detokenization (e.g.

cryptographic public key), as well as the system’s

cryptographic key (and iv) sk.

First, if required, a tokenization call is added to

the external database.

Then, the algorithm picks uniformly a 32 bit rand

and computes the 32 last bits of

hash

= SHA

224

(CN,expiry, auth,rand).

To ensure the uniformity of the output distribution,

this process is repeated with a new rand while hash

SECRYPT 2021 - 18th International Conference on Security and Cryptography

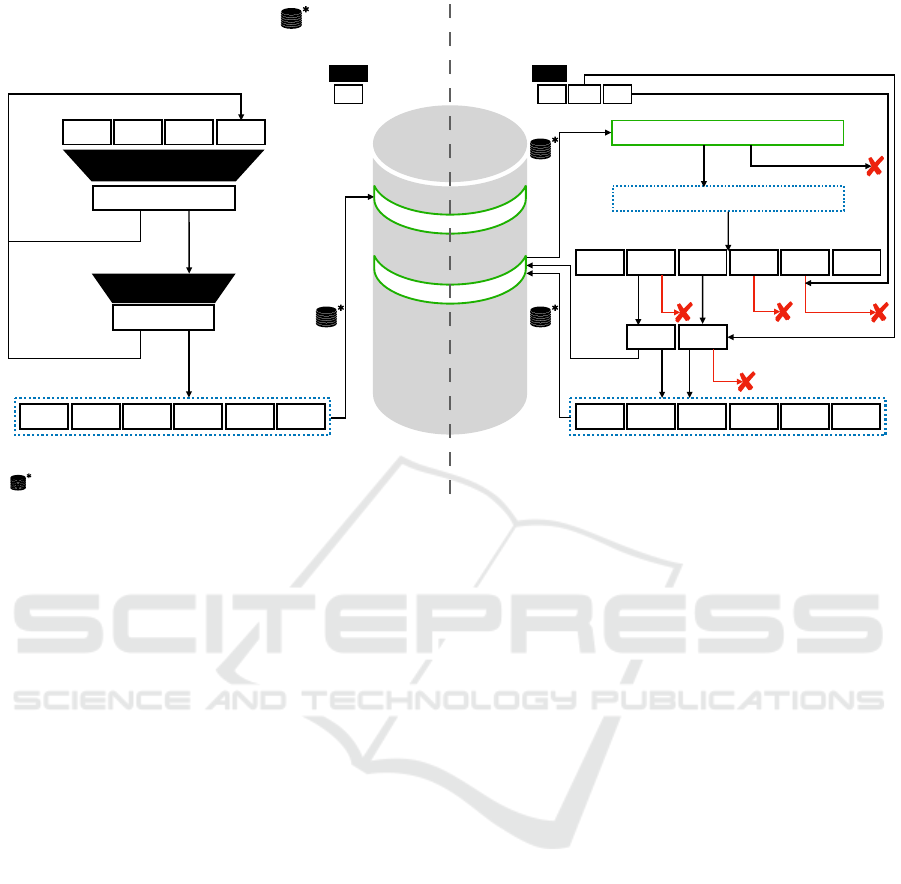
# of uses!

-=1

Balance

# of uses

@tok not free

TOK

mod 10

hash

SHA

234

@tok

> 2

- (2

% 10

)

encrypted under sk

empty

encrypted data

decrypt sk

@tok

≠ 0

= 0

≠ 0 = 0

Tokenization Detokenization

< now invalid

32 32/64 32

zeroes

TOK

Output

Inputs

Table

External database insertion

Exp

Auth

Rand

Debit

Sign

encrypted under sk

# of uses

Balance

Auth

Exp

Rand

# of uses

Balance

Auth

Exp

Rand

Balance

Auth

Exp

Rand

Balance!

-=Debit

≤ 0> 0

Figure 4: Upcycling Tokenization Table Algorithms.

is greater than the biggest multiple of 10

written in

32 bits (happens 0.1% of time).

Then, given n

max

the maximum number of rows it

computes tok = hash

mod n

max

This way, a token (8 open digits) is generated uni-

formly by hashing the data including rand and reduc-

ing the result into the token space by carrying out a

modulo n

max

operation on it.

num_uses is not included since it will vary over

time. Then, it checks whether tok corresponds to

an empty row of the table. If the token already

exists and is valid, then the process restarts and

tries with a fresh rand value until a new token

is found. Once an empty row is found, it inserts

Encrypt

in the row.

If the duration of the algorithm came to exceed

time f rame, the algorithm would stop with a failure

ﬂag. Else, it would return a success ﬂag and the 8-

digit token that got created.

The TSP should ensure to format properly the to-

ken back to a full token format by adding the TSP

identiﬁer and the checksums.

All ﬁelds required for audit purposes (e.g., the to-

ken number) are transmitted to the external database.

4.2.2 Detokenization

The detokenization process consists in retrieving a

credit card number CN from a token tok.

If needed (e.g., to detect malicious users request-

ing payments), the algorithm saves the detokenization

call in the external database.

The algorithm Detokenization(Tab, tok, debit,

verif, sk) takes as input the table Tab, the token tok

to verify (as an 8-digit value), verif the data possi-

bly required for authentiﬁcation (e.g., cryptographic

signature) and sk the system’s cryptographic key (and

iv).

It checks whether the table row indexed by tok

is empty or not. If it is empty, the token is invalid

and the algorithm stops with a failure ﬂag. Oth-

erwise, the row is deciphered with sk to retrieve

ken is depleted or invalid, or credit < debit the row

is deleted and the algorithm stops with a failure ﬂag.

Else, the algorithm Verify_signature(auth,verif) to

authenticate the consumer. If Verify_signature re-

turns a failure ﬂag, Detokenization stops and returns a

failure ﬂag. We further detail authentication methods

in Section 4.5.

Else, everything went well, num_uses is decre-

mented, debit is substracted from credit. If it reaches

0, the row is deleted, else the row is kept encrypted in

the table. Either way, the CCN is returned. It can be

sent to the card issuer for completion of the payment.

Also, any changes to the token can be reported in

the external database for audit purposes.

An Upcycling Tokenization Method for Credit Card Numbers

4.2.3 Cleaning the Table

To perform the cleaning, each row of the table is

checked and kept only if the token is still alive and

correct.

The algorithm Clean_table (Tab,sk) takes as in-

put the table Tab and sk the system’s cryptographic

key (and iv). For all rows, it deciphers the row to re-

The call to this function can be saved in the exter-

nal table if needed.

The number of remaining uses and the expiry date

are veriﬁed. If the validity date has passed or if the

maximum number of times the token has been used is

reached, then the row is erased. In order to detect er-

rors in the table, the algorithm can also compute if CN

is a valid CCN by verifying its checksum, and whether

SHA

224

(CN,expiry, auth,rand) mod n

max

is the in-

dex of the row. If no error is found, the token stays

as it was and the algorithm continues with the next

one. Each cleaned row can also be stored in the exter-

nal database.

Also, keeping the same secret key for a long

time is insecure, it should be changed regularly.

Clean_table could also be used as a key updater by

taking as additional input the new_key. Each row

is deciphered with sk, and after normal operations,

the rows are inserted back in the table encrypted with

new_key, which now acts as sk.

4.3 Conformity with Speciﬁcations

We prove that given a correct set of parameters, each

speciﬁcation is validated by our approach.

1. Unicity. Each token is unique because Tokeniza-

tion only returns a non-existing token.

2. Expiry. This is guaranteed by the veriﬁcation

process during Detokenization and the fact that

num_uses is decremented after each use. expiry

and num_uses are never incremented.

3. Formatting. The token format matches the one of

CCNs because of the formatting step at the end of

Tokenization.

4. Distribution. Any newly issued token has a num-

ber taken from a uniform distribution (property of

the hashing function).

5. Unlinkability. Since our systems includes random

values into the hash, there is no information de-

ductible from the observation of multiple tokens,

even with all other ﬁelds of the row being the

same. Therefore no link can be inferred between

tokens and consumers.

6. Timeframe. Tokenization times can be guaranteed

to be bounded, with the probability of failure to

deliver a new token being arbitrarily low. How-

ever, the implementation optimization, the com-

puter performances, and the value of T f have an

impact that we quantiﬁed in the upcoming para-

graph. Detokenization times are bounded because

the table access is in constant time.

7. Unforgeability. Without authentication of the cus-

tomer during a payment request, a merchant site

could submit a random illegitimate token and send

a payment request. The probability of success

is equal to the number of currently valid tokens

divided by the total number of tokens. In a to-

ken space of 10

, this causes a lot of design con-

straints. Therefore, authentication is needed to en-

sure this property.

8. Reusability. A properly sized system ensures by

cleaning regularly the table that all expired tokens

can be used again.

9. Auditability. All functions called and all tokens

created and modiﬁed can be stored in a permanent

external encrypted database according to TSP reg-

ulations.

10. Security. The table and the external database are

encrypted. Good key management is necessary.

11. Limited Storage Space. For normally sized au-

thentication data, the table can be in a computer’s

RAM. The external database should contain only

the required data to limit costs.

4.4 Probability of Tokenization Failure

Let us consider a token space of size n

max

, the num-

ber of already generated tokens n and the number of

tries T to generate a new token that can be done in the

given timeframe T f .

We study the maximum n, such that the probabil-

ity of a failure to create a new token is smaller than

−λ

, where λ is the security parameter. The probabil-

ity of failure is the probability of obtaining consecu-

tively T already existing tokens, which happens with

a probability of

max

. Thus we obtain the following

inequality:



max



⇐⇒ n < 2

log

max

)−

. (1)

When λ  T , n ≈ n

max

. Therefore with reasonable

security parameters, e.g., 128 or 256, we need to op-

timize enough the implementation so that T is big

enough. As long as this is the case, n ≈ n

max

, and any

failure to create a token in an upcycling table is proof

SECRYPT 2021 - 18th International Conference on Security and Cryptography

that either the system isn’t properly dimensioned or

that the 8-digit model is no longer big enough. (It

would imply that around ≈ 100Musers are instanta-

neously in a transaction.)

4.5 Authentication Methods

Here we propose three authentication solutions to en-

sure unforgeability.

1. Password: During the token request, the cus-

tomer chooses a password and sends a hash to the

TSP as auth. During detokenization the customer

submits verif, Verify_signature will just check

whether auth = verif (Halevi and Krawczyk,

1999). Note that using always the same pass-

word would allow an observer to infer that mul-

tiple detokenizations may be linked.

2. Signature: During the token request, the customer

sends a cryptographic public key auth. Dur-

ing detokenization the customer submits verif, its

cryptographic signature. Verify_signature is the

cryptographic veriﬁcation of the signature (John-

son et al., 2001). Note that no information can be

inferred from proper cryptographic signatures.

3. Multi-factor Authentication: During the token re-

quest, the customer sends contact data auth, such

as email address or phone number. During detok-

enization Verify_signature picks a code C, sends

it via email or SMS to the customer. If the cus-

tomer then submits verif = C, then the authentica-

tion is validated (N. Owen and Shoemaker, 2008).

Since C is chosen at random independently of the

user, no link can be inferred between two detok-

enizations.

5 PERFORMANCES

In this section, we evaluate our solution in terms of

table ﬁll rate and time taken by tokenization, detok-

enization, and the cleaning of the table. We also pro-

vide the RAM usage needed to run our solution.

We decided to use the C language to have good

memory management. This choice allows us not only

to reduce the amount of RAM used, but also to reduce

the token generation time by controlling precisely the

size of the data. For the sake of reproducibility, our

source code is publicly available on a repository (Al-

barel., 2021).

5.1 Tokenization Time and Table Fill

Rate

We performed our experiments on an AMD EPYC

7742 64-Core Processor. Each processor has an av-

erage speed of 3240.029MHz.

For each experiment, we generated tokens cor-

responding to random credit card numbers and then

ﬁlled our 10

rows table with tokens. We tried to

generate new tokens until the table is so full that a

new token could not be generated in less than the T

timeframe of 100ms. We repeated this experiment

10 times to obtain statistically signiﬁcant results. We

then evaluate several metrics: the table ﬁll rate be-

fore the ﬁrst failure happened, the number of missed

tries that lead to this ﬁrst failure, the maximum num-

ber of tries before inserting a correct value, and the

time needed to ﬁll the table before an insertion fails.

Hereafter, Figure 5 shows the box plot of these four

metrics computed for 10 ﬁll table operations.

Our results show that the table can be ﬁlled to

a median of 99.99% with a standard derivation of

0.002 (Figure 5a) before the ﬁrst failed token creation,

which is very satisfying.

The number of tries per timeframe can be bounded

between the number of tries before the ﬁrst failure

(Figure 5b) for which the median is 70,268, with a

small standard deviation equal to 634 and the number

of tries per timeframe is the number of tries before

inserting, which median is equal to 65,251.

The median time to ﬁll the table before a failure

occurs (Figure 5d) is 1344 seconds (i.e., 22 minutes

and 44 seconds), also with a very small standard de-

viation equal to 28 seconds.

Suppose a TSP wants to ensure a very low proba-

bility of failure e.g

128

. From 1, with T = 70000, we

ﬁnd a maximum table ﬁll rate of 99.8733%, which in-

dicates that the bottleneck is more the size of the table

than the performances.

Our experimentation show that single try for

tokenization lasts approximately 100ms/70,268 =

0.0014233ms. Since 99.99% of 10

tokens are cre-

ated in 1350s, an insertion took in average 0.0135ms,

or 75,750 tokens created per second.

To illustrate, credit cards can do 5000 transactions

per second. There is an average of 1 billion credit

card transactions per day worldwide, or an equivalent

of 11574 transactions per second (CardRates, 2020).

Our construction covers 6.5 times this rate. Further-

more, with a 10-minute token lifespan, with maxi-

mum token creation speed, a maximum of 45 million

valid tokens can be in the table at any given time. So

with Clean_table called every 10 minutes, there is no

possibility for the table ﬁll rate to go over the security

An Upcycling Tokenization Method for Credit Card Numbers

(a) Final table ﬁll

rate (%)

(b) Tries before ﬁrst

failure

tries before success

(d) Time to ﬁll the

table (s)

(e) Time to detok-

enize the table (s)

(f) Time to clean the

table (s)

Figure 5: Box plot of evaluation metrics for Tokenization, Detokenization and Clean_table.

threshold.

5.2 Detokenization and Cleaning Table

Time

Finally, we also measured the average time needed

to detokenize and clean the table. In addition to the

tokenization metrics, Figure 5 also provides statistics

about the Detokenization and Clean_table operations.

We observe that the Detokenization operation

(Figure 5e) for a table ﬁlled with tokens takes on av-

erage 660 seconds, i.e., 11 minutes, with a very low

standard deviation of 26 seconds. This represents

only 6µs for a single detokenization, which is far less

than the expected 100ms timeframe.

The Clean_table operation was also run on a ta-

ble ﬁlled with depleted tokens. The median time for

cleaning the table (Figure 5f) is 36.6 seconds with a

standard derivation of 0.43 seconds. This illustrates

that our upcycling tokenization technique can cope

well with large data as it is able to clean the table in a

very short time.

5.3 RAM Usage

The theoretical amount of RAM usage depends on the

row length and encryption design of the table. De-

pending on the security requirements, one can decide

whether to encrypt the table or not. If it is the case, the

table would be encrypted with Advanced Encryption

Standard (AES) and thus in 128-bit blocks.

For our experiments (64 bits expiry and a 64 bit

auth), the data in a row being stored on 232 bits, the

encryption would be done on 2 blocks of 128 bits.

With n

max

= 10

rows to store, 25.6GB of RAM are

necessary for the storage of the encrypted table. If we

choose not to encrypt the table, only 23.2 GB of RAM

are used for storage. Note that if auth is bigger, extra

AES blocks must be added which would increase the

memory requirements for the table.

6 CONCLUSIONS

In this paper, we proposed a solution for tokeniza-

tion systems for Credit card numbers. This system is

based on the possibility to keep a full table of tokens

in RAM so that computations are fast enough to guar-

antee a tokenization within a 100ms timeframe as long

as the table is not ﬁlled more than 99.87%. An exter-

nal database allows us to keep transaction data for au-

ditability while also allowing the table to be cleaned

regularly from expired tokens.

Our approach is still limited by its single point of

failure nature and extra mechanisms should be added

to improve availability and resilience.

For example, each modiﬁcation in the RAM could

be duplicated in a SSD, in order to have a non-volatile

backup almost up to date. The RAM can also be

duplicated into another RAM to increase availability

with minimal losses in case of failure. The TSP role

could also be split across multiple computers by allo-

cating a partition of the token space to each computer.

Also, in order to reduce the memory requirements

of the table and store more data per row, one could

implement a scalable data structure such as a binary

tree or more advanced dynamic storage mechanisms.

Our experiments showed that our implementa-

tion satisﬁes the speciﬁcations of the Token Service

Providers, and is efﬁcient enough to manage 6 times

the current number of worldwide credit card transac-

tions.

ACKNOWLEDGEMENTS

This work was done in cooperation with the BE YS

GROUP through its Pay and Research branches in RE-

DOCS 2020 based on the BE YS PAY TSP project.

The authors would also like to thank Pascal Lafour-

cade and Olivier Blazy for their support, as well as

Marius Lombard-Platet for his insights.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

REFERENCES

Albarel., D. L. (2021). Tokenization. https://github.com/

DianeLeblancAlbarel/Tokenisation.

Bellare, M., Ristenpart, T., Rogaway, P., and Stegers, T.

(2009). Format-Preserving Encryption. In Jacob-

son, M. J., Rijmen, V., and Safavi-Naini, R., edi-

tors, Selected Areas in Cryptography, pages 295–312.

Springer Berlin Heidelberg.

Cachin, C., Camenisch, J., Freire-Stögbuchner, E., and

Lehmann, A. (2017). Updatable Tokenization: Formal

Deﬁnitions and Provably Secure Constructions. In Ki-

ayias, A., editor, Financial Cryptography and Data

Security, pages 59–75. Springer International Publish-

ing.

CardRates (2020). The Average Number of

Credit Card Transactions Per Day &

Year. https://www.cardrates.com/advice/

number-of-credit-card-transactions-per-day-year/.

Díaz-Santiago, S., Rodriguez-Henriquez, L. M., and

Chakraborty, D. (2014). A cryptographic study of to-

kenization systems. In 11th International Conference

on Security and Cryptography (SECRYPT), pages 1–

Durak, F. B. and Vaudenay, S. (2017). Breaking the FF3

Format-Preserving Encryption Standard over Small

Domains. In Katz, J. and Shacham, H., editors, Ad-

vances in Cryptology – CRYPTO 2017, pages 679–

707, Cham. Springer International Publishing.

Halevi, S. and Krawczyk, H. (1999). Public-key cryptog-

raphy and password protocols. ACM Trans. Inf. Syst.

Secur., 2(3):230–268.

Hoang, V. T., Tessaro, S., and Trieu, N. (2018).

The Curse of Small Domains: New Attacks on

Format-Preserving Encryption. In Shacham, H. and

Boldyreva, A., editors, Advances in Cryptology –

CRYPTO 2018, pages 221–251, Cham. Springer In-

ternational Publishing.

International Organization for Standardization (2017).

ISO/IEC 7812-1:2017 Identiﬁcation cards – Identiﬁ-

cation of issuers – Part 1: Numbering system. Tech-

nical report, International Organization for Standard-

ization. https://www.iso.org/obp/ui/#iso:std:iso-iec:

7812:-1:ed-5:v1:en.

Johnson, D., Menezes, A., and Vanstone, S. (2001).

The elliptic curve digital signature algorithm (ecdsa).

1(1):36–63.

Krebs, Brian (2019). A Month After 2 Million Cus-

tomer Cards Sold Online, Buca di Beppo Par-

ent Admits Breach. https://krebsonsecurity.com/tag/

davinci-breach/.

Liu, Z., Jia, C., Li, J., and Cheng, X. (2010). Format-

preserving encryption for datetime. In 2010 IEEE In-

ternational Conference on Intelligent Computing and

Intelligent Systems, volume 2, pages 201–205. IEEE.

Luhn, H. P. (1960). Computer For Verifying Numbers.

US2950048A.

N. Owen, W. and Shoemaker, E. (2008). Multi-factor au-

thentication system.

NIST (2020). Methods for Format-Preserving

Encryption: NIST Requests Public Com-

ments on Draft Special Publication 800-

38G Revision 1. https://www.nist.gov/news-

events/news/2019/02/methods-format-

preserving-encryption-nist-requests

-public-comments-draft.

Payment Card Industry (2015). Tokenization Product Secu-

rity Guidelines – Irreversible and Reversible Tokens.

https://www.pcisecuritystandards.org/documents/

Tokenization_Product_Security_Guidelines.pdf.

Payment Card Industry (2020). Payment Card Industry Se-

curity Standards. https://www.pcisecuritystandards.

org/pci_security/maintaining_payment_security.

Sussman, B. (2020). ’BIGBADABOOM!’ Card-

ing Forum Selling Millions of Records

from Wawa Stores Data Breach. https:

//www.secureworldexpo.com/industry-news/

carding-forum-wawa-data-breach-update.

Thales group (2018). Card Data from 5M Customers Stolen

in Data Breach at Saks Fifth Avenue, Lord & Tay-

lor. https://dis-blog.thalesgroup.com/security/2018/

04/03/saksﬁfthavenuedatabreach/.

U.S. Department of Commerce (2020). Quarterly Retail E-

commerce Sales. https://www.census.gov/retail/mrts/

www/data/pdf/ec_current.pdf.

Voltage Security (2012). Voltage secure stateless tok-

enization. https://www.voltage.com/wp-content/

uploads/Voltage_White_Paper_SecureData_SST_

Data_Protection_and_PCI_Scope_Reduction_for_

Todays_Businesses.pdf.

Whatman, P. (2020). Credit card statistics 2020: 65+ facts

for Europe, UK, and US. https://blog.spendesk.com/

en/credit-card-statistics-2020.

An Upcycling Tokenization Method for Credit Card Numbers