Fractional Order PV/T Model Design and Estimation using the

Fractional Observer

Amer Aziz

, Muwahida Liaquat

, Aamer Iqbal Bhatti

and Lahoucine Ouhsaine

National University of Sciences and Technology, Pakistan

Capital University of Science and Technology, Pakistan

Université de Lorraine Nancy, France

Keywords: Fractional-order System, PV/T Hybrid System, Observation, Fractional-HOSMO, Estimation, Disturbance,

Pseudo State.

Abstract: In the last decade, the demand for renewable energy sources has been increased due to factors which include

the rising fuel price and pollution, and consequently research on solar energy sources has been increased to

improve their efficiency. Photovoltaic Thermal (PV/T) system provides electrical power and heat

simultaneously, which is the promising technology. This research paper illustrates the simulation of the

comprehensive thermal-based mathematical model of the PV/T system with the joint estimation of the system

states: the temperature at each node, and disturbance using Fractional-High Order Sliding Mode Observer

(HOSMO). A fractional-order differential equation describes the PV/T system because of its characterization

in heterogeneous media and its multilayers structure. Fractional–HOSMO is a robust observer that can be

used further for the reduced-sensor control of PVT, which can be comparatively cheap. The parameter values

are derived from the thermal configuration of the layers and the properties of constituents.

1 INTRODUCTION

The photovoltaics (PV) system is affected by external

climatic conditions, so its electrical efficiency

decreases rapidly as its temperature increases. In recent

years, researchers have studied PV/T, which combines

both PV solar cells and thermal collectors to enhance

the overall efficiency and performance (Lobera, 2013;

Cui Young, Abd El-Samie and Alayi, 2020). The

impact and importance of heat transfer fluid like water,

air, nanofluids, and the other fluid types have been

described on the characterization and performance of

the PV/T system (Esfe, Eisapour, Salari and Alayi,

2020; Jiang Q, 2018). A water-based PV/T system is

commonly used in domestic because it is quite simple

and economical as compared to other types. It shows

improved performance and enhanced efficiency of the

thermal PV/T from the indoor and outdoor experiments

(Al-Waeli, 2018). A thermal-based model for the PV

module, integrated with a solar air collector, is

presented. The PV module temperature can be

minimized and controlled from changing the mass flow

rate of air to optimize the performance of the module

(Joshi, 2009). The thermal and electrical-based model

of PVT is designed to study the rational behaviour of

thermal and electrical parameters such as PV

temperature, fluid outlet temperature, and open-circuit

voltage in (Sarhaddi, 2010). A thermal model of

building and heat transfer in heterogeneous media has

designed using a fractional-order approach. Fractional

derivative order is an indicator of the building's heat

capacity (Skruch, 2013). In (Sierociuk, 2013), general

equations for heat process in heterogeneous media is

suggested by considering dispersed heat flux in the air

around the beam. A fractional-order partial differential

equation is derived for the sub or hyper diffusion

process in that particular media.

Fractional differentiation operator is the

generalized form of the simple integer differentiation

operator. It is crucial to model real-world phenomena

because of its hereditary properties and applications,

and many basic concepts of control field like

observability, controllability concepts and stability

condition has extended to general FOS (Monje, 2010;

Sabatier, 2012; Birs, Yıldız, Giusti and Acay, 2020).

A generalized thermal-based PV/T system model is

discussed in (Ouhsaine et al., 2017). The performance

of the fractional observer is explained for the

proposed fractional-order systems for pseudo-state

estimation (Belkhatir, 2017). Many authors suggest

Aziz, A., Liaquat, M., Bhatti, A. and Ouhsaine, L.

Fractional Order PV/T Model Design and Estimation using the Fractional Observer.

DOI: 10.5220/0010512006490655

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 649-655

ISBN: 978-989-758-522-7

649

the integer-based high order sliding mode observer

using Levant differentiator under unknown input

(Levant, 2007; Chu and Feng, 2020).

This paper presents the fractional-order thermal-

based model of the PVT system in state-space

representation. Irradiation factor and PV cell

parameters, which are very critical to the PV/T, are

also taken into account in the proposed system.

System states and disturbances are estimated by using

fractional order high order sliding mode observer

from the output temperature state of the PV/T system

under some disturbance. The impact of the

differentiator gain of the observer is explained in the

estimation of states and disturbance.

The structure of this research paper as follows:

Section 2 describes the main problem statement and a

thermal-based model of the PV/T model by

fractional-order equations in state-space

representation. Fractional HOSMO is presented for

the system under disturbance in section 3. Simulation

is performed to illustrate its performance under

disturbance for the pseudo-states and disturbance

estimation of the given system, and the effect of the

differentiator gain on estimation error in section 4.

The research paper is concluded and delivers the

outlines for future work in section 5.

2 PROBLEM STATEMENT

External Temperature, Irradiation, and fluid

temperature are the inputs which have been applied to

the PV/T system in Figure 1.

Figure 1: Disturbance & States estimation of the system.

The main objective is to estimate all the

temperature states of PV/T model design described by

the fractional-order differential equations because of

its characterization in heterogeneous media and its

multilayers structure.

Fractional- HOSMO is used to estimate all the

node temperatures of each layer and disturbance

using the PV cell temperature as output. Fractional

HOSMO uses differentiators to converge the

estimated temperature states on the actual

temperature states.

3 PVT MATHEMATICAL

MODELLING

3.1 System Description

PV/T converts sunlight into electricity from the solar

cell, and it captures the residual heat energy and

eliminates it from the PV module using the solar

thermal collector. Figure 2 elaborates on the essential

heat transfer principle and specific arrangements of

its components in the 2D scheme.

Figure 2: PV/T multilayer structure.

In the first layer, there is a glass cover that

provides more extended durability to the solar cells

and higher design flexibility compared to other

encapsulating technologies. Then, the second layer is

made of Ethylene-vinyl acetate (EVA), which is an

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

650

electrical insulator. The third layer is the PV cell,

which is the most crucial component to generate

electricity from solar irradiation. In the fourth layer, a

copper absorber is employed to absorb the extra heat

directly from PV cells. After these layers, a heat

exchanger flows under fixed small channels to extract

the excessive heat from the system. The use of base

heat transfer fluid (HTF) is essential to ensure better

cooling for the PV panel and heat gain for the thermal

system's output. Then this thermal energy can be

utilized for domestic use or heating purposes. In this

particular model, the heat transfer fluid is water. In

the last layer, there is a thermal insulator, which

prevents the heat flows through the sink.

3.2 Mathematical Modelling

Let assume the HTF (water) temperature is uniform.

Then, the following equation proposes the dynamic

behaviour issued from the thermal balances in each

layer.

Following equation describes the fractional based

heat diffusion (Ouhsaine et al., 2017):

𝐻



𝑡,𝜆



𝜅









𝑇𝑡,𝜆 (1)

𝜌



𝑐



𝑒













𝑄





𝑄





(2)

Where i is the index number for each layer, and

ρ,c,e correspond to density, heat capacity, and

thickness of manufacturing materials in each layer,

respectively

𝜌



𝑐



𝑒













𝑈





𝑇



𝑇





𝑈





𝑇



𝑇





(3)

Fractional state-space representation:

𝐷





𝑥



𝑡





𝐴

𝑥



𝑡



𝐵𝑢



𝑡



𝑦



𝑡



𝐶𝑥



𝑡



(4)

Where A is the state matrix, B is the input matrix,

C is the input matrix of the system.

System matrix (A) is

Input matrix (B) is

Where

()

[

]

1, 2, 3, , 7

tTTT T=…

is the

state vector of temperature at each node, and

()

[]

,,Tut TextG=

is the input vector, here

, & TG Text

are irradiations, external

temperature, and fluid temperatures respectively.

4 FRACTIONAL HIGH ORDER

SLIDING MODE OBSERVER

Many sensors are required for the measurement of

states, so they are costly and complicated. System

state measurements may be too noisy due to the

presence of disturbance. Therefore, to solve this

problem, system states are estimated by the help of

Fractional HOSMO. The advantage of this observer

is that it also estimates the disturbance added in the

system if it is bounded.

Following assumptions should be satisfied by the

system (Belkhatir, 2017):

• Assumption 1: The system should be

completely observable

• Assumption 2: The relative degree of the

system concerning unknown input should be

n. It shows that the system is strongly

observable.

• Assumption 3: The unknown input and its

derivative should be bounded a function of

Lebesgue measurable.

The following equations give fractional HOSMO:

𝐷





𝑧



𝑡



𝐴𝑧



𝑡



𝐵𝑢



𝑡



𝐿𝑦𝐶𝑧



𝑡





(5)

Fractional Order PV/T Model Design and Estimation using the Fractional Observer

651

11 2 1 1 1

223 2 1 2 1

11 1

()

( )

tn n n

Dvw v M v yCz signv yCz

Dv w v M v w signv w

Dv Msignv w

−



==− −+ −+



==− − −





=− −





(6)

𝑥



𝑡



𝑧𝑡𝐾𝑣



𝑡



(7)

𝜉





𝑡





𝑑



𝑣







𝑎



𝑣



⋯𝑎



𝑣





 (8)

Where z∈ℝ



and L∈ℝ is the vector and gain of

Luenberger observer (5) respectively, v∈ℝ



and

M is the vector and gain of differentiator (6)

respectively where the sliding surface is defined,

constant 𝑑𝐶



𝐴𝐿𝐶





, x is pseudo-state

estimation vector and K is a correction gain which is

inverse of observability matrix in (7), a



∈ℝ are

coefficients of 𝐾



𝐴  𝐿𝐶𝐾 in the estimation of

disturbance 𝜁𝑡.

5 SIMULATION

Table 1: The values of important parameters.

The simulation illustrates the performance of the

observer for the given PV/T system. There are two

cases:

I. Disturbance free

II. Disturbed system

Now after putting the values of parameters as

given in table 1, system matrices are as follow:

𝐴

⎣

⎢

⎡

1.19 0.180 0 0 0 0 0

0.41 0.61 0.24 0 0 0 0

0 0.79 1000.5 1001 0 0 0

0 0 202 298 96 0 0

0 0 0 56.1 56.7 0.14 0

0 0 0 0 2.36 2.30 0.01

0 0 0 0 0 1 20.70

⎦

⎥

⎤

The parameter values are taken from the manual

of the apparatus (PVT system) in the laboratory of

National University of Sciences and Technology

Islamabad, Pakistan.

The output matrix will be

[0 0 0 0 0 0 1]C =

The following system is observable. The system

is at rest and taking initial condition zero. Inputs is

[30,900,18]. The different values of input can be

taken according to the model.

5.1 Case 1: Disturbance Free

Differentiator gain is M=5, and the gain of the linear

observer part is 𝐿  500 100 15 20 5 10 5



Figure 3: States estimation error without disturbance.

Figure 3 shows that, in the absence of unknown

input or disturbance, HOSMO will simultaneously

ignore modeling ambiguity and easily estimate the

system states.

5.2 Case 2: Under Disturbance

In this case, the system has perturbed by

incorporating the disturbance in the first state of the

system. The observer should estimate it accurately so

that some suitable controller can eliminate its effect

using this disturbance estimation. The disturbance

added in the system is 𝜁𝑡  10sin 2𝜋𝑡 .

Differentiator gain is M=25.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

652

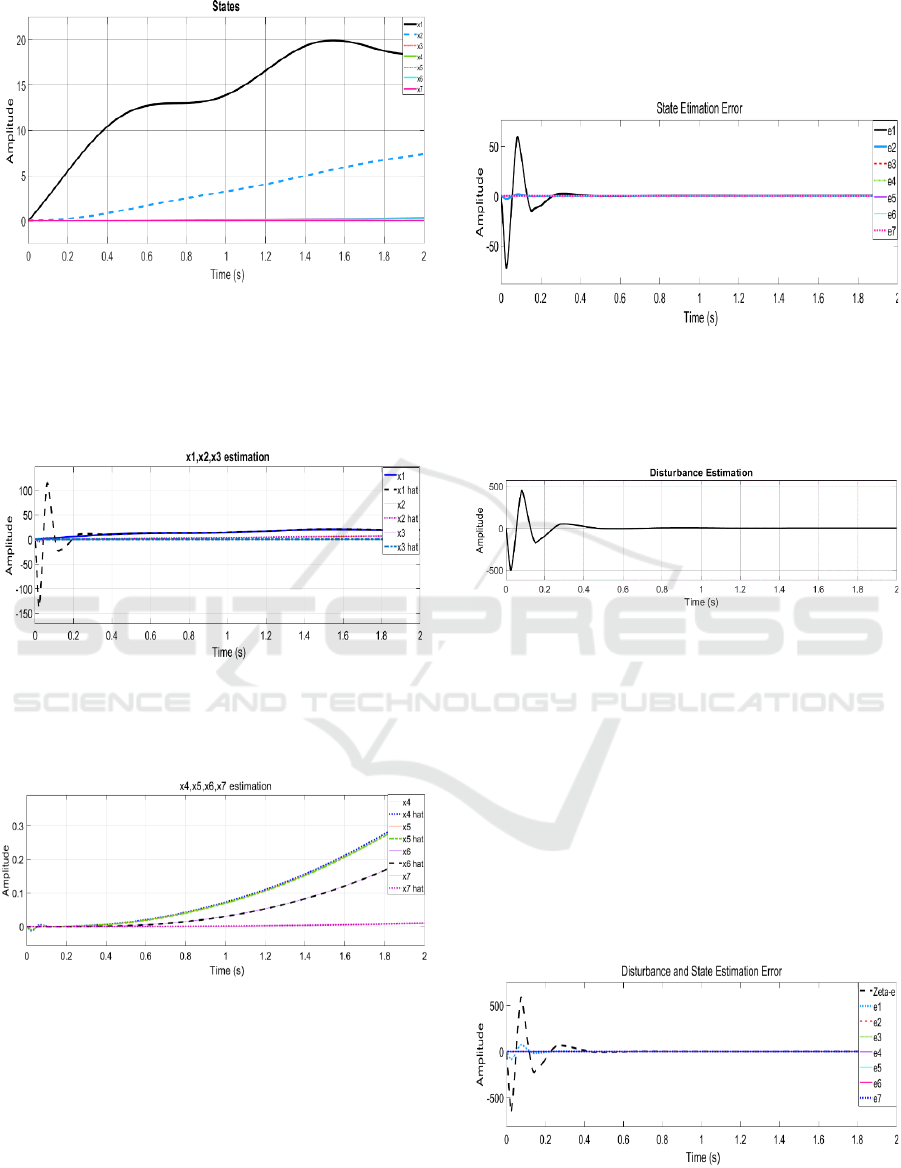
Figure 4: System states under the disturbance.

Figure 4 shows the effect of the disturbance in

which systems states have been disturbed. System

state showing the nonlinear behaviour due to

nonlinear disturbance.

Figure 5: States 𝑥



, 𝑥



, 𝑥



and their estimated states.

Figure 5 shows that the estimated states of (T1-

T3) converging on the system states at 0.25 second.

Figure 6: States 𝑥



, 𝑥



, 𝑥



, 𝑥



and their estimated states.

Figure 6 shows that the estimated states of (T4-

T7) converging on the system states at 0.15 second.

It is shown that observer is still estimating the

status smoothly under the disturbance because all the

estimated states of the observer are converging to the

systems states smoothly within 0.25 sec in Figures 5

and 6.

5.2.1 Estimation Error for Observer

The estimation error is the measure of the

performance of the given observer.

Figure 7: The estimation error for all the states.

Figure 7 shows that the estimation error for all

states is zero when all the estimated states converge

to the system states within 0.25 second.

Figure 8: The estimation error for disturbance.

Figure 8 shows that the estimation error for

disturbance is zero when the estimation of

disturbance is converging to the actual disturbance

within 0.3 second.

It is shown in figures 7 and 8 that states and

disturbance estimation error is high in the start, but it

becomes zero at 0.25 sec when estimated states

converge on system states. Therefore, these graphs

are evidence of the excellent performance of the

given observer.

5.2.2 Effect of the Gain M

Figure 9: State-estimation errors for M=50.

Fractional Order PV/T Model Design and Estimation using the Fractional Observer

653

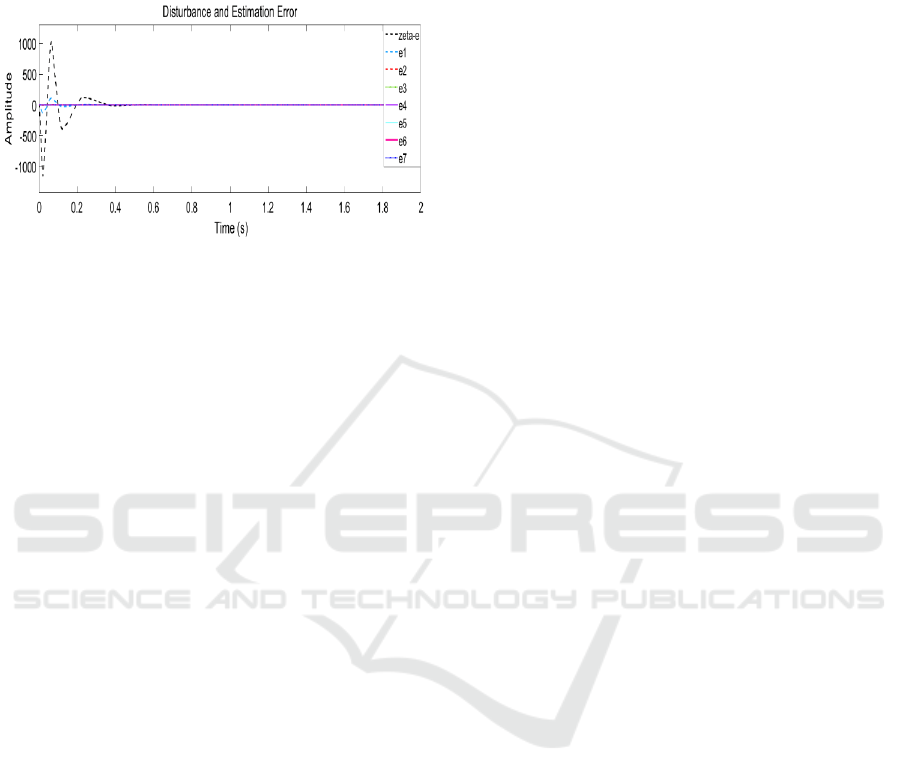
It illustrates the effect of the differentiator gain M on

the convergence and amplitude of error. There exists

a compromise between convergence and overshoot of

estimation error.

Figure 10: State-estimation errors for M=200.

The overshoot of estimation error is increasing

from 600 to 1000 as gain is increasing from 50 to 200.

While the convergence in the second scenario will be

better than in the first scenario

Figures 9 and 10 elaborate that there exists a

trade-off between estimation convergence and the

overshoot of estimation error because, when M gain

is increased, the overshoot of the estimation error will

also increase.

6 CONCLUSIONS

This paper presents the thermal-based modelling of

the multilayer structure PVT system by a fractional-

order derivative equation and then its state-space

representation. Fractional-HOSMO is implemented

to estimate the disturbance and system states under

disturbance. Simulation is performed to test the

performance of the given observer for both cases:

disturbance-free and disturbed systems. It describes

the effect of the gain on the performance of the

observer. It emphasizes on the hardware

implementation of this system and extends it to the

multiple inputs and multiple outputs system for future

work. It will be interesting to make further

suggestions for improvements in the system.

REFERENCES

Lobera, D. T., & Valkealahti, S. (2013). Dynamic thermal

model of solar PV systems under varying climatic

conditions. Solar energy, 93, 183-194.

Cui, Y., Yao, H., Zhang, J., Xian, K., Zhang, T., Hong, L.,

... & Hou, J. (2020). Single ‐ junction organic

photovoltaic cells with approaching 18% efficiency.

Advanced Materials, 32(19), 1908205.

Abd El-Samie, M. M., Ju, X., Zhang, Z., Adam, S. A., Pan,

X., & Xu, C. (2020). Three-dimensional numerical

investigation of a hybrid low concentrated

photovoltaic/thermal system. Energy, 190, 116436.

Alayi, R., Kasaeian, A., & Atabi, F. (2020). Optical

modeling and optimization of parabolic trough

concentration photovoltaic/thermal system.

Environmental Progress & Sustainable Energy, 39(2),

e13303.

Esfe, M. H., Kamyab, M. H., & Valadkhani, M. (2020).

Application of nanofluids and fluids in photovoltaic

thermal system: An updated review. Solar Energy, 199,

796-818.

Eisapour, M., Eisapour, A. H., Hosseini, M. J., &

Talebizadehsardari, P. (2020). Exergy and energy

analysis of wavy tubes photovoltaic-thermal systems

using microencapsulated PCM nano-slurry coolant

fluid. Applied Energy, 266, 114849.

Salari, A., Kazemian, A., Ma, T., Hakkaki-Fard, A., &

Peng, J. (2020). Nanofluid based photovoltaic thermal

systems integrated with phase change materials:

numerical simulation and thermodynamic analysis.

Energy Conversion and Management, 205, 112384.

Alayi, R., Kasaeian, A., & Atabi, F. (2020). Optical

modeling and optimization of parabolic trough

concentration photovoltaic/thermal system.

Environmental Progress & Sustainable Energy, 39(2),

e13303.

Yu, B., Jiang, Q., He, W., Liu, S., Zhou, F., Ji, J., ... & Chen,

H. (2018). Performance study on a novel hybrid solar

gradient utilization system for combined photocatalytic

oxidation technology and photovoltaic/thermal

technology. Applied Energy, 215, 699-716.

Al-Waeli, A. H., Chaichan, M. T., Kazem, H. A., Sopian,

K., Ibrahim, A., Mat, S., & Ruslan, M. H. (2018).

Comparison study of indoor/outdoor experiments of a

photovoltaic thermal PV/T system containing SiC

nanofluid as a coolant. Energy, 151, 33-44.

Joshi, A. S., Tiwari, A., Tiwari, G. N., Dincer, I., & Reddy,

B. V. (2009). Performance evaluation of a hybrid

photovoltaic thermal (PV/T)(glass-to-glass) system.

International Journal of Thermal Sciences, 48(1), 154-

164.

Sarhaddi, F., Farahat, S., Ajam, H., Behzadmehr, A. M. I.

N., & Adeli, M. M. (2010). An improved thermal and

electrical model for a solar photovoltaic thermal (PV/T)

air collector. Applied energy, 87(7), 2328-2339.

Skruch, P. (2013). A general fractional-order thermal model

for buildings and its properties. In Advances in the

Theory and Applications of Non-integer Order Systems

(pp. 213-220). Springer, Heidelberg.

Sierociuk, D., Dzieliński, A., Sarwas, G., Petras, I.,

Podlubny, I., & Skovranek, T. (2013). Modelling heat

transfer in heterogeneous media using fractional

calculus. Philosophical Transactions of the Royal

Society A: Mathematical, Physical and Engineering

Sciences, 371(1990), 20120146.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

654

Monje, C. A., Chen, Y., Vinagre, B. M., Xue, D., & Feliu-

Batlle, V. (2010). Fractional-order systems and

controls: fundamentals and applications. Springer

Science & Business Media.

Sabatier, J., Farges, C., Merveillaut, M., & Feneteau, L.

(2012). On observability and pseudo state estimation of

fractional order systems. European journal of control,

18(3), 260-271.

Birs, I., Nascu, I., Ionescu, C., & Muresan, C. (2020).

Event-based fractional order control. Journal of

Advanced Research.

Yıldız, T. A., Jajarmi, A., Yıldız, B., & Baleanu, D. (2020).

New aspects of time fractional optimal control

problems within operators with nonsingular kernel.

Discrete & Continuous Dynamical Systems-S, 13(3),

407.

Giusti, A. (2020). General fractional calculus and

Prabhakar’s theory. Communications in Nonlinear

Science and Numerical Simulation, 83, 105114.

Acay, B., Bas, E., & Abdeljawad, T. (2020). Non-local

fractional calculus from different viewpoint generated

by truncated M-derivative. Journal of Computational

and Applied Mathematics, 366, 112410.

Ouhsaine, L., Boukal, Y., El Ganaoui, M., Darouach, M.,

Zasadzinski, M., Mimet, A., & Radhy, N. E. (2017). A

General fractional-order heat transfer model for

Photovoltaic/Thermal hybrid systems and its observer

design. Energy Procedia, 139, 49-54.

Belkhatir, Z., & Laleg-Kirati, T. M. (2017). High-order

sliding mode observer for fractional commensurate

linear systems with unknown input. Automatica, 82,

209-217.

Levant, A. (2003). Higher-order sliding modes,

differentiation and output-feedback control.

International journal of Control, 76(9-10), 924-941.

Fridman, L., Levant, A., & Davila, J. (2007). Observation

of linear systems with unknown inputs via high-order

sliding-modes. International Journal of systems

science, 38(10), 773-791.

Ferreira de Loza, A., Fridman, L., Aguilar, L. T., & Iriarte,

R. (2019). High‐order sliding‐mode observer–based

input ‐ output linearization. International Journal of

Robust and Nonlinear Control, 29(10), 3183-3199.

Yin, X., Wang, B., Liu, L., & Wang, Y. (2019). Disturbance

observer-based gain adaptation high-order sliding mode

control of hypersonic vehicles. Aerospace Science and

Technology, 89, 19-30.

Chu, Z., Meng, F., Zhu, D., & Luo, C. (2020). Fault

reconstruction using a terminal sliding mode observer

for a class of second-order MIMO uncertain nonlinear

systems. ISA transactions, 97, 67-75.

Feng, Z., Liang, W., Ling, J., Xiao, X., Tan, K. K., & Lee,

T. H. (2020). Integral terminal sliding-mode-based

adaptive integral backstepping control for precision

motion of a piezoelectric ultrasonic motor. Mechanical

Systems and Signal Processing, 144, 106856.

Fractional Order PV/T Model Design and Estimation using the Fractional Observer

655