Ransomware Detection using Markov Chain Models over File Headers
Nicolas Bailluet
1
, H
´
el
`
ene Le Bouder
2
and David Lubicz
3
1
ENS Rennes, France
2
OCIF IMT Atlantique Campus Rennes, France
3
DGA MI, Bruz, France
Keywords:
Ransomware, Detection, Malware, Markov Chain, File Header.
Abstract:
In this paper, a new approach for the detection of ransomware based on the runtime analysis of their behaviour
is presented. The main idea is to get samples by using a mini-filter to intercept write requests, then decide if a
sample corresponds to a benign or a malicious write request. To do so, in a learning phase, statistical models
of structured file headers are built using Markov chains. Then in a detection phase, a maximum likelihood test
is used to decide if a sample provided by a write request is normal or malicious. We introduce new statistical
distances between two Markov chains, which are variants of the Kullback-Leibler divergence, which measure
the efficiency of a maximum likelihood test to distinguish between two distributions given by Markov chains.
This distance and extensive experiments are used to demonstrate the relevance of our method.
1 INTRODUCTION
Ransomware are a family of malware that ask a pay-
ment to the legitimate users for accessing their ma-
chine or computer files. They are one of the most se-
rious security threats on the Internet. The number of
attacks has increased drastically these last years, re-
sulting in huge losses and disruptions. There are two
types of ransomware: some prevent the usage of the
computer, others encrypt files. In this paper we are
interested in the last case called crypto-ransomware.
Crypto-ransomware are more and more efficient and
easy to operate by malicious individuals and organisa-
tions. They are provided as ready-to-use toolkit with
robust cryptographic algorithms, embed evasion tech-
niques to defeat intrusion detection and are capable
to spread in a network to infect many computers. In
order to mitigate this threat, it is important to be able
to detect and stop automatically the malicious activ-
ity of ransomware. In this paper, we present a new
method to detect ransomware that belongs to the class
of behavioural approach which consists in detecting
malign activity : the encryption data, by distinguish-
ing it from normal activity. In this paper, we explain:
how to use Markov chains in order to build a statis-
tical model of a normal behaviour by training it with
write requests; how to compute maximum likelihood
tests that distinguish samples drew following two dis-
tributions well described by Markov chains. We re-
port on extensive experiments to demonstrate the rel-
evance of our method. The main originality of the
paper, which is developped in Section 4, is related to
the remark that the Kullback-Leibler differential en-
tropy measures the efficiency of the maximum likeli-
hood test to distinguished the distributions given by
two Markov chains.
The state of the art of countermeasures are de-
scribed in Section 2. In Section 3, the basic defi-
nition and main theoretical ingredients that are used
in the paper, are introduced. Section 4 is devoted to
a preliminary analysis of the data. In Section 5, we
present the results of our first experiments to then re-
fine our approach in Section 6. The Section 7 tests our
approach against real-world ransomware-encrypted
files. Finally, conclusions are drawn in Section 8.
2 STATE OF THE ART
Different surveys have been published on ransomware
protections (Genc¸ et al., 2018; Al-rimy et al., 2018b;
Aurangzeb et al., 2017; Moussaileb, 2020). A first
idea to protect data against ransomware attacks is
to use data back-up as explained in (Castiglione and
Pavlovic, 2019; Baykara and Sekin, 2018). The clas-
sic detection techniques used for all malware, such as
as Network Intrusion Detection Systems, can be used
for ransomware. Network traffic is compared to previ-
ously well-known malware patterns, called signatures
as in (Moussaileb et al., 2019; Ahmadian et al., 2015;
Cabaj et al., 2018; Almashhadani et al., 2019). The
Bailluet, N., Bouder, H. and Lubicz, D.
Ransomware Detection using Markov Chain Models over File Headers.
DOI: 10.5220/0010513104030411
In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 403-411
ISBN: 978-989-758-524-1
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
403

limitation of these techniques is that they are unable to
detect new malware, never seen before. This is a seri-
ous problem with ransomware because a lot of attacks
come from new ransomware. The detection of spe-
cific behaviours of ransomware are used too. Some
detection mechanisms specific to ransomware can be
to watch how files are touched (Moussaileb et al.,
2018) or to detect ransom note writing (Yassine Lem-
mou, 2019). Some papers studies the transaction for
the ransom payment (Akcora et al., 2019). But, the
most specific behaviour of ransomware is to overwrite
files with encrypted data so that these methods still
generate a lot of false alarms. Often ransomware do
not come with their own cryptographic libraries and
rather rely on the victims own tools. So many protec-
tions are based on controlling accesses over the cryp-
tographic tools in Windows (Palisse et al., 2016; Chen
et al., 2017; Al-rimy et al., 2018a; Al-rimy et al.,
2019). One other way to detect ransomware is to
have honey pots. These are files that trigger an alarm
when they are modified (Moore, 2016; Patton et al.,
2019). Finally there is a family of ransomware de-
tection mechanisms which rely on encryption detec-
tion. Indeed encryption produces data which have a
pseudo-random distribution, therefore increasing the
entropy of the files. There is an important litera-
ture about statistical tests of randomness which can
be used to detect encrypted data (Scaife et al., 2016;
Continella et al., 2016; Kharraz and Kirda, ; Palisse
et al., 2017; Kharraz et al., 2016).
A recent study (Pont et al., 2020) presents limita-
tion of classical statistic tool to detect ransomware.
A drawback of these methods is that randomness
behaviour is not a complete characterisation of en-
crypted streams: compressed data streams behave in
the same manner. As a consequence, in order to avoid
too much false alarms it is necessary to combine de-
tection mechanism based on randomness with other
criteria. Another problem is that we want to distin-
guish malign activity from normal behaviour. But if
we have a clear statistical model for malign activity,
namely random data, we do not have its counterpart
for normal behaviour. In this situation, the use of clas-
sical χ
2
tests (Palisse et al., 2017) is problematic since
they are meant to detect improbable events under the
hypothesis that the stream of data is random where
we actually want to single out improbable events in
the case that the stream of data is a normal structured
file. This makes it impossible to carry out a precise
analysis of the efficiency of the statistical tests that
we use and to design the most efficient ones.
In this paper, we present a new method to detect
ransomware that belongs to the class of behavioural
approach. A well suited probe for the kind of ma-
lign activity involved by ransomware is provided by
write requests which are handled by the kernel and
is a mandatory call in order to perform a write ac-
cess on a hard drive. These requests can be monitored
by a specific driver running in kernel land, the opera-
tion of which can not be disrupted by the ransomware
(which is running in user land). Whereas most sta-
tistical models and machine learning techniques re-
cently implemented focus on neural networks or other
modern machine learning methods (Lee et al., 2019),
we chose to use Markov chains to model the stream
of data. Unlike modern machine learning methods,
Markov chains are fairly easy to understand and ma-
nipulate. They induce well understood probability
distributions and can be used in conjunction with a
maximum likelihood test that is known to be the most
powerful in a large class of statistical tests.
3 BASIC DEFINITIONS AND
NOTATIONS FOR MARKOV
CHAINS
Let bit = {0, 1} be an alphabet of cardinal 2 . ∀k ∈ N ,
let S
k
be the set of finite sequences of length k with
coefficients in bit. The data stream is represented by
a probability distribution on S
k
. This probability dis-
tribution can be: either the uniform U
k
distribution
which represents encrypted data; or an unknown dis-
tribution D
k
which represents normal header data. We
suppose that we can obtain samples drawn following
the distribution D
k
(and of course also following the
distribution U
k
). So, we can obtain information about
this distribution. The problems that we want to solve
efficiently are: obtain a model of the distribution D
k
by learning it from samples drawn following D
k
;and
for s a given sample, decide from which distribution
D
k
or U
k
it comes from. In order to learn the dis-
tribution D
k
, we use the model provided by Markov
chains. It is a fundamental and widely used model in
information theory and is particularly well suited to
statistically model a data stream. There exists more
general definition in the huge literature on the subject
(see (Ash, 1990) for instance), but we have chosen in
this paper to slightly adapt it to our needs.
Definition 3.1. We keep the previous notations for bit
and S
m
. Let P (S
m
) be a set of subsets of S
m
. The map
succ is defined as :
succ : S
m
→ P (S
m
)
s = s
1
...s
m
7→ {s
2
.. .s
m
b|b ∈ bit}.
A binary Markov chain X with memory m is a se-
quence (X
i
)
i≥0
of random variables with value in S
m
,
SECRYPT 2021 - 18th International Conference on Security and Cryptography
404

P(
b
X(k) = b
1
.. .b
k
) = P(X
n
= b
k−m+1
.. .b
k
|X
n−1
= b
k−m
.. .b
k−1
) · P(
b
X(k − 1) = b
1
.. .b
k−1
). (1)
P(
b
X(m) = b
1
.. .b
m
) = P(
b
X(m + 1) = b
1
.. .b
m
1) + P(
b
X(m + 1) = b
1
.. .b
m
0). (2)
the set of states, and such that ∀n ≥ k:
1. P(X
n
= x
n
|X
n−1
= x
n−1
,. .., X
n−k
= x
n−k
) =
P(X
n
= x
n
|X
n−1
= x
n−1
),
2. P(X
n
= x
n
|X
n−1
= x
n−1
) does not depend on n.
We suppose moreover that if x
n
/∈ succ(x
n−1
) then
P(X
n
= x
n
|x
n−1
= x
n−1
) = 0.
It is clear that succ maps any element s ∈
S
m
to the set of its possible successors. If
s
0
= s
0
1
.. .s
0
m
∈ succ(s) then the transition from s to s
0
is labelled by s
0
m
∈ bit.
A binary Markov chain is classically defined by
the following data: the memory m which is an integer,
the transition matrix T = t
x,y
such that, ∀x,y ∈ S
m
:
t
x,y
= P(X
n
= x|X
n−1
= y), an initial state X
0
which is
a random variable with value in S
m
.
Definition 3.2. An element X
k
0
of the Markov chain
(X
i
)
i≥0
is stable if, ∀k ≥ k
0
: X
k+1
= X
k
.
A Markov chain with memory m verifies the er-
godicity and irreducibility condition (Ash, 1990) so
that by (Ash, 1990) we know that any such Markov
chain has a unique stable element. A stable element
gives by definition a random variable on S
m
that we
denote by
b
X(m). More generally, it also defines ran-
dom variable
b
X(k) on S
k
, ∀k > m, by the induction (1)
Because of definition 3.1, the preceding formula does
not depend on n. One has to remark that
b
X(m + 1)
allows to recover
b
X(m) using (2). But, it means that
b
X(m + 1) allows to recover the transition matrix t
x,y
,
for x ∈ succ(y) using Equation (1) with k = m + 1.
The distribution
b
X(m + 1) can then be encoded by a
function
f
b
X
: S
m+1
→ [0,1]
b
1
.. .b
m+1
7→ P(
b
X(m + 1) = b
1
.. .b
m+1
).
(3)
This way of encoding the transition matrix takes
O(2
m
) memory bits and is more efficient that storing
all the t
x,y
,∀x, y ∈ S
m
(which takes O(2
2m
) memory
bits).
Finally, we denote by X(m, f
b
X
,X
0
) the Markov
chain with memory m, transition matrix encoded by
f
b
X
and initial state X
0
. From the knowledge of f
b
X
,
one can recover the stable state
b
X(m) from (2). Then
P(
b
X(k
0
) = s) for k
0
> m is given for s = b
1
.. .b
k
0
∈
S
k
0
by 4. In the preceding formula, the first equality
is obtained by an inductive application of (1) for k =
k
0
,k
0
− 1,.. .,m + 1 and the second equality comes
from (3).
4 MODELING DATA STREAM
USING MARKOV CHAINS
We have a corpus of files with different extensions
and we want to model the statistical properties of their
header with Markov chains in order to be able to dis-
tinguish them from encrypted files. A Markov chain
of memory m is used and trained, with the first N bits
of each file. In this section, we explain how to train
the model, compute the test and assess the efficiency
of the test.
4.1 Training the Model
Let H
N
be the list of the first N-bit sequences of each
file in the corpus. Let X(m, f
b
X
,X
0
) be the Markov
chain which represents the best statistical approxima-
tion of the sample H
N
. To define this Markov chain
X(m, f
b
X
,X
0
), we have to compute f
b
X
(s),∀s ∈ S
m+1
and P(X
0
= s), ∀s ∈ S
m
. ∀s ∈ S
m+1
, let c
H
N
(s) be
the occurrence count of s in every sequence of H
N
.
∀s ∈ S
m
, let c
H
N,0
be the number of sequences in H
N
such as s is the m first bits. Denote by |H
N
| the num-
ber of the list H
N
i.e the number of files. Finally, let
|H
N
|(k) = (N − k).|H
N
| be the number of sequences
of bits of length k in H
N
. We have:
∀s ∈ S
m+1
, f
b
X
(s) =
c
H
N
(s)
|H
N
|(m+1)
,
∀s ∈ S
m
, P(X
0
= s) =
c
H
N,0
(s)
|H
N
|
.
(5)
On the other side, let X
r
(m, f
b
X
r
,X
r
0
) be the Markov
chain with memory m which represents the best statis-
tical approximation of an encrypted file. As the statis-
tical behaviour the encrypted file is indistinguishable
from the one of a perfectly random sequence (Katz
and Lindell, 2007). Thus:
∀m ∈ S
m+1
, f
b
X
r
(s) =
1
2
m+1
,
∀m ∈ S
m
, P(X
r
0
= s) =
1
2
m
.
(6)
4.2 Testing Samples against Models
For i ∈ {1,2}, let X
i
(m, f
b
X
i
,X
i
0
) be two Markov
chains. Let s ∈ S
N
be a sample header. We want to
decide which of the two trained models X
i
(m, f
b
X
i
,X
i
0
)
for i = 1,2 is the more likely to match s. For this we
apply the likelihood ratio test.
Ransomware Detection using Markov Chain Models over File Headers
405

P

b
X(k
0
) = s

= P

b
X(m) = b
1
.. .b
m

k
0
∏
i=m+1
P(
b
X(m + 1) = b
i−m
.. .b
i
)
P(
b
X(m) = b
i−m
.. .b
i−1
)
(4)
Definition 4.1. Likelihood Ratio Test for Trained
Models. Let s ∈ S
k
be a sample, we define the like-
lihood ratio of s with respect to X
i
(m, f
b
X
i
,X
i
0
) for
i = 1,2, two Markov chains, as:
Λ

s,
b
X
1
(k),
b
X
2
(k)

=
P

b
X
1
(k) = s

P

b
X
2
(k) = s

.
The likelihood ratio test then is defined by:
T

c,s,
b
X
1
(k),
b
X
2
(k)

=
(
1 if Λ(s,
b
X
1
(k),
b
X
2
(k)) > c
0 otherwise
.
Here c is a constant that allows to set the significance
level of the test.
The Neyman-Pearson lemma (Huber and
Strassen, 1973) states that this likelihood-ratio
test is the most powerful test for a given signifi-
cance level. A variant uses the log-likelihood ratio
log

Λ(s,
b
X
1
(k),
b
X
2
(k)

.
4.3 Measuring the Relevance of the Test
For k ≥ m an integer, the expected value of
log

Λ(s,
b
X
1
(k),
b
X
2
(k)

, with s drawn from
b
X
1
(k)
is (7). It is nothing but the Kullback-Leibler di-
vergence (Kullback and Leibler, 1951; Hershey and
Olsen, 2007) of
b
X
1
(k) and
b
X
2
(k), denoted by:
KL

(
b
X
1
(k)||
b
X
2
(k)

. Thus, the Kullback-Leibler di-
vergence gives an assessment of the distance between
the distributions of
b
X
1
(k) and
b
X
2
(k). One has to re-
mark that it is particularly well suited for the likeli-
hood ratio test. The bigger the Kullback-Leibler di-
vergence is, the more the test will be able to success-
fully distinguish
b
X
1
(k) from
b
X
2
(k).
When a statistical model for a corpus of very
structure files is computed, it is not so uncommon that
some states of a Markov chain are almost never or
never reached. In the case where P

b
X
2
(k) = s

= 0,
KL

(
b
X
1
(k)||
b
X
2
(k)

is not defined and the computa-
tion of the likelihood ratio may fail. Indeed, in the
computation of likelihood ratio or in the Kullback-
Leibler divergence, there is the following quotient:
for k ≥ m and s ∈ S
k
:
Λ

s,
b
X
1
(k),
b
X
2
(k)

=
P

b
X
1
(k) = s

P

b
X
2
(k) = s

.
Of course if X
2

m, f
b
X
2,X
2
0

is the model cor-
responding to the random distribution, then,
Λ

s,
b
X
1
(s),
b
X
2
(s)

can always be computed. In
this case, we can also compute the Kullback-Leibler
divergence. But we would like to be able to compute
the divergence between two not random distributions.
Furthermore, it may also happen that P(
b
X
2
(k) =
s) is not zero but is very small, which corresponds to
very rare states. In this case, the statistics computed
during the training phase may happen to be not sig-
nificant, since they have been computed with a very
small sample. It could generate false negative for our
test. One of the main point of the present paper is to
explain how to deal with this situation by introduc-
ing a tweaked Kullback-Leibler divergence and use it
to choose the best parameters for our Markov chain
model.
5 FIRST EXPERIMENTS AND
RESULTS
In this section, we make a first analysis of our cor-
pus of files. The given corpus is split into two parts,
one is for training while the other is for testing the
model. The purpose of this corpus is to make a model
of legit and well-structured data that are commonly
present on anybody’s computer, as well as observing
how already-known ransomware encrypt data. The
training corpus is composed of 10134 files with 49
different extensions.
The model is built on file headers analyse. It
is possible to group extensions by header format.
For example: doc, docx, ppt, pptx, xls, xlsx
share the same header format in Microsoft Office
suite. The test corpus is composed of 27 plaintexts
files and their associated ciphertexts for different ran-
somware (Zppelin, GlobImposter, Gigsaw, Paradise,
Deadmin, Estemani, GlobImposter
half, Medusa-
Locker, NemtyRevenge, Ordinypt, StopDjvuMoka,
Unknown 6rndchar, MegaCortex, Phobos, Sodinok-
ibi,Eris, Maoloa, Nemsis, Seon2 and Xorist. ).
For the first experiments, we have trained multiple
models on different file formats: jpg, gif, msoffice
and pdf. These formats are the most present ones in
the corpus. Indeed, we have considered subsets of the
training corpus consisting of files with the same ex-
tensions because it seems reasonable to suppose that
their file headers have the same structure that will be
SECRYPT 2021 - 18th International Conference on Security and Cryptography
406

E

log

Λ(s,
b
X
1
(k),
b
X
2
(k))

=
∑
s∈S
k
P

b
X
1
(k) = s

· log
P(
b
X
1
(k) = s
P(
b
X
2
(k) = s
!
. (7)
captured by the Markov chain model. We wanted to
see how much our approach is sensitive to the type of
files of the corpus.
The parameters for the experiments have been
chosen based on the KL-divergence to randomness.
We trained multiple models with different parameters
m (memory) and N (header length). The parameter
N is ranging from 128 to 2048, which seem to be
reasonable sizes for file headers. The parameter m
is ranging from 4 to 16, a larger value would not be
reasonable knowing the number of states in a Markov
chain grows exponentially as the memory grows. The
results are shown in Table 1.
While the header length N seems to have a sig-
nificant effect on the divergence for each format, to
increase in memory m seems to globally decrease the
divergence. Based on those observations and the re-
sults in Table 1, we have chosen the following pa-
rameters for our experiments: m = 4 and N = 512.
Indeed, the choice for m is obvious, we have decided
to set N = 512, since it maximizes the divergence for
msoffice files.
To ensure the significance of the test, we have
recorded the evolution of the KL-divergence while
training the Markov chain model. It is important to
take a look at the evolution to check that the metric
converges to a non-null value. A null value would in-
dicate that the test would be unable to distinguish the
trained model from randomness. We verified that the
divergence seems to more or less converge in most
cases.
The divergence of msoffice files is really high
compared to other format. This is not surprising, this
format is known to have a header that leaves small
room for randomness. As for jpg and gif files, the
divergence is relatively smaller and this is again not
surprising because these formats do not have headers
as static as msoffice. Finally, the divergence for pdf
files seems to be almost zero because the pdf headers
are very varying.
The model trained over the whole corpus, without
taking into account file extension, seems to converge
to a divergence of approximately 0.069.
5.1 Test and Results
To test the trained models against randomness, we
have created for each format a corpus half composed
of randomly generated files and half composed of files
that match the format and were not in the original
training corpus. We have used the likelihood ratio test
with the constant c = 1. The test is positive if it says
that the sample corresponds to a structured header and
negative if it says that the sample is random. The re-
sults are shown in Table 2. One has to remark that the
success rate of positive test-cases for gif and pdf is
not maximal. By looking at the computation of the
likelihood ratio, we figured out the issue is due to rare
states and transitions that are not highly present in the
original corpus.
5.2 Explanation of False Negatives
The results showed that some positive test-cases are
categorized as negative by the test. We figured out
this behaviour is due to some states that are relatively
little present in the original corpus.
Let X(m, f
b
X
,X
0
) be a trained model, we say that
b
1
.. .b
m
∈ S
m
is a rare state if (with the notations
of Section 4.1): c
H
N
(b
1
.. .b
m
) = c
H
N
(b
1
.. .b
m
0) +
c
H
N
(b
1
.. .b
m
1) is small compared to the total num-
ber of transitions in the corpus. Said in another way,
a s ∈ S
m
is rare if
f
b
X
(s0) + f
b
X
(s1) < t,
for a t > 0 small. If s ∈ S
m
is a rare state it may happen
that





c
H
N
(b
1
.. .b
m
0) = 0
or
c
H
N
(b
1
.. .b
m
1) = 0
.
As a result, when such a state is encountered in a test-
case and the transition taken is the one of null prob-
ability, the numerator of the likelihood ratio becomes
zero and eventually the file is categorised as negative.
Since the global number of states is 2
m
, we observed
this behaviour to be more significant on the results
with greater values of m. For instance the proportion
of false negative was about 33% for m = 16.
The issue is that the test only takes into account
the transition probabilities, it does not take into ac-
count whether the state’s count in the corpus is repre-
sentative or not compared to other’s state counts. For
example, it is irrelevant to reject a file only because
of one state whose count in the corpus is only 4 while
the total number of transitions seen in the corpus is
greater than 400000. This means that in this case the
decision is taken on little information which only rep-
resent
1
100000
of the original corpus, this is like deduc-
ing generalities from specific cases.
Ransomware Detection using Markov Chain Models over File Headers
407

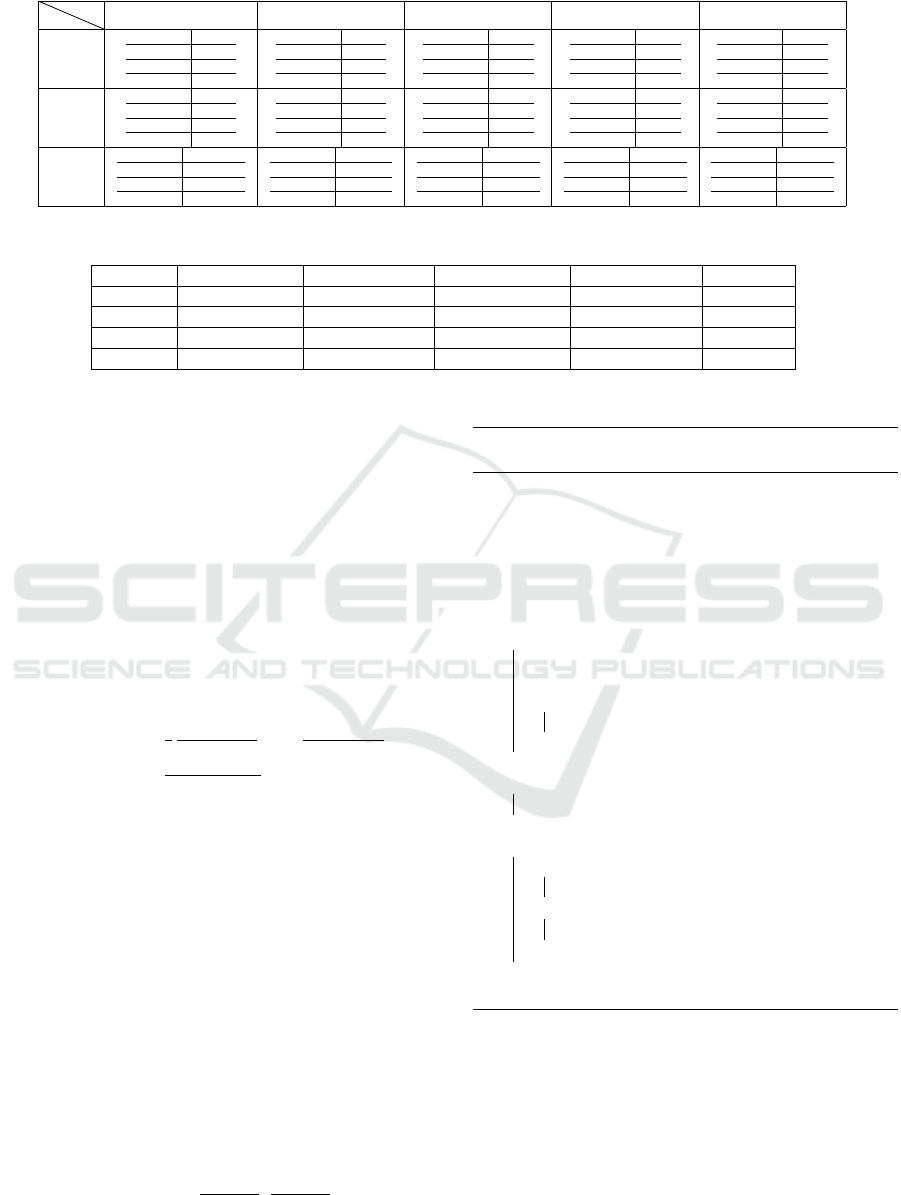
Table 1: KL-divergence for different choices of parameters m (memory) and N (header length), and for different file formats.
m
N
128 256 512 1024 2048
4
msoffice 0.25
jpeg 0.13
gif 0.11
pdf 0.01
msoffice 0.30
jpeg 0.12
gif 0.12
pdf 0.01
msoffice 0.39
jpeg 0.10
gif 0.09
pdf 0.02
msoffice 0.25
jpeg 0.09
gif 0.06
pdf 0.02
msoffice 0.14
jpeg 0.11
gif 0.04
pdf 0.03
8
msoffice 0.32
jpeg 0.11
gif 0.09
pdf 0.01
msoffice 0.32
jpeg 0.08
gif 0.10
pdf 0.02
msoffice 0.38
jpeg 0.08
gif 0.08
pdf 0.02
msoffice 0.23
jpeg 0.09
gif 0.06
pdf 0.02
msoffice 0.13
jpeg 0.11
gif 0.04
pdf 0.03
16
msoffice 0.29
jpeg 0.05
gif 0.06
pdf 0.00005
msoffice 0.32
jpeg 0.03
gif 0.06
pdf 0.0003
msoffice 0.33
jpeg 0.03
gif 0.05
pdf 0.0004
msoffice 0.17
jpeg 0.04
gif 0.04
pdf 0.0004
msoffice 0.09
jpeg 0.06
gif 0.02
pdf 0.0002
Table 2: First results of tests against randomness for multiple file formats.
Format # true positive # true negative # false negative # false positive Accuracy
msoffice 330 330 0 0 1.00
jpeg 330 330 0 0 1.00
pdf 322 330 8 0 0.98
gif 142 150 8 0 0.97
6 REFINE THE MODELS AND
TESTS
In this section we describe the solutions implemented
to overcome the issue of rare states. A modification of
the model is introduced to involve applying a thresh-
old to get rid of irrelevant information.
The main idea is to get rid of irrelevant informa-
tion, by applying a threshold on state probabilities in
the trained model X(m, f
b
X
,X
0
). That is to say, for a
threshold t ∈ [0, 1], ∀b
1
.. .b
m
∈ {0,1}
m
, during the
learning phase, we set:
f
b
X
(b
1
.. .b
m+1
) =



1
2
c
H
N
(b
1
...b
m
)
|H
N
|(m)
if
c
H
N
(b
1
...b
m
)
|H
N
|(m)
< t
c
H
N
(b
1
...b
m+1
)
|H
N
|(m+1)
otherwise
.
Intuitively, we remove any information based on rare
states, with t a tolerance coefficient. We deduce Al-
gorithm 1 to compute a Markov chain model of a data
stream taking into account t.
6.1 Threshold Benefits
In other words, once the likelihood ratio is computed,
we can distinguish between the transitions which are
relevant for the test from those who are not.
Let s ∈ S
N
be a header sample, we want to test this
sample for a model X
1
(m, f
b
X
1
,X
1
0
) with threshold t
against a model X
2
(m, f
b
X
2
,X
2
0
) with the same thresh-
old t.
We write s = b
1
.. .b
N
and we introduce:
Γ
X
1
,X
2
,t
(s) =

γ
X
1
,t
(s)
N − m
,
γ
X
2
,t
(s)
N − m

,
Algorithm 1: Computation of a Markov chain
model of a data stream with threshold.
input :
• m an integer ;
• H
N
a list of the first N-bit sequences
of each file in the corpus ;
• t ∈ [0, 1] a threshold.
output: X(m, f
b
X
,X
0
) a memory m Markov chain.
1 for i ← 1 to |H
N
| do
2 Let b
1
... b
N
= H
N
[i];
3 C
H
N,0
(b
1
... b
m
) = C
H
N,0
(b
1
... b
m
) + 1;
4 for j ← 1 to N − m do
5 C
H
N
(b
j
... b
j+m
) = C
H
N
(b
j
... b
j+m
) + 1;
6 end
7 end
8 for s ← S
m
do
9 P(X
0
= s) ← C
H
N,0
(s)/|H
N
|;
10 end
11 for s = b
1
... b
m+1
← S
m+1
do
12 if c
H
N
(b
1
... b
m
)/|H
N
(m)| < t then
13 f
b
X
(s) ← 1/2c
H
N
(b
1
... b
m
)/|H
N
|(m)
14 else
15 f
b
X
(s) ← c
H
N
(s)/|H
N
|(m + 1);
16 end
17 end
18 return X(m, f
b
X
,X
0
);
with (8). It is clear that Γ
X
1
,X
2
,t
(s) is the pair of pro-
portions of relevant transitions in the sample s for
both models X
1
and X
2
. The higher these values are,
the more relevant the test should be. The Algorithm
2 computes the likelihood ratio of a sample s ∈ S
k
and outputs Γ
X
1
,X
2
,t
(s) taking into account a certain
threshold t.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
408

γ
X,t
= |{s = b
i
.. .b
i+m−1
∈ S
m
,i = 1,.. .,N − m + 1 | f
b
X
(s0) + f
b
X
(s1) ≥ t}|. (8)
Table 3: Results of tests with thresholded models against randomness for pdf and gif files (m = 4, N = 512).
Format t # true positive # true negative # false negative # false positive Accuracy
pdf 0.05 330 330 0 0 1.00
gif 0.05 142 150 8 0 0.97
Table 4: Results of tests with thresholded models against randomness for pdf and gif files (m = 16, N = 512).
Format t # true positive # true negative # false negative # false positive Accuracy
pdf 0.0005 330 330 0 0 1.00
gif 0.05 149 150 1 0 0.99
We remark that if we increase t the proportion of rel-
evant transition in the computation of a sample s will
decrease but if a sample has only relevant transitions
with respect to t, we will be confident that the like-
lihood ratio is meaningful from a statistical point of
view. In order to choose t, we can compute the ex-
pectancy, that we denote by E(
b
X,t), that a sample
s ∈ S
N
drawn following the distribution
b
X(N) has only
relevant transitions that is:
E(
b
X,t) =
∑
s=b
1
...b
N
∈S
N
P(
b
X(N) = s)T
b
X(m)
(s), (9)
where T
b
X(N)
: S
N
→ {0,1} is the function such that
• T
b
X(N)
(s) = 0 for s = b
1
.. .b
N
if there is a i ∈
{1,. .., N − m + 1} such that f
b
X
(b
i
.. .b
i+m−1
0) +
f
b
X
(b
i
.. .b
i+m−1
1) < t
• and T
b
X(N)
(s) = 1 otherwise.
Then one can choose a E(
b
X,t) which give the proba-
bility that a test will be relevant which fixes a t.
6.2 Results
The same tests as in Section 5.1, have been ran, on the
same corpus, with threshold models for pdf and gif
formats. The results for the best observed t parameter
are shown in Table 3.
The results are optimal for pdf files, the thresh-
old achieves a success rate of 100%. However, it
does not work so well for gif files, the threshold
does not improve the success rate. This is not sur-
prising because with m = 4, the observed transitions
are only distributed over a set of 2
4
= 16 states. This
does not allow for a lot of precision in the choice of
the threshold since we are basically ignoring a whole
state, when m = 4 this represents
1
16
of the et of states.
According to the previous observation, it should
be easier to find a good threshold for greater m. Thus,
the threshold model has also been tested with different
values of m. The results are the best for m = 16 as
shown in Table 4.
Algorithm 2: Algorithm to compute the likelihood
ratio.
input :
• m an integer;
• X
i
(m, f
b
X
i
,X
i
0
), for i = 1,2 two Markov chains;
• s = b
1
... b
k
∈ S
k
a sample of length k with k ≥ m;
• t ∈ [0, 1] a threshold.
output:
• Λ

s,
b
X
1
(k),
b
X
2
(k)

the likelihood ratio;
• µ
1
,µ
2
∈ [0, 1]
2
measuring the relevance of the test.
1 Λ ←
P(X
1
0
=b
1
...b
m
)
P(X
2
0
=b
1
...b
m
)
;
2 n
1
← 0, n
1
← 0 ;
3 for i ← m + 1 to k do
4 for j ← 1 to 2 do
5 P
j
=
f
b
X
j
(b
i−m
...b
i
)
f
b
X
j
(b
i−m
...b
i−1
0)+ f
b
X
j
(b
i−m
...b
i−1
1)
;
6 if f
b
X
j
(b
i−m
... b
i−1
0) +
f
b
X
j
(b
i−m
... b
i−1
1) ≥ t then
7 n
j
← n
j
+ 1;
8 end
9 end
10 Λ ← Λ
P
1
P
2
;
11 end
12 return Λ, µ
1
= n
1
/(k − m), µ
2
= n
2
/(k − m) ;
7 EXPERIMENTS ON
REAL-WORLD RANSOMWARE
In this section we show and analyse the results of
our tests against files encrypted by real-world ran-
somware. We used a model trained over the whole
corpus for these tests. It is important to precise that
the ransomware are active only a short moment, so it
is difficult to compare two experimentations paper.
Ransomware Detection using Markov Chain Models over File Headers
409

7.1 Models and Parameters
As done in section 5, we compared the divergence
to randomness for different values of m and N and
selected the ones that maximize the metric. The re-
sults are shown in Table 5. According to the diver-
Table 5: Divergence to randomness (whole corpus) for dif-
ferent parameters m and N.
m
N
128 256 512 1024 2048
4 0.044 0.057 0.069 0.049 0.035
8 0.074 0.074 0.084 0.060 0.045
16 0.055 0.062 0.067 0.040 0.025
gence results we have selected the following param-
eters: m = 8 and N = 512. Then we have checked
the convergence of the divergence to randomness like
previously done.
7.2 Results and Analysis
Table 6: Results with a model trained over the whole corpus
tested against ransomware encrypted files (m = 8, N = 512).
Ransomware # true positive # true negative # false negative # false positive Accuracy
Gigsaw 25 16 2 0 0.95
Ordinypt 25 4 2 20 0.57
Maoloa 25 27 2 0 0.96
MedusaLocker 25 24 2 0 0.96
Phobos 25 12 2 15 0.69
Unknown 25 27 2 0 0.96
Nemsis 25 24 2 0 0.96
Deadmin 25 27 2 0 0.96
Seon2 25 23 2 0 0.96
Zppelin 25 27 2 0 0.96
Paradise 25 27 2 0 0.96
StopDjvuMoka 25 27 2 0 0.96
MegaCortex 25 24 2 0 0.96
NemtyRevenge 25 23 2 0 0.96
Globlmposter 25 22 2 5 0.87
Globlmposter half 25 27 2 0 0.96
Estemani 25 24 2 0 0.96
Sodinokibi 25 24 2 0 0.96
Eris 25 27 2 0 0.96
xorist 25 2 2 25 0.5
We have run a test for each ransomware in the cor-
pus, on both encrypted files (we removed the files that
were not encrypted by the ransomware) and original
files. The results are shown in Table 6. The tested
ransomware all give two false negatives. The for-
mats of those two files .exe and .7z are actually not
present in the corpus, thus we do not expect them to
be tested positive. That means the accuracy in most
cases is probably the maximum we can expect from
the model.
However, there are still significant issues with
some specific ransomware. Orinypt & Phobos: the
issues with these two ransomware is that they put a
padding of zeroes at the beginning of some encrypted
files, since the transition from the all-zero state to it-
self is quite common in the corpus and can also be an
initial state, the model has troubles distinguishing it.
xorist: we believe the issues with this one is due to its
ability to conserve more or less the original entropy
of encrypted files, thus it does not fit into our model
of encrypted data based on randomness.
As we can see, the main issue is that some ran-
somware encryption techniques do not fit into our
model of encrypted data. A possible way to solve
these issues would be to train a model over a large
number of files encrypted with those ransomware and
then perform a test against these newly trained mod-
els. However, this would ruin the preventive aspect of
this approach since these specific ransomware would
have to be known before being detectable.
8 CONCLUSION AND FUTURE
WORKS
We have introduced a new countermeasure based on
Markov Chains to detect ransomware based on their
encryption behaviour. We also define a metric asso-
ciated to our models to give an idea on how well the
test should work. Considering ransomware use se-
mantically secure encryption schemes, we represent
encrypted data by a complete randomn Markov chain
model and are able to distinguish the structured files
from random data. According to our observations we
have refined our approach and models to fix potential
issues and get better results. Finally, we have proved
our approach to be applicable to real-world cases by
successfully distinguishing structured files from files
encrypted with known ransomware whose encryption
schemes fit into our models.
While the results are quite encouraging, there are
still some points to be dealt with more in depth. We
have mentioned that all the metrics do not take into
account the initial state probabilities, defining new
metrics to fix this issue would help getting a more
precise idea on the significance of the tests. Finally,
all tests on ransomware were made on small corpora,
running a full benchmark on thousands of files would
be needed to ensure the reliability of the approach.
One limitation of this work is that it cannot de-
tect a ransomware which do not encrypt header of
files. This countermeasure is not enough on her own.
But it’s a pertinent additional tool to complete other
implemented countermeasures against ransomware.
In the fight against ransomware, more indicators we
have, better is the detection. Moreover, the Markov
chain models have a low cost in terms of computing.
So they can be deployed in the kernel to stop mali-
cious processes without slowing down too much the
computer.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
410

ACKNOWLEDGMENTS
The authors would like to thank Jean-Louis Lanet and
Aur
´
elien Palisse for their for their helpful comments
and discussions.
REFERENCES
Ahmadian, M. M., Shahriari, H. R., and Ghaffarian, S. M.
(2015). Connection-monitor & connection-breaker: A
novel approach for prevention and detection of high
survivable ransomwares. In (ISCISC).
Akcora, C. G., Li, Y., Gel, Y. R., and Kantarcioglu,
M. (2019). Bitcoinheist: Topological data analysis
for ransomware detection on the bitcoin blockchain.
arXiv preprint.
Al-rimy, B. A. S., Maarof, M. A., Prasetyo, Y. A., Shaid, S.
Z. M., and Ariffin, A. F. M. (2018a). Zero-day aware
decision fusion-based model for crypto-ransomware
early detection. International Journal of Integrated
Engineering.
Al-rimy, B. A. S., Maarof, M. A., and Shaid, S. Z. M.
(2018b). Ransomware threat success factors, taxon-
omy, and countermeasures: A survey and research di-
rections. Computers & Security.
Al-rimy, B. A. S., Maarof, M. A., and Shaid, S. Z. M.
(2019). Crypto-ransomware early detection model us-
ing novel incremental bagging with enhanced semi-
random subspace selection. Future Generation Com-
puter Systems.
Almashhadani, A. O., Kaiiali, M., Sezer, S., and O’Kane, P.
(2019). A multi-classifier network-based crypto ran-
somware detection system: a case study of locky ran-
somware.
Ash, R. B. (1990). Information theory. Dover Publications,
Inc., New York. Corrected reprint of the 1965 original.
Aurangzeb, S., Aleem, M., Iqbal, M. A., Islam, M. A., et al.
(2017). Ransomware: a survey and trends. J. Inf.
Assur. Secur.
Baykara, M. and Sekin, B. (2018). A novel approach to
ransomware: Designing a safe zone system. In ISDFS.
IEEE.
Cabaj, K., Gregorczyk, M., and Mazurczyk, W. (2018).
Software-defined networking-based crypto ran-
somware detection using http traffic characteristics.
Computers & Electrical Engineering.
Castiglione, J. and Pavlovic, D. (2019). Dynamic dis-
tributed secure storage against ransomware. IEEE
Transactions on Computational Social Systems.
Chen, Z.-G., Kang, H.-S., Yin, S.-N., and Kim, S.-R.
(2017). Automatic ransomware detection and analysis
based on dynamic api calls flow graph. In Proceedings
of the International Conference on Research in Adap-
tive and Convergent Systems.
Continella, A., Guagnelli, A., Zingaro, G., Pasquale,
G. D., Barenghi, A., Zanero, S., and Maggi, F.
(2016). ShieldFS: A Self-healing, Ransomware-aware
Filesystem. In ACSAC. ACM.
Genc¸, Z. A., Lenzini, G., and Ryan, P. Y. (2018). Next gen-
eration cryptographic ransomware. In Nordic Confer-
ence on Secure IT Systems. Springer.
Hershey, J. R. and Olsen, P. A. (2007). Approximating the
kullback leibler divergence between gaussian mixture
models. In IEEE-ICASSP.
Huber, P. J. and Strassen, V. (1973). Minimax tests and the
neyman-pearson lemma for capacities. The Annals of
Statistics.
Katz, J. and Lindell, Y. (2007). Introduction to Modern
Cryptography (Chapman & Hall/Crc Cryptography
and Network Security Series). Chapman & Hall/CRC.
Kharraz, A., Arshad, S., Mulliner, C., Robertson, W. K.,
and Kirda, E. (2016). UNVEIL: A Large-Scale,
Automated Approach to Detecting Ransomware. In
USENIX.
Kharraz, A. and Kirda, E. Redemption: Real-Time Pro-
tection Against Ransomware at End-Hosts. In RAID
2017.
Kullback, S. and Leibler, R. A. (1951). On information and
sufficiency. Ann. Math. Statistics.
Lee, K., Lee, S.-Y., and Yim, K. (2019). Machine learning
based file entropy analysis for ransomware detection
in backup systems.
Moore, C. (2016). Detecting ransomware with honeypot
techniques. In 2016 Cybersecurity and Cyberforensics
Conference (CCC). IEEE.
Moussaileb, R. (2020). Log Analysis for Malicious Software
Detection. PhD thesis.
Moussaileb, R., Bouget, B., Palisse, A., Le Bouder, H.,
Cuppens, N., and Lanet, J.-L. (2018). Ransomware’s
early mitigation mechanisms. In Proceedings of the
13th International Conference on Availability, Relia-
bility and Security. ACM.
Moussaileb, R., Cuppens, N., Lanet, J.-L., and Le Bouder,
H. (2019). Ransomware network traffic analysis for
pre-encryption alert. In FPS2019.
Palisse, A., Durand, A., Le Bouder, H., Le Guernic, C.,
and Lanet, J.-L. (2017). Data aware defense (dad):
towards a generic and practical ransomware counter-
measure. In Nordic Conference on Secure IT Systems.
Springer.
Palisse, A., Le Bouder, H., Lanet, J.-L., Le Guernic, C., and
Legay, A. (2016). Ransomware and the legacy crypto
api. In International Conference on Risks and Security
of Internet and Systems. Springer.
Patton, M. W., Scott, N., Gutierrez, R. R., and Giovannini,
S. (2019). Behavior-based ransomware detection us-
ing decoy files.
Pont, J., Arief, B., and Hernandez-Castro, J. (2020). Why
current statistical approaches to ransomware detection
fail. In International Conference on Information Se-
curity. Springer.
Scaife, N., Carter, H., Traynor, P., and Butler, K. R. B.
(2016). CryptoLock (and Drop It): Stopping Ran-
somware Attacks on User Data. In ICDCS. IEEE.
Yassine Lemmou, H
´
el
`
ene Le Bouder, J.-L. L. (2019). Dis-
criminating unknown software using distance model.
Ransomware Detection using Markov Chain Models over File Headers
411