AVX-512-based Parallelization of Block Sieving and Bucket Sieving for
the General Number Field Sieve Method
∗
Pritam Pallab and Abhijit Das
Indian Institute of Technology, Kharagpur, India
Keywords:
General Number Field Sieve Method, RSA Cryptanalysis, Line Sieving, Lattice Sieving, Block Sieving,
Bucket Sieving, Single Instruction Multiple Data (SIMD), Multi-core, Multi-thread, AVX-512, Skylake.
Abstract:
The fastest known general-purpose technique for factoring integers is the General Number Field Sieve Method
(GNFSM), in which the most time-consuming part is the sieving stage. For both line sieving and lattice sieving,
two cache-friendly extensions used in practical implementations are block sieving and bucket sieving. The
new AVX-512 instruction set in modern Intel CPUs offers some fast vectorization intrinsics. In this paper, we
report our AVX-512 based cache-friendly parallelization of block and bucket sieving for the GNFSM. We use
vectorization for both sieve-index calculations and sieve-array updates in block sieving, and for the insertion
stage in bucket sieving. Our experiments using Intel Xeon Skylake processors demonstrate a performance
boost in both single-core and multi-core environments. The introduction of cache-friendly sieving leads to a
speedup of up to 63%. On top of that, vectorization yields a speedup of up to 25%.
1 INTRODUCTION
The General Number Field Sieve Method (GN-
FSM) (Lenstra et al., 1993a) is the fastest known
technique for factoring large composite integers, like
RSA moduli. The RSA (Rivest–Shamir–Adleman)
algorithm (Rivest et al., 1978) is one of the earliest
and most widely used public-key cryptographic algo-
rithms, and exploits the difficulty of factoring prod-
ucts of pairs of large primes to derive its security.
The last published successful RSA factorization at-
tempt was that of an RSA modulus of length 795
bits (Boudot et al., 2020a). There is also an un-
published claim of successful factorization of RSA-
250 (Boudot et al., 2020b) which is a 829-bit RSA
modulus. All these attempts implement the GNFSM.
The GNFSM originates from a specialized form
called the Special Number Field Sieve Method
(SNFSM) (Lenstra et al., 1990) which is developed
to factor composite integers of the form r
e
± s, where
r, s,e ∈ Z and e > 0. It is asymptotically faster than
the GNFSM, and is used to factor the ninth Fermat
Number F
9
= 2
512
+ 1 (Lenstra et al., 1993b). The
SNFSM is later generalized to the GNFSM to work
for any composite integer (Buhler et al., 1993). This
method is based on a ring homomorphism (Briggs,
1998) Z[θ] → Z for a suitable algebraic number θ,
and is intended to discover a non-trivial Fermat con-
∗
Funded partially by the Ministry of Electronics and
Information Technology, India.
gruence of the form x
2
≡ y
2
(mod n).
The GNFSM consists of multiple stages, among
which sieving is the most time-consuming one taking
around 60–80% of the overall running time. There
are two main techniques used for sieving: line sieving
and lattice sieving. In this paper, we mainly focus on
line sieving. In both of these types of sieving, mem-
ory accessing plays a pivotal role. In order to mini-
mize costly cache misses, two new modifications are
introduced. These are called block sieving (Wambach
and Wettig, 1995) and bucket sieving (Aoki and Ueda,
2004). In the recent factorization attempts, the block
and bucket sieving ideas are extensively used. Earlier,
SSE2- and AVX-based SIMD parallelization tech-
niques are attempted (Sengupta and Das, 2017) for
line and lattice (Pollard, 1993) sieving. In that work,
the index-calculation part is vectorized, but the sieve-
array updating part is not. This is attributed to limited
and costly intrinsics available in previous generations
of CPUs. The recent introduction of AVX-512 offers
a new set of intrinsics, and thereby opens the opportu-
nities of exploring the potentials of fully vectorizing
the sieving stage. In this paper, we report our AVX-
512-based vectorization attempts for cache-friendly
block- and bucket-sieving variants of line sieving. We
are able to achieve speedup factors of up to 63% with
cache-friendly sieving and additional speedup factors
of up to 25% with vectorization.
The rest of the paper is organized as follows. Sec-
tion 2 deals with the background and a study of ex-
Pallab, P. and Das, A.
AVX-512-based Parallelization of Block Sieving and Bucket Sieving for the General Number Field Sieve Method.
DOI: 10.5220/0010515206530658
In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 653-658
ISBN: 978-989-758-524-1
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
653

isting factoring algorithms. Section 3 elaborates our
vectorization approaches for both block sieving and
bucket sieving. The experimental results for single-
core and multi-core environments are presented in
Section 4. Section 5 concludes the paper with notes
on possible extensions of our current work.
2 BACKGROUND
2.1 General Number Field Sieve
Method
In order to factor n, the GNFSM starts with the selec-
tion of two irreducible polynomials f
r
(x) and f
a
(x) of
degrees d
r
and d
a
and with a common root m modulo
n. Here, f
r
(with d
r
= 1) pertains to the rational side,
whereas f
a
(with d
a
> 1) pertains to the algebraic side.
We also let θ ∈ C be a root of f
a
(x). Next, the rational
(RFB) and the algebraic (AFB) factor bases are cre-
ated. RFB consists of small (integer) primes bounded
by a limit B
r
, while the AFB consists of prime ide-
als in the number ring Q[X]/h f
a
(X)i of prime norms
bounded by a limit B
a
. For each small prime p, the
prime ideals of norm p can be obtained by identifying
the roots of the equation f
a
(x) modulo p, that is, by
solving the congruence f
a
(r) ≡ 0 (mod p).
The sieving stage uses two integer parameters a
and b with gcd(a,b) = 1. If a + bm and a + bθ are
both smooth over the respective factor bases, a re-
lation is discovered. The integer a + bm is called
smooth if it factors completely over the RFB, whereas
the algebraic number a + bθ is called smooth if the
ideal ha + bθi factors completely over the prime ide-
als in AFB. A choice of the pair (a,b) gives a relation
if and only if both the integers (−b)
d
r
f
r
(−a/b) and
(−b)
d
a
f
a
(−a/b) factor completely over the primes ≤
B
r
and B
a
. Using the ring homomorphism η : Z[θ] →
Z/nZ taking θ 7→ m, each relation η(a + bθ) ≡ a +
bm (mod n) gives a linear congruence. The resulting
linear system is solved to reach the Fermat congru-
ence. If gcd(x − y, n) is a trivial factor of n, we go for
the other solutions else we report the factors.
2.2 Sieving
The main focus of this paper is on the efficient imple-
mentations of the sieving part mainly the line sieving
whereas the proposed methods are applicable to lat-
tice sieving in a straightforward manner. Block and
bucket sieving techniques are the cache-friendly ex-
tensions of normal sieving.
2.2.1 Block Sieving
Instead of accessing the whole sieve array S for each
factor f in the factor base FB, we divide S into multi-
ple blocks and perform sieving on one block at a time.
The entire sieve line of length 2MAX
A
+ 1 is subdi-
vided into b
n
blocks, where the size of each block
is b
s
= d(2MAX
A
+ 1)/b
n
e. This method is advan-
tageous if we keep the value of b
s
within the size of
the available cache memory. This enables the runtime
system to load a whole block of S at a time in the
cache, and for all f ∈ FB, accesses are made within
that block only. This reduces the cache misses sig-
nificantly, thereby speeding up the whole sieving pro-
cess. The factor base is subdivided into two parts:
0 ≤ f ≤ FB
S
and FB
S
< f ≤ FB
MAX
. For the smaller
factors ( f ≤ FB
S
), block sieving is used.
2.2.2 Bucket Sieving
In order to manage the cache memory efficiently for
large factors also, bucket sieving is introduced. In-
stead of performing normal sieving over large factors,
buckets are created, filled, and sieved only one at a
time. The main concept relies again on the use of
only a portion of the sieve array S during accessing
and log subtractions. Let B
n
be the number of buck-
ets under consideration, and B
s
= d(2MAX
A
+1)/B
n
e.
Bucket sieving employs a two-fold approach. For
each large factor f and for each of the sieving loca-
tion a we encounter, an element (a,log( f )) is inserted
in the b(a + MAX
A
)/B
s
c-th bucket. The size of each
bucket is kept within the limits of the available cache
memory. Later, we iterate over all the buckets one
by one, popping its elements and performing S up-
dates accordingly. As each of the buckets holds the
elements having a within the range of the cache size,
cache misses are reduced drastically.
3 OUR IMPLEMENTATION
APPROACH
In this section, we elaborate our approach of using
SIMD (Single Instruction Multiple Data) in the con-
text of block sieving and bucket sieving. The latest
SIMD feature added by Intel is AVX-512 which sup-
ports 512-bit registers. In the context of sieving, it
allows us to perform 16 index calculations and log
subtractions in a data-parallel fashion.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
654

Table 1: AVX-512 SIMD instructions used.
AVX-512 intrinsic Pseudo-function
mm512 load epi32 (void const*
mem addr)
simd load
mm512 store epi32 (void* mem addr,
m512i a)
simd store
mm512 add epi32 ( m512i a, m512i b) simd add
mm512 sub epi32 ( m512i a, m512i b) simd sub
mm512 reduce min epi32 ( m512i a) simd minimum
mm512 i32gather epi32 ( m512i vindex,
void const* base addr, int scale)
simd gather
mm512 i32scatter epi32 (void*
base addr, m512i vindex, m512i
a, int scale)
simd scatter
3.1 SIMD-based Block Sieving
In Intel’s AVX-512 intrinsics, a special data type
m512i can store sixteen 32-bit integers in a vec-
tor. In (Sengupta and Das, 2017), vectoriza-
tion of the subtraction phase of the sieve array
is avoided in line and lattice sieving because of
limitations of AVX. With AVX-512, we can per-
form SIMD-level parallelization of both index cal-
culations and sieve-array modifications. We pack
16 primes p
i
, p
i+1
,. .., p
i+15
= p[i : i + 15] from the
factor base FB into a m512i SIMD variable ∆
p
,
and their log values into another SIMD variable
∆
log p
. For a fixed b, we calculate the starting siev-
ing locations a
s
i
,a
s
i+1
,. ..,a
s
i+15
= a
s
[i : i + 15] for
(r[i : i + 15], p[i : i + 15]). Then, we pack another
m512i variable ∆
a
with a
s
[i : i + 15]. Now, we keep
on incrementing ∆
a
by ∆
p
over the entire a-line up
to MAX
A
to find out 16 sieving cell indices at a time.
Using the AVX-512 intrinsic gather, we collect the
values S[∆
a
] and store them in ∆
S
, and subtract ∆
log p
from ∆
S
. Then, we store the subtracted components
back to their corresponding locations using another
AVX-512 intrinsic scatter. This enables us to shorten
the outer factor-base loop by a factor of 16 at the
cost of some SIMD overhead. The index vector ∆
a
is
packed with the starting indices only once for a par-
ticular p[i : i + 15].
Moreover, the incremental addition of ∆
p
to ∆
a
Table 2: Details of the pseudo functions.
Pseudo-function Description
allocate memory Allocates memory to the array.
is incomplete Checks if an element has pending iterations.
process bucket For each (a,log p) stored in the bucket, S[a +
MAX
A
] − log p is performed emptying the
bucket.
insert element Inserts (a,log(p)) into a given bucket.
populate sieve array For a given b and a ∈ [A
L
,A
R
], S[a + MAX
A
] is
populated by log|(−b)
d
f (−a/b)|.
initialize Initializes array elements with given value.
Algorithm 1: SIMD-based block sieving.
1 for b ← B
L
to B
R
do
2 for A
L
← −MAX
A
to MAX
A
in steps of b
s
do
3 A
R
← minimum(A
L
+ b
s
,MAX
A
)
4 populate sieve array (S,b,A
L
,A
R
)
5 for each p[i : i + 15] ∈ FB such that p[ j] ≤ FB
S
,
i ≤ j ≤ i + 15, do
6 ∆
p
← simd load(p[i : i + 15])
7 ∆
log p
← simd load(log p[i : i + 15])
8 if A
L
equals −MAX
A
then
9 a
s
[i : i + 15] ← initial sieving points
10 ∆
a
← simd load(a
s
[i : i + 15])
11 while simd minimum(∆
a
)≤ A
R
do
12 ∆
S
← simd gather(S,∆
a
)
13 ∆
S
← simd sub(∆
S
,∆
log p
)
14 simd scatter(S,∆
S
,∆
a
)
15 ∆
a
← simd add(∆
a
,∆
p
)
16 a
s
[i : i + 15] ← simd store(∆
a
)
17 for j ← i to i +15 do
18 if is incomplete(a
s
[ j],A
R
) then
19 while a
s
[ j] ≤ A
R
do
20 S[a
s
[ j]+ MAX
A
] ←
S[a
s
[ j] + MAX
A
] − log(p[ j])
21 a
s
[ j] ← a
s
[ j] + p[ j]
does not require unpacking of any of the SIMD reg-
isters. Therefore we achieve effective vectorization
of sieving-index calculations with 16-fold speedup.
However, gathering and scattering costs after each in-
dex increment introduce some overhead. Algorithm 1
elaborates the steps of AVX-512-based block sieving.
Table 1 lists the AVX-512 intrinsics used in the im-
plementation of this algorithm.
3.2 SIMD-based Bucket Sieving
In bucket sieving, updating indices are calculated sep-
arately and stored in buckets. Later, the buckets are
emptied followed by sieve-array updates. The bucket-
filling part is SIMD-friendly. In bucket sieving, we
work with the large primes (p > FB
S
) of the factor
base FB. We take 16 primes p[i : i + 15] at a time, and
store them in an SIMD variable ∆
p
. We also calculate
the initial locations a
s
[i : i + 15], and store them in an-
other SIMD variable ∆
a
. Then, we keep on finding 16
new sieving locations using an SIMD increment of ∆
a
by ∆
p
, and fill the buckets.
We start by allocating memory to the array BARR
of buckets. In order to keep track of the numbers of
elements in the buckets in the array BARR, we main-
tain another array B
T
. For efficient memory usage,
we pre-allocate each bucket in the bucket array BARR
with a maximum element capacity of BUC
MAX
. The
AVX-512-based Parallelization of Block Sieving and Bucket Sieving for the General Number Field Sieve Method
655

value of BUC
MAX
is determined according to the size
of the cache memory so that during the bucket-pop
operation, cache-miss rates are minimized. During
each insertion, we keep a check whether any bucket
exceeds its capacity. If it so happens, we pop all
the elements from that bucket, and update the siev-
ing array at the stored locations. This strategy also
eliminates the need of malloc and free operations
of bucket entries after individual insert and pop op-
erations. These memory operations are atomic, so
avoiding them inside the loop boosts parallelism in
multi-threaded implementations.
Algorithm 2 summarizes these implementation
ideas. The workings of the pseudo-functions used in
this algorithm are explained in Table 2.
4 EXPERIMENTAL RESULTS
4.1 Hardware and Software Setup
We use Intel’s Xeon Gold Series (Model No. 6130)
processor clocked at 2.10 GHz with an L3 Cache of
size 22 MB. The gcc compiler (version 9.2.0), GMP
library (version 6.1.2)and OpenMP API (version 4.5)
is used. For calculating the prime ideals, we use
Victor Shoup’s NTL library (version 11.3.2) (Shoup
et al., 2020). The optimization flag -O3 and the in-
trinsic flag -mavx=native are used. In the multi-core
implementations, we use all of the 16 cores of a sin-
gle processor. The operating system is CentOS Linux
release 7.4.1708 (Core).
4.2 Data Setup
As a test bench, we here consider the two numbers
RSA-512 and RSA-768 which are factored as re-
ported in (Cavallar et al., 2000) and (Kleinjung et al.,
2010). In each of the cases, we consider the same
polynomials that are used in the actual factorization
attempts. Suitable partitioning of the factor base be-
tween block- and bucket-sieving primes has a ma-
jor impact on the overall running time. We vary the
small-versus-large demarcation boundary FB
S
based
on the sieving range MAX
A
across various test cases.
For our multi-threaded implementation, we use
the OpenMP directive #pragma omp parallel for
to launch 16 threads expected to map to the individ-
ual cores. We allocate different segments of b values
to the different threads in order to avoid concurrent
writes. The read-only p and log p arrays are shared
by all the threads, so that they can stay loaded in the
cache. We have chosen the same limiting values (up-
per) for both the factor bases: B
r
= B
a
= MAX
FB
.
4.3 Timing Results
Table 3 reports the timings T
±v
±b
of our implemen-
tations of sieving. The subscript indicates whether
cache-friendly (block/bucket) sieving is used (+b) or
not (−b), whereas the superscript indicates whether
vectorization is used (+v) or not (−v). For exam-
ple, T
−v
+b
indicates the timing of our non-vectorized
implementation with block and bucket sieving. All
the times are in seconds, and stand for the com-
bined times of rational sieving and algebraic siev-
ing. Each sieving includes the time taken by the pre-
computation of initial indices, index increments and
log subtractions, and locating potential sieving loca-
tions. The time for final trial divisions (relation gen-
eration) is excluded here. The number of threads uti-
lized is denoted as N
θ
. Each of the reported times is
the average over 100 test cases.
Based on these four sets of timings, we calculate
four relevant sets of speedup figures. The speedup
of [T+] over [T−] is calculated as

[T−] − [T+]
[T−]

×
100%, where both the signs ± appear either in the
subscript or in the superscript with the other kept
unchanged. For example, ψ
+b
=
T
−v
+b
− T
+v
+b
T
−v
+b
!
×
100% indicates the speedup obtained by vec-
torization on cache-friendly sieving, and ψ
−v
=
T
−v
−b
− T
−v
+b
T
−v
−b
!
× 100% indicates the speedup ob-
tained by cache-friendly sieving without vectoriza-
tion.
The experimental data establishes two facts. First,
AVX-512-based vectorization achieves a speedup of
up to 56% in non-cache-friendly sieving and up to
25% in cache-friendly block and bucket sieving over
non-vectorized implementations. Second, the effec-
tiveness of cache-friendly sieving is manifested by a
speedup of up to 63% both with and without vector-
ization. In particular, the best running times are ob-
tained with both cache-friendly sieving and vectoriza-
tion (the column headed T
+v
+b
).
5 CONCLUSION
In this paper, we report the practical effectiveness
of block and bucket sieving and AVX-512-based
vectorization. This study establishes the usefulness of
exploiting latest hardware features for implementing
time-consuming algorithms like the GNFSM for fac-
toring integers. There are several ways in which our
study can be extended. Both cache-friendly sieving
SECRYPT 2021 - 18th International Conference on Security and Cryptography
656

Algorithm 2: SIMD-based bucket sieving.
1 B
N
← (2 × MAX
A
+ 1)/B
s
// Total number of buckets
2 BARR ← allocate memory(B
N
× BUC
MAX
) // Memory for all buckets
3 B
T
← initialize(0) // All buckets are initially empty
4 for b ← B
L
to B
R
do
5 for A
L
← −MAX
A
to MAX
A
in steps of b
s
do
6 A
R
← minimum(A
L
+ b
s
,MAX
A
)
7 populate sieve array (S,b,A
L
,A
R
) // Initialize with log values
8 block sieving(A
L
,A
R
) // Use Algorithm 1 to handle small primes
9 for each p[i : i + 15] ∈ FB
LIST
such that p[ j] > FB
S
, i ≤ j ≤ i + 15 do
10 ∆
p
← simd load(p[i : i + 15])
11 a
s
[i : i + 15] ← initial sieving points
12 ∆
a
← simd load(a
s
[i : i + 15]) // Calculate next indices
13 while simd minimum(∆
a
) ≤ MAX
A
do
14 for each (a
s
[ j], p[ j]) in (a
s
[i : i + 15], p[i : i + 15]) do
15 b
n
← (a
s
[ j] + MAX
A
)/B
s
// The bucket number
16 if B
T
[b
n
] equals BUC
MAX
then
17 // Bucket capacity reached
18 process bucket(S,BARR,B
T
,b
n
)
19 B
T
[b
n
] ← 0 // Bucket flushed
20 insert element(S, BARR,B
T
,b
n
,a
s
[ j], log(p[ j]))
21 B
T
[b
n
] ← B
T
[b
n
] + 1 // Update entry stored
22 ∆
a
← simd add(∆
a
,∆
p
)
23 a
s
[i : i + 15] ← simd store(∆
a
)
24 for j ← i to i + 15 do
25 if is incomplete(a
s
[ j], MAX
A
) then
26 while a
s
[ j] < MAX
A
do
27 b
n
← (a
s
[ j] + MAX
A
)/B
s
28 if B
T
[b
n
] equals BUC
MAX
then
29 process bucket(S,BARR,B
T
,b
n
)
30 B
T
[b
n
] ← 0
31 insert element(S,BARR,B
T
,b
n
,a
s
[ j], log(p[ j]))
32 B
T
[b
n
] ← B
T
[b
n
] + 1
33 a
s
[ j] ← a
s
[ j] + p[ j]
34 for b
n
← 1 to B
N
do
35 process bucket(S,BARR,B
T
,b
n
) // Use all non-empty buckets
and the use of vectorization are expected to boost lat-
tice sieving by the same margins as line sieving. How-
ever, explicit experiments are not carried out with lat-
tice sieving. Block sieving is effectively vectorized,
but bucket sieving has further rooms for investigation,
particularly in the bucket emptying process.
The current processor technology imposes restric-
tions on the processing speed in the presence of SIMD
utilization. For Xeon 6130 processors, individual
cores work at a speed of 2.1 GHz, but enabling AVX2
or AVX-512 reduces the frequency to 60–65% (Wi-
kiChip, 2020). Further reduction happens with the
increasing number of cores. This is one of the main
reasons behind not achieving the ideal speedup in the
case of multi-threaded implementations. Finding a
balance between the use of multiple cores and the use
of SIMD features remains a challenging practical area
of investigation.
REFERENCES
Aoki, K. and Ueda, H. (2004). Sieving using bucket sort.
In International Conference on the Theory and Appli-
cation of Cryptology and Information Security, pages
92–102. Springer.
AVX-512-based Parallelization of Block Sieving and Bucket Sieving for the General Number Field Sieve Method
657

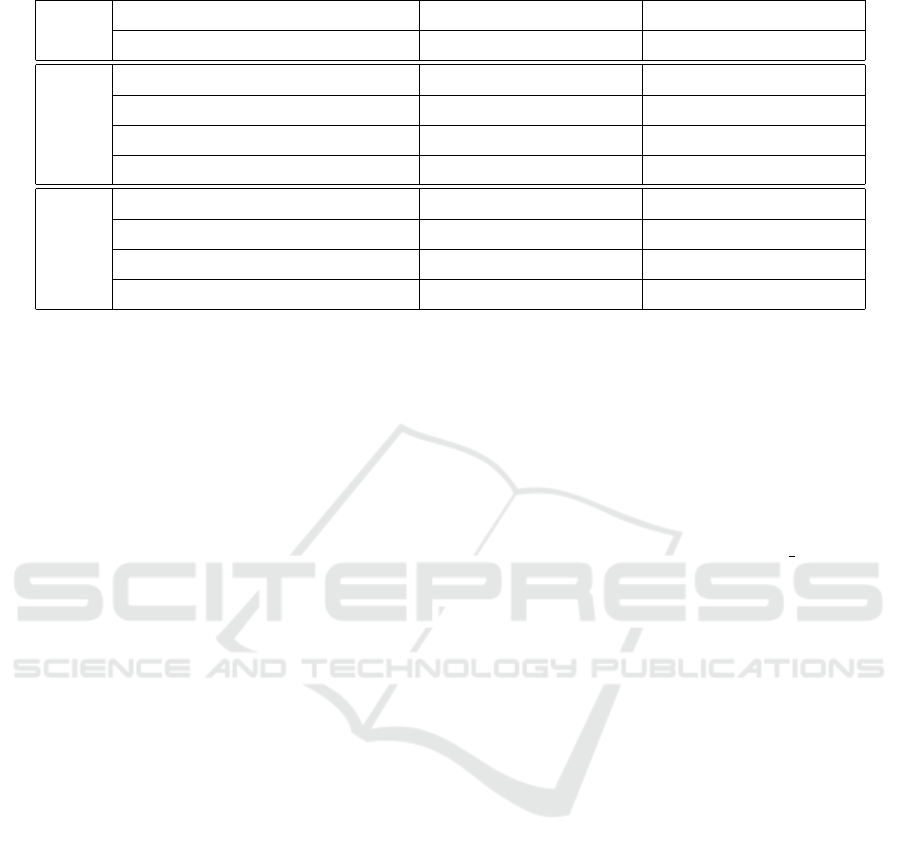
Table 3: Timing and speedup figures.
n
Parameters Sieving time (sec) Percentage speedup
MAX
A
MAX
B
N
θ
FB
S
MAX
FB
T
−v
−b
T
−v
+b
T
+v
−b
T
+v
+b
ψ
−b
ψ
+b
ψ
−v
ψ
+v
RSA-512
5 × 10
5
11 1 4.5 × 10
4
5 × 10
4
0.281 0.131 0.151 0.098 46.26 25.19 53.38 35.10
3 × 10
6
11 1 4.5 × 10
4
5 × 10
4
2.056 0.968 1.270 0.737 38.23 23.86 52.92 41.97
3 × 10
6
11 1 2
18
3 × 10
5
2.255 1.068 1.300 0.805 42.35 24.63 52.64 38.08
3 × 10
6
161 16 2
18
3 × 10
5
6.299 2.321 5.929 2.212 5.87 4.70 63.15 62.69
RSA-768
5 × 10
5
11 1 4.5 × 10
4
5 × 10
5
0.386 0.192 0.171 0.160 55.70 16.67 50.26 6.43
3 × 10
6
11 1 4.5 × 10
4
5 × 10
5
2.506 1.368 1.332 1.137 46.85 16.89 45.41 14.64
3 × 10
6
11 1 2
19
3 × 10
6
2.947 1.427 1.511 1.186 48.73 16.89 51.58 21.51
3 × 10
6
161 16 2
19
3 × 10
6
7.499 4.072 6.691 3.763 10.77 7.59 45.70 43.76
Boudot, F., Gaudry, P., Guillevic, A., Heninger, N., Thom
´
e,
E., and Zimmermann, P. (2020a). Comparing the dif-
ficulty of factorization and discrete logarithm: a 240-
digit experiment. arXiv preprint arXiv:2006.06197.
Boudot, F., Gaudry, P., Guillevic, A., Heninger, N., Thom
´
e,
E., and Zimmermann, P. (2020b). Factorization of
rsa-250. https://caramba.loria.fr/rsa250.txt. Accessed:
2021-02-08.
Briggs, M. E. (1998). An introduction to the general number
field sieve. PhD thesis, Virginia Tech.
Buhler, J. P., Lenstra, H. W., and Pomerance, C. (1993).
Factoring integers with the number field sieve. In The
development of the number field sieve, pages 50–94.
Springer.
Cavallar, S., Dodson, B., Lenstra, A. K., Lioen, W., Mont-
gomery, P. L., Murphy, B., Te Riele, H., Aardal, K.,
Gilchrist, J., Guillerm, G., et al. (2000). Factoriza-
tion of a 512-bit rsa modulus. In International Confer-
ence on the Theory and Applications of Cryptographic
Techniques, pages 1–18. Springer.
Kleinjung, T., Aoki, K., Franke, J., Lenstra, A. K., Thom
´
e,
E., Bos, J. W., Gaudry, P., Kruppa, A., Montgomery,
P. L., Osvik, D. A., et al. (2010). Factorization of a
768-bit rsa modulus. In Annual Cryptology Confer-
ence, pages 333–350. Springer.
Lenstra, A. K., Hendrik Jr, W., et al. (1993a). The develop-
ment of the number field sieve, volume 1554. Springer
Science & Business Media.
Lenstra, A. K., Lenstra, H. W., Manasse, M. S., and Pollard,
J. M. (1993b). The factorization of the ninth fermat
number. Mathematics of Computation, 61(203):319–
349.
Lenstra, A. K., Lenstra Jr, H. W., Manasse, M. S., and Pol-
lard, J. M. (1990). The number field sieve. In Proceed-
ings of the twenty-second annual ACM symposium on
Theory of computing, pages 564–572. ACM.
Pollard, J. M. (1993). The lattice sieve. In The development
of the number field sieve, pages 43–49. Springer.
Rivest, R. L., Shamir, A., and Adleman, L. (1978). A
method for obtaining digital signatures and public-
key cryptosystems. Communications of the ACM,
21(2):120–126.
Sengupta, B. and Das, A. (2017). Use of simd-based data
parallelism to speed up sieving in integer-factoring
algorithms. Applied Mathematics and Computation,
293:204–217.
Shoup, V. et al. (2020). Ntl: A library for doing number
theory.
Wambach, G. and Wettig, H. (1995). Block sieving algo-
rithms. Citeseer.
WikiChip (2020). Intel xeon gold 6130.
https://en.wikichip.org/wiki/intel/xeon gold/6130.
Accessed: 2021-02-08.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
658