Time Delay Investigation in Telerobotic Surgery
Vivian Chai and Dan-Sorin Necsulescu
Department of Mechanical Engineering, University of Ottawa, Ottawa, ON, Canada
Keywords:
Contact Forces, Robotic Arm Manipulator, Soft Tissue Modelling, Telerobotics, Time Delay.
Abstract:
Telerobotic surgery is a medical technology that allows a surgeon to operate on a patient from a distance, via
a communication network. As with all telerobotic procedures, factors such as time delay or limited bandwidth
may affect the performance of the robotics. In addition, surgeries require contact with soft tissues of the body,
resulting in unaccounted external forces on the robotic manipulator. The paper investigates the effects of
time delay on the desired trajectory of a telerobotic arm that undergoes forces due to contact with skin tissue.
Two behaviours will be explored through simulation, under different time delays, with the robotic arm’s end
effector sliding across the surface of the skin, as well as compressing the skin perpendicularly. Simulation
results are compared with the expected behaviour of existing telerobotic performance. It was found that
tangential forces across the skin’s surface do not significantly impact telerobotic performance but when subject
to normal contact, the robotic arm fails under shorter time delays than expected. Further experimentation with
trajectories, not limited to parallel or perpendicular motion of the effector on the skin, and trials involving real
tissues and manipulators will provide greater insight for understanding telerobotic performance in surgery.
1 INTRODUCTION
With the improvements of modern technology, teler-
obotic applications are becoming more prominent in
the medical field. These procedures are carried out
through a communication network between a user-
controlled master console and a semi-autonomous,
slave robot that moves based on directions from the
user (Avgousti et al., 2016). This networking enables
medical treatment to be performed without direct con-
tact between patient and doctor. As telerobotic appli-
cations, in the medical field, are still a relatively new
subject of research, there are many areas that require
progress, which may offer various improvements to
the existing health care systems.
Telerobotic surgery, in particular, is a topic of
great interest, as it presents many advantages over
current surgical procedures. When compared with
traditional surgical methods, surgical robots have a
significantly greater range of motion and can be
smaller than a human hand, allowing for more com-
plex and dexterous movements (Ho et al., 2011).
These robots can be small and equipped with various
sensors and cameras, resulting in less invasive opera-
tions, fewer surgical complications and blood loss, as
well as significant reductions in patient recovery time
(Buia et al., 2015). Furthermore, with telerobotics,
treatment of infectious diseases or surgeries in remote
locations can be performed (Arata et al., 2007). These
advantages, and many more, encourage the techno-
logical advancements of robotics in this field.
However, telerobotic surgeries still have many is-
sues that have yet to be resolved. As these surgeries
are highly dependent on the communication feedback
from the slave controller, any feedback problems will
greatly influence the robot’s performance. In partic-
ular, time delay during the transmission of informa-
tion to and from the slave robot is always prevalent
in telerobotic operations. These delays prevent up-
to-date knowledge from reaching the operator, which
may in turn impact performance, depending on the
length of the delay. For surgeries, which are time
sensitive, these delays are dangerous and can pose a
threat to the patient’s well being.
This paper explores the effects of time delay on a
3-linkage planar robotic arm, operating in a surgical
environment. Different interactions, such as tangean-
tial surface contact and compression between the soft
tissue and robotic arm, will be modeled and simu-
lated under different time delays, and performance of
the robot will be compared to its desired movement.
Simulations were performed using MATLAB
TM
and
Simulink
TM
.
Chai, V. and Necsulescu, D.
Time Delay Investigation in Telerobotic Surgery.
DOI: 10.5220/0010515603750382
In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 375-382
ISBN: 978-989-758-522-7
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
375

2 BACKGROUND
The concepts of time delay, manipulator control, and
soft tissue behaviour in the surgical environment must
be understood. The following section presents the
knowledge about these topics that is required for mod-
eling.
2.1 Time Delay
All telerobotic operations have time delays, which
stem from a combination of delays from image
capturing, communications, signal processing for
the controllers and many more factors (Vazquez-
Santacruz et al., 2017)(Velasco-Villa et al., 2013).
Many studies have shown that as time delay increases,
the number of moves required, the time to com-
plete the task, as well as the number of errors all
increase (Fabrizio et al., )(Anvari et al., 2005)(Lum
et al., 2009)(Korte et al., 2014)(Hristu et al., 1996)(M.
Uebel et al., 1994). However, it is important to note
that while time delays cannot be completely elimi-
nated from a system, shorter time delays are beneficial
to the system’s performance. Table 1 below shows
the effects of different time delays on their perfor-
mance, gathered from various papers (Orosco et al.,
2020)(Perez et al., 2015)(Xu et al., 2014).
Table 1: Time Delay Effects on Telerobotic Performance.
Delay Length (ms) Telerobotic Performance
No Time Delay No Effect.
0−300
Task duration increased.
No performance effects.
300−500
Task duration increased.
Increase in errors.
500−700
Possible task failure.
Increase in errors.
700+ Error in every task.
For tasks with time delays between 500ms -
700ms, performance is heavily dependent on the op-
erator’s experience. More experienced operators may
have fewer errors and succeed in tasks that inexperi-
enced ones would fail (Ladoiye et al., 2018).
2.2 Manipulator Control
2.2.1 Model Predictive Control
Model Predictive Controllers (MPCs) are effective
controllers that use an iterative prediction and op-
timization process to generate ideal outputs. This
is done by combining actual values, obtained from
the slave manipulator, with predicted values from the
master controller, and reference values from the in-
put, to create variety of possible control signal out-
puts over a specified prediction horizon (Camacho
and Bordons, 2007)(Wang, 2009). From these out-
puts, the best trajectory is selected based on a cost
function, and a single time step from the prediction
is applied to the system. The process is then repeated
for the next time step. Figure 1 below shows the MPC
prediction process for a given prediction horizon of p.
Figure 1: Model Predictive Control Output Prediction Pro-
cess (Simon, 2014).
An advantage of MPCs is its compatibility with
multiple input and multiple output (MIMO) systems.
This is useful for robotic arm applications, as torques
from the torque from the joints affect one another.
2.2.2 System Dynamics
The motion of a manipulator can be described by its
equations of motion, which define a relationship be-
tween the input torques and the output manipulator
movement (Spong et al., 2005). The general matrix
formulation of the equations of motion are shown in
Equation (1) below.
M(q) ¨q +V (q, ˙q) ˙q + g(q) = τ (1)
where D(q), V (q,
˙
(q)), and g(q) represent the mass
matrix, the joint velocity terms, and the gravity vector
respectively. The joint velocity matrix can be split
into two terms: the centrifugal, C(q) and coriolis,
B(q) forces.
A method of obtaining the system dynamics is via
the Lagrangian formulation, which is derives equa-
tions using the energies of the system (Asada and Slo-
tine, 1986). Equation (2) is the Euler-Lagrange that
must be computed to obtain the equations of motion,
while Equation (3) provides the Lagrangian, which is
the difference between kinetic and potential energies.
d
dt
∂L
∂ ˙q
i
−
∂L
∂q
i
= τ (2)
L = K −V (3)
Implementing the computed energies into Equation
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
376

(2) and Equation (3) will give the system dynamics
in the form of Equation (1).
2.3 Soft Tissue Modeling
2.3.1 Soft Tissue Behaviour
To model and simulate interactions between the robot
and soft tissue, the soft tissue properties must be
fully understood. Tissues exhibit hyperelastic and vis-
coelastic behaviour and factors such as its composi-
tion affect how the material reacts to contact. These
combined characteristics make it very difficult to ac-
curately model soft tissues
The hyperelastic behaviour of the tissue indicates
that deformations do not occur linearly with applied
force. A study, summarized in (Misra et al., 2008),
showed that the stress-strain relationship is linear,
only if deformations are within 1-2% of the tissues
original shape. Successful models, such as the Og-
den, Yeoh, and Arruda-Boyce models, which accu-
rately represent this hyperelastic behaviour, have been
developed (Bergstr
¨
om, 2015). Figure 2 below shows
a general stress-strain curve for the behaviour of hy-
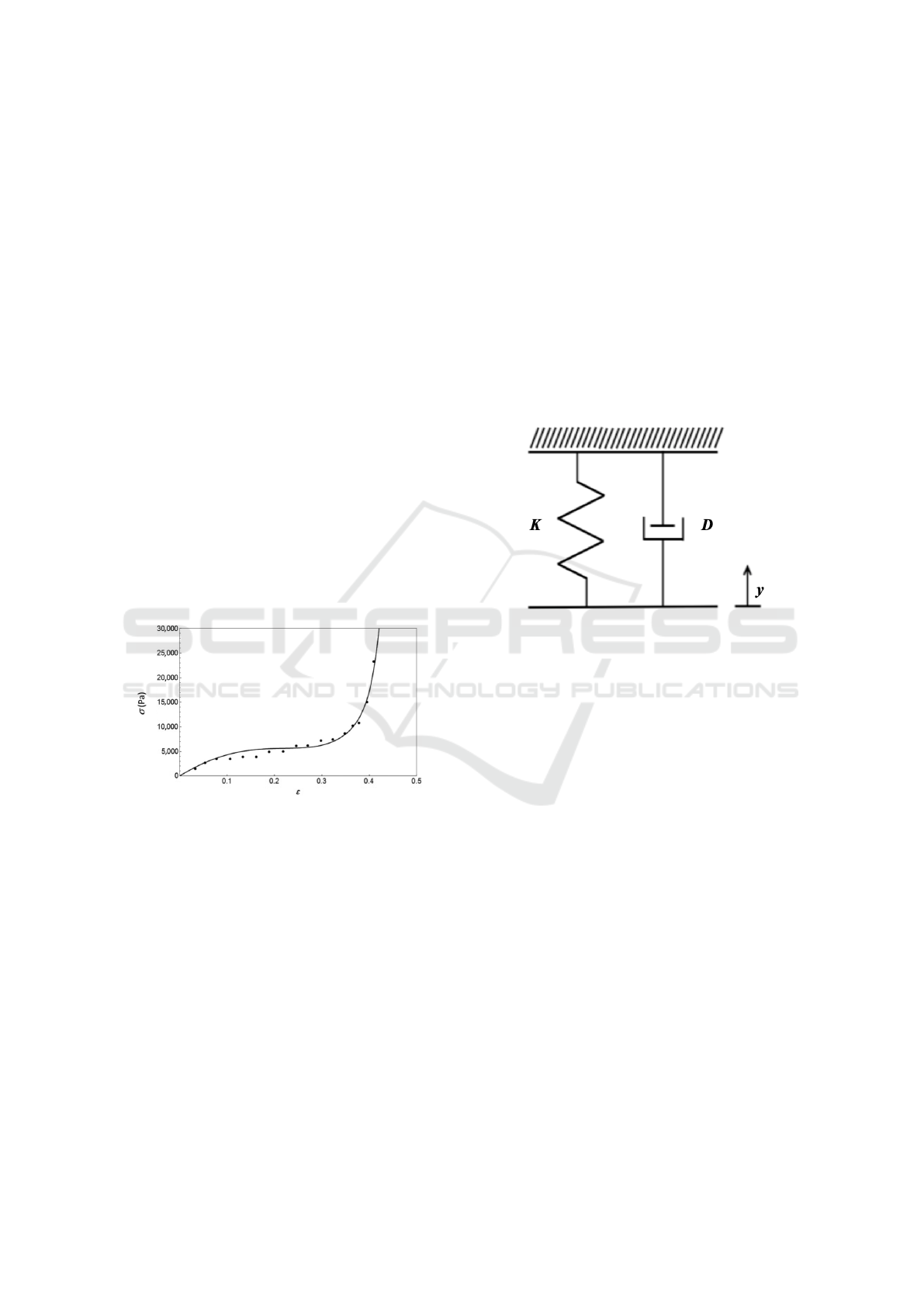
perelastic materials, where the curved line represents
the line of best fit for experimental results.
Figure 2: General Stress-Strain Relationship of a Hypere-
lastic Material (Amabili, 2018).
Soft tissues, with their viscoelastic properties, will
have both ’elastic’ and ’viscous’ behaviour. The
‘elastic’ term indicates that the tissues will return
back to their original form after deformation, and
the ‘viscous’ term indicates that stress on the tissue
increases with strain, meaning that the material be-
comes more resistant to deformation the more it is
compressed/stretched (Gould et al., 2019). When
modeling these characteristics, the elastic and viscous
behaviours can be modeled by springs and dampers
respectively.
Another factor to consider when modeling tissues
is the effect of its composition. Different tissue types,
such as epithelial, muscle, etc., will have different
properties. In addition, tissues are made of different
quantities of cells, elastin, collagen, and other com-
ponents, set in different arrangements and at different
orientation (Famaey and Sloten, 2008). These quan-
tities, arrangements, and orientations can change how
the material reacts to various forces applied to it. The
composition of the tissues, which differs from patient
to patient, make accurate modeling very difficult.
2.3.2 Hunt-Crossley Method
An established non-linear model, called the Hunt-
Crossley method, is able to capture both hyperelastic
and viscoelastic behaviour of soft tissues (Pappalardo
et al., 2016). This model is shown below, in Figure 3,
and its corresponding equation is described by (4).
Figure 3: Hunt-Crossley Soft Tissue Model (Amabili,
2018).
F = ky
β
(t)+λy
β
(t)˙y(t) (4)
where parameters k, β, and λ are obtained experimen-
tally. Thus, from Figure 3 and (4), variables K and D
are defined as K = ky
β−1
(t) and D = λy
β
(t) respec-
tively. The exponential factor, β, illustrates the non-
linear stress-strain tissue relationship, due to hyper-
elasticity, while the first and second terms show the
elastic and viscous characteristics of the tissue respec-
tively (Pappalardo et al., 2016). The Hunt-Crossley
method is currently one of the most accurate soft tis-
sue models that can be solved without the use of com-
plex operations such as continuum-mechanics and fi-
nite element analysis.
3 SYSTEM SETUP
The block diagram from Figure 4 shows the general
setup of a telerobotic system in a surgical setting. It
consists of an operating the master console, a slave
console, and a communication network that connects
the two. Note that the network can experience time
delay and/or discontinuity when transferring informa-
tion between the two locations.
Time Delay Investigation in Telerobotic Surgery
377

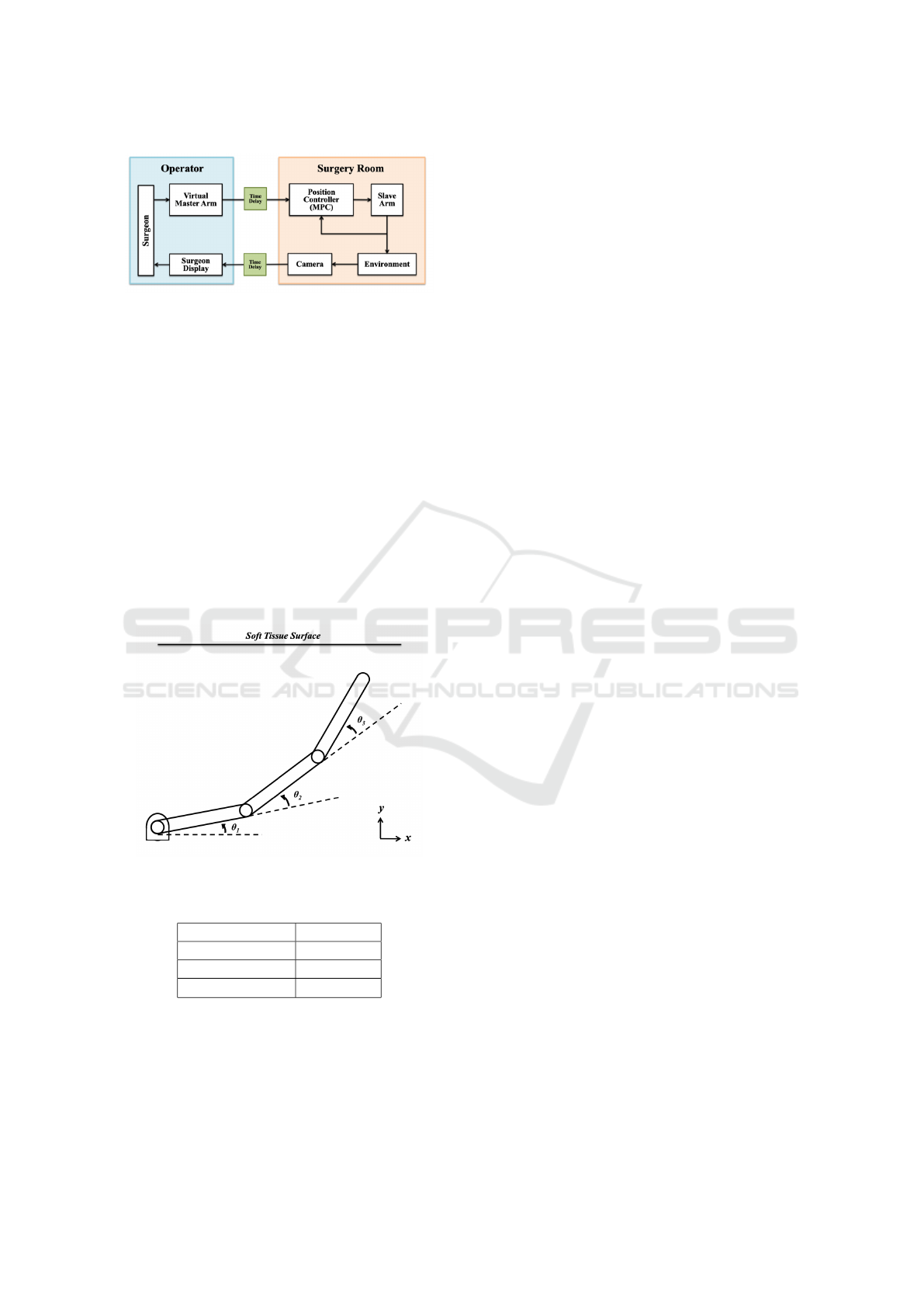
Figure 4: Block Diagram Showing a Telerobotic Surgery
Setting.
For simulations, two main components must be
modeled for the setup: the slave robot manipula-
tor and the surrounding environment, the soft tissue.
The simulation focuses on the slave manipulator with
transport delays used to model the telerobotic aspect
of the system. Models for these parts are described
below.
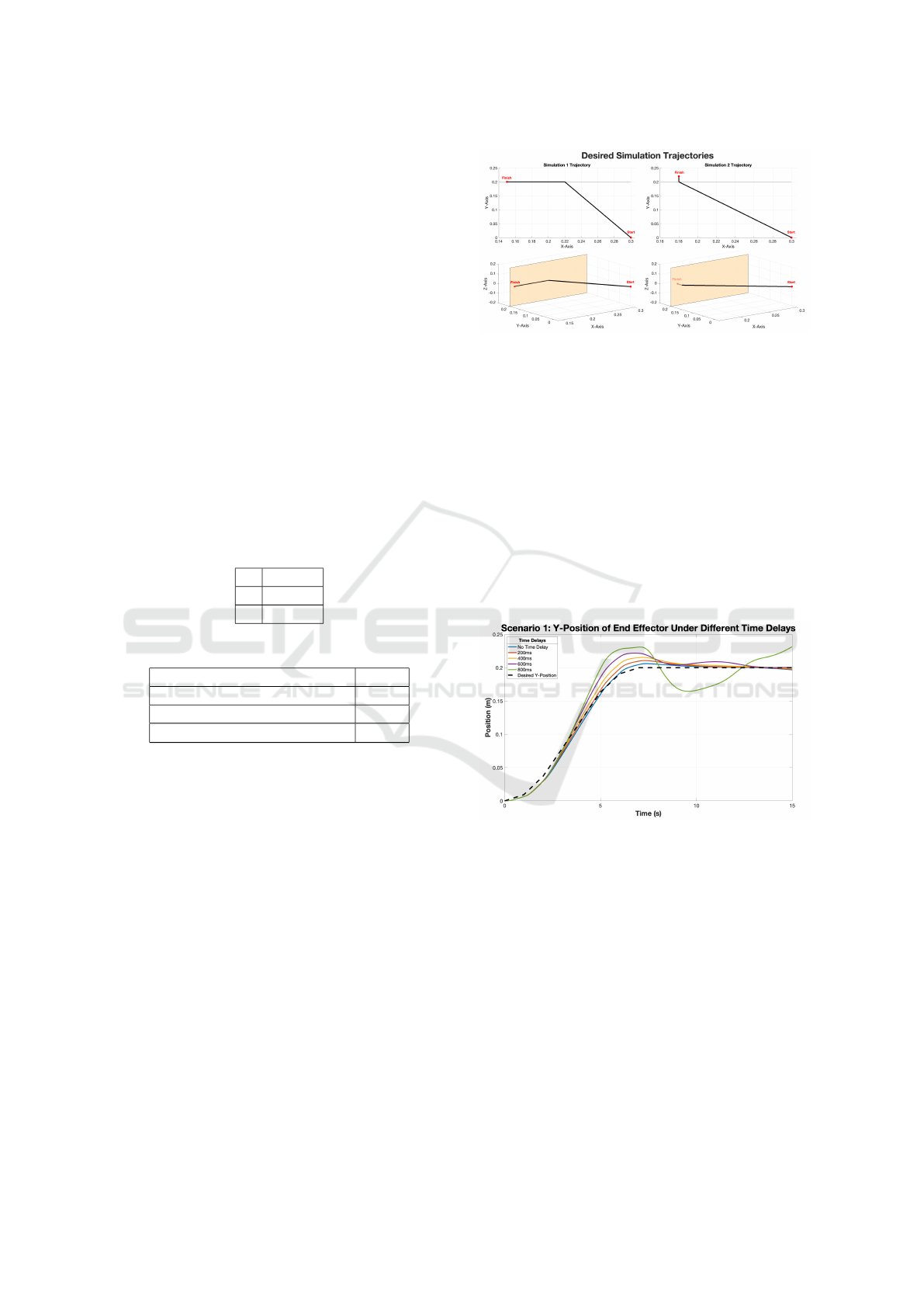
3.1 Robot Manipulator
The robotic arm used in this paper is a planar 3DOF
RRR robot, as shown below in Figure 5. An MPC will
be used to control that arm. All linkages are the same
length and its properties are shown in Table 2 (Atlas
Steels Technical Department, 2013).
Figure 5: 3DOF Robotic Arm and Surface Diagram.
Table 2: 3DOF Robotic Arm Diagram.
Property Magnitude
Length (cm) 10
Radius (cm) 1
Density (g/cm
2
) 7.95
Robotic arms used for surgical purposes are usu-
ally very small, as shown by the small dimensions in
the table above. While these dimensions do not come
from any existing robotic arm, they are selected to
give a size similar to the da Vinci SP surgical robot
(Cruz et al., 2019).
The equations of motion for the arm, derived using
the Lagrangian Formulation, are presented in Equa-
tion (5).


A
1
B
1
C
1
D
1
E
1
F
1
G
1
H
1
I
1




¨
θ
1
¨
θ
2
¨
θ
3


+


A
2
B
2
C
2
D
2
E
2
F
2
G
2
H
2
I
2




˙
θ
2
1
˙
θ
2
2
˙
θ
2
3


+


A
3
B
3
C
3
D
3
E
3
F
3
G
3
H
3
I
3




˙
θ
1
˙
θ
2
˙
θ
1
˙
θ
3
˙
θ
2
˙
θ
3


=


τ
1
τ
2
τ
3


(5)
where
A
1
= 0.5ml
2
[(c
1+12
− s
1+12
)
2
+ (c
1+12+123
−
s
1+12+123
)
2
] +ms
2
1
B
1
= D
1
= 0.5ml
2
[(c
12
− s
12
)(c
1+12
− s
1+12
) −(c
12+123
−
s
12+123
)(c
1+12+123
− s
1+12+123
)] −ms
1
s
2
C
1
= G
1
= 0.5ml
2
(c
123
− s
123
)(c
1+12+123
− s
1+12+123
)
E
1
= 0.5ml
2
[(c
12+123
− s
12+123
)
2
+ (c
12
− s
12
)
2
] +ms
2
2
F
1
= H
1
= 0.5ml
2
(c
123
− s
123
)(c
12+123
− s
12+123
)
I
1
= 0.5ml
2
(c
123
− s
123
)
2
A
2
= 0.5ml
2
[(c
1+12+123
− s
1+12+123
)(c
1+12+123
+
s
1+12+123
) +(c
1+12
+ s
1+12
)(c
1+12
− s
1+12
)] −mc
1
s
1
B
2
= 0.5ml
2
[(c
12+123
+ s
12+123
)(c
12+123
− s
12+123
) +
(c
12
− s
12
)(c
12
+ s
12
)]
C
2
= 0.5ml
2
(c
123
− s
123
)(c
123
+ s
123
)
D
2
= 0.5ml
2
[(c
12
+ s
12
)(c
1+12
− s
1+12
) + (c
12+123
+
s
12+123
)(c
1+12+123
− s
1+12+123
)]
E
2
= 0.5ml
2
[(c
12+123
+ s
12+123
)(c
12+123
− s
12+123
) +
(c
12
− s
12
)(c
12
+ s
12
)] −mc
2
s
2
F
2
= 0.5ml
2
(c
123
− s
123
)(c
123
+ s
123
)
G
2
= 0.5ml
2
(c
123
+ s
123
)(c
1+12+123
− s
1+12+123
)
H
2
= 0.5ml
2
(c
123
+ s
123
)(c
12+123
− s
12+123
)
I
2
= 0.5ml
2
(c
123
− s
123
)(c
123
+ s
123
)
A
3
= 0.5ml
2
[(c
12
+ s
12
)(c
1+12
− s
1+12
) + (c
12+123
−
s
12+123
)(c
1+12+123
+ s
1+12+123
) + (c
12
− s
12
)(c
1+12
+
s
1+12
) + (c
12+123
+ s
12+123
)(c
1+12+123
− s
1+12+123
)] −
mc
1
s
2
B
3
= 0.5ml
2
[(c
123
− s
123
)(c
1+12+123
+ s
1+12+123
) +
(c
123
+ s
123
)(c
1+12+123
− s
1+12+123
)]
C
3
= 0.5ml
2
[(c
123
+ s
123
)(c
12+123
− s
12+123
) + (c
123
−
s
123
)(c
12+123
+ s
12+123
)]
D
3
= 0.5ml
2
[(c
12
+ s
12
)(c
1+12
− s
1+12
) + (c
12+123
+
s
12+123
)(c
1+12+123
− s
1+12+123
) + (c
12+123
+
s
12+123
)(c
12+123
− s
12+123
) + (c
12
− s
12
)(c
12
+ s
12
)] −
mc
2
s
1
E
3
= 0.5ml
2
[(c
123
− s
123
)(c
12+123
+ s
12+123
) + (c
123
+
s
123
)(c
1+12+123
− s
1+12+123
)]
F
3
= 0.5ml
2
[(c
123
+ s
123
)(c
12+123
− s
12+123
) + (c
123
−
s
123
)(c
12+123
+ s
12+123
)]
G
3
= 0.5ml
2
[(c
123
+ s
123
)(c
12+123
− s
12+123
) + (c
123
+
s
123
)(c
1+12+123
− s
1+12+123
)]
H
3
= 0.5ml
2
[(c
123
+ s
123
)(c
1+12+123
− s
1+12+123
) +
(c
123
− s
123
)(c
123
+ s
123
)]
I
3
= 0.5ml
2
[(c
123
+ s
123
)(c
12+123
− s
12+123
) + (c
123
−
s
123
)(c
123
+ s
123
)]
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
378

Note that c
ab
represents cos(a + b) while c
a+b
represents cos(a) + cos(b). All s terms represent
the sine counterparts. There is also no gravity term
because the gravitational force acts in the axis of the
joint rotation, therefore it does not significantly affect
the motion of the arm.
3.2 Soft Tissue
The Hunt-Crossley method will be used to model the
soft tissue, as this method is able to capture various
characteristics of the tissue, while maintaining model
simplicity. The parameters below, provided in Table 3
and Table 4 will be used. Table 3 shows the parame-
ters for perpendicular contact forces between the soft
tissue and a metal part, while Table 4 provides corre-
sponding properties for skin tissue (Liang and Bop-
part, 2010)(Veijgen, 2013). The selected parameters
for the normal force are average values obtained from
five experimental trials of a robot interacting with soft
tissue reported in (Yamamoto et al., 2009).
Table 3: Experimental Hunt-Crossley Parameters.
k 5.5432
λ 0.1496
β 1.5826
Table 4: Soft Tissue Behavioural Parameters.
Parameters Value
Coefficient of Static Friction 0.52
Coefficient of Kinetic Friction 0.36
Skin Density (kg/m
3
) 1.02
4 RESULTS
Two scenarios will be simulated for the robot and soft
tissue interaction under different time delays. The
first simulation involves a robotic arm moving to ap-
proach a soft tissue surface, where it will then slide
tangentially across the surface of the skin. For the
second scenario, the robotic arm will come in con-
tact with the tissue surface, where it will then attempt
to compress the tissue. Figure 6 below shows the in-
tended trajectories for both simulations.
The input trajectory, from Figure 6 is converted
from Cartesian coordinates to joint coordinates, via
inverse kinematics, and is then converted into joint
torques using the controller.
Figure 6: Desired Trajectory of the Robotic Arm for Both
Simulations.
4.1 Scenario 1: Movement across the
Tissue
In scenario 1, the path of the robotic arm’s end effec-
tor will be traced, namely the movement across the
skin, in the Y-direction, and the frictional and normal
forces will be recorded. The tissue sample is located
0.2m away from the robot’s starting position and the
surface should be reached, in the simulation, in 7 sec-
onds. Results of the simulations are shown below and
will be compared to the expected performance results
presented in Table 1.
Figure 7: End Effector Position in the Y-Direction.
From Figure 7, it can be seen that all simulations,
with the exception of the 800ms time delay trial, reach
the desired final position of 0.2m. It is noted, how-
ever, that with increased time delay, the magnitude
of the errors also increases, and the system requires
more time to reach its desired value. In addition, al-
though the simulation trajectory is planned to have no
contact with the soft tissue, all scenarios are shown to
have slight interactions, which result in forces on the
tissue and robot. This behaviour can be seen in more
detail in Figure 8 and Figure 9, which show the con-
tact and frictional forces computed during simulation.
The simulation for a time delay 800ms is not included
in friction results as the task has already failed.
Time Delay Investigation in Telerobotic Surgery
379

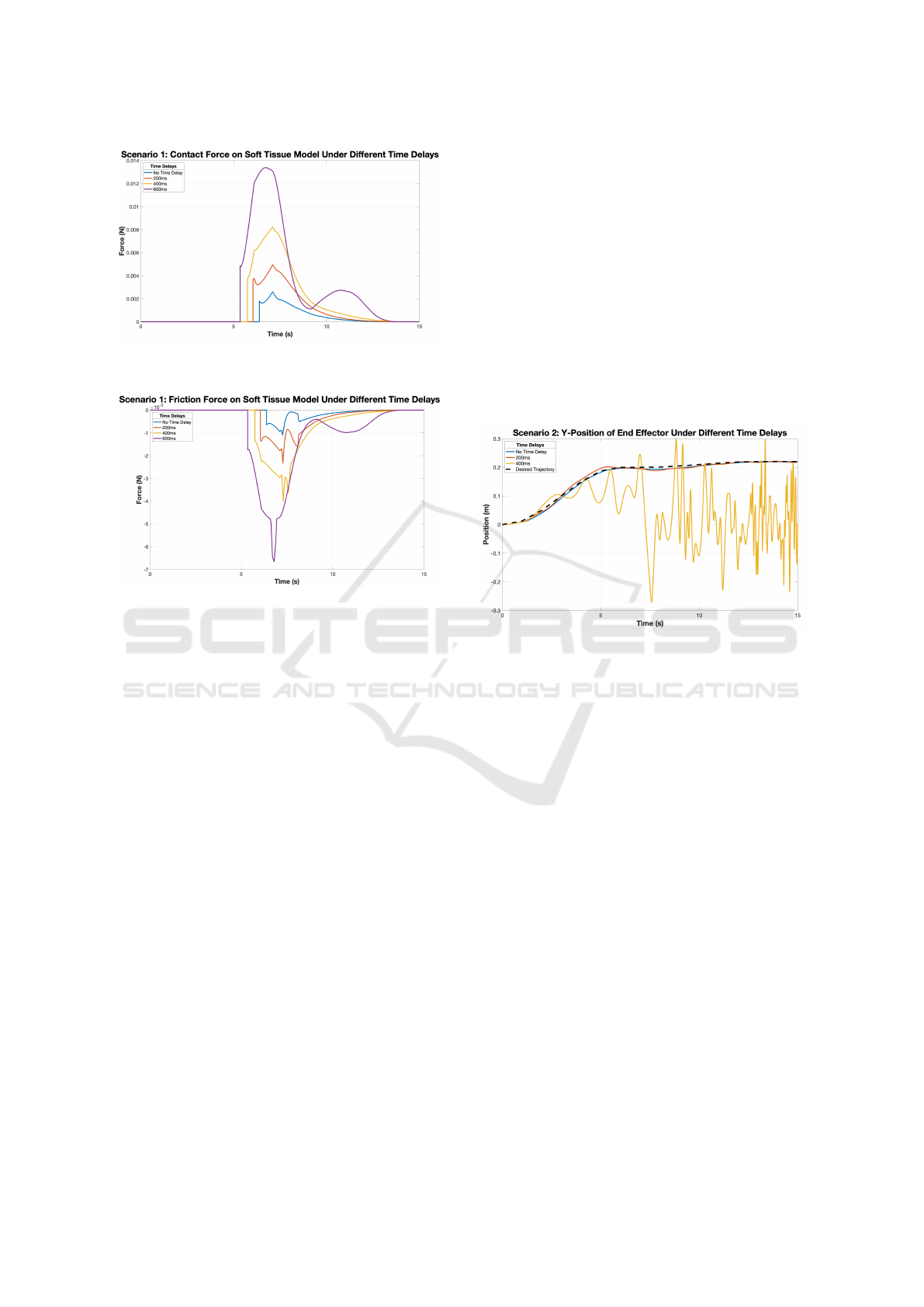
Figure 8: Contact Force between the End Effector and Soft
Tissue along the Y-Direction.
Figure 9: Frictional Force between the End Effector and
Soft Tissue along the X-Direction.
Note that the normal force and frictional force
points correspond with one another, as both will oc-
cur once the robot is in contact with tissue. These
points also correspond to points from Figure 7, where
the end effector position peaks and is recorded to be
above 0.2m. Greater contact and frictional forces also
occur for longer time delays. It is interesting to note
that although the planned trajectory is to move the
robot across the surface of the tissue, the normal con-
tact forces are stronger than the frictional forces.
Upon immediate contact with the skin, at 7 sec-
onds, the robotic arm briefly moves slightly away
from its position, before continuing to penetrate the
skin surface. Figure 8 shows the reduction in contact
force due to this movement. This behaviour is likely
due to the interaction with the soft tissue. As pre-
viously explained, soft tissue exhibits a viscoelastic
property, which would result in the end effector being
repelled from the surface of the skin. This results in
unstable contact.
The observations from this simulation match with
the expected behaviour of telerobotics under time de-
lay, as presented in Table 1. Increasing time delay
increases the system errors and the time required to
complete the desired task. In addition, the simulated
trial with a time delay of over 700ms failed, as ex-
pected.
4.2 Scenario 2: Movement into the
Tissue
In this scenario, the tissue sample is located 0.2m
away from the skin surface, and the robot attempts
to penetrate the skin by 2cm, for a total desired dis-
placement of 0.22m. Initial contact with the skin oc-
curs at 6 seconds, and the robot arm is held in place,
at a desired compression of 0.22m, after 13 seconds.
Interesting properties to observe include the path of
the robot, as it attempts to compress the skin tissue,
as well as the total penetration into the tissue and the
corresponding contact forces. Figure 10 below shows
the movement of the tip of the robot compared to the
desired movement.
Figure 10: End Effector Position in the Y-Direction.
For this scenario, only time delay simulations of
up to 400ms are included, as the erratic movement of
the arm indicates system failure. Given that the pur-
pose of these robots is for surgery, an uncontrolled
and large displacement is very dangerous and unsuit-
able for the application.
Figure 11 shows the penetration distance of the
soft tissue. The simulated 400ms time delay is not
included in these results, due to failure. Again, the
trial with no time delay approaches the desired state
much faster than the trial with a 200ms delay. Fur-
thermore, the penetration error is larger for the 200ms
delay trial, with more oscillations, indicating greater
instability in the system. Errors are expected to be
even larger for larger delays.
Figure 12 shows the normal contact forces, which
correspond to the penetration distances above. Recall
that the contact force is proportional to the penetra-
tion distance, but the relationship is non-linear, as de-
scribed by the Hunt-Crossley model in Equation 4.
When compared with Scenario 1, where contact
and penetration were not intended, the contact forces
due to compression are significantly larger. Frictional
forces were neglected for this scenario, as they are
expected to be very small, since motion is penetrative.
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
380

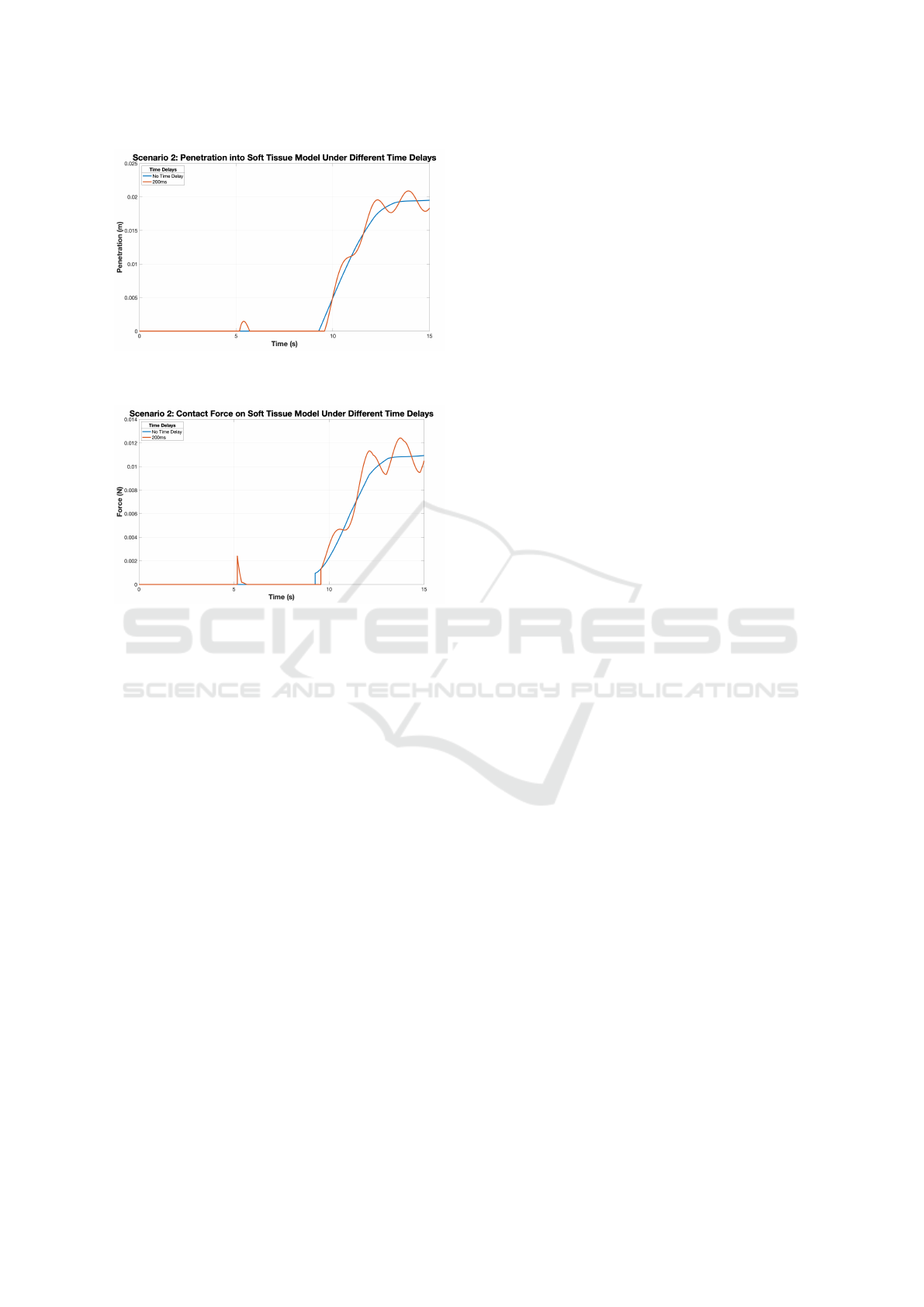
Figure 11: Penetration Depth of the End Effector into the
Soft Tissue.
Figure 12: Contact Force between the End Effector and Soft
Tissue.
It should be noted that the rebounding behaviour
upon initial contact, mentioned in Scenario 1, can
clearly be seen in both Figure 11 and Figure 12. The
change in motion and force, shown for the simulation
with a time delay of 200ms, indicates instability from
contact with the body.
In general, the performance of the robot during
compression of soft tissue, is similar to the behaviour
described by Table 1. As time delay increases, the er-
rors increase, and the desired position is achieved at a
much slower rate. However, in this scenario the sys-
tem fails at a delay of 400ms, instead of the 700ms+
time delay expected from the performance informa-
tion in Table 1. It is likely that this occurred because
the system was unable to adapt to the force from the
contact with the tissue in combination with the de-
layed feedback response. The time delay increases the
position error, resulting in greater compression and a
larger rebounding force, resulting in uncontrolled dis-
placement of the arm. Thus, under these conditions,
the desired task cannot be completed with a time de-
lay of 400ms.
5 CONCLUSION
This paper and the performed simulations are de-
signed to help get a better understanding of the be-
haviour of telerobotic contact with soft tissues. Un-
der small time delays, it appears that the 3DOF RRR
robotic arm is able to carry out desired tasks in a
surgical environment. However, large time delays,
as well as large forces from contact with the tissues
result in task failure. The motion, due to the these
forces, is difficult to predict, and the system is unable
to compensate for large, unpredicted forces.
In addition, the direction in which the robot comes
in contact with the surface also influences the success
of a task. The forces generated by perpendicular con-
tact with a surface are significantly larger than those
that are tangential and as a result they destabilize the
system more and have a greater effect on robot per-
formance. Simulating trials with different trajecto-
ries, which have both significant frictional and normal
contact forces, and examining the force effects may
be considered for future work. Experimentation with
real tissue and telerobotic manipulators would also be
beneficial for further investigation.
REFERENCES
Amabili, M. (2018). Hyperelasticity of Soft Biological and
Rubber Materials, page 151–224. Cambridge Univer-
sity Press.
Anvari, M., Broderick, T., Stein, H., Chapman, T.,
Ghodoussi, M., Birch, D. W., Mckinley, C., Trudeau,
P., Dutta, S., and Goldsmith, C. H. (2005). The Im-
pact of Latency on Surgical Precision and Task Com-
pletion during Robotic-Assisted Remote Telepresence
Surgery. Computer Aided Surgery, 10(2):93–99.
Arata, J., Takahashi, H., Pitakwatchara, P., Warisawa,
S., Tanoue, K., Konishi, K., Ieiri, S., Shimizu, S.,
Nakashima, N., Okamura, K., Fujino, Y., Ueda, Y.,
Chotiwan, P., Mitsuishi, M., and Hashizume, M.
(2007). A Remote Surgery Experiment between
Japan and Thailand over Internet using a Low Latency
CODEC System. In Proceedings 2007 IEEE Interna-
tional Conference on Robotics and Automation, pages
953–959, Rome, Italy. IEEE. ISSN: 1050-4729.
Asada, H. and Slotine, J. (1986). Robot Analysis and Con-
trol. A Wiley-Interscience Publication. Wiley.
Atlas Steels Technical Department (2013). Stainless Steel
Grade Datasheets. Atlas Technical Handbook of Stain-
less Steels.
Avgousti, S., Christoforou, E., Panayides, A., Voskarides,
S., Novales, C., Nouaille, L., Pattichis, C., and
Vieyres, P. (2016). Medical Telerobotic Systems: Cur-
rent Status and Future Trends. BioMedical Engineer-
ing Online, 15.
Time Delay Investigation in Telerobotic Surgery
381

Bergstr
¨
om, J. (2015). 5 - Elasticity/Hyperelasticity. In
Bergstr
¨
om, J., editor, Mechanics of Solid Polymers,
pages 209 – 307. William Andrew Publishing.
Buia, A., Stockhausen, F., and Hanisch, E. (2015). La-
paroscopic Surgery: A Qualified Systematic Review.
World Journal of Methodology, 5:238–54.
Camacho, E. F. and Bordons, C. (2007). Introduction to
Model Predictive Control. In Camacho, E. F. and Bor-
dons, C., editors, Model Predictive Control, pages 1–
11. Springer London, London.
Cruz, C., Yang, H., Kang, I., Kang, C., and Lee, W.
(2019). Technical Feasibility of da Vinci SP Single-
Port Robotic Cholecystectomy: A Case Report. An-
nals of Surgical Treatment and Research, 97:217.
Fabrizio, M., Lee, B., Chan, D., Stoianovici, D., Jarrett,
T., Yang, C., and Kavoussi, Louis, m. . m. y. . . p. . .
Effect of Time Delay on Surgical Performance during
Telesurgical Manipulation. Journal of Endourology /
Endourological Society, 14.
Famaey, N. and Sloten, J. V. (2008). Soft Tissue Mod-
elling for Applications in Virtual Surgery and Surgical
Robotics. Computer Methods in Biomechanics and
Biomedical Engineering, 11(4):351–366.
Gould, T. E., Jesunathadas, M., Nazarenko, S., and Piland,
S. G. (2019). Chapter 6 - Mouth Protection in Sports.
In Subic, A., editor, Materials in Sports Equipment
(Second Edition), pages 199–231. Woodhead Publish-
ing.
Ho, C., Tsakonas, E., Tran, K., Cimon, K., Severn, M.,
Mierzwinski-Urban, M., Corcos, J., and Pautler, S.
(2011). Robot-Assisted Surgery Compared with Open
Surgery and Laparoscopic Surgery: Clinical Effec-
tiveness and Economic Analyses.
Hristu, D., Kontarinis, D. A., and Howe, R. D. (1996). A
Comparison of Delay and Bandwidth Limitations in
Teleoperation. 13th World Congress of IFAC, 1996,
San Francisco USA, 30 June - 5 July, 29(1):5709–
5714.
Korte, C., Nair, S., Nistor, V., Low, T., Doarn, C., and
Schaffner, G. (2014). Determining the Threshold
of Time-Delay for Teleoperation Accuracy and Effi-
ciency in Relation to Telesurgery. Telemedicine Jour-
nal and E-Health : The Official Journal of the Ameri-
can Telemedicine Association, 20.
Ladoiye, J., Necsulescu, D., and Sasiadek, J. (2018). Force
Control of Surgical Robot with Time Delay using
Model Predictive Control. pages 202–210.
Liang, X. and Boppart, S. A. (2010). Biomechanical Prop-
erties of In Vivo Human Skin from Dynamic Opti-
cal Coherence Elastography. IEEE Transactions on
Bio-Medical Engineering, 57(4):953–959. Edition:
2009/10/09.
Lum, M., Rosen, J., King, H. H., Friedman, D., Lendvay,
T., Wright, A., and Hannaford, B. (2009). Teleoper-
ation in Surgical Robotics - Network Latency Effects
on Surgical Performance. Conference Proceedings :
Annual International Conference of the IEEE Engi-
neering in Medicine and Biology Society, 2009:6860–
3.
M. Uebel, M. Ali, and I. Minis (1994). The Effect of
Bandwidth on Telerobot System Performance. IEEE
Transactions on Systems, Man, and Cybernetics,
24(2):342–348.
Misra, S., Ramesh, K. T., and Okamura, A. M. (2008).
Modeling of Tool-Tissue Interactions for Computer-
Based Surgical Simulation: A Literature Review.
Presence: Teleoperators and Virtual Environments,
17(5):463–491.
Orosco, R., Lurie, B., Matsusaki, T., Funk, E., Divi, V.,
Holsinger, C., Hong, S., Richter, F., Das, N., and Yip,
M. (2020). Compensatory Motion Scaling for Time-
Delayed Robotic Surgery. Surgical Endoscopy.
Pappalardo, A., Albakri, A., Liu, C., Bascetta, L., De Momi,
E., and Poignet, P. (2016). Hunt–Crossley Model
based Force Control for Minimally Invasive Robotic
Surgery. Biomedical Signal Processing and Control,
29:31–43.
Perez, M., Xu, S., Chauhan, S., Tanaka, A., Simpson, K.,
Abdul-Muhsin, H., and Smith, R. (2015). Impact
of Delay on Telesurgical Performance: Study on the
Robotic Simulator dV-Trainer. International Journal
of Computer Assisted Radiology and Surgery, 11.
Simon, D. (2014). Model Predictive Control in Flight Con-
trol Design - Stability and Reference Tracking. PhD
thesis.
Spong, M., Hutchinson, S., and Vidyasagar, M. (2005).
Robot Modeling and Control. Wiley.
Vazquez-Santacruz, J. A., Velasco-Villa, M., Portillo-Velez,
R. d. J., Marin-Urias, L. F., and Vigueras-Zuniga, M.
(2017). Autonomous Navigation for Multiple Mobile
Robots under Time Delay in Communication. Journal
of Intelligent & Robotic Systems, 86(3-4):583–597.
Veijgen, N. (2013). Skin Friction: A Novel Approach to
Measuring In Vivo Human Skin. PhD thesis, Univer-
sity of Twente, Netherlands.
Velasco-Villa, M., Castro-Linares, R., Rosales-Hern
´
andez,
F., del Muro-Cu
´
ellar, B., and Hern
´
andez-P
´
erez, M.
(2013). Discrete-Time Synchronization Strategy for
Input Time-Delay Mobile Robots. Journal of the
Franklin Institute, 350(10):2911–2935.
Wang, L. (2009). Model Predictive Control System Design
and Implementation Using MATLAB
R
. ISSN: 1430-
9491.
Xu, S., Perez, M., Yang, K., Perrenot, C., Felblinger, J.,
and Hubert, J. (2014). Determination of the Latency
Effects on Surgical Performance and the Acceptable
Latency Levels in Telesurgery Using the dV-Trainer
(R) simulator. Surgical Endoscopy, 28.
Yamamoto, T., V
´
agv
¨
olgyi, B., Balaji, K., Whitcomb, L.,
and Okamura, A. (2009). Tissue Property Estima-
tion and Graphical Display for Teleoperated Robot-
Assisted Surgery. 2009 IEEE International Confer-
ence on Robotics and Automation, pages 4239–4245.
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
382