A Novel and Dedicated Machine Learning Model for Malware

Classiﬁcation

Miles Q. Li

, Benjamin C. M. Fung

2 a

, Philippe Charland

and Steven H. H. Ding

School of Computer Science, McGill University, Montreal, Canada

School of Information Studies, McGill University, Montreal, Canada

Mission Critical Cyber Security Section, Defence R&D Canada, Quebec, Canada

School of Computing, Queen’s University, Kingston, Canada

Keywords:

Cybersecurity, Malware Classiﬁcation, Reverse Engineering, Clustering.

Abstract:

Malicious executables are comprised of functions that can be represented in assembly code. In the assembly

code mining literature, many software reverse engineering tools have been created to disassemble executables,

search function clones, and ﬁnd vulnerabilities, among others. The development of a machine learning-based

malware classiﬁcation model that can simultaneously achieve excellent classiﬁcation performance and provide

insightful interpretation for the classiﬁcation results remains to be a hot research topic. In this paper, we

propose a novel and dedicated machine learning model for the research problem of malware classiﬁcation.

Our proposed model generates assembly code function clusters based on function representation learning

and provides excellent interpretability for the classiﬁcation results. It does not require a large or balanced

dataset to train which meets the situation of real-life scenarios. Experiments show that our proposed approach

outperforms previous state-of-the-art malware classiﬁcation models and provides meaningful interpretation of

classiﬁcation results.

1 INTRODUCTION

Malware has been an increasingly serious threat to ne-

tizens all over the world, as there has been a tremen-

dous growth in the volume of new malware broadcast-

ing on the Internet (Kumar et al., 2019). To manually

analyze malware samples is not efﬁcient enough to

prevent them from releasing their payload and caus-

ing damages. Most malware samples are variants of

existing ones that fall into a known malware fam-

ily (Nataraj et al., 2015; Kalash et al., 2018). Mal-

ware samples in the same family present similar be-

haviors and often share similar goals. Thus, it is cru-

cial to build an effective malware classiﬁcation sys-

tem to automatically recognize the family of a new

malware sample to discern its malicious intent. It is

also important for the malware classiﬁcation system

to be able to explain its classiﬁcation result so that

malware analysts can validate the outcome and ac-

quire new insights.

Nowadays, general-purpose machine learning

models are applied to many kinds of classiﬁcation

https://orcid.org/0000-0001-8423-2906

tasks including malware classiﬁcation (Moskovitch

et al., 2008; Santos et al., 2013; Nataraj et al., 2011;

Han et al., 2014; Yang and Wen, 2017; Kalash et al.,

2018). However, there are several limitations com-

ing with them. First, it is hard for ordinary machine

learning models to both achieve good classiﬁcation

performance and provide good interpretability. Linear

models are simple and thus have inferior classiﬁca-

tion performance but excellent interpretability. Non-

linear models, however, have better modelling power,

so they can achieve better performance, but lose inter-

pretability from complexity (Cerna et al., 2019). Sec-

ond, it is commonly known that the training of ordi-

nary machine learning models (Bishop, 2006; Mur-

phy, 2012) requires a large volume of data. The num-

ber of samples in each class is supposed to be sev-

eral times larger than the number of features, or they

tend to overﬁt the training set. This means that the

models just memorize the labels of the training data,

but cannot correctly classify unseen samples. Third,

when the dataset is unevenly distributed among dif-

ferent malware families, ordinary machine learning

models, in particular discriminative models, may fail

to achieve a satisfying performance. Those issues are

Li, M., Fung, B., Charland, P. and Ding, S.

A Novel and Dedicated Machine Learning Model for Malware Classiﬁcation.

DOI: 10.5220/0010518506170628

In Proceedings of the 16th International Conference on Software Technologies (ICSOFT 2021), pages 617-628

ISBN: 978-989-758-523-4

617

problematic since different malware families could

have quite different numbers of samples. The num-

ber of samples of some malware families could be

small and thus much less than the number of fea-

tures. Therefore, the performance of ordinary ma-

chine learning models are limited.

To overcome the aforementioned issues, instead

of using an existing machine learning model, we

propose a dedicated machine learning model that

is speciﬁcally designed to classify a malicious exe-

cutable to a malware family. Typically, an executable

contains hundreds or thousands of functions. Even a

small dataset with about one hundred executables has

hundreds of thousands of functions in total. There-

fore, our model handles the executable-level classiﬁ-

cation task at the function level. It is thus feasible to

train the model even if the dataset is not very large

in terms of number of executables. Unlike an ordi-

nary classiﬁcation approach, ours is developed based

on the concept of discriminative assembly code func-

tion cluster, or simply discriminative cluster for con-

ciseness. Discriminative clusters are sets of functions

that are only common in certain malware families.

They can serve as signatures for malware families and

are robust against uneven class (i.e., malware family)

distribution scenarios. We use the clone relation be-

tween functions in a target executable and functions

in the clusters to determine the malware family of

the executable. Thus, the classiﬁcation results are in-

terepretable.

We summarize the contributions of this paper as

follows:

1. Our proposed malware classiﬁcation model is

novel because it not only achieves excellent clas-

siﬁcation accuracy and but also provides inter-

pretable results to justify the classiﬁcation result.

Our method can precisely pinpoint which func-

tions of the target executable belong to which

clusters. The constituents of the formed clusters

can also be visualized. This capability makes

our model much more than just a classiﬁcation

system. The interpretability provides an addition

layer of insights and evidence to reverse engi-

neers.

2. Our model is more robust against the overﬁtting

problem than the general-purpose machine learn-

ing models on small datasets. It is well known that

training a classiﬁcation system on a small dataset

is more challenging than training it on a large

one. Unlike an ordinary machine learning model

that is directly applied to features extracted from

samples, our method is dedicated for this speciﬁc

classiﬁcation problem. It does not require a large

training set, since it handles the executable-level

classiﬁcation task at the function level.

3. We formally deﬁne the concept of discriminative

cluster to effectively solve the uneven class dis-

tribution issue in malware classiﬁcation. We also

develop an optimized algorithm to efﬁciently con-

struct discriminative clusters based on our novel

locality sensitive hashing-based method, which

signiﬁcantly reduces the time complexity of func-

tion clustering.

The rest of the paper is organized as follows. Sec-

tion 2 introduces related work. Section 3 provides the

details of our proposed method. Section 4 presents the

experiment results and analyses. Section 5 concludes

the paper.

2 RELATED WORK

Schultz et al. (2001) propose to use imported DLLs,

functions, printable strings, and bigram byte se-

quences as features for malware detection. Since

the number of different bigram byte sequences is too

large for in-memory processing, they separate them

into multiple sets and feed them to several Naive

Bayes models. To solve this issue, Kolter and Mal-

oof (Kolter and Maloof, 2004) propose to use infor-

mation gain to select the most informative byte se-

quences as features, which improves both accuracy

and scalability. Further research (Moskovitch et al.,

2008; Dai et al., 2009; Santos et al., 2013) suggests

that opcode sequences are more effective features

than byte sequences because the meaning of instruc-

tion operands, e.g., memory addresses, constants,

varies in different contexts. Therefore, the operands

should not be included in any features. Since byte se-

quences include the operands while opcodes do not,

opcodes are thus better features. Due to the fact

that malware programs may use obfuscation, pack-

ing, polymorphism, and metamorphism to hide their

original malicious code, some researchers therefore

propose dynamic approaches. It involves running tar-

get executables in an isolated environment and moni-

toring the executed instructions and invoked system

calls as features (Fredrikson et al., 2010; Ye et al.,

2010; Dahl et al., 2013; Kolosnjaji et al., 2016; Huang

and Stokes, 2016). The disadvantage of dynamic ap-

proaches is that running executables and logging their

behaviors are time-consuming and do not reveal all

possible execution paths (Bayer et al., 2006).

All of the aforementioned works apply machine

learning models on their proposed features to classify

executables. In contrast, we use function clusters as

the basis for the classiﬁcation. Chen et al. (2015) also

ICSOFT 2021 - 16th International Conference on Software Technologies

618

Executable Disassembling

Asm2Vec

Representation

Learning

Function

Representation

Database

Discriminative

Function

Clustering

Function

Cluster

Database

Function Clone

Classiﬁcation

Classiﬁcation Result

Visualization

Training

Test

Cluster

Visualization

Figure 1: Workﬂow of our approach.

propose to classify malware using function clusters.

They assume ﬁles belonging to the same malware

family share some common functions. They group

functions of samples from the same malware family

in clusters, where any two functions can be connected

directly or indirectly using a clone relation. They pick

one function from each cluster as an exemplar to be a

signature of its malware family. Among all kinds of

clone detection methods Ding et al. (2016); Farhadi

et al. (2014, 2015); Cordy and Roy (2011); Ding et al.

(2019), they use the NiCad clone detector (Cordy and

Roy, 2011) to determine whether two functions are

a clone of each other. In the testing phase, they de-

tect whether a target ﬁle contains any function that

is a clone of an exemplary function that represents a

signature of a malware family. If a match is found,

the ﬁle is classiﬁed to be an instance of that malware

family. Their method is primitive and suffers from the

following issues:

1. Using one exemplar function to represent a cluster

of functions is problematic. As the same func-

tion evolves over different generations of mal-

ware samples in the same family, the newest ver-

sion may be quite different than the older ver-

sions (Cabaj et al., 2017). If the oldest version

is picked as the exemplar, there is a large chance

for the clone detector to fail in identifying some

of its new unknown generations.

2. Their function clusters may not be discriminative.

Some function clusters may be common in most

malware families or even legitimate software. In-

tuitively, they are not appropriate to serve as sig-

natures. There is no mechanism in their method

to ﬁlter out those function clusters.

3. The NiCad clone detector (Cordy and Roy, 2011)

cannot recognize function clone pairs that are se-

mantically similar, but syntactically very differ-

ent.

4. Their task is malware classiﬁcation of Android

applications, which are written in Java. Neither

in their approach nor with NiCad do they explain

how they handle obfuscation, which is quite com-

mon in Java malware.

Our model addresses all of these issues.

Another related topic to this paper is locality sen-

sitive hashing (LSH). LSH is proposed to serve as a

fast and approximate solution to the nearest neighbor

problem (Indyk and Motwani, 1998). It is based on

the property that LSH functions lead to the results that

data points that are close to each other in their vec-

tor space have relatively high probability to have the

same hash value. Although LSH is mostly used for

real-life nearest neighbor problems (Ding et al., 2016;

Bawa et al., 2005; Jain et al., 2008; Kulis and Grau-

man, 2009; Sæbjørnsen et al., 2009), it can also be

used for data clustering. Koga et al. (2007) apply LSH

to ﬁnd the closest cluster to an intermediate data clus-

ter in their agglomerative hierarchical clustering algo-

rithm. In a different way, Ravichandran et al. (2005)

use LSH functions to accelerate the speed of ﬂat clus-

tering. Their objective is to cluster similar nouns from

a collection of nouns. The vectors of nouns have very

large dimension in their case, so they minimize the

number of times to compute their cosine similarities

by generating signatures with LSH functions to sort

items and only compare objects near each other in

the sorted lists and with similar signatures. The sub-

problem of this paper to cluster similar functions is

the same as theirs at an abstract level. However, in

our case, the dimension of the vectors representing

functions is small and the number of functions could

be very large. In our LSH-based clustering algorithm,

we do not have to avoid the cosine similarity compu-

tation, but we avoid the sorting procedure.

3 OUR APPROACH

Figure 1 illustrates an overview of our approach. The

executables are ﬁrst disassembled and the assembly

A Novel and Dedicated Machine Learning Model for Malware Classiﬁcation

619

code functions are fed into the representation learning

module of a clone search engine to generate function

vector representations, such that semantically simi-

lar functions have a high cosine similarity measure.

Next, the function representations are fed into a clus-

tering algorithm to construct function clusters that can

be used to discriminate malicious executables of some

families from others. In the testing phase, we disas-

semble a target executable and use the function clone

search engine to determine whether each function of it

is a clone of any function belonging to a cluster. The

results are used to calculate the conﬁdence at which

the target executable belongs to each malware family.

3.1 Disassembling

In the ﬁrst step, we use IDA Pro

, a commercial dis-

assembler, to disassemble the executable samples in

E. The output is a set of assembly code functions of

the executables.

3.2 Function Representation Learning

In this step, we learn the vector representations of

the disassembled code functions with Asm2Vec (Ding

et al., 2019), an open source function clone search en-

gine based on representation learning. In the literature

of function clone search, when the semantic similar-

ity between two functions is larger than a threshold,

which is automatically decided by a clone search en-

gine or deﬁned by a user, they are considered to be a

clone of each other. Given a target function, the ob-

jective of a clone search engine is to retrieve the top-

k semantically similar functions indexed in the code

repository, which have semantic similarities with the

target function larger than the threshold. The mech-

anism of Asm2Vec is to train an unsupervised learn-

ing model to generate vector representations of func-

tions. The cosine similarity of the vector representa-

tions of two functions represents their semantic sim-

ilarity: cos(θ(u, v)) =

|u·v|

√

|u||v|

where vector u and v

are the semantic representations of two functions and

θ(u, v) is the angle between vector u and v. We use the

representation learning module of Asm2Vec to gener-

ate the representations of functions disassembled in

the previous step. We choose Asm2Vec because it has

been taken as one of the best solutions for single-

platform clone search (Zuo et al., 2018; Massarelli

et al., 2019b,a) for the following reasons:

1. It is capable to recognize semantically similar

function pairs, even though they may appear syn-

tactically different.

https://www.hex-rays.com/products/ida/

2. It has been shown to be more resilient to code

obfuscation and compiler optimization than other

clone search engines.

To learn function representations, Asm2Vec uses co-

occurrence relationships among assembly tokens (i.e.,

opcodes and operands) and discovers rich lexical se-

mantic relationships among them. It learns vector

representations of assembly tokens and of assembly

code functions simultaneously in the training phase

and computes the representations of target functions

in the testing phase. We refer the readers to the origi-

nal paper for more details (Ding et al., 2019).

3.3 Discriminative Function Clustering

Consider an undirected graph where the vertices are

assembly functions and edges exist between functions

that are clones of each other, then a function cluster is

a connected component of the graph. In other words,

functions that are in the same cluster are connected

directly or indirectly through clone relations. Some

clusters resemble the commonality of malware fam-

ilies, but others do not, because the clusters are too

common in all kinds of malware families or also in

legitemate software. In other words, they are not dis-

criminative for the classiﬁcation problem. Therefore,

we want to exclude them and keep only the discrim-

inative ones. In contrast, Chen et al. (2015) isolate

functions from each malware family and then cluster

them for each family separately. Their solution cannot

identify or exclude non-discriminative function clus-

ters.

3.3.1 Discriminative Assembly Code Function

Cluster

Before describing the algorithms to construct dis-

criminative clusters, we ﬁrst deﬁne the discrimina-

tive power of a cluster. Intuitively, the larger the per-

centage of executables in a malware family contain a

function that belongs to a cluster, the more likely the

cluster is a commonality of that family. However, if

for every malware family there is a large percentage

of executables containing a function that belongs to

a cluster, the cluster is not discriminative anymore,

since it is a commonality of all malware families.

Therefore, a large difference on the popularity of a

cluster among different malware families indicates a

good discriminative power. Figure 2 illustrates this

idea. We give a formal deﬁnition of a discriminative

cluster below.

Consider a set of predeﬁned malware families C =

, . . . ,C

}, a collection of executable samples E,

a set of assembly functions F = {f

, . . . , f

}, and a

ICSOFT 2021 - 16th International Conference on Software Technologies

620

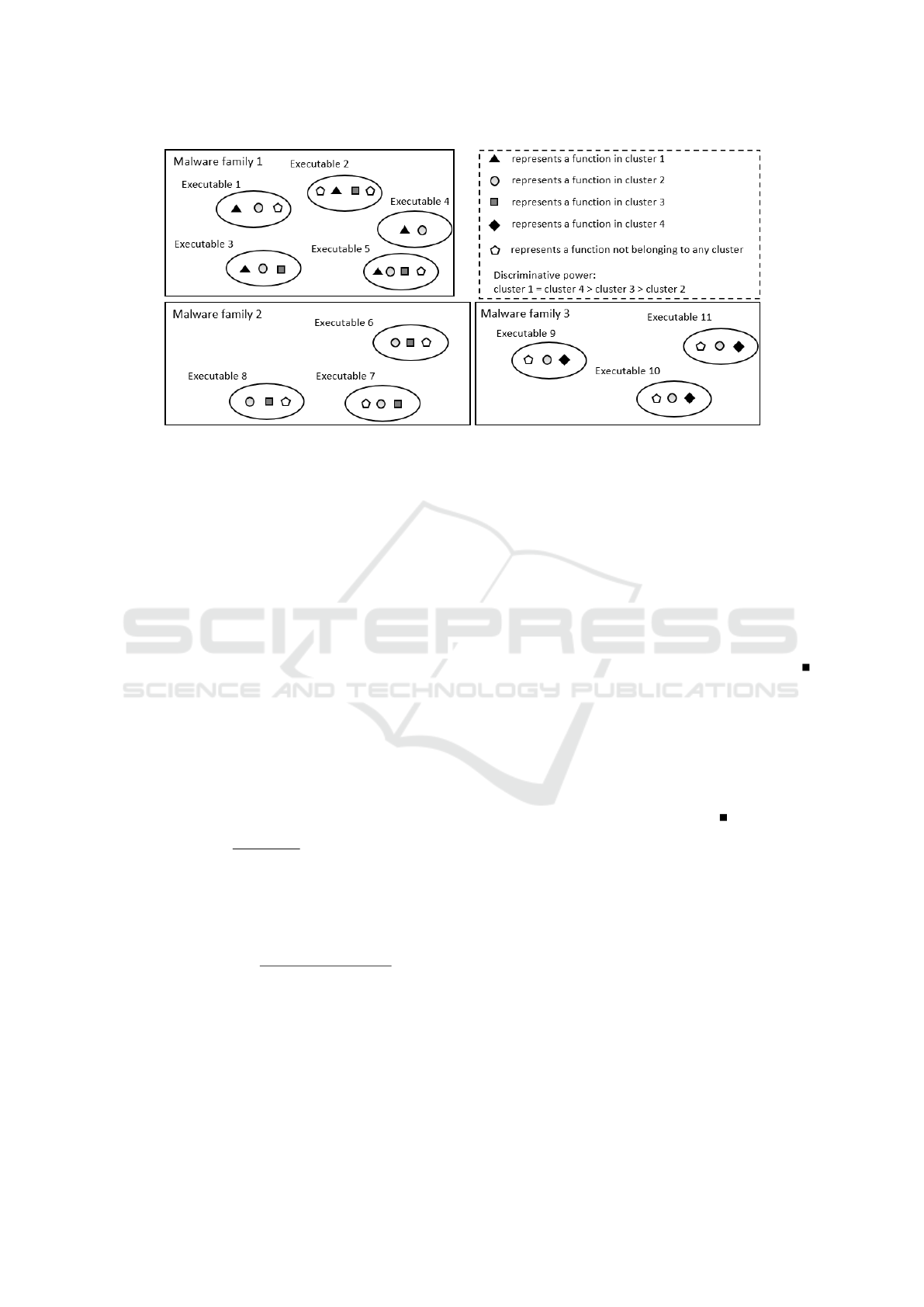
Figure 2: Comparison of different discriminative powers of clusters. Function cluster 1 is only popular in malware family 1

and every executable in the family contains a function of cluster 1. Therefore, cluster 1 has the highest discriminative power.

The same applies to cluster 4. Cluster 3 is popular among family 1 and family 2 and no executable in family 3 contains one

of its functions. Hence, it still has some discriminative power. Functions in cluster 3 are from all three families. Cluster 3 has

thus a low discriminative power.

set of assembly function clusters G = {G

, . . . , G

where each G

⊆ F. Each executable sample e ∈ E

is a subset of assembly functions e ⊆ F. Each ex-

ecutable sample e ∈ E belongs to a malware fam-

ily C

∈ C. Let exe(G

) denotes the set of executa-

bles that have function(s) in cluster G

. Formally,

exe(G

) = {e|∃f , f ∈ e ∧ f ∈ G

Next, we deﬁne the notion of overlapping be-

tween a malware family and a cluster in terms of

common functions. com f (G

) denotes the set of

functions in executables of family C

that are also

in cluster G

. Formally, com f (G

) = {f |∀f , f ∈

e ∧e ∈ C

∧ f ∈ G

}. |com f (G

)| is the cardi-

nality of com f (G

) and denotes the number of

overlapping functions between G

and C

in this con-

text. kcom f (G

)k denotes the |com f (G

)| nor-

malized by the number of executables in family C

kcom f (G

)k=

|com f (G

. To put in plain words,

kcom f (G

)k is the percentage of executables in

family C

that has at least one function in cluster G

The popularity of a malware family C

in cluster G

denoted by pop(G

), is shown in Equation 1.

pop(G

) =

kcom f (G

∑

j=1

kcom f (G

(1)

We have

∑

j=1

pop(G

) = 1. If a cluster contains

functions from only one executable, then it probably

characterizes only that executable itself rather than

the malware family it belongs to. Therefore, the dis-

criminative power only exists in clusters that consist

of functions from at least two executables. Intuitively,

if the difference between the popularity of different

malware families of a cluster is large, then the dis-

criminative power of the cluster is high. We deﬁne

the discriminative power of a cluster G

, denoted by

d p(G

), based on this intuition.

Deﬁnition 3.1 (Cluster Discriminative Power). We

deﬁne the discriminative power of cluster G

as fol-

lows. If |exe(G

)| = 1, then d p(G

) = 0. Otherwise,

d p(G

) = max

{pop(G

)}−min

{pop(G

)}.

Discriminative assembly code function clusters

are the clusters that have high disciminative powers.

In other words, the clusters that can be used to differ-

entiate malware families.

Deﬁnition 3.2 (Discriminative Assembly Code Func-

tion Cluster). A cluster G

is a discriminative as-

sembly code function cluster if d p(G

) ≥ θ

, where

0 ≤ θ

≤ 1 is a prespeciﬁed threshold.

3.3.2 LSH-based Discriminative Clustering

Algorithm

To construct discriminative clusters, we do it in two

steps. The ﬁrst step is to construct function clus-

ters. The second step is to calculate the discriminative

power of the clusters and keep only those with a high

discriminative power.

The most straightforward way to group functions

in clusters is also done in two steps. The ﬁrst step

is to compute the semantic similarity between every

function pair and ﬁnd all function clones. The second

is to use a Union-Find (a.k.a. Disjoint Set) algorithm

to combine the unions of two functions that are

clones of each other. For the latter part, we adopt the

A Novel and Dedicated Machine Learning Model for Malware Classiﬁcation

621

Algorithm 1: LSH_Separation.

Data: a set of functions F, the maximum

number of LSH functions to apply

h_max

, the lower boundary of the

number of functions in a bucket n

f _b

Result: A set of buckets R

R ←

0 ;

f _hash ← {f → 0|f ∈ F};

n_hash ← 0;

while sizeo f (F) > 0 do

Cur_buckets ←

LSH_ f unc ←new_LSH_ f unc();

for f ∈ F do

old_hash ← f _hash.get( f );

cur_hash ← LSH_ f unc( f );

new_hash ←(old_hash <<

1) + cur_hash;

f _hash.put( f , new_hash);

if new_hash 6∈Cur_buckets.keys then

Cur_buckets.put(new_hash,

0);

end

buck ←Cur_buckets.get(new_hash);

buck.add( f );

end

for hash,buck ∈Cur_buckets.KV Pairs

if sizeo f (buck) ≤ n

f _b

then

R.add(buck);

F ← F −buck;

end

n_hash = n_hash +1;

if n_hash ≥ n

h_max

then

for

hash, buck ∈Cur_buckets.KVPairs

if sizeo f (buck) > n

f _b

then

R.add(buck);

F ← F −buck;

end

break;

end

Weighted Quick-Union with Path Compression algo-

rithm (Sedgewick and Wayne, 2011), since it is the

most efﬁcient one. The problem is that the ﬁrst step

requires to iterate very function pair with a complex-

ity of O(n

), where n is the number of functions. This

is not efﬁcient enough when the number of functions

is large. Therefore, we propose an LSH-based algo-

rithm to signiﬁcantly improve the efﬁciency.

We use a family of LSH functions as follows: each

hash function corresponds to a random vector r which

has the same dimension as the assembly code function

vector representation. The hash value of an assembly

code function vector representation u is computed as

follows:

(u) =



1 u ·r > 0

0 u ·r ≤0

It has been proven (Indyk and Motwani, 1998) that

for vector u and vector v, the probability that they

have the same hash value of the same LSH function is

as follows:

Pr[h

(u) = h

(v)] = 1 −

θ(u, v)

(2)

Two functions that are clones of each other

are semantically similar and have a large cosine

similarity cos(θ(u, v)), i.e., small value of θ(u, v).

They thus stand a better chance to have the same

hash value. Therefore, we propose the algorithm

LSH_Separation described as Algorithm 1 to put po-

tentially semantically similar assembly functions in

the same bucket. First, we gradually apply LSH func-

tions on the assembly functions and form a signa-

ture composed of hash values produced by the hash

functions for each assembly code function. Then, we

place the assembly functions having the same signa-

ture in the same bucket. If the number of functions of

a bucket is less than a certain number n

f _b

, the bucket

is saved and excluded from the subsequent procedure.

If a certain number n

h_max

of hash functions have been

applied, even though there could still be some buck-

ets holding more than n

f _b

functions, the procedure

stops and all the remaining buckets are saved. Each

saved bucket contains potentially semantically simi-

lar assembly functions, so we compute the semantic

similarity between every function pair in a bucket and

feed all function clone pairs to the Union-Find algo-

rithm to group them in clusters.

It is still possible that semantically similar as-

sembly functions are separated in different buck-

ets. To solve this issue, we repeat the algorithm

LSH_Separation l times and compute the similarities

between functions in every bucket produced by the al-

gorithm in the l times. Practically, l does not have to

be large and l = 2 is usually enough. Let us use an ex-

ample to illustrate this idea. Consider a function clus-

ter of m functions. It is separated in two buckets by

an LSH function when we apply LSH_Separation for

the ﬁrst time. Then, we compare the semantic similar-

ity between every function pair in each bucket to ﬁnd

function clone pairs. If we apply the Union-Find al-

gorithm on the function clone pairs that we ﬁnd from

the two buckets, we form two separate clusters with

the functions from the original function cluster. Then,

when we apply LSH_Separation for the second time,

ICSOFT 2021 - 16th International Conference on Software Technologies

622

Figure 3: Visualization of clusters.

the original cluster is probably not separated the same

way as in the ﬁrst time. Any two functions that are

a clone of each other in the cluster and separated in

different buckets the ﬁrst time, but in the same bucket

the second time, are recognized as a function clone

pair. The two clusters they belong to are combined

and we get the original cluster.

The time complexity of applying

LSH_Separation algorithm l times is

O(l × (n

h_max

× n)) = O(ln

h_max

n). The time

complexity to compute the semantic similarity

between every function pair in all generated buck-

ets is O(l × (

f _b

× n

f _b

)) = O(ln

f _b

n). The

total time complexity is O(ln

h_max

n + ln

f _b

n) =

O(l(n

h_max

+ n

f _b

)n). Since l, n

h_max

, and n

f _b

are

constants and much smaller than n, we reduce the

time complexity of ﬁnding all function clone pairs

from O(n

) to a practically linear procedure.

After we use our optimized algorithm to ﬁnd func-

tion clone pairs and the Union-Find algorithm to con-

struct the clusters, we just need to compute their dis-

criminative powers according to our deﬁnition and re-

move the non-discriminative ones.

3.3.3 Cluster Labeling

Chen et al. (2015) assign a hard malware family label

to a cluster, since their clusters are formed within in-

dividual families. We also assign a label to be the

family which takes the largest popularity in cluster

: label(G

) = argmax

{pop(G

)}. However, a

function cluster may be common in multiple malware

families. Therefore, we still keep all pop(G

) of a

cluster G

for classifying target executables.

3.4 Function Clone Search

For a target executable, we use Asm2Vec to detect

clone relations between all its functions and the func-

tions in the clusters. Since each cluster is considered

to be a set of semantically equivalent functions, if a

function of the target executable is a clone of any

function in a cluster, it is also considered to be a mem-

ber of that cluster. As most functions of the executa-

bles in the training set do not belong to a discrimina-

tive cluster, they are abandoned. By keeping only dis-

criminative clusters, we also greatly reduce the time

consumption of this step.

3.5 Malicious Executable Classiﬁcation

To classify a target executable, we calculate an afﬁli-

ation score for each malware family. If the target exe-

cutable contains a function that is a member of cluster

, then pop(G

) for all j = 1, . . . , m of that cluster

is added to the scores of those malware families.

The absolute score accumulated in this way cannot

tell the conﬁdence at which a target executable be-

longs to a malware family. Therefore, for each fam-

ily, we calculate the scores in the same way for all

executables of that family in the training set and ﬁnd

the median. Then, we divide the accumulated score

of a target executable by that median to be the conﬁ-

dence at which the executable belongs to that family.

If the conﬁdence is larger than 100%, it will be set to

100%.

3.6 Visualization

Our approach supports visualizing the composition of

the formed clusters and the interpretation of the clas-

siﬁcation results. For each cluster, the family popu-

larity and its function composition can be viewed to

examine whether they are good signatures of the cor-

responding families. An example is given in Figure 3.

If some clusters are found to be not reasonably good

signatures or some functions should not be included

in a cluster, they can be manually deleted. This abil-

ity to allow human-in-the-loop is a unique advantage

of our classiﬁcation model. To provide a justiﬁcation

for the classiﬁcation of a target executable, its func-

tions that belong to a cluster and the functions in the

clusters that are clones of them can also be viewed.

A Novel and Dedicated Machine Learning Model for Malware Classiﬁcation

623

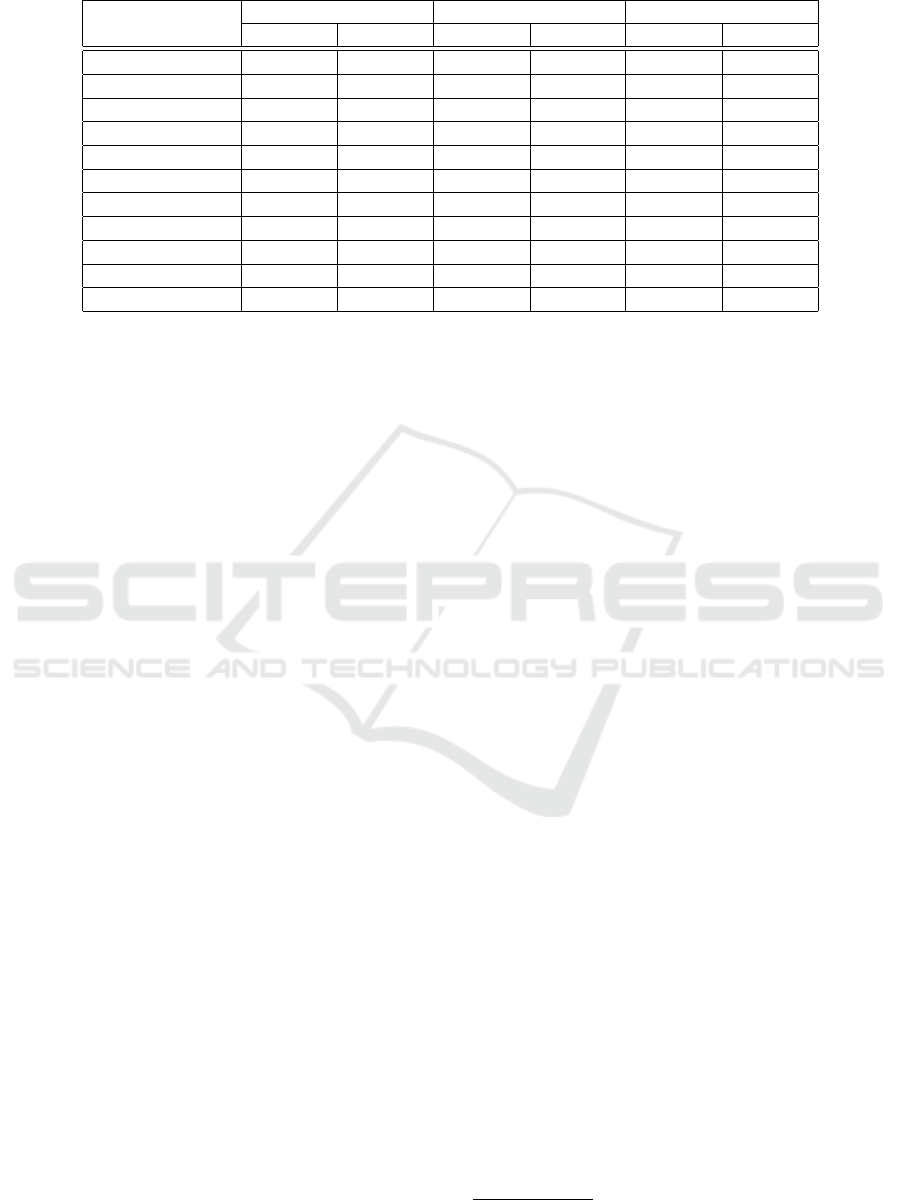
Table 1: Statistics of the dataset.

Class

Training Validation Test

# of exec # of func # of exec # of func # of exec # of func

Autoit 80 141,763 26 44,145 27 46,732

Bundlore 186 72,674 61 24,436 61 24,500

Emotet 175 8,714 57 3,405 57 3,460

Fireseria 131 68,605 43 22,516 44 23,109

Gamarue 96 141,312 32 55,676 33 56,276

Hotbar 80 124,977 26 40,633 27 41,712

Imali 121 79,108 40 25,279 41 26,159

Loadmoney 151 39,296 50 13,442 51 13,323

Softpulse 79 58,289 26 19,218 27 19,536

Speedingupmypc 80 38,692 27 12,488 28 13,735

Total 1,179 773,430 388 261,238 396 268,542

An example is given in Figure 4. This interpretabil-

ity can help malware analysts better understand the

function grouping phenomena among some malware

families.

4 EXPERIMENTS

The objectives of our experiments are to (1) evalu-

ate the performance of our dedicated machine learn-

ing model for malware classiﬁcation, compared with

other state-of-the-art machine learning solutions, (2)

demonstrate that using the proposed concept discrim-

inative power to select function clusters is effective

and necessary, and (3) illustrate the interpretability of

our classiﬁcation model.

4.1 Dataset

We evaluate the classiﬁcation model with a dataset of

10 malware families. It is separated into three parts:

training set, validation set, and test set. The valida-

tion set is used to tune hyper-parameters, which is the

discriminative power threshold in our case. We did

not tune the hyper-parameters of Asm2Vec, including

the dimension of vectors representing the functions

and the threshold to determine clone relation, as we

use the default values. There is no overlapping of

executables between the training, validation, and test

sets. To evaluate the generalizability of all classiﬁca-

tion methods, the dataset is organized in a time split

setting (Saxe and Berlin, 2015), i.e., the samples in

the test set are chosen as the ones that are compiled

later than the samples in the training and validation

set. In Table 1, we present the statistics. The dataset

is not very large in terms of number of executables in

each malware family and the class distribution is un-

even by nature. These conditions make it challenging

for machine learning-based classiﬁcation models.

We collect the malware samples from MalShare

and VirusShare. We use the AVClass malware label-

ing tool (Sebastián et al., 2016) to generate the mal-

ware family label of the malware samples, based on

analysis reports from VirusTotal

. It should be noted

that some malware samples use packing, polymor-

phism, or metamorphism. For them, IDA Pro can

identify zero or only one function. We do not include

those samples in our dataset, since our focus is not

on accounting for those techniques but on classify-

ing malware samples based on the functions that are

already revealed. Asm2Vec can identify the clone re-

lation between an obfuscated function and its original

function, so obfuscation is not a concern.

Our experiment focuses on evaluating the accu-

racy of the classiﬁcation results. We also evaluate the

precision, recall, and F1 for each family. The classiﬁ-

cation of an executable is correct if the predicted fam-

ily, i.e., the class with the highest conﬁdence, matches

its real family label.

4.2 Comparing with State-of-the-Art

Models

We compare our approach with the following state-

of-the-art static malware classiﬁcation methods.

• Mosk2008OpBi: Moskovitch et al. (2008) pro-

pose to use TF or TF-IDF of opcode bi-grams as

features and use document frequency (DF), infor-

mation gain ratio, or Fisher score as the criteria

for feature selection. They apply Artiﬁcial Neural

Networks, Decision Trees, Naïve Bayes, Boosted

Decision Trees, and Boosted Naïve Bayes as their

malware classiﬁcation models.

https://www.virustotal.com/

ICSOFT 2021 - 16th International Conference on Software Technologies

624

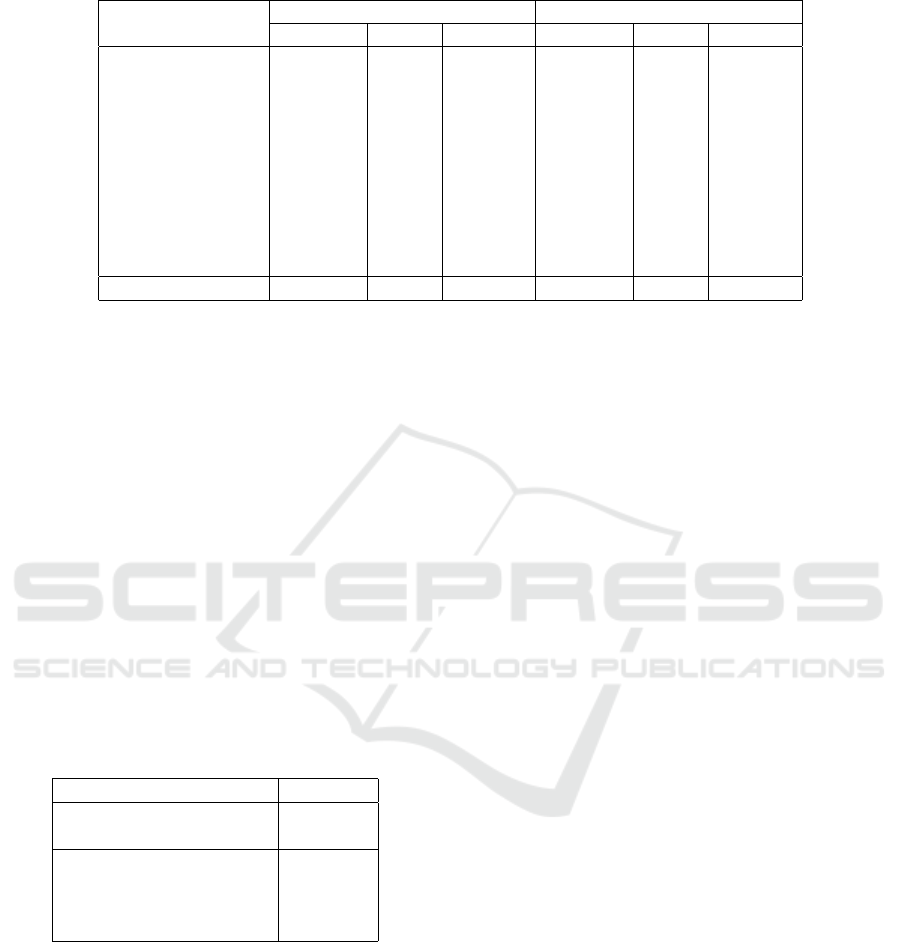
Table 2: Experiment results on each malware family.

Malware family

Our method Bald2013Meta

Precision Recall F1-score Precision Recall F1-score

Autoit 1.00 1.00 1.00 0.96 0.89 0.92

Bundlore 1.00 0.97 0.98 0.98 1.00 0.99

Emotet 0.98 0.96 0.97 1.00 0.98 0.99

Firseria 0.98 1.00 0.99 1.00 1.00 1.00

Gamarue 0.97 0.94 0.95 0.94 0.91 0.92

Hotbar 0.96 1.00 0.98 0.96 0.89 0.92

Imali 0.98 1.00 0.99 0.98 1.00 0.99

Loadmoney 0.96 0.98 0.97 0.98 1.00 0.99

Softpulse 1.00 1.00 1.00 0.93 0.93 0.93

Speedingupmypc 1.00 1.00 1.00 0.90 1.00 0.95

Weighted Average 0.98 0.99 0.98 0.96 0.97 0.97

• Bald2013Meta: Baldangombo et al. (2013) pro-

pose to extract multiple raw features from PE

headers and use information Gain and calling fre-

quencies for feature selection and PCA for dimen-

sion reduction. They apply SVM, J48, and Naïve

Bayes as their malware classiﬁcation models.

• Saxe2015Deep: Saxe and Berlin (2015) propose

a deep learning model that works on four differ-

ent features: byte/entropy histogram features, PE

import features, string 2D histogram features, and

PE metadata numerical features.

• Mour2019CNN: Mourtaji et al. (2019) convert

malware binaries to grayscale images and apply a

convolutional neural network (CNN) on malware

images for malware classiﬁcation. Their CNN

network has two convolutional layers followed by

a fully-connected layer.

Table 3: Accuracy of different models on the test set.

Method Accuracy

Our Method 98.2%

Our Method (all clusters) 94.2%

Mosk2008OpBi 82.3%

Bald2013Meta 97.0%

Saxe2015Deep 96.7%

Mour2019CNN 55.1%

4.3 Classiﬁcation Results

We show the classiﬁcation accuracy of our approach

and the state-of-the-art models for comparison in Ta-

ble 3. The ﬁrst row is the results of the exact model

we proposed and the second row shows the results

of our model without excluding clusters of low dis-

criminative power. From the table, we can see that

by keeping only the discriminative clusters, our ap-

proach achieves signiﬁcantly better results. This ver-

iﬁes the effectiveness of our proposed concept of dis-

criminative power and the importance of using it to

exclude the interference of irrelevance functions in

non-discriminative clusters. The previous methods

for comparison achieve different performances and

the accuracy is lower than what they report in their

papers. This may be due to the fact that the dataset is

relatively small and ordinary machine learning mod-

els require a large dataset to train, while our model

works at the assembly function level to mitigate this

issue. This result shows the advantage of our pro-

posed model since in real-life scenarios, some mal-

ware families do not contain a lot of samples.

In Table 2, we compare our method with

Bald2013Meta, which is the best model for compari-

son, regarding precision, recall and F1 for each mal-

ware family. We can see that Bald2013Meta achieves

lower F1 on malware families with less training sam-

ples such as Autoit and Hotbar, while our model have

no such issue. This conﬁrms our statement that gen-

eral machine learning models are less robust with

datasets of uneven class distribution, while our model

uses the concept of Discriminative assembly code

function clusters, which takes uneven class distribu-

tion into consideration, and thus does not suffer from

this issue.

4.4 Visualizing Clusters

The clusters of each family and the functions that

form them can be visualized. An example is shown

in Figure 3. We can see the list of clusters for each

malware family, the functions in each cluster, and the

class popularity pop(G

) of each cluster.

To provide an in-depth understanding of the clus-

ters, we carefully examined the formed clusters of the

two datasets. According to our observation, we ﬁnd

min

{pop(G

)} = 0 for all saved clusters. This

means that for every saved cluster, there is always at

least one malware family that has no function in it.

A Novel and Dedicated Machine Learning Model for Malware Classiﬁcation

625

Figure 4: An example of the detailed interpretation of classiﬁcation results.

The two reasons leading to this result are as follows:

(1) some of the 10 malware families are quite dif-

ferent from each other. The chance that all of them

share some semantically similar functions is very

low. (2) A few clusters with min

{pop(G

)} > 0

are automatically ﬁltered, because their discrimina-

tive power is low. Therefore, for each cluster G

that is saved, we have d p(G

) = max

{pop(G

)}−

min

{pop(G

)} = max

{pop(G

)}.

We also provide the statistics on the number

of classes (n

) that have functions in a cluster and

the discriminative power (d p(G

) or equivalently

max

{pop(G

)}) of a cluster. They are shown in

Table 4. Most clusters (i.e., 4,723) are homogeneous:

all of their functions are from the same family, i.e.,

the number of n

= 1 or max

{pop(G

)} > 0.99.

If there is only one family taking up a large popu-

larity (e.g., max

{pop(G

)} > 0.90) of cluster G

the cluster is obviously a good signature of the fam-

ily. 988 clusters contain functions from two malware

families. We manually examined those clusters con-

cerning two malware families and found that many of

them are shared by related malware families that have

similar behaviors. Therefore, those clusters charac-

terize both malware families and provide insights on

the commonalities of the malware families to reverse

engineers.

4.5 Interpretable Classiﬁcation Results

To interpret the classiﬁcation results, the executable’s

functions that are clones of functions in a cluster and

the corresponding cluster are presented. Figure 4

shows an example. The target executable belongs to

malware family Autoit. The ﬁgure presents a list of

functions of it that are clones of functions in a clus-

ter. Its function sub_40B6D0 belongs to cluster Au-

toit_Cluster186, which we have introduced in Fig-

ure 3, since it is a clone of the listed functions in the

training set that belong to Autoit_Cluster186. Fig-

Table 4: Statistics of clusters. n

is the number of classes

that have functions in a cluster. d p(G

) is the discriminative

power of the clusters. The second and the fourth columns

are the numbers of clusters that satisfy the numbers in the

ﬁrst column and the ranges in the third column, respectively.

# of clusters d p(G

) # of clusters

1 4,723 [0,0.20] 0

2 988 (0.20,0.40] 0

3 45 (0.40,0.60] 260

4 22 (0.60,0.80] 228

5 30 (0.80,0.99] 615

6 17 (0.99,0.100] 4,723

7 1

≥ 8 0

ures 3 shows that Autoit_Cluster186 consists of 112

functions. However, Figure 4 shows that only 13 of

them are found to be clones of sub_40B6D0 in the

target executable. Chen et al. (2015) use one ex-

emplary function to represent a cluster in their mal-

ware classiﬁcation system. Their method would fail

to identify that sub_40B6D0 belongs to cluster Au-

toit_Cluster186, if one of the 99 functions in Au-

toit_Cluster186 that were not determined as clones of

sub_40B6D0 in the target executable, was chosen as

the exemplar. Our model does not have this concern,

as we keep all the functions of a cluster.

5 CONCLUSION

This work is the result of a fruitful collaboration with

some reverse engineers in a government agency. The

accuracy of a malware classiﬁcation system is impor-

tant for system security monitoring usage. Yet, in-

terpretability is also crucial if further investigation or

justiﬁcation is needed on the classiﬁcation results. In

this paper, we propose a novel and dedicated machine

learning model for malware classiﬁcation that has

several advantages over the ordinary machine learn-

ICSOFT 2021 - 16th International Conference on Software Technologies

626

ing classiﬁcation models for this task. First, it does

not require a large number of samples in each mal-

ware family to train the model. Second, using the con-

cept of discriminative power to select discriminative

function clusters, our approach can handle datasets

with uneven class distribution. Third, unlike ordinary

machine learning models, our approach provides in-

terpretable evidence to justify its classiﬁcation results.

It is a practical solution for malware classiﬁcation.

ACKNOWLEDGMENT

This research is supported by Defence Research

and Development Canada (contract no. W7701-

176483/001/QCL), NSERC Discovery Grants

(RGPIN-2018-03872), and Canada Research Chairs

Program (950-230623).

REFERENCES

Baldangombo, U., Jambaljav, N., and Horng, S.-J. (2013).

A static malware detection system using data mining

methods. arXiv preprint arXiv:1308.2831.

Bawa, M., Condie, T., and Ganesan, P. (2005). Lsh forest:

self-tuning indexes for similarity search. In Proceed-

ings of the 14th International Conference on World

Wide Web, pages 651–660. ACM.

Bayer, U., Moser, A., Kruegel, C., and Kirda, E. (2006).

Dynamic analysis of malicious code. Journal in Com-

puter Virology, 2(1):67–77.

Bishop, C. M. (2006). Pattern recognition and machine

learning. springer.

Cabaj, K., Gawkowski, P., Grochowski, K., Nowikowski,

A., and

Zórawski, P. (2017). The impact of mal-

ware evolution on the analysis methods and infras-

tructure. In Proceedings of the Federated Conference

on Computer Science and Information Systems (Fed-

CSIS), pages 549–553. IEEE.

Cerna, A. E. U., Pattichis, M., VanMaanen, D. P., Jing, L.,

Patel, A. A., Stough, J. V., Haggerty, C. M., and Forn-

walt, B. K. (2019). Interpretable neural networks for

predicting mortality risk using multi-modal electronic

health records. arXiv preprint arXiv:1901.08125.

Chen, J., Alalﬁ, M. H., Dean, T. R., and Zou, Y. (2015). De-

tecting android malware using clone detection. Jour-

nal of Computer Science and Technology, 30(5):942–

956.

Cordy, J. R. and Roy, C. K. (2011). The nicad clone

detector. In Proceedings of the 19th IEEE In-

ternational Conference on Program Comprehension

(ICPC), pages 219–220. IEEE.

Dahl, G. E., Stokes, J. W., Deng, L., and Yu, D. (2013).

Large-scale malware classiﬁcation using random pro-

jections and neural networks. In Acoustics, Speech

and Signal Processing (ICASSP), 2013 IEEE Interna-

tional Conference on, pages 3422–3426. IEEE.

Dai, J., Guha, R. K., and Lee, J. (2009). Efﬁcient virus

detection using dynamic instruction sequences. JCP,

4(5):405–414.

Ding, S. H. H., Fung, B. C. M., and Charland, P. (2016).

Kam1n0: MapReduce-based assembly clone search

for reverse engineering. In Proceedings of the 22nd

ACM International Conference on Knowledge Dis-

covery and Data Mining (SIGKDD), pages 461–470.

ACM Press.

Ding, S. H. H., Fung, B. C. M., and Charland, P. (2019).

Asm2vec: Boosting static representation robustness

for binary clone search against code obfuscation and

compiler optimization. In Proceedings of the 40th

International Symposium on Security and Privacy

(S&P), pages 38–55. IEEE Computer Society.

Farhadi, M. R., Fung, B. C. M., Charland, P., and Deb-

babi, M. (2014). Binclone: Detecting code clones

in malware. In Proceedings of the 8th IEEE Interna-

tional Conference on Software Security and Reliabil-

ity (SERE), pages 78–87, San Francisco, CA. IEEE.

Farhadi, M. R., Fung, B. C. M., Fung, Y. B., Charland,

P., Preda, S., and Debbabi, M. (2015). Scalable code

clone search for malware analysis. Digital Investiga-

tion (DIIN): Special Issue on Big Data and Intelligent

Data Analysis, 15:46–60.

Fredrikson, M., Jha, S., Christodorescu, M., Sailer, R., and

Yan, X. (2010). Synthesizing near-optimal malware

speciﬁcations from suspicious behaviors. In Security

and Privacy (SP), 2010 IEEE Symposium on, pages

45–60. IEEE.

Han, K., Kang, B., and Im, E. G. (2014). Malware analysis

using visualized image matrices. The Scientiﬁc World

Journal, 2014.

Huang, W. and Stokes, J. W. (2016). Mtnet: a multi-task

neural network for dynamic malware classiﬁcation. In

Proceedings of the International Conference on De-

tection of Intrusions and Malware, and Vulnerability

Assessment, pages 399–418. Springer.

Indyk, P. and Motwani, R. (1998). Approximate nearest

neighbors: towards removing the curse of dimension-

ality. In Proceedings of the thirtieth annual ACM

symposium on Theory of computing, pages 604–613.

ACM.

Jain, P., Kulis, B., and Grauman, K. (2008). Fast image

search for learned metrics. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recogni-

tion, pages 1–8. IEEE.

Kalash, M., Rochan, M., Mohammed, N., Bruce, N. D.,

Wang, Y., and Iqbal, F. (2018). Malware classiﬁcation

with deep convolutional neural networks. In Proceed-

ings of the 9th IFIP International Conference on New

Technologies, Mobility and Security (NTMS), pages

1–5. IEEE.

Koga, H., Ishibashi, T., and Watanabe, T. (2007). Fast

agglomerative hierarchical clustering algorithm using

locality-sensitive hashing. Knowledge and Informa-

tion Systems, 12(1):25–53.

A Novel and Dedicated Machine Learning Model for Malware Classiﬁcation

627

Kolosnjaji, B., Zarras, A., Webster, G., and Eckert, C.

(2016). Deep learning for classiﬁcation of malware

system call sequences. In Proceedings of the Aus-

tralasian Joint Conference on Artiﬁcial Intelligence,

pages 137–149. Springer.

Kolter, J. Z. and Maloof, M. A. (2004). Learning to de-

tect malicious executables in the wild. In Proceedings

of the 10th ACM International Conference on Knowl-

edge Discovery and Data Mining (SIGKDD), pages

470–478. ACM.

Kulis, B. and Grauman, K. (2009). Kernelized locality-

sensitive hashing for scalable image search. In Pro-

ceedings of the International Conference on Computer

Vision (ICCV), volume 9, pages 2130–2137.

Kumar, N., Mukhopadhyay, S., Gupta, M., Handa, A., and

Shukla, S. K. (2019). Malware classiﬁcation using

early stage behavioral analysis. In Proceedings of the

14th Asia Joint Conference on Information Security

(AsiaJCIS), pages 16–23. IEEE.

Massarelli, L., Di Luna, G. A., Petroni, F., Baldoni, R.,

and Querzoni, L. (2019a). Safe: Self-attentive func-

tion embeddings for binary similarity. In Proceedings

of the International Conference on Detection of In-

trusions and Malware, and Vulnerability Assessment,

pages 309–329. Springer.

Massarelli, L., Di Luna, G. A., Petroni, F., Querzoni, L., and

Baldoni, R. (2019b). Investigating graph embedding

neural networks with unsupervised features extraction

for binary analysis. In Proceedings of the 2nd Work-

shop on Binary Analysis Research (BAR).

Moskovitch, R., Feher, C., Tzachar, N., Berger, E., Gitel-

man, M., Dolev, S., and Elovici, Y. (2008). Unknown

malcode detection using opcode representation. In

Proceedings of the IEEE International Conference on

Intelligence and Security Informatics, pages 204–215.

Springer.

Mourtaji, Y., Bouhorma, M., and Alghazzawi, D. (2019).

Intelligent framework for malware detection with con-

volutional neural network. In Proceedings of the 2nd

International Conference on Networking, Information

Systems & Security, pages 1–6.

Murphy, K. P. (2012). Machine learning: a probabilistic

perspective. MIT press.

Nataraj, L., Karthikeyan, S., Jacob, G., and Manjunath, B.

(2011). Malware images: visualization and automatic

classiﬁcation. In Proceedings of the 8th international

symposium on visualization for cyber security, page 4.

ACM.

Nataraj, L., Karthikeyan, S., and Manjunath, B. (2015).

Sattva: Sparsity inspired classiﬁcation of malware

variants. In Proceedings of the 3rd ACM Workshop on

Information Hiding and Multimedia Security, pages

135–140.

Ravichandran, D., Pantel, P., and Hovy, E. (2005). Random-

ized algorithms and nlp: Using locality sensitive hash

functions for high speed noun clustering. In Proceed-

ings of the 43rd Annual Meeting of the Association for

Computational Linguistics (ACL’05), pages 622–629.

Sæbjørnsen, A., Willcock, J., Panas, T., Quinlan, D., and

Su, Z. (2009). Detecting code clones in binary ex-

ecutables. In Proceedings of the 18th International

Symposium on Software Testing and Analysis, pages

117–128. ACM.

Santos, I., Devesa, J., Brezo, F., Nieves, J., and Bringas,

P. G. (2013). Opem: A static-dynamic approach

for machine-learning-based malware detection. In

Proceedings of the International Joint Conference

CISIS’12-ICEUTE 12-SOCO 12 Special Sessions,

pages 271–280. Springer.

Saxe, J. and Berlin, K. (2015). Deep neural network based

malware detection using two dimensional binary pro-

gram features. In Proceedings of the 10th Interna-

tional Conference on Malicious and Unwanted Soft-

ware (MALWARE), pages 11–20. IEEE.

Schultz, M. G., Eskin, E., Zadok, F., and Stolfo, S. J. (2001).

Data mining methods for detection of new malicious

executables. In Proceedings of the IEEE Symposium

on Security and Privacy (S&P), pages 38–49. IEEE.

Sebastián, M., Rivera, R., Kotzias, P., and Caballero, J.

(2016). Avclass: A tool for massive malware labeling.

In Proceedings of the International Symposium on Re-

search in Attacks, Intrusions, and Defenses, pages

230–253. Springer.

Sedgewick, R. and Wayne, K. (2011). Algorithms.

Addison-Wesley Professional.

Yang, M. and Wen, Q. (2017). Detecting android malware

by applying classiﬁcation techniques on images pat-

terns. In Proceedings of the 2nd International Con-

ference on Cloud Computing and Big Data Analysis

(ICCCBDA), pages 344–347. IEEE.

Ye, Y., Li, T., Huang, K., Jiang, Q., and Chen, Y. (2010). Hi-

erarchical associative classiﬁer (hac) for malware de-

tection from the large and imbalanced gray list. Jour-

nal of Intelligent Information Systems, 35(1):1–20.

Zuo, F., Li, X., Zhang, Z., Young, P., Luo, L., and Zeng,

Q. (2018). Neural machine translation inspired binary

code similarity comparison beyond function pairs.

arXiv preprint arXiv:1808.04706.

ICSOFT 2021 - 16th International Conference on Software Technologies

628