Applications of Learning Methods to Imaging Issues in Archaeology,

Regarding Ancient Ceramic Manufacturing

K. Dia

1,3 a

, V. L. Coli

1,3 b

, L. Blanc-F

eraud

2 c

, J. Leblond

3 d

, L. Gomart

4 e

and D. Binder

1 f

University C

ote d’Azur, CNRS, CEPAM, 06300 Nice, France

University C

ote d’Azur, CNRS, INRIA, I3S Lab., Sophia Antipolis, France

University C

ote d’Azur, INRIA, Team Factas, B.P. 93, 06902 Sophia Antipolis Cedex, France

University Paris 1 Panth

eon-Sorbonne, CNRS-UMR 8215 Trajectoires, 92023 Nanterre, France

Keywords:

Machine Learning Algorithms, Convolution Neural Network, Support Vector Machine, Image Classiﬁcation

and Analysis, Hough Transform, Archaeology, Neolithic Pottery.

Abstract:

Archaeological studies involve more and more numerical data analyses. In this work, we are interested in the

analysis and classiﬁcation of ceramic sherds tomographic images in order to help archaeologists in learning

about the fabrication processes of ancient pottery. More speciﬁcally, a particular manufacturing process (spiral

patchwork) has recently been discovered in early Neolithic Mediterranean sites, along with a more traditional

coiling technique. It has been shown that the ceramic pore distribution in available tomographic images of

both archaeological and experimental samples can reveal which manufacturing technique was used. Indeed,

with the spiral patchwork, the pores exhibit spiral-like behaviours, whereas with the traditional one, they are

distributed along parallel lines, especially in the experimental samples. However, in archaeological samples,

these distributions are very noisy, making analysis and discrimination hard to process. Here, we investigate

how Learning Methods (Deep Learning and Support Vector Machine) can be used to answer these numerically

difﬁcult problems. In particular, we study how the results depend on the input data (either raw data at the output

of the tomographic device, or after a preliminary pore segmentation step), and the quality of the information

they could provide to archaeologists.

1 INTRODUCTION

Back in the seventh and sixth millennia BC, when

farming was introduced to Europe, pottery was a cen-

tral practice for storing and food processing. For the

archaeologists, the techniques used to manufacture

ancient pottery can act as a powerful marker of the so-

cial identity of their producers. A previously unrecog-

nised pottery manufacturing technique was recently

identiﬁed (Gomart et al., 2017) at the Pendimoun

rock shelter (early Neolithic layers dated to the early

6th millennium BCE) in southeastern France (Alpes-

Maritimes) and named spiralled patchwork technol-

https://orcid.org/0000-0002-4526-2851

https://orcid.org/0000-0002-4777-3217

https://orcid.org/0000-0002-9693-6924

https://orcid.org/0000-0001-7950-0283

https://orcid.org/0000-0003-0793-2292

https://orcid.org/0000-0001-8232-5367

ogy (SPT). The construction of pottery using SPT re-

lies on juxtaposing and fusing circular patches, see

Figure 1, right. This manufacturing technique is con-

temporary to the coiling technology (CoT), which is

often observed in European early farming contexts

(Salanova et al., 2010; Gomart, 2014; Gomart, 2010)

and is characterised by superimposition of coils, see

Figure 1, left.

Micro-computed tomographic (µ-CT) 3-D images

of pottery sherds formed using these techniques were

acquired, revealing their internal structure. In partic-

ular, in 2-D cross-sections, the distribution of pores

(i.e., voids trapped inside the clay forming the sherd

structure during the building process) revealed curvi-

linear patterns for the SPT sherds and mainly paral-

lel linear patterns for the CoT sherds, see Figure 2

(mostly visible in the ﬁrst and second columns).

The goal of the present work is to analyse and

classify pottery manufacturing sequences using the

images acquired by µ-CT from available archaeolog-

Dia, K., Coli, V., Blanc-Féraud, L., Leblond, J., Gomar t, L. and Binder, D.

Applications of Learning Methods to Imaging Issues in Archaeology, Regarding Ancient Ceramic Manufacturing.

DOI: 10.5220/0010519101090116

In Proceedings of the 2nd International Conference on Deep Learning Theory and Applications (DeLTA 2021), pages 109-116

ISBN: 978-989-758-526-5

109

Figure 1: Coiling Technology (superimposition of coils, left), Spiral Patchwork Technology (juxtaposed spiral patches, right).

ical sherds and from experimental sherds that were

recently manufactured in controlled conditions using

both coiling and spiral patchwork techniques. These

scans allow to access the complete internal structure

of these sherds and, after a segmentation process, to

isolate the regions corresponding to pores, showing

their spatial distribution, see Figure 2, bottom line.

The purpose of this work is to provide a quan-

titative characterisation of Neolithic pottery forming

techniques using 3-D datasets. To the authors knowl-

edge, it represents a ﬁrst attempt to achieve this goal.

The dataset considered in this study is composed

of sixteen sherds:

• four CoT sherds (one archaeological and three ex-

perimental sherds);

• twelve SPT sherds (ﬁve archaeological and seven

experimental sherds).

The ﬁrst and second columns of Figure 2, which show

2-D cross-sections images of CoT and SPT experi-

mental sherds, reveal that pore distribution varies ac-

cording to the manufacturing technique used. The

third and fourth columns of Figure 2, which represent

archaeological CoT and SPT sherds, show that man-

ufacturing technique is much more difﬁcult to detect

in archaeological samples as patterns are not visually

distinguishable, most probably because of fragment

alteration through time. The pore distribution of both

archaeological and experimental sherds is accessible

by analysing the segmented images (as in Figure 2,

bottom line). Detecting pore alignments, which are

visible in Figure 2 down-left image, allows to iden-

tify the CoT technique. This is obtained by using the

Hough transform as in (Coli et al., 2020), an auto-

matic way to detect aligned patterns in images. We

ﬁrst select the lines that intersect the highest quan-

tity of pore regions, and we analyse their parallelism

by computing the scalar product between their direc-

tional vectors. As expected, CoT-like images reveal

parallel lines characterised by values of the scalar

products close to 1, whereas other techniques as SPT

show other / random distributions, see (Dia, 2020).

To classify ceramic sherd images, we investigate

in this work classical Machine Learning (ML) algo-

rithms. The Support Vector Machine (SVM) method

(Widodo and Yang, 2007) is applied to preliminary

features given by the scalar products between the

detected lines, while Deep Learning (DL) method

is initially run on the segmented images (extracted

pores). We use Convolutional Neural Network (CNN)

(Krizhevsky et al., 2012) with the pre-trained network

GoogLeNet (Szegedy et al., 2015) for transfer learn-

ing to classify segmented images. Finally, as CNN-

based methods result in automatic feature extraction,

the pore segmentation step appears not be necessary.

The same CNN based classiﬁcation procedure, with

the learning phase, has been applied directly on the

2D slices of tomographic images and good classiﬁca-

tion results have been obtained.

Below, we describe the data, the considered ana-

lytical protocol and classiﬁcation methods, and show

how they can answer archaeological questions. In

Section 2 we precise some information on data ac-

quisition and treatments. Section 3 is devoted to a

brief overview of the exploited learning algorithms

(ML/SVM and DL/CNN). In Section 4, classiﬁcation

results for the above dataset including both pottery

forming techniques are given and analysed. Finally,

a brief conclusion is provided in Section 5.

2 DATA PROCESSING

We describe here the data acquisition process, the pre-

processing step of the images, that consists in pore

segmentation, and the way we proceed to feature ex-

traction, using Hough transform.

2.1 Image Acquisition

The experimental and archaeological pottery sherds

were scanned using a SkyScan-1178 X-ray µ-CT sys-

tem (Bruker) with two 1280x1024 X-ray cameras,

beam energy of 60kV, a 0.5mm thick aluminium ﬁlter,

0.7

◦

rotation. Each reconstructed image has a resolu-

tion of 81 µm. To reduce the data size, a box volume

surrounding each sherd is cropped from the 3-D stack

and used in the analysis. In this work we considered

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

110

Figure 2: Pores segmentation results. The ﬁrst line shows 2-D tomographic images and the second line the corresponding

segmented images. From left to right: CoT and SPT experimental sherds, CoT and SPT archaeological sherds.

central 2-D cross sections of tomographic images of

sherds (see Figure 2, ﬁrst row, for an example of CoT

and SPT experimental and archaeological sherds).

2.2 Image Processing

The spatial distribution of pores inside pottery de-

pends on the manufacturing sequence used, as air

tends to be trapped between building elements during

the forming process. Thus, CoT sherds are charac-

terised by pores showing linear patterns, while SPT

sherds reveal more dispersed patterns, which in some

cases suggest circular dispositions by visual interpre-

tation. Therefore, the segmentation of pores inside to-

mographic images reveals useful information for the

characterisation of the building technique.

The procedure we use to segment pore regions

is as follows. First, the pixels with low intensity

grey-scale values are selected as corresponding to air.

Then, a volume binarisation is applied to separate air

pixels from the rest of the materials characterising the

pottery (i.e. clay and mineral inclusions). Finally, a

connected components detection is performed in or-

der to remove unwanted connected components cor-

responding to the air surrounding the sherd. This pro-

cedure is applied to 3-D stack of tomographic images

and more details can be found in (Coli et al., 2020).

The 2-D cross-section images which we chose to use

in this work are successively extracted from the 3-D

stack. In Figure 2, bottom line, we show examples

of results of this segmentation process, where only

the porosity contrast is kept visible in the images.

In the rest of this work, we refer to these images as

segmented images. After segmentation, the images

show mostly aligned patterns for the pores in the CoT

sherds, while the distribution appears to be more cir-

cular and random for the SPT ones (Figure 2, bottom

line). Then, the distribution of pores is investigated

by means of the Hough transform.

2.3 Feature Extraction

The Hough transform is a classical technique which

is often used to detect alignments or other patterns

in images (Ballard, 1981; Beltrametti et al., 2013;

Mukhopadhyay and Chaudhuri, 2015). In order to de-

tect lines in 2-D images, the Hough transform relates

points in the image to sinusoidal curves in an asso-

ciated Hough space. The intersections between sinu-

soids account for the presence of points along lines in

the original image. Keeping the points where most si-

nusoids intersect provides us with the main alignment

directions of pores. In the analysis of the segmented

images, only the ﬁve lines which have the greater

amount of aligned pore pixels are retained in each im-

age for both classes (e.g., see Figure 3). The paral-

lelism between these ﬁve lines is tested by computing

the scalar products between their directional vectors

(Dia, 2020; Coli et al., 2020). These scalar products

constitute the main feature which will be provided to

the SVM classiﬁer.

A second feature is provided by the number of in-

tersection points between the recovered lines in the

image. Indeed, these lines are almost parallel for CoT

sherds and may intersect outside the image region,

while this is not the case for SPT sherds for which

these lines admit quite a few intersection points close

to the image centre (see Figure 3).

Applications of Learning Methods to Imaging Issues in Archaeology, Regarding Ancient Ceramic Manufacturing

111

Figure 3: Hough transform results. The red lines represent the detected alignments. From left to right: CoT and SPT

experimental sherds, CoT and SPT archaeological sherds.

3 CLASSIFICATION WITH

LEARNING ALGORITHMS

In this section, we brieﬂy introduce the two classi-

cal ML methods we used to classify the dataset. The

Support Vector Machine (SVM) (Widodo and Yang,

2007) and Convolutional Neural Network (CNN)

(Krizhevsky et al., 2012; de Rezende et al., 2018),

both are supervised learning methods, meaning that

they require a labeled dataset to be trained. In this

study, labels correspond to CoT and SPT techniques.

The big difference between these two methods is

that a feature extraction procedure is essential for the

SVM in order to classify the data. These features may

also provide important additional information in view

of archaeological interpretations. In this archaeologi-

cal sherd study, features are based on the alignments

in the pores structure. While, CNN do not require this

preliminary process, instead the algorithm detects and

extracts necessary features throughout its hidden lay-

ers. In the following two sections we provide a short

overview of these standard methods in the context of

this sherd study.

3.1 Support Vector Machine

Support Vector Machine is a ML method used to per-

form classiﬁcation tasks. It was initially introduced as

a two-class classiﬁcation technique, which can be ex-

tended to multiple-class classiﬁer (Widodo and Yang,

2007; Abe, 2010). For data in a n-dimensional space

with two classes, the objective of the SVM classiﬁer

is to ﬁnd a hyperplane in the n-dimensional space that

separates the two classes. Among all possible hyper-

planes, the objective is to ﬁnd the one that has the

maximum margin, i.e. the maximum distance to data

points of both classes (see Figure 4, left).

Usually, real-life problems contain noisy data and

may not be efﬁciently separated by such a hyperplane.

Indeed, if it exists, this hyperplane may have a very

small margin (minimal distance to the points, see Fig-

ure 4, left). To deal with this problem, an additional

Figure 4: Left: an example of how a dataset is separated

in two different classes by a hyperplane. Right: a non-

separable case, with an example of slack variables.

term weighted by a parameter C ∈ R

is introduced in

the SVM, in order to specify how many errors can be

accepted in the classiﬁcation. The parameter C allows

to tune the trade-off between having a wide margin

and the number of admitted errors (that correspond to

the slack variables in Figure 4, right).

Moreover, data may not be separable by a hyper-

plane (see an example Figure 5). In such general

cases, they are projected onto a higher dimensional

feature space, where linear classiﬁcation is possible.

This is done by the use of a kernel transformation

such as linear, polynomial and Gaussian Radial Ba-

sis Function (RBF) (Widodo and Yang, 2007).

Figure 5: The left picture shows a 2-D set of points impos-

sible to separate using linear SVM. The right picture shows

a kernel transformation of these data in a 3-D space where

they can be easily separated (https://commons.wikimedia.

org/wiki/File:Nonlinear SVM example illustration.svg).

Based on the archaeological question of identify-

ing the CoT or SPT manufacturing techniques on the

basis of sherds, it seems natural to ﬁrst detect align-

ment of pores in segmented images and then classify

data from these lines. More precisely, the considered

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

112

features for SVM classiﬁcation are line intersections

points and dot products between the Hough-detected

lines, as described in Section 2.3. Due to non-linearity

of the data, a RBF Kernel, depending on a parameter

γ, is used to increase the accuracy rate. See Section 4

for technical details and values.

3.2 Convolutional Neural Network

Classiﬁcation Convolutional Neural Network is a

Deep Learning method (Krizhevsky et al., 2012; de

Rezende et al., 2018) which generally consists of

three main parts (see Figure 6 as an example): an in-

put layer part, where the image is given to the clas-

siﬁer, a feature extraction (or a hidden layer) part,

and a classiﬁcation part that uses fully connected lay-

ers (i.e. each neuron of a layer is connected to ev-

ery neurons of the following layer). This overall net-

work provides as an output the probability values for

an input image to belong to each of the classes. In

this work two classes are considered, CoT and SPT.

CNN have shown unequalled performances in image

classiﬁcation. Such performances are mainly due to

the learning of the hidden network from a huge num-

ber of images. Indeed, a feature extraction network

is classically composed of a sequence of layers, each

one containing bias addition, convolution ﬁlters, ac-

tivation function (Rectiﬁed Linear Unit, ReLu), and

pooling operation.

We choose to use a transfer-learning procedure

with a pre-modeled and pre-trained network, specif-

ically the GoogLeNet architecture (Szegedy et al.,

2015). The architecture and huge quantity of parame-

ters of the ﬁrst two parts of this CNN network which

compute image characteristics (e.g. bias, coefﬁcients

of the convolution ﬁlters) remained unchanged. Only

the parameters of the third fully connected layer part

were estimated and tested using our dataset, which is

one of the main advantages of using such a network.

For this estimation, we used the DL Matlab toolbox

All parameters of SVM and CNN are provided in

Section 4.

4 CLASSIFICATION RESULTS

This section presents the classiﬁcation results ob-

tained on lines, segmented images (see Section 2.2),

and 2-D cross-sections of raw tomographic images.

The considered datasets are as follows:

• 360 segmented binary images (130 from CoT

https://it.mathworks.com/help/deeplearning/ref/

trainnetwork.html

sherds and 130 from SPT sherds), used for SVM

and CNN classiﬁcation.

• 460 grey-scale images (230 from CoT sherds and

230 from SPT sherds), used for CNN classiﬁca-

tion.

Note that the dataset of segmented images is smaller

than the dataset of tomographic images, because the

pore segmentation process can produce empty images

(dark images, which correspond to a slice where no

pores were detected).

As Figure 2 (ﬁrst line) shows, the CoT experimen-

tal sherds usually have a squared shape, while the SPT

ones are round-shaped. Since this shape is not rel-

evant for manufacturing characterisation, it may in-

duce bias in the classiﬁcation. To avoid this phe-

nomenon, only the central part of each grey-scale im-

age is considered in the experiments (see Figure 7).

Whatever the classiﬁcation methods and the input

data, the learning step is performed on 80% of the

dataset and the remaining 20% are used for testing.

4.1 Results with Support Vector

Machine

As mentioned in Section 3.1, a cost parameter C and

the Kernel parameter γ must be tuned in order to pre-

vent under- or over-ﬁtting phenomena. A grid search

is performed to determine the optimal values of these

parameters. From these multiple tests, C was set to

100 and γ to 10. The dataset is randomly shufﬂed

1000 times and different learning and testing sets are

picked for each run. The prediction accuracy results

averaged over 1000 runs on 72 test images are shown

in Table 1.

4.2 Results with Convolutional Neural

Network

The second method we consider is the classiﬁcation

by CNN, ﬁrst on segmented images, and then on raw

images.

As presented in Section 3.2, we use a transfer-

learning procedure with GoogLeNet network which

requires three-dimensional 224 × 224 × 3 images as

inputs; the images are thus resized accordingly. As

the images of our dataset are either binary or grey-

scale, each image is replicated three times to obtain

the desired form. The training and validation set is

composed by 80% of the images of each dataset (more

precisely, 64% of the dataset is used for training and

16% for validation), while the testing set is composed

by the remaining 20% of the images.

The CNN classiﬁer was tested multiple times with

Applications of Learning Methods to Imaging Issues in Archaeology, Regarding Ancient Ceramic Manufacturing

113

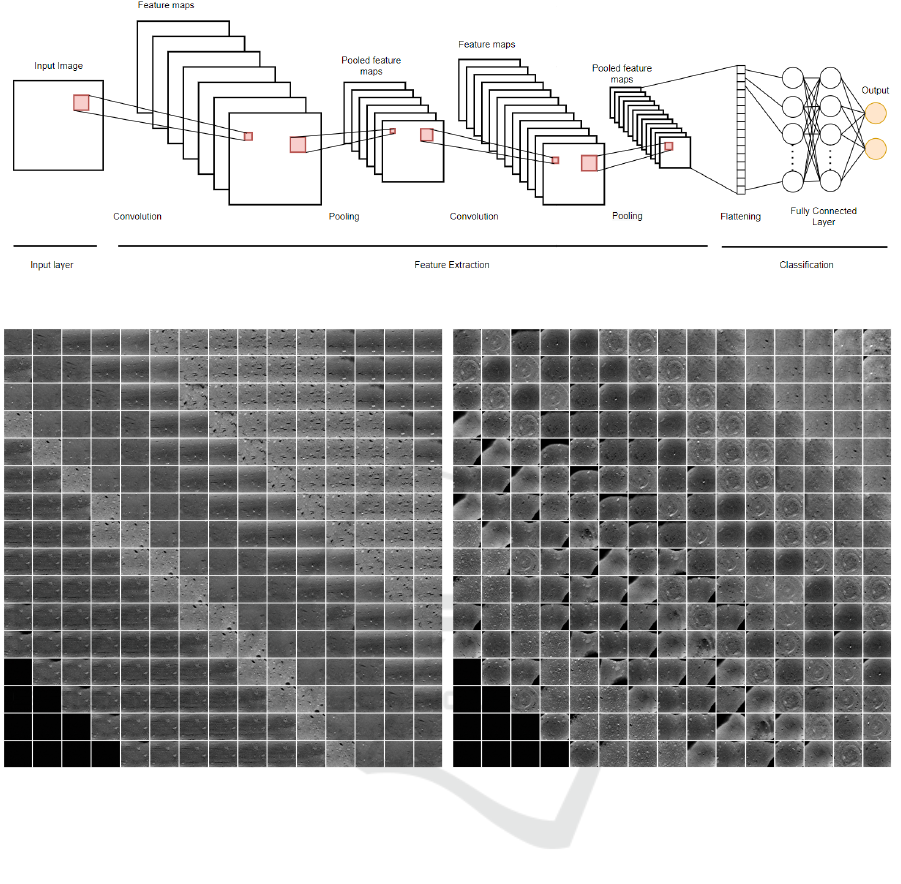
Figure 6: CNN architecture.

Figure 7: Grey-scale tomographic images, cropped central regions. Left: the 230 images composing the CoT dataset. Right:

the 230 images composing the SPT dataset. The 10 black images displayed in the bottom-left corners of each set are not

included in the datasets.

different input parameters, in order to determine their

suitable values for our data. The following parame-

ters are set for each run: number of epochs (number

of complete passes through the training dataset) = 15,

batch size (number of training samples that are fed

to the classiﬁer at once to reduce the computational

time) = 40 images, validation frequency (number of

iterations after which the validation set is fed to clas-

siﬁer to test its accuracy and update the weights of

the fully connected layers) = 20 iterations, and learn-

ing rate (step size) = 0.0001. These parameter values

are the same for both experiments described below,

i.e. for segmented and grey-scale images.

4.2.1 Segmented Images

The CNN classiﬁer was ﬁrst tested on segmented im-

ages, in order to take into account the fact that we

are interested in pore alignments for CoT while ran-

dom/spiral distribution are expected in SPT. The pre-

diction accuracy results on 72 test images are shown

in Table 1.

4.2.2 Grey-scale Images

As the CNN classiﬁer showed remarkable improve-

ment in classiﬁcation with respect to the SVM perfor-

mances, the classiﬁer is tested on the more challeng-

ing set of grey-scale images of Figure 7. The predic-

tion accuracy results on 92 test images are shown in

Table 1.

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

114

Table 1: Prediction accuracy for each object category and all considered classiﬁcation methods. The number of images in the

testing dataset is indicated between parentheses. The results are averaged over 1000 runs for the SVM method.

Object category SVM (segmented images + features) CNN (segmented images) CNN (grey-scale images)

SPT 77.7% (36) 88.8% (36) 100% (46)

CoT 79.5% (36) 100% (36) 93.4% (46)

Overall accuracy 78.6% (72) 94.4% (72) 96.7% (92)

4.3 Discussion

Considering the methods applied to segmented im-

ages, the CNN method appears more accurate than

the SVM one. Indeed, the accuracy rates for SVM

roughly hit less than 80%, while they are higher than

90% for CNN for most of the tested situations (see

Table 1). Despite the differences between the classiﬁ-

cation methods, it could be that the features captured

by CNN on segmented images are richer than those

extracted from the lines obtained by the Hough trans-

form on pores.

From these results, it appears that the Deep Learn-

ing method is more competent than the SVM Ma-

chine Learning method in classifying the testing set,

where it provided signiﬁcantly more accurate results.

Moreover, CNN automatically performs the feature

detection / extraction steps with transfer learning,

whence only the classiﬁcation network needs to be

trained. For SVM however, each image had to be pre-

processed in order to extract the retained features. Fi-

nally, SVM is 5 times more computationally costly (in

time) than the CNN one.

Ultimately, the CNN procedure gives slightly bet-

ter classiﬁcation results from grey-scale images than

from segmented images. Yet, some information might

be lost during by the segmentation / pore extraction

procedure.

5 CONCLUSION

Promising results were obtained with Machine Learn-

ing and Deep Learning algorithms for classiﬁcation

of ancient pottery samples, running on 2-D cross-

sections extracted from a set of µ-CT images. This

will be useful to classify archaeological sherds which

are often damaged and difﬁcult to distinguish from

noisy images. As CNN methods give good results,

different conﬁgurations of these techniques can be

further investigated. To improve the classiﬁcation, we

also plan to acquire more samples and images, with

other modalities and at different resolutions.

However, one of the most important drawbacks of

CNNs is their lack of interpretation in terms of mod-

elling. The advantage of the more traditional image

analysis approaches (like the SVM one) is that it pro-

vides archaeologists with visual and quantitative el-

ements for image interpretation (e.g. the quantity of

parallel pore lines in CoT sherds) that are very useful

for their analysis of the manufacturing process. Many

additional features can also be considered, as for ex-

ample the positions of lines intersection points.

With the same goal, the Hough transform can be

adapted in order to catch circular or spiral-like be-

haviour of pores in SPT images, see (Coli et al.,

2020). Finally, note that higher dimensional versions

of the Hough transform are able to detect surfaces

in 3-D images, see (Beltrametti et al., 2013; Ballard,

1981). They could provide good results on sherd im-

ages.

The quantitative analysis proposed here to dis-

criminate between CoT and SPT manufacturing tech-

niques using pore distribution in µ-CT scans of sherds

can be applied to other pottery building processes.

These promising results address similar issues con-

cerning other markers of the micro-structures inher-

ited from the building process. More speciﬁcally,

the spatial organisation of mineral inclusions also re-

ﬂects the technical gestures implemented during pot-

tery making. The present approach may provide use-

ful complementary classiﬁcation results on such in-

clusions, though their segmentation from µ-CT im-

ages is more difﬁcult than those of the pores due to

the variety of materials (hence of intensities in im-

ages). Next step will be to jointly process these dif-

ferent markers in order to reﬁne the diagnostic and to

furnish more robust and accurate information.

ACKNOWLEDGEMENTS

This work was supported by the French National

Research Agency, with the reference number ANR-

15-IDEX-0001, IDEX UCA

JEDI

“Multiscale Tomog-

raphy: Imaging and Modelling Ancient Materials,

Technical Traditions and Transfers - TOMAT” project

and through the 3IA C

ote d’Azur Investments, with

the reference number ANR-19-P3IA-0002.

We thank the reviewers for their comments and

Applications of Learning Methods to Imaging Issues in Archaeology, Regarding Ancient Ceramic Manufacturing

115

suggestions.

REFERENCES

Abe, S. (2010). Support Vector Machines for Pattern Clas-

siﬁcation. Springer Publishing Company, Incorpo-

rated, 2nd edition.

Ballard, D. (1981). Generalizing the Hough transform to de-

tect arbitrary shapes. Pattern Recognition, 13(2):111–

22.

Beltrametti, M., Massone, A., and Piana, M. (2013). Hough

Transform of Special Classes of Curves. SIAM Jour-

nal on Imaging Sciences, 6(1):391–412.

Coli, V. L., Gomart, L., Pisani, D., Cohen, S., Blanc-

eraud, L., Leblond, J., and Binder, D. (2020). Micro-

computed tomography for discriminating between dif-

ferent forming techniques in ancient pottery: new seg-

mentation method and pore distribution recognition.

Under revision for publication.

de Rezende, E. R., Ruppert, G. C., Th

eohilo, A., Tokuda,

E. K., and Carvalho, T. (2018). Exposing computer

generated images by using deep convolutional neural

networks. Signal Processing: Image Communication,

66:113 – 126.

Dia, K. (2020). Machine learning for imaging issues in ar-

chaeology. Master’s thesis, Universit

e Savoie Mont

Blanc.

Gomart, L. (2010). Variabilit

e technique des vases du

Ruban

e r

ecent du Bassin parisien (RRBP) et du

Villeneuve-Saint-Germain (VSG) : un cas d’

etude

dans la vall

ee de l’Aisne. Bulletin de la Soci

ehistorique franc¸aise, 107(3):537–48.

Gomart, L. (2014). Traditions techniques et production

eramique au N

eolithique ancien.

Etude de huit sites

ruban

es du Nord-Est de la France et de Belgique. Lei-

den: Sidestone.

Gomart, L., Weiner, A., Gabriele, M., Durrenmath, G.,

Sorin, S., Angeli, L., Colombo, M., Fabbri, C., Maggi,

R., Panelli, C., Pisani, D., Radi, G., Tozzi, C., and

Binder, D. (2017). Spiralled patchwork in pottery

manufacture and the introduction of farming to South-

ern Europe. Antiquity, 91(360):1501–14.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).

Imagenet classiﬁcation with deep convolutional neu-

ral networks. In Proceedings of the 25th Interna-

tional Conference on Neural Information Processing

Systems - Volume 1, NIPS’12, page 1097–1105, Red

Hook, NY, USA. Curran Associates Inc.

Mukhopadhyay, P. and Chaudhuri, B. (2015). A survey of

Hough Transform. Pattern Recognition, 48(3):993–

1010.

Salanova, L., Vieugu

e, J., and Gomart, L. (2010). Meth-

ods of study of large ceramic complexes: series and

sets of Neolithic pottery from Kovachevo (Bulgaria).

Arheologia Soﬁa, (3–4):7–23.

Szegedy, C., Wei Liu, Yangqing Jia, Sermanet, P., Reed, S.,

Anguelov, D., Erhan, D., Vanhoucke, V., and Rabi-

novich, A. (2015). Going deeper with convolutions. In

2015 IEEE Conference on Computer Vision and Pat-

tern Recognition (CVPR), pages 1–9.

Widodo, A. and Yang, B.-S. (2007). Support vector ma-

chine in machine condition monitoring and fault di-

agnosis. Mechanical Systems and Signal Processing,

21(6):2560 – 2574.

DeLTA 2021 - 2nd International Conference on Deep Learning Theory and Applications

116