Proof-of-Useful-Randomness: Mitigating the Energy Waste in

Blockchain Proof-of-Work

Efe Ulas Akay Seyitoglu

, Attila Altay Yavuz

and Thang Hoang

Department of Computer Science and Engineering, University of South Florida, Tampa FL, U.S.A.

Department of Computer Science, Virginia Tech, Blacksburg VA, U.S.A.

Keywords:

Blockchain, Proof-of-Work.

Abstract:

Proof-of-Work (PoW) is one of the fundamental and widely-used consensus algorithms in blockchains. In

PoW, nodes compete to receive the mining reward by trying to be the ﬁrst to solve a puzzle. Despite its fairness

and wide-availability, traditional PoW incurs extreme computational and energy waste over the blockchain.

This waste is considered to be one of the biggest problems in PoW-based blockchains and cryptocurrencies.

In this work, we propose a new useful PoW called Proof-of-Useful-Randomness (PoUR) that mitigates the

energy waste by incorporating pre-computed (disclosable) randomness into the PoW. The key idea is to inject

special randomness into puzzles via algebraic commitments that can be stored and later disclosed. Unlike the

traditional wasteful PoWs, our approach enables pre-computed commitments to be utilized by a vast array of

public-key cryptography methods that require ofﬂine-online processing (e.g., digital signature, key exchange,

zero-knowledge protocol). Moreover, our PoW preserves the desirable properties of the traditional PoW and

therefore does not require a substantial alteration in the underlying protocol. We showed the security of our

PoW, and then fully implemented it to validate its signiﬁcant energy-saving capabilities.

1 INTRODUCTION

The Proof-of-Work (PoW) algorithm provides a

means of consensus in blockchains and therefore

plays a central role in various blockchain applications.

The traditional PoW puzzle has been shown to be fair

and is widely adopted in practice. Speciﬁcally, a tradi-

tional PoW (at minimum) satisﬁes the following prop-

erties: (i) Hardness: Each attempt to solve the PoW

puzzle should succeed in a similar probability. This

gives incentives to invest in computational resources

because the puzzle rate (i.e., the hashing effort) grows

linearly with the possibility of ﬁnding a solution. (ii)

Efﬁciency: A puzzle must have a solution, and should

be generated/veriﬁed in polynomial time. (iii) Com-

pleteness: Only a valid puzzle solution should be ac-

cepted by the veriﬁer (Ball et al., 2018).

The traditional PoW accounts for about 90% of

the total market in digital cryptocurrencies (Gervais

et al., 2016), as well as dominating the blockchain-

based applications. However, despite its merits and

wide-use in practice, the traditional PoW also has

been shown to be extremely energy costly. For in-

stance, Bitcoin was measured to have consumed 39

TWh of electricity in 2018 which at the time was

more than the electricty consumption of Qatar and

Bulgaria (Bahri and Girdzijauskas, 2018). A big

chunk of these electricity consumption are due to the

computational wastefulness of traditional PoW algo-

rithms. This severe energy waste is considered as one

of the biggest disadvantage of traditional PoW (Ger-

vais et al., 2016). Various alternative consensus al-

gorithms have been developed to reduce the energy

waste in blockchains. Below, we ﬁrst outline some

of the prominent approaches related to our work, and

then elaborate our contributions in this paper.

2 RELATED WORK

The existing PoW algorithms can be classiﬁed into

three groups: (i) Traditional Proof-of-Work, (ii)

Proof-of-Non-Wasteful-Work, (iii) Proof-of-Useful-

Work.

• Traditional Proof-of-Work. The most common

example for such consensus algorithms is the hash-

based Bitcoin PoW algorithm. These type of algo-

rithms are based on the fact that the hash function

output is pseudorandom. The puzzle is constructed

in a way that, every miner in the network tries to cou-

412

Seyitoglu, E., Yavuz, A. and Hoang, T.

Proof-of-Useful-Randomness: Mitigating the Energy Waste in Blockchain Proof-of-Work.

DOI: 10.5220/0010519204120419

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 412-419

ISBN: 978-989-758-524-1

ple an arbitrary nonce with the block content whose

hash will be satisfying the puzzle (Meng et al., 2018).

The more computational power a miner has, the more

nonce values they can try which can potentially end

up satisfying the requirements of the puzzle. We take

the Bitcoin PoW algorithm as a starting point and

thus, will elaborate on this idea further in the pro-

posed PoW algorithm section.

Note. There are other variants of PoW algorithm such

as Number Theoretic PoW which is used in popu-

lar cryptocurrencies such as PrimeCoin (King, 2013).

Another important variants are linear algebra based

(e.g. (Ball et al., 2017)) or graph theoretic ones (e.g.

(Tromp, 2015)). However, the focus of this paper is

going to be a hash-based approach for two reasons:

(i) our construction is on top of the traditional hash-

based Bitcoin PoW, (ii) the hash-based PoW domi-

nates the cryptocurrency market (Loe and Quaglia,

2018).

• Proof-of-Non-Wasteful-Work. A proof-of-non-

wasteful-work, is an algorithm that does not consume

computational resources for establishing consensus.

One good example is the the proof-of-stake (PoS) al-

gorithm. In this algorithm, the nodes deposit certain

amount of ﬁnancial resources as stakes. The node

that will add a new block to the blockchain is cho-

sen with a probability that is linear to the stake they

deposit. PoS is a clever attempt to solve the electric-

ity/computation waste problem. An instantiation of

the PoS puzzle idea can be found in (Bentov et al.,

2016). PoS has also been partially used in other novel

PoW schemes (e.g. (Bentov et al., 2014)). Further-

more, Krol et. al. proposed Proof-of-Prestige (PoP)

which is built on top of PoS. In PoP, the users earn

prestige via performing useful work which in turn in-

creases their chances of obtaining the mining reward

(Król et al., 2019).

However, PoS is not perfect due to its innate

foundational differences (i.e. incentivizing the miner

via stakes instead of compuatation power) compared

to PoW. This is a problem because many popular

blockchains (e.g. Bitcoin) use the wasteful PoW as

the consensus algorithm (Nakamoto, 2009). There-

fore, a big algorithmic jump from PoW to a com-

pletely different consensus algorithm (PoS) would re-

quire costly development efforts. Furthermore, coin

holders in the network would need to be convinced to

participate in a whole different consensus algorithm

which could be problematic (Kiayias et al., 2017).

Another fundamental difference between traditional

PoW algorithms and the PoS algorithm is the source

of pseudorandomness. In a desirable PoW algorithm,

the pseudorandomness should be external. In other

words, ﬁnding the solution to the PoW puzzle should

have no relation with the cryptocurrency itself but

should be a process that is dependent on external fac-

tors such as hash output. In the PoS algorithm, the

pseudorandomness is internal (Brown-Cohen et al.,

2019).

The PoS variants also suffer from the "nothing

at stake" problem. In PoS, validators can maximize

their earning by joining various forks (and generat-

ing clashing blocks) without taking on extra risk for

losing the stake (Li et al., 2017). Some important ap-

proaches to mitigate this problem can be found in (Ki-

ayias et al., 2017). Another concern with PoS is the

security impact of stale blocks as described in (Ger-

vais et al., 2016). GHOST protocol works to solve

this problem (Gervais et al., 2016).

Another good example is the Intel’s proof-of-

elapsed-time (PoET) which is based on time instead

of execution power. The ﬁrst node to ﬁnish waiting

gets the mining reward (Chen et al., 2017). This al-

gorithm is a good candidate to solve the PoW elec-

tricity consumption problem, but it does not incen-

tivize nodes and has a considerable deployment cost

on PoW dominated blockchains.

• Proof-of-Useful-Work (PoUW). This type of al-

gorithms produce a useful component during consen-

sus. One good example is from Ball et. al. who pro-

posed a PoUW that helps tackle computational prob-

lems (3SUM, Orthagonal Vectors etc.) while solv-

ing the PoW puzzle (Ball et al., 2017). Another good

approach is by (Loe and Quaglia, 2018) who gener-

ated an instance of the Travelling-Salesman problem

which is known to be NP-Hard during the PoW con-

sensus. There are other notable approaches such as

Hastings et. al., who proposed a PoUW algorithm

that computes the discrete logarithm of a cyclic group

during consensus (Hastings et al., 2019) or by Lihu et.

al. who incorporates ML training into puzzle solving

(Lihu et al., 2020) to save energy.

To sum up, the traditional (wasteful) PoW is still

the most widely adopted consensus algorithm despite

its wastefulness. Therefore, we need a new useful

PoW algorithm that stays in the realm of traditional

PoW consensus but also mitigates its energy waste

problem (Nakamoto, 2009).

3 OUR CONTRIBUTION

In this work, to the best of our knowledge,

we proposed the ﬁrst PoUW that creates useful-

randomnesses, which not only substantially reduces

the energy waste, but also preserves the main PoW

architecture, thereby avoid the hurdles of heavy

transition costs of alternative consensus algorithms.

Proof-of-Useful-Randomness: Mitigating the Energy Waste in Blockchain Proof-of-Work

413

We name our scheme as proof-of-useful-randomness

(PoUR).

Main Idea. In the traditional PoW, one-time ran-

domnesses (nonces) are used as a solution to the puz-

zle. However, this is expensive and wasteful, as gen-

erating a bitcoin block takes on average 2

attempts

(O’Dwyer and Malone, 2014), and mostly impor-

tantly, those nonces are just discarded (wasted). Our

key observation is that the wasted randomness gen-

eration in PoW can be turned into an opportunity, if

one can produce (special) useful randomness that can

be harnessed by the cryptographic algorithms. Our

PoUR algorithm randomly generates (one-way) al-

gebraic commitments that not only serve as the ran-

domness source for PoW but also can be integrated

into a vast range of public key cryptographic prim-

itives. We call these useful randonmness as Pre-

computed Algebraic Commitments (PAC), which can

be integrated into various cryptographic schemes in

ofﬂine-online settings (e.g., digital signatures, key ex-

change). We further elaborate the desirable properties

of our scheme as follows:

• Energy-Saving and Efﬁcient Consensus. PoUR

saves considerable energy by creating useful-

randomnesses that can be used by various crypto-

graphic operations as needed. For example, after

puzzle-solving attempts, PoUR saves around

2.18 · 10

J worth of energy in elliptic-curve set-

tings. This energy-saving process does not come

with the cost of any additional efﬁciency overhead

to the protocol since the target value of the puz-

zle could be adjusted to accommodate the desired

hardness (i.e. the necessary number of attempts to

solve the puzzle on average).

• Security and Open-Source Implementation. We

present a security discussion for PoUR and pro-

vide the implementation of our proposed scheme

on commodity hardware. We will open-source our

implementation.

• Potential Use-cases. PoUR is applicable to a

wide-array of cryptographic schemes that admit

an ofﬂine-online phase, in which PACs can be

generated via PoUR and then later consumed by

cryptographic scheme. Some example crypto-

graphic schemes that receive beneﬁt from PoUR

includes ,but not limited to digital signatures, key-

exchange, public-key encryption, zero-knowledge

proofs, random beacons and their quantum-safe

variants. We have shown two speciﬁc PoUR in-

stantiations with elliptic-curve and lattice based

digital signatures.

• Ease-of-Integration. PoUR algorithm requires

minimal alteration to the existing and traditional

PoW algorithms in popular platforms such as Bit-

coin. We save commitments during consensus

without impacting the other parts of the system.

4 PRELIMINARIES

We now present the prelimineries of our scheme.

Deﬁnition 1. An Algebraic One-way function AOWF

consist of two algorithms Gen, F(Catalano et al.,

2013):

1. K ← Gen(1

). Given the security parameter κ,

Gen(1

) outputs a key K. The key K determines

the order of the groups A

and B

for F.

2. F

: A

→ B

. For input a ∈ A

, there is an

output b ∈ B

such that b = F

(a) is computed

in polynomial-time. However, given b, it should

be infeasible for a probabilistic polynomial-time

(PPT) adversary A to come up with a function F

such that Pr[F

) = b] ≥ ε.

3. ∀ κ ∈ N, K ← Gen(1

) such that K constitutes an

order for A

and B

in F

: A

→ B

4. We Can Perform Efﬁcient Group Operations.

F(A

)

F(B

) = F(A

) where

is an

operator over the ring R.

AOWF is popular in many cryptographic domains

such as ECDLP, DLP and Post-Quantum Cryptogra-

phy. We leverage them in PoUR for energy saving

purposes.

One of the most popular AOWF is the hash func-

tion H. A hash function is a one-way function takes

in an arbitary length input and produces a ﬁxed out-

put. We leveraged SHA-256 in our constructions as

an AOWF. Bitcoin also leverages the SHA-256 hash

function durining consensus (Nakamoto, 2009).

Deﬁnition 2. Given an elliptic curve E(F

) over a

ﬁnite ﬁeld F

, ECDLP asks to ﬁnd a value k ∈ Z

such that P

= k · P

where P

, P

are points on E(F

)

(Behnia et al., 2019).

Deﬁnition 3. Short Integer Solution Problem (SIS).

Given a collection of n-dimensional modulo q (prime

number) vectors

, . . . ,

∈ Z

, the SIS problem

asks to ﬁnd a collection of non-trivial s

, . . . , s

∈

{−1, 0, 1} such that s

+ . . . + s

∈

where

is an n-dimensional vector that contains

all zeros (Peikert, 2016).

Deﬁnition 4. Learning with Errors Problem (LWE).

Given dimension n, modulo q, an error distribution e

such that

√

n ≤ e ≤ q, and b ∈ Z

, the LWE problem

asks to ﬁnd a secret s ∈ Z

, such that b = hs, ai + e ∈

where a ∈ Z

and hs, ai denotes the inner-product

SECRYPT 2021 - 18th International Conference on Security and Cryptography

414

between s and a. The decision version of the same

problem asks to distinguish a collection of pairs from

truly random pairs (Peikert, 2016).

Deﬁnition 5. Cryptographic Pseudorandom Num-

ber Generators (CPRNG). A CPRNG, G is a deter-

ministic algorithm that takes a uniform input seed and

produces a pseudorandom output. Given a short uni-

form seed s, G is a CPRNG satisﬁes the following

properties:

• ∀s, L(G(s)) > L(s) where L is gives the string

length.

• |Pr[T (G(s)) = 1] - Pr[T [(r) = 1]]| ≤ ε where ε is a

negligible value, T is an efﬁcient statistical random-

ness test (distinguisher), and r ∈ {0, 1}

L(G(s))

(Katz

and Lindell, 2014).

Deﬁnition 6. Pre-computed Algebraic Commit-

ments (PAC). PACs are expensive cryptographic to-

kens created in the ofﬂine phase and directly used in

the online phase for computational saving. Creation

of a PAC consists of three steps:

1. r

← D for all i = 1 to K where r

is selected from

is selected from a speciﬁed distribution D which

is random-uniform.

2. R

← AOWF(r

) for all i = 1 to K (All R

are dis-

closable randomnesses)

3. U ← U ∪{(r

, R

)} for all i = 1 to K where U is

a set that stores the commitments.

Deﬁnition 7. A PoW scheme has three algorithms

(Ball et al., 2018):

• c ←Gen(1

): Generates the challange c given the

security parameter κ.

• π ← Solve(c) : Satisﬁes the requirements of the

challenge c and generates the proof π.

• {0, 1} ← Ver(c, π): Veriﬁes that the proof π satis-

ﬁes the requirements of the challenge c.

Miners try to solve the puzzle by ﬁnding a nonce v

such that H(B

|| v) < T (target value) where || denotes

concatenation and B

denotes the block content. The

ﬁrst miner with such a nonce keeps the reward.

5 PROPOSED PROOF-OF-WORK

ALGORITHM

The classical PoW compares the target value with

H(B

|| v) (v is the nonce). If the comparison fails,

PoW increases the nonce by one and compares the

hash output against the target value. The idea in tradi-

tional Bitcoin PoW is that the miners try out different

nonces for which when appended with the block con-

tent, will result in a hash output that is smaller than

the target. In PoUR we replace the duty of nonces

with disclosable PACs and store them for energy-

saving. Storing PACs is essential for our scheme be-

cause the usage of PACs are common in blockchain-

based public-key infrastructure where ofﬂine-online

cryptography is leveraged. Furtermore, in our PAC

creation we leverage B

. This prevents miners to pre-

create and use these PACs prior to mining.

PoUR Energy Saving. PACs are computationally ex-

pensive to create and are neccessary in cryptographic

operations. Our PoUR construction pre-computes

PACs during consensus and stores them. The stored

PACs results in energy-efﬁciency because instead of

creating them in future cryptographic methods, we

fetch the stored ones.

Generic PoUR Algorithm. We now present the

generic construction of our PoUR algorithm. We use

this construction as a starting point to show the us-

age of PoUR in other cryptographic settings such as

ofﬂine-online cryptographic settings as well as instan-

tiations in elliptic-curve and post-quantum settings.

We note that

−→

m : (m

, . . . m

) means a vector of mes-

sages. {0, 1}

∗

denotes a string with arbitrary length

and B

denotes the block randomness.

Algorithm 1: Generic Constructions of PoUR.

c ← PoUR.Gen(1

) :

1: Target value T is determined

2: Let (B

, B

) ∈ {0, 1}

∗

3: return c = (B

, T, B

)

π ← PoUR.Solve(c = (B

, T, B

)):

1: i = 0

2: do

3: s

← D

4: r

← G(s

|| B

)

5: R

← AOWF(r

)

6: U ← U ∪{(r

, R

)}

7: i = i + 1

8: while H(B

|| R

) ≥ T

9: return π = (s

i−1

, R

i−1

)

Note. We disclose only a single PAC out of the

(on average) PACs we save. Therefore, our

(on average) -1 PACs are processable and we

save the energy that would have been needed to

create the commitments.

{0, 1} ← PoUR.Ver(c = (B

, T, B

), π = (s, R)):

1: r

← AOWF(G(s || B

))

2: if AOWF(r

) = R & G(B

|| R) < T then

3: return 1

4: return 0

Proof-of-Useful-Randomness: Mitigating the Energy Waste in Blockchain Proof-of-Work

415

In our PoUR.Solve method, we store the PACs.

These pre-computed PACs could later be utilized in

many cryptographic methods instead of creating them

from stratch (which results in energy efﬁciency). In

the subsequent sections, we show how we leverage

PoUR in cryptographic applications.

Usage in Ofﬂine-Online Cryptography. In

blockchains with public-key infrastructure, online

stage execution time is crucial. Thus, we store the

pre-computed and compuationally expensive alge-

braic commitments in U during the ofﬂine-phase for

faster execution in the online phase. CryptOp.process

is a function for cryptographic operations like encryp-

tion, signing etc. whereas CryptOp.verify refers to its

veriﬁcation.

Algorithm 2: Ofﬂine-Online Settings with PoUR.

U ← PoUR.Oﬄine(1

)

1: c ← PoUR.Gen(1

)

2: π ← PoUR.Solve(c) //PACs are in U

3: if PoUR.Verify(c, π) = 0 then

4: Go Back to Step 1

(F , R ) ← PoUR.Online(

−→

m , U)

1: for i = 1 to n do

2: (r

, R

) ← Pick and remove from U

3: R ← R ∪{(R

)}

4: F ← F ∪CryptOp.process(r

, R

, m

)

return (F , R )

{0, 1} ← PoUR.Verify(

−→

m , F , R )

1: Let F : ( f

, .., f

)

2: Let R : (R

, .., R

)

−→

m = (m

, .., m

)

4: for i = 1 to n do

5: f

← Pick from F

6: R

← Pick from R

7: if CryptOp.verify(R

, f

, m

) = 0 then

8: return 0

9: return 1

5.1 Generic Constructions of PoUR

We now describe our elliptic-curve and lattice instan-

tiations with PoUR. The core idea is to generate com-

mitments during consensus and use them in crypto-

graphic operations later. If it were not for the PoUR,

these commitments would need to be created from

scratch which would be computationally costly.

Note. The type of commitments that are saved in

PoUR.Solve is dependent on the underlying crypto-

graphic instantiation.

PoUR Construction in Elliptic Curves. We now

show how PoUR uses PACs and saves energy

in ECDLP settings. We chose SchnorrQ signa-

tures (Schnorr, 1991) but any digital signature with

special features (e.g., forward-security, aggregation

(e.g. (Seyitoglu et al., 2020)) would beneﬁt from

PoUR. We denote (k, K) as a public, private key pair.

The key generation, signature generation and veriﬁ-

cation functions are denoted by Kg, Sig, Ver respec-

tively. R

is the x-coordinate of R. P is the elliptic

curve generator.

Algorithm 3: PoUR Construction in Elliptic-Curves and its

usage in SchnorrQ Signature.

c ← PoUR.Gen(1

) :

1: Target value T is determined

2: Let (B

, B

) ∈ {0, 1}

∗

3: return c = (B

, T, B

)

π ← PoUR.Solve(c = (B

, T, B

)):

1: i = 0

2: do

3: s

← Z

∗

4: r

← H(s

|| B

)

5: R

← r

·P //P: Elliptic Curve Generator

6: U ← U ∪{(r

, R

)}

7: i = i + 1

8: while H(B

|| R

) ≥ T

9: return π = (s

i−1

, R

i−1

)

(0, 1) ← PoUR.Ver(c = (B

, T, B

), π = (s, R)):

1: t ← H(s || B

)

2: if P ·t = R & H(B

|| R)) < T then

3: return 1

4: return 0

(k, K) ← SchnorrQ.Kg(1

1: (k, K) ← Pick and remove from U

2: return (k, K)

σ ← SchnorrQ.Sig(k, M):

1: (r, R) ← Pick and remove from U

2: e ←H(M || R

) //R

: x coordinate of the point R

3: s ←r −e ·k

4: return σ = (s, e)

{0, 1} ← SchnorrQ.Ver(K, M, σ = (s, e)):

1: R

← K ·e + P ·s

2: if e = H(M || R

) then

3: return 1

4: else return 0

SECRYPT 2021 - 18th International Conference on Security and Cryptography

416

PoUR Construction in Lattices. PoUR can be useful

in Lattices. ϕ is the coefﬁcient threshold. R

is a vec-

tor with l elements. R

m×l

is a matrix with dimensions

m ×l. S

∈ R

and G is the generator in R

m×l

. We

use the sampling in lattices Samp() to incorporate the

in our secret. β is the maximum coefﬁcient. High

and Low refer to high and low bits due to signature

compression in Dilithium (Ducas et al., 2018). ||z|| is

the norm operation on z. ∞ is the norm inﬁnity.

Algorithm 4: PoUR Construction in Lattices and its usage

in Dilithium Signature (Ducas et al., 2018).

c ← PoUR.Gen(1

) :

1: Target value T is determined

2: Let (B

, B

) ∈ {0, 1}

∗

3: return c = (B

, T, B

)

π ← PoUR.Solve(c = (B

, T, B

1: i = 0

2: do

3: s

← S

, r

← Samp(s

, B

), R

← G ·r

4: e

← S

, U ← U ∪(r

, e

), i = i + 1

5: while H(B

|| R

i−1

) ≥ T

6: return π = (s

i−1

, R

i−1

)

(0, 1) ← PoUR.Ver(c = (B

, T, B

), π = (s, R)):

1: x ← Samp(s, B

)

2: return G ·x = R & H(B

|| R)) < T

(k, K) ← Dilithium.Kg()

1: (r, e) ← Pick and remove from U

2: t = G ·r + e

3: return (k = (r, e, G,t), K = (G, t))

σ ← Dilithium.Sig(k, M)

1: do

2: (r, e) ← pick from U

3: w ← G ·r, c ← H(High(w) || M)

4: z ← y + c ·r

5: b1 ← ||z||

∞

≥ ϕ

−β

6: b2 ← ||Low(w −c ·e), M)||

∞

≥ ϕ

−β

7: while b1 or b2

8: return σ ← (z, c)

(0, 1) ← Dilithium.Ver(K, M, σ)

1: a ← H(High(G ·z - c ·t) || M)

2: b

← ||z||

∞

< ϕ

−β, b

← H(M || a) = c

3: if b

& b

then

4: return 1

5: else return 0

5.2 Security Analysis of PoUR

We base our security claim on the fact that the disclos-

able commitments we save in PoUR operates identi-

cal as the nonce in the original hash-based PoW. The

difference between the traditional hash-based PoW

and our PoUR is that we replace the nonce in tradi-

tional hash-based PoW algorithm with the disclosable

PAC component in our construction.

The secret component of PACs in PoUR is

selected from a uniformly distributed set of numbers.

Furthermore, the disclosable commitment portion is

created as a AOWF of the secret. Thus, the discloable

PAC component operates identical as the traditional

nonce since the probability of selecting the same

disclosable secret component is neglible by κ. Fur-

thermore, we assume a collusion-free AOWF. The

collusion-freeness property is preserved in Schnorr

(Schnorr, 1991) variants or discrete log based prob-

lems. Even if the AOWF is not collusion-free, PoUR

still preserve its security but can potentially cause a

slight (negligible) performance drawback.

Remark. The security of SchnorrQ (Schnorr, 1991),

Dilithium (Ducas et al., 2018), and, CryptoOp are

presevered when instantiated with PoUR since the

corresponding commitments (which are located in U)

with PoUR are identical to the original corresponding

commitments.

Therefore, since our disclosable commitment

component operates identical as the original nonce in

the traditional consensus, PoUR is as secure as the

traditional Bitcoin PoW.

5.3 Alternative Constructions of PoUR

We now discuss alternative constructions of PoUR.

Key-exchange. PACs created during PoUR can be

used as session keys during key-exchanges.

Signcryption. PACs created during PoUR can be

used in signcryption when the public-keys are known

prior to mining.

Zero-knowledge Proofs. PoUR provides support for

creating PACs for zero-knowledge proof construc-

tions such as (Biasse et al., ) the same way it provides

support with digital signatures.

Cryptographic Beacons. We could store the random

beacon outputs during consensus with PoUR (Bünz

et al., 2017).

Remark. Due to the generation of PACs, a single

iteration in PoUR can take more time than a single it-

eration in a traditional PoW. However, this does not

result in a loss in performance because it is possible

Proof-of-Useful-Randomness: Mitigating the Energy Waste in Blockchain Proof-of-Work

417

to adjust the target value of the puzzle and use PoUR

instead of PoW so that we do not give up on the hard-

ness of the puzzle and also leverage a useful PoW.

6 PERFORMANCE ANALYSIS

We now present our evaluation metrics and experi-

mental setup.

6.1 Evaluation Metrics and

Experimental Setup

Hardware. We fully-implemented the PoUR on com-

modity hardware with an Intel i7-8750H 2.20 GHz

processor on a 32GB of RAM.

Implementation. Our implementation is based on the

Bitcoin infrastructure (Nakamoto, 2009). We replace

the classical hash-based Bitcoin

PoW with PoUR.

This allows for the creation of commitments during

consensus to be used at a later time and thus, prevents

energy and execution-time waste.

www.github.com/efeseyitoglu/PoUR

Open-source Tools. We executed the open-source

code of Dilithium

(Ducas et al., 2018) for generating

post-quantum commitments. For elliptic-curve com-

mitment savings, we measured SchnorrQ (Schnorr,

1991) implementation of the FourQlib library

We chose Dilitium (Ducas et al., 2018) and

SchnorrQ (Schnorr, 1991) due to their popularity and

leveraged the FourQlibrary because it is a fast ellip-

tic curve library. We obtained the energy savings

and power consumption by executing Intel’s power-

top tool

Performance. We calculate the performance efﬁ-

ciency in terms of execution and energy savings we

acquire via PACs. Considering that a traditional com-

mitment pair (e.g. (Schnorr, 1991)) would require

around 32KB of storage, this is a small price to pay

considering our efﬁciency results.

Methodology. Since it would be difﬁcult to create

large number of commitments (e.g. 2

), we mea-

sured the execution time and power requirements for

generating 2

, 2

commitments and extrapolated

with Matlab for larger number of commitments 2

, 2

https://github.com/bitcoin/bitcoin

https://github.com/pq-crystals/dilithium

https://github.com/Microsoft/FourQlib

https://github.com/fenrus75/powertop

6.2 Performance Evaluation

We focused on the savings that PoUR enables on ex-

ecution time and energy consumption. J and W mean

Joule and Watt. Our experiments showed a linear re-

lation between the puzzle solving attempts and the en-

ergy/execution time savings.

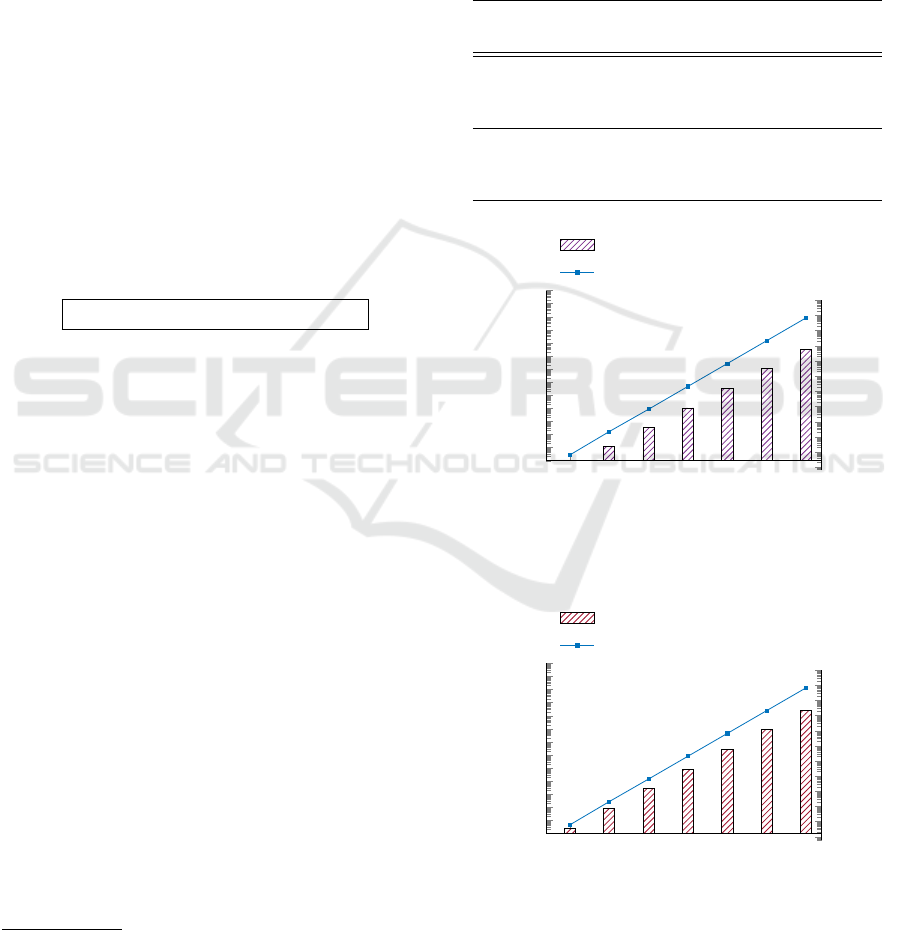
Table 1: Experimental Results for Savings in Elliptic-Curve

and Post-Quantum Settings.

Puzzle

Solving

Attempts

Execution Time

Savings (ms)

Energy

Savings (J)

Power

Consumption

Rate (W = J/Sec)

Elliptic-Curve Commitments

0.306 0.0065

10.6 0.2248 21.2

314.74 6.6724

Post-Quantum Commitments

2.47 0.06

84.60 2.12 25.2

2596.295 65.85

−3

−2

−1

Puzzle Solving Attempts

Execution Time Savings (ms) (log scale)

Energy Savings (J) (log scale)

Execution Time Savings (ms)

Energy Savings (J)

Figure 1: Execution Time (ms) and Energy (J) Savings for

Elliptic-Curve Commitments.

−2

−1

Puzzle Solving Attempts

Execution Time Savings (ms) (log scale)

Energy Savings (J) (log scale)

Execution Time Savings (ms)

Energy Savings (J)

Figure 2: Execution Time (ms) and Energy (J) Savings for

Post-Quantum Commitments.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

418

7 CONCLUSION

We propose PoUR: a PoW algorithm that requires

minial alteration to the existing hash-based consen-

sus. Our experiments showed that PoUR saves around

2 ·10

J in post-quantum and 2 ·10

J in elliptic-curve

settings. We fully-implemented PoUR to demonstrate

its’ energy-saving capabilities. We also algorithmi-

cally showed how the PACs we save with PoUR could

be used in a wide array of cryptographic schemes.

ACKNOWLEDGEMENTS

We thank the anonymous reviewers for their feed-

back. This work is supported by the NSF CAREER

Award CNS-1917627.

REFERENCES

Bahri, L. and Girdzijauskas, S. (2018). When trust saves

energy: a reference framework for proof of trust (pot)

blockchains. In Companion Proceedings of the The

Web Conference 2018, pages 1165–1169.

Ball, M., Rosen, A., Sabin, M., and Vasudevan, P. N.

(2017). Proofs of useful work. Cryptology ePrint

Archive, Report 2017/203. https://eprint.iacr.org/

2017/203.

Ball, M., Rosen, A., Sabin, M., and Vasudevan, P. N.

(2018). Proofs of work from worst-case assump-

tions. In Annual International Cryptology Confer-

ence, pages 789–819. Springer.

Behnia, R., Ozmen, M. O., and Yavuz, A. A. (2019). Aris:

Authentication for real-time iot systems. ICC 2019 -

2019 IEEE International Conference on Communica-

tions (ICC), pages 1–6.

Bentov, I., Lee, C., Mizrahi, A., and Rosenfeld, M. (2014).

Proof of activity: Extending bitcoin’s proof of work

via proof of stake [extended abstract]y. SIGMETRICS

Perform. Eval. Rev., 42(3):34–37.

Bentov, I., Pass, R., and Shi, E. (2016). Snow white: Prov-

ably secure proofs of stake. IACR Cryptology ePrint

Archive, 2016:919.

Biasse, J.-F., Chellappan, S., Kariev, S., Khan, N., Menezes,

L., Seyitoglu, E., Somboonwit, C., and Yavuz, A.

Trace-σ.

Brown-Cohen, J., Narayanan, A., Psomas, A., and Matthew

Weinberg, S. (2019). Formal barriers to longest-chain

proof-of-stake protocols?

Bünz, B., Goldfeder, S., and Bonneau, J. (2017). Proofs-

of-delay and randomness beacons in ethereum. IEEE

Security and Privacy on the blockchain (IEEE S&B).

Catalano, D., Fiore, D., Gennaro, R., and Vamvourellis, K.

(2013). Algebraic (trapdoor) one-way functions and

their applications. In Theory of Cryptography Confer-

ence, pages 680–699. Springer.

Chen, L., Xu, L., Shah, N., Gao, Z., Lu, Y., and Shi, W.

(2017). On security analysis of proof-of-elapsed-time

(poet).

Ducas, L., Kiltz, E., Lepoint, T., Lyubashevsky, V.,

Schwabe, P., Seiler, G., and Stehlé, D. (2018).

Crystals-dilithium: A lattice-based digital signature

scheme. IACR Transactions on Cryptographic Hard-

ware and Embedded Systems, 2018(1):238–268.

Gervais, A., Karame, G. O., Wüst, K., Glykantzis, V., Ritz-

dorf, H., and Capkun, S. (2016). On the security

and performance of proof of work blockchains. In

Proceedings of the 2016 ACM SIGSAC conference on

computer and communications security, pages 3–16.

Hastings, M., Heninger, N., and Wustrow, E. (2019). Short

paper: The proof is in the pudding. In International

Conference on Financial Cryptography and Data Se-

curity, pages 396–404. Springer.

Katz, J. and Lindell, Y. (2014). Introduction to modern

cryptography. CRC press.

Kiayias, A., Russell, A., David, B., and Oliynykov, R.

(2017). Ouroboros: A provably secure proof-of-stake

blockchain protocol. In CRYPTO, pages 357–388.

Springer.

King, S. (2013). Primecoin: Cryptocurrency with prime

number proof-of-work. July 7th, 1(6).

Król, M., Sonnino, A., Al-Bassam, M., Tasiopoulos, A., and

Psaras, I. (2019). Proof-of-prestige: A useful work re-

ward system for unveriﬁable tasks. In 2019 IEEE In-

ternational Conference on Blockchain and Cryptocur-

rency (ICBC), pages 293–301. IEEE.

Li, W., Andreina, S., Bohli, J.-M., and Karame, G.

(2017). Securing proof-of-stake blockchain protocols.

In Data Privacy Management, Cryptocurrencies and

Blockchain Technology, pages 297–315. Springer.

Lihu, A., Du, J., Barjaktarevic, I., Gerzanics, P., and

Harvilla, M. (2020). A proof of useful work for ar-

tiﬁcial intelligence on the blockchain.

Loe, A. F. and Quaglia, E. A. (2018). Conquering generals:

an np-hard proof of useful work. In Proceedings of the

1st Workshop on Cryptocurrencies and Blockchains

for Distributed Systems, pages 54–59.

Meng, W., Wang, J., Wang, X., Liu, J., Yu, Z., Li, J., Zhao,

Y., and Chow, S. S. M. (2018). Position paper on

blockchain technology: Smart contract and applica-

tions. In Au, M. H., Yiu, S. M., Li, J., Luo, X.,

Wang, C., Castiglione, A., and Kluczniak, K., editors,

Network and System Security, pages 474–483, Cham.

Springer International Publishing.

Nakamoto, S. (2009). Bitcoin: A peer-to-peer electronic

cash system.

O’Dwyer, K. J. and Malone, D. (2014). Bitcoin mining and

its energy footprint.

Peikert, C. (2016). A decade of lattice cryptography. Foun-

dations and Trends® in Theoretical Computer Sci-

ence, 10(4):283–424.

Schnorr, C. (1991). Efﬁcient signature generation by smart

cards. Journal of Cryptology, 4(3):161–174.

Seyitoglu, E. U. A., Yavuz, A. A., and Ozmen, M. O.

(2020). Compact and resilient cryptographic tools for

digital forensics. In 2020 IEEE Conference on Com-

munications and Network Security (CNS), pages 1–9.

Tromp, J. (2015). Cuckoo cycle: a memory bound graph-

theoretic proof-of-work. In International Conference

on Financial Cryptography and Data Security, pages

49–62. Springer.

Proof-of-Useful-Randomness: Mitigating the Energy Waste in Blockchain Proof-of-Work

419