A New MILP Model for Matrix Multiplications with Applications
to KLEIN and PRINCE
Murat Burhan
˙
Ilter
1,2 a
and Ali Aydın Selc¸uk
3 b
1
Institute of Applied Mathematics, Middle East Technical University, Ankara, Turkey
2
Aselsan Inc., Ankara, Turkey
3
Dept. of Computer Eng., TOBB Univ. of Economics and Tech., Ankara, Turkey
Keywords:
MILP, Cryptanalysis, Differential Cryptanalysis, Optimization.
Abstract:
Mixed integer linear programming (MILP) models are applied extensively in the field of cryptanalysis. Find-
ing the minimum number of active S-boxes and the best differential characteristic in a differential attack are
two main problems examined using the MILP approach. In this study, KLEIN and PRINCE block ciphers are
modeled with MILP to search for an exact solution to these problems. Both ciphers contain matrix multiplica-
tion operations, which can be calculated using multiple xor operations. The standard MILP model for multiple
xors increases the number of variables significantly, which extends the solution time. In this work, an alterna-
tive xor model is proposed using fewer variables than the standard xor model. The new model is much more
efficient in terms of the number of variables involved and the execution time. Using the new model, we analyze
the differential properties of KLEIN and PRINCE. We obtain the exact minimum number of active S-boxes
of these ciphers with full rounds and also discover the best differential characteristics for various numbers of
rounds. For KLEIN and PRINCE ciphers we achieve the best single differential characteristic of probability
2
−56
. These results improve the best single-key differential attacks on these ciphers in the literature.
1 INTRODUCTION
In recent years, mixed integer linear programming
(MILP) has seen widespread applications in the field
of cryptography. Block ciphers, stream ciphers, and
hash functions have been analyzed using MILP mod-
els. Mouha et al. (Mouha et al., 2011) used the MILP
approach to count the minimum number of active S-
boxes. In that study, equations that describe S-box op-
erations, linear permutation layers, and xor operations
were modeled by MILP. Following Mouha et al.’s
work, much research in cryptanalysis has been done
using MILP. Various cryptanalysis methods such as
differential (Zhu et al., 2019), linear (Fu et al., 2016),
impossible differential (Sasaki and Todo, 2017b), and
conditional cube attacks (Li et al., 2017) have been
also modeled by this approach.
MILP models are extensively used to minimize
or to maximize an objective function under specified
conditions by modeling each step of a cipher as a con-
straint. An objective function is identified depending
a
https://orcid.org/0000-0002-4399-2594
b
https://orcid.org/0000-0002-8963-1647
on the cryptanalysis method. For instance, for a dif-
ferential attack, an objective function minimizes the
number of active S-boxes or maximize the charac-
teristic’s probability. Constraints are constructed by
modeling the S-boxes, the permutation layer, matrix
multiplications, or modular addition operations.
Cipher-specific automated search algorithms were
used before MILP applications emerged, which were
generally hard to implement. Implementation of
MILP methods is known to be easier and more ef-
fective. With efficient models, more rounds can be
analyzed. So, MILP has become an essential tool for
analyzing and attacking ciphers.
In MILP models, it is of crucial importance to de-
crease the number of variables and the solution time.
Sasaki and Todo (Sasaki and Todo, 2017a) proposed
a reduction method to minimize the number of con-
straints used to represent the H-representation of S-
boxes. Yin et al. (Yin et al., 2017) proposed an effi-
cient way to model an equation of two xor operations,
reducing the number of variables significantly com-
pared to the previous MILP models.
In this paper, we extend the work of Yin et al. (Yin
et al., 2017) to equations of multiple xor operations
420
˙
Ilter, M. and Selçuk, A.
A New MILP Model for Matrix Multiplications with Applications to KLEIN and PRINCE.
DOI: 10.5220/0010519504200427
In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 420-427
ISBN: 978-989-758-524-1
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

and use this method to model matrix multiplication
operations over Galois fields of characteristic 2. Us-
ing the new model for multiple xor operations and
matrix multiplications, we examined KLEIN (Gong
et al., 2011) and PRINCE (Borghoff et al., 2012) ci-
phers with regard to two problems: finding the min-
imum number of active S-boxes involved in a differ-
ential attack and computing the best differential char-
acteristic. We obtained the exact minimum number of
active S-boxes required in differential attacks on these
ciphers. We also discovered the best differential char-
acteristics for various numbers of rounds. The results
are given in Table 4.These results improve the best
single-key differential attacks on these two ciphers to
the extent of our knowledge.
The rest of this paper is organized as follows: In
Section 2, related work is reviewed. Description of
the standard and the new MILP xor models are pre-
sented in Section 3. The MILP modeling of the differ-
ence propagation in a block cipher is described in Sec-
tion 4. In Section 5 and Section 6, the MILP models
of KLEIN and PRINCE are presented, respectively.
We conclude the paper in Section 7.
2 RELATED WORK
Mouha et al. (Mouha et al., 2011) suggested a
method to find the minimum number of active S-
boxes for word-oriented ciphers using the MILP ap-
proach. They analyzed the minimum number of ac-
tive S-boxes for linear and differential cryptanalysis
of the AES and Enocoro ciphers.
Sun et al. (Sun et al., 2013) proposed a MILP
model to find the minimum number of active S-
boxes for bit-oriented block ciphers. In that work,
PRESENT-80 was modeled with MILP for single-
key and related-key differential cryptanalysis. Sun
et al. (Sun et al., 2014b) gave the first analysis us-
ing the H-representation and logical condition model-
ing to give an exact representation of an S-box with
a greedy algorithm to model S-boxes. The authors
analyzed the ciphers SIMON, Serpent, LBlock, and
DESL. They obtained significant results of differen-
tial cryptanalysis and related key attacks on these ci-
phers.
Sun et al. (Sun et al., 2014a) recommended a
method to find the best characteristic. In this work,
the probability information of possible differential
patterns was added to the S-box representation. The
authors studied the SIMON48, LBlock, DESL, and
PRESENT-128 ciphers and obtained improved results
on differential cryptanalysis, linear cryptanalysis, and
related key attacks on these ciphers.
Sasaki and Todo (Sasaki and Todo, 2017a) devel-
oped a new reduction method that enabled represent-
ing S-boxes as constraints. Unlike the greedy algo-
rithm, which was proposed by Sun et al. (Sun et al.,
2014b), this new method ensured the minimum num-
ber of inequalities for the representation of an S-box.
Yin et al. (Yin et al., 2017) suggested a new
method to model two xor operations in the MILP ap-
proach. This method is based on Sasaki and Todo’s
reduction algorithm (Sasaki and Todo, 2017a). In this
paper, HIGHT was analyzed against differential and
linear cryptanalysis with a new two xor model.
3 A NEW MODEL FOR n-xor
In this work, we write “n-xor” to denote the xor of
n + 1 binary variables. For instance, y = x
1
⊕ x
2
⊕ x
3
is a 2-xor. There are two different methods that can be
used to model an equation of multiple xor operations,
which we call the standard xor model and the new
n-xor model. In the standard xor model, each 1-xor
is modeled separately to model multiple xors. This
model uses too many variables which increases the
solution time. In order to reduce the solution time, a
new model for n-xor is proposed that uses fewer vari-
ables. We explain these two models below.
3.1 Standard xor Model
In this model, in order to model multiple xors each
1-xor is modeled individually. For y,x
1
,x
2
∈ F
2
, let
y = x
1
⊕ x
2
. 1-xor is modeled as follows:
−x
1
+ x
2
+ y ≥ 0, x
1
− x
2
+ y ≥ 0
x
1
+ x
2
− y ≥ 0, −x
1
− x
2
− y ≥ −2
The model for 2-xor can be constructed with dummy
variable d
0
∈ (0,1) as follows: Let y = x
1
⊕ x
2
⊕ x
3
,
−x
1
+ x
2
+ d
0
≥ 0, −d
0
+ x
3
+ y ≥ 0
x
1
+ x
2
− d
0
≥ 0, d
0
− x
3
+ y ≥ 0
x
1
− x
2
+ d
0
≥ 0 d
0
+ x
3
− y ≥ 0
−x
1
− x
2
− d
0
≥ −2 −d
0
− x
3
− y ≥ −2
where y,x
1
,x
2
,x
3
∈ F
2
.
3.2 New Model for n-xor
The new n-xor model is an extension of the work by
Yin et al. (Yin et al., 2017). In their study, 2-xor was
modeled with a method using the work of Sasaki and
Todo (Sasaki and Todo, 2017a).
The model for 2-xor can be obtained as fol-
lows: Let y = x
1
⊕ x
2
⊕ x
3
where y,x
1
,x
2
,x
3
∈
A New MILP Model for Matrix Multiplications with Applications to KLEIN and PRINCE
421

F
2
. The valid points (y, x1,x2,x3) for this opera-
tion are (0,0,0,0), (0,0,1,1), (0,1,1,0), (1,1, 0,0),
(1,0, 1,0), (0,1,0, 1), (0,1,1,0), and (1,1,1,1). An
H-representation is a representation of a polyhedron
that contains a set of given valid points. The H-
representation of these valid points are calculated and
16 constraints are obtained, some of which are redun-
dant. The aim is to find the minimum number of equa-
tions that represent the 2-xor operation while avoiding
all impossible points (0,0, 0,1), (0,0, 1,0), (0,1, 0,0),
(1,0, 0,0), (1, 1,1,0), (1,1,0,1), (1,0,1,1), and
(0,1, 1,1). This operation is done with Sasaki and
Todo’s reduction method. In the end, it is ensured that
all impossible points are eliminated and the following
8 constraints are obtained for the 2-xor model.
x1 + x2 − x3 + y ≥ 0, x1 + x2 + x3 − y ≥ 0
−x1 + x2 + x3 + y ≥ 0, x1 − x2 + x3 + y ≥ 0
−x1 − x2 + x3 − y ≥ −2, x1 − x2 − x3 − y ≥ −2
−x1 + x2 − x3 − y ≥ −2, −x1 − x2 − x3 + y ≥ −2
These inequalities are added to the MILP model as
constraints for the 2-xor operation. For n-xor case,
H-representation of possible points in F
n+2
2
are calcu-
lated. Then, the minimum number of equations that
can eliminate the impossible points is determined us-
ing Sasaki and Todo’s reduction algorithm. The num-
ber of constraints to eliminate all impossible points
are given in Table 1.
Table 1: Number of variables and constraints used to repre-
sent n-xor.
Standard xor Model New n-xor Model
n-Xor # var. # const. # var. # const.
1 3 4 3 4
2 5 8 4 8
3 7 12 5 16
4 9 16 6 32
5 11 20 7 64
6 13 24 8 128
7 15 28 9 256
As shown in the Table 1, the new n-xor model uses
fewer variables to model xor operation, leading to
shortening solution time.
4 MODELING THE DIFFERENCE
PROPAGATION
In this section, the construction of the MILP model
for two different types of problems is examined. The
first problem is to find the exact minimum number of
differentially active S-boxes, and the second problem
is to find the best differential characteristic. Except
for the modeling of an S-box, all other constraints are
the same in these problems. For the first problem, the
inequalities that represent the S-box are formed from
possible differential patterns. For the second prob-
lem, the probability information is also added to the
S-box’s representation.
We will represent a matrix multiplication over a
Galois field of characteristic 2 by multiple xor opera-
tions and model it using the new xor model. To model
the remaining operations such as the S-boxes and bit
permutations, we will use the well-known models in
the literature.
4.1 S-box
In order to denote the activity of an S-box, we use
the method proposed by Sun et al. (Sun et al., 2014b).
The activity of an S-box is denoted by A
i
, a binary
variable. If S-box is active A
i
= 1, otherwise A
i
= 0.
Let (x
1
,x
2
,x
3
,x
4
) be the input and (y
1
,y
2
,y
3
,y
4
) be
the output of a 4 × 4 S-box. Also, the activity of
the input and output bits are denoted by binary vari-
ables x
i
and y
j
, 0 ≤ i, j ≤ 3, respectively. With these
notations, the following constraints are added to the
model.
x
1
− A
i
≤ 0,x
2
− A
i
≤ 0,x
3
− A
i
≤ 0,x
4
− A
i
≤ 0
x
1
+ x
2
+ x
3
+ x
4
− A
i
≥ 0
4(x
1
+ x
2
+ x
3
+ x
4
) − (y
1
+ y
2
+ y
3
+ y
4
) ≥ 0
4(y
1
+ y
2
+ y
3
+ y
4
) − (x
1
+ x
2
+ x
3
+ x
4
) ≥ 0
In order to find the minimum number of differen-
tially active S-boxes, MILP model constructed by ap-
plying the method in (Sun et al., 2014b). In this
model, the objective function is selected to mini-
mize the number of active S-boxes. First, Differ-
ence Distribution Table (DDT) of an S-box is com-
puted. Possible differential patterns in DDT, i.e,
Pr[(x
1
,x
2
,x
3
,x
4
) → (y
1
,y
2
,y
3
,y
4
)] 6= 0, are used for
computing H-representation. However, redundant in-
equalities will exist in the H-representation, which
should be removed in order to shorten the solution
time. Sun et al. (Sun et al., 2014b) proposed a greedy
algorithm to get rid of the redundant inequalities.
Sasaki and Todo (Sasaki and Todo, 2017a) proposed
an optimal reduction algorithm, which guarantees the
minimum number of inequalities that avoids all re-
dundant inequalities. These inequalities are added
to the MILP model as constraints that represent the
properties of S-box.
In order to find the best differential characteristic,
we change the objective function to maximize the dif-
ferential probability in the MILP model by using the
method proposed by Sun et al. (Sun et al., 2014a).
SECRYPT 2021 - 18th International Conference on Security and Cryptography
422

For each possible differential pattern, the probabil-
ity information is encoded into the objective func-
tion. For instance, if there are three possible distinct
probabilities in DDT, then 2-bit information (p
0
, p
1
)
is enough for encoding. As in the first problem, the
method of Sasaki and Todo is applied to avoid redun-
dant inequalities. H-representation of possible pat-
terns with the corresponding probability information,
i.e., (x
1
,x
2
,x
3
,x
4
,y
1
,y
2
,y
3
,y
4
, p
0
, p
1
), is calculated.
A new MILP model is constructed to find the mini-
mum number of equations, and the solution is used
for representing an S-box with the probability infor-
mation. We give applications of this approach in Sec-
tion 5 and Section 6.
4.2 Permutation
In order to model permutation operation, new binary
variables b
i
are introduced. Let c
i
be the input and
P(c
i
) be the output of a permutation. New variables
are initialized to the result of the permutation so that
the constraints in this step become equalities, i.e., b
i
=
P(c
i
).
4.3 MDS Matrix Multiplication
The exact representation of a (MDS) matrix multipli-
cation is crucial to find exact results in MILP models.
Mouha et al. (Mouha et al., 2011) modeled MDS ma-
trix multiplications only by the branch number of the
MDS matrix. Lower bounds can be obtained by us-
ing only the branch number for MDS multiplication.
However, this kind of modeling is not suitable to find
exact solutions.
In this work, we modeled (MDS) matrix multi-
plication operations over a Galois field of character-
istic 2 by multiple xor operations using the prim-
itive representation decomposition as proposed by
Sun et al. (Sun et al., 2019). In order to apply this
method, entries of a matrix are represented via matri-
ces that are calculated using the reduction polynomial
of GF(2
n
). An application of this matrix representa-
tion method can be seen in Section 5.
5 MILP MODEL FOR KLEIN
In this section, we give our MILP model for KLEIN
cipher. We explain the details of the MILP model’s
construction for finding the minimum number of dif-
ferentially active S-boxes and the best differential
characteristic. As a result of this model, we obtain the
exact minimum number of active S-boxes of KLEIN-
64 as 46. Moreover, we obtain the best differential
characteristics for KLEIN-64 with up to 6 rounds, af-
ter which any single-key differential attack becomes
impossible.
5.1 KLEIN Cipher
KLEIN (Gong et al., 2011) is a lightweight block ci-
pher family which is designed for embedded systems.
The block size is fixed to 64 bits, and the key sizes
are 64, 80, and 96 bits with 12, 16, and 20 rounds,
respectively. Round operations are SubNibbles, Ro-
tateNibbles, and MixNibbles.
5.1.1 SubNibbles
KLEIN cipher uses a single 4 × 4 S-box, given in Ta-
ble 2.
Table 2: S-box of KLEIN.
Input 0 1 2 3 4 5 6 7
Output 7 4 A 9 1 F B 0
Input 8 9 A B C D E F
Output C 3 2 6 8 E D 5
5.1.2 MixNibbles
In the MixNibbles step, finite field multiplication is
carried out on GF(2
8
) = GF(2)/ <x
8
+ x
4
+ x
3
+ x +
1>. The MDS matrix M is defined as follows, where
the entries are in GF(2
8
):
M =



2 3 1 1
1 2 3 1
1 1 2 3
3 1 1 2



.
5.2 Construction of the MILP Model
for KLEIN-64
In this part, we describe the details of the construc-
tion of the MILP model for KLEIN-64. First, the
minimum number of differentially active S-boxes is
analyzed with the standard xor method and the new
n-xor method. Later, results for the best differential
characteristics are given.
SubNibbles. DDT of KLEIN S-box has 106 non-zero
entries. H-representation of these possible differential
patterns is calculated, and 311 equations are obtained.
Applying Sasaki and Todo’s reduction algorithm, it is
shown that 21 constraints are sufficient to represent
the S-box of KLEIN.
MixNibbles. In this step, 64 new binary variables
d
i
j
[k] are defined. The notation d
i
j
[k] is used for the
result of the MDS multiplication. In this notation, the
A New MILP Model for Matrix Multiplications with Applications to KLEIN and PRINCE
423

round number is denoted by i, and j denotes the po-
sition of a nibble, 0 ≤ j ≤ 15. Furthermore, k is the
position of a bit within the nibble, 0 ≤ k ≤ 3.
The entries, 1,2 and 3, of the MDS matrix (M) of
the KLEIN cipher, are given in the primitive represen-
tation as proposed by Sun et al. (Sun et al., 2019). The
representation which is given in the following matri-
ces is calculated with the underlying primitive poly-
nomial x
8
+x
4
+x
3
+x +1 for the field multiplication:
1 =











1 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1











2 =











0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 0 0 1 0 0 0 0
1 0 0 0 1 0 0 0
1 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
1 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0











3 =











1 1 0 0 0 0 0 0
0 1 1 0 0 0 0 0
0 0 1 1 0 0 0 0
1 0 0 1 1 0 0 0
1 0 0 0 1 1 0 0
0 0 0 0 0 1 1 0
1 0 0 0 0 0 1 1
1 0 0 0 0 0 0 1











Matrices corresponding to the primitive representa-
tions of 1, 2, and 3 are substituted in the M matrix,
and a new 32 × 32 binary matrix is obtained, which
can be used to model a matrix multiplication as a set
of xor operations.
For instance, in the first round output the follow-
ing equations are obtained for (d
1
0
||d
1
1
):
d
1
0
[0] =c
1
4
[1] ⊕ c
1
6
[0] ⊕ c
1
6
[1] ⊕ c
1
8
[0] ⊕ c
1
10
[0]
d
1
0
[1] =c
1
4
[2] ⊕ c
1
6
[1] ⊕ c
1
6
[2] ⊕ c
1
8
[1] ⊕ c
1
10
[1]
d
1
0
[2] =c
1
4
[3] ⊕ c
1
6
[2] ⊕ c
1
6
[3] ⊕ c
1
8
[2] ⊕ c
1
10
[2]
d
1
0
[3] =c
1
4
[0] ⊕ c
1
5
[0] ⊕ c
1
6
[0] ⊕ c
1
6
[3] ⊕ c
1
7
[0] ⊕ c
1
8
[3]
⊕ c
1
10
[3]
d
1
1
[0] =c
1
4
[0] ⊕ c
1
5
[1] ⊕ c
1
6
[0] ⊕ c
1
7
[0] ⊕ c
1
7
[1] ⊕ c
1
9
[0]
⊕ c
1
11
[0]
d
1
1
[1] =c
1
5
[2] ⊕ c
1
7
[1] ⊕ c
1
7
[2] ⊕ c
1
9
[1] ⊕ c
1
11
[1]
d
1
1
[2] =c
1
4
[0] ⊕ c
1
5
[3] ⊕ c
1
6
[0] ⊕ c
1
7
[2] ⊕ c
1
7
[3] ⊕ c
1
9
[2]
⊕ c
1
11
[2]
d
1
1
[3] =c
1
4
[0] ⊕ c
1
6
[0] ⊕ c
1
7
[3] ⊕ c
1
9
[3] ⊕ c
1
11
[3]
These equations of multiple xors are written as in-
equalities and added to the MILP model as con-
straints. For instance, for the representations of d
1
0
[0]
and d
1
0
[3], 4-xor and 6-xor models are used, respec-
tively. In general, in order to model this 32 × 32 ma-
trix multiplication, it is enough to use 4-xor and 6-xor
models.
In this study, Gurobi optimizer (Gurobi Optimiza-
tion, 2018) v.9.0.2 is used for solving the MILP prob-
lems. The experiments are done on a 2.3 GHz Quad-
Core Intel Core i5 processor with 8 GB RAM. Sage-
Math (The Sage Developers, 2020) is used for com-
puting the H-representations.
KLEIN-64 is modeled using the standard and the
new xor models. The results are given in Table 4.
In order to find the best differential characteris-
tic, the S-box differential values are represented with
probability information. There exist three non-zero
probabilities 1, 2
−2
, and 2
−3
in DDT. These prob-
abilities are encoded with the corresponding possi-
ble patterns as described by Sun et al. (Sun et al.,
2014a). The H-representation is calculated, and 2489
inequalities are obtained. Adopting the reduction
method of Sasaki and Todo, 21 equations are shown
to be enough for the representation of the S-box. The
best differential characteristics with new model and
standard model are presented in Table 5. The best
single-key differential characteristic for 6 rounds with
a probability of 2
−56
which is given in Table 3.
Table 3: The best 6-round differential characteristic of
KLEIN-64.
Round Diff. Prob.
Input E0E0000000005000 1
1 000000000000D0B0 2
−6
2 00000000E0E04000 2
−12
3 00E0709060303050 2
−20
4 0000001090D00000 2
−44
5 00D0B00000000000 2
−52
6 A05050F020206040 2
−56
SECRYPT 2021 - 18th International Conference on Security and Cryptography
424

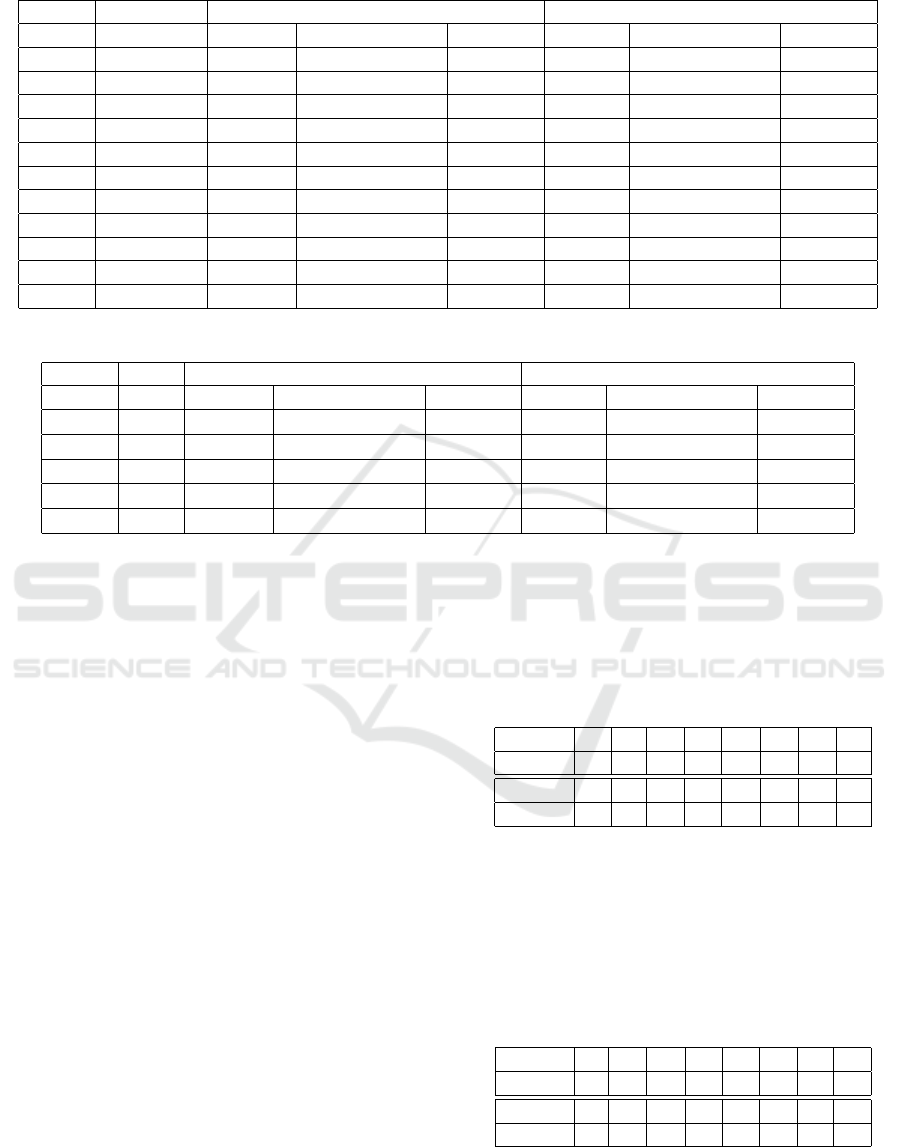
Table 4: Minimum number of differentially active S-box of KLEIN-64 with new n-xor and standard xor model.
Standard xor model New n-xor model
Round Act. S-box # of var. # of Constraints Time (s.) # of var # of Constraints Time (s.)
2 5 464 1748 1 224 4881 2
3 8 848 3412 80 368 9681 132
4 15 1232 5076 447 512 14484 202
5 18 1616 6740 877 656 19284 584
6 20 2000 8407 1989 800 24087 1760
7 24 2384 10071 3648 944 28887 3331
8 30 2768 11736 10285 1088 33688 5526
9 34 3152 13401 6129 1232 38489 7923
10 36 3536 15066 11687 1376 43290 20248
11 39 3920 16731 112950 1520 48091 39246
12 46 4304 18395 61070 1664 52892 110088
Table 5: The best differential characteristics of KLEIN-64 with new n-xor and standard xor model.
Standard xor model New n-xor model
Round Prob. # of var. # of Constraints Time (s.) # of var # of Constraints Time (s.)
2 2
−10
528 2113 2 288 5249 4
3 2
−18
944 3777 1064 464 10049 888
4 2
−32
1360 5444 3321 640 14852 2355
5 2
−48
1776 7108 27721 816 19652 17231
6 2
−56
2192 8772 533062 992 24452 557971
6 MILP MODEL FOR PRINCE
In this section, we give our MILP model for PRINCE
cipher. We explain the details of the construction of
the MILP model for finding the minimum number
of differentially active S-boxes and the best differen-
tial characteristic. As a result of this model, we ob-
tain the exact minimum number of active S-boxes of
PRINCE as 48. Moreover, we obtain the best differ-
ential characteristics for PRINCE with up to 7 rounds,
after which any single-key differential attack becomes
impossible.
6.1 PRINCE Cipher
PRINCE (Borghoff et al., 2012) is a 12-round cipher,
the block size is 64 bits and the key size is 128 bits.
The cipher is designed for low latency and low hard-
ware cost. The round operations are the S-box layer
and the linear layer. In the first 5 rounds, the S-box
layer and the linear layer are applied. In the 6th round,
only the S-box layer is applied. For the 7th round, the
M
0
matrix multiplication and the inverse S-box layer
are applied. In the last 5 rounds, the inverse linear
layer and the inverse S-box layer are executed.
6.1.1 S-box Layer
There is a single, 4 × 4 S-box used in PRINCE. The
S-box is given in Table 6.
Table 6: S-box of PRINCE.
Input 0 1 2 3 4 5 6 7
Output B F 3 2 A C 9 1
Input 8 9 A B C D E F
Output 6 7 8 0 E 5 D 4
6.1.2 Linear Layer
The linear layer consists of a shift row (SR) operation,
and the matrix M multiplication. The shift row oper-
ation changes the position of nibbles. This operation
is given in Table 7.
Table 7: Permutation of PRINCE.
Input 0 1 2 3 4 5 6 7
Output 0 5 A F 4 9 E 3
Input 8 9 A B C D E F
Output 8 D 2 7 C 1 6 B
For the details of linear layer, M = SR ◦ M
0
,
see (Borghoff et al., 2012).
A New MILP Model for Matrix Multiplications with Applications to KLEIN and PRINCE
425

Table 8: Minimum number of differentially active S-box of PRINCE with new n-xor and standard xor model.
Standard xor model New n-xor model
Round Act. S-box # of var. # of Constraints Time (s.) # of var. # of Constraints Time (s.)
2 4 288 1121 1 224 1121 1
3 7 560 2161 19 432 2161 7
4 16 832 3204 20 640 3204 5
5 19 1104 4244 57 848 4244 45
6 20 1376 5284 599 1056 5284 208
7 23 1648 6262 437 1264 6262 404
8 32 1920 7303 1245 1472 7303 1425
9 35 2192 8343 1890 1680 8343 1688
10 36 2464 9384 5602 1888 9384 4981
11 39 2736 10425 19374 2096 10425 12272
12 48 3008 11466 26889 2304 11466 21780
Table 9: The best differential characteristics of PRINCE with new n-xor and standard xor model.
Standard xor model New n-xor model
Round Prob. # of var. # of Constraints Time (s.) # of var # of Constraints Time (s.)
2 2
−8
480 1475 1 416 1475 1
3 2
−14
784 2500 233 656 2500 73
4 2
−32
1088 3524 21008 896 3524 4291
5 2
−40
1392 4548 44738 1136 4548 78283
6 2
−48
1696 5575 83315 1376 5575 64532
7 2
−56
1937 6536 128549 1552 6536 82610
6.2 Construction of MILP Model of
PRINCE
In this section, we describe the details of the con-
struction of the MILP model of PRINCE. First, the
minimum number of differentially active S-boxes are
obtained by the standard and the new n-xor models.
Then, the best differential characteristics are given.
S-box Layer. DDT of the S-box of PRINCE has
106 non-zero entries. H-representation of these pos-
sible patterns is calculated, and 300 inequalities are
obtained. Applying Sasaki and Todo’s reduction
method, 22 inequalities are obtained to represent the
S-box difference patterns of PRINCE.
Linear Layer. In the linear layer, there is a 64 × 64
binary matrix M
0
multiplication. There are three 1s
in each row of matrix M
0
. Hence the equations of the
matrix multiplications have the form:
d
1
0
[0] = c
1
1
[0] ⊕ c
1
2
[0] ⊕ c
1
3
[0].
Therefore, we need 2-xor models to represent the ma-
trix multiplication M
0
. They are written as inequali-
ties and added to the MILP model as constraints.
PRINCE is modeled using the standard and the
new 2-xor models. The results are compared in Ta-
ble 8.
In the design paper of PRINCE (Borghoff et al.,
2012), the authors calculated the minimum number
of differentially active S-boxes to be at least 48. By
our MILP model, we showed that the actual number
is exactly 48.
In order to find the best differential characteris-
tic, the probability information of DDT is added to
the representation of the S-box and the inverse S-box.
There exist three non-zero probabilities, 1, 2
−2
, and
2
−3
in DDT. These probabilities are encoded with
the corresponding possible differential patterns as de-
scribed by Sun et al. (Sun et al., 2014a). The H-
representation is calculated, and 1975 constraints are
obtained. Adopting the reduction method of Sasaki
and Todo, 22 constraints are shown to be enough for
the representation of the S-box and the inverse S-box.
In Table 9, the best differential characteristics are pre-
sented for various numbers of rounds.
Previously, the best single-key differential char-
acteristic on PRINCE in the literature was obtained
for 6 rounds, with a probability of 2
−62
(Ankele and
K
¨
olbl, 2018). Using the MILP model, we discovered
a single-key differential characteristic for 7 rounds
with a probability of 2
−56
which is given in Table 10.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
426

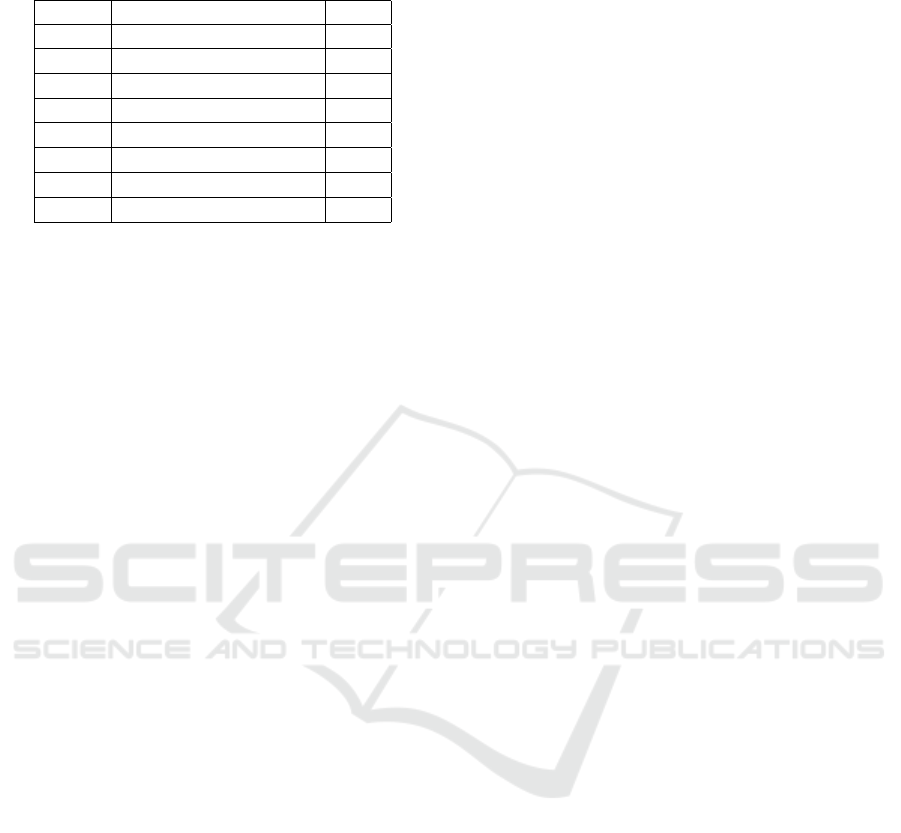
Table 10: The best 7-round differential characteristic of
PRINCE.
Round Diff. Prob.
Input 0041C80000000000 1
1 1100000000000110 2
−8
2 0000001101100000 2
−16
3 0000110010010000 2
−24
4 0110000000000011 2
−32
5 0000008808800000 2
−40
6 0000044000440000 2
−48
7 9A3B3B9A9A2B9A3B 2
−56
7 CONCLUSIONS
An improved, more efficient way to model equations
of multiple xor operations in the MILP approach is
proposed in this work. The new n-xor method is used
to model matrix multiplications over Galois fields of
characteristic 2. Using this method, we develop MILP
models for KLEIN and PRINCE ciphers. These mod-
els enable us to calculate the actual minimum number
of differentially active S-boxes in these ciphers and
to discover the optimal single-key differential char-
acteristics for different numbers of rounds. The best
single differential characteristic of probability 2
−56
is
obtained for KLEIN and PRINCE ciphers.
The developed method is quite general and can be
applied to other ciphers that utilize matrix multiplica-
tions over Galois fields of characteristic 2 in their dif-
fusion layers. By this way, it can be possible to obtain
improved results on differential and linear properties
of these ciphers.
REFERENCES
Ankele, R. and K
¨
olbl, S. (2018). Mind the gap-a closer
look at the security of block ciphers against dif-
ferential cryptanalysis. In International Conference
on Selected Areas in Cryptography, pages 163–190.
Springer.
Borghoff, J., Canteaut, A., G
¨
uneysu, T., Kavun, E. B.,
Knezevic, M., Knudsen, L. R., Leander, G., Nikov,
V., Paar, C., Rechberger, C., et al. (2012). PRINCE–a
low-latency block cipher for pervasive computing ap-
plications. In International conference on the theory
and application of cryptology and information secu-
rity, pages 208–225. Springer.
Fu, K., Wang, M., Guo, Y., Sun, S., and Hu, L. (2016).
Milp-based automatic search algorithms for differen-
tial and linear trails for speck. In International Con-
ference on Fast Software Encryption, pages 268–288.
Springer.
Gong, Z., Nikova, S., and Law, Y. W. (2011). KLEIN: a
new family of lightweight block ciphers. In Interna-
tional Workshop on Radio Frequency Identification:
Security and Privacy Issues, pages 1–18. Springer.
Gurobi Optimization, I. (2018). Gurobi optimizer reference
manual. URL http://www. gurobi. com.
Li, Z., Bi, W., Dong, X., and Wang, X. (2017). Improved
conditional cube attacks on keccak keyed modes with
milp method. In International Conference on the The-
ory and Application of Cryptology and Information
Security, pages 99–127. Springer.
Mouha, N., Wang, Q., Gu, D., and Preneel, B. (2011). Dif-
ferential and linear cryptanalysis using mixed-integer
linear programming. In International Conference on
Information Security and Cryptology, pages 57–76.
Springer.
Sasaki, Y. and Todo, Y. (2017a). New algorithm for mod-
eling S-box in MILP based differential and division
trail search. In International Conference for Infor-
mation Technology and Communications, pages 150–
165. Springer.
Sasaki, Y. and Todo, Y. (2017b). New impossible differ-
ential search tool from design and cryptanalysis as-
pects. In Annual International Conference on the The-
ory and Applications of Cryptographic Techniques,
pages 185–215. Springer.
Sun, L., Wang, W., and Wang, M. Q. (2019). MILP-aided
bit-based division property for primitives with non-
bit-permutation linear layers. IET Information Secu-
rity, 14(1):12–20.
Sun, S., Hu, L., Song, L., Xie, Y., and Wang, P. (2013).
Automatic security evaluation of block ciphers with S-
bP structures against related-key differential attacks.
In International Conference on Information Security
and Cryptology, pages 39–51. Springer.
Sun, S., Hu, L., Wang, M., Wang, P., Qiao, K., Ma, X., Shi,
D., Song, L., and Fu, K. (2014a). Towards finding the
best characteristics of some bit-oriented block ciphers
and automatic enumeration of (related-key) differen-
tial and linear characteristics with predefined proper-
ties. IACR Cryptology ePrint Archive, 747:2014.
Sun, S., Hu, L., Wang, P., Qiao, K., Ma, X., and Song, L.
(2014b). Automatic security evaluation and (related-
key) differential characteristic search: application to
SIMON, PRESENT, LBlock, DES (L) and other bit-
oriented block ciphers. In International Conference
on the Theory and Application of Cryptology and In-
formation Security, pages 158–178. Springer.
The Sage Developers (2020). SageMath, the Sage
Mathematics Software System (Version 9.2).
https://www.sagemath.org.
Yin, J., Ma, C., Lyu, L., Song, J., Zeng, G., Ma, C., and Wei,
F. (2017). Improved cryptanalysis of an ISO stan-
dard lightweight block cipher with refined MILP mod-
elling. In International Conference on Information Se-
curity and Cryptology, pages 404–426. Springer.
Zhu, B., Dong, X., and Yu, H. (2019). MILP-based differ-
ential attack on round-reduced GIFT. In Cryptogra-
phers’ Track at the RSA Conference, pages 372–390.
Springer.
A New MILP Model for Matrix Multiplications with Applications to KLEIN and PRINCE
427