A Comparison of Interpolation Techniques in Producing a DEM

from the 5 m National Geospatial Institute (NGI) Contours

Prevlan Chetty and Solomon Tesfamichael

Department of Geography, Environmental Management and Energy Studies,

University of Johannesburg, Johannesburg, South Africa

Keywords: GIS, Remote Sensing, Interpolation, LiDAR, Kriging, Inverse Distance Weighting, Spline, Nearest

Neighbour, Topo to Raster, ANUDEM, Chief Directorate National Geospatial Information, NGI.

Abstract: Continuous elevation surfaces, which are commonly referred to as Digital Elevation Models (DEM), are vital

sources of information in flood modelling. Due to the multitude of interpolation techniques available to create

DEMs, there is a need to identify the best suited interpolation techniques to represent a localised hydrological

environment. This study investigated the accuracies of commonly applied interpolation techniques including

Inverse Distance Weighting (IDW), Nearest Neighbour (NN), Kriging, Spline and Topo to Raster

interpolation techniques as applied to a 5-m interval elevation contours as a precursor to simulate a flood zone

in the Roodepoort region in Johannesburg, South Africa. A 50 cm resolution DEM derived from aerial Light

Detection and Ranging (LiDAR) point cloud was used as a reference to compare the five interpolations

techniques. The Topo to Raster results were not significantly different from the reference data (P = 0.79 at

95% confidence level), where elevation values were on average underestimated by 0.93 m. In contrast, the

spline interpolation showed the highest significant difference from the reference data (P = 0.00 at 95%

confidence level), with an average underestimation of the elevation by 69.84 m. Outlier identification using

standardized residual analysis flagged significant elevation outliers that were produced in the interpolation

process, and it was noted that most of the outliers across all techniques coincide with areas that showed

frequent topographical changes. Specifically, the largest significant differences using the Topo to Raster

technique were overestimations of the elevation that occur in the upstream section of the tributary. The Spline

technique in contrast showed significant underestimations of the elevation throughout the river system.

Overall, the results indicate that the Topo to Raster technique is preferred to accurately represent the

topography around a river system of the study area.

1 INTRODUCTION

Flooding is a globally occurring phenomenon that

causes property loss and casualties all around the

world (Teng et al., 2017). A flood is characterised by

an overflow of water that submerges land that would

usually be dry which is often referred to as the flood

inundation area (Merz and Blöschl, 2008). The extent

to which a given river will flood to is commonly

referred to as a flood-line (the maximum extent of the

flood inundation area) and is related to the effect that

a specific volume of water has on a hydrological

system through rainfall events (Nkwunonwo et al.,

2020). The statistical likelihood of a rainfall volume

is commonly translated to 10-Year, 50-Year and a

100-Year, and a flood event (Smithers, 2012). As part

of South Africa’s Council for Scientific and Industrial

Research’s (CSIR) Guidelines for Human Settlement,

Planning and Design (CSIR, 1999), no urban

development should be allowed in the demarcated 50-

year flood-line extent. The requirement itself

originates from the National Building Regulation and

Building Standards Act of South Africa (Act 103 of

1997) and is solely based on safety considerations.

The establishment of the flood-line extents therefore

play a crucial role in any development along a river.

In deterministic computer aided techniques of

demarcating a flood-line, one of the most important

aspects is the input elevation data that defines the

geometry of the river and its surrounding basin

(Saksena & Merwade, 2015). Flood-line mapping

often produces results that vary with different sources

of elevation data. The outputs are affected by the

vertical accuracy which is determined by the

Chetty, P. and Tesfamichael, S.

A Comparison of Interpolation Techniques in Producing a DEM from the 5 m National Geospatial Institute (NGI) Contours.

DOI: 10.5220/0010525100370047

In Proceedings of the 7th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2021), pages 37-47

ISBN: 978-989-758-503-6

topography of the region and the spatial resolution of

the elevation data (Li et al., 2010). In addition, the

importance of interpolation algorithm accuracy is

recognised as an integral component in representing

the topography in numerical form (Chaplot et al.,

2006). If interpolation forms an integral component

of defining topography, and the topography forms an

important part of the flood-line process, it can be

inferred that the interpolation procedure of elevation

data plays an important role in the development of

flood-line extents.

For elevation data to be accurately incorporated

into the flood-line modelling process, there needs to

be spatial continuity in the elevation dataset by

creating a raster surface referred to as a Digital

Elevation Model (DEM). DEMs are derived through

the process of interpolation, which refers to the

prediction of a series of unknown values located

between a limited number of sample points (Manuel,

2004). Interpolation techniques, of which numerous

techniques are available, are commonly used for

geographic data that are represented as points or lines

having elevation information. These techniques are

commonly grouped into local/global,

deterministic/geostatistical and exact/approximate

classes (Erdogan, 2009). Local methods of

interpolation include the Inverse Distance Weighting

(IDW) and the Nearest Neighbour (NN) technique.

Geostatistical methods of interpolation include the

kriging method, which uses the spatial location of

data points rather than relying on the elevation

attribute values alone (Arun, 2013). The spline

(sometimes referred to as rubber sheet) method is

mathematical in nature and takes the form of a cubic

equation whereby each known data point has a cubic

equation where all splines pass through (Robinson &

Metternicht, 2003).

Different interpolation techniques applied to the

same set of elevation data can result in varying DEM

outputs (Arun, 2013). There is therefore a need to

evaluate the suitability and accuracy of these

interpolation techniques for a specific data and

purpose. Erdogan (2009) investigated the relative

accuracy of various interpolation algorithms for an

area with high topographical variance in Turkey. The

research evaluated various deterministic interpolation

algorithms against a baseline survey grade dataset.

The best results were obtained using the thin plate

spline algorithm, a derivative of the spline algorithm

itself. Zimmerman et al. (1999) compared the outputs

of the IDW versus the kriging methodology and

showed that the kriging method was able to adjust

itself to the spatial variability of the data and by doing

so, yielded better estimation of altitude for unknown

sample points. In contrast, Aguilar et al. (2005)

presented research from their study area in Almeria,

Spain, that indicated that the IDW method was

marginally better than the accuracy from the kriging

model output.

In 1984, Mark was the first to propose an

algorithm for automatically delineating a drainage

network from DEM data for specific applications in

hydrological modelling (Mark, 1984). This study

gave rise to the need for hydrological correction

algorithms in the DEM interpolation process which

includes the development of the Australian National

University Digital DEM (ANUDEM), known as the

Topo to Raster feature in ArcGIS, to generate

elevation models that are hydrologically conducive to

network extraction (Callow et al., 2007). The

ANUDEM method creates an interpolated surface

that preserves the critical geometry components

required to define a hydrological system which

includes ridgelines and stream networks (Arun,

2013). Pavlova (2017) presented research conducted

in the Omsk region in Russia which evaluated the

outputs from IDW, Kriging, Topo To Raster, Spline,

Nearest Neighbour (NN) and the Triangulated

Irregular Network (TIN) techniques. The findings

indicated that on relatively flat areas, the best results

were obtained using the Spline and IDW techniques.

In a contrasting environment, Salekin et al. (2018)

conducted research into utilising Global Navigation

Satellite Systems (GNSS) as a data source to generate

a DEM in a landscape with a large degree of

topographical variation in Marlborough, New

Zealand. The GNSS data were used in various

interpolation techniques including NN, Topo to

Raster and IDW techniques. The quantitative research

showed that the Topo to Raster technique showed the

most accurate DEM results, while the IDW showed

the least accurate results.

Chaplot et al. (2006) investigated the suitability of

various interpolation techniques across a

mountainous region in Laos and undulating

landscapes in France. The recommendations

following the results of the study indicated that the

accuracy of the various interpolation techniques

needs to be tested in terms of their applicability to

multiple resolution data (Chaplot et al., 2006). Many

studies have been focused on modelling and

identifying the spatial distribution of errors associated

with DEM’s in order to remove DEM errors (Aguilar

et al., 2010; Hu et al., 2009; Stal et al., 2012).

The above studies show that the accuracy of

interpolated elevation is affected by the topography

of the area of interest and the interpolation techniques

used to create the continuous surface. assessment,

GISTAM 2021 - 7th International Conference on Geographical Information Systems Theory, Applications and Management

with different interpolation techniques being more

and less effective in varying landscapes. In South

Africa, the Chief Directorate for National Geospatial

Institute (NGI) produces a 5 m resolution elevation

dataset that can be used by the public for different

purposes. There is a significant gap in assessing the

accuracy of the various interpolation outputs based on

the NGI dataset against survey-grade elevation data

sources. The limitations associated with the

application of the 5 m resolution NGI dataset needs

to be understood in terms of the identification of

spatial distribution errors and the circumstances that

lead to these errors. This study therefore aims to

compare various interpolation techniques to derive a

DEM data for the eventual development of flood-

lines using the 5 m NGI elevation contours in the

Roodepoort region in Johannesburg, South Africa.

The specific objectives of the study are to (1) compare

various interpolation techniques conducted on the

NGI elevation data source which includes the IDW,

NN, Kriging, Spline and Topo to Raster techniques

and (2) identify limitations associated with the

interpolation accuracy of the NGI dataset. The

performances of the interpolators will be evaluated

using a high-resolution Light Detection and Ranging

(LiDAR) derived DEM. It is expected that the

comparisons of the various interpolators will

contribute to hydrological modelling in South Africa

by listing recommendations and limitations of the

application of specific interpolation techniques to the

5 m NGI data source for DEM outputs.

2 METHODS

2.1 Study Area

The study area focuses on a 5-kilometre length of a

river that is a tributary of the Wilgespruit River,

between Willowbrook and Strubens Valley in

Roodepoort, Johannesburg (Figure 1). The channel

width ranges from between 5 and 20 m over the length

of the study area and flows seasonally between

October and March (Climate-data.org, 2019). The

study area is composed of an urban residential

composition, which is amongst the highest affected

land-use classes affected by the effects of flooding

(Davis-Reddy et al., 2017).

The Roodepoort region receives approximately

610 mm of rain per year, with the majority occurring

during the summer months from November to

February (Climate-data.org, 2019). The region is

classified as warm and temperate according to the

Köppen and Geiger climate classification (Conradie,

2012). The warmest months by average temperature

are between November and February.

Figure 1: Research Area - Tributary of the Wilgespruit

River, displayed in true colour Red-Greed-Blue (RGB)

band combination.

2.2 Data

2.2.1 5 m Chief Directorate National

Geospatial Contours

The 5 m-resolution contour dataset from the DRDLR

is generated by the Intergraph Dual Mass Camera

(DMC) which captures stereo imagery at a GSD of

0.5 m (NGI, 2018). The NGI also contracts service

providers with similar cameras to acquire data owing

to the scale of the operation. Currently, the NGI aims

to capture 40% of the country every 3 years and the

remaining areas every 5 years. The dataset included

in this research is the 5 m contour dataset (referred to

as the NGI dataset), which was last updated 8

December 2009, for the study area.

The 5 m resolution contour dataset has the largest

spatial coverage compared with more recent high-

resolution survey campaigns that have been

commissioned by the City of Johannesburg (COJ)

Municipality. While higher resolution (that is, to

smaller GSD) datasets are available for metropolitan

areas in South Africa, sites that fall outside of the

metropolitan area demarcations are at best covered by

the 5 m contour offering. As such, the 5 m NGI

dataset is a popular choice among specialists who

seek to apply topographical elements to their

respective studies.

2.2.2 Light Detection and Ranging Point

Cloud

The LiDAR data for the study area was obtained from

the COJ Municipality Corporate Geo-informatics

Department. LiDAR is a popular method of surveying

A Comparison of Interpolation Techniques in Producing a DEM from the 5 m National Geospatial Institute (NGI) Contours

that uses an active remote sensing system composed

of at least three sensors, the Inertial Measurement

Unit (IMU), the Global Positioning System (GPS)

and the laser scanner (Csanyi & Toth, 2007). A target

is illuminated by a light source through a laser beam

and the time taken for the reflected beam to return to

the sensor allows for the calculation of survey-grade

measurements relating to the linear position of the

target from the sensor (Vosselman, 2003).

Advancements in optical and computing technologies

have seen the emergence of LiDAR as a rapid and

accurate terrain mapping tool (Lohani & Ghosh,

2017). The COJ municipality region distributes an

aerial-based LiDAR data that is acquired by a

contracted service provider every three years. The

data sourced for this study was acquired in June 2012.

The native format for the LiDAR data includes

American Standard Code for Information Interchange

(ASCII)-based text files that contain information

relating to each point’s location and elevation, which

collectively form a point cloud. The LiDAR point

clouds used in the present study had a point density

of 0.2 points per square meter with an approximate

average spacing between neighbouring points of 2 m.

Therefore, LiDAR is acknowledged for its survey-

grade level of accuracy (Vosselman, 2003; Lohani &

Ghosh, 2017). The horizontal accuracy of the LiDAR

data had a 0.048 m root mean square error (RMSE),

and a vertical accuracy of 0.32 m RMSE as verified

using a network of seven ground control points. The

points were classified into ground and non-ground

points by the data supplier, with the ground points

representing the physical ground level, while the non-

ground points represented all features above ground

including vegetation and structures. The ground

points were used in the present study to serve as the

baseline dataset to evaluate the relative accuracy of

the different interpolation techniques applied to the 5

m elevation contour dataset.

2.3 Analysis

To produce continuous digital representations of a

surface, interpolation techniques were derived to

calculate unknown values that lie between known

values. In this study, five interpolation techniques

conducted on the 5 m resolution NGI dataset were

compared, namely IDW, NN, kriging, spline, and

Topo to Raster algorithms.

IDW is a non-linear, deterministic interpolation

technique that computes a weighted average of a

value from sample points in close vicinity to

determine the value of non-sampled points (Robinson

& Metternicht, 2003). The IDW principle was first

presented by Shepard (1968) for improved efficiency

of the central processing unit time. Today, the IDW

process is one of the most widely applied methods of

interpolation in the hydrological environment. The

IDW principle assumes that values which are close

together are more alike than values that are further

away. To calculate the value of an unknown point at

a location, the weighted average of the surrounding

known values is calculated and assigned to the

unknown point. Known values that are closer to the

location of the unknown point are given a higher

weighting ranking in the calculation, and therefore

have a larger influence on the determination of the

unknown value, opposed to known values that are

further away. Definitions of the neighbouring radius

for the calculation and the power function

representing the inverse distance relationship

between the points are critical parametres for this

interpolation method. The formula for the IDW

interpolation is defined as 𝑍





∑









.





∑











, where 𝑍



= value of variable Z in point I; 𝑍



= the sample in

point I; 𝑑



= distance to the sampled point from the

unknown point; N = coefficient that defines the

weight that will be based on the inverted distance

function; n = total number of predictions allowed for

each validation (Shepard, 1968).

The NN Interpolation model is based on the

Sibson interpolation model, where values are

assigned to un-sampled points based on the

construction of Thiessen polygons which work

together to form areas of overlap (Sibson, 1980). The

polygons are formed across all known values

surrounding the unknown value by connecting all

common values into a network of Thiessen polygons

which represent all known values. A new Thiessen

polygon is then generated over the unknown value,

and the proportion of the overlap between this new

polygon versus the network of intersecting polygons

previously generated define the weighting system to

be used. The formula used for the NN interpolation is

identical to IDW, with the only difference coming

from the method used to calculate the weightings. The

NN interpolation formula is defined as 𝑍



𝑢

∑

λu  z







, where λ



u

    

   

and u = (x,y) location of

query point (Rukundo & Cao, 2012).

Kriging is a stochastic local interpolation

technique that computes the value of non-sampled

points in a similar way to IDW, with the exception

that there is more control on the weighting system that

determines unknown values based on distance

(Robinson & Metternicht, 2003). The kriging model

GISTAM 2021 - 7th International Conference on Geographical Information Systems Theory, Applications and Management

was developed by Danie Krige, who formed the basis

of what would later be called the kriging process in

1951 through research presented in the Journal of the

Chemical, Metallurgical and Mining Society of South

Africa in the 1960s (Cellmer, 2014). Krige (1951)

applied the kriging technique to survey two gold

mines to understand resource estimation based on

borehole data. An ordinary kriging equation is

defined as 𝑍𝑠



 

∑

λ zs









, where, λ = weights

assigned to each known value, where all weights sum

to a unity which enables unbiased estimations which

are defined as

∑







 1. The matrix equation

calculating the weights is defined as C = 𝐴



𝑏

,where 𝐴 = matrix of semi-variance between the

known values; 𝑏 = estimated semi-variances between

the known values and unknown value, represented by

a vector (Krige, 1951; Krige, 1952).

The spline interpolation is a piecewise polynomial

interpolation method that creates a smooth raster

surface from the known sample points using a 2-D

minimum curve technique (Robinson & Metternicht,

2003). The resulting surface passes through all known

sample points. The spline method is mathematical in

nature and takes the form of a cubic equation whereby

each known data point has a cubic equation through

which all splines pass (Robinson & Metternicht,

2003). Jenkins (1927) and Schoenberg (1946) can be

credited with the origins of the spline method of

interpolation. The spline cubic equation is defined as

𝑆



𝑥,𝑦



𝑇



𝑥,𝑦





∑

𝜆



𝑅𝑟









, where 𝑗 =

1,2,… 𝑁, 𝑁 is the number of points, 𝜆



are the

coefficients found by the linear equation solution and

𝑟



is the distance from the point (x,y) to the 𝑗



point

(Meijering, 2002).

ANUDEM is based on a program developed to

interpolate elevation values across a topographical

surface by Hutchinson (1988). The algorithm

generates elevation models that are hydrologically

conducive to network extraction (Callow et al.,

2007). In the 1980s, a study done by Mark (1984)

proposed an algorithm for automatically delineating a

drainage network from DEM data. This study gave

rise to the need for hydrological correction algorithms

in the DEM interpolation process which includes the

development of the ANUDEM. This interpolation

technique provides a compromise between local

interpolation methods such as IDW and global

interpolation methods such as kriging, by allowing

the resultant DEM values to follow abrupt changes in

terrain which include streams, ridges and cliffs, thus

preserving topographical continuity (Pavlova, 2017).

The Topo to Raster interpolation is the only algorithm

featured in ArcGIS that is preferentially applied to

contour datasets. The Topo to Raster interpolation is

defined by the equation 𝐽





𝑓







𝑓





 𝑓





𝑑𝑥𝑑𝑦,

where 𝐽



is known as a local interpolation technique

that is well-suited for features with a better resolution.

Then 𝐽





𝑓







𝑓





 𝑓





𝑓





𝑑𝑥𝑑𝑦, where 𝐽



known to create unrealistically flat surfaces as

commonly seen by global interpolation techniques.

Hutchinson's ANUDEM program revolves around a

compromise between 𝐽



𝑎𝑛𝑑𝐽



as follows: 𝐽



𝑓





0.5  ℎ



𝐽





𝑓



 𝐽



𝑓, where ℎ is the spatial

resolution of the output surface model (Hutchinson,

1988).

2.4 Accuracy Assessment

A buffer measuring 100 m was created around the

river’s centreline. Points were then generated at 100

m intervals along the extent of the buffer, from which

LiDAR elevations were extracted within a 5 m

average distance from each point, resulting in a total

of 103 LiDAR spot elevations. Figure 2 shows the

positions of the spot elevation points, plotted against

a 2018 WorldView-2 derived satellite image that is

rendered in red, green and blue (RGB). These

elevation values, along with their X and Y positions,

represent the most accurate remotely sensed dataset

available for this study and were therefore used as

reference data to compare the different surfaces

created using the five interpolators applied to the 5 m

contour data. While a field-collected differential real-

time kinematic GPS system will provide the highest

level of accuracy, the intention of the research

presented is to utilise practical and readily available

datasets, such as the COJ distributed LiDAR.

Elevation values of the five interpolated surfaces

were extracted at each of the above-mentioned

LiDAR spot elevation locations. The T-test and

residual analysis was used to compare the

interpolated surfaces against the baseline LiDAR

elevation values.

2.4.1 Comparing the Output Elevations of

the Interpolated DEMs against the

Reference LiDAR Elevations

The T-test is a statistical procedure that is commonly

used when investigating the relationship between

variables by comparing the means on the dependent

variables against the baseline or independent variable

(Green & Salkind, 2012). The T-test was chosen due

to the flood extent comparisons involved at each

measurement station, where more than one dependent

set of results is be compared to the baseline LiDAR

flood-line extents. The P-value from the T-test output

A Comparison of Interpolation Techniques in Producing a DEM from the 5 m National Geospatial Institute (NGI) Contours

is used to assess the degree of difference between the

means of the interpolation elevation versus the

baseline LiDAR elevation. The applied T-test

formula is a generalisation of a two-sample T-test

(Ostertagova & Ostertag, 2013) and is defined as 𝐹

    

  

where 𝑀𝑆𝐺 

∑















 



/







and 𝑅𝑀𝑆

∑∑









∑































where 𝑌



is the observation distances from the stream

centreline for each output, 𝑇



is the sum of each group

of distances from the stream centreline, G is the total

of all observations being compared for the variance

(model output being assessed versus baseline LiDAR

output), 𝑛



is the number of observations in group i

and n is the total number of observations being

analysed for the variance. The T-test and associated

P-values were calculated using Microsoft Excel

(Microsoft Corporation, 2019).

Figure 2: Location of observations for analysis, displayed

in true colour RGB band combination.

2.4.2 Identification of Outliers from the

Interpolated DEMs against the LiDAR

Reference Data

Analysis of residuals forms part of a regression

analysis which is designed to assess model adequacy

(Martin et al., 2017). Regressions are typically

applied to assess the accuracy of a predicted model

against actual values (Martin et al., 2017). Because

the research purpose is accuracy assessment, as

opposed to model fitting, regression analysis was not

chosen as an accuracy assessment tool in this

research. However, components of the regression

analysis remain useful tools in location-based

analytics, such as the residual analysis which allows

for reference to a specific observation and its

associated spatial location. Residuals are defined as

the vertical distance 𝑟



) between the observed

measurement and the predicted measurement (𝑟



𝑦



 𝑦., represented by a linear regression line. In

this research, the observed distance (𝑦



) represents the

linear regression from the baseline LiDAR elevation

while the predicted measurement (𝑦) represents the

vertical elevation difference between the

interpolation surface being assessed (Topo to Raster,

kriging, NN, IDW, spline).

Outlier identifications in data have been applied

successfully through the usage of standardised

residuals (Sousa et al., 2012; Miller, 1993, Salekin et

al., 2018) and are defined by the formula 𝑟









where the standardised residual (𝑟



) is the residual

value (𝑟



) divided by its standard deviation (𝑠. At a

95% confidence level, it is expected that 95% of the

data falls within 2 standard deviations of the mean

(Sousa et al., 2012). Data points falling lower than -2

and higher than 2 on the standardised residual plot

will therefore represent outliers. The incorporation of

a standardised residual analysis allows for the

identification of interpolated elevation output

observations that are significantly different to the

baseline LiDAR elevation values, which in turn

allows for a spatial expression of the results observed.

The methodology starts with the running of the

various interpolation procedures. As the focus of the

assessment is on the influence of interpolation

techniques on hydrological modelling environments,

a streamflow analysis was run on the baseline LiDAR

dataset, from which a 100 m buffer was generated.

LiDAR points were then selected using proximity

analyses at every 100 m interval along the extent of

the buffer. Interpolated elevation values were then

extracted from each interpolation process at each

LiDAR elevation point every 100 m along the buffer

zone. All GIS-based processing procedures were

conducted using ArcGIS (ESRI, 2019). The

interpolated elevation observations were then

compared against the LiDAR elevations using a T-

test and residual analysis in Microsoft Excel

(Microsoft Corporation, 2019).

A buffer measuring 100 m was created around the

river’s centreline. Points were then generated at 100

m intervals along the extent of the buffer, from which

LiDAR elevations were extracted within a 5 m

average distance from each point, resulting in a total

of 103 LiDAR spot elevations. These elevation

values, along with their X and Y positions, represent

the most accurate remotely sensed dataset available

for this study and were therefore used as reference

data to compare the different surfaces created using

the five interpolators applied to the 5 m contour data.

While a field-collected differential real-time

kinematic GPS system will provide the highest level

GISTAM 2021 - 7th International Conference on Geographical Information Systems Theory, Applications and Management

of accuracy, the intention of the research presented is

to utilise practical and readily available datasets, such

as the COJ distributed LiDAR. Elevation values of

the five interpolated surfaces were extracted at each

of the above-mentioned LiDAR spot elevation

locations. The T-test and residual analysis was used

to compare the interpolated surfaces against the

baseline LiDAR elevation values.

3 RESULTS

3.1 Differences between Interpolated

Elevations and LiDAR Elevations

The T-test presented in this section yields information

on the degree of variance between the elevation

values obtained from each interpolation against the

baseline LiDAR elevation values. The T-test was run

at an alpha = 5%. The outputs from the T-test for the

various interpolation algorithms are presented in

Table 1 which has been sorted from most accurate to

least accurate.

The Topo To Raster interpolation had the highest

correlation with the baseline LiDAR elevation with a

P value of 0.75. The lowest P value obtained indicates

a relatively strong correlation to the LiDAR baseline

elevations when compared against the other

interpolation techniques. The mean value from the

Topo to Raster techniques elevation values are close

to the mean value of the LiDAR elevations (1553.99),

with the Topo To Raster interpolation generally

underestimating the elevation by 1.10 m.

The T-test results indicate NN to have the second

highest correlation to the baseline LiDAR elevation

with P value of 0.78. The P value indicates a relatively

good correlation to the LiDAR baseline elevations

when compared against the other interpolation

techniques. The mean value from the NN techniques

elevation values are close to the mean value of the

LiDAR elevations (1553.99), with the NN

interpolation generally underestimating the elevation

by 0.96 m. The Kriging T-test results show this

technique to marginally be the third most accurate

interpolator with results similar to the NN technique

with a P value of 0.79. The IDW T-test results are

within close range of the Kriging and NN

interpolators, showing a relatively good correlation to

the baseline LiDAR elevations with P value of 0.79.

Both Kriging and IDW mean outputs indicate a

general underestimation of the elevation by 0.95 m

and 0.93 m respectively in relation to the LiDAR

mean value.

The spline T-test results show the highest variance

to the baseline LiDAR by far with a P value of 0.00.

The negligible P value and highest mean deviation

from the LiDAR elevation with a general

overestimation of -69.84 m indicate that the spline

interpolation technique is unsuitable for deriving a

suitable DEM from the NGI 5 m dataset.

Table 1: T-test results across all interpolation techniques

results. Each interpolation was compared against the

LiDAR mean elevation of 1553.9 m.

Interpolation

Technique

Mean Elevation

(Meters above

mean sea level)

Mean

Difference

between

LiDAR and

Interpolator

(

meter

)

*P Value

Topo To Raster

(

ANUDEM

)

1553.06

0.93

0.754

NN 1553.04

0.95

0.787

Kri

1553.04

0.95

0.787

1552.89

1.10

0.791

line 1623.83

-69.84

0.000

*P value was measured using 95% confidence level

3.2 Identification of Outliers from the

Interpolated DEMs Relative to the

LiDAR Data

The plotted residual results are presented for each

interpolation technique in Figure 3. The results

graphically illustrate the outliers of significance that

can be related to a spatial location, which forms a

platform for the subsequent discussion around the

results seen. Residuals of Topo to Raster, NN, IDW

and kriging share a similar distribution throughout the

plot. The spline residual plot results resemble the

same general distribution as the other interpolators

but appear to have larger variances along the residual

plot.

The Topo to Raster, NN, kriging and IDW

residual points all show a dependent positive

correlation to the LiDAR elevations with a wave-

form trend about the Y-axis. Elevations of 1500–1540

m and 1560–1600 m show a general underestimation

of elevation values by the Topo to Raster

interpolation. For elevation values of 1540–1560 m,

the Topo to Raster interpolation overestimates the

elevations. Highly significant outliers occur at higher

elevation values at around 1600 m. The IDW and

kriging interpolation outputs have similar

A Comparison of Interpolation Techniques in Producing a DEM from the 5 m National Geospatial Institute (NGI) Contours

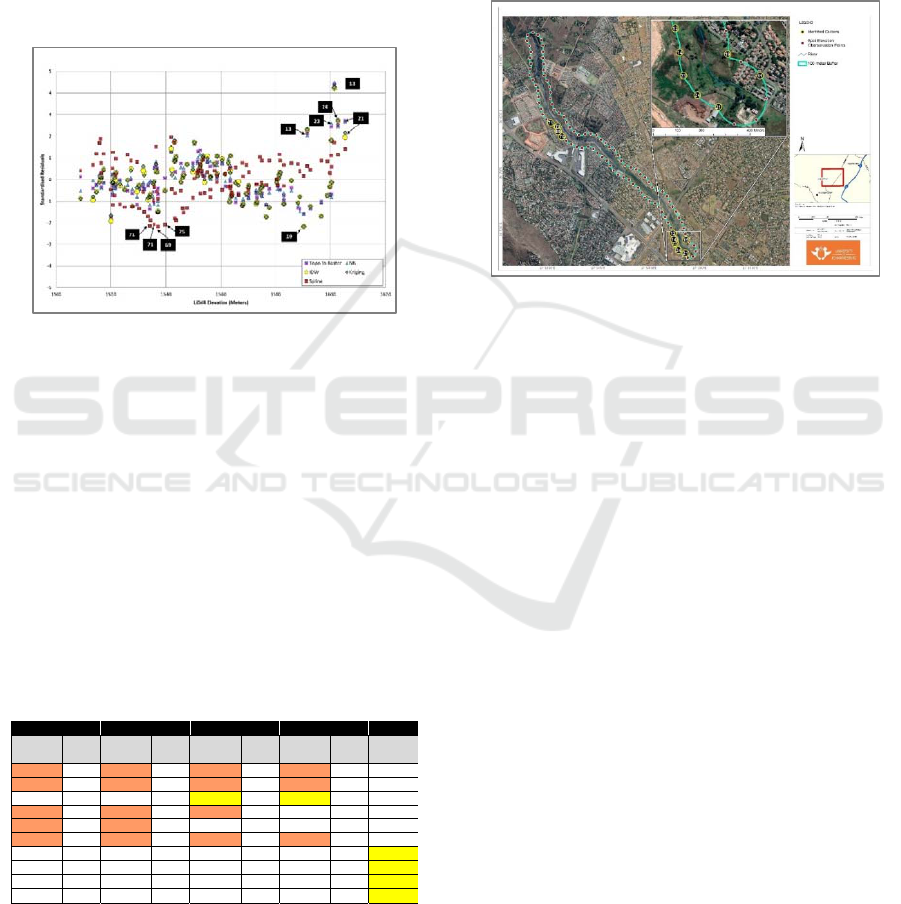
standardised residual plots, while the Topo to Raster

and NN interpolation outputs share similarities in

their standardised residual plots. The spline

interpolation residual points also show a general

dependent positive correlation to the LiDAR

elevations, but in comparison to the other

interpolators, the spline results have a larger residual

variance. Larger underestimations in elevation values

are seen at 1530–1550 m, with the same general

observation of higher overestimations of elevations at

1600 m.

Figure 3: Combined standardised residuals across all

interpolation techniques with significant outliers identified

with labels.

Table 2 shows the name and location of the

elevation values that were identified through the

residual plot shown in Figure 3. Observations 13, 14,

21, 23 and 24 show overestimations of the elevation

across all interpolation techniques except for the

spline technique. Observation 19 shows

underestimations of elevation in the kriging and IDW

technique while observations 69, 70, 71 and 75 show

underestimations of the elevation only in the spline

technique.

Table 2: Significant outliers Identified from standardised

residual plot analysis.

Figure 4 shows the identified locations of the

significant residual outliers in the upper section of the

tributary (Locations 11, 13, 14, 19, 21, 23 and 24).

The downstream section of the tributary shows a

higher correlation between the LiDAR elevation and

interpolated algorithms that are within a 95%

confidence level of vertical elevation difference. A

large concentration of outliers can be seen in the

upstream section of the tributary, where 5 of the 6

observation outliers identified are overestimations of

elevation. The remainder of residual outliers

identified (69, 70, 71 and 75) are all identified from

the spline interpolation with significant elevation

deviations (all 13 m under the LiDAR elevation).

Figure 4: Identified standardised residual outlier locations,

displayed in true colour RGB band combination.

4 DISCUSSION

The results obtained in the interpolation output

compared against the reference LiDAR data indicate

that the Topo to Raster interpolation technique yields

marginally more accurate DEM surfaces than the

other interpolators, based on the T-test. The Topo to

Raster results agree with existing bodies of research

(Arun, 2013; Salekin et al., 2018) indicating that the

Topo to Raster technique preserves critical

components of the hydrological environment and by

doing so, is the most accurate under these conditions.

The spline interpolation technique was the most

inaccurate and is unsuitable for the application on the

5 m NGI dataset to create a DEM. These results from

the spline methodology are inconsistent with findings

from Erdogan (2009) and Pavlova (2017) who found

that the spline methodology yielded marginally more

accurate results in comparison to other interpolations

assessed. It must, however, be noted that Erdogan

(2009) utilised a thin-plate spline algorithm which is

a derivative of the original spline technique; this was

not used in the research presented here, and Pavlova’s

(2017) findings are representative of an area with low

topographical variations. All other interpolation

techniques assessed in the results presented as part of

this research show good applicability with marginal

differences in variation to the baseline LiDAR.

TopoToRaster NN Kriging IDW Spli

Standardised

Residual

Distance

toLiDAR

Elevation

Standardised

Residual

Distance

toLiDAR

Elevation

Standardised

Residual

Distance

toLiDAR

Elevation

Standardised

Residual

Distance

toLiDAR

Elevation

Standardised

Residual

2.14 5.20 2.02 4.91 2.30 5.74 2.29 5.75 0.62

4.39 10.63 4.46 10.83 4.24 10.60 4.22 10.60 1.71

‐1.61 ‐3.90 ‐1.61 ‐3.90 ‐2.16 ‐5.41 ‐2.17 ‐5.44 0.17

2.73 6.62 2.67 6.49 2.15 5.37 1.95 4.89 1.42

2.45 5.93 2.62 6.35 1.82 4.56 1.81 4.55 1.10

2.52 6.12 2.44 5.91 2.74 6.86 2.73 6.85 1.14

‐0.69 ‐1.67 ‐1.18 ‐2.86 ‐1.51 ‐3.77 ‐1.49 ‐3.74 ‐2.17

‐1.06 ‐2.57 ‐1.13 ‐2.74 ‐0.13 ‐0.32 ‐0.12 ‐0.29 ‐2.07

‐1.38 ‐3.34 ‐1.17 ‐2.84 ‐0.80 ‐2.00 ‐0.78 ‐1.97 ‐2.14

0.07 0.17 ‐0.51 ‐1.24 ‐0.54 ‐1.34 ‐0.52 ‐1.31 ‐2.09

GISTAM 2021 - 7th International Conference on Geographical Information Systems Theory, Applications and Management

Spatial representations of the outliers as identified

from the residual analysis reveal a large concentration

of points to the upper part of the tributary which fall

on a garden refuse site (Figure 4). Due to the

differences in the temporal acquisition of the data, the

garden refuse site would have undergone

topographical changes to its the baseline LiDAR

(acquired in June 2012) compared to NGI (acquired

in December 2009). Figure 5 illustrates the

progression of the area, identified as the Weltevreden

Park PickitUp garden refusal site, between 2006 and

2019 which shows the visible changes in topography

over 13 years. Changes in the surface topography

across this site over time have a direct influence on

the elevation values observed during the LiDAR and

NGI data acquisitions. These elevation value

differences are prominent in the residual analysis,

which shows a large concentration of residuals with a

variance larger than 5 m in and around the refuse site.

The residual interpretation further indicates the spline

interpolation’s output is unsuitable for accurate DEM

interpolation from the 5 m NGI data source.

Figure 5: PickitUp garden refuse site surface changes:

2006-2019, displayed in true colour RGB band

combination.

The differences in elevation values between the

NGI versus the LiDAR data reveals large differences

in elevation values in the refuse site region, located in

the upper section of the tributary (Figure 2.7). The

NGI surface along this section is almost constantly

below the LiDAR surface which shows clear

definitions of a dump feature (Figure 2.8). This is

indicative of changes in the surface between the

acquisition of the 5 m NGI dataset (December 2009)

and the LiDAR dataset (June 2012) which is

statistically shown with the underestimation of the

elevation values with the 5 m NGI dataset. The profile

comparisons show a high degree of variance with

regards to topographic changes that have occurred

over the dumpsite, highlighting differences in

temporal resolution as shown in Figure 6.

Figure 6: Profile comparisons for LiDAR (Left) versus NGI

(Right) along A-B.

5 CONCLUSION

The findings of this study indicate that the Topo to

Raster interpolation technique is the most favourable

for the 5 m contour data of the localised study area.

The results also indicate that while the application of

the Topo to Raster technique yielded the most

accurate results, the NN, kriging and IDW techniques

were close to the Topo to Raster technique. These

results imply that the application of the NN, kriging

and IDW interpolation techniques to the 5 m NGI

dataset will yield DEMs with similar vertical

accuracy.

While the results indicate that the Topo to Raster

technique is the most accurate, it must be

acknowledged that certain interpolation techniques

are likely to yield the most favourable results in the

environments for which they were originally

developed. The Topo to Raster interpolation

algorithm was specifically formulated for its

application in hydrological environments

(Hutchinson, 1988), while the geostatistical method

evaluated in this research (kriging) and local methods

(NN and IDW) are limited by the resolution and

spread of data (Al Mashagbah et al., 2012). Research

into the interpolation technique to be applied and its

favourability to different spatial distributions of data

should always be taken into account when

interpolating elevation datasets (Cellmer, 2014). Due

to advancements in technology and information, it is

also likely that the defining geometry (point, line or

polygon) of the elevation data sources may change

from line-based contour elevations to point-cloud

elevation formats, which will also play a significant

role in determining the ideal interpolation technique

to apply.

The results presented in this research are specific

to the application on the freely and nationally

A Comparison of Interpolation Techniques in Producing a DEM from the 5 m National Geospatial Institute (NGI) Contours

distributed South African NGI contour dataset. The

residual analysis indicated substantial differences in

elevation between areas for the reference LiDAR and

NGI datasets, which is attributed to differences in

temporal resolution. As access to spatial information

in South Africa increases in association with

advancements in survey techniques, future

assessments should be performed on the most

temporally relevant data available. The findings

indicate that while the usage of lower spatial

resolution datasets such as the 5 m data used in the

present study may be acceptable in terms of RMSE,

the need for access to more temporally relevant

datasets is crucial to accurately represent

topographical information for an area.

REFERENCES

Aguilar, F.J., F. Agu¨era, M.A. Aguilar. & F. Carvajal.

(2005). Effects of terrain morphology, sampling

density, and interpolation methods on grid DEM

accuracy. Photogrammetric Engineering and Remote

Sensing, 71: 805–816.

al Mashagbah, A., R. Al-Adamat. & E. Salameh. (2012).

The use of Kriging Techniques within GIS

Environment to Investigate Groundwater Quality in the

Amman-Zarqa Basin/Jordan. Research Journal of

Environmental and Earth Sciences, 4: 177-185.

Arun, P. V. (2013). A comparative analysis of different

DEM interpolation methods. The Egyptian Journal of

Remote Sensing and Space Sciences, 16(2): 133-139.

Academy of Science of South Africa (ASSAf), (2020).

Quest: Science for South Africa, 16(2).

Callow, J, N., G.S Boggs. & K. P van Niel. (2007). How

does modifying a DEM to reflect known hydrology

affect subsequent terrain analysis? Journal of

hydrology, 332(1-2): 30-39.

Cellmer, R. (2014). The possibilities and limitations of

geostatistical methods in real estate market analyses.

Real Estate and Valuation, 22(3): 54-62.

Chaplot, V., F. Darboux, H. Bourennane, S. Leguedois, N.

Silvera. & K. Phachomphon. (2006). Accuracy of

Interpolation Techniques for the Derivation of Digital

Elevation Models in Relation to Landform Types and

Data Density. Geomorphology, 77: 126-141.

Climate-data.org. (2019). Roodepoort Climate. Available

from https://en.climate-data.org/africa/south-

africa/gauteng/roodepoort-232/.

Conradie, D. C. U. (2012). South Africa’s Climatic Zones:

Today, Tomorrow. International Green Building

Conference and Exhibition, Future Trends and Issues

Impacting on the Built Environment, Sandton, July 25-

26.

Council for Scientific and Industrial Research (CSIR).

(1999). Ecologically Sound Urban Development.

Available from

https://www.csir.co.za/sites/default/files/Documents/

Chapter_05_08_02_-Vol _I.pdf.

Csanyi, N. & C.K. Toth. (2007). Point positioning accuracy

of airborne lidar systems: A rigorous analysis.

International Archives of Photogrammetry, Remote

Sensing and Spatial Information Systems, 36(1):107-

111.

Davis-Reddy, C.L. & K.Vincent. (2017). Climate risk and

vulnerability: A handbook for Southern Africa (2nd

Edition), CSIR, Pretoria, South Africa.

Department of Water and Sanitation (DWS). 2017. The

quaternary drainage regions. Available from

http://www.dwa.gov.za/iwqs/wms/data/000key2data.a

sp.

Erdogan, S. (2009). A comparison of interpolation methods

for producing digital elevation models at the field scale.

Earth Surface Processes and Landforms, 34: 366-376.

ESRI 2019. ArcGIS Desktop: Release 10.7. Redlands, CA:

Environmental Systems Research Institute.

Green, S.B. & N.J. Salkind. (2010). Using SPSS for

Windows and Macintosh: Analysing and understanding

data (5th Edition). Upper Saddle River, New Jersey:

Pearson Education Incorporated.

Hutchinson, M.F. (1988). Calculation of hydrologically

sound digital elevation models, Third International

Symposium on Spatial Data Handling at Sydney,

Australia, vol. 3, no. 1, pp.120–127.

Jenkins, W.A. (1927). Graduation based on a modification

of osculatory interpolation. Trans. Actuar. Soc. Amer,

28:198-215.

Johnson, M. R., C.R. Anhaeusser. & R.J. Thomas. (2006).

The Geology of South Africa. Council for Geoscience.

Krige, D.G. (1951). A statistical approach to some basic

mine valuation problem on the Witwatersrand. Journal

of the Chemical, Metallurgical and Mining Society of

South Africa. 12: 119–139.

Krige, D.G. (1952). A statistical analysis of some of the

borehole values in the Orange Free State goldfield.

Journal of the Chemical, Metallurgical and Mining

Society of South Africa, 9: 47–64.

Lohani, B. & S. Ghosh. (2017). Airborne LiDAR

technology: A review of data collection and processing

systems. Proceedings of the National Academy of

Sciences, India Section A: Physical Sciences,

87(1):567-579.

Manuel, P. (2004). Influence of DEM interpolation

methods in drainage analysis. GIS in Water Resources,

8: 32-28.

Mark, D.M. (1984). Automatic detection of drainage

networks from digital elevation models. Cartographica,

21(2-3): 168-178.

Martin, J., A. David. & A. Garcia Asuero. (2017). Fitting

Models to Data: Residual Analysis, a Primer. Intech.

Available from: http://dx.doi.org/10.5772/68049.

Matheron, G. (1963). Principles of geostatistics. Economic

Geology, 58: 1246-1266.

Meijering, E. (2002). A chronology of interpolation: From

ancient astronomy to modern signal and image

processing. Proceedings of the IEEE, 90(3): 319-342.

GISTAM 2021 - 7th International Conference on Geographical Information Systems Theory, Applications and Management

Merz, R. & G. Blöschl. (2008). Flood frequency hydrology:

Temporal, spatial, and causal expansion of information.

Water Resources Research, 3:13-20.

Microsoft Corporation, 2019. Microsoft Excel (Windows

10 version), Available at: https://office.microsoft. com/

excel.

Miller, J.N. (1993). Outliers in experimental data and their

treatment. Analyst, 118(5):455-461.

Nkwunonwo, U.C., M. Whitworth. & B. Baily. (2020). A

review of the current flood modelling for urban flood

risk management in the developing countries. Scientific

African. 7: e00269.

Ostertagova, E. & O. Ostertag. (2013). Methodology and

application of one-way ANOVA. American Journal of

Mechanical Engineering, 1(7):256-261.

Pavlova, A.I. (2017). Analysis of elevation interpolation

methods for creating digital elevation models.

Optoelectron. Instrument. Proc, 53(2): 171–177.

Robinson, T. B. & G. Metternicht. (2003). A comparison of

inverse distance weighting and ordinary kriging for

characterizing within-paddock spatial variability of soil

properties in Western Australia. Cartography, 32(1):

11-24.

Rukundo, O. & H. Cao. (2012). Nearest Neighbor Value

Interpolation. International Journal of Advanced

Computer Science and Applications, 3: 25-30.

Saksena, S. & V. Merwade. (2015). Incorporating the effect

of DEM resolution and accuracy for improved flood

inundation mapping. Journal of Hydrology, 530(1):80-

194.

Salekin, S., J.H. Burgess., J. Morgenroth., E.G. Mason.,

D.F. Meason. (2018). A comparative study of three

non-geostatistical methods for optimising digital

elevation model interpolation. ISPRS International

Journal of Geoinformatics, 7: 300-308.

Shepard, D. (1968). A two-dimensional interpolation for

irregularly-spaced data. 23rd ACM National

Conference, Brandon Systems Press, Princeton, New

Jersey, pp. 517–524.

Sibson, R. (1980). Interpolating Multivariate Data: A Brief

Description of Natural Neighbour Interpolation. New

York: Wiley.

Smithers, J. C. (2012). Methods for design flood estimation

in South Africa, Water SA, 38(4): 633–646.

Sousa, J.A., A.M. Reynolds. & A.S. Ribeiro. (2012). A

comparison in the evaluation of measurement

uncertainty in analytical chemistry testing between the

use of quality control data and a regression analysis.

Accredited Quality Assurance, 17(1):207-214.

South Africa. Department of Rural Development and Land

Reform, Chief Directorate: National Geo-spatial

Information (NGI). (2018). Chief Directorate for

Surveys and Mapping. Available from:

http://www.cdsm.gov.za.

South Africa. Department of Rural Development and Land

Reform, Chief Directorate: National Geo-spatial

Information (NGI). (2014). National Landcover

Classification – Geo Terra Image. Available from

http://www.geoterraimage.com/uploads/GTI%202013-

14%20SA%20LANDCOVER%20REPORT%20-

%20CONTENTS%20vs%2005%20DEA%

20OPEN%20ACCESS%20vs2b.pdf.

Stal, C., A. De Wulf., P. De Maeyer., R. Goosens., T.

Nuttens., F. Tack. (2012). Statistical comparison of

urban 3D models from photo modelling and airborne

laser scanning. International Multidisciplinary

Scientific GeoConference-SGEM, 12: 901-908.

Teng, J., A.J. Jakeman, J. Vaze, S. Kim, B. Croke. & D.

Dutta. (2017). Flood inundation modelling: A review of

methods, recent advances and uncertainty analysis.

Environmental Modelling and Software, 90: 201-216.

Vosselman, G. (2003). 3D reconstruction of roads and trees

for city modelling. The International Archives of the

Photogrammetry, Remote Sensing and Spatial

Information Sciences, 34(1): 211-216.

Zimmerman, D., C. Pavlik, A. Ruggles. & M. Armstrong.

(1999). An experimental comparison of ordinary and

universal kriging and inverse distance weighting.

Mathematical Geology, 31: 475-390.

A Comparison of Interpolation Techniques in Producing a DEM from the 5 m National Geospatial Institute (NGI) Contours