Scalable k-anonymous Microaggregation: Exploiting the Tradeoff

between Computational Complexity and Information Loss

Florian Thaeter

and R

udiger Reischuk

Institut f

ur Theoretische Informatik, Universit

at zu L

ubeck, Ratzeburger Allee 160, L

ubeck, Germany

Keywords:

Microaggregation, k-anonymity, Data Clustering.

Abstract:

k-anonymous microaggregation is a standard technique to improve privacy of individuals whose personal data

is used in microdata databases. Unlike semantic privacy requirements like differential privacy, k-anonymity

allows the unrestricted publication of data, suitable for all kinds of analysis since every individual is hidden in

a cluster of size at least k. Microaggregation can preserve a high level of utility, that means small information

loss caused by the aggregation procedure, compared to other anonymization techniques like generalization

or suppression. Minimizing the information loss in k-anonymous microaggregation is an NP-hard clustering

problem for k ≥3. Even more, no efﬁcient approximation algorithms with a nontrivial approximation ratio are

known. Therefore, a bunch of heuristics have been developed to restrain high utility – all with quadratic time

complexity in the size of the database at least.

We improve this situation in several respects providing a tradeoff between computational effort and utility.

First, a quadratic time algorithm ONA

∗

is presented that achieves signiﬁcantly better utility for standard bench-

marks. Next, an almost linear time algorithm is developed that gives worse, but still acceptable utility. This

is achieved by a suitable adaption of the Mondrian clustering algorithm. Finally, combining both techniques a

new class MONA of parameterized algorithms is designed that deliver competitive utility for user-speciﬁed time

constraints between almost linear and quadratic.

1 INTRODUCTION

k-anonymous microaggregation is a technique de-

signed to improve privacy of individual-related data,

still keeping the data useful for research. It has been

introduced by Anwar, Defays and Nanopoulus (An-

war, 1993; Defays and Nanopoulos, 1993) in 1993.

Higher dimensional numerical data is clustered into

groups of size at least k. We will call the result

a k-member clustering in contrast to a k-clustering

where the number of clusters is bounded by k. As

ﬁnal output each data point is represented by the cen-

troid of its cluster and thus the modiﬁed database is

k-anonymous (Samarati, 2001; Sweeney, 2002).

While k-anonymity is quite a simple condition,

other more complex properties have been considered

to guarantee privacy like `-diversity (Machanava-

jjhala et al., 2007), t-closeness (Li et al., 2007) or ε-

differential privacy (Dwork et al., 2006). `-diversity

and t-closeness may sound theoretically more appeal-

ing, but it is unclear whether and how efﬁciently

https://orcid.org/0000-0002-6870-5643

https://orcid.org/0000-0003-2031-3664

these properties can be achieved in practice. In ad-

dition, they require a strict separation of attributes

into so-called quasi-identiﬁers (QI) and conﬁdential

attributes (CA) which decreases the ﬂexibility when

using the anonymized data. On the other hand, differ-

ential privacy is restricted to a setting where instead

of anonymizing the database and making it publicly

known, only a predeﬁned type of questions can be

sent to the owner of the database. The answers pro-

tect private information by adding a suitable amount

of noise depending on the diversity of the data and

the type of questions. The usability is therefore lim-

ited and highly diverse data may yield quite useless

answers because of larger deviations. For a more de-

tailed discussion why these measures cannot replace

k-anonymity entirely see (Li et al., 2012).

Minimizing the information loss in k-anonymous

microaggregation is an NP-hard optimization prob-

lem for k ≥ 3 (Oganian and Domingo-Ferrer, 2001;

Thaeter and Reischuk, 2020). Even more, no ef-

ﬁcient approximation algorithms with a nontrivial

approximation ratio are known. Several heuris-

tics with quadratic time complexity in the number

Thaeter, F. and Reischuk, R.

Scalable k-anonymous Microaggregation: Exploiting the Tradeoff between Computational Complexity and Information Loss.

DOI: 10.5220/0010536600870098

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 87-98

ISBN: 978-989-758-524-1

of individuals have been developed to achieve k-

anonymity (see e.g. (Domingo-Ferrer and Torra,

2005; Thaeter and Reischuk, 2018; Soria-Comas

et al., 2019)). Quadratic time may be acceptable for

small databases, but large ones with millions of indi-

viduals cannot be handled in reasonable time.

Our work tries to mitigate this problem. In 2006

LeFevre et al. introduced MONDRIAN, a clustering al-

gorithm that achieves k-anonymity in O(n logn) time

(LeFevre et al., 2006). The optimization goal of the

MONDRIAN algorithm are clusters with sizes as close

to k as possible. This algorithm has not been devel-

oped for microaggregation, still it creates clusterings

with cluster size at least k. Hence, this strategy can

be used to perform k-anonymous microaggregation

by calculating and reporting centroids for each clus-

ter created. However, the question arises whether the

resulting information loss is comparable to state-of-

the-art heuristics designed to minimize information

loss. Our investigations have shown that this is not

the case. Therefore we modify and improve this strat-

egy to design two new algorithms MONDRIAN V and

MONDRIAN V2D that have the same time complexity as

the original one, but achieve reasonable utility. The

information loss occurring is larger than that of the

best quadratic time algorithms, but still on the same

order. These results will be presented in section 4.

Most competitive k-anonymous microaggregation

algorithms are based on the MDAV (maximum dis-

tance to average vector) principle initially formulated

by Domingo-Ferrer et al. in (Domingo-Ferrer and

Torra, 2005). The idea is to start with an element ¯x

of greatest distance to the centroid c(X) of the whole

database X and to form clusters by grouping ¯x with

its k −1 nearest neighbours. If less than k elements

are left, the remaining elements are assigned to their

closest cluster. Since the distance of many pairs of el-

ements has to be computed this results in quadratic

time complexity. While no approximation guaran-

tees have been shown for this strategy and further im-

provements, these algorithms seem to perform well

on benchmark databases.

In (Thaeter and Reischuk, 2018) we have pro-

posed an extension called MDAV

∗

. Instead of creating

a new group in every step, one is given the additional

option to add the current most distant element ¯x to the

closest cluster already created. The decision is made

by comparing the impact on cluster cost in the local

area. Without increasing the time complexity signif-

icantly the results in (Thaeter and Reischuk, 2018)

show that MDAV

∗

outperforms MDAV and other MDAV

variants. Another approach named PCL has been pre-

sented in (Rebollo-Monedero et al., 2013) using clus-

tering techniques for the case that an upper bound is

given on the number of clusters – the k-means prob-

lem – instead of a lower bound on the size. However,

no analysis of its computational complexity seems to

have been made.

In 2019 Soria-Comas et al. presented an algorithm

named ONA (Near-Optimal microaggregation Algo-

rithm) (Soria-Comas et al., 2019). It is based on the

Lloyd algorithm for efﬁciently clustering high dimen-

sional data that starts with a random clustering and

then iteratively improves the clustering by reassign-

ing data points to closer clusters until a stopping con-

dition holds (Lloyd, 1982). As the Lloyd algorithm

is not tailored to guarantee a lower bound on cluster

sizes it has to be modiﬁed. ONA starts with a randomly

created k-member clustering and repeats the follow-

ing steps for several rounds. Iterate over all elements

x and consider their cluster C

. If C

has more than

k elements try to lower the information loss by reas-

signing x to another cluster. If |C

| = k try to improve

the clustering by dissolving C

and redistribute its el-

ements to other clusters nearby. Finally, split all clus-

ters that have grown to size at least 2k by applying

ONA recursively. This rearrangement of elements is

stopped when within a round no change has occurred

or a preset number of rounds has been reached.

Regarding information loss ONA seems to be com-

parable to previous quadratic time heuristics on real

and synthetic benchmark databases. However, it was

not possible for us to reproduce the excellent results

claimed in (Soria-Comas et al., 2019). We have inves-

tigated how the strategy of rearranging clusters can be

improved. It turned out that iterating over data points

in an arbitrary order, which seems to be a good strat-

egy for k-clustering, is not as good for k-member clus-

tering. Instead iterating over clusters in a well chosen

order is computationally more efﬁcient and according

to the benchmarks applied gives better utility. This

new strategy called ONA

∗

will be presented in sec-

tion 3. Finally, by combining both methods – almost

linear time complexity with a larger information loss

and quadratic time with better utility – we design two

new classes of algorithms called MONA

and MONA 2D

that are scalable by the parameter ρ between almost

linear and quadratic time. They deliver competitive

utility shown by benchmark tests in section 5.

Summarizing the results of this paper, the perfor-

mance of state-of-the-art quasi-linear, resp. quadratic

time heuristics for k-anonymity are signiﬁcantly im-

proved. Furthermore, we have exploited the tradeoff

between computational effort and data quality provid-

ing a whole range of algorithms that suit different de-

mands in practice.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

2 PRELIMINARIES

Deﬁnition 1 (Database). A data point, element or in-

dividual is a d-dimensional vector x

= (x

,...,x

) ∈

of numerical attributes. A database X = x

,...,x

is a sequence of data points, potentially including du-

plicates. X is k-anonymous if each data point occur-

ring in X has a multiplicity of at least k.

The common property of all microaggregation al-

gorithms is the use of a k-member clustering to gener-

ate a partition of the data. Once clusters are deﬁned,

elements of the database are replaced by the centroid

of their cluster. As a result one obtains a k-anonymous

database which protects privacy of its individuals by

the principle hiding in a group of k.

Deﬁnition 2 (k-member clustering). A k-member

clustering of a database X is a partition C of its mem-

bers into clusters C

,...,C

such that each cluster

contains at least k elements.

Let δ(x,x

) denote the Euclidean distance between

two elements and c(C

) =

∑

x∈C

x the centroid

of a cluster C

The diversity of a cluster C

is deﬁned as

Cost(C

) :=

∑

x∈C

δ(x,c(C

))

and the total cost of a clustering C by

Cost(C ) :=

∑

∈C

Cost(C

Cost(C ) measures the closeness of elements within

clusters. Once the clusters are established, creating a

k-anonymous database is straight-forward by select-

ing the centroid as the anonymous version of each

data point. Thus the data disturbance of such a proce-

dure is related to Cost(C ) and should be as small as

possible. Let us note

Fact 1: Given a clustering C , for each cluster C

the

centroid c(C

) and Cost(C

) can be computed in

O(|C

| d) arithmetic operations.

Hence, Cost(C ) can be estimated in time O(n d) given

C . Note that the input size is N = n ·d real numbers,

thus this computation takes only linear time.

Deﬁnition 3 (k-anonymous microaggregation).

Given a database X the k-anonymous microaggre-

gation problem is to ﬁnd a k-member clustering C

with minimum cost.

It has been shown that this is an NP-hard optimiza-

tion problem for k ≥3 (Oganian and Domingo-Ferrer,

2001; Thaeter and Reischuk, 2020). Even approxima-

tion algorithms with a nontrivial approximation ratio

are not known. Hence, several heuristics have been

developed.

To compare the data disturbance between several

databases of different sizes and dimensionality, the

notion information loss has been introduced. By di-

viding cost by the worst possible clustering (cluster

all elements in one big cluster), one obtains a utility

measure ranging from 0 for perfect utility and 1 for

worst possible utility. Typically, information loss is

stated as percentages, see e.g. (Soria-Comas et al.,

2019).

Deﬁnition 4 (Information loss). The diversity ∆(X )

of a database X is the sum of squared distances of all

elements to the global centroid:

∆(X) :=

∑

i=1

δ(x

,c(X))

The information loss of a clustering C of X is deﬁned

L(C,X) :=

Cost(C )

∆(X)

Thus, for a given database X minimizing Cost(C )

minimizes the information loss, too.

2.1 Benchmarks and Test Setting

To compare different heuristics several benchmark

databases have been used, in particular Census, Tar-

ragona and EIA from the CASC project (Domingo-

Ferrer and Mateo-Sanz, 2002) as well as Cloud1,

Cloud2, the Adult data set and the credit card clients

data set from the UCI Machine Learning Repository

(Lichman, 2013). Census, Tarragona, EIA, Cloud1

and Cloud2 are relatively small databases used to

compare algorithms with quadratic time complexity.

The Adult and Credit Card databases are much bigger

and can only be handled by subquadratic algorithms

in reasonable time. More details are given in the ap-

pendix.

For a meaningful test the attributes of the

databases should be standardized to mean value 0 and

variance 1 prior to anonymization. This ensures that

all dimensions have equal impact on the anonymiza-

tion process and information loss evaluation. As mi-

croaggregation is dimension and order conserving,

this standardization can be reversed after anonymiza-

tion. All information losses given in this paper are ex-

pressed in percentages to be directly comparable with

previously published results. The computations have

been performed based on Java implementations on a

PC equipped with an Intel Core i7 6850K with 4GHz

core frequency and 32 GB of RAM.

Scalable k-anonymous Microaggregation: Exploiting the Tradeoff between Computational Complexity and Information Loss

3 MICROAGGREGATION IN

QUADRATIC TIME WITH

LOWER INFORMATION LOSS

A popular class of k-anonymous microaggregation al-

gorithms is based on the MDAV principle explained

in the introduction. The ﬁrst algorithm MDAV has been

presented in (Domingo-Ferrer and Torra, 2005). The

currently best version of this methodology is MDAV

∗

(Thaeter and Reischuk, 2018). Algorithm 1 gives a

speciﬁcation.

Algorithm 1: MDAV

∗

(Thaeter and Reischuk, 2018).

input : database X and min cluster size k

output: k-member clustering C

1 Let U ← X ; Let C ←

2 repeat

3 Let ¯x ∈U be the unassigned element furthest

away from c(X)

4 Let N

k−1

( ¯x,U) be a cluster consisting of ¯x and

its k −1 nearest unassigned neighbours

5 Let N

k−1

(ν( ¯x),U \{¯x}) be a cluster consisting

of the nearest unassigned neighbour ν( ¯x) of ¯x

and the k −1 nearest unassigned neighbours

of ν( ¯x)

6 Let clos( ¯x) be the closest cluster to ¯x

7 Let Cost

←

Cost(N

k−1

( ¯x,U))

8 Let Cost

←

Cost(clos( ¯x)+ ¯x)−Cost(clos( ¯x))+Cost(N

k−1

(ν( ¯x),U \{¯x}))

k+1

9 if Cost

≤ Cost

then

10 C ∪{N

k−1

( ¯x,U)}

11 U \N

k−1

( ¯x,U)

12 else

13 clos( ¯x) ∪ ¯x

14 U \{¯x}

15 until |U| < k

16 Assign each x ∈U to clos(x)

Our improvements build on this algorithm. Therefore

let us estimate its time complexity precisely. For this

we use the following facts:

Fact 2: For any data point x a list L

x,U

of the dis-

tances to all points of a set U can be computed in

O(|U| d) arithmetic operations.

Fact 3: Given L

x,U

, for every 1 ≤` ≤|U|the `’s near-

est neighbour of x and the set of its ` closest neigh-

bours can be found by O(|U|) comparisons.

Thus, line 3 to 5 of Algorithm 1 each take at most

O(n d) time since |U| ≤ n. Line 6 requires O(n d/k)

steps because there can be at most n/k clusters. Com-

puting the cost in line 7 and 8 takes time O(k d). Thus,

a single execution of the loop requires at most O(n d)

steps. The number of executions can range between

n/k and n. Typically, the case generating a new clus-

ter (line 10 to 11) should be much more likely. Thus,

on average the number of executions should be on the

order n/k. This gives a worst-case time bound O(n

and an average bound O(n

d/k).

The ONA algorithm (Soria-Comas et al., 2019)

uses a different approach for k-anonymous micro-

aggregation. Its strategy has already been presented

above. A pseudo code of ONA is shown as Algo-

rithm 2. While for large values of k the algorithm de-

livers slightly lower information loss than MDAV vari-

ants on benchmark databases, there are some open is-

sues.

Algorithm 2: ONA (Soria-Comas et al., 2019).

input : database X and min cluster size k

output: k-member clustering C

1 Randomly generate a set of clusters

C ← {C

,.. . ,C

} such that each cluster contains

at least k elements

2 repeat

3 foreach x ∈ X do

4 Let C

i(x)

be the cluster that contains x

5 if |C

i(x)

| > k then

// Should x be reassigned to

another cluster? (case 1)

6 Extract x from C

i(x)

7 Compute distance between x and the

centroids of the clusters in C

8 Add x to the cluster whose centroid is

closest to x

9 else if |C

i(x)

| = k then

// Should cluster C

i(x)

dissolved? (case 2)

10 For s ∈C

i(x)

let C

j(s)

be the cluster

with the closest centroid to s among

those in C \C

i(x)

11 Let L ←{j(s) : s ∈C

i(x)

}

12 Let C

←C

∪{s ∈C

i(x)

: j(s) = `},

for each ` ∈ L

13 Let Cost

←

Cost(C

i(x)

) +

∑

`∈L

Cost(C

)

14 Let Cost

←

∑

`∈L

Cost(C

)

15 if Cost

> Cost

then

16 C ← {C

: ` ∈ L}∪{C

: ` 6∈

(L ∪{i(x)})}

// Split large clusters

17 foreach C ∈ C do

18 if |C| ≥ 2k then

19 C ← C \{C}; C ← C ∪ONA(C, k)

20 until convergence condition

It is unclear when to stop the iteration – the conver-

SECRYPT 2021 - 18th International Conference on Security and Cryptography

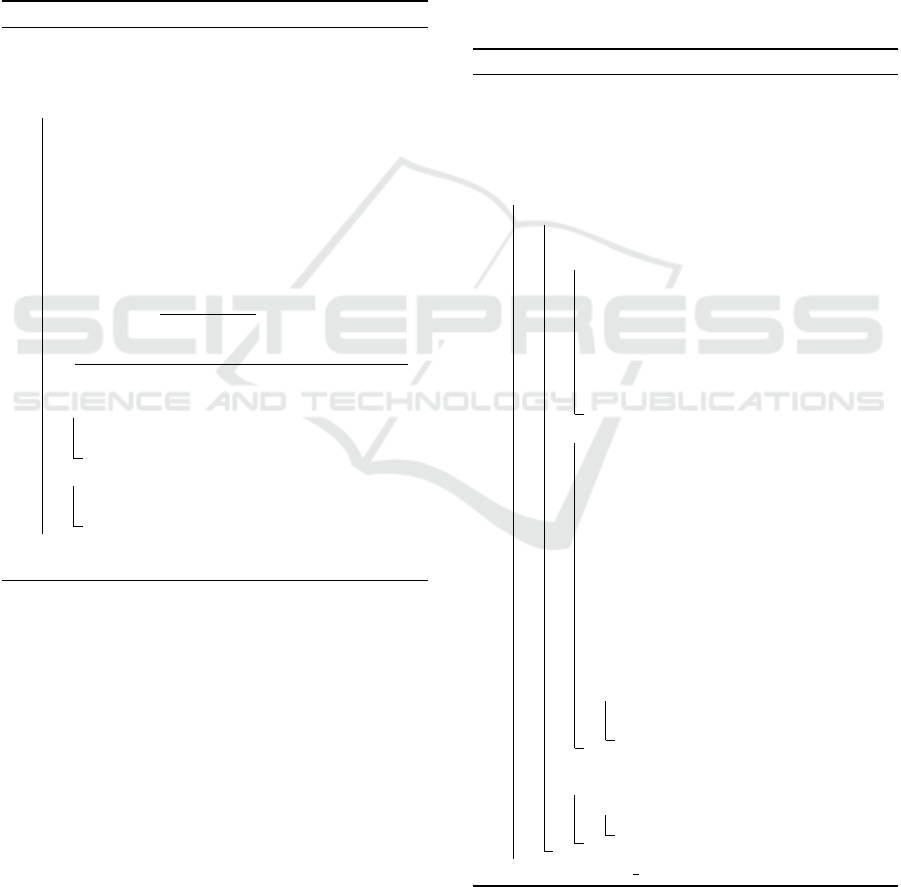
Figure 1: Histogram of the information losses of 1000 ONA

runs on the Census database for k = 10.

gence criteria. An obvious condition is that nothing

has changed within a round, but it is not clear how

many rounds this may require, even more whether this

situation will always be reached. In the implementa-

tion to generate the benchmark results presented be-

low we have stopped the iteration when this condition

has not been fulﬁlled within 30 rounds. This has hap-

pened very rarely in our tests.

Another problem is caused by the probabilistic

initialization with a randomly generated k-member

clustering. As for the Lloyd algorithm, a bad initial-

ization inevitably leads to a bad output. Hence, the

results may differ quite a lot and indeed, they range

from better to worse than those of MDAV algorithms.

In Figure 1 and Table 2 in the appendix this behavior

is shown on the benchmark database Census.

While the authors do not provide any guidelines

on how to tackle this problem, the standard approach

would be to repeat the algorithm several times, let this

number be µ, and output the clustering with the best

solution found. As can be seen in Table 3, there is

some improvement to be gained by increasing µ. But

when a good conﬁdence is aimed at, this increases the

runtime signiﬁcantly.

We have analyzed the methodology of generating

and rearranging clusters in detail and propose a new

algorithm, subsequently called ONA

∗

that uses better

selection strategies. In Table 1 ONA and ONA

∗

are com-

pared with a previous state-of-the-art heuristic based

on the MDAV principle.

Replacing the random initial clustering by a good

deterministic process increases the performance sig-

niﬁcantly,. Our experiments have shown that using an

optimized variant of MDAV like MDAV

∗

gives better re-

sults typically with lower information loss compared

to the original ONA algorithm with µ = 100 repetitions.

MDAV

∗

does not guarantee a limit on the maxi-

mum cluster size, however a split is guaranteed if

2k or more elements are given. As a result, inputs

of 3k −1 or less elements cannot result in a cluster

of size 2k or more. To guarantee a maximum clus-

ter size throughout the ONA

∗

algorithm, after initial-

ization with MDAV

∗

we apply the variant MDAV

(see

(Thaeter and Reischuk, 2018)) to all clusters of size

2k or more. MDAV

delivers slightly worse informa-

tion loss in general, but guarantees a maximum cluster

size of 2k −1 within the same time frame. In practice,

the inﬂuence of MDAV

on ONA

∗

is very limited, as sit-

uations in which MDAV

∗

returns large clusters are very

rare.

Concerning reassignment, ONA

∗

makes a more

precise estimation (line 22). Whereas ONA bases its

decision, whether and where to move an element x,

on the distances to centroids, ONA

∗

compares the ac-

tual costs before and after a change.

A ﬁnal modiﬁcation simpliﬁes matters substan-

tially. Every cluster in step 21 of ONA has between

2k and 3k − 1 elements and should be divided into

2 parts. For this task ONA is not likely to ﬁnd bet-

ter solutions than MDAV algorithms, but requires more

time and works probabilistically. Hence, we have

replaced the recursive execution of ONA by a call to

MDAV

∗

which ﬁrst creates 2 clusters with exactly k el-

ements on opposite sides of the global centroid and

afterwards assigns remaining elements to their clos-

est cluster which is likely to yield an optimal solution

in this special case. A complete description of ONA

∗

is given as Algorithm 3.

To evaluate the improvements by replacing ONA

with ONA

∗

, we have performed several benchmarks

on established benchmark sets (see Table 1 and Ta-

ble 4). The best out of 100 ONA runs is able to out-

perform MDAV

∗

in most of the tests. With bigger k, the

percental difference between MDAV

∗

and ONA becomes

larger. Compared to MDAV

∗

, ONA

∗

is able to lower the

information loss in all test cases with improvements

ranging from 2% for Cloud1 and k = 2 to 31% for EIA

and k = 10. The average improvement from MDAV

∗

ONA

∗

is 11% over all experiments. While the average

improvement from ONA to ONA

∗

is just 3% over all

experiments, its deterministic behaviour takes much

lower runtime.

To determine the time complexity of ONA

∗

con-

sider its basic building blocks and let ζ be the number

of repetitions until convergence. There are at most

n/k clusters C

of size k which might be dissolved in

phase 1. For each element s of such a cluster its clos-

est centroid j(s) can be found in time O(n/k d). For

each cluster C

evaluating the cost function for it and

the at most k neighbours C

j(s)

takes time O(k

d).

Splitting a cluster C

by MDAV

∗

requires O(|C

time. Each cluster C

can give rise to at most k splits

of a cluster C

of size less than 3k, which adds up

Scalable k-anonymous Microaggregation: Exploiting the Tradeoff between Computational Complexity and Information Loss

Algorithm 3: ONA

∗

input : database X and min cluster size k

output: k-member clustering C

1 Let C = {C

,.. . ,C

} ← MDAV

∗

(X, k)

// Split large clusters

2 foreach C ∈ C do

3 if |C| ≥ 2k then

4 C ← C \{C}; C ← C ∪MDAV

(C,k)

5 repeat

// Phase 1: dissolving clusters

6 foreach C

∈ C with |C

| = k do

7 For s ∈C

let C

j(s)

be the cluster with the

closest centroid to s in C \{C

}

8 Let L ←{j(s) : s ∈C

}

9 Let C

←C

∪{s ∈C

: j(s) = `}, for each

` ∈ L

10 Let Cost

← Cost(C

) +

∑

`∈L

Cost(C

)

11 Let Cost

←

∑

`∈L

Cost(C

)

12 if Cost

> Cost

then

13 C ←{C

: ` ∈L}∪{C

: ` 6∈(L∪{i})}

// Split large clusters

14 foreach ` ∈ L do

15 if |C

| ≥ 2k then

16 C ← C \{C

}

17 C ← C ∪MDAV

∗

,k)

// Phase 2: reassigning elements

18 foreach C

∈ C with |C

| > k do

19 repeat

20 foreach s ∈C

21 Let C

j(s)

be the cluster with the

closest centroid to s among

those in C \C

22 Let improvement(s) ←

(Cost(C

) −Cost(C

\{s})) −

(Cost(C

j(s)

∪{s})−Cost(C

j(s)

))

23 Let s

← argmax

s∈C

improvement(s)

24 if improvement(s

) ≤ 0 then

25 break

26 else

27 C

←C

\{s

}

28 C

j(s

)

←C

j(s

)

∪{s

}

// Split large clusters

29 if |C

j(s

)

| ≥ 2k then

30 C ← C \{C

j(s

)

}

31 C ← C ∪MDAV

∗

j(s

)

,k)

32 until |C

| = k

33 until convergence condition

to O(k

d) computational effort. Thus the total time

of phase 1 can be bounded by n/k ·(k ·O(n/k d) +

O(k

d + k

d)) = O((n

/k + n k

) d) .

For phase 2 one has to consider less than n/k

clusters of size between k + 1 and 2k − 1. The

loop starting in line 19 is executed less than k

times. In each execution, again for each ele-

ment s of a cluster to compute its closest cen-

troid and its improvement takes time O(n/k d) and

O(k d) respectively. Now there can be at most

one split adding time O(k

d). Hence, per cluster

O(n k d) + O(k

d) time is needed. All together this

gives an upper bound n/k ·(O(n k d) + O(k

d)) =

O((n

+ n k

) d) for phase 2.

If the time O(n

d) for the initialization by MDAV

∗

is added we ﬁnally get

Lemma 1. If ONA

∗

needs ζ iterations till conver-

gence its runtime is bounded by O((n

+ ζ (n

n k

)) d).

To establish a time bound for ONA seems to be

more difﬁcult. The time used for random initial-

ization can be considered linear in n, a reassign-

ment check takes time O(n/k d) and a dissolve check

O((n + k

) d). Iterating over n elements this already

adds up to O((n

+ nk

) d). This has to be multi-

plied by the number ζ of executions of the main loop

till convergence and furthermore by the number µ of

probabilistic repetitions The correct time bound may

even be larger because in this calculation the recursive

splitting has been ignored for which an analysis does

not seem to be obvious.

4 MICROAGGREGATION IN

ALMOST LINEAR TIME

In 2006 LeFevre et al. introduced MONDRIAN,

an anonymization algorithm which achieves k-

anonymity in O(nlog n) time (LeFevre et al., 2006).

The optimization goal of MONDRIAN is to create clus-

ters with cluster sizes as close to k as possible.

Algorithm 4: MONDRIAN (LeFevre et al., 2006).

input : database X and min cluster size k

output: k-member clustering C

1 if |X | < 2k then

2 return X

3 Let dim ←

argmax

j∈{1,...,d}



max

∈X

−min

∈X



4 Let median ← median({x

dim

| x

∈ X})

5 Let lhs ←

0; Let rhs ←

6 foreach x

∈ X do

7 if x

dim

≤ median then

8 lhs ←lhs ∪{x

}

9 else

10 rhs ←rhs ∪{x

}

11 return MONDRIAN(lhs,k) ∪ MONDRIAN(rhs, k)

SECRYPT 2021 - 18th International Conference on Security and Cryptography

Table 1: Comparison of quadratic time microaggregation algorithms on the benchmark databases for different values of k. For

ONA the best result out of 100 runs is stated, ONA

∗

, MDAV and MDAV

∗

are run only once as they are deterministic.

Information Loss in % on Census

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV 3.18 5.69 7.49 9.09 11.60 14.16

MDAV

∗

3.17 5.78 7.44 8.81 11.37 14.01

ONA 3.44 5.47 6.92 8.16 10.08 12.45

ONA

∗

3.06 5.26 6.81 7.99 10.07 12.46

Information Loss in % on Tarragona

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV 9.33 16.93 19.55 22.46 27.52 33.19

MDAV

∗

9.44 16.14 19.19 22.25 28.40 34.75

ONA 9.19 15.01 17.66 20.88 26.50 30.95

ONA

∗

9.06 15.11 17.79 20.69 26.34 31.15

Information Loss in % on EIA

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV 0.31 0.48 0.67 1.67 2.17 3.84

MDAV

∗

0.22 0.45 0.62 0.91 2.03 2.63

ONA 0.21 0.40 0.59 0.81 1.60 2.01

ONA

∗

0.20 0.37 0.52 0.79 1.63 1.99

Information Loss in % on Cloud1

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV 1.21 2.22 3.74 4.31 5.70 7.05

MDAV

∗

1.16 2.11 3.65 4.09 5.54 6.70

ONA 1.21 2.16 3.18 3.82 4.97 6.35

ONA

∗

1.15 2.02 3.25 3.92 5.07 6.28

Information Loss in % on Cloud2

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV 0.68 1.21 1.70 2.03 2.69 3.40

MDAV

∗

0.64 1.10 1.52 1.87 2.51 3.28

ONA 0.67 1.08 1.46 1.73 2.28 2.96

ONA

∗

0.60 1.04 1.40 1.70 2.22 2.92

MONDRIAN is not deﬁned as a microaggregation al-

gorithm, but it creates a k-member clustering in the

process of anonymization. Hence, this strategy can

be used to perform k-anonymous microaggregation

by calculating and reporting centroids for each clus-

ter created. However, the question arises, whether the

resulting information loss is comparable to state-of-

the-art heuristics designed to minimize information

loss. We have developed two extensions of MONDRIAN

and compared the resulting runtimes and information

losses to those of the original MONDRIAN algorithm as

well as to MDAV

∗

and ONA

∗

The lower time complexity of MONDRIAN is caused

by the fact that no distances between elements are

computed. Instead, MONDRIAN resembles the pro-

cess of sub-dividing a d-dimensional space by d-

dimensional trees. A database is interpreted as a

d-dimensional space with the elements being points

in that space. In the ﬁrst step, MONDRIAN splits the

database into two clusters by projecting it onto one

of its d dimensions and dividing elements at the me-

dian. Subsequently clusters are divided further, po-

tentially using different splitting dimensions for dif-

ferent (sub)clusters. A cluster is no longer split and

considered ﬁnal, if a split at the median would result

in at least one new cluster having less than k elements.

Thus, in the ﬁnal clustering the size of each cluster is

between k and 2k −1.

Choosing a good splitting dimension for each

cluster is a crucial part of the algorithm. Especially

for higher-dimensional data, choosing a less optimal

splitting dimension might result in big and sparsely

populated clusters, resulting in high information loss.

MONDRIAN chooses the splitting dimension for any

cluster as the attribute dimension with widest range

of values in that cluster, a strategy aimed at reducing

the area of clusters as far as possible. A pseudo code

of MONDRIAN is given as Algorithm 4.

As can be seen in Table 6 in the appendix,

MONDRIAN is not able to deliver information loss as

low as ONA or MDAV variants. However, its computa-

tion takes far less time. Its strategy can be interpreted

as acting in rounds of cutting every existing cluster

of size at least 2k into two smaller clusters. There

are O(log n) cutting rounds where every element is

assigned to a new, smaller cluster. Computation of

the splitting dimension is linear in d and n and com-

putation of the median is linear in n. Hence, the total

Scalable k-anonymous Microaggregation: Exploiting the Tradeoff between Computational Complexity and Information Loss

time complexity of MONDRIAN is O(n d logn).

Choosing splitting dimensions according to the

widest range rule might be problematic as informa-

tion loss is deﬁned by cluster density rather than

cluster area. We have investigated several alterna-

tive splitting criteria with the same asymptotic time

complexity and come to the conclusion that a signiﬁ-

cant improvement could be achieved by choosing the

splitting dimension as the dimension with the largest

variance of values. Our resulting algorithm called

MONDRIAN V achieves 20% lower information loss on

average over MONDRIAN in the test cases provided in

Table 6. The splitting rule of MONDRIAN V has the

same time complexity of O(nd) and can be formal-

ized as

dim = argmax

j∈{1,...,d}

∑

∈X



−c(X )



The improvement going from MONDRIAN to

MONDRIAN V shows that even for low-dimensional

data, the choice of the right way to cut is quite

important. A natural next step is to increase the

number of options for splits. Up to this point we

have considered cuts according to attribute values

in a single dimension only. The largest possible set

of cuts would be the set of all hyperplanes dividing

the database in two parts with a varying amount of

elements on each side. However, deciding which

splitting hyperplane to choose is a time consuming

process, eliminating the performance gains made by

MONDRIAN V over ONA

∗

In MONDRIAN V splits can be interpreted as hy-

perplanes perpendicular to one of the unit vectors

,. ..,e

of the data space R

dividing the ele-

ments into two clusters. The second algorithm called

MONDRIAN V2D considers additional splits. We now

also allow hyperplanes that are perpendicular to a

combination e

of a pair of unit vectors e

√

·(e

+ e

) and e

−

√

·(e

−e

). In other

words, we expand the set of possible splits by hyper-

planes which are 45

◦

and 315

◦

between any two unit

vectors. As before, splits are made at the median of

the dimension (or combination of dimensions) with

largest variance. Note that, by the prefactor

√

we en-

sure measuring variances in an orthonormal basis re-

sulting in values comparable to those measured along

original dimensions.

The number of possible splits for any given cluster

increases from d to 2·





+d = d

since there are





pairs of dimensions to choose from and two orienta-

tions for each pair together with the d options to cut

along a single dimension as before. The time com-

plexity of MONDRIAN V2D increases to O(nd

logn),

but information loss further decreases by 6% on av-

erage on the Adult data set (low-dimensional data)

and by 25% on average on the Credit Card data

set (higher-dimensional data). A pseudo code for

MONDRIAN V2D is given as Algorithm 5.

Of course, one could extend this further and take

combinations of 3 or more unit vectors increasing the

time bound by additional factors of d. However, the

largest gain seems to be the step from 1 to 2 dimen-

sions.

Algorithm 5: MONDRIAN V2D.

input : database X and min cluster size k

output: k-member clustering C

1 if |X | < 2k then

2 return X

3 Let

(dim1,dim2,o) ← argmax

, j

∈{1,...,d},o∈{−1,1}



∑

∈X



√



+ o ·x



4 Let median ← median({x

dim1

+ o ·x

dim2

| x

∈ X})

5 Let lhs ←

0; Let rhs ←

6 foreach x

∈ X do

7 if x

dim

≤ median then

8 lhs ←lhs ∪{x

}

9 else

10 rhs ←rhs ∪{x

}

11 return MONDRIAN V2D(lhs,k) ∪

MONDRIAN V2D(rhs,k)

5 COMBINING ONA

∗

AND

MONDRIAN V

As can be seen in Table 6, no MONDRIAN variant can

compete with MDAV* or ONA* with respect to infor-

mation loss. How can one still get the best of both

worlds? We propose to combine both methods, the

fast one at the beginning to split large clusters and

the one of better quality for a ﬁne grained clustering

of small clusters, and name this MONA. The combina-

tion is ﬂexible governed by a parameter ρ that can be

chosen between 0 and 1. It deﬁnes the switch from

MONDRIAN V to ONA

∗

: clusters of size larger than n

are iteratively split by MONDRIAN V, smaller ones are

then handled by ONA

∗

. Thus, we get a family of algo-

rithms MONA

, where MONA

equals MONDRIAN V and

MONA

is identical to ONA

∗

. The code of MONA

is de-

scribed in Algorithm 6. Analogously the algorithm

MONA 2D

combines MONDRIAN V2D and ONA

∗

Since ONA* has quadratic time complexity, but is

only applied to a bunch of smaller datasets, the to-

tal runtime in the ONA*-phase is reduced. Further-

more, most computation of MDAV or ONA variants is

SECRYPT 2021 - 18th International Conference on Security and Cryptography

0.3

0.35

0.4

0.45

0.5

0.55

0.6

0.65

0.7

0.75

0.8

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Information Loss in %

Split limit exponent ρ

MONDRIAN_V MONDRIAN_V2D ONA* MONA MONA_2D

(a) Adult database: n = 48842, d = 3, k = 10.

5.0

10.0

15.0

20.0

25.0

30.0

35.0

40.0

45.0

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Information Loss in %

Split limit exponent ρ

MONDRIAN_V MONDRIAN_V2D ONA* MONA MONA_2D

(b) Credit Card database: n = 30000, d = 24, k = 10.

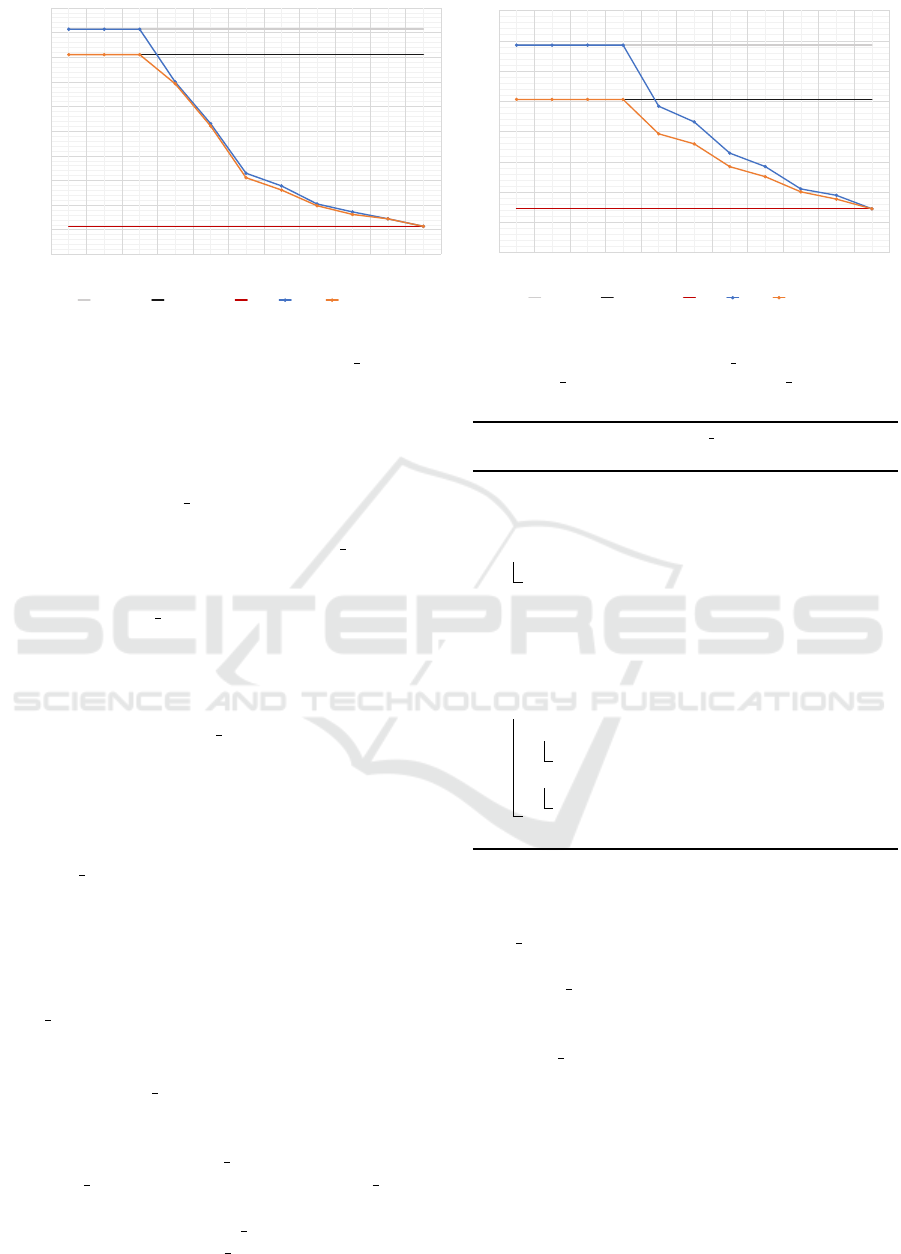
Figure 2: Information Losses of MONA and MONA 2D for different split limits compared to MONDRIAN V variants and ONA

∗

two different databases. As n

< 2k for small values of ρ, both MONA and MONA 2D behave like their MONDRIAN V counterparts.

due to distance calculations between far apart ele-

ments. But this has little inﬂuence on the local ar-

rangements of elements. Thus, saving these estima-

tions in the MONDRIAN V-phase does not increase the

information loss much. Still, there might occur a

decrease of data quality in the MONDRIAN V-phase if

ONA* would have clustered elements together that lie

on both sides of the median of a splitting dimension

used by MONDRIAN V and now are assigned to differ-

ent subproblems. However, for larger datasets such

cases can be expected to have only a small inﬂuence.

In the ONA*-phase MONA

has to manage O(

) =

O(n

1−ρ

) instances with input size n

at most. The

runtime of the MONDRIAN V-phase is obviously not

larger than a complete run of this algorithm. Hence,

the total time complexity of MONA

can be bounded by

O(nd log n) + O



1−ρ



·O((n

2ρ

+ ζ(n

2ρ

+ n

))d)

= O(nd log n) + O((n

1+ρ

+ ζ(n

1+ρ

+ nk

))d) .

For MONA 2D

the ﬁrst term gets an additional factor

d. For ρ > 0 the ﬁrst term is majorized by the second.

If k is small compared to n, which for larger databases

typically holds, and ζ is considered as a constant we

get

Lemma 2. For 0 < ρ ≤ 1 the runtime of MONA

and

MONA 2D

is bounded by O(n

1+ρ

d).

The information loss of both algorithms for differ-

ent ρ are shown in Figure 2. Additionally, runtimes

for MONA and MONA 2D on Credit Card are listed in Ta-

ble 5.

To give a more complete overview of the perfor-

mance of MONA

and MONA 2D

, in Table 6 MONA

0.5

and MONA 2D

0.5

are compared to MONDRIAN V and

ONA

∗

on Adult and Credit Card. It can be ob-

served that MONA

0.5

and MONA 2D

0.5

deliver better re-

sults than pure MONDRIAN V approaches. On the

Algorithm 6: MONA

(MONDRIAN V combined with

ONA

∗

, split limit n

input : database X , min cluster size k and split

limit n

output: k-member clustering C

1 if |X | < n

then

2 return ONA

∗

(X, k)

3 Let

dim ← argmax

j∈{1,...,d}



∑

∈X



−c(X)





4 Let median ← median({x

dim

| x

∈ X})

5 Let lhs ←

0; Let rhs ←

6 foreach x

∈ X do

7 if x

dim

≤ median then

8 lhs ←lhs ∪{x

}

9 else

10 rhs ←rhs ∪{x

}

11 return MONA(lhs,k, n

) ∪ MONA(rhs,k,n

)

low-dimensional database Adult, MONA

0.5

is in reach

of quadratic time algorithms like ONA

∗

whereas

MONA 2D

0.5

is not able to improve much compared to

MONA

0.5

. On the higher dimensional database Credit

Card, MONA 2D

0.5

achieves a notable improvement to

MONA

0.5

. However, both have higher information loss

than the quadratic time algorithms. But compared to

MONDRIAN V the improvement is signiﬁcant.

6 CONCLUSION

The contribution of this paper is threefold. The ONA-

approach has been optimized and transformed into a

deterministic variant that works considerably faster

and is at least as good as ONA w.r.t. information loss,

Scalable k-anonymous Microaggregation: Exploiting the Tradeoff between Computational Complexity and Information Loss

according to the evaluation by standard benchmarks.

Further, the clustering algorithm MONDRIAN has

been adapted to perform well in microaggregation ap-

plications. Two variants, namely MONDRIAN V and

MONDRIAN V2D have been presented, both delivering

superior information loss compared to MONDRIAN and

operating at different ratios of performance to data

quality. For lower-dimensional data the MONDRIAN

technique can achieve almost the same data quality

as much more time consuming algorithms.

Combining both advantages, the data quality

of ONA

∗

and the performance of MONDRIAN V, we

have designed new classes of algorithms MONA

and

MONA 2D

that achieve high quality data anonymiza-

tion even for huge databases where quadratic time

would be far too expensive.

What could be the next steps in further improv-

ing microaggregation techniques? An obvious ques-

tion is whether there are even better splitting rules

for MONDRIAN? On the other hand, is it possible

to decrease the information loss further by spending

more than quadratic time? By design, any improve-

ment here could be applied to the MONA

approach

to get fast solutions with better quality. How well

k-anonymous microaggregation can be approximated

is still wide open. There is hope to achieve approxi-

mation guarantees for ONA

∗

by carefully designing an

initial clustering similar to the k-means++ algorithm

(Arthur and Vassilvitskii, 2007). We plan to investi-

gate this issue in more detail.

REFERENCES

Anwar, N. (1993). Micro-aggregation-the small aggregates

method. Technical report, Internal report. Luxem-

bourg: Eurostat.

Arthur, D. and Vassilvitskii, S. (2007). k-means++: The

advantages of careful seeding. In Proceedings of the

eighteenth annual ACM-SIAM symposium on Discrete

algorithms, pages 1027–1035. Society for Industrial

and Applied Mathematics.

Defays, D. and Nanopoulos, P. (1993). Panels of enterprises

and conﬁdentiality: the small aggregates method. In

Proceedings of the 1992 symposium on design and

analysis of longitudinal surveys, pages 195–204.

Domingo-Ferrer, J., Mart

ınez-Ballest

e, A., Mateo-Sanz,

J. M., and Seb

e, F. (2006). Efﬁcient multivariate

data-oriented microaggregation. The VLDB Jour-

nal—The International Journal on Very Large Data

Bases, 15(4):355–369.

Domingo-Ferrer, J. and Mateo-Sanz, J. M. (2002).

Reference data sets to test and compare sdc

methods for protection of numerical microdata.

https://web.archive.org/web/20190412063606/http:

//neon.vb.cbs.nl/casc/CASCtestsets.htm.

Domingo-Ferrer, J. and Torra, V. (2005). Ordinal, continu-

ous and heterogeneous k-anonymity through microag-

gregation. Data Mining and Knowledge Discovery,

11(2):195–212.

Dwork, C., McSherry, F., Nissim, K., and Smith, A. (2006).

Calibrating noise to sensitivity in private data analy-

sis. In Theory of cryptography conference, pages 265–

284. Springer.

LeFevre, K., DeWitt, D. J., and Ramakrishnan, R.

(2006). Mondrian multidimensional k-anonymity. In

22nd International conference on data engineering

(ICDE’06), pages 25–25. IEEE.

Li, N., Li, T., and Venkatasubramanian, S. (2007).

t-closeness: Privacy beyond k-anonymity and l-

diversity. In 2007 IEEE 23rd International Confer-

ence on Data Engineering, pages 106–115. IEEE.

Li, N., Qardaji, W., and Su, D. (2012). On sam-

pling, anonymization, and differential privacy or, k-

anonymization meets differential privacy. In Pro-

ceedings of the 7th ACM Symposium on Information,

Computer and Communications Security, pages 32–

33. ACM.

Lichman, M. (2013). UCI machine learning repository.

http://archive.ics.uci.edu/ml.

Lloyd, S. P. (1982). Least squares quantization in pcm.

IEEE transactions on information theory, 28(2):129–

137.

Machanavajjhala, A., Kifer, D., Gehrke, J., and Venkita-

subramaniam, M. (2007). l-diversity: Privacy beyond

k-anonymity. ACM Transactions on Knowledge Dis-

covery from Data (TKDD), 1(1):3.

Oganian, A. and Domingo-Ferrer, J. (2001). On the com-

plexity of optimal microaggregation for statistical dis-

closure control. Statistical Journal of the United Na-

tions Economic Commission for Europe, 18(4):345–

353.

Rebollo-Monedero, D., Forn

e, J., Pallar

es, E., and Parra-

Arnau, J. (2013). A modiﬁcation of the Lloyd algo-

rithm for k-anonymous quantization. Information Sci-

ences, 222:185–202.

Samarati, P. (2001). Protecting respondents identities in mi-

crodata release. IEEE transactions on Knowledge and

Data Engineering, 13(6):1010–1027.

Soria-Comas, J., Domingo-Ferrer, J., and Mulero, R.

(2019). Efﬁcient near-optimal variable-size microag-

gregation. In International Conference on Modeling

Decisions for Artiﬁcial Intelligence, pages 333–345.

Springer.

Sweeney, L. (2002). k-anonymity: A model for protecting

privacy. International Journal of Uncertainty, Fuzzi-

ness and Knowledge-Based Systems, 10(05):557–570.

Thaeter, F. and Reischuk, R. (2018). Improving anonymiza-

tion clustering. In Langweg, H., Meier, M., Witt,

B. C., and Reinhardt, D., editors, SICHERHEIT 2018,

pages 69–82, Bonn. Gesellschaft f

ur Informatik e.V.

Thaeter, F. and Reischuk, R. (2020). Hardness of

k-anonymous microaggregation. Discrete Applied

Mathematics.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

APPENDIX

Benchmarks

The Census database contains 13 numerical attributes and 1080 elements. It was created using the Data Extraction

System of the U.S. Bureau of Census in 2000. Tarragona contains 13 numerical attributes and 834 elements. It

contains data of the Spanish region Tarragona from 1995. The EIA data set consists of 15 attributes and 4092

records. As in previous works (see e.g. (Domingo-Ferrer et al., 2006)) only a subset of 11 attributes precisely 1

and 6 to 15 have been used. Cloud1 and Cloud2 have been created using statistics from AVHRR images. These

databases are commonly used for the training and evaluation of machine learning algorithms, and both contain

1024 elements with 10 attributes each. Adult consists of 48842 elements with 14 attributes. As for EIA, only

a subset of numerical attributes namely age, education number and hours per week is used. This particular

selection was suggested in (Rebollo-Monedero et al., 2013). It is used to test subquadratic algorithms on low-

dimensional data. The Credit Card clients data set consists of 30000 elements in 24 numeric attributes. It contains

inputs and predictive results from six data mining methods and is used to evaluate subquadratic algorithms on

higher-dimensional data.

Experimental Results

Table 2: Statistics of the consistency of outputs on 1000 ONA executions on the Census benchmark database for different k.

The information loss of MDAV

∗

is included for reference. Information losses (IL) are stated in percentages.

ONA on Census MDAV

∗

on Census

lowest IL highest IL median mean variance IL

k = 2 3.43 3.90 3.63 3.63 0.01 3.17

k = 3 5.42 6.24 5.70 5.71 0.01 5.78

k = 4 6.94 7.74 7.25 7.25 0.02 7.44

k = 5 8.12 9.10 8.47 8.48 0.02 8.81

k = 7 10.04 11.11 10.43 10.44 0.03 11.37

k = 10 12.36 13.66 12.77 12.80 0.04 14.01

Table 3: Statistics of the consistency of outputs on different numbers of ONA executions on the Census benchmark database

for k = 10. The runtime and information loss of MDAV

∗

is included for reference. As MDAV

∗

is deterministic, it is run only

once.

ONA on Census for k = 10 MDAV

∗

on Census

lowest IL highest IL median mean variance runtime IL runtime

10 runs 12.54 13.00 12.74 12.76 0.02 1s 14.01 0s

100 runs 12.41 13.39 12.79 12.80 0.04 9s 14.01 0s

1000 runs 12.36 13.66 12.77 12.80 0.04 100s 14.01 0s

Table 4: Comparison of quadratic time microaggregation algorithms on the EIA benchmark database for different values of

k. For ONA the total runtime for 100 runs is stated, ONA

∗

and MDAV

∗

are run only once as they are deterministic.

Runtime on EIA

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV

∗

2s 1s 1s 0s 0s 0s

ONA 162s 255s 138s 327s 41s 36s

ONA

∗

2s 1s 1s 1s 0s 0s

Scalable k-anonymous Microaggregation: Exploiting the Tradeoff between Computational Complexity and Information Loss

Table 5: Runtimes of MONA

and MONA 2D

for different ρ and k on Credit Card. Compare with information losses stated in

Figure 2b.

Runtime on Credit Card

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MONA

0.3

0s 0s 0s 0s 0s 0s

MONA

0.4

0s 0s 0s 0s 0s 0s

MONA

0.5

1s 0s 0s 0s 0s 0s

MONA

0.6

4s 2s 2s 2s 1s 1s

MONA

0.7

8s 5s 4s 4s 3s 3s

MONA

0.8

33s 24s 19s 16s 13s 11s

MONA

0.9

67s 48s 39s 37s 30s 25s

MONA

306s 226s 174s 146s 123s 101s

MONA 2D

0.3

2s 1s 1s 1s 1s 1s

MONA 2D

0.4

2s 1s 1s 1s 1s 1s

MONA 2D

0.5

2s 2s 2s 1s 1s 2s

MONA 2D

0.6

5s 3s 3s 2s 2s 2s

MONA 2D

0.7

8s 6s 5s 4s 4s 4s

MONA 2D

0.8

34s 24s 20s 18s 14s 12s

MONA 2D

0.9

70s 49s 42s 37s 31s 25s

MONA 2D

309s 216s 176s 146s 124s 98s

Table 6: Comparison of several microaggregation algorithms on benchmarks Adult with d = 3 and Credit Card with d = 24.

Information Loss in % on Adult

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV

∗

0.04 0.09 0.14 0.18 0.28 0.42

ONA

∗

0.04 0.08 0.12 0.16 0.24 0.36

MONDRIAN 0.25 0.51 0.51 0.51 0.92 0.92

MONDRIAN V 0.21 0.41 0.41 0.41 0.76 0.76

MONDRIAN V2D 0.19 0.38 0.38 0.38 0.71 0.71

MONA

0.5

0.05 0.11 0.16 0.21 0.32 0.46

MONA 2D

0.5

0.05 0.10 0.16 0.21 0.30 0.46

Information Loss in % on Credit Card

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV

∗

3.65 6.44 8.48 10.21 12.36 14.68

ONA

∗

3.50 5.86 7.53 8.64 10.23 12.24

MONDRIAN 30.33 30.33 41.47 41.47 43.75 50.71

MONDRIAN V 24.05 24.05 32.54 32.54 34.12 39.27

MONDRIAN V2D 15.81 15.81 21.93 21.93 23.23 27.34

MONA

0.5

7.74 12.56 15.99 18.53 22.45 26.59

MONA 2D

0.5

6.87 10.96 13.89 16.16 19.50 22.95

Runtime on Adult

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV

∗

211s 141s 89s 77s 50s 40s

ONA

∗

538s 358s 267s 218s 163s 116s

MONDRIAN 0s 0s 0s 0s 0s 0s

MONDRIAN V 0s 0s 0s 0s 0s 0s

MONDRIAN V2D 0s 0s 0s 0s 0s 0s

MONA

0.5

1s 0s 0s 0s 0s 0s

MONA 2D

0.5

1s 0s 0s 0s 0s 0s

Runtime on Credit Card

k = 2 k = 3 k = 4 k = 5 k = 7 k = 10

MDAV

∗

223s 158s 120s 95s 78s 61s

ONA

∗

292s 209s 174s 145s 123s 106s

MONDRIAN 0s 0s 0s 0s 0s 0s

MONDRIAN V 0s 0s 0s 0s 0s 0s

MONDRIAN V2D 1s 1s 1s 1s 1s 1s

MONA

0.5

1s 0s 0s 0s 0s 0s

MONA 2D

0.5

2s 2s 2s 1s 1s 2s

SECRYPT 2021 - 18th International Conference on Security and Cryptography