Practically Efﬁcient RFID Scheme with Constant-time Identiﬁcation

Ferucio Laurent¸iu T¸ iplea

1,2 a

and Cristian Hristea

2 b

Department of Computer Science, Alexandru Ioan Cuza University of Ias¸i, Ias¸i, Romania

Simion Stoilow Institute of Mathematics of the Romanian Academy, Bucharest, Romania

Keywords:

RFID System, Security, Privacy.

Abstract:

Complex systems based on RFID technology, such as healthcare or people identiﬁcation, raise various scala-

bility problems, timely identiﬁcation of tags, security, privacy, and efﬁcient, practical implementation. This is

because such systems contain many tags, operate with private personal data, and respond promptly in concrete,

practical situations to avoid malfunctions (errors in the decision process, trafﬁc congestion, and so on). This

paper proposes an RFID protocol that achieves the properties mentioned above, namely mutual authentication,

destructive privacy, and constant-time identiﬁcation in Vaudenay’s model with temporary state disclosure. The

protocol employs just an IND-CPA secure symmetric-key encryption scheme, which makes it very efﬁcient

in implementation. To protect the secret key against adversaries with corruption capabilities, physically un-

clonable functions (PUFs) are used to mask it. As far as we know, this is the most practically efﬁcient RFID

protocol that achieves mutual authentication, destructive privacy, and constant-time identiﬁcation. All these

key features make it suitable for applications as those above.

1 INTRODUCTION

Radio Frequency Identiﬁcation (RFID) is a technol-

ogy that allows over the air identiﬁcation of objects,

animals or persons. The central ﬁgure of an RFID sys-

tem is a small resource constrained device called tag.

It communicates through radio waves with an uncon-

strained device capable of much more computation,

called reader. The reader is connected through a se-

cure channel with a back-end database that contains

information about all tags. The result of communica-

tion between reader and tag is the identiﬁcation of the

entity the tag is attached to.

In recent years, the applicability of RFID systems

has expanded to increasingly diverse and complex

domains and systems. It is worth mentioning here

animal monitoring systems, medical healthcare sys-

tems, pharmaceutical systems, people identiﬁcation

systems, and so on. Each of these areas raises spe-

ciﬁc issues of identiﬁcation and authentication, secu-

rity, privacy, and implementation efﬁciency.

Healthcare for example offers a rich palette of po-

tential applications of the RFID technology. Besides

traditional uses such as tracking of medical equip-

ment and devices or access control, RFID technol-

https://orcid.org/0000-0001-6143-3641

https://orcid.org/0000-0003-0132-9310

ogy can provide even greater beneﬁts to the domain.

The misidentiﬁcation of patients, drugs, blood bags

and so on, which frequently occurs in hospitals, con-

stitutes a real threat to patients’ safety (Haddara and

Staaby, 2018). The use of an RFID-based infras-

tructure would allow medical staff to largely allevi-

ate this issue and to signiﬁcantly reduce the medi-

cal errors. Likewise, tracking the movement of pa-

tients and visitors throughout the hospital by means

of RFID bracelets has also been proven to help pre-

vent infectious diseases (Lahtela, 2009; Haddara and

Staaby, 2018). It would be desirable for the next gen-

eration of RFID healthcare services to ensure contin-

uous monitoring of patients, whether they are in the

hospital or are discharged (but not in full health).

Despite all these advantages, the adoption process

of RFID technology in healthcare systems has stag-

nated over the past decade. There are several rea-

sons for this but probably the most important reason is

that the scientiﬁc and technological research was not

yet sufﬁciently mature to offer truly secure and pri-

vate RFID systems at affordable implementation costs

(Lahtela, 2009; Yao et al., 2010; Yao et al., 2012;

Haddara and Staaby, 2018).

The main key properties that healthcare RFID

schemes must satisfy are:

• Efﬁcient, or even constant, identiﬁcation time:

¸Tiplea, F. and Hristea, C.

Practically Efﬁcient RFID Scheme with Constant-time Identiﬁcation.

DOI: 10.5220/0010544804950506

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 495-506

ISBN: 978-989-758-524-1

495

healthcare systems can be very large (millions of

tags) and thus, linear identiﬁcation time propor-

tional to the size of the database can lead to fre-

quent system crashes and disfunctionalities;

• Good security properties to avoid identity or per-

sonal data theft, even if the tag is corrupted;

• Good privacy level to avoid illegal tracking or

monitoring of patients, drugs, and so on, even if

the associated tag is corrupted;

• Efﬁcient software and hardware implementation:

the operations performed by tags, including the

communication protocol, must be performed in

timely manner to avoid system congestion.

The properties mentioned above are speciﬁc to

other RFID-based systems too and not only to the

healthcare ones.

If we translate these properties into Vaudenay’s

security and privacy RFID model (Vaudenay, 2007;

Paise and Vaudenay, 2008), we see that we are inter-

ested in building RFID schemes to ensure efﬁcient or

even constant-time tag identiﬁcation, security against

strong adversaries, at least a destructive level of pri-

vacy, and efﬁcient (software and hardware) imple-

mentation. By efﬁcient implementation we under-

stand, among others, that the RFID schemes we are

interested in should avoid public-key cryptography,

which is still very expensive (Preneel, 2018) espe-

cially if implemented on low power devices.

Thus, we have reached the main goal of our pa-

per, namely to design an RFID scheme that achieves

mutual authentication, destructive privacy, constant-

time tag identiﬁcation, and efﬁcient implementation

in practice. In addition, the model in which we want

these properties to be satisﬁed is the one proposed by

Vaudenay and subsequently extended with the possi-

bility for the corruption oracle to disclose the tempo-

rary state of the tag and not only its permanent state

(Armknecht et al., 2010).

Related Work: The ﬁrst attempts to propose RFID

schemes that satisfy all four properties mentioned

above at the same time are those in (Kardas¸ et al.,

2012; Akg

un and C¸ aglayan, 2015). We say that these

were only attempts because the analysis from (iplea

and Hristea, 2021) showed that these schemes do

not satisfy the authors’ privacy requirements. Also,

in (iplea and Hristea, 2021), a general method was

presented by which the RFID schemes from (Kardas¸

et al., 2012; Akg

un and C¸ aglayan, 2015) can be ﬁxed

in terms of privacy in Vaudenay’s model with tempo-

rary state disclosure. Even with this ﬁx, the resulting

schemes are not very efﬁcient. Besides, they use ran-

dom number generators, and the scheme in (Kardas¸

et al., 2012) has linear identiﬁcation time and not

constant. But let us review the effort to build RFID

schemes with the four properties mentioned above.

Efﬁcient Identiﬁcation but Loss of Privacy: In

any RFID protocol, the tag transmits certain infor-

mation from which the reader extracts a speciﬁcation

by which it initiates the tag identiﬁcation process in

its back-end database. This speciﬁcation is named

tag identiﬁer (Hristea and T¸ iplea, 2019b). Several

authors have developed RFID schemes in which the

tag identiﬁer is updated only at the end of the com-

munication protocol (tag identiﬁers with this property

are called constant tag identiﬁers (Dimitriou, 2005;

Tsudik, 2006; Alomair et al., 2010; Lu et al., 2010;

Alomair et al., 2012; Hristea and T¸ iplea, 2019)). The

great advantage of using constant tag identiﬁers is that

the identiﬁcation is done in time proportional to log n,

where n is the size of the database (Hristea and T¸ iplea,

2019b). Some authors have proposed special tech-

niques of organizing databases to get better identiﬁca-

tion time than log n (Alomair et al., 2010). But what is

very clear about such RFID schemes is that they lose

privacy in a dramatic way: as it was recently shown

(Hristea and T¸ iplea, 2019b), no stateful RFID scheme

with constant tag identiﬁers achieves any form of pri-

vacy in Vaudenay’s model (with or without temporary

state disclosure).

More recently, the authors of (Akg

un and

C¸ aglayan, 2015) have proposed a PUF-based RFID

scheme that achieves constant time tag identiﬁcation.

They also claimed that the scheme achieves destruc-

tive privacy in Vaudenay’s model with temporary state

disclosure. Unfortunately, this is not true as it was

shown in (Hristea and T¸ iplea, 2019a; iplea and Hris-

tea, 2021). Although the technique in (iplea and

Hristea, 2021) ﬁxes this issue, the resulting scheme

is still not very efﬁcient. Moreover, it uses a ran-

dom number generator (RNG) and the XOR opera-

tion to build messages that are transmitted between

reader and tag. However, sending secrets XOR-ed

with “random” strings raises the issue of the gener-

ator’s security (Arslan et al., 2018). This is because

lightweight tags may only implement short length

RNGs and thus are susceptible to prediction. For in-

stance, the EPC compliant Class-1 Generation-2 stan-

dard (EPCglobal, 2016) states that RFID tags should

accommodate RNGs capable of providing 16-bit long

random numbers. However, this might not be quite

secure. More secure RNGs require more than 1000

gate equivalents (GEs), which is actually more than

the number of GEs needed to implement lightweight

symmetric-key ciphers (Armknecht et al., 2014).

Efﬁcient Identiﬁcation but Inefﬁcient Implemen-

tation: An elegant RFID protocol that allows

constant-time identiﬁcation is the one proposed in

SECRYPT 2021 - 18th International Conference on Security and Cryptography

496

(Vaudenay, 2007; Paise and Vaudenay, 2008) and

based on public-key cryptography (PKC). The main

idea is quite simple. Each tag has the reader’s public-

key and, therefore, can send its identity encrypted by

it. Only the reader can decrypt the message, extract

the tag’s identity, and convert it into a hash index.

This makes the search in the database to be imple-

mented in constant time (by hash indices). Vaude-

nay’s PKC-based RFID scheme has two major dis-

advantages. First of all, it does not provide destruc-

tive privacy, but only forward privacy in Vaudenay’s

model without temporary state disclosure and only

weak privacy in Vaudenay’s model with temporary

state disclosure (Armknecht et al., 2010). Secondly, it

uses PKC, which for the nowadays technology is still

very expensive, especially if it is to be implemented

on low-power devices like RFID tags (Preneel, 2018).

Although the technique proposed in (iplea and Hris-

tea, 2021) makes this RFID scheme resistant to cor-

ruption with temporary state disclosure, the two is-

sues still persist: the scheme does not achieve destruc-

tive privacy and the use of PKC makes it inefﬁcient.

Destructive Privacy but Inefﬁcient Identiﬁcation:

When Vaudenay’s model was proposed, ﬁnding an

RFID scheme to provide destructive privacy remained

an open problem. This was solved in (Sadeghi et al.,

2010) by using PUFs. However, the scheme provides

only unilateral authentication and it is inefﬁcient from

the tag identiﬁcation point of view (which is linear

in time). As the scheme uses pseudo-random func-

tions (PRFs), PUFs, and pseudo-random generators

(PRGs), we may say that it achieves a certain degree

of practical efﬁciency. The scheme was extended in

(Hristea and T¸ iplea, 2019a) with mutual authentica-

tion, but tag identiﬁcation inefﬁciency persists.

Contribution: In this paper we propose a PUF-

based RFID scheme that achieves mutual authenti-

cation and destructive privacy in Vaudenay’s model

with temporary state disclosure. Moreover, it pro-

vides constant-time identiﬁcation and is very efﬁcient

in practical implementation.

The scheme employs a symmetric-key encryption

scheme that is IND-CPA secure. To protect the se-

cret key on tags we mask it with PUF values. To

avoid the use of temporary variables that might com-

promise privacy, we use the reader-ﬁrst authentication

approach, where the tag authenticates ﬁrst the reader.

Detailed security and privacy proofs of the scheme,

are provided.

The use of PUFs should not be seen as an incon-

venience to our scheme. This is because reader au-

thentication and narrow forward privacy are not possi-

ble together by means of standard cryptography, when

corruption with temporary state disclosure is allowed

(Armknecht et al., 2010). The only technique known

so far to bypass this limitation is by using PUFs

(Sadeghi et al., 2010; Kardas¸ et al., 2012; Akg

un and

C¸ aglayan, 2015; Hristea and T¸ iplea, 2019a; iplea and

Hristea, 2021). On the other hand, the PUF tech-

nology is becoming more and more mature, with a

wide variety of hardware implementations at the mo-

ment (Maes and Verbauwhede, 2010; Delvaux et al.,

2015b) (please see Section 6 in the paper).

Due to the fact that the scheme employs just a

symmetric-key encryption scheme and a PUF, it can

be efﬁciently implemented in practice. We also em-

phasize that the scheme does not need RNGs on tags

(please see our discussion above on RNGs). As far as

we know, this is the most practically efﬁcient RFID

scheme that achieves mutual authentication, destruc-

tive privacy, and constant-time identiﬁcation.

Paper Structure: The paper is divided into seven

sections, the ﬁrst being the introductory section. The

basic concepts and notations used in this paper are

presented in Sections 2 and 3 (the latter being es-

pecially dedicated to RFID systems). Section 4 dis-

cusses on general issues regarding tag identiﬁcation

complexity. In Section 5 we propose our main RFID

scheme and prove its security and destructive privacy.

The last two sections focus on implementation issues,

comparison with other schemes, and conclude the pa-

per. Due to space limitations, the proofs are presented

in a separate appendix to allow reviewers to assess the

correctness of the results presented in the paper.

2 BASIC DEFINITIONS AND

NOTATION

We recall in this section a few concepts from cryptog-

raphy. For details, the reader is referred to standard

textbooks, such as (Katz and Lindell, 2014).

We use probabilistic polynomial time (PPT) algo-

rithms A as deﬁned in (Sipser, 2012) that can consult

oracles. An oracle is a black box that can perform

a particular computation. When considering an ora-

cle, we do not care about its implementation or how

it works. Whenever a PPT algorithm A sends a value

x to some oracle O, the oracle returns to A a given

value in O(1) time, that can be used further by A.

For a set A, a ← A means that a is uniformly at

random chosen from A. If A is a probabilistic algo-

rithm, then a ← A means that a is an output of A for

some given input.

The asymptotic approach to security makes use of

security parameters, denoted by λ in our paper. A

positive function f (λ) is called negligible if for any

Practically Efﬁcient RFID Scheme with Constant-time Identiﬁcation

497

positive polynomial poly(λ) there exists n

such that

f (λ) < 1/poly(λ), for any λ ≥ n

. f (λ) is called over-

whelming if 1 − f (λ) is negligible.

A physically unclonable function (PUF) (Maes,

2013) can be seen as a physical object that, when

queried with a challenge x generates a response y that

depends on both x and the speciﬁc physical proper-

ties of the object. PUFs are typically assumed to be

physically unclonable (it is infeasible to produce two

PUFs that cannot be distinguished based on their chal-

lenge/response behavior), unpredictable (it is infeasi-

ble to predict the response to an unknown challenge),

and tamper-evident (any attempt to physically access

the PUF irreversible changes its challenge/response

behavior). As PUFs are subject to noise induced by

the operating conditions, they return slightly differ-

ent responses when queried with the same challenge

multiple times. As there are practical techniques to

alleviate this, from a theoretical point of view it is

assumed that PUFs return a similar response when

queried with the same challenge multiple times (this

is usually called robustness).

Based on these, we adopt here the concept of an

ideal PUF slightly different than in (Sadeghi et al.,

2010). Namely, an ideal PUF is a physical object

with a challenge/response behavior that implements

a function P : {0,1}

→ {0,1}

, where p and k are of

polynomial size in λ, such that:

1. P is computationally indistinguishable from a ran-

dom function (that is, no PPT algorithm can

decide with more than a negligible probability

whether a given value is an output of P or it was

chosen uniformly at random);

2. Any attempt to physically tamper with the object

implementing P results in destruction of P (P can-

not be evaluated any more).

Why ideal PUFs? In cryptography and security

we typically build a cryptographic system and prove

its security under the assumption that we have used

secure ingredients (building blocks) such as collision-

resistant hash functions, PRFs, or ideal PUFs. These

secure ingredients are a kind of “ground truth” of

applied cryptography. “Provable security” typically

starts only above the level of these secure ingredients.

A proof based on experiments and simulations may

only show that the scheme is secure with respect to

those experiments and simulations. A proof based on

ideal primitives has a major advantage: if a crypto-

graphic primitive is assumed ideal and later is proved

(by experiments) insecure, we may change it by an-

other one of the same type that we believe is secure.

The entire scheme remains unchanged and the secu-

rity analyses is moved to the cryptographic primitives.

A symmetric-key encryption (SKE) scheme is a

triple of PPT algorithms S = (G,E,D), where G out-

puts a secret key K when takes as input a security

parameter λ, E outputs a ciphertext y when takes as

input a key K and a message x, and D is determinis-

tic and outputs a plaintext when takes as input a key

K and a ciphertext, such that x = D(K,y), for any

y ← E(K,x). Usually, SKE schemes are obtained by

iterating block ciphers. For the sake of simplicity, we

use {x}

({y}

−1

) to denote encryption (decryption)

of x (y) by K. When two or more messages are con-

catenated for encryption, we will use “k” to denote

the concatenation operation.

S is called IND-CPA secure if no PPT algorithm

A that is allowed to query the encryption algorithm

E of S has a non-negligible advantage to distinguish

between two equally length plaintexts, given a cipher-

text of one of them.

3 (PUF BASED) RFID SCHEMES

We recall in this section basic notions regarding RFID

schemes and Vaudenay’s security and privacy model.

For details, the reader is referred to (Vaudenay, 2007;

Paise and Vaudenay, 2008).

An RFID scheme is typically composed of three

main entities: a reader, a set of tags, and a radio fre-

quency communication protocol between reader and

tags. The reader is a powerful device not compu-

tationally restricted so it can perform any crypto-

graphic operation. It stores tag related information in

a database to which it has secure access. On the other

side, tags are small devices that are considered to be

resource constrained.

The memory of a tag is typically split into perma-

nent (or internal), used to store the state values of the

tag, and temporary (or volatile), used to carry out the

calculations required by the communication protocol.

RFID Schemes: Let R be a reader identiﬁer and T

be a set of tag identiﬁers whose cardinal is polyno-

mial in some security parameter λ. An RFID scheme

over (R , T ) (Vaudenay, 2007; Paise and Vaudenay,

2008) is a triple S = (SetupR, SetupT, Ident) of PPT

algorithms, where:

1. SetupR(λ) inputs a security parameter λ and out-

puts a triple (pk,sk,DB) consisting of a key pair

(pk,sk) and an empty database DB. pk is public,

while sk is kept secret by reader;

2. SetupT (pk, ID) initializes the tag identiﬁed by

ID. It outputs an initial tag state S and a tag-

speciﬁc secret K. The identity ID together with K

is stored as a pair (ID,K) in the reader’s database;

SECRYPT 2021 - 18th International Conference on Security and Cryptography

498

3. Ident(pk; R (sk, DB); ID(S)) is an interactive

protocol between the reader identiﬁed by R (with

its private key sk and database DB) and a tag iden-

tiﬁed by ID (with its state S) in which the reader

ends with an output consisting of ID or ⊥. The

tag may end with no output (unilateral authenti-

cation), or it may end with an output consisting of

OK or ⊥ (mutual authentication).

The correctness of an RFID scheme means that,

regardless of how the system is set up, after each com-

plete execution of the interactive protocol between the

reader and a legitimate tag, the reader outputs tag’s

identity with overwhelming probability. For mutual

authentication RFID schemes, correctness means that

the reader outputs tag’s identity and the tag outputs

OK with overwhelming probability.

Adversaries: In order to formalize the security and

privacy requirements for RFID schemes, the concept

of an adversary model is needed. Such a model de-

ﬁnes the capabilities of an adversary by means of a

set of oracles that simulate the interaction with the

RFID system. There have been several proposal for

this, such as (Vaudenay, 2007; Paise and Vaudenay,

2008; Juels and Weis, 2009; Canard et al., 2010; Deng

et al., 2010; Bohli and Pashalidis, 2011; Hermans

et al., 2011; Hermans et al., 2014). One of the most

inﬂuential, which we follow in this paper, is Vaude-

nay’s model (Vaudenay, 2007; Paise and Vaudenay,

2008). Within this model, the adversary is given ac-

cess to several oracles to create tags, initiate proto-

col sessions, and communicate with the tags and the

reader. There are two special oracles, Corrupt and

Result that play an important role in classifying the

adversaries. The Corrupt oracle allows an adversary

to get the internal state of the tag, while the Result or-

acle allows the adversary to know the authentication

result of a protocol session.

It is customary to assume that the RFID tags can

be corrupted to reveal not only their permanent mem-

ory (internal state) but also the temporary variables

that get values in a protocol step and then are used in

another protocol step (and not the temporary variables

that are used locally in doing computations in a given

protocol step). When the Corrupt oracle is consid-

ered in such a way, we will refer to Vaudenay’s model

as being with temporary state disclosure.

The adversaries are classiﬁed into classes accord-

ing to the access they get to these oracles:

• Weak adversaries: they do not have access to the

Corrupt oracle;

• Forward adversaries: if they access the Corrupt

oracle, then they can only access this oracle;

• Destructive adversaries: after the adversary has

queried Corrupt(vtag) and obtained the corre-

sponding information, the tag identiﬁed by vtag

is destroyed and the temporary identiﬁer vtag will

no longer be available. The database DB will still

keep the record associated to this tag (the reader

does not know the tag was destroyed). As a conse-

quence, a new tag with the same identiﬁer cannot

be created (in this approach, the database cannot

store multiple records for the same tag identiﬁer);

• Strong adversaries: there are no restrictions on

the use of oracles.

An adversary that does not have access to the ora-

cle Result is called narrow. The narrow property can

be combined with any of the previous properties in

order to get another four classes of adversaries, nar-

row weak, narrow forward, narrow destructive, and

narrow strong.

Security: Security of RFID schemes in Vaudenay’s

model (Vaudenay, 2007; Paise and Vaudenay, 2008)

means tag and reader authentication.

An RFID scheme S achieves tag authentication if

no strong adversary has more than a negligible prob-

ability to authenticate itself to the reader as an uncor-

rupted legitimate tag.

An RFID scheme S achieves reader authentica-

tion if no strong adversary has more than a negligible

probability to authenticate itself to some uncorrupted

legitimate tag as the reader.

Privacy: Privacy in Vaudenay’s model generalizes

anonymity (which means that the tag ID cannot be

inferred) and untraceability (which means that the

equality of two tags cannot be inferred). Thus, pri-

vacy requires that no adversary can infer non-trivial

tag ID relations from the protocol messages. The in-

formation provided by a protocol is trivial when the

adversary may learn it without making effective use

of the protocol messages. To formalize this, Vaude-

nay’s model introduces the concept of a blinder that

simulates the protocol for adversary without know-

ing any secret information of the tags or the reader. If

this simulation does not change the adversary’s output

compared to the case when the adversary plays with

the real protocol, then the protocol achieves privacy.

Thus, according to the adversary’s class, we thus

obtain eight concepts of privacy: strong privacy, nar-

row strong privacy, destructive privacy, and so on.

PUF Tags and PUF based RFID Schemes: The

newest technologies allow PUF tags that are tags with

PUFs inside them. An RFID scheme with PUF tags

will sometimes be called PUF based RFID scheme.

In order to adapt Vaudenay’s model to PUF based

RFID schemes, we have to clarify what corruption

means in this case. Taking into account that PUFs

Practically Efﬁcient RFID Scheme with Constant-time Identiﬁcation

499

are tamper-evident, the approach we follow is that

corruption on a PUF tag reveals the permanent (and

temporary, if the model is with temporary state dis-

closure) memory of the tag, but the tag is consid-

ered destroyed. By corruption, the values computed

by PUFs cannot be obtained (except when they were

saved in the permanent memory or in global tempo-

rary variables). For more details the reader is referred

to (T¸ iplea et al., 2021).

4 IDENTIFICATION TIME IN

RFID SCHEMES

With the increase in the applicability of RFID sys-

tems, the number of tags to be managed by the back-

end server has increased. This raises the problem of

tag identiﬁcation time by the reader. In fact this is

an on-line search problem of a speciﬁc record in a

large database. The tag has to provide the reader with

some identiﬁcation information, and the reader has to

search the database for some related information. The

information provided by tag for identiﬁcation, gener-

ically called tag identiﬁer, may facilitate more or less

the identiﬁcation process.

A tag identiﬁer should not be confused with the

tag’s identity. It may be a tag identity, but it may also

be a hash of a tag identity, or any other information

that uniquely identiﬁes the tag without loosing secu-

rity and privacy. A tag identiﬁer may also be a con-

stant value (as in the case of the tag’s identity), it may

be derived from the tag’s state, or from the tag’s state

and some message received from reader. Therefore, a

tag identiﬁer may change dynamically and this is why

the tag identiﬁcation in the back-end database might

not always be very efﬁcient.

The tag identiﬁcation time in the back-end

database depends on how the tag identiﬁers are

viewed as search indices (Silberschatz et al., 2010).

There are two main approaches along this line: or-

dered indices and hash indices.

An ordered index is a pair that consists of a search

key value and a pointer to the corresponding record or

to a disk block containing it in the back-end database.

Ordered indices are sorted by the search key value.

Therefore, the identiﬁcation time of a tag is propor-

tional to log n (n being the database size). When the

tag is identiﬁed and the tag’s state is updated, as it is

for instance in (Dimitriou, 2005; Tsudik, 2006; Vau-

denay, 2007; Paise and Vaudenay, 2008; Hristea and

T¸ iplea, 2019), the tag identiﬁer changes. Therefore,

the index structure has to be updated as well. This can

simply be done by deleting the old index entry and in-

serting the new one in the right position, which takes

time proportional to log n. Therefore, the entire pro-

cess is proportional to log n. Remark also that the new

index entry is obtained from the old one by replacing

the search key value (the pointer remains unaltered).

The sequential organization of indices has the

main disadvantage that performance degrades as the

index ﬁle grows. In such a case, one may think to

organize indices on multiple levels or even as a B

tree. Lookup on B

-trees is efﬁcient; deletion and

insertion are somewhat more complicated but still ef-

ﬁcient. Thus, if the number of pointers in a non-leaf

node is k, the height of the B

-tree is proportional to

log

n, and the identiﬁcation and updating time is pro-

portional to log

k/2

n. The value of k is often around

50 or 100 (Silberschatz et al., 2010).

The hash organization of a database uses a hash

function that maps the search key value to the ad-

dress of the desired record or to a bucket containing

it (a bucket is a unit of storage containing one or more

records; typically, a bucket is a disk block). In such

a case, the lookup time is usually a constant, inde-

pendent of the database size. This approach can be

used with all RFID schemes for which the tag identi-

ﬁer is constant, such as the PKC-based RFID scheme

in (Vaudenay, 2007).

There is also another approach based on hash in-

dices. Namely, we compute hash indices for all pos-

sible search keys of each tag, we associate the corre-

sponding pointers to the database records, and view

the hash index (the hash ﬁle structure) such obtained

as secondary (hash) indices. For this hash index we

may use the ﬁrst hashing approach to search within it.

However, the search time might not be constant.

In this paper we will look for constant-time iden-

tiﬁcation by using constant tag identiﬁers. This will

also allow for scalability. However, to avoid loss of

privacy, the constant tag identiﬁers need to be en-

capsulated. In (Vaudenay, 2007; Paise and Vaude-

nay, 2008), the PKC-based RFID scheme does this

by means of PKC. To get more efﬁciency, we would

like to do this by means of SKC. The details follow in

the next section.

5 DESTRUCTIVE PRIVACY

WITH CONSTANT-TIME

IDENTIFICATION

The PKC-based RFID scheme proposed in (Paise and

Vaudenay, 2008) achieves forward privacy and mu-

tual authentication. Moreover, it allows constant-time

identiﬁcation of tags in the reader’s database. This is

because the reader has a public key that is distributed

SECRYPT 2021 - 18th International Conference on Security and Cryptography

500

to all tags, while it keeps the corresponding private

key. Therefore, each tag can safely send its iden-

tity encrypted by the reader’s public key. The search

procedure in the database may then be organized by

means of hash indices computed on tag identities (as

we have discussed in Section 4).

This idea cannot be put into practice only by SKC

because the secret key is used for both encryption and

decryption. Sharing the secret key to all tags and the

reader raises serious security and privacy problems:

corruption of a tag reveals the secret key and the entire

system is compromised. However, if the secret key is

protected by PUFs, then it may act as a master key

known only to tags and reader. Trying to extract the

key from tags by corruption destroys the tags without

disclosing the key.

The ﬁrst attempt to design a destructive private

and mutual authentication RFID scheme by using

PUF protected secret keys was proposed in (Akg

and C¸ aglayan, 2015). Unfortunately, the scheme in

(Akg

un and C¸ aglayan, 2015) does not achieve de-

structive privacy in Vaudenay’s model with tempo-

rary state disclosure, as it was claimed by its authors.

This is because the scheme uses temporary variables

to carry crucial information from one tag step to an-

other one, and this information can be obtained by

corruption. For a detailed attack on the scheme the

reader is referred to (Hristea and T¸ iplea, 2019a).

However, if we combine the idea in (Akg

un and

C¸ aglayan, 2015) of using PUF protected secret keys

with the reader-ﬁrst authentication approach to avoid

the use of temporary variables, we arrive to an RFID

scheme that achieves destructive privacy and mutual

authentication in Vaudenay’s model with temporary

state disclosure, together with constant-time identiﬁ-

cation of tags in the back-end database.

We thus propose an RFID scheme based on an

SKE scheme {·}

whose block-length and key-

length are `, where ` is polynomial in the security

parameter λ. The secret key K

, also called the

master key of the scheme, is stored on reader and

all tags. However, to avoid key disclosure by tag

corruption, K

is stored on tags in a masked form

= K

⊕ P(s), where P is a PUF and s is a seed,

both of them speciﬁc to the tag.

Each tag is identiﬁed by its identity ID and is ini-

tially endowed with a random value x needed to ran-

domize the encryption. The value x is incremented

each time a tag is queried. For the simplicity of the

exposition we assume that ID, x, s, and P(s) are all of

the same length `.

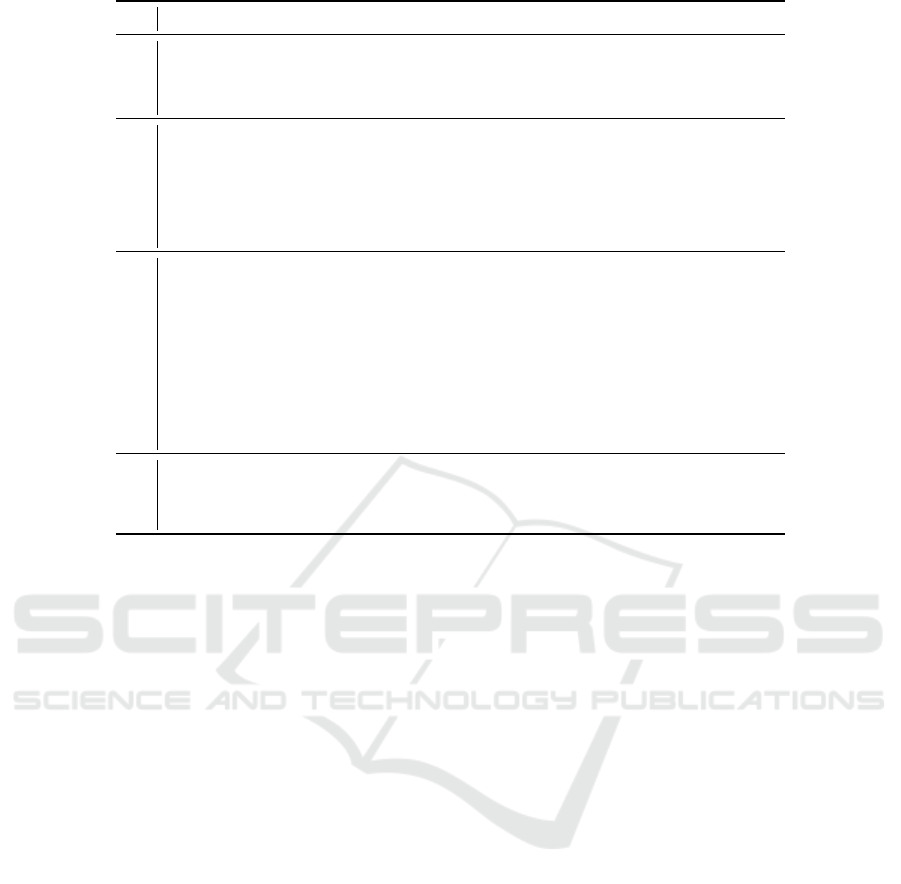
The mutual authentication protocol is represented

in Figure 1. The tag evaluates its PUF P on s, extracts

from K

with the help of P(s), and sends its en-

crypted credentials (x,ID) to the reader (in Figure 1,

k stands for string concatenation). Remark that x is

the ﬁrst block to be encrypted (using some operation

mode) because it will get a new value next time when

the protocol is initiated. In this why, the encryption

gets randomized

When the reader receives the message from tag,

decrypts it and looks for a corresponding record in

its database. If this is found, which means that the

reader identiﬁed the tag, an “authentication code” w

obtained from a random v and x is returned (remark

that v is the ﬁrst block to be encrypted). The tag

decrypts w and checks the x-values. If they match,

authenticates the reader and prepares an “authentica-

tion code” w

for reader. Note again that w

is built

by placing x on the ﬁrst position after it has been in-

cremented. When receiving w

, the reader checks it

against the value {(y + 2) k (v + 1)}

computed by

itself. If they match, the tag is authenticated and x

is synchronized (by incrementing it) with the corre-

sponding value on tag.

It is straightforward to check the correctness of

this scheme. We list below a few properties of it:

1. A tag may be queried multiple times without com-

pleting the protocol. In this case, the x-value on

tag gets greater than (but never less than) the cor-

responding value stored in the database. When

the tag is identiﬁed, the reader synchronizes its

x-value with the one used by tag to compose the

message w;

2. The scheme does not use temporary variables to

carry information between protocol steps. There-

fore, the scheme is secure and private in Vau-

denay’s model with temporary state disclosure if

and only if it is secure and private in Vaudenay’s

model without temporary state disclosure;

3. The tag identiﬁcation process takes constant time

if the database is organized by means of hash in-

dices computed on tag identities;

4. The scheme does not use RNGs on tags, which

might be a source of insecurity if they are not suf-

ﬁciently long. Secure RNGs require more than

1000 GEs (Armknecht et al., 2014);

5. There are lightweight block ciphers that are con-

sidered to be sufﬁciently secure at the moment and

which can efﬁciently be implemented on RFID

tags (please see the last section of the paper for

more details on this).

Remark 5.1. One can see from Figure 1 that mes-

sages to be encrypted have length 2`. According to

Formally, the encryption will be required to be IND-

CPA secure.

Practically Efﬁcient RFID Scheme with Constant-time Identiﬁcation

501

Reader (DB,K

) Tag (ID, x, K

,P,s)

1 K = P(s), K

= K

⊕ K,

x = x + 1, z = {x k ID}

←−

erase K, K

{z}

−1

= x k ID

If ∃(ID,y) ∈ DB and y < x

then y = x − 1, v ← {0,1}

w = {v k (y + 1)}

else w ← {0,1}

−→

3 K = P(s), K

= K

⊕ K,

{w}

−1

= v

k x

If x = x

then output OK, x = x + 1

= {x k (v

+ 1)}

else output ⊥, x = x + 1

= {x k (v

+ 2)}

←−

erase K, K

4 If w

= {(y + 2) k (v + 1)}

then output ID, y = y + 2

else output ⊥

Figure 1: Destructive private and mutual authentication scheme in Vaudenay’s model with temporary state disclosure.

our assumption, each message to be encrypted con-

sists of two blocks. Therefore, it sufﬁces for the SKE

scheme to be IND-CPA secure for such messages.

However, although the messages consist of only two

blocks, some operation mode has to be used. When

we proposed the scheme we have taken into consider-

ation the CBC operation mode. Under this operation

mode, the incrementation of x and the random choice

of v randomizes the ﬁrst block of the ciphertext. As

this block is then used to encrypt the next message

block, the entire encryption gets randomized.

What we have said above is just an explanation

that underpins the construction of our scheme. In

general it is sufﬁcient to ask the SKE scheme to be

IND-CPA secure in order to get security and privacy

of the RFID scheme (without any other constraints on

the operation mode).

The following theorems establish the security and

privacy properties of our scheme. Their proofs are

omitted due to space limitations, but the reader can

ﬁnd them in the appendix to assess their correctness.

The ﬁrst result is on tag authentication.

Theorem 1. The RFID scheme in Figure 1 achieves

tag authentication in Vaudenay’s model with tempo-

rary state disclosure, provided that the SKE scheme is

IND-CPA and the tags are endowed with ideal PUFs.

As with respect to the reader authentication prop-

erty, we have the following result.

Theorem 2. The RFID scheme in Figure 1 achieves

reader authentication in Vaudenay’s model with tem-

porary state disclosure, provided that the SKE scheme

is IND-CPA and the tags are endowed with ideal

PUFs.

Finally, we have the following privacy result.

Theorem 3. The RFID scheme in Figure 1 achieves

destructive privacy in Vaudenay’s model with tempo-

rary state disclosure, provided that the SKE scheme is

IND-CPA and the tags are endowed with ideal PUFs.

Remark 5.2. The RFID scheme in Figure 1 can be

easily transformed into a weak private scheme. What

we have to do is to remove the PUF from each tag

and to keep the master key K

in the tag’s permanent

memory. Although this might seem a good idea from

the constant-time identiﬁcation point of view, this so-

lution should be taken with great care. This is because

disclosure of K

compromises the entire scheme.

6 IMPLEMENTATION ISSUES

Practical implementation of the RFID scheme in the

previous section is conditioned by the existence of

lightweight symmetric-key encryption schemes. An

RFID tag has very few gates, and many of these are

taken up by logic required for basic operation. In

SECRYPT 2021 - 18th International Conference on Security and Cryptography

502

RFID

Scheme

Efﬁciency

Ident.

time

Auth. Privacy

(Paise and Vaudenay,

2008) and (iplea and

Hristea, 2021)

1 PKE + 2 PUF

+ 1 RNG

Constant Mutual

Destructive private in V TSD

(iplea and Hristea, 2021)

(Sadeghi et al., 2010)

1 PRF + 1 PUF

+ 1 RNG

Linear Unilateral Destructive private in V

(Hristea and T¸ iplea,

2019a)

2 PRF + 1 PUF

+ 1 RNG

Linear Mutual Destructive private in V

(Kardas¸ et al., 2012)

and (iplea and Hristea,

2021)

4 Hash + 4 PUF

+ 2 RNG

Linear Mutual

Destructive private in V TSD

(iplea and Hristea, 2021)

(Akg

un and C¸ aglayan,

2015) and (iplea and

Hristea, 2021)

4 Hash + 4 PUF

+ 1 RNG

Constant Mutual

Destructive private in V TSD

(iplea and Hristea, 2021)

This paper 3 SKE + 2 PUF Constant Mutual Destructive private in V TSD

Figure 2: Comparisons between RFID scheme trying to achieve destructive privacy in Vaudenay’s model: V stands for

Vaudenay’s model, V TSD stands for Vaudenay’s model with temporary state disclosure.

(Weis et al., 2004) it was estimated that about 5,000

gate equivalents (GEs) are left over in a typical RFID

tag for cryptographic functions. This somehow al-

lows compact implementations of the Advanced En-

cryption Standard (AES) cryptosystem on RFID tags,

that use around 2,400 GEs (Moradi et al., 2011;

Banik et al., 2016). However, with processors getting

smaller and faster, and with more devices becoming

mobile, the AES cryptosystem has become clunky,

while RFID technology developers are seeking some-

thing that consumes smaller area of about 2,000 GEs.

During the last ﬁfteen years a lot of effort has

been dedicated to propose lightweight block ciphers.

Among them, it is worth to mention PRESENT (Bog-

danov et al., 2007), Piccolo (Shibutani et al., 2011),

SIMON and SPECK (Beaulieu et al., 2015), and

Simeck (Yang et al., 2015). There are some similar-

ities between Simon/Speck and Simeck. For 32/64-

(48/96-, 64/128-) bit size, they require less than 580

(800, 1030) GEs. They also have comparable secu-

rity properties. As a conclusion, all of them can meet

the area, power consumption, and throughput require-

ments in the passive RFID tags, and they are promis-

ing candidates for resource-constrained devices, such

as passive RFID tags and wireless sensor networks.

Since their introduction, PUFs have been inte-

grated in various cryptographic protocols. Usually,

PUFs serve two main purposes: identiﬁcation and

cryptographic key generation. A primary example of

the former situation is (Devadas et al., 2008), where a

PUF has actually been integrated in an RFID tag. Key

generation by PUFs is a bit more delicate because we

need to overcome the PUF’s noisy nature and its lack

of entropy. Therefore, additional mechanisms such as

error correction codes, hash functions and helper data

algorithms are needed (Delvaux et al., 2015a).

Fortunately, this situation has changed recently

when new PUF constructions with very low bit er-

ror rates were proposed (Yoshimoto et al., 2016; Liu

et al., 2015; Chuang et al., 2017; Chuang et al., 2018).

The PUF design in (Chuang et al., 2017; Chuang

et al., 2018), based on the randomness of the soft

breakdown position of CMOS transistors, is such an

example. Denoted as BD-PUF, it represents a promi-

nent candidate for constructing PUF-based key gen-

eration mechanisms with good entropy.

7 CONCLUSIONS

We have proposed in this paper an RFID scheme

that achieves mutual authentication, destructive pri-

vacy, constant-time identiﬁcation, and is efﬁcient in

practical implementation. The scheme is based on

symmetric-key encryption. To avoid key disclosure

on tags, we have masked the key by PUF values. To

reach destructive privacy in Vaudenay’s model with

temporary state disclosure we avoided the use of tem-

porary variables by following the reader-ﬁrst authen-

tication approach. Constant-time identiﬁcation fol-

Practically Efﬁcient RFID Scheme with Constant-time Identiﬁcation

503

lows from the fact that each tag sends its encrypted

identity to the reader.

As far as we know, this is the most practically ef-

ﬁcient RFID scheme that achieves mutual authentica-

tion, destructive privacy, and constant-time identiﬁca-

tion in Vaudenay’s model with temporary state dis-

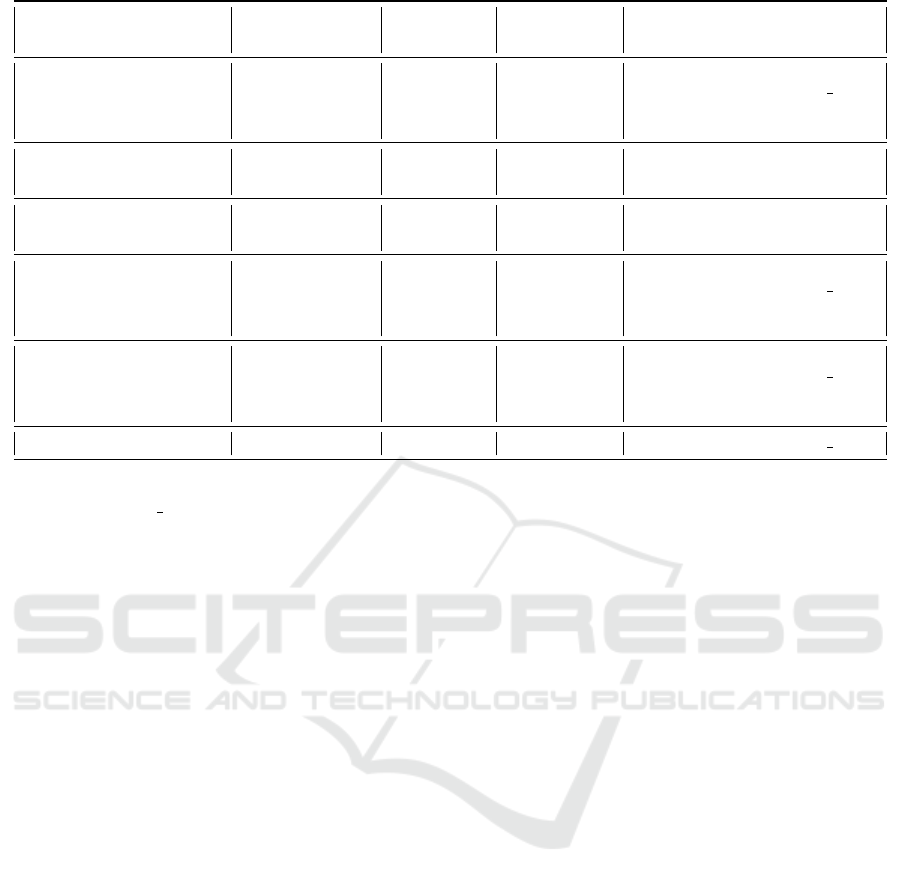
closure. The table in Figure 2 provides comparisons

between our scheme and the closest schemes to ours.

We would like to emphasize that reader authen-

tication and destructive privacy are not possible to-

gether only by means of standard cryptography, when

corruption with temporary state disclosure in allowed

(Armknecht et al., 2010). The only technique known

so far to bypass this limitation is by using PUFs.

REFERENCES

Akg

un, M. and C¸ aglayan, M. U. (2015). Providing de-

structive privacy and scalability in RFID systems us-

ing PUFs. Ad Hoc Netw., 32(C):32–42.

Alomair, B., Clark, A., Cu

ellar, J., and Poovendran, R.

(2012). Scalable RFID systems: A privacy-preserving

protocol with constant-time identiﬁcation. IEEE

Transactions on Parallel and Distributed Systems,

3(8):1536–1550.

Alomair, B., Lazos, L., and Poovendran, R. (2010). Secur-

ing low-cost RFID systems: An unconditionally se-

cure approach. In Li, Y. and Zhou, J., editors, Radio

Frequency Identiﬁcation System Security, volume 4 of

Cryptology and Information Security Series, pages 1–

17. IOS Press.

Armknecht, F., Hamann, M., and Mikhalev, V. (2014).

Lightweight authentication protocols on ultra-

constrained RFIDs – myths and facts. In Saxena,

N. and Sadeghi, A.-R., editors, Radio Frequency

Identiﬁcation: Security and Privacy Issues, pages

1–18, Cham. Springer International Publishing.

Armknecht, F., Sadeghi, A.-R., Scafuro, A., Visconti, I., and

Wachsmann, C. (2010). Impossibility results for RFID

privacy notions. In Gavrilova, M. L., Tan, C. J. K.,

and Moreno, E. D., editors, Transactions on Com-

putational Science XI, pages 39–63. Springer-Verlag,

Berlin, Heidelberg.

Arslan, A., Kardas¸, S., C¸ olak, S. A., and Ert

urk, S. (2018).

Are RNGs Achilles’ heel of RFID security and pri-

vacy protocols? Wireless Personal Communications,

100(4):1355–1375.

Banik, S., Bogdanov, A., and Regazzoni, F. (2016). Atomic-

AES: A compact implementation of the aes encryp-

tion/decryption core. In INDOCRYPT.

Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S.,

Weeks, B., and Wingers, L. (2015). The SIMON and

SPECK lightweight block ciphers. In Proceedings

of the 52Nd Annual Design Automation Conference,

DAC ’15, pages 175:1–175:6, New York, NY, USA.

ACM.

Bogdanov, A., Knudsen, L. R., Leander, G., Paar, C.,

Poschmann, A., Robshaw, M. J. B., Seurin, Y.,

and Vikkelsoe, C. (2007). PRESENT: An ultra-

lightweight block cipher. In Paillier, P. and Ver-

bauwhede, I., editors, Cryptographic Hardware and

Embedded Systems – CHES 2007, pages 450–466,

Berlin, Heidelberg. Springer Berlin Heidelberg.

Bohli, J.-M. and Pashalidis, A. (2011). Relations among

privacy notions. ACM Trans. Inf. Syst. Secur.,

14(1):4:1–4:24.

Canard, S., Coisel, I., Etrog, J., and Girault, M. (2010).

Privacy-preserving RFID systems: Model and con-

structions. https://eprint.iacr.org/2010/405.pdf.

Chuang, K.-H., Bury, E., Degraeve, R., Kaczer, B., Groe-

seneken, G., Verbauwhede, I., and Linten, D. (2017).

Physically unclonable function using cmos break-

down position. In 2017 IEEE International Reliability

Physics Symposium (IRPS), pages 4C–1. IEEE.

Chuang, K.-H., Bury, E., Degraeve, R., Kaczer, B., Linien,

D., and Verbauwhede, I. (2018). A physically unclon-

able function with 0% ber using soft oxide breakdown

in 40nm cmos. In 2018 IEEE Asian Solid-State Cir-

cuits Conference (A-SSCC), pages 157–160. IEEE.

T¸ iplea, F. L., Andriesei, C., and Hristea, C. (2021). Security

and privacy of PUF-based RFID systems. In Cryptog-

raphy - Recent Advances and Future Developments.

IntechOpen, London, UK. Online ﬁrst.

Delvaux, J., Gu, D., Schellekens, D., and Verbauwhede, I.

(2015a). Helper data algorithms for PUF-based key

generation: Overview and analysis. IEEE Transac-

tions on Computer-Aided Design of Integrated Cir-

cuits and Systems, 34(6):889–902.

Delvaux, J., Peeters, R., Gu, D., and Verbauwhede, I.

(2015b). A survey on lightweight entity authentication

with strong PUFs. ACM Comput. Surv., 48(2):26:1–

26:42.

Deng, R. H., Li, Y., Yung, M., and Zhao, Y. (2010). A new

framework for RFID privacy. In Proceedings of the

15th European Conference on Research in Computer

Security, ESORICS’10, pages 1–18, Berlin, Heidel-

berg. Springer-Verlag.

Devadas, S., Suh, E., Paral, S., Sowell, R., Ziola, T.,

and Khandelwal, V. (2008). Design and implemen-

tation of PUF-based unclonable RFID ICs for anti-

counterfeiting and security applications. In 2008

IEEE international conference on RFID, pages 58–64.

IEEE.

Dimitriou, T. (2005). A lightweight RFID protocol to pro-

tect against traceability and cloning attacks. In Pro-

ceedings of the First International Conference on Se-

curity and Privacy for Emerging Areas in Commu-

nications Networks, SECURECOMM ’05, pages 59–

66, Washington, DC, USA. IEEE Computer Society.

EPCglobal (2016). Interoperability test system for EPC

compliant Class-1 Generation-2 UHF RFID devices.

Technical report, GS1 EPCglobal Inc.

Haddara, M. and Staaby, A. (2018). Rﬁd applications and

adoptions in healthcare: A review on patient safety.

Procedia computer science, 138:80–88.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

504

Hermans, J., Pashalidis, Andreasand Vercauteren, F., and

Preneel, B. (2011). A new RFID privacy model. In

Atluri, V. and Diaz, C., editors, Computer Security –

ESORICS 2011, pages 568–587, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Hermans, J., Peeters, R., and Preneel, B. (2014). Proper

RFID privacy: Model and protocols. IEEE Transac-

tions on Mobile Computing, 13(12):2888–2902.

Hristea, C. and T¸ iplea, F. L. (2019a). Destructive pri-

vacy and mutual authentication in Vaudenay’s RFID

model. Cryptology ePrint Archive, Report 2019/073.

https://eprint.iacr.org/2019/073.

Hristea, C. and T¸ iplea, F. L. (2019b). Privacy of state-

ful RFID systems with constant tag identiﬁers. IEEE

Transactions on Information Forensics and Security,

15:1920–1934. early access.

Hristea, C. and T¸ iplea, F. L. (2019). A PUF-based destruc-

tive private mutual authentication RFID protocol. In

Lanet, J.-L. and Toma, C., editors, Innovative Security

Solutions for Information Technology and Communi-

cations, pages 331–343, Cham. Springer International

Publishing.

iplea, F. L. and Hristea, C. (2021). PUF protected variables:

A solution to rﬁd security and privacy under corrup-

tion with temporary state disclosure. IEEE Transac-

tions on Information Forensics and Security, 16:999–

1013.

Juels, A. and Weis, S. A. (2009). Deﬁning strong privacy for

RFID. ACM Trans. Inf. Syst. Secur., 13(1):7:1–7:23.

Kardas¸, S., C¸ elik, S., Yildiz, M., and Levi, A. (2012). PUF-

enhanced ofﬂine RFID security and privacy. J. Netw.

Comput. Appl., 35(6):2059–2067.

Katz, J. and Lindell, Y. (2014). Introduction to Modern

Cryptography. Chapman & Hall/CRC, 2nd edition.

Lahtela, A. (2009). A short overview of the rﬁd technol-

ogy in healthcare. In 2009 Fourth International Con-

ference on Systems and Networks Communications,

pages 165–169. IEEE.

Liu, R., Wu, H., Pang, Y., Qian, H., and Yu, S. (2015).

Experimental characterization of physical unclon-

able function based on 1 kb resistive random ac-

cess memory arrays. IEEE Electron Device Letters,

36(12):1380–1383.

Lu, L., Liu, Y., and Li, X.-Y. (2010). Refresh: Weak pri-

vacy model for RFID systems. In Proceedings of

the 29th Conference on Information Communications,

INFOCOM’10, pages 704–712, Piscataway, NJ, USA.

IEEE Press.

Maes, R. (2013). Physically Unclonable Functions: Con-

structions, Properties and Applications. Springer Ver-

lag.

Maes, R. and Verbauwhede, I. (2010). Physically unclon-

able functions: A study on the state of the art and fu-

ture research directions. In Sadeghi, A.-R. and Nac-

cache, D., editors, Towards Hardware-Intrinsic Secu-

rity: Foundations and Practice, pages 3–37. Springer

Berlin Heidelberg, Berlin, Heidelberg.

Moradi, A., Poschmann, A., Ling, S., Paar, C., and Wang,

H. (2011). Pushing the limits: A very compact and a

threshold implementation of AES. In Paterson, K. G.,

editor, Advances in Cryptology – EUROCRYPT 2011,

pages 69–88, Berlin, Heidelberg. Springer Berlin Hei-

delberg.

Paise, R.-I. and Vaudenay, S. (2008). Mutual authentication

in RFID: Security and privacy. In Proceedings of the

2008 ACM Symposium on Information, Computer and

Communications Security, ASIACCS ’08, pages 292–

299, New York, NY, USA. ACM.

Preneel, B. (2018). Cryptography best practices. Online

communication at https://secappdev.org/handouts-

2018.html.

Sadeghi, A.-R., Visconti, I., and Wachsmann, C. (2010).

PUF-enhanced RFID security and privacy. In Work-

shop on secure component and system identiﬁcation

(SECSI), volume 110.

Shibutani, K., Isobe, T., Hiwatari, H., Mitsuda, A., Ak-

ishita, T., and Shirai, T. (2011). Piccolo: An ultra-

lightweight blockcipher. In Preneel, B. and Takagi,

T., editors, Cryptographic Hardware and Embedded

Systems – CHES 2011, pages 342–357, Berlin, Hei-

delberg. Springer Berlin Heidelberg.

Silberschatz, A., Korth, H., and Sudarshan, S. (2010).

Database Systems Concepts. McGraw-Hill Educa-

tion, Inc., New York, NY, USA, 6 edition.

Sipser, M. (2012). Introduction to the Theory of Computa-

tion. Cengage Learning.

Tsudik, G. (2006). YA-TRAP: Yet another trivial RFID

authentication protocol. In Proceedings of the 4th

Annual IEEE International Conference on Pervasive

Computing and Communications Workshops, PER-

COMW ’06, page 640, Washington, DC, USA. IEEE

Computer Society.

Vaudenay, S. (2007). On privacy models for RFID. In Pro-

ceedings of the Advances in Crypotology 13th Interna-

tional Conference on Theory and Application of Cryp-

tology and Information Security, ASIACRYPT’07,

pages 68–87, Berlin, Heidelberg. Springer-Verlag.

Weis, S. A., Sarma, S. E., Rivest, R. L., and Engels,

D. W. (2004). Security and privacy aspects of low-

cost radio frequency identiﬁcation systems. In Hut-

ter, D., M

uller, G., Stephan, W., and Ullmann, M.,

editors, Security in Pervasive Computing, pages 201–

212, Berlin, Heidelberg. Springer Berlin Heidelberg.

Yang, G., Zhu, B., Suder, V., Aagaard, M. D., and Gong,

G. (2015). The simeck family of lightweight block

ciphers. In G

uneysu, T. and Handschuh, H., ed-

itors, Cryptographic Hardware and Embedded Sys-

tems – CHES 2015, pages 307–329, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Yao, W., Chu, C.-H., and Li, Z. (2010). The use of rﬁd in

healthcare: Beneﬁts and barriers. In 2010 IEEE Inter-

national Conference on RFID-Technology and Appli-

cations, pages 128–134. IEEE.

Practically Efﬁcient RFID Scheme with Constant-time Identiﬁcation

505

Yao, W., Chu, C.-H., and Li, Z. (2012). The adoption

and implementation of rﬁd technologies in health-

care: a literature review. Journal of medical systems,

36(6):3507–3525.

Yoshimoto, Y., Katoh, Y., Ogasahara, S., Wei, Z., and

Kouno, K. (2016). A reram-based physically unclon-

able function with bit error rate ¡ 0.5% after 10 years at

125

◦

c for 40nm embedded application. In 2016 IEEE

Symposium on VLSI Technology, pages 1–2. IEEE.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

506