EPredictor: An Experimental Platform for Community Evolution

Prediction Tests

Narimene Dakiche

1 a

, Fatima Benbouzid-Si Tayeb

, Karima Benatchba

, Yahya Slimani

Abdelouahab Khelifati

and Hadjer Chabane

Laboratoire des M

ethodes de Conception de Syst

emes (LMCS), Ecole Nationale Sup

erieure d’Informatique (ESI),

BP 68M, 16270 Oued Smar, Alger, Algeria

Computer Science Department, ISAMM, Institute of Manouba, 2010 Manouba, Tunisia

Keywords:

Dynamic Social Network, Community Detection, Community Evolution, Evolution Prediction.

Abstract:

This paper presents “EPredictor” an experimental platform which enables testing, verifying and validating

models related to community evolution prediction in dynamic social networks. Community evolution pre-

diction is one of the most interesting issues in the ﬁeld of social network analysis. It is usually handled by

following four main steps: (1) split the network into timeframes; (2) detect communities in each timeframe;

(3) track their evolutionary behavior and (4) build a predictive model to forecast the future events. The main

objective of EPredictor is to provide a ﬂexible environment that handles the entire process of community evo-

lution prediction with a rich set of literature methods for each step; thus enabling researchers to make valuable

comparisons and consistent analysis.

1 INTRODUCTION

Social networks have become ubiquitous and increas-

ingly popular. They have interesting properties that

gave rise to the very active ﬁeld of Social Network

Analysis (SNA). SNA exploit network and graph the-

ories in order to understand the relationship between

members involved in an interaction for numerous use-

ful purposes. Social networks are usually represented

by graphs in which the nodes represent the social en-

tities (e.g., individuals) and the edges describe so-

cial interactions (e.g., friendship, collaboration, trust,

etc) (Tabassum et al., 2018). A further abstraction of

the network concept is the dynamic network in which

changes occur over time. These changes happen when

new nodes join the network, existing ones leave it, or

when existing pairs of nodes establish a new relation

or terminate an existing one over time.

One important characteristic of social networks is

community structure, i.e., groups of nodes closer to

each other in comparison to other nodes of the net-

work. On a community scale, network dynamics re-

sult in certain evolutionary events such as growth,

merge, split and survive (Br

odka et al., 2013). Model-

ing and detecting community evolution have become

https://orcid.org/0000-0003-2371-616X

a subject of great interest and many researchers have

contributed to the understanding of the phenomena

(Dakiche et al., 2018). Indeed, the study of commu-

nity evolution plays a prominent role in understand-

ing the changes of networks and predict their future

(Saganowski et al., 2019).

In the related literature, the main issues are how to

detect critical events a community can undergo, how

to track communities over time and how to predict

their future. Existing approaches of predicting com-

munity evolution (Br

odka et al., 2013; Takaffoli et al.,

2014; Diakidis et al., 2015;

Ilhan and

u, 2016;

Pavlopoulou et al., 2017; Saganowski et al., 2019; Ra-

jita et al., 2020; Dakiche et al., 2021) are typically ad-

dressed through the same main steps: (1) split the net-

work into timeframes also called snapshots; (2) detect

communities in each timeframe; (3) track their evolu-

tionary behavior and (4) build a predictive model to

forecast the future events.

For each one of the listed steps, there exist several

literature methods that can be used. However, to the

best of our knowledge, no research tool that handles

the entire process for predicting community evolution

were proposed.

Dakiche, N., Benbouzid-Si Tayeb, F., Benatchba, K., Slimani, Y., Khelifati, A. and Chabane, H.

EPredictor: An Experimental Platform for Community Evolution Prediction Tests.

DOI: 10.5220/0010547502950302

In Proceedings of the 11th Inter national Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2021), pages 295-302

ISBN: 978-989-758-528-9

295

In this paper, we present “EPredictor” an exper-

imental platform that enables testing, verifying and

validating models related to predicting community

evolution in dynamic social networks. Our challenge

is to provide a ﬂexible environment to conduct com-

munity evolution prediction with a rich set of litera-

ture methods for each step; thus enabling researchers

to make valuable comparisons and consistent analy-

sis. Besides, EPredictor can be enriched by adding

other options and methods in each step.

The remainder of this paper is organized as fol-

lows. Section 2 brieﬂy introduces the community evo-

lution prediction approach. Section 3 presents the

EPredictor platform and illustrates its features and

functionalities. Finally, Section 4 gives a resume and

outlines future developments.

2 COMMUNITY EVOLUTION

PREDICTION

Community evolution prediction is usually handled

as a supervised learning task, where the history of a

community is used to predict its future. Often, three

or four past instances are used to train a classiﬁer.

It consists of four main steps as shown in Fig.1: (1)

The dynamic social network data are segmented into

a series of timeframes also called snapshots; (2) Each

timeframe is partitioned using a community detection

algorithm and for each community a set of features,

mostly related to the link structure, such as the size,

cohesion, and density are computed; (3) Then evolu-

tion events of communities in consecutive timeframes

are identiﬁed; (4) Finally, a predictive model to fore-

cast community future occurring events is built. The

rest of this section deals with a detail description of

Figure 1: Community evolution prediction process.

these steps.

2.1 Network Splitting

A dynamic social network G = (V, E

) is deﬁned by

a set of nodes V and a set of time-stamped edges

describing the interactions among them. Each edge

e ∈ E

represents an interaction between two nodes

u, v ∈ V at time t (Holme and Saram

aki, 2012).

In order to analyze the dynamic network G, it is

split into τ consecutive timeframes, thus obtaining a

set of graphs G = (G

, ..., G

)., where G

= (V

, E

)

represents a graph with only the set of nodes and

edges that appears in the interval (t

i+1

2.2 Community Detection

Partitioning a network into communities is a difﬁ-

cult task; thus, several methods have been proposed

during the last decade, each one of them tailored to

extract communities carrying speciﬁc characteristics

(El Moussaoui et al., 2019).

Formally, given a dynamic social network G =

, ..., G

) as input, for each snapshot, its corre-

sponding communities are detected. The k commu-

nities detected in the i

snapshot are denoted by C

, ...,C

) where community C

∈ C

, 1 ≤ p ≤ k,

is also a graph denoted by (V

, E

2.3 Community Matching

The crucial goal of this phase is to detect commu-

nity evolution between consecutive snapshots. It con-

sists in ﬁnding series of similar communities in differ-

ent snapshots. Thus, a dynamic community is repre-

sented by its constituent communities ordered by time

snapshots. Formally, the dynamic community is de-

noted by DC = {C

, ...,C

}, where t

< t

< ... <

and C

represents its instance community at time

. Besides, the evolution is represented by the events

a community may undergo from one snapshot to an-

other i.e., events like splitting, growing, merging, dis-

solving and so on. This raises the problem of ﬁnding

a given community at time t

among those of time t

i+1

There are several taxonomies in the literature that

categorize the changes which are likely to occur to

a community. For example, Asur et al. (2009) dis-

tinguish ﬁve possible events, i.e., the communities

may dissolve, form, continue, merge and split; while

odka et al. (2013), in turn, describe seven no-

ticeable event types: continuing, shrinking, growing,

splitting, merging, dissolving and forming. The com-

munity evolution can then be deﬁned as a sequence

of communities ordered by time, from the timeframe

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

296

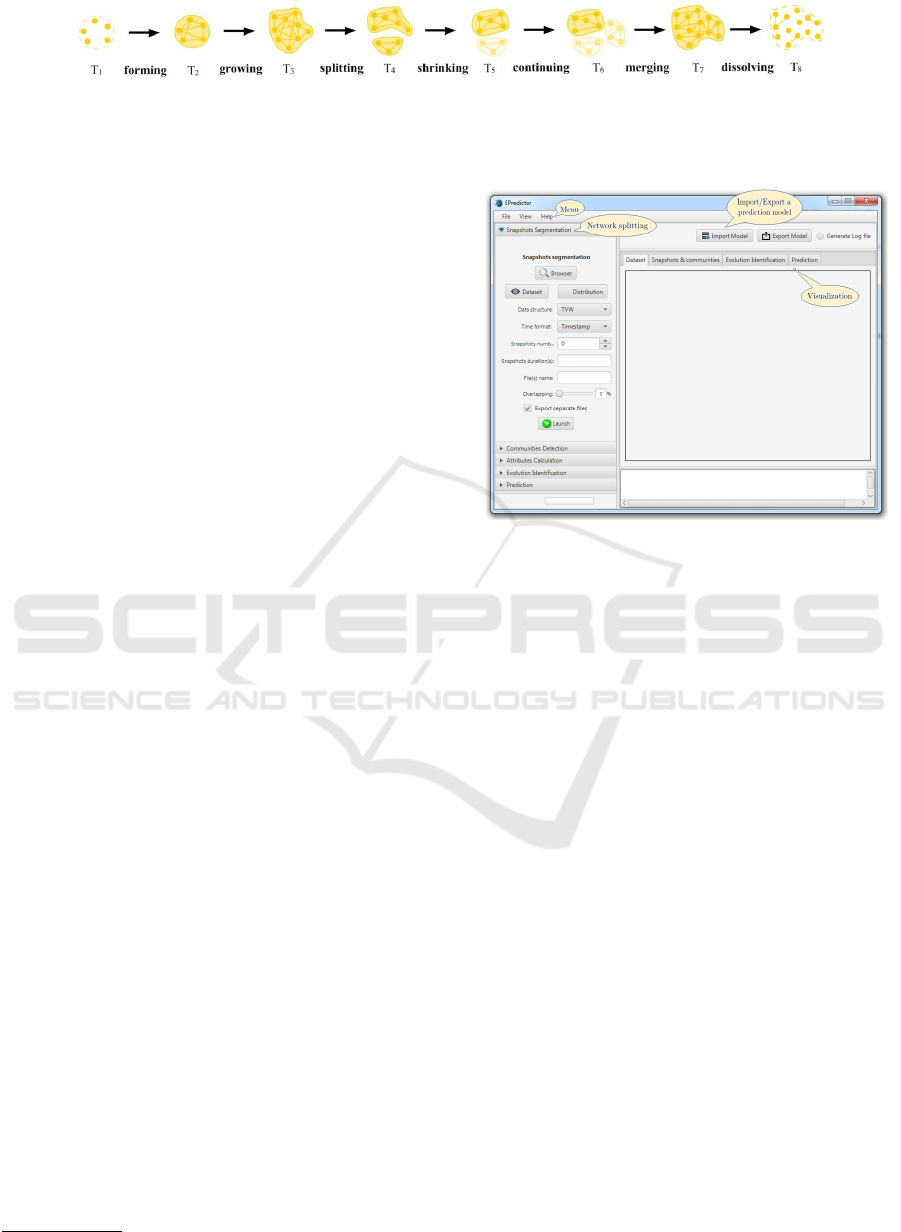
Figure 2: Community evolution in a dynamic network (Br

odka et al., 2013).

where it ﬁrst appears to the timeframe where it is last

observed (Fig. 2).

2.4 Prediction

In this step, the predictive model is built. The fea-

tures previously computed and the identiﬁed evolu-

tion events are used to create community evolution

sequences. A collection of community evolution se-

quences is the ﬁnal form of the data used for training

and testing the classiﬁers.

A community evolution sequence contains a com-

munity and its several past instances from the previ-

ous frames. Formally, it consists of the current com-

munity C

, the p

community of timeframe t

, and

its previous instances C

i−1

, C

i−2

, ..., C

i−n

. It looks as

follows:

input = (C

i−n

, ...,C

i−2

i−1

) (1)

Each community instance at a speciﬁc timeframe is

described by its structural features and its identiﬁed

evolution event. Vector (2) represents the structure of

each community instance.

= [ f

p,t

, f

p,t

, ..., f

p,t

, event] (2)

The goal of classiﬁcation is to predict the next

event for a given community. In what follows, we

present in details the EPredictor platform.

3 THE EPredictor PLATFORM

EPredictor

is an experimentation platform (Fig.3)

which handle the entire prediction process. It is ded-

icated to test and validate community evolution pre-

diction models. The main objective of EPredictor is

to provide a variety of community evolution predic-

tion experimental scenarios for various real social net-

works. This experimental platform allows to conduct

the prediction process passing through its main steps,

offering for each step the possibility to use different

literature methods. Thus, it offers the possibility to

get a signiﬁcant number of experiments for only one

network. Besides, it is possible to enrich the platform

by adding other options and methods in each step.

Moreover, EPredictor allows to conduct the predic-

tion process by starting from any step, importing and

https://github.com/NarimeneDakiche/EPredicror

exporting multiple kinds of data and visualizing re-

sults of different methods.

Figure 3: The EPredictor platform.

The EPredictor architecture is based on the com-

munity evolution prediction process steps as shown

in Fig.4. It is composed of the following six modules:

a data input/output module allowing to start commu-

nity evolution prediction from any step of the predic-

tion process; a network segmentation module to split

the network into several timeframes; a community de-

tection module to identify corresponding communi-

ties of each timeframe; an attribute computation mod-

ule to compute communities structural features; an

evolution identiﬁcation module to provide communi-

ties evolution events; a prediction module to forecast

communities future events and a visualization mod-

ule to visualize the results of each one of the previous

modules. In the following subsections, we detail the

functionalities of each module.

3.1 Data Input/Output Module

EPredictor offers the possibility to load different for-

mats and types of data: dynamic network data, time-

frame data, community data, and learning data.

• Loading data from a dynamic network in order to

be split into several timeframes.

As it is shown in Fig.5, EPredictor allows to vi-

sualize some lines of the data source ﬁle in order to

observe the information carried on each edge. In-

deed, the edges must be time-stamped and this times-

tamp can have different types. It can be recorded as

EPredictor: An Experimental Platform for Community Evolution Prediction Tests

297

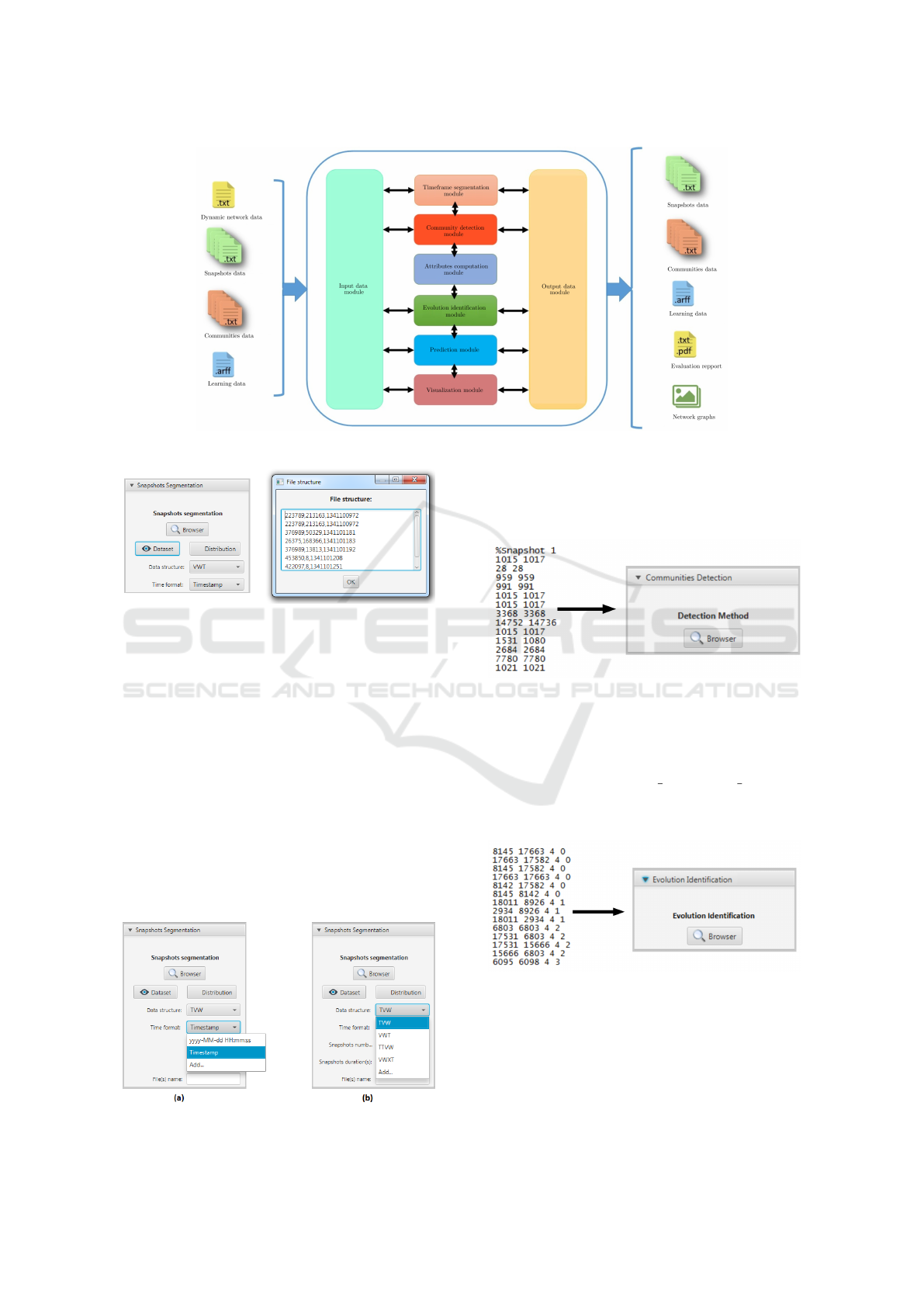
Figure 4: The EPredictor modules.

Figure 5: Loading dynamic network data.

a unix-timestamp “1284101485” or as a human date

“2010-09-10 06:51:25”. It is also possible to add a

new type if needed (see Fig.6-(a)). To correctly pro-

cess the network splitting, the user should specify the

adequate type describing the edges. Besides, the order

of information carried on each edge is important and

should be indicated carefully. For example, an edge

between two nodes V and W can be stored according

to different formats such as node1|node2|Stamp or

Stamp|node1|node2. For this reason, the user should

specify how these three elements are stored in the ﬁle

data. The ﬁrst node is represented by ’V’, the second

node by ’ W’, time by ’T’ and any other information

by ’X’. It is also possible to add a new structure of

data if needed (see Fig.6-(b)).

Figure 6: Timestamp and network data types.

• Loading data from timeframe ﬁles (Fig.7): each

ﬁle contains data of one snapshot. This data is

used in the step of community detection.

Figure 7: Loading timeframe data.

• Loading data from community ﬁles (Fig.8): each

ﬁle contains data of detected communities into

one timeframe according to the following format:

node1|node2|community id|snapshot id. This

data is used to compute community attributes and

to identify their evolution events.

Figure 8: Loading community data.

• Loading data from an ARFF ﬁle (Hall et al., 2009)

containing the learning instances to be used in the

prediction model.

• Loading a prediction model (.log ﬁle) containing

all the methods used in the different steps with all

their required parameters (Fig.9).

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

298

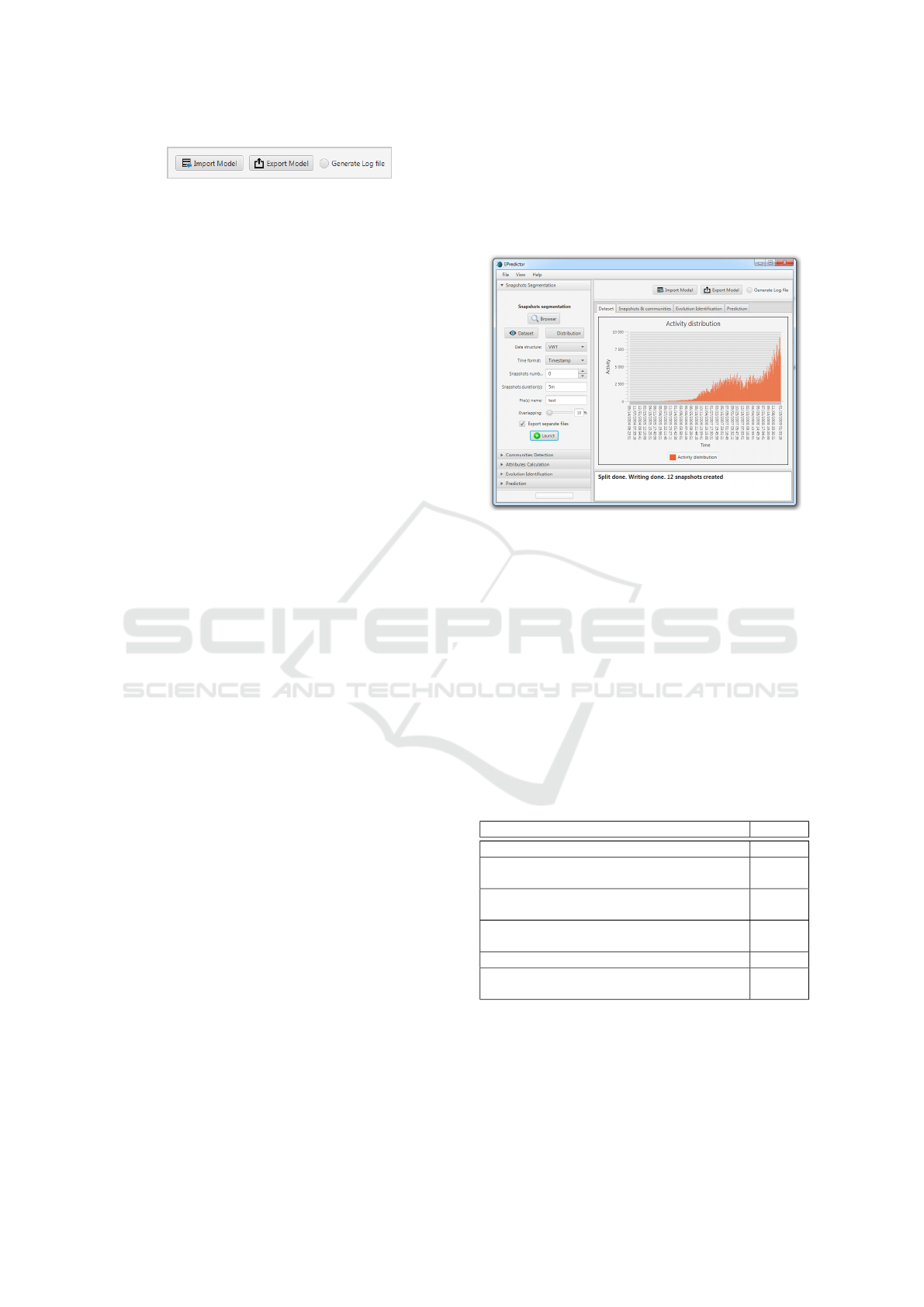
Figure 9: Import / Export of a prediction model.

At the end of each step the results are automat-

ically exported into a folder in the directory of the

executable such as timeframe ﬁles, detected commu-

nities, evolution sequences, learning instances and the

ﬁnal evaluation report.

3.2 The Timeframe Segmentation

Module

This module allows starting the community evolution

prediction from the ﬁrst step which consists of split-

ting the network data into several timeframes. EPre-

dictor offers several parameters to perform the seg-

mentation which is done according to one or more of

the given parameters as shown in Fig.10. The most

important are the following:

• Timeframe number where EPredictor generates a

set of timeframes covering equal durations.

• Timeframe duration which is an alternative op-

tion to the previous one; indeed, instead of giving

the resulting number of timeframes, the segmenta-

tion can be done according to the duration of each

timeframe. There are two scenarios for using this

parameter:

– One time duration. Giving a single duration

as a parameter means that the durations of all

timeframes must be equal to this duration.

– Multiple durations. The network data may

not be uniformly distributed, so the segmented

timeframes with equal duration can result in a

sequence of empty timeframes. To solve this,

splitting can be done using unequal durations

and thus gathering the successive empty time-

frames in a single one.

Furthermore, EPredictor supports different time

units. In order to introduce a duration, it should be

given in the form “dU” where d is an integer repre-

senting the value of the duration and U is the unit of

time. The time unit could be {H: Hour, D: day, W:

week, M: month, Y: year}.

• The overlapping rate: is the percentage of the

intersection between two consecutive time-

frames. This parameter is used to create common

elements between the various consecutive time-

frames and consequently slow down the evolution

between them in order to better identify the

evolution events. This continuity will be used

for the identiﬁcation phase of the subsequent

evolution.

The timeframe data will be exported, following

the user’s choice, either in separate ﬁles or in one ﬁle

with a supplement ﬁeld indicating the adequate time-

frame. The name of the ﬁles in which the data is ex-

ported should be given.

Figure 10: Timeframe segmentation.

3.3 The Community Detection Module

The EPredictor platform offers the possibility to

choose one among several community detection

methods. Indeed, in order to compare the perfor-

mance of different community detection algorithms

on prediction of the community evolution, we in-

cluded various algorithms commonly used in social

network analysis studies (El Moussaoui et al., 2019),

which are presented in Table 1. Two of them detect

disjoint communities, while the others can ﬁnd com-

munities that overlap which is more realistic in real

social networks.

Table 1: Community detection algorithms.

Method Overlap

CPM (Clique Percolation Method) 3

CONGA (Cluster-Overlap Newman Girvan

Algorithm)

COPRA (Community Overlap PRopagation

Algorithm)

CONCLUDE (COmplex Network CLUster

DEtection)

CM (CliqueMod) 7

SLPA (Speaker-listener Label Propagation

Algorithm)

No matter which algorithm is used, at the end of

the community detection on all timeframes, the re-

sults are displayed as shown in Fig.11. In this step,

communities of all timeframes are detected. It is pos-

sible to locate the timeframe data on the disk directly,

without going through the segmentation step. Then

EPredictor: An Experimental Platform for Community Evolution Prediction Tests

299

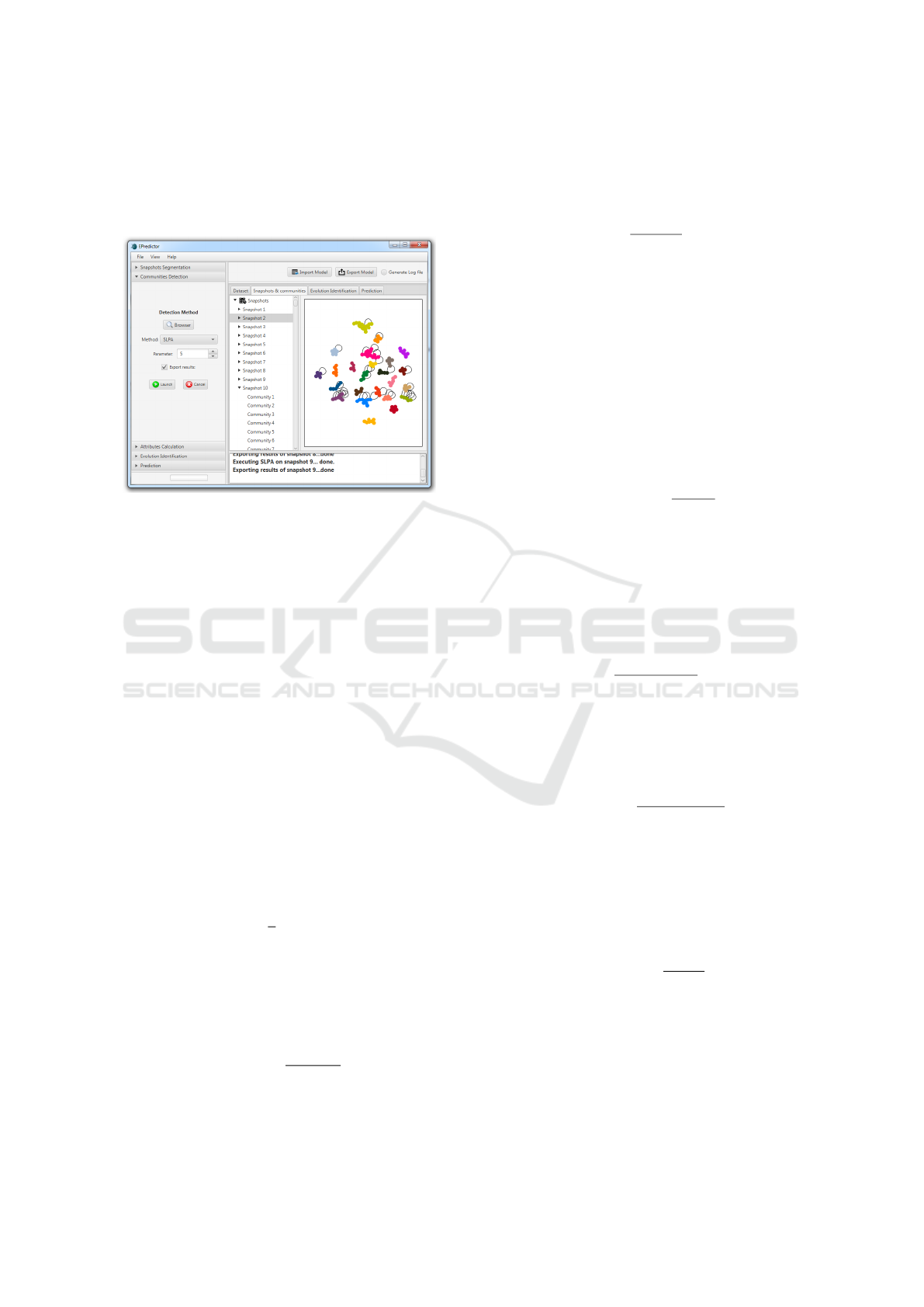
the method of detection is selected as well as its re-

quired parameter, if it exists, otherwise the parameter

ﬁeld is not editable. The user could choose whether

or not to export the detection results.

Figure 11: Community detection.

3.4 The Attributes Computation

Module

The next step of EPredictor is to compute a set of

community features that may be important to deter-

mine community evolution and measure the commu-

nities from structural aspects (Tabassum et al., 2018)

(Fig.12). These features encompass many structural

properties; they can describe the community itself

such as size, average density, cohesion, leadership,

reciprocity, and so on. Alternatively, they can deﬁne

the nodes belonging to a community such as the total

degree of nodes, the incoming and outgoing degrees,

the intermediate centrality, and so on. The explana-

tions for the features/structural measures, available in

EPredictor, are presented below:

• Size: the number of nodes in the community (n).

• Average Degree: the ratio of the sum of degrees

of the nodes in the community to the number of

nodes in the community:

∑

u=1

where d

means the degree value of node u in the

community.

• Clustering Coefﬁcient: a measure of how com-

plete a node’s neighborhood is to the number of

nodes in the community.

u−1

)

where t

is the the number of triangles in which

node u participates.

• Density: a measure expressing how many con-

nections between nodes are present in the com-

munity in relation to all possible connections be-

tween them:

2 · E

n(n − 1)

where E

is the number of edges within the com-

munity.

• Diameter: the greatest shortest paths between any

pair of nodes in the community:

max(σ(u, v)) ∀u, v ∈ V

where function σ(u, v) is the shortest path from

node u to v.

• Betweenness Centrality: a node measure describ-

ing the number of the shortest paths from all nodes

to all others that pass through that node.

∑

u6=v6=w

(w)

where σ

align is the total number of the shortest

paths from node u to v and σ

(w) is the number

of those paths that pass through w.

• Cohesion: a measure characterizing strength of

connections inside the group in relation to the

connections outside the group:

2 · E

− n)

out

(n − 1)

where E

out

is the set of outer edges of the commu-

nity and n

is the number of nodes in the network.

• Leadership: a measure describing centralization

in the graph or community:

L =

∑

u=1

max

− d

(n − 2)(n − 1)

where d

max

means the maximum value of degree

in the community and n the number of nodes in

the community.

• Closeness Centrality: a node measure deﬁned as

the inverse of the farness, which in turn, is the sum

of distances to all other nodes:

∑

u6=v

d(u, v)

where function d(u, v) is distance from node

u to v.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

300

Figure 12: Attribute computation.

3.5 The Evolution Identiﬁcation Module

This step consists in applying a community tracker in

order to determine the events depicting the evolution-

ary behavior of each detected community. Right now,

there are two methods implemented in the EPredictor

platform: GED (Group Evolution Discovery) (Br

odka

et al., 2013) and Asur’s method. For both, it is possi-

ble to introduce the required parameters. For example

GED depends on two parameters (α and β) as well

as a node’s importance measure that could be chosen

among the list of attributes previously computed.

The results are displayed in a chart depicting the

numbers of each identiﬁed event as shown in Fig. 13.

If the user starts the prediction process from this step,

community data is loaded directly from the disk. In

this case, the attributes will be automatically com-

puted before starting the evolution events identiﬁca-

tion. According to the user’s choice, the results will

be exported to a database ﬁle containing the detected

community evolution sequences.

Figure 13: Evolution event identiﬁcation.

3.6 The Prediction Module

In the last step, users have the possibility to choose

the classiﬁer to be used for the prediction task. EPre-

dictor includes several Weka classiﬁers: NaiveBayes,

BayesNet, J48, SMO, randomForest, decisionStump,

perceptron, Logistic, RandomTree, iBk, oneR and

Bagging (Hall et al., 2009). Given the fact that classi-

ﬁcation algorithms are sensitive to data, it is pertinent

to use several classiﬁers to perform credible compar-

isons.

As previously explained, community evolution

sequences are used to train the classiﬁer. Users

could specify the length of community evolution se-

quences as well as the attributes describing a commu-

nity instance from the list of the computed attributes

(Fig.14). For the classiﬁcation, it is possible to choose

the attribute selection technique; it could be either

manual, by ﬁltering or by encapsulation. The manual

selection considers the attributes notched by the user.

For the selection by ﬁltering or encapsulation, the user

has to choose a research method that deﬁnes a subset

of attributes to be used for the prediction. Then, the

predictive capacity of this subset of attributes is eval-

uated. To export the results, if notched, an evaluation

report will be exported in Pdf containing a synthesis

of the built model of prediction. It is also possible to

start the prediction process from this step by loading

the community evolution sequences stored in an .arff

ﬁle directly from the disk.

Figure 14: Evolution prediction results.

3.7 Results Visualization

EPredictor allows to visualize the results of the differ-

ent treatments of the community evolution prediction

process. More speciﬁcally, the distribution of network

activity over time (Fig.10), the detected communi-

ties and their timeframes (Fig.11, Fig.12), evolution

EPredictor: An Experimental Platform for Community Evolution Prediction Tests

301

identiﬁcation results (Fig.13) and prediction results

(Fig.14). It also allows to export an evaluation report

containing all user entries and statistics of different

results throughout the prediction process.

4 CONCLUSION

In this paper, the EPredictor platform, a research tool,

was described and its usability was presented in de-

tail for the community evolution prediction issue. To

the best of our knowledge, no other research tools,

that handle the entire community evolution predic-

tion process, were proposed for predicting commu-

nity evolution in dynamic social networks. We have

presented step by step all the options offered by the

platform in order to make visible the range of func-

tionalities which can be involved for one particular

network. Several experiments were conducted by stu-

dents for their Master dissertation, which proved the

usability of the current version of the EPredictor plat-

form for educational purposes. We meant, through

this paper, to present the EPredictor platform to the

researchers in the ﬁeld of social network analysis in

order to prove its usability for research purposes. Yet,

the platform is still being developed and new func-

tionalities are constantly incorporated in order to en-

rich the set of methods proposed by the platform for

each step. The EPredictor platform is now available

for academic and other non-commercial purposes.

REFERENCES

Asur, S., Parthasarathy, S., and Ucar, D. (2009). An event-

based framework for characterizing the evolutionary

behavior of interaction graphs. ACM Transactions on

Knowledge Discovery from Data (TKDD), 3(4):1–36.

odka, P., Saganowski, S., and Kazienko, P. (2013).

Ged: the method for group evolution discovery in so-

cial networks. Social Network Analysis and Mining,

3(1):1–14.

Dakiche, N., Benbouzid-Si Tayeb, F., Benatchba, K., and

Slimani, Y. (2021). Tailored network splitting for

community evolution prediction in dynamic social

networks. New Generation Computing, pages 1–38.

Dakiche, N., Benbouzid−Si Tayeb, F., Slimani, Y., and Be-

natchba, K. (2018). Tracking community evolution in

social networks: A survey. Information Processing &

Management.

Diakidis, G., Karna, D., Fasarakis-Hilliard, D., Vogiatzis,

D., and Paliouras, G. (2015). Predicting the evolution

of communities in social networks. In Proceedings of

the 5th International Conference on Web Intelligence,

Mining and Semantics, pages 1–6. ACM.

El Moussaoui, M., Agouti, T., Tikniouine, A., and El Ad-

nani, M. (2019). A comprehensive literature review on

community detection: Approaches and applications.

Procedia Computer Science, 151:295–302.

Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,

P., and Witten, I. H. (2009). The weka data min-

ing software: an update. ACM SIGKDD explorations

newsletter, 11(1):10–18.

Holme, P. and Saram

aki, J. (2012). Temporal networks.

Physics reports, 519(3):97–125.

Ilhan, N. and

u, S¸. G. (2016). Feature identiﬁcation

for predicting community evolution in dynamic social

networks. Engineering Applications of Artiﬁcial In-

telligence, 55:202–218.

Pavlopoulou, M. E. G., Tzortzis, G., Vogiatzis, D., and

Paliouras, G. (2017). Predicting the evolution of com-

munities in social networks using structural and tem-

poral features. In 2017 12th International Workshop

on Semantic and Social Media Adaptation and Per-

sonalization (SMAP), pages 40–45. IEEE.

Rajita, B., Ranjan, Y., Umesh, C. T., and Panda, S. (2020).

Spark-based parallel method for prediction of events.

Arabian Journal for Science and Engineering, pages

1–17.

Saganowski, S., Br

odka, P., Koziarski, M., and Kazienko,

P. (2019). Analysis of group evolution prediction in

complex networks. PloS one, 14(10):e0224194.

Tabassum, S., Pereira, F. S., Fernandes, S., and Gama, J.

(2018). Social network analysis: An overview. Wiley

Interdisciplinary Reviews: Data Mining and Knowl-

edge Discovery, 8(5):e1256.

Takaffoli, M., Rabbany, R., and Za

ıane, O. R. (2014). Com-

munity evolution prediction in dynamic social net-

works. In 2014 IEEE/ACM International Conference

on Advances in Social Networks Analysis and Mining

(ASONAM), pages 9–16. IEEE.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

302