Multi-Party Private Set Intersection Protocols for Practical Applications
Asli Bay
1
, Zeki Erkin
2,4
, Mina Alishahi
3
and Jelle Vos
2
1
Antalya Bilim University, Turkey
2
Delft University of Technology, The Netherlands
3
Eindhoven University of Technology, The Netherlands
4
Radboud University, The Netherlands
Keywords:
Multi-Party Private Set Intersection, Bit-set Representation, Threshold PKE, Privacy-preserving Protocols.
Abstract:
Multi-Party Private Set Intersection (MPSI) is an attractive topic in research since a practical MPSI protocol
can be deployed in several real-world scenarios, including but not limited to finding the common list of cus-
tomers among several companies or privacy-preserving analyses of data from different stakeholders. Several
solutions have been proposed in the literature however, the existing solutions still suffer from performance re-
lated challenges such as long run-time and high bandwidth demand, particularly when the number of involved
parties grows. In this paper, we propose a new approach based on threshold additively homomorphic encryp-
tion scheme, e.g., Paillier, which enables us to process the bit-set representation of sets under encryption. By
doing so, it is feasible to securely compute the intersection of several data sets in an efficient manner. To prove
our claims on performance, we compare the communication complexity of our approach with the existing
solutions and show performance test results. We also show how the proposed protocol can be extended to
securely compute other set operations on multi-party data sets.
1 INTRODUCTION
Multi-party Private Set Intersection (MPSI) is the pro-
cess of finding the common elements in several data
sets without revealing any information about the data
but the intersection itself. Formally, t parties P
1
,...,P
t
owning the sets S
P
1
,...,S
P
t
, respectively, are inter-
ested in finding S
P
1
∩ ... ∩ S
P
t
without revealing their
data sets. Multi-party private set intersection has wide
application in real-world scenarios: MPSI can be used
among several commercial companies to find the in-
tersection of customer lists. The list of common cus-
tomers can be used to plan promotions for such cus-
tomers (Cheon et al., 2012); MPSI can be used among
the community of medical professionals to find out
the patients of a hospital who have participated in the
medical tests of different research labs (Cao et al.,
2017); MPSI can also be used in multi-party access
control, where several co-owners of a common con-
tent each specify a set of users who are permitted to
access data. The ones in the intersection are allowed
to access the content (Sheikhalishahi et al., 2019).
Given the relevance of the problem, several works
have been proposed in the literature. While the pro-
posed approaches provide solutions for the MPSI
problem in different scenarios, they mainly suffer
from computation and communication complexity
that grow when the number of involved parties in-
creases. To solve this issue, in this study we pro-
pose an efficient MPSI protocol which its complex-
ity is more efficient than the existing ones in terms
of the number of parties. The main intuition behind
protocol is that the data sets are converted to a bit-set
representation, i.e., a vector of bits is assigned to each
data set S in which the i’th element of this bit-vector
(bit-set) is equal to 1, if the i’th element of an ordered
domain of elements belongs to S, and 0 otherwise.
This new representation makes the protocols’ com-
putation and communication complexity (mainly) de-
pendent on domain size. Our proposed approach is
an effective MPSI solution when the domain size is
small enough and the number of parties increases.
The growth of the number of parties is particu-
larly an issue in certain real-world applications. For
instance the problem of recommending items from a
limited-size catalogue to customers: There is a grow-
ing number of customers but a limited size catalogue.
An MPSI protocol can identify the items that a group
of customers have all bought or looked at. In general,
these protocols are particularly interesting for creat-
Bay, A., Erkin, Z., Alishahi, M. and Vos, J.
Multi-Party Private Set Intersection Protocols for Practical Applications.
DOI: 10.5220/0010547605150522
In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 515-522
ISBN: 978-989-758-524-1
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
515

ing social groups with similar interests.
The design of our MPSI protocol relies on thresh-
old additively homomorphic encryption. Threshold
schemes are important in settings in which no indi-
vidual party knows the secret key, i.e., it provides a
strong security guarantee. An additive homomorphic
scheme supports the addition of two ciphertexts with-
out needing them to be decrypted, which is an appeal-
ing property for MPSI protocol enabling the server
to find the common elements in data sets without de-
crypting the individual messages. Our experimental
results show that for a domain of 2
8
elements, where
each party owns 16 elements out of domain, the total
runtime stays within 16 seconds for a group of t = 50
parties (with collusion threshold of ` = b
t
2
c). This re-
sult is significantly better than the most efficient MPSI
protocol in the literature proposed by Kolesnikov et.
al. (Kolesnikov et al., 2017). The contribution of this
study can be summarized as follows:
• Based on the bit-set representation of data sets and
threshold additively homomorphic encryption, we
design an efficient MPSI protocol: MPSI-1.
• We improve the communication complexity in
MPSI-2, which reduces the server interaction with
clients from O (dt ) to O (d`), where ` < t.
• We provide the correctness, complexity analy-
sis, and formal simulation-based security proof of
both protocols in semi-honest adversary model.
• We show how to extend our solution to other
privacy-preserving set operations, e.g. set union,
threshold set intersection, and set subtraction.
• We provide a theoretical comparison of our proto-
cols’ complexity with the existing MPSI protocols
in the literature.
• We validate the efficiency of our MPSI protocol
implementation by comparing its runtime with the
most efficient MPSI approach in the literature.
The rest of this paper is organized as follows: Sec-
tion 2 discusses related work.Section 3 describes pre-
liminary background. Section 4 presents an exten-
sion of Ruan’s PSI protocol, and Section 5 improves
it based on the bit-set representation. Section 6 pro-
vides experimental results of our protocol. Section 7
concludes and provides directions for future work.
2 RELATED WORK
In recent years, many works in literature has been
devoted to private set intersection. The first re-
search investigated the use of cryptographic tech-
niques in the context of two-party private set inter-
section (PSI). For instance, in (Dong et al., 2013), a
new approach named oblivious Bloom intersection is
Table 1: The comparison of previous designs with ours;
where n is the number of elements in a data set; d is the
domain size; t is number of parties; ` is the threshold of
Homomorphic PKE; κ and λ are the computational and sta-
tistical security parameter; Ω is the size of each bin of Gar-
bled Bloom filter; and log
|
X
|
is the bit-size of ciphertext
X.
Protocol
Communication Computation
bits encryptions
Server Client Server Client
(Kissner and Song, 2005) O (λ`tn log
|
X
|
) O

`tn
2

(Cheon et al., 2012) O

λt
2
n

O (tn)
(Miyaji et al., 2015) O (λtn log
|
X
|
) O (λtn log
|
X
|
) O (λn ) O (λn )
(Hazay et al., 2017) O (tnλ) O (nλ ) O (tn logn) O (n )
(Kolesnikov et al., 2017) O (tnλ ) O (n`λ) O (tκ) O (`κ )
(Inbar et al., 2018) O (tnκΩ) O (tnκΩ) O (tnκΩ) O (tnκΩ)
MPSI-1 (Section 4) O (dt log
|
X
|
) O (d log
|
X
|
) O (d ) O (d )
MPSI-2 (Section 5) O (d` log
|
X
|
) O (d log
|
X
|
) O (d ) O (d )
proposed which uses the combination of symmetric
key operations and garbled Bloom filters, or in (Cao
et al., 2017), which uses a combination of commu-
tative encryption and hash-based commitments. Al-
though these works provide effective solutions for ad-
dressing the PSI problem, they are not applicable for
Multi-party PSI. Thus, further research attempts to
address PSI in the multi-party setting.
In (Kissner and Song, 2005), with the use of
mathematical properties of polynomials, the compos-
able protocols over multiset operations are designed.
In polynomial computations, the multiplication (over
encrypted coefficients) generally imposes quadratic
computational and communicational complexities in
the degree of polynomials. To mitigate this issue,
(Cheon et al., 2012) propose an approach in which
a polynomial f (x) is represented by several points
on the curve y = f (x). To solve the MPSI prob-
lem, a scalable and flexible approach is proposed in
(Miyaji and Nishida, 2015) in which the data set size
of each party is independent to each other and the
computational complexity is independent to the num-
ber of parties. A new approach for MPSI using two-
party set intersection protocols is developed in (Hazay
and Venkitasubramaniam, 2017). The proposed ap-
proach addresses the challenges of using two-party
protocols for intermediate computations without vi-
olating the privacy of the multi-party construction. A
new paradigm for MPSI using oblivious evaluation of
a programmable pseudorandom function (OPPRF) is
proposed in (Kolesnikov et al., 2017). The proposed
protocols avoid expensive public-key operations and
are secure in the presence of any number of semi-
honest participants. In (Inbar et al., 2018), two pro-
tocols based on Bloom filters and threshold Homo-
morphic Public Key Encryptions (PKE) are proposed
in the multi-party setting. Table 1 reports the com-
plexity of existing MPSI approaches and ours i.e.,
MPSI-1 and MPSI-2. The MPSI-2 is the optimized
version of MPSI-1 in which the communication com-
SECRYPT 2021 - 18th International Conference on Security and Cryptography
516

plexity of server has been reduced from O (dt log
|
X
|
)
to O (d`log
|
X
|
) where ` < t.
3 PRELIMINARIES
3.1 Security Model
The security of our protocols are proven in the semi-
honest model with static adversaries. So, the num-
ber of corrupted parties are known before the proto-
col starts and they follow the protocol honestly. Due
to space limitations, we briefly mention the security
concepts and give a reference link to the reader. The
proofs of the protocols are based on the the security
definition of the semi-honest security for determinis-
tic functionalities in (Goldreich and Warning, 1998).
In our protocols, we use the threshold variant of
Paillier PKE scheme proposed in (Fouque et al., 2000)
which is additively homomorphic that is, if given two
ciphertexts c
1
= Enc(pk, M
1
) and c
2
= Enc(pk, M
2
)
one can efficiently compute Enc(pk,M
1
+ M
2
) with-
out the knowledge of the secret key. Also, we use
the approach proposed in (Hazay and Venkitasubra-
maniam, 2017) which provides an extension of the
decryption algorithm of an additively homomorphic
threshold PKE that allows the involved parties to learn
whether a ciphertext is encryption of zero or not, but
nothing else. We will call such decryption algorithm
“decryption-to-zero” and denote it by ShDec0. This
property can typically be achieved by randomizing the
ciphertext by each of the involved parties, combining
the results in a new value, and jointly decrypting this
obtained value.
3.2 Bit-set Representation
We adopt the data set representation in terms of bit
vectors as employed by (Ruan et al., 2019), namely
bit-set representation. Formally, assume that parties’
data sets are selected from a fixed and ordered domain
that consists of d elements S = {s
1
,s
2
,...,s
d
}. Let a
bit vector
−→
B = (b
1
,b
2
,...,b
d
) denotes a set S which
is a subset of S , where if b
j
= 1, 1 ≤ i ≤ d, then s
j
∈ S,
otherwise, s
j
/∈ S. Regardless of the size of S, the size
of
−→
B is always d. Thus, the bit-set representation has
the advantage of hiding the cardinality of subsets.
The bit-set representation is used to perform the
intersection of two data sets S
1
and S
2
, namely S
1
∩S
2
,
with
−→
B
1
and
−→
B
2
bit vector representations of size d as
follows:
−→
B
1
∗
−→
B
2
= (b
1
1
× b
2
1
, b
1
2
× b
2
2
, . . . , b
1
d
× b
2
d
).
Our Multi-party Private Set Intersection Protocol (MPSI-1)
P
1
... P
t−1
P
t
(server)
−−→
B
1
...
−−−−→
B
t−1
, S = {}
−−→
B
1
∗
...
−−−−→
B
t−1
∗
−→
B
t
computes c = (c
1
,c
2
,. . . ,c
d
),c
i
= E(b
t
i
) ∀ i
c = (c
1
,c
2
,. . . ,c
d
)
←−−−−−−−−−−−−−−−−−−−−−−−
...
c = (c
1
,c
2
,. . . ,c
d
)
←−−−−−−−−−−−
e
i
j
= c
b
i
j
j
E
PK
(0)
e
i
j
, ∀ j
−−−−−−−−−−−−−−−−−−−−−−−→
computes E (b
j
) =
∏
t−1
i=1
e
i
j
∀ j
((E(b
1
),. . . ,E(b
d
))
←−−−−−−−−−−−−−−−−−−−−−−−
...
((E(b
1
),. . . ,E(b
d
))
←−−−−−−−−−−−−−−−−−
sh
1, j
= ShDec0(sk
1
,E(b
j
))
sh
1, j
,∀ j
−−−−−−−−−−−−−−−−−−−−−−−→
... sh
i, j
= ShDec0(sk
i
,E(b
j
))
sh
i, j
,∀ j
−−−−−−−−→
D(E(b
j
)) ← Comb(sh
1, j
,. . . ,sh
t−1, j
), ∀ j
if b
j
= 0 and b
t
j
= 1 then S = {y
j
} ∪ S,
else discard y
j
, ∀ j
Output S
Figure 1: MPSI-1.
Also, the cardinality of the set intersection |S
1
∩ S
2
| is
done by computing the dot product of
−→
B
1
and
−→
B
2
:
−→
B
1
·
−→
B
2
= b
1
1
× b
2
1
+ b
1
2
× b
2
2
+ ··· + b
1
d
× b
2
d
.
3.3 The Ruan PSI Protocol
Ruan et al. (Ruan et al., 2019) propose a secure
PSI protocol based on the bit-set representation (Sec-
tion 3.2). In the proposed methodology, two parties P
1
and P
2
own respectively the data sets S
1
and S
2
drawn
from a fixed domain S = (s
1
,s
2
,...,s
d
) of d elements.
In the setup phase, both parties generate their bit vec-
tors
−→
B
1
= (b
1
1
,b
1
2
,...,b
1
d
) and
−→
B
2
= (b
2
1
,b
2
2
,...,b
2
d
) out
of their data sets S
1
and S
2
, respectively. Party P
2
gen-
erates his public/private key pair (pk
2
,sk
2
) and shares
pk
2
with P
1
. The protocol works as follows:
• P
2
computes c
j
= E
pk
2
(b
2
j
) for all j, 1 ≤ j ≤ d and
sends c = (c
1
,c
2
,...,c
d
) to P
1
.
• P
1
computes e
j
= (c
j
)
b
1
j
E
pk
2
(0) for all j, 1 ≤ j ≤
d, then sends e = (e
1
,e
2
,...,e
d
) to P
2
.
• Upon receiving e, P
2
decrypts every e
j
, namely
b
j
= D
sk
2
(e
j
), and decides if b
j
= 1, then s
j
∈
S = S
1
∩ S
2
, else s
j
/∈ S = S
1
∩ S
2
.
We refer the reader to (Ruan et al., 2019) for details.
4 MPSI-1
We extend the Ruan’s PSI protocol into the multi-
party setting. To this end, let assume there are t par-
ties P = {P
1
,...,P
t
} each holding a private data set
S
i
are interested in obtaining the intersection of their
data sets. As previously, the data sets contain n
i
num-
ber of elements, where 1 ≤ i ≤ t. Among all parties,
P
t
is the server who computes the intersection and the
remaining parties are the clients. Differently from the
two-party setting, in the multi-party setting we make
use of secret shares to protect the privacy of clients so
that the server cannot decrypt himself to find mutual
intersection of clients with his own data set.
Multi-Party Private Set Intersection Protocols for Practical Applications
517

Let pk be the public key of a secret key sk which
is shared among t − 1 clients. The encryption is done
by the threshold Paillier PKE scheme (Fouque et al.,
2000)
1
. The protocol execution goes as follows:
• Each party P
i
, where 1 ≤ i ≤ t, generates the vec-
tor representation
−→
B
i
of their data set S
i
.
• Each client P
i
(1 ≤ i ≤ t −1) inverts his bit vectors
−→
B
i
∗
= (b
i
1
,b
i
2
,...,b
i
d
).
• P
t
then encrypts his bit vector
−→
B
t
with pk by
the threshold Paillier PKE scheme and sends
(c
1
,c
2
,...,c
d
) to each client P
i
(1 ≤ i ≤ t − 1).
• Each party P
i
computes e
i
= (e
i
1
,e
i
2
...,e
i
d
) by e
i
j
=
c
b
i
j
j
E(0) and then sends e
i
to P
t
.
• Upon receiving e
i
’s, the server P
t
computes
E(b
j
) =
∏
t−1
i=1
e
i
j
and asks ` participants among
t − 1 to run ShDec0 protocol to generate their
shares sh
i, j
= ShDec0(sk
i
,E(b
j
)) for all j (1 ≤
j ≤ n). Then, they send their shares sh
i, j
’s to P
t
.
• P
t
combines these shares by D(E(b
j
)) ←
Comb(sh
1, j
,...,sh
t−1, j
), ∀ j, 1 ≤ j ≤ d.
• Finally, P
t
computes the intersection S by check-
ing: if b
j
= 0 and b
t
j
= 1 both hold, then s
j
∈ S,
otherwise s
j
/∈ S.
Figure 1 summarizes the communications among
clients and server for executing the MPSI-1 protocol.
4.1 Correctness
We start by expanding E(b
j
) as
E(b
j
) =
t−1
∏
i=1
e
i
j
= c
b
1
j
j
× c
b
2
j
j
× ··· × c
b
t−1
j
j
E(0)
t−1
= E(b
t
j
)
b
1
j
+b
2
j
+···+b
t−1
j
E(0)
t−1
= E(b
t
j
× (b
2
j
+ ··· + b
t−1
j
) + 0).
It can be seen that when b
t
j
= 0, P
t
always gets b
j
= 0
and so he concludes that s
j
is not in the intersection
S. Furthermore, if b
t
j
= 1 and b
j
= r, then at least one
client does not have s
j
. Hence, P
t
again decides that
s
j
is not in S. Only, the element s
j
is in S, when b
t
j
= 1
and b
j
= 0 both hold.
4.2 Complexity Anaylsis
Communication Complexity. The server P
t
sends d
ciphertexts to each client in the first, the third, and
during the execution of ShDec0. Hence, P
t
sends
O (dt ) ciphertexts in total. Similarly, each client
sends O (d ) ciphertexts in total. To compare the
communication complexity in bits with the previous
1
Note that any additively homomorphic threshold PKE
scheme can also be used.
works, we multiply the number of ciphertexts with
log
|
X
|
which is the size of the ciphertext X in bits.
Therefore, the communication complexities of P
t
and
each client in terms of the number of bits sent are
O (dt log
|
X
|
) and O (d log
|
X
|
), respectively.
Computational Complexity. The server P
t
makes
d encryptions in the first round. Then, he makes
O (d t ) multiplications in the third round. Each client
performs O (d ) encryptions and exponentiations in
round two. During the execution of the decryt-to-zero
protocol which essentially consists of two parts, each
client first randomizes the ciphertext by raising it to
the power of a random value and sends back to the
server. The server multiplies all randomized cipher-
texts performing O (t ) multiplications for each ele-
ment and sends back to the clients. Then, each client
calculates his decryption share. This requires O (d )
exponentiation for each client. The server makes
O (d`) multiplications in total with the last round.
4.3 Security Analysis
The privacy of clients is protected, as when b
t
j
= 0
(that is s
j
/∈ S
t
), the server P
t
can not learn any in-
formation of the clients’ private data sets. When,
b
t
j
= 1, due to ShDec0 protocol, unless b
i
j
= 0 for all
1 ≤ i ≤ t −1 simultaneously, the decryption result will
be random. So, there is no information leakage to P
t
.
The security of the protocol is based on the as-
sumption of the IND-TCPA (Fouque and Pointcheval,
2001) security of additively homomorphic threshold
PKE scheme T Π with threshold ` < t. A corrupted
party is assumed to be an adversary who is curi-
ous but honest. We shall denote I =
{
i
1
,...,i
ω
}
⊂
{
1,2,...,t − 1
}
and the complement of I by
¯
I . Let
the inputs of the clients be Inp
i
= (S
i
,pk,sk
i
), i ∈
{1,...,t − 1} and of the server be Inp
t
= (S
t
,pk). The
output of the protocol is only provided by the server
which is the intersection S =
T
t
j=1
S
j
. The clients pro-
duce no output. We consider two scenarios; (1) the
server P
t
is honest and a subset P
I
of the clients are
corrupted, where ω < `; (2) the server P
t
is corrupted
a subset P
I
of the clients are corrupted, where ω < `.
In the first scenario, where a number of (ω < `)
clients are corrupted, the simulator S has Inp
I
but
no output (as server is honest). S is going to sim-
ulate the view of corrupted parties (clients) which
is indistinguishable from the real view of the proto-
col. Namely, the simulator will make simulated ˜c =
( ˜c
1
, ˜c
2
,..., ˜c
d
) indistinguishable from the real string
c = (c
1
,c
2
,...,c
d
). The simulator S chooses a ran-
dom binary vector of length d for each honest parties’
set, namely the simulated server set B
t
and the sets of
SECRYPT 2021 - 18th International Conference on Security and Cryptography
518

honest clients B
¯
I
s. S follows the protocol and gen-
erates ( ˜c
1
, ˜c
2
,..., ˜c
d
). Suppose that there is an adver-
sary A who can distinguish two strings c and ˜c with a
non-negligible probability. This implies A can break
IND-TCPA security of Homomorphic PKE. This con-
tradicts the security of the PKE scheme. In addition,
other inputs to the corrupted clients are E(b
j
)’s for
1 ≤ j ≤ d. By following the protocol, S then gener-
ates
˜
E(b
j
)’s. As previously, the security of T Π does
not allow to distinguish E(b
j
) and
˜
E(b
j
) with a non-
negligible probability.
In the second scenario, apart from a subset P
I
of
corrupted clients, the server is also corrupted, where
number of corrupted clients ω is less than `. Note
that we do not count the server in the number of ` as
he does not have a secret key share. As the server
is among the corrupted parties, the corrupted parties
know the intersection S =
T
t
j=1
S
j
. Hence, the sim-
ulator S has to simulate the output S of the protocol,
too. S starts by choosing random strings for the in-
put set of the honest parties
˜
B
i
, i ∈
¯
I in such a way
that
T
j∈I
S
j
∩
T
j∈
¯
I
˜
S
j
= S. Then, S follows the pro-
tocol and produces simulated ( ˜c
1
, ˜c
2
,..., ˜c
n
t
). Then,
he generates ˜e = ( ˜e
1
, ˜e
2
,..., ˜e
d
) for the honest parties
and corrupted parties. Later, S generates
˜
E(b
j
)’s for
1 ≤ j ≤ d and sends it to a subset of ` parties among
t parties. As for the number of corrupted parties we
have ω < `, there is at least one honest client in this
set who receives
˜
E(b
j
)’s. Now, the simulator has to
simulate the decryption shares of honest parties with-
out knowing their secret key shares as follows: The
simulator knows there are ` − ω honest parties and
simulates the decryption shares of the honest parties
by invokes the share decryption algorithm ShDec0 on
˜
E(b
j
) and random element from the secret key space,
˜
sk
k
for each of ` − ω − 1 honest parties. For the last
remaining honest party, if y
j
∈ S , the simulator com-
putes the decryption share from the decryption shares
of the corrupted parties and the simulated honest par-
ties, such that the combining algorithm Comb out-
puts 0. If y
j
/∈ S, it forces the output to a random
value that is a result of the randomness in data. Now
clearly the simulated ˜e’s are indistinguishable from
the real ones, otherwise the IND − TCPA security of
the TPKE breaks. Also, the decryption shares are pro-
duced by a simulator for ShDec0, so the adversary can
not distinguish them from the real execution. Note
that such a simulator exists for threshold Pailler PKE.
5 MPSI-2
In this section, we propose a similar protocol which is
slightly more efficient protocol than MPSI-1. That is,
in MPSI-2 we could reduce the server’s communica-
tion complexity from O (dt ) to O (d`), where ` < t.
The reason is that, the server interacts with the clients
only in the shared decryption phase. The key set-up
phase is same as in Sec. 4. The protocol follows the
steps below:
• Each party P
i
, 1 ≤ i ≤ t, generates the vector
−→
B
i
of
their data set S
i
and inverts it to
−→
B
i
∗
.
• Every party P
i
, 1 ≤ i ≤ t, computes the en-
cryption of their inverted vectors E(
−→
B
i
∗
) =
(E(b
i
1
),. .. , E(b
i
n
)) by a threshold homomorphic
PKE scheme.
• Clients send their encrypted inverted binary vec-
tors E(
−→
B
i
∗
), 1 ≤ i ≤ t − 1, to the server P
t
.
• P
t
then makes entry-wise homomorphic addition
to obtain
(E(b
1
),. .. , E(b
n
)) =
(E(b
1
1
+ b
2
1
+ ··· + b
t
1
),. .. , E(b
1
n
+ b
2
n
··· + b
t
n
)).
• The server sends (E(b
1
),E(b
2
),. .. , E(b
d
)) to `
parties among t − 1 clients and asks them to mu-
tually decryption-to-zero each E(b
j
)
2
. We al-
low ` ≤ t − 1 for more flexibility, although often
` = t − 1.
• Each client P
i
involved in the decryption com-
putes their decryption share sh
i, j
for all j ∈
{1,...,d} as follows: They first send a random-
ized E(b
j
)
r
i, j
to the server; the server combines
them into
˜
E(b
j
) = E(b
j
)
Σr
i, j
and sends
˜
E(b
j
) to
each party. Now each party decrypts it to obtain
their shares sh
i, j
for all j ∈ {1, . . . , d}. Finally the
shares are sent to the server.
3
• For each j ∈ {1,. . . , d}, the server runs the com-
bining algorithm on the obtained shares and com-
putes Dec(
˜
E(b
j
)) ← Comb(sh
1, j
,...,sh
t−1, j
).
• For each j ∈ {1,...,d}, if Dec(
˜
E(b
j
)) = 0, then
the server makes corresponding c
j
= 1, otherwise
c
j
= 0. Here, (c
1
,c
2
,...,c
d
) is the bit-set repre-
sentation of the intersection set S = ∩
d
i
S
i
.
5.1 Correctness
The protocol is correct, because when b
1
j
+ b
2
j
+ ··· +
b
t
j
= 0 holds, this means that all b
i
j
’s are zero at the
2
Note that by randomizing bit vectors of all parties, we
have the same functionality of ShDec0.
3
Note that in Figure 1 we have modified the notations
to improve the readability, and this whole step of produc-
ing shares with the ShDec0 algorithm is denoted as sh
i, j
=
ShDec0(sk
i
,E(b
j
)) for all j ∈ {1,. .., d}.
Multi-Party Private Set Intersection Protocols for Practical Applications
519

same time. As this bits are inverted, this implies b
i
j
’s
are all one. Therefore, we set c
j
= 1, and the ele-
ment s
j
corresponding c
j
= 1 is in the intersection
S = ∩
d
i
S
i
. For the case where b
1
j
+ b
2
j
+ ·· · + b
t
j
6= 0
(which let the ShDec0 output a random value), at least
one data set does not contain the element correspond-
ing to j-th element in the domain. Hence, we set
c
j
= 0, and the element s
j
corresponding c
j
= 0 is not
in the intersection. The protocol works for all data
sets, so the error probability of MPSI-2 is zero.
5.2 Complexity Analysis
Communication Complexity. The server P
t
sends d
ciphertexts to ` clients among t − 1 in the second and
the fourth rounds (during the execution of ShDec0).
Hence, P
t
sends O (d` log
|
X
|
) bits in total, where
log
|
X
|
is the size of the ciphertext X in bits. Like-
wise, each client sends O (d log
|
X
|
) bits in total.
Computational Complexity. Each client and the
server perform O (d ) encryptions in the first round.
Then, in the second round, P
t
performs dt homomor-
phic addition, which corresponds to the modular mul-
tiplication in Paillier PKE scheme. During the execu-
tion of the decrypt-to-zero protocol, each client first
randomizes the ciphertext by raising it to the power
of a random value and sends back to the server. The
server multiplies all randomized ciphertexts perform-
ing O (d`) multiplications and re-sends to the clients.
Then, each client calculates his decryption share. This
requires O (d ) exponentiation for each client. The
server makes O (d`) multiplications in total with the
last round. Hence, the dominated complexity for each
client and the server is O (d ) encryptions.
Note that the protocol is still applicable when the
server computes the set intersection and does not have
a data set. This leads to that the server does not
make any encryption, which reduces the computa-
tional overhead for the server significantly.
5.3 Security Analysis
The security of MPSI-2 protocol is guaranteed based
on the IND-TCPA security of additively homomor-
phic threshold PKE scheme T Π with threshold ` < t
(Fouque and Pointcheval, 2001). As the steps of the
protocols are similar, the security proof of MPSI-1 is
can similarly be adopted for MPSI-2. Therefore, to
avoid repetitions and save space, we refer readers to
Section 4.3 for the proof of this protocol.
5.4 Extension to Other Set Operations
There are three parts in the MPSI protocol presented
at the start of Section 5 that can be altered to al-
low the same scheme to perform different set oper-
ations: Whether the bit-set encoding is inverted or
not, what the server does after aggregating the bit-
sets (in the MPSI protocol the server chooses which
bits to decrypt-to-zero at this point) and how the
server extracts the final bit-set from the results of the
decryption-to-zero. Some of these protocols require
the use of a multi-party Secure Comparison Protocol
(SCP) such as that by (Kerschbaum et al., 2009) or
a Secure Equality Protocol (SEP). The protocols can
also be composed for more complex operations by re-
placing the intermediate decrypt-to-zero with a SEP.
Set Union (MPSU). Multi-party Private Set Union
(MPSU) is the process of finding the elements that
appeared in at least one of the data sets owned by the
participating parties. More precisely, let assume t par-
ties P
1
,...,P
t
own the data sets S
P
1
,...,S
P
t
, respec-
tively, are interested in finding S
P
1
∪ .. . ∪ S
P
t
without
revealing their data sets. Now, we explain how to de-
sign MPSU based on MPSI-2 protocol as follows:
• Clients do not invert the bit-sets (i.e., if x
i
belongs
to S
j
, then the associated element in the bit-set is
equal to 1) before sending them to the server.
• Aggregation is the same as before, but the en-
tire aggregated bit-set is chosen for a collaborative
decryption-to-zero.
• Finally, the server keeps every bit that results as 0
stays 0, and sets every other value to 1. The bits of
the aggregated bit-set that equal 1 are the ones that
belong to at least one data set, i.e., to set union.
Threshold MPSI (T-MPSI). The Threshold Multi-
party Private Set Intersection (T-MPSI) is the process
of finding the elements that appeared in the combined
sets of parties at least T times. Based on the MPSU
protocol, it is as follows:
• The first step is the same as the first step in MPSU
protocol, i.e., the bits remain non-inverted.
• Before decryption-to-zero (in the second step of
MPSU), the secure comparison protocol (SCP) is
used to understand if b
j
≥ T for every bit b
j
.
• Finally, every bit that results as 0 and every other
value becomes 1. The bits which are equivalent to
1 are the ones appeared in more than T data sets.
The server can choose to recover only those elements
that they themselves possess by only submitting those
bits for decryption, or they can choose to reveal all
elements surpassing the threshold by submitting the
full bit-set.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
520

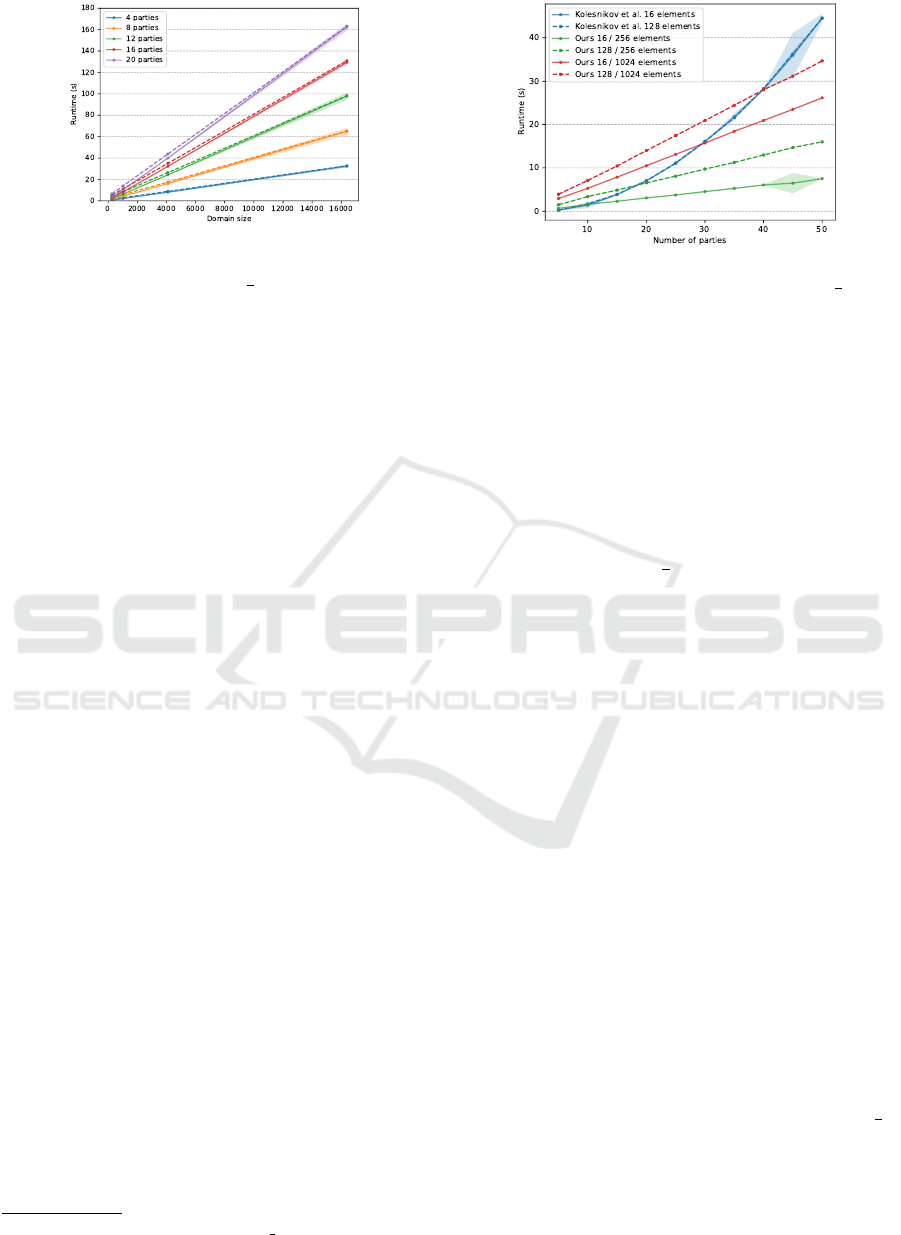
Figure 2: Our runtime over a growing domain size and
different number of parties. n = 16 for the solid line and
n = 128 for the dashed line. ` = b
t
2
c.
Private Set Cardinality (CA). The cardinality is
the number of elements in a set S, and it is generally
denoted as |S|. In some applications it is only neces-
sary to compute the cardinality of a set without know-
ing which specific elements are inside it. For instance,
to privately estimate the number of users in the Tor
network. (Fenske et al., 2017) To extend our protocol
for this purpose, the decryption-to-zero is replaced by
secure equality protocol (SEP), and for the MPSI pro-
tocol, SEP evaluates whether b
j
= 0 or not, while for
the MPSU and T-MPSI, SEP evaluates b
j
= 1 or not.
After that, all bits can be summed homomorphically
to reveal the resulting set’s cardinality.
Set Subtraction. Given two data sets S
A
and S
B
, the
subtraction of S
B
from S
A
, denoted by S
A
−S
B
consists
of elements that are in S
A
but not in S
B
. To compute
the subtraction of two encrypted bit-sets, the first one
should be inverted, but, the second one remains un-
changed. After aggregating the bit-sets, a decryption-
to-zero is applied on the resulting bit-set. Then, the
server changes the bits that are 0 to 1, while the other
bits become 0. The bits with value 1 show the ele-
ments that belong to the first set but not the second.
6 RESULTS
We have developed a reference implementation
4
of
both protocols in C++. The implementation relies on
the GMP and NTL libraries. Although the code runs
on one machine, it spawns one thread for each client
for concurrency; the main thread represents the server.
Set-up. We evaluate the runtime of the protocol by
performing 10 set intersections for each choice of pa-
rameters, and all sets contain n random elements. Our
benchmarks were executed on a 64-bit Unix machine
4
https://github.com/jellevos/bitset mpsi
Figure 3: Runtime of our protocol and Kolesnikov et al.’s
protocol for n = 16,128, d = 256, 1024, and ` = b
t
2
c.
with an INTEL CORE
TM
I7-1065G7 processor at 8
× 1.30GHz and 16GB of memory. For our work, we
choose κ = 1024 as is common for public-key encryp-
tion. We determine the standard deviation σ, and plot
the 3σ confidence interval as a shaded area.
Protocol Performance. As the domain size d is a
dominant factor in computation and communication
costs (Table 1) of our protocols, we evaluate the run-
time over a growing domain size in Figure 2. The col-
lusion threshold is ` = b
t
2
c. The solid and dashed lines
represent are when a party owns n = 16 and n = 128
elements, respectively. The number of parties t in the
figure are from the set {4,8,12,16,20}. It can be in-
ferred that the runtime is linearly dependent on do-
main size. The negligible distance between the solid
and dashed lines show that the number of elements
has negligible impact on the computation cost. For
small domain sizes (i.e d ≤ 4000), the growth in the
number of parties has small effect on runtime. How-
ever, as the domain size grows, the difference between
the runtime of different number of parties increases.
We compare the runtime of our MPSI protocol
with the protocol proposed by (Kolesnikov et al.,
2017) (with κ = 128) as its empirical runtime is gen-
erally superior to that of similar works. Note that their
approach is efficient in the number of elements n, but
it scales quadratically in terms of the number of par-
ties t. Asymptotically, the computation and commu-
nication in our approach is dominated by the domain
size d, but for lower values the number of parties t and
number of elements n have a linear impact on runtime.
Figure 3 compares the runtime of our implement-
ing proposed approach with Kolesnikov et al.’s ap-
proach for n = 16, 128, d = 256,1024, and ` = b
t
2
c.
Note that for a small number of elements and small
domain (n ≤ 16,d ≤ 256), our protocol outperforms
the other protocol consistently for any number of par-
ties. However, when the number of elements in each
party’s set increases, our protocol is more strongly af-
Multi-Party Private Set Intersection Protocols for Practical Applications
521

fected than the other work. Still, for many parties, our
MPSI protocol becomes considerably more efficient.
In the following table we highlight the parameters
for which our MPSI protocol is more efficient than
Kolesnikov’s protocol. In short, for any domain size
d = 2
8
d = 2
10
n = 16 t ≥ 11 t ≥ 29
n = 128 t ≥ 19 t ≥ 40
d, number of elements n and collusion threshold `,
our MPSI protocol is more efficient than Kolesnikov
et al.’s protocol when the number of parties is large
enough. For a domain size of 2
8
elements, regardless
of the number of elements in each party’s set, the to-
tal runtime stays within 16 seconds for a group of 50
parties. For a larger domain of 2
10
elements, the total
runtime stays within 35 seconds for such a group. As
expected our protocol is especially efficient for small
domains d ≈ 2
8
and a low number of owned elements
n ≈ 16, where our runtime is significantly lower than
the other work, starting from 11 parties.
7 CONCLUSION
Multi-Party Private Set Intersection (MPSI) has been
proposed to enable several data owners to find the
common elements in their data sets without revealing
their data sets. However, the existing solutions suf-
fer from computation and communication costs when
the number of parties grows. In this paper, we have
proposed a new MPSI approach based on bit-set rep-
resentation and threshold Paillier PKE, which is effi-
cient for a large number of parties. We show theo-
retically and empirically that our proposed approach
considerably outperforms the existing MPSI solutions
when the number of parties increases.
ACKNOWLEDGEMENT
This work has been supported by the H2020 EU
funded project SECREDAS [GA #783119].
REFERENCES
Cao, X., Li, H., Dang, L., and Lin, Y. (2017). A two-party
privacy preserving set intersection protocol against
malicious users in cloud computing. Comput. Stand.
Interfaces, 54(P1):41–45.
Cheon, J. H., Jarecki, S., and Seo, J. H. (2012). Multi-Party
Privacy-Preserving Set Intersection with Quasi-Linear
Complexity. IEICE Transactions on Fundamentals of
Electronics Communications and Computer Sciences,
95(8):1366–1378.
Dong, C., Chen, L., and Wen, Z. (2013). When private set
intersection meets big data: An efficient and scalable
protocol. In the ACM SIGSAC Conference on Com-
puter and Communications Security, CCS ’13, page
789–800.
Fenske, E., Mani, A., Johnson, A., and Sherr, M. (2017).
Distributed measurement with private set-union cardi-
nality. In ACM SIGSAC Conference on Computer and
Communications Security, CCS, pages 2295–2312.
ACM.
Fouque, P., Poupard, G., and Stern, J. (2000). Sharing de-
cryption in the context of voting or lotteries. In Finan-
cial Cryptography, 4th International Conference, FC,
volume 1962 of Lecture Notes in Computer Science,
pages 90–104. Springer.
Fouque, P.-A. and Pointcheval, D. (2001). Threshold cryp-
tosystems secure against chosen-ciphertext attacks. In
Boyd, C., editor, Advances in Cryptology — ASI-
ACRYPT 2001, pages 351–368, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Goldreich, O. and Warning, A. (1998). Secure multi-party
computation.
Hazay, C. and Venkitasubramaniam, M. (2017). Scalable
multi-party private set-intersection. In Fehr, S., edi-
tor, Public-Key Cryptography (PKC), pages 175–203.
Springer Berlin Heidelberg.
Inbar, R., Omri, E., and Pinkas, B. (2018). Efficient scalable
multiparty private set-intersection via garbled bloom
filters. In 11th International Conference on Security
and Cryptography for Networks, pages 235–252.
Kerschbaum, F., Biswas, D., and de Hoogh, S. (2009). Per-
formance comparison of secure comparison protocols.
In Database and Expert Systems Applications, DEXA,
pages 133–136.
Kissner, L. and Song, D. X. (2005). Privacy-preserving set
operations. In Annual International Cryptology Con-
ference (CRYPTO), volume 3621 of Lecture Notes in
Computer Science, pages 241–257. Springer.
Kolesnikov, V., Matania, N., Pinkas, B., Rosulek, M., and
Trieu, N. (2017). Practical multi-party private set in-
tersection from symmetric-key techniques. In ACM
SIGSAC Conference on Computer and Communica-
tions Security, CCS, pages 1257–1272. ACM.
Miyaji, A. and Nishida, S. (2015). A scalable multiparty
private set intersection. In Network and System Secu-
rity Conference, NSS, volume 9408 of Lecture Notes
in Computer Science, pages 376–385. Springer.
Ruan, O., Wang, Z., Mi, J., and Zhang, M. (2019). New ap-
proach to set representation and practical private set-
intersection protocols. IEEE Access, 7:64897–64906.
Sheikhalishahi, M., Tillem, G., Erkin, Z., and Zannone, N.
(2019). Privacy-preserving multi-party access control.
In ACM Workshop on Privacy in the Electronic Soci-
ety, WPESCCS, pages 1–13.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
522