Balancing Quality and Efﬁciency in Private Clustering

with Afﬁnity Propagation

Hannah Keller, Helen M

ollering, Thomas Schneider and Hossein Yalame

Technical University of Darmstadt, Darmstadt, Germany

Keywords:

Privacy-preserving Machine Learning, Clustering, Secure Computation.

Abstract:

In many machine learning applications, training data consists of sensitive information from multiple sources.

Privacy-preserving machine learning using secure computation enables multiple parties to compute on their

joint data without disclosing their inputs to each other. In this work, we focus on clustering, an unsupervised

machine learning technique that partitions data into groups. Previous works on privacy-preserving clustering

often leak information and focus on the k-means algorithm, which provides only limited clustering quality and

ﬂexibility. Additionally, the number of clusters k must be known in advance. We analyze several prominent

clustering algorithms’ capabilities and their compatibility with secure computation techniques to create an

efﬁcient, fully privacy-preserving clustering implementation superior to k-means. We ﬁnd afﬁnity propagation

to be the most promising candidate and securely implement it using various multi-party computation techniques.

Privacy-preserving afﬁnity propagation does not require any input parameters and consists of operations that

are relatively efﬁcient with secure computation. We consider passive security as well as active security with an

honest and dishonest majority. We offer the ﬁrst comparison of privacy-preserving clustering between these

scenarios, enabling an understanding of the exact trade-offs between them. Based on the clustering quality and

the computational and communication costs, privacy-preserving afﬁnity propagation offers a good trade-off

between quality and efﬁciency for practical privacy-preserving clustering.

1 INTRODUCTION

The ﬁeld of machine learning (ML) has received con-

siderable attention in recent years thanks to its mani-

fold applications. Furthermore, the increased storage

capabilities and computational power of devices enable

models to be trained on immense data pools. Train-

ing data is often aggregated from multiple sources to

increase the utility of the resulting model, and cloud

providers such as Amazon SageMaker and the Google

AI Platform offer the necessary storage and compu-

tation as a service. However, as the availability of

training data for such algorithms increases, the rele-

vance of protecting its security and privacy also grows.

Regulations such as GDPR restrict the use of personal

information, and a need for privacy-preserving solu-

tions arises.

For this reason, using secure multi-party computa-

tion (MPC) for privacy-preserving machine learning

(PPML) has become a hot research topic (Juvekar et al.,

2018; Mishra et al., 2020; Rathee et al., 2020; Patra

et al., 2021). MPC uses cryptographic techniques to

allow several parties to compute the output of a func-

tion without revealing the private input values to each

other. Using MPC, multiple data owners can securely

train an ML model without any information leakage to

an (internal or external) adversary.

In this work, we focus on clustering, a form of

unsupervised ML in which similar data points are

grouped together. Clustering algorithms are useful,

for example, to segment a market using consumer

preferences (Chaturvedi et al., 1997) or group photos

of diseased organs in medical imaging (Masulli and

Schenone, 1999). A well-known and simple clustering

algorithm is k-means (Steinhaus, 1956), which itera-

tively updates cluster centers and assignments. This al-

gorithm has been the focus of much privacy-preserving

clustering research (cf.

6); however, the quality of

clustering results from this algorithm is limited (cf.

3).

Furthermore, k-means requires the number of clus-

ters k to be chosen in advance, which is a challenge

if no party has access to the full pool of training data,

as is the case in many privacy-preserving settings. In

general, choosing parameter values for clustering al-

gorithms becomes signiﬁcantly less trivial when algo-

rithms are executed in a privacy-preserving manner.

Keller, H., Möllering, H., Schneider, T. and Yalame, H.

Balancing Quality and Efﬁciency in Private Clustering with Afﬁnity Propagation.

DOI: 10.5220/0010547801730184

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 173-184

ISBN: 978-989-758-524-1

173

Furthermore, privacy research has focused on private

clustering in the passive security model (cf.

2.2), ne-

glecting the stronger active security model needed to

securely perform secure computation between mutu-

ally distrusting parties.

Contributions and Outline.

After discussing the pre-

liminaries in

2, we provide the following contribu-

tions:

•

We give a comprehensive analysis of multiple clus-

tering algorithms with respect to their potential

for efﬁcient and high-quality privacy-preserving

clustering with MPC techniques (cf. §3).

•

Based on our analysis, we identify afﬁnity propaga-

tion as a promising candidate. Afﬁnity propagation

is used in a wide variety of privacy-critical med-

ical applications, such as epilepsy (Leone et al.,

2007) and cancer detection (John et al., 2016). It

automatically determines the number of clusters

and is tolerant to outliers (cf.

4). We provide the

ﬁrst fully privacy-preserving afﬁnity propagation

protocol with MPC usable in the passive and active

security model.

•

We provide an experimental evaluation of our pro-

tocol in multiple security models, i.e., considering

an active/passive adversary and honest/dishonest

majority (cf.

5). Our results enable the assess-

ment of the overhead associated with stronger se-

curity, which is important for meaningfully balanc-

ing privacy and efﬁciency in privacy-preserving

clustering applications. Our code is available

at https://encrypto.de/code/ppAfﬁnityPropagation.

We discuss related work on privacy-preserving cluster-

ing in §6 and conclude with §7.

2 PRELIMINARIES

This section introduces the preliminaries of clustering

(cf. §2.1) and secure computation (cf. §2.2).

2.1 Clustering

Clustering is an unsupervised ML technique that

groups data points into clusters. Since it is an unsuper-

vised ML technique, learning occurs without knowl-

edge of any true grouping of points or any data labels.

The goal is to group similar records into the same

cluster, while elements in different clusters should be

maximally different (Jain et al., 1999).

Clustering Algorithm Types.

We differentiate be-

tween partitioning-based, hierarchical, distribution-

based, and density-based clustering algorithms.

Partitioning-based algorithms separate the data set into

several non-overlapping groups, whose center is con-

sidered the center of the data points in this group (Xu

and Tian, 2015). Often these algorithms optimize an

objective function in an iterative fashion (Xu et al.,

1998). Examples are k-means (Steinhaus, 1956) and

afﬁnity propagation (AP) (Frey and Dueck, 2007),

which we both examine closely in this work (cf.

3).

This approach realizes a hard clustering, i.e., every

input record is assigned to exactly one cluster, whereas

soft clustering, e.g., based on distributions, may assign

a point to several clusters with varying probabilities.

Distribution-based clustering approximates the origi-

nal distributions from which data points are assumed to

have been drawn (Xu and Tian, 2015), as is the case for

Gaussian mixture models clustering (GMM). Hierar-

chical clustering algorithms represent a data set as a bi-

nary tree of data points and iteratively merge or divide

clusters based on the derived tree structure (Xu and

Tian, 2015). The computational complexity of these

algorithms is very high; already the ﬁrst step of most hi-

erarchical clustering algorithms, computing pair-wise

distances and performing a sort, requires

O(n

logn)

time complexity (Xu and Tian, 2015). Therefore, we

do not consider them as candidates for our privacy-

preserving algorithm. Density-based algorithms, such

as Density-Based Spatial Clustering of Applications

with Noise (DBSCAN) (Ester et al., 1996), cluster data

points that lie closely together in a dense area.

Clustering Quality Scores.

To measure clustering

quality, internal or external clustering indices are used.

External indices compare the clustering result to a

known ground truth, which is a known true assign-

ment of each point to a cluster. A ground truth is only

available for benchmark data sets and not present for

practical applications, since clustering is an unsuper-

vised ML technique. In those cases, internal indices

are used instead to assess the quality of a clustering

result. These indices focus on internal characteristics,

i.e., they measure the compactness of the elements

assigned to one cluster and the separation between

different clusters (Arbelaitz et al., 2013). To provide

a comprehensive quality assessment in

3 and

5, we

use an external and an internal clustering quality index:

The adjusted rand index (

ARI

) (Hubert and Ara-

bie, 1985) is a widely used (Arbelaitz et al., 2013;

Vinh et al., 2010) external index that assesses all inner-

cluster and inter-cluster data point pairs, where the 2

points were assigned to the same cluster and to differ-

ent clusters, respectively. Any pairs correctly identiﬁed

as belonging to the same cluster or to different clusters

increase the ARI value. The ARI lies in a range of

[−1,1]

, and a value of 1 indicates that the clustering

result is equal to the ground truth.

The silhouette index (

) (Rousseeuw, 1987) is a

SECRYPT 2021 - 18th International Conference on Security and Cryptography

174

Table 1: MPC protocols for different security models, cat-

egorized by their security level and number of corruptions.

Names are from MP-SPDZ (Keller, 2020).

Passive Active

Dishonest Majority Semi2k SPDZ2k

Honest Majority Replicated2k PsReplicated2k

well-known internal index (Arbelaitz et al., 2013) with

range

[−1,1]

and quantiﬁes the relation between inner-

cluster and inter-cluster distance between points. A

good result has an SI value close to 1, indicating a

small inner-cluster and large inter-cluster distance.

2.2 Multi-Party Computation (MPC)

MPC protocols allow the realization of privacy-

preserving clustering algorithms. They privately evalu-

ate an algorithm under “encryption” s.t. the inputs and

intermediate values remain hidden and only the output

is revealed. The two most prominent cryptographic

protocols for MPC are constant-round garbled circuits

(GC) by (Yao, 1986) and the multi-round Arithmetic or

Boolean Sharing protocol by (Goldreich et al., 1987).

Honest/Dishonest Majority.

This terminology spec-

iﬁes the fraction of possible corruptions among the

parties involved in MPC. In a dishonest majority set-

ting, the adversary may corrupt all but one party. This

setting is more complex and, thus, more expensive

than an honest majority setting, where only a minority

of parties are assumed to be corrupted.

Passive/Active Security.

Adversarial behavior can be

passive or active, which implies speciﬁc assumptions

about the adversary’s capabilities in an MPC protocol.

Passive security protects against passive adversaries,

who adhere to the protocol’s speciﬁcations while at-

tempting to learn as much as possible about that data

of other parties (Goldreich, 2009). In the active secu-

rity model, an active adversary can arbitrarily deviate

from the protocol, i.e., this model provides stronger

security guarantees. However, a trade-off between efﬁ-

ciency and security must often be made, since actively

secure protocols incur signiﬁcant overhead (Lindell

and Pinkas, 2015).

Tab. 1 contains an overview of several MPC

protocols used in our evaluation. We implement

privacy-preserving afﬁnity propagation (cf.

4) with

the MP-SPDZ framework for MPC (Keller, 2020):

SPDZ2k (Cramer et al., 2018) is the ﬁrst protocol for

the active, dishonest majority setting over

, and

was implemented by (Damg

ard et al., 2019). Semi2k

is a trimmed-down version of SPDZ2k for the passive,

dishonest majority setting. Replicated2k is a passively

secure protocol for 3 parties and honest majority based

on (Araki et al., 2016). PsReplicated2k (Eerikson et al.,

2019) extends (Lindell and Nof, 2017) to the ring set-

ting and uses ideas from (Cramer et al., 2018), offering

protection in the passive, honest majority setting.

3 ANALYSIS OF CLUSTERING

ALGORITHMS

In order to determine promising algorithm candidates

for privacy-preserving clustering, we compare the fol-

lowing prominent algorithms: k-means (Steinhaus,

1956), Gaussian mixture models (GMM) (Dempster

et al., 1977), afﬁnity propagation (AP) (Frey and

Dueck, 2007), and Density-Based Spatial Clustering

of Applications with Noise (DBSCAN) (Ester et al.,

1996). These algorithms were selected based on (1)

their widespread use (Bano and Khan, 2018; Xu and

Tian, 2015; Xu and Wunsch, 2005) and (2) simplicity,

which is crucial for efﬁciency with MPC. K-means

and AP are partitioning-based algorithms (cf.

2.1).

GMM is a distribution-based clustering algorithm, and

DBSCAN is a density-based clustering algorithm.

The input parameters of these algorithms have a

direct impact on the clustering result and its quality. In

the following, we discuss and visualize the inﬂuence

of these parameters, as well as other characteristics

such as the tolerance to outliers, ﬂexibility for multiple

cluster shapes, and other non-visual components on

the clustering quality. Furthermore, we investigate the

algorithms’ suitability for a privacy-preserving realiza-

tion via MPC.

3.1 Tolerance to Outliers

Data sets often contain outliers, i.e., data records that

are very untypical compared to the majority of the

set. Therefore, in the context of clustering, it is im-

perative that the clustering result, including identiﬁed

cluster centers and cluster assignments, is not distorted

or greatly affected by these data records. If a cluster-

ing algorithm either explicitly identiﬁes outliers or if

outliers do not distort the result, this algorithm can

be considered as tolerant to outliers. Especially in a

privacy-preserving context, data owners may not know

whether their own data contains an outlier or not, since

the other data owners’ input data is unknown.

DBSCAN deﬁnes a special notion of noise that

allows outliers to be ﬂagged as such (Ester et al., 1996;

Xu and Tian, 2015). Since AP does not require the

number of clusters as input parameter, outliers are typ-

ically detected as small, separate clusters, which can

be marked as outliers based on their size and which do

not affect the attributes of other identiﬁed clusters (Xu

and Tian, 2015). Therefore, both DBSCAN and AP

Balancing Quality and Efﬁciency in Private Clustering with Afﬁnity Propagation

175

(a) K-means (k=3) (b) Afﬁnity Propagation

Figure 1: Example for outlier tolerance of four clustering

algorithms. The red crosses mark the clusters’ centers in the

respective clustering algorithm’s output.

are tolerant to outliers. In contrast, k-means and GMM

are both sensitive to outliers. Speciﬁcally, k-means

requires all data points to be assigned to one cluster,

even if a point does not ﬁt to any cluster. Since the

algorithm speciﬁes the cluster center as the mean of

all points, outliers heavily distort these centers or form

an own cluster, forcing other true clusters in the data

to become merged (Xu and Wunsch, 2005). Similarly,

the clusters resulting from GMM are assumed to have

been drawn from a Gaussian distribution, so the center

of all clusters is also the mean of data points, which is

inherently sensitive to outliers (Xu and Tian, 2015).

To demonstrate these strengths and weaknesses

of the four clustering algorithms with respect to out-

liers, we provide an example in Fig. 1. We show the

clustering results for a data set with three circular clus-

ters, each drawn from a 2-dimensional Gaussian dis-

tribution, and 4 manually added outliers. DBSCAN

(Fig. 1d) does not include the concept of cluster centers.

We provided both k-means and GMM with the correct

number of clusters k=3. However both algorithms are

sensitive to outliers. K-means (Fig. 1a) marks one

outlier as a single cluster while it merges two true

clusters to a combined one, thus, it returns a result

that is far from optimal. GMM (Fig. 1c) groups the

3 clusters correctly; however, one centroid is affected

by the outliers and, thus, not centered in the “core”

cluster. AP and DBSCAN, on the other hand, perform

well; AP (Fig. 1b) identiﬁes the outliers as additional

clusters that do not inﬂuence the 3 other clusters and

can be identiﬁed as outliers based on their cluster size.

DBSCAN inherently identiﬁes all outliers as such.

(a) K-means (k=2) (b) Afﬁnity Propagation

Figure 2: Effect of setting the wrong numer of clusters k

for clustering with k-means and GMM, whereas DBSCAN

and AP determine the number of clusters automatically. The

red crosses mark the clusters’ centroids in the respective

clustering algorithm’s output.

3.2 Clustering Parameters

Another problem of k-means and GMM is the neces-

sity to choose the number of clusters k in advance (Xu

and Tian, 2015). Especially in a privacy-preserving

setting, it may be difﬁcult to set parameters like k in ad-

vance without knowledge of the entire data set. Fig. 2

shows that when the number of clusters k is set to the

wrong value (k=2 instead of 3), the clustering result of

k-means and GMM can be heavily distorted.

AP and DBSCAN do not require k to be chosen

in advance and are initialized with other parameters.

DBSCAN requires 2 parameters,

minPts

and

, where

minPts

quantiﬁes the minimal number of data points

required to form a cluster, while

is the maximum

distance between 2 data points considered “neighbors.”

Especially setting

can be challenging in a privacy-

preserving clustering application, as each data owner

only holds a subset of the input data. AP depends on

the preference parameter, which can be tuned manu-

ally by testing several possible values, running the AP

clustering with them, and then choosing the best one

(using a clustering quality index). Alternatively, pref-

erence can be set to the minimum or median Euclidean

squared distance between data points (Frey and Dueck,

2007). Therefore, AP is the most simple to initialize,

which is important in a privacy-preserving setting.

3.3 Other Attributes and Summary

The clustering quality scores ARI and SI (cf.

2.1)

for the example data sets from

3.1 and

3.2 can be

found in Tab. 2; the underlying distributions from

which these data sets were drawn are considered as the

SECRYPT 2021 - 18th International Conference on Security and Cryptography

176

ground truth. The scores conﬁrm the visual observa-

tions discussed in the previous subsections.

We summarize the strengths and weaknesses of all

clustering algorithms in Tab. 3 including additional

attributes of each algorithm, namely ﬂexible choice of

distance metrics, determinism, cluster shapes, compu-

tational complexity, and complex operations.

Since k-means averages input records to deter-

mine cluster centers and GMM uses the Gaussian

distribution, they do not directly support nominal

variables (Huang and Ng, 1999); AP and DBSCAN

are more ﬂexible, as they can use any distance func-

tion (Ester et al., 1996; Frey and Dueck, 2007). Fur-

thermore, the original k-means and GMM algorithms

are instances of the expectation-maximization (EM)

algorithm, which is non-deterministic and often uses

random initialization. This initialization strategy can

lead to convergence at a local optimum (Pe

na et al.,

1999). AP is deterministic (Frey and Dueck, 2007),

and DBSCAN only varies in rare cases for elements

that lie exactly in the neighborhood of elements from

different clusters (Ester et al., 1996).

So far, we focused on circular or spherical clusters,

which are non-convex. However, data can also come

in the form of elongated or irregularly shaped clus-

ters inﬂuenced, e.g., by the data’s dimensions. Since

some clustering algorithms, such as k-means and AP,

depend on a dissimilarity measure like Euclidean dis-

tance and assign points to the cluster with the closest

center, these algorithms do not perform as well on ir-

regular data sets (Xu and Tian, 2015). GMM assumes

that data is drawn from Gaussian distributions and

is therefore more ﬂexible, since oval-shaped distribu-

tions still fall within this assumption; however, GMM

performs poorly on other irregular cluster shapes (Xu

and Tian, 2015). Since DBSCAN is based on density

of points rather than the distance to a cluster center,

DBSCAN can detect arbitrarily shaped clusters (Ester

et al., 1996). These observations are conﬁrmed by our

experiments reported in Tab. 2.

Secure computation protocols add signiﬁcant over-

head to their plaintext equivalents; therefore, we must

balance clustering quality and complexity. We in-

clude the computational complexity of all algorithms

in Tab. 3. The naive implementation of k-means and

AP have a computational complexity of

O(n

) (Xu and

Tian, 2015; Frey and Dueck, 2007; Ester et al., 1996),

where

is the number of data points. DBSCAN and

GMM, in contrast, have a complexity of

O(n

) when

implemented using MPC. GMM requires an expen-

sive matrix inversion operation, and DBSCAN uses

a queue or stack for cluster expansion; to obliviously

realize this queue, the computational complexity of

the original baseline DBSCAN algorithm (Ester et al.,

Table 2: Clustering quality measured with ARI and SI

(cf.

2.1) of the four clustering algorithms k-means, AP,

GMM, and DBSCAN for different data sets. Larger values

(best in bold) indicate a better clustering result.

Attribute Algorithm ARI SI

Outliers

(Fig. 1, §3.1)

k-means (k=3) 0.55 0.67

AP 0.96 0.85

GMM (k=3) 0.98 0.79

DBSCAN 0.96 0.83

# of Clusters

(Fig. 2, §3.2)

k-means (k=3) 0.47 0.55

AP 1.00 0.73

GMM (k=3) 0.57 0.60

DBSCAN 0.93 0.65

Shape

(§3.3)

k-means (k=3) 0.52 0.51

AP 0.61 0.50

GMM (k=3) 1.00 0.45

DBSCAN 0.95 0.45

1996) increases from

O(n

) to

O(n

) (Bozdemir et al.,

2021). Thus, privacy-preserving DBSCAN and GMM

are signiﬁcantly more costly than the other algorithms.

Based on the results for the four clustering algo-

rithms, we ﬁnd AP to offer a good trade-off between

clustering quality and complexity, taking its favorable

handling of outliers and easily determinable clustering

parameters into account.

4 PRIVACY-PRESERVING

AFFINITY PROPAGATION

Afﬁnity propagation (AP) is an iterative message-

passing algorithm, where intuitively, each data point

sends two messages to all other points in every iter-

ation. A point’s ﬁrst message communicates the at-

tractiveness of another point as its cluster center, or

exemplar. This message is known as the

responsibil-

ity

. Based on all received responsibility values, each

data point replies with a message quantifying its suit-

ability as a cluster center for each other point, known

as the

availability

. These messages are revised in each

iteration until a consensus emerges, which identiﬁes

exemplars and point assignments to those exemplars.

All message updates are based on the previous changes

and the distance between data points in general. Com-

putationally, message passing is implemented through

iterative matrix updates of the availability and respon-

sibility matrices, which store the pair-wise values.

Adapting AP for MPC (cf.

2.2) requires an in-

depth analysis of the necessary operations of the al-

gorithm. Fortunately, AP mainly consists of multi-

plication and addition in terms of arithmetic, which

have efﬁcient MPC instantiations based on Arithmetic

Balancing Quality and Efﬁciency in Private Clustering with Afﬁnity Propagation

177

Table 3: Suitability of plaintext clustering algorithms for privacy-preserving clustering.

indicates that the algorithm provides

the property, while 7 indicates that it does not.

Attributes

k-means

(Steinhaus, 1956)

Afﬁnity Propagation

(Frey and Dueck, 2007)

GMM

(Dempster et al., 1977)

DBSCAN

(Ester et al., 1996)

Automatic choice of # clusters k 7 3 7 3

Tolerance to outliers 7 3 7 3

Non-spherical cluster support 7 7 3 3

Flexible choice of distance metrics 7 3 7 3

Determinism 7 3 7 3

MPC-friendly operations 3 3 7 7

Computational Complexity in MPC O(n

) O(n

)

Private Clustering

Protocols (cf. §6)

Leakage of intermediate

values

e.g., (Vaidya and Clifton, 2003),

(Jagannathan and Wright, 2005)

(Zhu et al., 2012)

(Lin et al., 2005),

(Hamidi et al., 2019)

e.g., (Liu et al., 2013),

(Rahman et al., 2017)

Fully private

(Bunn and Ostrovsky, 2007),

(Patel et al., 2012),

aschke and Armknecht, 2019),

(Mohassel et al., 2020)

This work (Bozdemir et al., 2021)

sharing (cf.

2.2). Furthermore, the iterative matrix

updates of AP often require maximum or minimum

operations, which can be implemented with compar-

isons using special subprotocols for secure computa-

tion. In

4.1 to

4.3, we formalize protocols for the

constituent parts of privacy-preserving AP, where all

deﬁned variables are secret shared among all participat-

ing parties, excluding the loop indices. This approach

hides all intermediate results, making our private AP

fully privacy-preserving, as discussed in

4.4.

4.1

discusses the necessary setup operations, including

distance calculations and a private calculation for the

preference parameter value.

4.2 and

4.3 describe

how responsibility and availability matrices are up-

dated, respectively. In practice, each update is damped

with the previous update using a weighted average of

the previous and current updates. The computation and

communication costs reported in

5.2 to

5.4 omit the

damping step to enable integer-only computation; how-

ever, including damping does not signiﬁcantly change

the runtime and communication costs, since its addi-

tion only incurs two arithmetic operations per iteration:

multiplication by the damping coefﬁcient and addition

of the components.

4.1 Setup and Output

Alg. 1 speciﬁes the modular steps of our privacy-

preserving AP protocol for both the ﬁrst distance cal-

culation, solely with addition and multiplication, and

the ﬁnal choice and assignment of exemplars, mainly

using comparison operations. Before the ﬁrst iteration,

the algorithm begins with the calculation of pair-wise

squared Euclidean distances for all points in the data

set in Step 5, whose additive inverses are stored in the

similarity matrix

. Alternatively, other distance met-

rics could be used. Our protocol automatically selects

the minimal negative difference between 2 data points

as the preference value in Step 7, as recommended

by (Frey and Dueck, 2007). This calculation easily

integrates into the initial calculation of the distance

between data points and is therefore not expensive.

Using the calculated distances, the availability and

responsibility matrices are iteratively updated until

convergence, when cluster centroids and assignments

no longer change with additional iterations. In a ﬁnal

step, the state of availability and responsibility values

determines which data points are chosen as exemplars,

i.e., cluster centers.

4.2 Responsibility Update

Intuitively, the responsibility value between two data

points quantiﬁes how likely one point is to serve as an

exemplar for the other point. The updates for responsi-

bility

based on availaibility

and similarity

in AP

are executed using the following rule:

r(i, k) ← s(i,k) − max

s.t.k

6=k

{a(i,k

) + s(i, k

)},

where responsibility

r(i, k)

quantiﬁes the evidence for

point k as an exemplar for point

. Expanding and mod-

ularizing this equation for use in secure computation

yields Alg. 2.

4.3 Availability Update

The availability of one data point for another represents

how likely one point is to choose the other point as its

exemplar. Availability is quantiﬁed using two rules.

The availability

of a point

to another point

based

on responsibility r is:

a(i,k) ← min

(

0,r(k, k) +

∑

s.t.i

/∈{i,k}

max{0,r(i

,k)}

)

where availability

a(i,k)

quantiﬁes the evidence for

point

to choose point

as an exemplar. The self-

availability, or availability for a data point

to itself,

SECRYPT 2021 - 18th International Conference on Security and Cryptography

178

Algorithm 1: Privacy-Preserving Afﬁnity Propagation.

Input:

iterations iter, data set

with N points of

dimension features

Output: E, exemplars of all points exEach

1: S = zeros((N,N))

2: for i in range(N) do

3: for j in range(N) do

4: for k in range(features) do

5: d=(D[k][i]-D[k][j])·(D[k][i]-D[k][j])

6: S[i][j] = S[i][j] + d

7: pref = pref>S[i][j]?pref:S[i][j]

8: end for

9: end for

10: end for

11: S = -S

12: for i in range(n) do

13: S[i][i] = preference

14: end for

15: N=size(S)

16: A=zeros(N,N), R=zeros(N,N)

17: λ=0.5

18: for it in range(iter) do

19: AS = A+S

20: UpdateResponsibilityMatrix(AS,S,R)

21: UpdateAvailabilityMatrix(AS,S,A,R)

22: end for

23: E = R+A

24: ex = zeros(N)

25: exEach = zeros(N)

26: for i in range(N) do

27: ex[i] = (E[i][i]>0)?1:0

28: end for

29: for i in range(N) do

30: for j in range(N) do

31:

exEach[i]=((ex[j]

∧

(exEach[i]

≥

∧

(E[i][j]

E[i][exEach[i]])

∨

(ex[j]>0)∧(exEach[i]<0))?j:exEach[i]

32: end for

33: end for

34: return E, exEach

is calculated differently:

a(k, k) ←

∑

s.t.i

6=k

max{0,r(i

,k)}.

We combine, expand, and modularize these update

rules for implementation with a secure computation

protocol in Alg. 3.

4.4 Security Discussion

The security of our privacy-preserving AP protocol

follows from the security of the employed MPC tech-

niques. These techniques guarantee that a passive

Algorithm 2: Update Responsibility Matrix.

Input: AS, S, oldR

Output: R

1: R = oldR

2: row = zeros(N)

3: idx = zeros(N)

4: Y = zeros(N)

5: for r in range(N) do

6: for p in range(N) do

7: index = idx[r]

8: max = row[r]

9: idx[r] = AS[r][p]>max?AS[r][p]:index

10: row[r] = AS[r][p]>max?AS[r][p]:max

11: end for

12: end for

13: R = S-repeat(row, columnRep=N, rowRep=1)

14: for index in idx do

15: AS[index] = -inf

16: end for

17: for r in range(N) do

18: for p in range(N) do

19: Y[r] = AS[r][p]>Y[r]?AS[r][p]:Y[r]

20: end for

21: end for

22: for i in range(N) do

23: R[i,idx[i]] = S[i, idx[i]] - Y[i]

24: end for

25: return R = (1-λ)·R + λ·oldR

or active adversary learns nothing beyond what can

be learned from the output. Initially, all data owners

secret-share their clustering input among themselves

or among several non-colluding parties in an outsourc-

ing scenario (Kamara and Raykova, 2011). As these

parties have access only to secret shares, no private

information can be extracted. The distance calcula-

tions for the similarity matrix and for the preference

value are realized with Arithmetic or Boolean shar-

ing (Yao, 1986; Goldreich et al., 1987; Beaver et al.,

1990). MP-SPDZ also includes conversions between

these realizations, which are also provably secure (Ro-

taru and Wood, 2019). The same techniques are used

for all other calculations in the protocol. All data but

the output of the clustering remains secret-shared dur-

ing the entire protocol, so our privacy-preserving AP

protocol is fully privacy-preserving.

5 EVALUATION

In this section, we benchmark our privacy-preserving

AP implementation (cf.

4) w.r.t. the achieved clus-

tering quality, its efﬁciency in comparison to related

Balancing Quality and Efﬁciency in Private Clustering with Afﬁnity Propagation

179

Algorithm 3: Update Availability Matrix.

Input: AS, S, oldA, R

Output: A

1: RP = zeros(N)

2: for r in range(N) do

3: for p in range(N) do

4: RP[r] = R[r][p]>0?R[r][p]:0

5: end for

6: end for

7: for i in range(N) do

8: RP(i,i) = R(i,i)

9: end for

10: sum = sum(R, dimension=1)

11:

A = repeat(sum, columnRep=1, rowRep=N) - RP

12: AP = zeros(N)

13: for r in range(N) do

14: for p in range(N) do

15: AP[r] = A[r][p]>0?0:A[r][p]

16: end for

17: end for

18: for i in range(N) do

19: AP(i,i) = A(i,i)

20: end for

21: A = AP

22: return A = (1-λ)·A+λ·oldA

Table 4: Data sets and parameter values.

Data Set Size # Clusters Iterations Preference

LSUN 400 3 127 24

Blobs

100 2 28 6

200 2 61 8

300 2 104 20

400 2 95 23

500 2 126 18.8

100 6 23 3

100 10 23 40

works, as well as its scalability.

MP-SPDZ.

We implement our protocol using the MP-

SPDZ framework for MPC (Keller, 2020). It realizes

secure multi-party computation (MPC) in the active

and passive security models with honest and dishonest

majorities. The MPC protocols of MP-SPDZ speciﬁed

in Tab. 1 run over a ring

with

k = 64

bits. All

experiments are run on a 16-core machine for each

party, with a 2.8 GHz Intel Core i9-7960X processor

and 128GB RAM, running Linux. We evaluated a

LAN setting with bandwidth 10Gbps and RTT 0.2ms.

Data Sets.

Several data sets were used in our eval-

uation. First, we chose the LSUN cluster bench-

marking data set (Ultsch, 2005) for a comparison of

privacy-preserving AP’s efﬁciency with other works on

privacy-preserving clustering (Mohassel et al., 2020;

aschke and Armknecht, 2019). It contains 400 2-

dimensional data points and 3 rectangular clusters, but

no outliers. Furthermore, we created artiﬁcial “blob”

data sets to benchmark privacy-preserving AP’s scala-

bility with respect to the data set’s size. For simplicity,

all clusters are spherically shaped and have a standard

deviation of 0.3, as we only use them for demonstra-

tion purposes on how to choose a preference value, as

well as runtime and communication cost benchmarks

with varying data set sizes. The artiﬁcial data sets are

also 2-dimensional, and their sizes range from 100 to

500 elements.

5.1 Clustering Quality & Input

Parameters

We ﬁrst discuss the effect of input parameters on the

clustering quality. We measure the quality of a clus-

tering output with the adjusted rand index (ARI) and

silhouette index (SI), cf.

2.1. Here we do not focus

on other aspects, e.g., the tolerance to outliers, the

handling of nominal variables, or determinism as dis-

cussed in

3, but rather on the question of how to

determine AP’s input parameter, i.e., the preference, in

a privacy-preserving setting. This is a crucial question

for practical applications of privacy-preserving cluster-

ing, but was completely neglected so far by previous

work.

Tab. 4 lists the manually tuned values for prefer-

ence and the number of iterations until convergence

for all data sets that we used in this work. For the arti-

ﬁcial “blob” data sets, AP yields a perfectly clustered

result that reﬂects exactly the ground truth. The result

of clustering LSUN with AP corresponds to an ARI

score (cf.

2.1) of 0.53 and a SI of 0.54. In comparison,

k-means (with k set to the true number of clusters as

shown in Tab. 4) results in a lower and hence worse

ARI of 0.44 and SI of 0.50.

As the data set size increases, the number of iter-

ations until convergence also increases. Furthermore,

more complex data sets like LSUN (i.e., not simply

spherical shaped clusters) require additional iterations

to converge. However, increasing the number of clus-

ters within a data set in general affects only the optimal

preference value, but not the number of iterations. Of-

ten, the optimal preference value also tends to grow

with the data set size and the number of clusters.

In a privacy-preserving setting, participants are

likely not able to tune the preference value before the

clustering given that they only have access to a subset

of the input data. In such cases, we recommend follow-

ing the suggestion of the original work that introduced

AP (Frey and Dueck, 2007) and set the preference

to a privately calculated median or minimum sum of

SECRYPT 2021 - 18th International Conference on Security and Cryptography

180

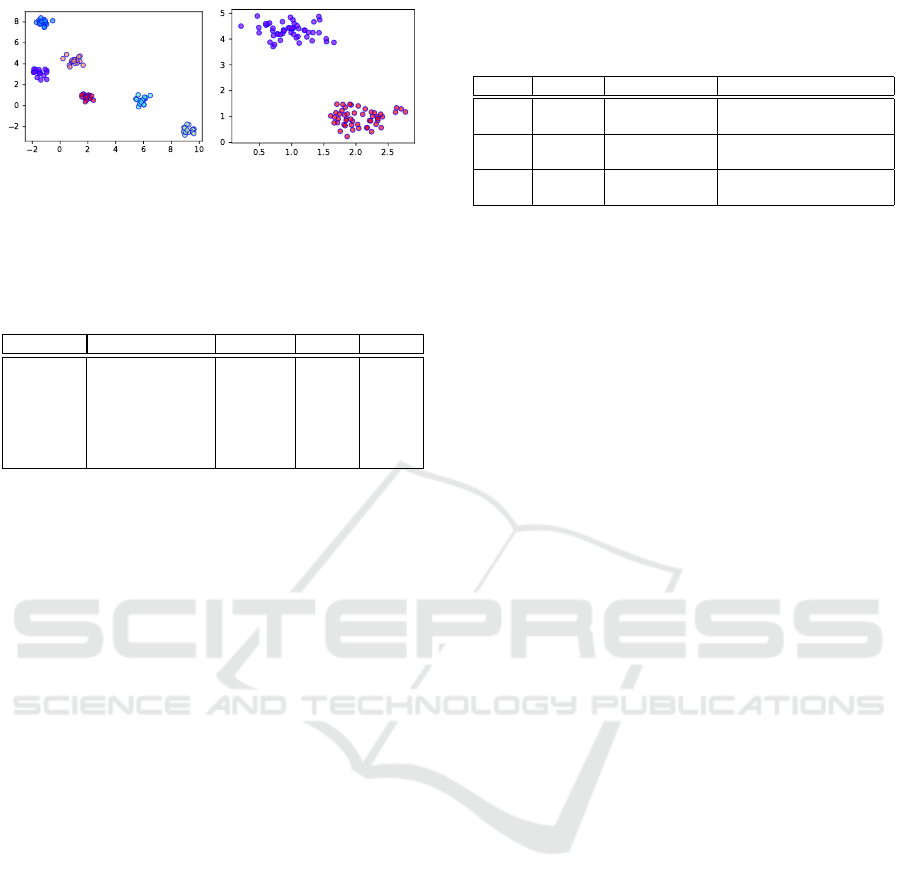
(a) Median

(b) Minimum sum

Figure 3: Example results when setting the preference value

to the median or minimum sum of squared distances between

the input records.

Table 5: Effect of the preference on number of iterations for

the “Blob” data sets with 100 elements and 2 or 6 clusters.

# Clusters Preference Iterations ARI SI

2 tuned: −6 28 1.0 0.85

2 min: −23.65 52 1.0 0.85

2 med: −4.10 27 0.50 0.32

6 tuned: −3 23 1.0 0.85

6 min: −242.78 280 0.54 0.62

6 med: −22.11 51 1.0 0.85

squared distances, which we simply call the distance

between data points. To do so, e.g., (Makri et al.,

2021; Aggarwal et al., 2010) propose efﬁcient MPC-

protocols for computing minimum and median. This

approach often yields a good clustering result (Frey

and Dueck, 2007). For example, we give the clustering

results for our 2 artiﬁcial 100-element “Blobs” data

sets with 2 and 6 clusters in Fig. 3. Setting the prefer-

ence value to the minimum distance yields a perfect

clustering result when the data set comprises 2 clus-

ters in Fig. 3b. Similarly, the 6-cluster data set can be

clustered perfectly when the preference value is set to

the median distance as shown in Fig. 3a.

However, the preference value affects the cluster-

ing result and the number of iterations until conver-

gence. We show this effect in Tab. 5. After preference

tuning, AP converges on the 2-cluster “Blobs“ data set

after 28 iterations, while it takes 52 iterations when the

preference is set to the minimum distance (yielding the

same clustering result). Similarly, although choosing

the median distance results in a good clustering result

for the 6-cluster data set, the algorithm converges after

51 iterations, rather than 23 with tuning.

5.2 MPC Performance

We evaluate privacy-preserving AP on a wide range of

MPC protocols and give an intuition for the efﬁciency-

security trade-off in different security models for

privacy-preserving AP. Therefore, we benchmark the

costs associated with our privacy-preserving AP im-

plementation for all settings described in Tab. 1 on the

public data set LSUN (Ultsch, 2005). Furthermore,

Table 6: Computation and communication costs for cluster-

ing LSUN in the passive (P)/active (A) security model, as

well as for honest (H)/dishonest (D) majority.

# Parties Runtime (hr) Communication (GBytes)

P H 3 22.67 103

A H 3 33.01 550

P D 3 107.18 42,658

A D 3 660.05 312,127

P D 2 54.92 17,471

A D 2 500.19 156,079

we carried out experiments for 3 parties in an hon-

est majority setting and for both 2 and 3 parties for a

dishonest majority of parties. We executed each exper-

iment 5 times and report the average cost per iteration

(see Tab. 4 and Tab. 5 for examples how many iter-

ations are needed). All resulting computational and

communication costs for clustering LSUN in these

settings are given in Tab. 6. As expected, the honest-

majority protocols (H) are signiﬁcantly more efﬁcient

than dishonest-majority protocols (D). Compared to

passive security (P), the active security model (A) in-

creases computational costs by a factor of about

9×

for the dishonest-majority (2 parties) and about

1.5×

for the honest-majority setting (3 parties). For the

same scenarios, communication costs grow by a factor

of approximately

9×

with dishonest-majority and

5×

with honest majority protocols. To choose the most

efﬁcient protocol, it is important to realistically assess

the behavior and capabilities of a potential adversary

w.r.t. the speciﬁc application (cf. §2.2).

5.3 Comparison to Related Work

We use the LSUN benchmark data set to compare

the efﬁciency of privacy-preserving AP with state-of-

the-art privacy-preserving clustering algorithms and

gauge costs for the standardized data set LSUN. Tab. 7

lists the runtime necessary to cluster LSUN using

three state-of-the-art efﬁcient privacy-preserving k-

means and DBSCAN protocols from (J

aschke and

Armknecht, 2019; Mohassel et al., 2020; Bozdemir

et al., 2021) compared to our work. Although (Mohas-

sel et al., 2020) is by a factor of 3,674

faster than

ours, we discussed in

3 that AP yields a better cluster-

ing result for many data sets (including LSUN), mak-

ing the additional costs acceptable. Similarly, the par-

allel and independent work by (Bozdemir et al., 2021)

on private DBSCAN is about 194

faster than ours.

However, they use an optimized hybrid combination

of secure two-party computation techniques (Demmler

et al., 2015) which is not possible with MP-SPDZ. Ad-

ditionally, (Bozdemir et al., 2021) reduce the complex-

ity of DBSCAN on LSUN to close to

O(n

)

by ﬁxing

a low number of neighborhood expansions which will

likely not be possible for all kinds of datasets.

Balancing Quality and Efﬁciency in Private Clustering with Afﬁnity Propagation

181

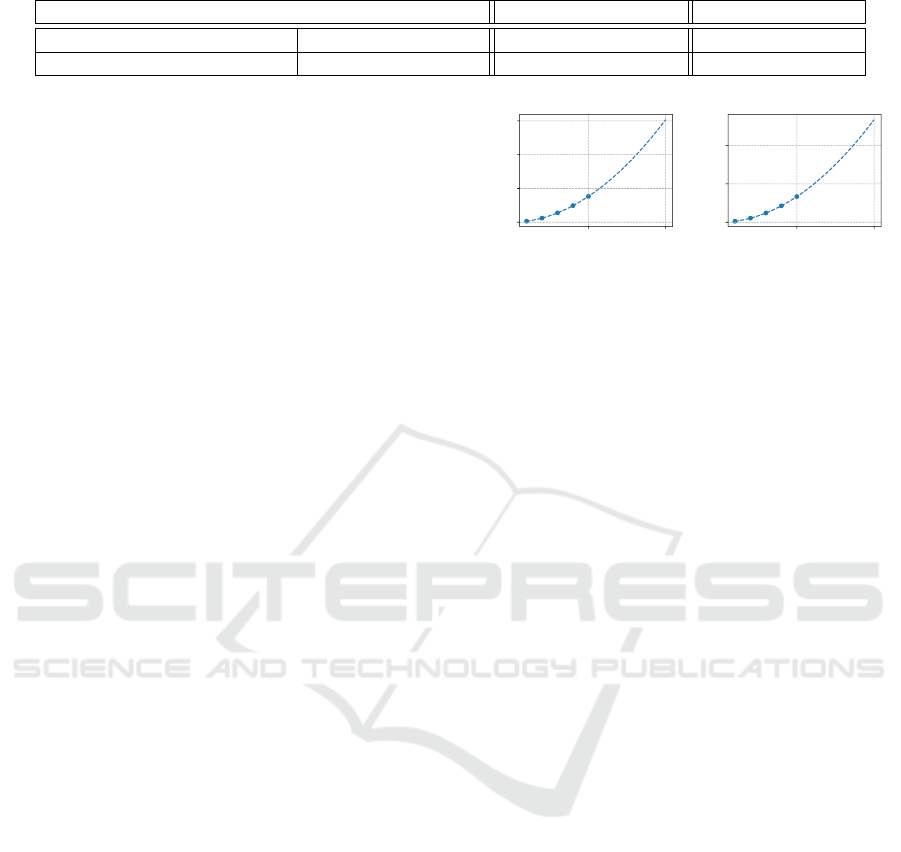
Table 7: Runtime comparison for privately clustering the LSUN data set with 2 parties and passive security.

k-means DBSCAN Afﬁnity Propagation

aschke and Armknecht, 2019) (Mohassel et al., 2020) (Bozdemir et al., 2021) This work

25.79 days 22.21 seconds 420.72 seconds 22.67 hours

5.4 Scalability

We evaluate the runtime and computation costs of

privacy-preserving AP on the “Blobs” data sets (cf.

Tab. 4) with varying sizes (100, 200, 300, 400, and

500 data points) to assess the scalability of privacy-

preserving AP. This evaluation was carried out for

2 parties and the passive security model. Note that

all other MPC instantiations from Tab. 1 scale sim-

ilarly with

and the results are, thus, transferable

to the other security settings. Since the evaluated

data sets have different optimal preference values and

converge after a varying number of iterations, which

would inﬂuence the scaling of cost values, we re-

strict our analysis to the computational and commu-

nication costs per iteration. We listed the required

number of iterations for the data sets in Tab. 4 such

that the runtimes of the full clustering can also be

derived. Fig. 4 presents our benchmark results. As

expected based on AP’s complexity (

O(n

)

), the costs

grow quadratically with the number of data points

n.We extrapolate the ﬁtted polynomial to a maximum

data set size of

n = 1000

. The ﬁtted polynomials

are

0.0001505n

+ 0.001638n − 0.1583

minutes for

runtime and

0.0005357n

+ 0.000001406n − 0.0001

GBytes for communication.

We note that the cost per iteration is not dependent

on the number of clusters in the original data set, since

the calculations executed will be the same. The op-

timal choice of preference value and the number of

iterations required for convergence may be affected

by the true number of clusters, as discussed in

5.1.

Therefore, our previous observations and benchmark-

ing results hold not only for the 2-cluster data sets

evaluated, but for data sets with arbitrary numbers of

clusters. This characteristic is a clear advantage of AP

over the k-means clustering algorithm, which becomes

increasingly expensive as the number of clusters k in

the data set grows.

6 RELATED WORK

Privacy-preserving machine learning (PPML) is an

active research ﬁeld, with much focus placed on cryp-

tographic methods for privacy-preserving supervised

and deep learning (Juvekar et al., 2018; Mishra et al.,

2020; Rathee et al., 2020; Boemer et al., 2020; Patra

500 1000

data points n

100

150

time (min)

(a) Runtime

500 1000

data points n

200

400

data sent (GBytes)

(b) Communication

Figure 4: Efﬁciency benchmark per clustering iteration for

privacy-preserving AP with 2 parties and passive security.

et al., 2021). As training data, often without labels,

is increasingly available, the relevance of privacy in

unsupervised learning, e.g., clustering, has also grown.

Some approaches to privacy-preserving clustering add

noise to the clustering process, providing provable

differential privacy (DP) guarantees (Su et al., 2017;

Balcan et al., 2017; Cai et al., 2020). DP is a privacy-

utility trade-off. Instead, we analyze cryptographic

approaches for achieving privacy, which yield full ac-

curacy but are more complex, so they are not directly

comparable to approaches based on DP.

Existing research on private clustering has mainly

proposed protocols for the k-means algorithm. To-

day’s most efﬁcient protocol is (Mohassel et al., 2020).

Their work is based on MPC and provides a privacy-

preserving k-means implementation that fully pre-

serves privacy and does not incur signiﬁcant compu-

tational overhead. For this reason, we compare our

privacy-preserving implementation of AP to their work

using the standard benchmark data set LSUN (cf.

5.3).

Other work on k-means provides privacy as well; how-

ever, some protocols use homomorphic encryption and

hence typically are signiﬁcantly slower, e.g., (Bunn

and Ostrovsky, 2007; J

aschke and Armknecht, 2019)

or are applicable only in certain settings, requiring

more than 2 non-colluding servers (Patel et al., 2012)

or horizontally partitioned data (Gheid and Challal,

2016). Some privacy-preserving k-means implemen-

tations have fundamental issues, leaking intermediate

cluster centers (Vaidya and Clifton, 2003; Jagannathan

and Wright, 2005; Jha et al., 2005) or information

about cluster sizes (Wu et al., 2020). In general, k-

means is a simple clustering algorithm, which explains

its popularity in privacy-preserving clustering. Un-

fortunately, its clustering capabilities and quality are

limited, as discussed in §3.

A few passively secure privacy-preserving variants

of clustering algorithms more advanced than k-means

SECRYPT 2021 - 18th International Conference on Security and Cryptography

182

have been proposed. (Bozdemir et al., 2021) design

a fully privacy-preserving DBSCAN clustering proto-

col. Unfortunately, most other protocols do not pre-

serve full privacy. For example, (Jagannathan et al.,

2010) tackle privacy-preserving hierarchical cluster-

ing, but their protocol reveals merging patterns. The

private DBSCAN protocols by (Jiang et al., 2008; Liu

et al., 2013; Rahman et al., 2017) leak information

such as parameter values, distances, cluster sizes, and

neighborhoods. (Zhu et al., 2012) propose a privacy-

preserving AP protocol for vertically partitioned data

in the passive security model using additively homo-

morphic encryption. Their protocol leaks the permuted

sensitivity values of all data records to one data owner.

7 CONCLUSION

In this work, we explored the suitability of k-means,

AP, GMM, and DBSCAN for efﬁcient crypto-oriented

clustering. While the clustering quality of k-means is

limited for many data sets, GMM and DBSCAN are

expensive to implement using MPC techniques. AP

provides more ﬂexibility in terms of all attributes, so

we design the ﬁrst fully privacy-preserving AP with

MPC techniques and implement it with the MP-SPDZ

framework. We evaluated the resulting cluster quality

and scalability, as well as the computational and com-

munication costs for all combinations of passive/active

security and honest/dishonest majority. With this, we

are the ﬁrst who evaluate the performance of a private

clustering algorithm on all 4 scenarios.

ACKNOWLEDGEMENTS

This project received funding from the European Re-

search Council (ERC) under the European Union’s

Horizon 2020 research and innovation program (grant

agreement No. 850990 PSOTI). It was co-funded

by the Deutsche Forschungsgemeinschaft (DFG) –

SFB 1119 CROSSING/236615297 and GRK 2050

Privacy & Trust/251805230, and by the BMBF and

the HMWK within ATHENE.

REFERENCES

Aggarwal, G., Mishra, N., and Pinkas, B. (2010). Secure

computation of the median (and other elements of spec-

iﬁed ranks). In Journal of Cryptology.

Araki, T., Furukawa, J., Lindell, Y., Nof, A., and Ohara,

K. (2016). High-throughput semi-honest secure three-

party computation with an honest majority. In CCS.

Arbelaitz, O., Gurrutxaga, I., Muguerza, J., P

erez, J., and

Perona, I. (2013). An extensive comparative study of

cluster validity indices. Pattern Recognition.

Balcan, M. F., Dick, T., Liang, Y., Mou, W., and Zhang,

H. (2017). Differentially private clustering in high-

dimensional euclidean spaces. In International Confer-

ence on Machine Learning (ICML).

Bano, S. and Khan, N. (2018). A survey of data clustering

methods. In International Journal of Advanced Science

and Technology.

Beaver, D., Micali, S., and Rogaway, P. (1990). The round

complexity of secure protocols. In ACM Symposium

on Theory of Computing (STOC).

Boemer, F., Cammarota, R., Demmler, D., Schneider, T.,

and Yalame, H. (2020). MP2ML: A mixed-protocol

machine learning framework for private inference. In

ARES.

Bozdemir, B., Canard, S., Ermis, O., M

ollering, H.,

Onen,

M., and Schneider, T. (2021). Privacy-preserving

density-based clustering. In ASIACCS.

Bunn, P. and Ostrovsky, R. (2007). Secure two-party k-

means clustering. In CCS.

Cai, H., Wang, J., Liu, X., and Li, X. (2020). Dp-ap: Differ-

ential privacy-preserving afﬁnity propagation cluster-

ing. In International Conference on Big Data Science

and Engineering (BigDataSE).

Chaturvedi, A., Carroll, J., Green, P., and Rotondo, J. A.

(1997). A feature-based approach to market segmenta-

tion via overlapping k-centroids clustering. Journal of

Marketing Research.

Cramer, R., Damg

ard, I., Escudero, D., Scholl, P., and Xing,

C. (2018). SPD

: Efﬁcient MPC mod

for dishon-

est majority. In CRYPTO.

Damg

ard, I., Escudero, D., Frederiksen, T., Keller, M.,

Scholl, P., and Volgushev, N. (2019). New primitives

for actively-secure mpc over rings with applications to

private machine learning. In IEEE S&P.

Demmler, D., Schneider, T., and Zohner, M. (2015). Aby-

a framework for efﬁcient mixed-protocol secure two-

party computation. In NDSS.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).

Maximum likelihood from incomplete data via the em

algorithm. In Journal of the Royal Statistical Society.

Eerikson, H., Orlandi, C., Pullonen, P., Puura, J., and Simkin,

M. (2019). Use your brain! arithmetic 3PC for any

modulus with active security. In Information-Theoretic

Cryptography.

Ester, M., Kriegel, H. P., Sander, J., and Xu, X. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In International

Conference on Knowledge Discovery and Data Mining

(KDD).

Frey, B. J. and Dueck, D. (2007). Clustering by passing

messages between data points. Science.

Gheid, Z. and Challal, Y. (2016). Efﬁcient and privacy-

preserving k-means clustering for big data mining. In

IEEE Trustcom/BigDataSE/ISPA.

Goldreich, O. (2009). Foundations of Cryptography: Volume

2, Basic Applications. Cambridge University Press.

Balancing Quality and Efﬁciency in Private Clustering with Afﬁnity Propagation

183

Goldreich, O., Micali, S., and Wigderson, A. (1987). How

to play any mental game or A completeness theorem

for protocols with honest majority. In STOC.

Hamidi, M., Sheikhalishahi, M., and Martinelli, F. (2019).

Privacy preserving Expectation Maximization (EM)

clustering construction. In DCAI.

Huang, Z. and Ng, M. K. (1999). A fuzzy K-modes algo-

rithm for clustering categorical data. IEEE Transac-

tions on Fuzzy Systems.

Hubert, L. and Arabie, P. (1985). Comparing partitions.

Journal of Classiﬁcation.

Jagannathan, G., Pillaipakkamnatt, K., Wright, R. N., and

Umano, D. (2010). Communication-efﬁcient privacy-

preserving clustering. Transactions on Data Privacy.

Jagannathan, G. and Wright, R. N. (2005). Privacy-

preserving distributed k-means clustering over arbi-

trarily partitioned data. In International Conference on

Knowledge Discovery in Data Mining (KDD).

Jain, A. K., Murty, M. N., and Flynn, P. J. (1999). Data

clustering: A review. In ACM Computing Surveys.

aschke, A. and Armknecht, F. (2019). Unsupervised ma-

chine learning on encrypted data. SAC.

Jha, S., Kruger, L., and McDaniel, P. (2005). Privacy pre-

serving clustering. In ESORICS.

Jiang, D., Xue, A., Ju, S., Chen, W., and Ma, H. (2008).

Privacy-preserving DBSCAN on horizontally parti-

tioned data. In International Symposium on IT in

Medicine and Education.

John, T., Jin, J., Dauwels, J., Cash, S., and Westover, B.

(2016). Clustering of interictal spikes by dynamic time

warping and afﬁnity propagation. In International Con-

ference on Acoustics, Speech and Signal Processing

(ICASSP).

Juvekar, C., Vaikuntanathan, V., and Chandrakasan, A.

(2018).

GAZELLE

: A low latency framework for se-

cure neural network inference. In USENIX Security’18.

Kamara, S. and Raykova, M. (2011). Secure outsourced

computation in a multi-tenant cloud. IBM Workshop

on Cryptography and Security in Clouds.

Keller, M. (2020). MP-SPDZ: A versatile framework for

multi-party computation. In CCS.

Leone, M., Sumedha, S., and Weigt, M. (2007). Clustering

by soft-constraint afﬁnity propagation: Applications to

gene-expression data. Bioinformatics.

Lin, X., Clifton, C., and Zhu, M. (2005). Privacy-preserving

clustering with distributed EM mixture modeling. In

Knowledge and Information Systems.

Lindell, Y. and Nof, A. (2017). A framework for construct-

ing fast mpc over arithmetic circuits with malicious

adversaries and an honest-majority. In CCS.

Lindell, Y. and Pinkas, B. (2015). An efﬁcient protocol

for secure two-party computation in the presence of

malicious adversaries. In Journal of Cryptography.

Liu, J., Xiong, L., Luo, J., and Huang, J. Z. (2013). Privacy

preserving distributed DBSCAN clustering. Transac-

tions on Data Privacy.

Makri, E., Rotaru, D., Vercauteren, F., and Wagh, S. (2021).

Rabbit: Efﬁcient comparison for secure multi-party

computation. In FC.

Masulli, F. and Schenone, A. (1999). A fuzzy clustering

based segmentation system as support to diagnosis in

medical imaging. Artiﬁcial Intelligence in Medicine.

Mishra, P., Lehmkuhl, R., Srinivasan, A., Zheng, W., and

Popa, R. A. (2020). Delphi: A cryptographic inference

service for neural networks. In USENIX Security.

Mohassel, P., Rosulek, M., and Trieu, N. (2020). Practical

privacy-preserving k-means clustering. In PETS.

Patel, S., Garasia, S., and Jinwala, D. (2012). An efﬁcient

approach for privacy preserving distributed k-means

clustering based on shamir’s secret sharing scheme. In

Trust Management VI.

Patra, A., Schneider, T., Suresh, A., and Yalame, H. (2021).

Aby2. 0: Improved mixed-protocol secure two-party

computation. In USENIX Security.

na, J., Lozano, J., and Larra

naga, P. (1999). An empirical

comparison of four initialization methods for the k-

means algorithm. Pattern Recognition.

Rahman, M. S., Basu, A., and Kiyomoto, S. (2017). Towards

outsourced privacy-preserving multiparty DBSCAN.

In Paciﬁc Rim International Symposium on Depend-

able Computing.

Rathee, D., Rathee, M., Kumar, N., Chandran, N., Gupta,

D., Rastogi, A., and Sharma, R. (2020). CrypTFlow2:

Practical 2-party secure inference. In CCS.

Rotaru, D. and Wood, T. (2019). Marbled circuits: Mixing

arithmetic and boolean circuits with active security. In

INDOCRYPT.

Rousseeuw, P. (1987). Silhouettes: A graphical aid to the in-

terpretation and validation of cluster analysis. Journal

of Computational and Applied Mathematics.

Steinhaus, H. (1956). Sur la division des corp materiels en

parties. Bulletin L’Acad

emie Polonaise des Science.

Su, D., Cao, J., Li, N., Bertino, E., Lyu, M., and Jin, H.

(2017). Differentially private k-means clustering and a

hybrid approach to private optimization. ACM Trans-

actions on Privacy and Security.

Ultsch, A. (2005). Clustering with SOM. In Workshop on

Self-Organizing Maps.

Vaidya, J. and Clifton, C. (2003). Privacy-preserving k-

means clustering over vertically partitioned data. In

International Conference on Knowledge Discovery and

Data Mining (KDD).

Vinh, N., Epps, J., and Bailey, J. (2010). Information the-

oretic measures for clusterings comparison: Variants,

properties, normalization and correction for chance.

Journal of Machine Learning Research.

Wu, W., Liu, J., Wang, H., Hao, J., and Xian, M. (2020).

Secure and efﬁcient outsourced k-means clustering

using fully homomorphic encryption with ciphertext

packing technique. IEEE Transactions on Knowledge

and Data Engineering.

Xu, D. and Tian, Y. (2015). A comprehensive survey of

clustering algorithms. Annals of Data Science.

Xu, R. and Wunsch, D. (2005). Survey of clustering algo-

rithms. IEEE Transactions on Neural Networks.

Xu, X., Ester, M., Kriegel, H.-P., and Sander, J. (1998). A

distribution-based clustering algorithm for mining in

large spatial databases. In International Conference on

Data Engineering.

Yao, A. C. (1986). How to generate and exchange secrets

(extended abstract). In FOCS.

Zhu, X., Liu, M., and Xie, M. (2012). Privacy-preserving

afﬁnity propagation clustering over vertically parti-

tioned data. In International Conference on Intelligent

Networking and Collaborative Systems.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

184