Optimized Line-of-Sight Assessment Algorithm for 5G mmW Network

Design using LiDAR Information

Reza Soosahabi and Magdy Bayoumi

Department of Electrical & Computer Engineering, University of Louisiana at Lafayette, Lafayette, LA 70504, U.S.A.

Keywords:

5G-NR, mmW Network Design, Fixed-Wireless Access, Line-of-Sight Assessment, LiDAR Application,

Visibility Algorithm.

Abstract:

Utilizing mmW carrier frequency bands (aka above-6 GHz) at the network edge, is a key enabling factor to

achieve near Gbps throughput in 5G-NR technology. The propagation characteristics of mmW signals in out-

door environment complicates 5G mmW network design. Previously used in backhaul networks, the service

availability of mmW radio technologies signiﬁcantly relies on the Line-of-Sight (LoS) signal path between the

communicating radios. LiDAR is considered a popular source of high-resolution aerial survey data suitable

for accurate LoS assessment. Maintaining low radio mounting height is another cost-related factor in practical

5G mmW network design. In this work we present a comprehensive LoS assessment problem incorporating

radio mounting height. Then we propose a new LoS assessment algorithm using LiDAR data that is compu-

tationally optimized for the practical aspects of 5G mmW network design. Empowered by a novel method to

topologically sort terrain data, it achieves constant-time, O(1), complexity to execute LoS assessment per user

location, whereas the complexity of retroﬁtted LoS algorithms for the same task grows linearly with respect to

the data dimensions. The improvements in the run-time efﬁciency are veriﬁed in numerical results for a real

deployment scenario.

1 INTRODUCTION

Superseding the Long-Term Evolution wireless tech-

nology, 5G is envisioned to be the prominent unify-

ing connectivity solution for a wide range of applica-

tions in the present decade. In terms of mobile and

broadband services, it is designed to offer near Gbps

throughput over wireless links at extremely low la-

tency. This is achieved by 5G-NR advanced radios

utilizing transmission bandwidths in the scale of hun-

dreds of MHz available in millimeter-wave (mmW)

carrier frequency bands (aka above-6 GHz) as well

as other physical layer advancements, such as beam-

forming and massive MIMO (Ghosh et al., 2019).

The propagation characteristics of mmW signals

in outdoor environment complicates 5G mmW net-

work design, particularly for broadband application

scenarios such as Fixed Wireless Access (FWA).

This requires deploying a higher number of cell sites

meticulously designed with respect to both terrain

and expected user locations data (Medin and Louie,

2019). As in legacy applications of the mmW in back-

haul networks, the Line-of-Sight (LoS) signal path

between both ends of a wireless link is the key factor

in service availability determination. Thus, a practical

approach to the complex design problem involves per-

forming LoS assessment between the candidate cell

site locations and expected user locations using high-

resolution areal survey data.

Light Detection and Ranging (LiDAR) is a re-

mote sensing technology offering very high resolution

aerial survey data invaluable in many applications.

Becoming popular in recent years, LiDAR has been

adopted by operators and software vendors engaged

in 5G network design. Basic LoS assessment (aka

viewshed or visibility problem) in large terrain envi-

ronment has been subject of extensive studies in com-

puter science due its relevance to other ﬁelds (Floriani

and Magillo, 2003).

In this work we present a more comprehensive

LoS assessment problem incorporating radio mount-

ing height that is a key practical variable in select-

ing 5G mmW cell sites. Keeping the required radio-

mounting height at minimum leads to signiﬁcant re-

duction in the infrastructure cost. Then we propose a

new LoS assessment algorithm using LiDAR data that

is computationally optimized for the practical aspects

of 5G mmW network design. It achieves remarkable

Soosahabi, R. and Bayoumi, M.

Optimized Line-of-Sight Assessment Algorithm for 5G mmW Network Design using LiDAR Information.

DOI: 10.5220/0010548100170024

In Proceedings of the 18th International Conference on Wireless Networks and Mobile Systems (WINSYS 2021), pages 17-24

ISBN: 978-989-758-529-6

computational efﬁciency compared to the retroﬁtted

LoS assessment algorithms that operate in linear-time

complexity at best with respect to the terrain size.

Empowered by a novel method to topologically sort

terrain data, it takes constant-time, O(1), complexity

to execute LoS assessment per user location.

The rest of this article organized as follows: LoS

assessment problem investigated in Section 2 fol-

lowed by Section 3 outlining possible solutions using

LiDAR data. Section 4 is designated to mathematical

details of proposed algorithm followed by numerical

results and conclusion, respectively in Sections 5 and

2 SCOPE OF PROBLEM

This section is dedicated to the practical challenges

of designing 5G mmW networks in outdoor environ-

ment. Although being used in other wireless applica-

tions, the propagation characteristics of mmW signals

in outdoor environment poses signiﬁcant design over-

head in terms of infrastructure cost and the computa-

tional complexity of coverage prediction models. The

problem of LoS assessment using high-resolution ter-

rain data is outlined towards the end of this section. It

captures a common design methodology used in cur-

rent deployments to properly select the radio installa-

tion sites.

2.1 Characteristics of mmW Signals

Utilizing mmW frequency bands is a key advance-

ment in 5G new radio (NR) technology. Radios op-

erating in mmW carrier frequency have the luxury of

larger transmission bandwidths with smaller antenna

elements. Therefore, they can house large antenna

arrays in the same form-factor as their sub-6 GHz

counterparts. Antenna arrays can be used for creat-

ing multiple highly-directional beams for both trans-

mitting and receiving the radio signals. However,

mmW radio signals suffer much higher attenuation

(path-loss) in the environment compared to their sub-

6 GHz counterparts that is attributed to their shorter

wavelengths. They cannot penetrate most obstacles

nor beneﬁt much from multipath reﬂections to reach

far distances without a LoS signal path. Focusing

on the link throughput, some of these propagation

losses are compensated for by utilizing higher band-

width and the beam-forming gains. Presence of LoS

signal path coupled with beam-forming can signiﬁ-

cantly boost per-user throughput and overall cell ca-

pacity by enabling SDM (Spatial Diversity Multiplex-

ing) in common point-to-multi-point scenarios. It en-

ables reusing time-frequency resources across multi-

ple beams, given sufﬁcient angular spread among the

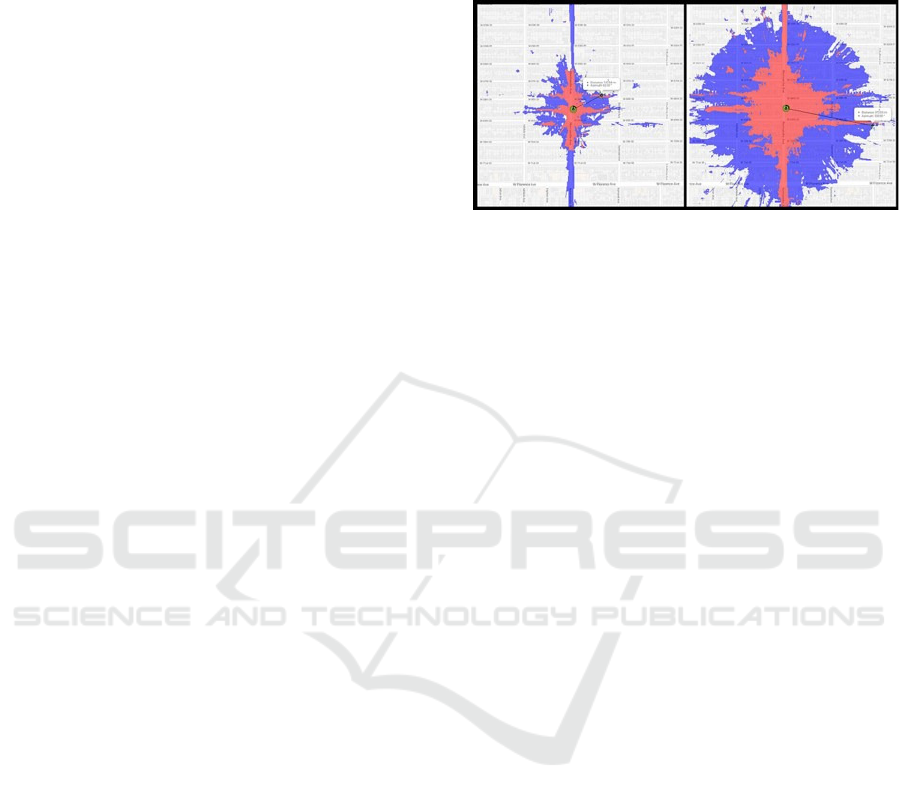
users. Figure 1 (excerpted from (Medin and Louie,

Figure 1: Comparing 5G-NR Coverage: above-6 GHz (left)

v.s sub-6 GHz (right) excerpted from (Medin and Louie,

2019). Red and Blue shades indicate high-throughput and

low-throughput areas, respectively.

2019)) depicts the throughput comparison between

identical 5G cell deployments in 28 GHz (mmW

band) and 3.4 GHz (sub-6 band) in the same serving

area, where the red and blue shades respectively de-

note the maximum achievable throughput in 1.0 Gbps

and 100 Mbps ranges. The key observations about

5G cell deployments in mmW band compared to sub-

6 band are:

• Smaller Serving Area Per Cell: this could be

confused as a disadvantage in the ﬁrst glance,

however smaller cells means the achievable cell

capacity is divided among fewer users leading

to higher average throughput per-user. To cover

the same geographical area more cells are de-

ployed with less inter-cell interference, thanks to

the fast attenuation of mmW signals. Utility poles

and other alternative radio mounting structures are

discussed in (Medin and Louie, 2019) as common

choices for the operators deploying 5G mmW

cells, whereas the technologies in sub-6 bands can

still rely on the existing designated telecom tow-

ers.

• Signiﬁcance of LoS Signal Path: unlike the sub-

6 band, the presence of LoS signal path signiﬁ-

cantly correlates with service availability. There-

fore, the signal quality undergoes drastic varia-

tion depending on LoS signal path availability at

instantaneous user location, particularly near the

cell edge. This phenomenon has already been

incorporated in 3GPP standard channel model

(3GPP, 2018a) and still subject of study as in

(Haneda et al., 2016).

2.2 Design Problem Objectives

Here we consider the problem of designing 5G mmW

radio network infrastructure for a given geographic

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

area without any prior 5G service deployment. There

are two typical deployment scenarios: mobility and

Fixed-Wireless Access (FWA). Mobility services are

offered to mobile user devices (UE) while FWA is

offering broadband connectivity over mmW links to

subscriber devices (CPE) installed on subscribers’

properties (typically in sub-urban / rural areas).

The design process in both scenarios starts with

collecting: topographical survey information (e.g.

terrain, buildings map), property information (e.g.

residential, commercial, public venues), and candi-

date cell deployment sites (e.g. telecom towers, util-

ity poles). Then the desired coverage targets are de-

termined for each scenario considering the following

factors:

• 5G Mobility Coverage Targets: this includes

polygons representing the areas with high user

density / trafﬁc. Since the users are mobile, there

is no need for guaranteed service at any particu-

lar location in the polygon. This is a design relief

since existing approximate predictions model can

still be used to guarantee average service across

each polygon.

• 5G FWA Coverage Targets: Since the wireless

link is used to offer broadband services equiv-

alent to wired technologies (e.g. ﬁber and ca-

ble modems), the guarantee of service per user

is a more stringent requirement in this scenario.

Thus, the service availability for each subscriber

property (residential, or commercial) should be

individually evaluated in the design phase. there

should be at least a CPE installation point on each

target property with guaranteed service connectiv-

ity.

Although applicable to both scenarios, the proposed

solution in this work is optimized more towards the

more challenging problem of 5G-FWA design.

Maintaining low radio mounting height is another

key practical design objective. Depending on CU-

DU split scenario (3GPP, 2018b) a combination of

directional antennas and other radio hardware com-

ponents should be mounted on candidate site loca-

tions, preferably above the foliage (aka clutter line) to

provide connectivity to the surrounding user devices.

These hardware components exert structural loads

such as wind-loading on their bearing structure (Tra-

vanca et al., 2019). The structural load is proportional

to the mounting height, so the higher the mounting

height, the higher structural reinforcement cost (De-

Grasse, 2013). Considering the increased number of

cells in 5G mmW and the height and load limitations

on the cell candidates (such as utility poles), the struc-

tural cost can become prohibitive without controlling

the mounting height in the design phase.

The 5G mmW design problem is a complex inte-

ger programming task whose output includes a set of

cell site coordinates, mounting height and the angular

orientation of antennas.

2.3 LoS Assessment Problem

As stated in Section 2.1, Existence of LoS signal path

between the user devices and the serving radio can

be accounted as a reliable service availability metric.

This evidently becomes a trade-off based on the fact

that the higher the mounting height, the more user lo-

cations with LoS signal path (Haneda et al., 2016).

Hence, a solution to the sophisticated cellular design

problem will depend on solving the following prob-

lem for each cell site candidate:

Problem 1. (LoS Query): For a given cell deploy-

ment coordinate (on XY -plane) and any user location

point (in XYZ-space), compute the minimum radio

mounting height at the cell site (minRMH) to achieve

LoS between the user and the cell radio.

Computing minRMH for every combination of

candidate site location and user point is a prerequisite

to any design decision. Solving Problem 1 requires

very high-resolution Digital Elevation Model (DEM)

of the serving area that come in considerable data vol-

umes. Hence, any solution algorithm should be efﬁ-

cient in terms of computation complexity per query

since this computation can be repeated in several iter-

ations per each cell site candidate through the design

process.

3 SCOPE OF SOLUTION

This section details the required data source and the

process to solve Problem 1, including: geometric

formulation of LoS problem in terms of minRMH

and they elements of the existing and proposed algo-

rithms.

3.1 Creating DEM from LiDAR Data

Light Detection and Ranging (LiDAR) offers com-

prehensive areal survey data with very high reso-

lution suited for accurate LoS assessment. It is a

high-resolution remote sensing technology using the

pulsed laser transceiver typically mounted under an

aircraft to scan the surface below a raster ﬂight path.

Similar in concept to radar technology, the character-

istics of the returned pulses are used to estimate the

coordinates of the reﬂection points. The output of

raw LiDAR scan is commonly called a point-cloud

Optimized Line-of-Sight Assessment Algorithm for 5G mmW Network Design using LiDAR Information

which is a scattered set of 3D points (in UTM co-

ordinate system) (Wandinger, 2005). Projected in

3D XY Z-space, the points are distributed almost uni-

formly on XY -plane (base-plane) with a ﬁxed step

size. Due to its high demand in various survey appli-

cations in some countries, the government agencies

(e.g. (USGS, 2018)) collect and publicly distribute

LiDAR data on periodic basis for most of the areas.

The raw LiDAR data are normalized and pre-

sented in the form of a Cartesian DEM to study the el-

evation information, where Z-axis values show the el-

evation across the base plane. An example of outdoor

DEM displayed in Fig. 2. In each iteration of LoS as-

sessment, the candidate cell site is usually mapped to

the origin of XY -plane with possible radio mounting

points along the Z-axis.

Figure 2: Example of outdoor DEM.

LiDAR provides ample resolution compared to

common clutter models using terrain approximation.

For example, the public data provided by USGS offers

70cm leading to a DEM with an enormous data set in

most survey projects. Therefore, efﬁcient algorithms

are required to perform LoS assessment task. DEMs

representing LiDAR data have disproportionate value

range across their dimensions. In a Cartesian system,

expanding the area under study pushes the limit along

X-axis and Y -axis in the scales of kilometers, while

the elevations along Z-axis remain within the range

of hundreds of meters in most topographies.

Remark. To incorporate the scale of DEM size in

algorithm complexity notation, it is modeled as an

N ×N grid of elevation values quantized into K digi-

tal levels. In the subsequent analysis, the algorithmic

complexities are expressed in orders of N while K is

considered an O(1) constant.

3.2 LoS Assessment Geometry

Problem 1 is a classic 3D visibility problem that can

be reduced to a 2D sub-problem in the following sec-

tion.

3.2.1 Creating 2D Sub-problem

Considering a DEM in Cartesian space where the ra-

dio mounted along ”Z-axis, a ray is a line connect-

ing a point on the Z-axis to a user location under

study. This ray together with the Z-axis will form

a half-plane that we refer to as a ray-plane. A ray

indicates a LoS (visibility) condition, if it is not ob-

structed with any other DEM object in between its

two end-points. Hence, examining the DEM points

residing on the ray-plane should be sufﬁcient to deter-

mine LoS condition. More sophisticated propagation

models evaluate LoS conditions for a cluster of rays to

predict signal levels which is outside the scope of this

work. Since the ray-plane will always be perpendicu-

lar to the XY -plane (base-plane), it is simple to iden-

tify the DEM points intersecting with the ray-plane

by projecting the ray onto XY -plane and selecting the

DEM grid points it crosses. Once selected through

this process, the DEM points on the ray-plane can be

represented in a new 2D Cartesian coordinate system

Z, where a values on X

-axis shows the distance of

the point from the Z-axis, and the Z values are pre-

served as the radio mounting height. An example of

ray-plane has been illustrated in Fig. 3 constructed

with Z-axis and a DEM point P

Henceforth, P = {P

, P

, ··· , P

} denotes an

enumerated set of N DEM points P

= (x

, z

) in a

ray-plane indexed in asceding order according to their

values for 0 ≤ j ≤ N. The origin is ﬁxed at P

and

denotes farthest point along the X

axis, i.e. the

horizon. Here we assume that all elevation values are

normalized by the lowest possible value. The base

ground elevation is assumed to be 0.

Figure 3: Visualizing the ray-plane and a solution for Prob-

lem 2.

Now the LoS query problem for each point in the

ray-plane can be formulated as:

Problem 2. (2D LoS Query): Given the set of ray-

plane points P , and a point P

∈ P , compute the

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

Figure 4: Proposed LoS assessment algorithm.

minRMH value h

∗

to reach LoS between the pair of

points: P

and (0, h

∗

) on X

Z-plane.

The value h

∗

should be computed such that none

of the intermediate DEM points appear above the line

connecting (0, h

∗

) to P

. The minimality condition

implies that there would be at least a DEM point P

with 0 < j < m barely residing on this line. The

dashed purple line in Fig. 3 demonstrates an exam-

ple solution to Problem 2.

3.2.2 Solving 2D Sub-problem

One can show that each point independently con-

tributes in the value of h

∗

. Let h

∗

(m, j) denote the

minRMH for P

given the condition that all the inter-

mediate points are eliminated except P

, 0 < j < m.

One can draw a line connecting P

and P

represent-

ing the ray which barely meets LoS. Extending this

line towards Z axis lands at (0, h

∗

(m, j)), where

∗

(m, j) =

−z

−x

(1)

. Applying the max-min technique, it can be shown

that

∗

= max{h

∗

(m, i)}

m−1

i=1

(2)

3.3 Using Existing Visibility Algorithms

Discovering LoS for pairs of points in a 3D space is a

classic computational geometry problem with wide-

ranging applications (Floriani and Magillo, 2003).

The most common algorithms are optimized to com-

pute what known as viewshed, where all the points in

a DEM with LoS path to a single point are discov-

ered. They are not optimized to accurately compute

minRMH queries as articulated in Problem 1. Re-

purposing viewshed algorithms for this problem may

require iteratively computing viewshed for all possi-

ble radio-mounting values, in O(K), and extracting

minRMH for user locations. In doing so, one of the

best known algorithm developed by Van Kreveld in

(Van Kreveld, 1996) that results in a solution com-

plexity in order of O(KN

logN).

R3 algorithm proposed in (Sorensen and Lanter,

1993) is one of the early algorithms that operates in

query fashion and can be modiﬁed to solve Problem

2. The computational complexity of (2) is O(N) per

query since (1) should be computed for all the preced-

ing points to P

. Put in perceptive to (Van Kreveld,

1996), computing minRMH for the entire DEM using

R3 will result in O(N

) complexity.

3.4 Elements of Proposed Algorithm

The proposed algorithm is optimized to process the

Problem 2 queries in constant time, O(1), indepen-

dent to the distance of the query point from the tower

location, proportional to N. Exhaustively solving (2)

for all the DEM points in a ray-plane leads to a O(N

)

complexity. The key distinction of the proposed al-

gorithm is using a fast-constructable data structure in

form of a Directed Acyclic Graph (DAG) to reduce

computation complexity of (2). As illustrated in Fig-

ure 4, the proposed algorithm comprised of and extra

ofﬂine processing step to construct the DAG and an

online query-handling process.

The reprocessing steps starts with common data

normalization and DEM creation. Then given the can-

didate cell site location, the DEM points are grouped

into a set of possible ray-planes. The set of all pos-

sible ray-planes can be created by considering each

point at the fringe of the DEM and the cell site at the

origin. Then each ray-plane independently undergoes

DAG construction process.

The query handling consists of two steps: ray-

plane determination and minRMH computation. The

ﬁrst step requires a simple ray-plane look-up based

on the angular orientation of the query point on the

base plane. The second step involves computing (1)

for a collection of points while traversing the pre-

constructed ray-plane DAG.

4 Proposed Algorithm

The key elements of proposed LoS assessment al-

gorithm are detailed in this section by focusing on

the components of an optimal solution to Problem 2

within a given ray-plane.

4.1 DAG Construction

The following proposition provides the key insight to

skip the redundant iteration in (2).

Optimized Line-of-Sight Assessment Algorithm for 5G mmW Network Design using LiDAR Information

Proposition 1. Given a point Pm ∈P and a pair of its

preceding points P

and P

such that 0 < x

< x

satisfying h

∗

(m, i) > h

∗

(m, j) requires z

> z

It is straightforward to prove Proposition 1 using

the formula in (1). Since the max operation is used

across h

∗

(m, i) values to compute h

∗

, this can be used

in its negative form to ignore points that produce in-

signiﬁcant h

∗

(m, i) values. Starting from P

and iter-

ating backwards to P

, after computing h

∗

(m, j) for a

point P

, we shall jump to computing h

∗

(m, i) for the

next preceding point P

with greater elevation z

> z

We need to continue these jumps until there is no pre-

ceding point with higher elevation. This can save lots

of computation cycles by skipping low intermediate

points in between the jumps. Since this operation may

be repeated to compute minRMH for any points in

a ray-plane, it would be beneﬁcial to determine the

preceding higher point to each point in a single pre-

processing step. This will be a simple variation of

the classic nearest smallest point problem in computer

science, where extremely efﬁcient solution algorithms

are available in (Berkman et al., 1993) and (Berkman

et al., 1998).

In the context of a ray-plane, the enumerated set

of points in P are augmented in the format of P

, z

, p

) for 0 < i ≤N, where p

stands for a pointer

(index) the next-greater-elevation-point (NGP) pre-

ceding P

. In each ray-plane there could be some peak

points where p

= Null, implying the minimum radi-

ation center be zero. The augmented P can be graph-

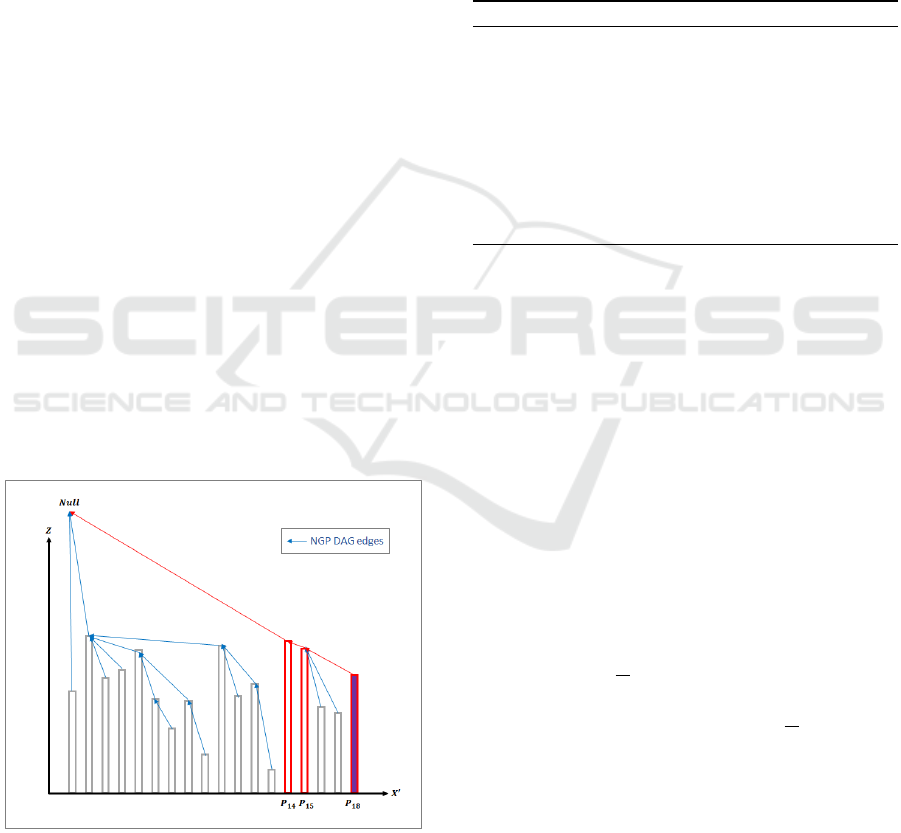
ically represented as a DAG demonstrated in Fig. 5,

where the blue arrows show the added pointers, i.e.

DAG edges.

Figure 5: NGP-DAG visualization in a ray-plane.

4.2 DAG Traversal

After constructing the DAG for a given ray-plane with

augmented point set P , the minimum radiation cen-

ter h

∗

is computed for each P

∈ P by only travers-

ing DAG predecessors of P

and computing (1) whose

maximum value reported as minRMH. This proce-

dure is outlined in Algorithm 1.

The red arrows in Fig. 5 depict the DAG traversal

path to compute minRMH for a sample point P

. It

shows that Problem 2 can be efﬁciently solved in 2 it-

erations (evaluating (1) for P

and P

) using the pro-

posed algorithm, whereas an exhaustive algorithms

requires 17 iterations to evaluate (1) for all the points

to P

Algorithm 1: Proposed DAG-traversal Algorithm.

1: procedure (2D LoS Query): P

, P

2: h

∗

← 0

3: i ← m

4: while p

6= Null do

5: h

∗

← max(h

∗

(m, i), h

∗

)

6: i ← p

7: end while

8: return h

∗

9: end procedure

4.3 Complexity Analysis

Using the algorithm outlined in (Berkman et al.,

1993) the DAG can be constructed in a near-

constant time O(loglogN) one-shot operation that can

be further improved to an absolute constant order

O(logloglogK) utilizing a hyper-threaded computing

environment (Berkman et al., 1998).

The complexity of the Algorithm 1 determined by

the expected number of the while-loop iterations. The

loop continues as long as there is an NGP with higher

elevation. Therefore, the total number of loop iter-

ations is bounded by the constant K, the number of

possible elevation levels in the DEM. It can be shown

that the expected number of loop iterations is rela-

tive to the expected length of the underlying longest-

increasing-sequence of elevations in each ray-plane,

proved to be O(

√

K) in (Odlyzko and Rains, 2000).

Remark. Combining the two steps, the proposed al-

gorithm achieves a constant-time O(

√

K) solution to

compute minRMH queries in Problem 1.

This algorithm can also be used to compute

minRMH for the entire DEM points (viewshed mode)

in some scenarios such as mobility applications in

municipal areas. The table in Figure 6 summarizes

the performance of the proposed algorithm compared

to the existing algorithms discussed in Section 3.3 for

both scenarios.

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems

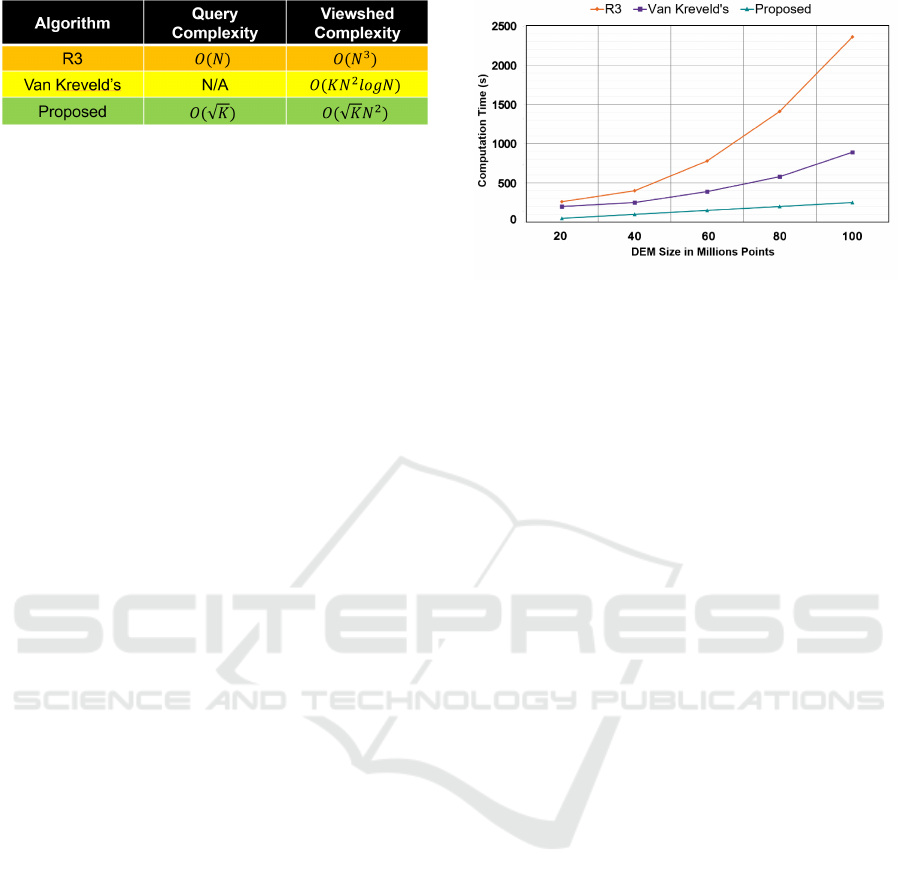
Figure 6: Algorithms’ computational complexities.

5 NUMERICAL RESULTS

In this section, we present the implementation de-

tails for the proposed LoS Assessment algorithm for

a commercial 5G-FWA deployment scenario. Then

compare the computation time with the existing algo-

rithms described in Section 3.3 in the same settings to

demonstrate the predicted efﬁciency gains.

5.1 Test Environment

The public LiDAR data set for a suburban residen-

tial neighborhood in the central area of the State of

Mississippi are obtained from Mississippi Automated

Resource Information System (MARIS) at (Woolpert,

2014). All algorithms are implemented in C++14

using PDAL (https://pdal.io) utility API to pre-

process the LiDAR data set and create a basic DEM.

The subsequent codes are compiled with gcc -Ofast

utility into executable libraries. The run-time envi-

ronment hosted on a RHEL

Linux virtual machine

with access to 16 GB of RAM and 2 Intel XEON

processors.

5.2 Test Scenario

The DEM has been created for a maximum of 8 km

radius area around a cell tower of maximum height

60 m as a potential deployment site for 5G FWA in

n257 band ( 28 GHz). To achieve a fair comparison

with (Van Kreveld, 1996), the analysis is performed

in viewshed mode for the proposed algorithm and R3

in (Sorensen and Lanter, 1993). We have computed

minRMH for all the DEM points within a circle cen-

tered at the origin with different radii to achieve dif-

ferent number of point queries shown Figure 7. The

execution time in seconds has been plotted in Figure

7 for all 3 algorithms for different number of DEM

points. Considering the values in horizontal axis is

proportional to N

, the execution times follow the ex-

pected complexity trends indicated in Figure 6 table

for the viewshed scenario.

Figure 7: Comparing execution time of the algorithms.

6 CONCLUSION

Considering the practical challenges of 5G mmW net-

work design, we present a comprehensive LoS assess-

ment problem incorporating radio mounting height.

Then we propose a new LoS assessment algorithm

using LiDAR data that is computationally optimized

for the practical aspects of 5G mmW network design.

Empowered by a novel method to topologically sort

terrain data, it achieves constant-time, O(1), com-

plexity to execute LoS assessment per user location,

whereas the complexity of retroﬁtted LoS algorithms

for the same task grows linearly, O(1) with respect to

the data dimensions. The improvements in the run-

time efﬁciency are veriﬁed in numerical results for

a real deployment scenario. It is worth investigat-

ing means of leveraging this algorithm to reduce the

computational complexity of coverage prediction al-

gorithms based on ray-tracing.

ACKNOWLEDGMENTS

We would like to express our appreciation to Infolink-

USA Inc. staff for providing the opportunity to study

the practical challenges in deploying 5G-FWA net-

works and motivating us to deploy our solution as a

joint venture with their clients.

REFERENCES

3GPP (2018a). LTE; 5G; Study on channel model for fre-

quency spectrum above 6 GHz. Technical Speciﬁca-

tion (TS) 38.900, 3rd Generation Partnership Project

(3GPP). Version 15.0.0.

3GPP (2018b). Study on Central Unit (CU) - Distributed

Unit (DU) lower layer split for NR. Technical

Speciﬁcation (TS) 38.816, 3rd Generation Partnership

Project (3GPP). Version 15.0.0.

Optimized Line-of-Sight Assessment Algorithm for 5G mmW Network Design using LiDAR Information

Berkman, O., Matias, Y., and Ragde, P. (1998). Triply-

logarithmic parallel upper and lower bounds for mini-

mum and range minima over small domains. Journal

of Algorithms, 28(2):197–215.

Berkman, O., Schieber, B., and Vishkin, U. (1993). Optimal

doubly logarithmic parallel algorithms based on ﬁnd-

ing all nearest smaller values. Journal of Algorithms,

14(3):344–370.

DeGrasse, M. (2013). Tower loading chal-

lenges wireless infrastrucure providers.

https://www.rcrwireless.com/20131002/network-

infrastructure/tower-loading-challenges-wireless-

infrastrucure-providers. Accessed: 2017-09-30.

Floriani, L. and Magillo, P. (2003). Algorithms for visibility

computation on terrains: a survey. Environment and

planning B: Planning and design, 30(5):709–728.

Ghosh, A., Maeder, A., Baker, M., and Chandramouli, D.

(2019). 5g evolution: A view on 5g cellular technol-

ogy beyond 3gpp release 15. IEEE Access, 7:127639–

127651.

Haneda, K., Zhang, J., Tan, L., Liu, G., Zheng, Y., Asplund,

H., Li, J., Wang, Y., Steer, D., Li, C., et al. (2016). 5g

3gpp-like channel models for outdoor urban microcel-

lular and macrocellular environments. In 2016 IEEE

83rd vehicular technology conference (VTC spring),

pages 1–7. IEEE.

Medin, M. and Louie, G. (2019). The 5g ecosystem: Risks

and opportunities for dod. Technical report, Defense

Innovation Board Washington DC United States.

Odlyzko, A. and Rains, E. (2000). On longest increasing

subsequences in random permutations. Contemporary

Mathematics, 251:439–452.

Sorensen, P. A. and Lanter, D. (1993). Two algorithms for

determining partial visibility and reducing data struc-

ture induced error in viewshed analysis. Photogram-

metric Engineering and Remote Sensing, 59:1149–

1160.

Travanca, R., de J. Souza, T., and Andr

e, J. (2019). Struc-

tural safety assessment of 5g network infrastructures.

Wiley 5G Ref: The Essential 5G Reference Online,

pages 1–21.

USGS (2018). Lidar Base Speciﬁcation. Standard 11-B4,

U.S. Geological Survey Standards. Version 1.3.

Van Kreveld, M. (1996). Variations on sweep algorithms:

efﬁcient computation of extended viewsheds and class

intervals, volume 1996. Utrecht University: Informa-

tion and Computing Sciences.

Wandinger, U. (2005). Introduction to lidar. In Lidar, pages

1–18. Springer.

Woolpert (2014). United States Geological Sur-

vey NRCS Laurel MS 0.7 NPS LIDAR.

https://www.maris.state.ms.us/HTML/DATA/

data Elevation/REPORTS/Lidar%20Rpt USGS%

20LaurelMS%20Lidar Dec2014.pdf.

WINSYS 2021 - 18th International Conference on Wireless Networks and Mobile Systems