Multi-domain Modeling and Simulation of an Oximeter:

PVT Variations Impact of Opto-electronic Devices

on the SpO

Quantification

Songlin Li

, Julien Denoulet

, Olivier Tsiakaka

2,3 c

and Sylvain Feruglio

CNRS UMR 7606, LIP6, Sorbonne Université, Paris, France

CERVO, University of Laval, Quebec, Canada

Biomedical Microsystems Laboratory, Université Laval, Quebec, Canada

Keywords: Heterogeneous System, Modeling, Monte-Carlo Simulation, Multi-domain, Near-Infrared Spectroscopy

(NIRS), Oxygen Saturation (SpO

), PhotoPlethysmoGraphy (PPG), PVT (Process, Voltage, Temperature),

SystemC(-AMS).

Abstract: Oxygen concentration quantification in the blood (SpO

) has been used as a mean to diagnose and prevent

critical medical conditions thanks to pulse oximetry. In spite of its theoretical precision, this method suffers

from intrinsic deviations from the components used in such monitoring devices (PVT) that can lead to SpO

measurement errors. In this paper, we propose a multi-domain modeling of a NIRS-based blood oxygen

saturation monitoring system and its biological environment using SystemC(-AMS) for virtual prototyping,

to analyze the impact of PVT variations of opto-electrical components, thanks to Monte-Carlo simulation

correlated with transient analysis. We simulated the blood flow of the finger tissue and the dynamic

attenuation of the red and infrared light passing through the tissue. The Monte-Carlo simulation method was

used to analyze different PVT parameters that may cause measurement deviations separately. Finally, we

found that the red/IR LED peak wavelength deviation and the temperature of the system have an important

impact on the SpO

quantification, especially red LED peak wavelength deviation. This result shows that the

choice of the red-light source is of prime importance for accurate SpO

quantification.

1 INTRODUCTION

SpO

(oxygen saturation)

index is measured to show

the level of oxygenation in blood using an oximeter

device. It is based on Near-InfraRed Spectroscopy

(NIRS) and on PhotoPlethysmoGraphy (PPG)

technologies (Webster, 1997). Typically, as shown in

Fig.1, two colored light sources (red and infrared) are

used on body parts, usually a finger, to detect

volumetric changes of blood. However, deviations

always occur when performing a measurement.

Therefore, device calibration is indispensable to

obtain an acceptable error rate (Maxim, 2019).

Many well-known factors have an impact on the

SpO

measurement, for instance motion artifacts,

ambient light, skin color, etc. However, so far,

influences coming from the system itself haven’t been

https://orcid.org/0000-0003-4717-1328

https://orcid.org/0000-0003-1354-961X

https://orcid.org/0000-0001-8723-7825

https://orcid.org/0000-0002-6444-2671

carefully studied. We propose to contribute to this

field through the study of the impact of PVT (Process,

Voltage, Temperature) variations in the SpO

monitoring system. To do this, we intend to model

and simulate the embedded system in association with

the monitored biological tissue.

Evaluating PVT variations is difficult to achieve

through experimental methods, because it is not easy

to vary certain parameters in the monitoring system

(such as the peak wavelength of the red/IR LED

spectrum, the spectral sensitivity of the photo-

detector, etc.) to evaluate their impact on SpO

quantification. Parasitic signals and noise might also

influence the results. Therefore, we will add these

features in our modeling methodology, to give us a

better knowledge of the measurement device.

Li, S., Denoulet, J., Tsiakaka, O. and Feruglio, S.

Multi-domain Modeling and Simulation of an Oximeter: PVT Variations Impact of Opto-electronic Devices on the SpO2 Quantiﬁcation.

DOI: 10.5220/0010548903030310

In Proceedings of the 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2021), pages 303-310

ISBN: 978-989-758-528-9

303

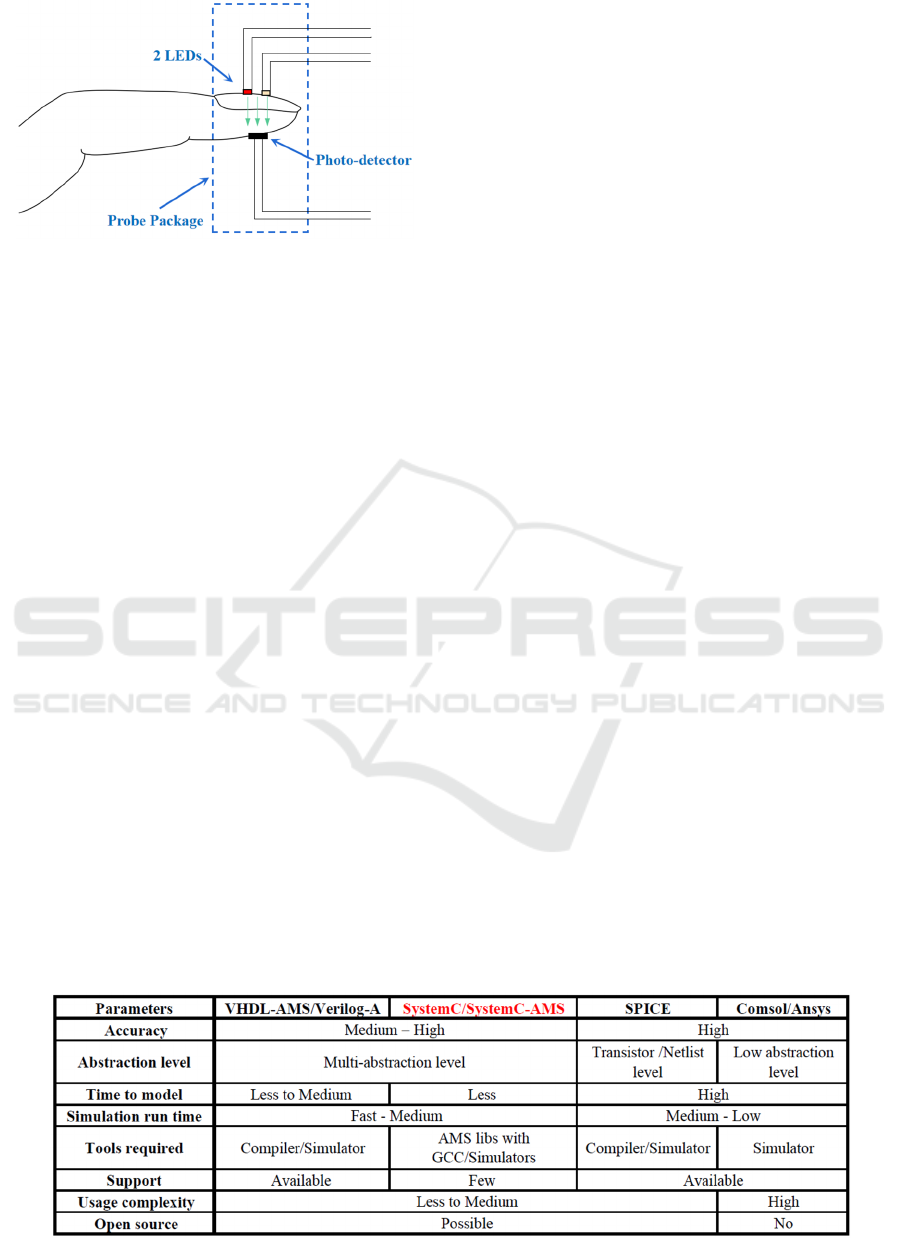
Figure 1: The principle of oximeter.

We chose the SystemC and SystemC-AMS

modeling tools to develop our models due to three

main advantages compared to other modeling

tools/languages, which are summarized in Table 1:

 Multi models of computation: SystemC/

SystemC-AMS offer several Models of

Computation (MoC) with Discrete Event (DE),

Timed Data Flow (TDF), Linear Signal Flow

(LSF) and Electrical Linear Networks (ELN).

Each MoC operates at different abstraction

levels and can therefore be chosen according to

the desired precision;

 Fast simulation: with well-chosen abstraction

level and simulation time step, simulation run

time can be shortened as much as possible;

 Open source: SystemC and SystemC-AMS are

freely distributed C++ libraries, which means

we have access to these tools as well as all C++

supported functions. If necessary, it is also

relatively easy to integrate other software in our

model by implementing interfaces.

Other advantages, like high data accuracy,

lightweight installation and simplicity of usage, are

also reasons why we chose this tool. We used

versions 2.3.2 of SystemC and 2.1 of SystemC-AMS.

Both of these libraries can be freely downloaded on

Accellera's website (Accellera, n.d.).

SystemC/SystemC-AMS was proposed as an

efficient tool for modeling complex systems,

especially in the biomedical domain (Pecheux, et al.,

2010), but it doesn’t natively include Monte-Carlo

(MC) statistical analysis method (Menčík, 2016).

Indeed, this analysis is particularly relevant to

observe the impact of key parameters on the system

behavior. Therefore, a MC simulation method in

SystemC-AMS must be developed.

Nowadays, modeling and simulation analysis

methods have been widely used in the field of

biomedicine (e.g., bionic nervous systems modeling

(Cacciapuoti, 2015)) and the research of medical

device (Mundt, 2000). The interaction modeling

between medical device and the human body also

exists, such as the interaction between ears and

cochlear implants (Tran, 2015), and the interaction

simulation between the cardiac rhythm and

pacemakers (Greenhut, 1993).

In this context, the main objective of this article is

to present our modeling and simulation approach of a

highly multi-domain application with open-source

tools, and to explore impacts of PVT variations in this

biomedical device.

The paper is organized as follows. In section 2, we

present our model structure. Then, the simulation

process and the model validation method are shown

in section 3. PVT variation analysis is described in

section 4. Finally, we conclude in the last section.

2 MODEL STRUCTURE

There are mainly two parts in our model: the

monitoring system, with opto-electrical components

and the biological environment. Figure 2 shows the

model block diagram (with the MoC used for each

sub-block), with the finger as the monitored

biological medium.

Table 1: SystemC/SystemC-AMS versus other modeling tools.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

304

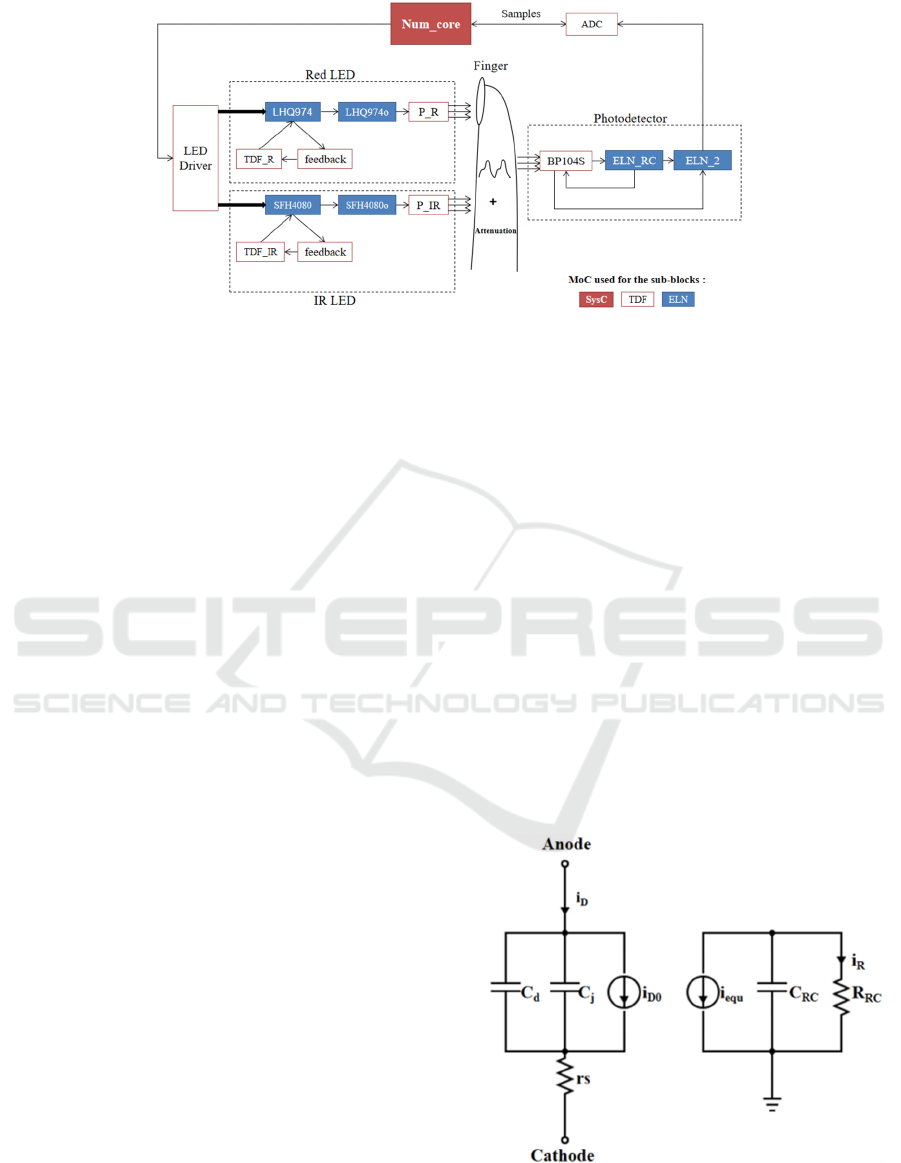
Figure 2: Model structure to emulate oximeter on finger in SystemC/SystemC-AMS.

In this figure, Num_core block was modeled in

SystemC, and a state machine was implemented to

emulate a micro-controller. This block was also used

to provide pulsed power supply for both LEDs by

controlling a LED Driver, and to receive data from

the ADC channel.

2.1 LED

A red LED (LHQ974) and an IR LED (SFH4080)

manufactured by OSRAM were modeled in

SystemC-AMS (note that any other type of light

source can subsequently be modeled, as long as

parameters describing it are available). Both LED

models are similar, except for their optical and

electronic parameters. The LED model is divided into

five sub-blocks to simulate static and dynamic

behaviors, in association with its optical

characteristics. Sub-block TDF_R, simulates the

static behavior described by Shockley equation (Sze,

et al., 2006), mainly. Blue sub-blocks are

implemented with the ELN MoC to simulate the

dynamic behavior of the LED. Figure 3 (left) shows

the physical equivalent circuit of both LHQ974 and

SFH4080 sub-blocks. In this equivalent circuit, C

and C

represent the diffusion and the junction

capacitance, respectively. i

is the equivalent current

source, which takes the value of the output current of

TDF_R and TDF_IR. The feedback sub-blocks are

used to transfer two

feedback

parameters: the current

and the voltage V

of the LED, from LHQ974 to

TDF_R or from SFH4080 to TDF_IR. Figure 3 (right)

represents the equivalent circuit of LHQ974o and

SFH4080o, which are used to take into account the

intrinsic opto-electrical effect of the device. i

equ

equal to i

. The RC pole, represented by the

resistance R

and the capacitance C

, designates the

frequency characteristic of the LED (Bian, et al.,

2008). Then, the P_R and P_IR sub-blocks are used

to convert the output current i

of LHQ974o and

SFH4080o into luminous intensity in Watt. The

actual spectral distribution of both LEDs is usually

modeled by a Gaussian curve (Tsiakaka, et al., 2020)

and the total radiant flux is the integral of the entire

spectrum.

For the oxygen rate calculation, since the molar

extinction ε(λ) varies according to the wavelength,

the attenuation for different wavelengths of light is

calculated separately, when a beam of light passes

through the biological tissue. Therefore, we should

separate the luminous intensity of each wavelength in

the LED model. Still, we cannot consider all

wavelengths of the LED spectrum, since it would

greatly increase the amount of calculation and,

therefore, the simulation time. As a result, we

approximated the LED spectrum by dividing it into

five intervals around the peak wavelength. For the red

LED (LHQ974), the peak wavelength is ideally

660nm. Thus, we chose five wavelengths from

Figure 3: Equivalent circuit of LED in dynamic mode. On

the left is the physical equivalent circuit. The block on the

right has no physical reality, but is used to consider the

device intrinsic opto-electrical effect.

Multi-domain Modeling and Simulation of an Oximeter: PVT Variations Impact of Opto-electronic Devices on the SpO2 Quantiﬁcation

305

640nm to 680nm with an interval of 10nm. For the IR

LED (SFH4080), with its peak at 880nm, the chosen

range was 860nm to 900nm, with the same interval.

2.2 Photo-detector

A model of the BP104S photo-detector (PD), also

manufactured by OSRAM, was developed. The PD

operates in reverse bias. It provides a spectral

sensitivity in accordance with the spectrum of the

received light to convert the light intensity into

electric power. The current generated by the PD

mainly consists of two parts:

 I

: the photonic current generated by the light

received from the external environment by the

PD, which carries the detection information;

 I

: the parasitic dark current generated by the

PD in the absence of wanted light.

Sub-block BP104S in Fig.2 is used to describe the

PD spectral sensitivity and the dark current. ELN_RC

and ELN_2 are made to simulate the dynamic

behavior, as in Fig.3. The PD output is sent to the

ADC block, so that the pulsed current can be sampled,

after amplification and voltage conversion, and data

can be registered in Num_core.

2.3 Biological Environment

A model of a finger was constructed to simulate the

oxygen concentration variation in the blood and its

detection with lights through the tissue. In the blood,

there are mainly two chromophores that impact the

measurement of SpO

: HbO

(oxy-hemoglobin) and

HHb (deoxy-hemoglobin). The light attenuation by

the biological tissue is given by the Beer-Lambert

Law, shown in equation (1):

dHHbHbO

HHbHbO

eII





])[][(

)()(





(1)

with I

(λ) the input light intensity at the wavelength λ,

I(λ) the output light intensity passing through and

attenuated by the biological tissue, ε

HbO2

, ε

HHb

the

molar extinction of HbO

and HHb, respectively,

[HbO

] and [HHb] the concentration of HbO

and

HHb, and d the length of optical path.

The change of blood volume according to time is

simulated by the normalized equation (2), where f

the cardiac frequency in Hz.

)22sin(

)2sin(

tftfA 



(2)

3 SIMULATION PROCESS AND

MODELS VALIDATION

This section first introduces the simulation process.

Then, in subsection 3.2, the accuracy of our models

(at the device and at the system level) is evaluated by

comparing our simulation with other experimental

results in the existing literature.

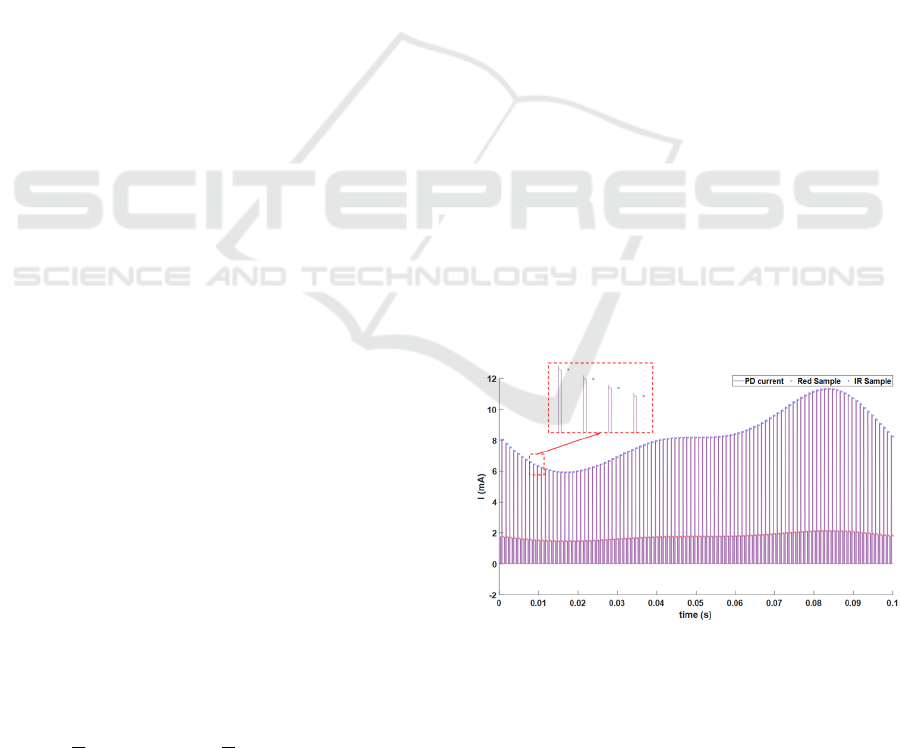
3.1 Simulation Process

Once all models were implemented, basic transient

simulation was performed to get two PPG signals that

represent the red and IR responses generated by the

PD after passing through the biological medium.

Then, as shown in Figure 2, data was sampled every

1ms by the ADC block. The result is presented in

Figure 4, where inputs for each LED are light pulses

of 150µs every 1ms. The simulation step was set to

1µs, to be able to observe the devices transient

behaviors. The heart rate was set to 10Hz (10 times

higher than in reality), to reduce the simulation time.

In this figure, the pink signal is the pulsed current

generated by the PD. The top envelope corresponds

to the IR LED, while the bottom envelope is due to

the red LED. The red LED signal amplitude is lower

because the luminous intensity of red light is

relatively weaker, when the same voltage is applied

to both LEDs. The crosses (in the zoomed block) are

samples of LED signals. On a laptop with an Intel

Core i5 9

Gen processor (2.4GHz, 8 CPUs) and

8192M of RAM,

it takes 29s to simulate a 0.1s

duration.

Figure 4: Red signal (bottom), IR signal (top) generated by

photo-detector and the samples of the signals (crosses on

the top and on the bottom).

Then, after detecting the peak and valley of the

red/IR signals by signal processing (filtering and

extremum detection, mainly), we can calculate the

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

306

(Ratio-of-ratio) value with the following

equation (Webster, 1997):



























(3)

Here, R

are the valley and peak value of the red

signal, respectively, and IR

correspond to the

valley and peak value of the IR signal.

SpO

value was set before simulation run-time, by

setting [HbO

] and [HHb] in the biological

environment, according to equation (4) (Webster,

1997). We set [HbO

] + [HHb] = 0.3mM, which is an

approximate value for the human body (Dash, et al.,

2010). In any case, in the simulation, the value of

SpO

can be easily and dynamically changed by

modifying the ratio of [HbO

] and [HHb].

%100

][][

][







HHbHbO

HbO

SpO

(4)

With a single period of both PPG (red and IR

responses), only one R

value can be obtained for

one specific SpO

value. However, to obtain a

quadratic SpO

-R

curve (Maxim, 2019), we need to

vary this SpO

value. In our simulation, we varied this

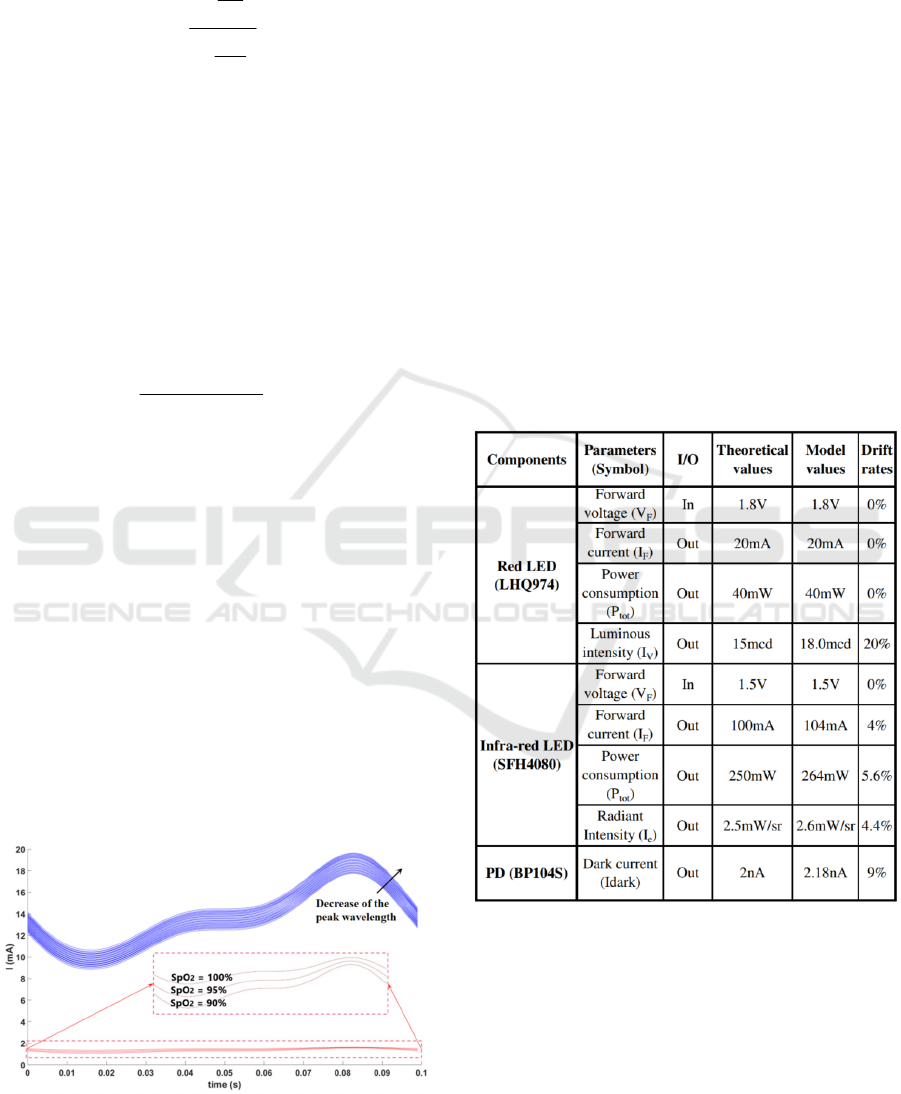
parameter from 90% to 100% (a below 90% SpO

value means the person is in a danger state). Figure 5

shows several simulation periods. Red lines

correspond to PPG due to the red source for three

different SpO

settings (90%, 95%, and 100%). For

IR responses (blue curves), a shift of the peak

wavelength has also been taken into account, to

illustrate PVT variation, albeit in a basic manner. We

chose four values above and four values below the

880nm nominal value, each with a 5nm step

increment, to constitute nine peak wavelength values

in the [860nm; 900nm] interval. Combined with the

Figure 5: PPG obtained with red and IR sources for three

SpO

value. IR LED curves (in blue) also feature variation

of the peak wavelength.

three different SpO

parameter values, we were able

to simulate twenty-seven configurations. Section 4

will present a more thorough approach to evaluate the

influence of PVT variations.

3.2 Models Validation

There are two steps to validate our models. First, we

individually validate each component (i.e., both

LEDs and PD) by comparing the simulation output

data with key-parameters in the datasheets. These

results are summarized in Table 2 (obtained by time

domain simulation). Only the optical parameters

weren’t modeled very well, but with acceptable

errors

according to datasheets

. We assume that it was due to

approximations made to model certain

characterizations and also to the fact that we had the

influence of the other parameters.

In any case, we can

calibrate this error rate by ourselves in the modeling, to be

closer to the datasheet value.

Table 2: Models key-parameters compared to datasheets.

The second step is to validate the whole system by

comparing our simulation data with previous results

(Tsiakaka, et al., 2020), where authors used six

different pairs of red/IR LED to plot six SpO

-R

curves. We were able to measure these LEDs optical

and electrical characteristics, in order to simulate

these devices with our developed model. For the PD,

a model of the BP104S was used. As for the

biological medium, we applied the same finger model.

Results are presented in Figure 6.a. It shows the “110-

Multi-domain Modeling and Simulation of an Oximeter: PVT Variations Impact of Opto-electronic Devices on the SpO2 Quantiﬁcation

307

25R

” curve, as it is a widely used reference to

basically estimate SpO

. We then compared our

simulations to Figure 9.b in (Tsiakaka, et al., 2020),

with the only difference being the used PD (BP104S

for us and FDS100 for the previous work). Figure 6.b

shows the SpO

deviation curves between our models

and the previous results, for all six red/IR LED pairs.

We can notice that the absolute value of ΔSpO

always less than 1%. Then, we also calculated the

SpO

Root-Mean-Square Deviation (RMSD) for each

pair of SpO

-R

curves in both works. It ranges from

0.22% to 0.77%, which proves that our simulation

results correlate well with the previous results. In this

way, our whole system model is validated.

Figure 6: a) Simulation result with our models for the six

different red/IR LED pairs; b) SpO

deviation curves

between our works and (Tsiakaka, et al., 2020).

4 PVT VARIATION ANALYSIS

The dispersion of the IR LED peak wavelength, as

simulated in Figure 5, relies on a deterministic

approach. For a more in-depth analysis of the impact

of PVT variations, it is necessary to introduce a

randomness factor. As a result, we performed a MC

analysis on our system, based on the variation of

selected parameters. As their impact on SpO

quantification can be rather unpredictable, a Corner

simulation will not necessarily give us enough

information. Therefore, MC analysis will allow us to

get a more complete view of the system behavior.

4.1 MC Simulation in SystemC-AMS

In this analysis, we varied selected parameters in a

reasonable range, with a chosen Probability Density

Function (PDF) of amplitude centered in a specific

value. Since this feature isn’t natively included in

SystemC-AMS, we had to develop our own code.

Firstly, we wrote a function to generate a set of

numbers varying within a certain range in a specific

distribution around 1. In this article, we used a

Gaussian distribution. However, other PDF are

possible (e.g., uniform). Then, these numbers were

multiplied by the nominal value of the parameter to

be varied. It constituted a set of input values. Then,

we assigned these input values to a SystemC signal

and connected it to the systemC-AMS input port of

the target parameter. A loop was then implemented in

the top file, where we assigned the random input

values to the SystemC signal, one by one, to do

repeated simulations. Finally, we generated a .dat file

to save the output data.

4.2 Introduction of Different PVT

Parameters in the System

PVT considers the variation of selected parameters in

an electronic system: Process (P) dispersion due to

manufacturing, mainly, supply Voltage (V) of the

various system components, and the operating

Temperature (T) of the device. The parameters we

took into account are presented in Table 3, with their

typical values and variation ranges.

T-variation in the device is mainly due to self-

heating during operation and also to the light sources

during emission. Note that a variation of more than

4K is generally unacceptable in a medical device.

A device power supply voltage is often affected

by many factors causing instability and fluctuations

(IR-drop due to current draw, crosstalk because of

electromagnetic interference, etc.). Moreover, in an

embedded system with battery, the voltage supply

decreases with the battery usage. Such instability may

impact the accuracy of our SpO

measure. In this

study, we focused on the power supply of both LEDs

and of the PD, knowing that the V

REF

for the ADC

doesn’t result in any error at all.

Table 3: PVT parameters to be varied and analyzed in the system.

90 92 94 96 98 100

SpO

(%)

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Approx 110-25R

Typical

VSMD66694

SMT660/890

SFH7050

led#1

led#2

-2 -1 0 1 2 3

ΔSpO

(%)

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Typical

VSMD66694

SMT660/890

SFH7050

led#1

led#2

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

308

P-variation is the deviation of component

attributes during fabrication. For both LEDs, n is the

ideality factor, a key parameter describing the diode

junction and a solar cell’s electrical behavior (Hadj,

et al., 2018). n can slightly vary during fabrication. As

shown in equation (5), it has an influence on the

forward current I, which is directly proportional to the

optical power of the light source. V

the threshold

voltage of the LED is also affected by manufacturing

dispersion. Both parameters can be concatenated in a

same Gaussian PDF.

)1( 





eII

(5)

In equation (5), I

is the saturation current, and V

the thermal voltage. We found in the datasheets that

the maximal V

for the red and IR LED is 2.5V and

1.8V, respectively. From simulations, we estimated

the maximal value of n for both LEDs. It is 2.55 and

1.64, respectively, and can’t be less than 1 (Sze, et al.,

2006). So, we varied n from 1 to 2.55 for the red LED

and from 1 to 1.64 for the IR LED.

Deviation of the LED peak wavelength is another

relevant parameter. Even for the same type of LED,

the peak wavelength of the optical spectrum is subject

to deviation due to the fabrication process. We found

a typical range of ±20nm for the peak wavelength of

both LEDs in their datasheets.

The FWHM (Full Width at Half Maximum)

parameter of the optical spectrum can also be

impacted by process dispersion. Based on

experimental results found in (Filippo, et al., 2017),

we chose a range of ±10% of the typical value.

Finally, the PD spectral sensitivity is also affected

by an offset due to process variation. Thus, we studied

the impact of this factor by shifting the PD optical

response spectrum vertically and laterally.

4.3 Simulation Results

To get an idea of the influence of each of the

parameters presented above, we first performed the

MC simulation (consisting of 200 runs), varying only

one single parameter. We were then able to calculate

for this parameter the maximal SpO

RMSD for its

two extreme values. These results are presented in the

last line of Table 3. We found that the main factors

that impact the SpO

quantification come from the

deviation of both LED peak wavelengths (RMSD is

11.31% for the red LED and 1.79% for the IR LED)

and from temperature (RMSD is 3.19%). The gap

between both LED RMSD values can be explained by

the fact that around the red-light band (660nm), the

slope of molar extinction curves of HbO

and HHb is

greater than around the IR light band (880nm). The

impact of other parameters is negligible.

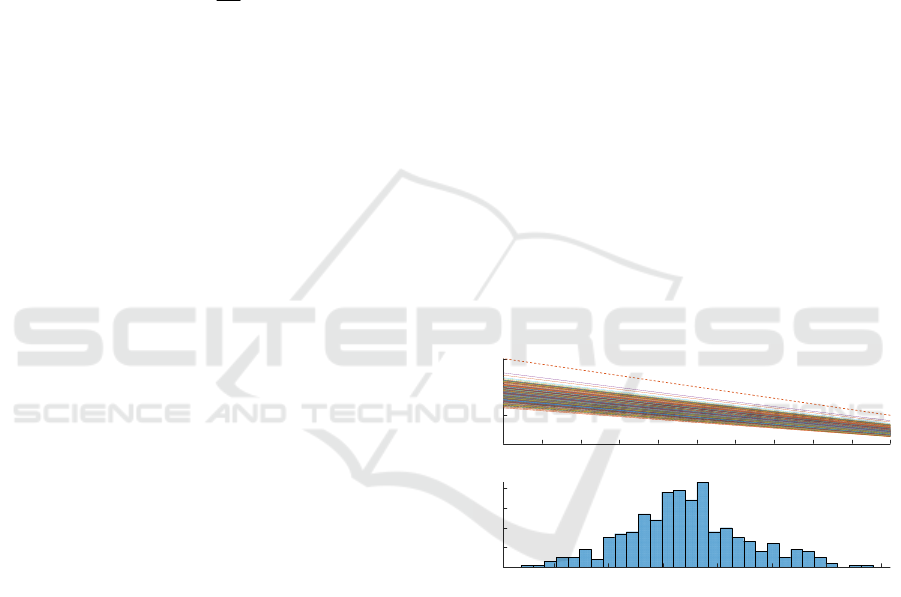
After that, we investigated the combined

influence of several parameters dispersion on the

quantification of SpO

. Figure 7 presents the result of

the MC simulation correlated with the transient

analysis. We varied three key parameters (both LED

peak wavelengths and T). We performed 400 runs

(i.e., different configurations) to obtain 400 SpO

-R

curves, as in Figure 7.a. To get these results, the

simulation time was around 11h. Figure 7.b shows the

distribution of SpO

when R

is equal to 0.4. The

RMSD of SpO

for the two extreme cases is 9.32% in

the critical 90–100% saturation window, which is

close to the dispersion value associated to the red

LED peak wavelength variation. Consequently, it

could be said that the red LED peak wavelength

variation has the greatest impact.

We can conclude from the above results that in the

oximeter manufacturing process, it is necessary to

tightly control the peak wavelength deviation of the

light source, to avoid an otherwise necessary

calibration. At the same time, the device operating

temperature influence on the SpO2 measurement

accuracy cannot be ignored. For other parameters of

our discussion, there is no strict requirement.

Figure 7: Simulation result of the variation of three key

factors at the same time.

5 CONCLUSIONS

In this paper, the process to quantify SpO

on the

finger with an oximeter is simulated with an opto-

electronic model built in SystemC/SystemC-AMS.

Then, the impact of PVT variations in the device on

the SpO

quantification is explored, through a MC

method combined with transient simulation,

performed on the developed models. We found that

the main influence parameters of PVT variations on

the quantification of SpO

were the red/IR LED peak

90 91 92 93 94 95 96 97 98 99 100

SpO

(%)

0.2

0.4

0.6

0.8

93 94 95 96 97 98 99

SpO

(%)

number

110-25R

Multi-domain Modeling and Simulation of an Oximeter: PVT Variations Impact of Opto-electronic Devices on the SpO2 Quantiﬁcation

309

wavelength deviation and temperature. Other factors

seem to have a negligible impact individually.

This modeling method in SystemC/SystemC-

AMS, which associates the monitoring system,

including its opto-electronic components, and the

biological environment, is proved fast, accurate and

flexible. This methodology can be employed for any

cyber-physical system to estimate its performances,

to optimize the design phase, and to help the

understanding of measurement data (e.g., reproduce

results close to the experimental measurements in the

simulation and vary certain parameters to understand

their impacts).

REFERENCES

Webster, J.G., ed. 1997. Design of Pulse Oximeters. Bristol;

Philadelphia: Institute of Physics Pub, doi:

10.1201/9780367802592.

Maxim, 2019. Guidelines for SpO2 measurement using the

Maxim MAX32664 sensor hub. https://pdfserv.maxim

integrated.com/en/an/SpO2-Measurement-Maxim-

MAX32664-Sensor-Hub.pdf

Accellera. (n.d.). SystemC. Retrieved February 27, 2021,

from https://www.accellera.org/downloads/standards/

systemc

Pecheux, F., et al., 2010. Is SystemC-AMS an Appropriate

“Promoter” for the Modeling and Simulation of Bio-

Compatible Systems? IEEE ISCAS, doi:

10.1109/ISCAS.2010.5537669.

Menčík, J., 2016. Concise Reliability for Engineers. InTech,

doi: 10.5772/62009.

Cacciapuoti, A.S., et al., 2015. Receiver Design for a Bionic

Nervous System: Modeling the Dendritic Processing

Power. IEEE Internet of Things Journal, 11, doi:

10.1109/JIOT.2015.2438098

Mundt, C.W., et al., 2000. Applications of SPICE for

Modeling Miniaturized Biomedical Sensor Systems.

IEEE Transactions on Biomedical Engineering, 47(2):

149–54, doi: 10.1109/10.821733.

Tran, P., et al., 2015. Development of HEATHER for

Cochlear Implant Stimulation Using a New Modeling

Workflow. IEEE Transactions on Biomedical

Engineering, 62(2): 728–35, doi: 10.1109/TBME.

2014.2364297.

Greenhut, S.E., et al., 1993. A Stochastic Network Model of

the Interaction between Cardiac Rhythm and Artificial

Pacemaker. IEEE Transactions on Biomedical

Engineering, 40(9): 845–58, doi: 10.1109/10.245605.

Bian, J., et al., 2008. A Novel Spice Model of Photodetector

for OEIC Design, edited by Liwei Zhou, 66211E.

Beijing, China, doi: 10.1117/12.790834.

Tsiakaka, O., et al., 2020. Source–Detector Spectral

Pairing-Related Inaccuracies in Pulse Oximetry:

Evaluation of the Wavelength Shift, MDPI Sensors,

20(11), doi: 10.3390/s20113302.

Dash, R.K., et al., 2010. Erratum to: Blood HbO2 and

HbCO2 Dissociation Curves at Varied O2, CO2, PH,

2,3-DPG and Temperature Levels. Annals of

Biomedical Engineering, 38(4), doi: 10.1007/s10439-

010-9948-y

Hadj, B., et al., 2018. Theoretical Models for Anomalously

High Ideality Factor in a Au/SnO2-Si(n)/Al Solar Cell,

Silicon, 10(3), doi: 10.1007/s12633-017-9572-7.

Sze, S.M., 2006. Physics of Semiconductor Devices:

Sze/Physics. Hoboken, NJ, USA: John Wiley & Sons,

Inc., doi: 10.1002/9780470068328.

Filippo, R., et al., 2017. LEDs: Sources and Intrinsically

Bandwidth-Limited Detectors, MDPI Sensors 17(7),

doi: 10.3390/s17071673.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

310