Towards the Formal Modeling Methodology of WSN through the

Transformation of SysML into DSPNs

Amel Berrachedi

, Malika Ioualalen

and Ahmed Hammad

Faculty of Exact Sciences and Informatics, Hassiba Benbouali University of Chlef, Chlef, Algeria

Department of Computing Science, MOVEP Laboratory, USTHB University, Algiers, Algeria

DISC/Femto-ST Department, Franche Comt

e University, Besanc¸on, France

Keywords:

Model-based Systems Engineering, Mapping, SysML, Activity Diagram, Deterministic Stochastic Petri Nets.

Abstract:

When developing critical and complex systems, the requirement of the systems design veriﬁcation is

paramount. We address the problem of how to design these ones in order to satisfy their requirements. Wire-

less Sensor Networks (WSNs) are examples of such systems, which consist of a large amount of distributed

and autonomous nodes. We aim to propose a Model-Based Systems Engineering speciﬁcation and veriﬁcation

methodology for designing WSNs. The proposed approach uses SysML language to describe the WSNs re-

quirements, behaviors and performance parameters. Then, it translates the SysML elements to a Deterministic

Stochastic Petri Net (DSPNs) and integrates them into an analytic model. This allows designing WSNs and

studying their behaviors and their performances, namely energy consumption. The current paper reﬁnes the

ﬁrst part of this project by transforming the activity diagram of SysML to a DSPN. To show the applicability

of the mapping technique, a case study that presents a hierarchical WSN is used.

1 INTRODUCTION

Since their appearance, Wireless Sensor Networks

(WSNs) increasingly invade the scientiﬁc and indus-

trial communities. They are used in a wide range

of applications such as environmental monitoring,

robotic exploration, trafﬁc control, military applica-

tions, medical systems and so on. A WSN consists of

a set of miniature, autonomous and multi-functional

sensor nodes which are distributed on a capture zone

to measure a physical magnitude or monitor an event.

These nodes sense information from their environ-

ment and relay them to a base station (BS) which is

generally supposed powerful and away from the cov-

erage area (Akyildiz et al., 2002).

As sensor nodes are primarily powered by irre-

placeable and limited batteries, they should work with

a low energetic balance. So, when designing WSNs,

it is important to consider these constraints for max-

imizing the network lifetime and to verify that this

design satisﬁes the system requirements. To do so,

it is attractive to reap the beneﬁts of Model-Based

Systems Engineering (MBSE) approaches (Estefan,

2008). This helps to produce easy and clear models,

to reduce the time and the maintenance costs, and to

increase the efﬁciency and the productivity.

Nowadays, Systems Modeling Language

(SysML), which is a general-purpose graphical

modeling language for the Systems-Engineering

domain, is the most adopted modeling language

because of its intuitive notations (Friedenthal et al.,

2008). In addition, it provides several improvements,

speciﬁcally, it considers the requirements modeling

and takes into account the strong interaction between

hardware and software system parts, which is an

important condition for effective modeling. However,

SysML is not formal. Accordingly, it does not

provide the detailed execution semantics of models

that allows the qualitative and quantitative analysis.

Therefore, integrating SysML with other engineering

analysis such as formal methods is necessary. Formal

methods are well adapted for analyzing and validating

complex systems that require rigorous veriﬁcation.

Different formalisms can be used to analyze WSNs

and to evaluate their performances. Among these

formalisms, Petri Nets (PN) (Peterson, 1977) have

many advantages, particularly, Deterministic and

Stochastic Petri Nets (DSPNs) could be the most

appropriate. In fact, they are very expressive and

they represent a widely used high-level formalism for

modeling concrete and discrete-event systems where

events may occur either without consuming time,

Berrachedi, A., Ioualalen, M. and Hammad, A.

Towards the Formal Modeling Methodology of WSN through the Transformation of SysML into DSPNs.

DOI: 10.5220/0010549200830091

In Proceedings of the 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2021), pages 83-91

ISBN: 978-989-758-528-9

after a deterministic time, or after an exponentially

distributed time (Marsan and Chiola, 1987).

The current work represents two contributions.

The main one is to provide an overview of the

proposed methodology of the speciﬁcation and the

veriﬁcation of the non-functional properties in the

WSN systems especially the energy dissipation. This

methodology is based on SysML and DSPNs. We use

SysML for describing the requirements, the behaviors

and the parametric aspects of the WSN. Then, we es-

tablish the SysML behavioral speciﬁcation, and there-

after, we construct the DSPN analytic model, which

will be used to compute the elementary performance

values of the designed WSN. In this step, TimeNET

model-checker is used as an analysis and evaluation

tool. The methodology might comprise a feedback,

i.e. the results of the performance evaluation should

be exploited by the SysML designers. These latter

check if the requirements are satisﬁed regarding the

computed performances values. The second contribu-

tion is to elaborate the ﬁrst part of this methodology

in proposing mapping rules from the SysML activity

diagram to its equivalent DSPN, and thereafter, un-

rolling them via an example of WSN.

The remainder of the paper is organized as fol-

lows. Section 2 presents the background with tools

and languages used in our approach. The next section

cites works related to methodologies dealing with the

formalization of SysML diagrams, and then we com-

pare them to our own. Section 4 explains the proposed

methodology and the mapping rules. After that, we

run in the section 5 these latter through an example

of an hierarchical routing protocol in a WSN. At the

end, we close the paper with some conclusions and

possible improvements to the work.

2 BACKGROUND

WSNs are so complex so that we can not design

them without adequate high-level tools. This section

presents the tools used during this work.

2.1 SysML

SysML is an OMG standard modeling language sup-

ported by leading organizations from the systems en-

gineering industry, including the INternational Coun-

cil On Systems Engineering (INCOSE) (Friedenthal

et al., 2008). SysML is an UML proﬁle proposed to

specify systems that include heterogeneous compo-

nents. It reuses a subset of UML diagrams, extends

others and deﬁnes new ones to provide speciﬁc sys-

tems engineering features. SysML diagrams cover

four views of system modeling. The Requirement

Diagram (RD) is used for better organizing require-

ments at different levels of abstraction and showing

explicitly the various kinds of relationships between

requirements and model elements. The PacKage Di-

agram (PKD), The Block Deﬁnition Diagram (BDD)

and the Internal Block Diagram (IBD) are used to de-

scribe the structural aspects. The State Machine Dia-

gram (SMD), the Sequence Diagram (SD) and the Ac-

tivity Diagram (AD) are used to specify behavioral as-

pects. Finally, the Parametric Diagram (PD) is used to

describe the mathematical relations between the sys-

tem parameters.

One of the tools used to elaborate the SysML di-

agrams is Eclipse Modeling Framework (EMF). This

project is a modeling framework and code generation

facility for building tools and other applications based

on a structured data model. From a model speciﬁca-

tion described in XMI, EMF provides tools and run-

time support to produce a set of Java classes for the

model, along with a set of adapter classes that enable

viewing and command-based editing of the model,

and a basic editor. Even if the models are described

in XMI, they can be speciﬁed in UML/SysML docu-

ments. In order to create a working environment ori-

ented to this speciﬁc area, toolkits can be added to

EMF. This is the case of Papyrus which aims to pro-

vide an integrated environment for editing any kind

of EMF model and particularly supporting UML and

related modeling languages such as SysML.

2.2 Deterministic Stochastic Petri Nets

Deterministic and Stochastic Petri Nets (DSPNs) in-

troduced by Ajmone Marsan and Chiola in (Marsan,

1990) are a stochastic modeling formalism with

graphical representation which include both exponen-

tially distributed and deterministic delays. A DSPN is

a 9-tuple (P, T, I, O, V, W, Π, D, M

), where:

• P is a ﬁnite set of places. P = {p

, ..., p

};

• T is a ﬁnite set of transitions, disjoint from P, par-

titioned into three disjoint sets, T

, T

, and T

, of

immediate, exponential, and deterministic transi-

tions respectively. T = {t

, ..., t

};

• I is a set of the input arcs. I ⊆ (P × T );

• O is a set of the output arcs. O ⊆ (T × P);

• V is a set of the inhibitor arcs. V ⊆ (P×T ), where

V ∩ I =

• W deﬁnes the weights of all arcs;

• Π is the priority function assigning a priority to

each transition. Π : T → N

, N

the set of the

positive natural numbers;

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

• D deﬁnes the ﬁring times. D : T → {0} ∪ R

∪

Ω, where R

is the set of positive real numbers

and Ω = {λ

, ..., λ

} is the set of random variables

with a given distribution;

• M

is the initial marking.

DSPNs have the same graphical notation of places

and arcs in traditional PNs. However, immediate tran-

sitions drawn as thin bars ﬁre without delay, expo-

nential transitions drawn as empty bars ﬁre after an

exponentially distributed delay, whereas determinis-

tic transitions drawn as black bars ﬁre after a constant

delay.

TimeNET (Timed Petri Net Evaluation

Tool) (Zimmermann, 2012) is a software pack-

age and an interactive toolkit for the modeling and

evaluation of PNs in which the ﬁring times of the

transitions may be immediate, deterministic or more

exponentially distributed. It has been developed

at the Real-Time Systems and Robotics group of

Technische University at Berlin, Germany. The

project has been motivated by the need for powerful

software for the efﬁcient evaluation of Timed Petri

Nets with arbitrary ﬁring delays.

3 RELATED WORK

A methodology is deﬁned in (Estefan, 2008) as a col-

lection of related processes, methods, and tools. A

MBSE methodology can be characterized as the col-

lection of related processes, methods, and tools used

to support the discipline of systems engineering in

a model-based or model-driven context. The author

has provided a brief overview of MBSE methodolo-

gies. In this section, we relate existing research to

our methodology, especially those which deal with

the formalization of SysML.

In (Wolny et al., 2020), the authors conduct a

systematic mapping study to analyze SysML publi-

cations from 2005 to 2017. It has been found that

this language is mostly used in the design or valida-

tion phase. In addition, there are approaches focus-

ing on translation like transformation to PNs, Mod-

elica, SystemC or Matlab/Simulink in order to build

frameworks for the veriﬁcation and the validation of

systems design. SysML is also used in combination

with OCL, LTL or MARTE to support the implemen-

tation of an executable architecture that provides a

feasible systems engineering solution. Furthermore,

most of the publications deal with SysML proﬁles for

facilitating the veriﬁcation of functional and/or non-

functional requirements and improving the applica-

tion of SysML to complex systems.

A great number of methodologies deals with re-

quirements that can be abstract when describing sys-

tem objectives and can be more concrete when they

relate to speciﬁc behaviors in the system or techni-

cal choices relating to its components. Specifying

the structure and the behavior of a system is to de-

scribe it by conceptual models. The validation of

the systems from the ﬁrst design phases is necessary

to assure the correction of the abstract models. In

this context, works were proposed, in particular the

method AVATAR (Pedroza et al., 2011) which is one

surround including an equipped and adapted method

to the real-time and distributed systems, and assisted

by the tool Ttool. The language AVATAR is a pro-

ﬁle of SysML. It extends SysML by proposing the

language TEPE (Knorreck et al., 2011) for the ex-

pression of the properties. This methodology con-

cerns only the veriﬁcation of the properties by model

checking. The traceability of the requirements and

the validation of the not functional requirements are

not taken into account in this environment. The ap-

proach OMEGA2 (Ahmad et al., 2013), includes a

feasible proﬁle UML/SysML dedicated for the speci-

ﬁcation and the formal validation of Real-time critical

systems. The model OMEGA2 uses the tool IFx or

the simulation for the veriﬁcation of the properties.

A lot of other works proposed methodologies in

the same area. (Gauthier et al., 2015) and (Zhu et al.,

2019) propose a MBSE methodology for the capture

and the deﬁnition of functional requirements in com-

plex systems like the avionics domain. The goal is

also to validate these functional requirements through

functional simulation, and verify efﬁciently the con-

sistency of these functional requirements.

All of these studies have in common that they

do not consider PNs as a target formalism. Sev-

eral initiatives have emerged such as (Foures et al.,

2012) and (Gutierrez et al., 2015). These papers out-

line methodologies for modeling embedded systems.

They transform SysML models in PNs and generate

VHDL code and allow to execute and simulate a sys-

tem behaviour modeled by improved SysML ADs.

Another improvement is the subject of the approach

cited in (Huang et al., 2020) which uses ADs from

UML/SysML, providing a standard object-oriented

graphical notation and enhancing reusability. The au-

thors show that a behavior model represented by a set

of compliant modeling elements in SysML ADs can

be transformed into an equivalent PN, so that the anal-

ysis capability of PN can be applied. They deﬁne thus

a formal mathematical notation for a set of modeling

elements in ADs, show the mapping rules between PN

and ADs, and ﬁnally propose a formal transformation

algorithm.

Towards the Formal Modeling Methodology of WSN through the Transformation of SysML into DSPNs

An other attractive work focusing on the veriﬁca-

tion of complex systems is that presented in (Rahim

et al., 2017). The authors deﬁne a complete process to

formalize and verify SysML functional requirements

related to ADs. At ﬁrst, they deﬁne a new language

called AcTRL for the formalization of functional re-

quirements at SysML level. Then, The veriﬁcation is

enabled by formalizing SysML activities with Hierar-

chical Coloured Petri Nets (HCPNs) and by automat-

ically translating SysML requirements expressed on

AcTRL into temporal logic.

According to the study that was done in (Wolny

et al., 2020), the non-functional properties did not

have a big place compared to the functional ones.

Among the works that propose methodologies deal-

ing with quantitative properties, we cite (Baouya

et al., 2015) and (Huang et al., 2015). They associate

SysML bihavioral diagrams (a SMD for the ﬁrst pa-

per and an AD for the second one) with the MARTE

proﬁle for the describing of the real-time embedded

systems behaviors, and then, transforming these ex-

tended diagrams into timed automata that is expressed

in a model checker. To check the functional correct-

ness of the system under test, the time properties are

expressed in temporal logic.

We have encountered another work that veriﬁes

the non-functional properties of a WSN by transform-

ing SysML Diagrams to a target formalism which is

different from PNs. It’s the case of (Berrani et al.,

2013) who specify a model transformation from RD,

PD, SD, BDD and IBD SysML diagrams, to their

corresponding textual elements in Modelica. Be-

sides, they have veriﬁed and validated a WSNs non-

functional property which is the energy constraint.

However, Modelica is not considered as a model

checker. In fact, it is executable but not provable.

Among the formalisms which are very efﬁcient in

performance evaluation and which are different from

the proﬁles extended to SysML, there are stochas-

tic formalisms such as Markov chains and Stochastic

Petri Nets (SPNs). According to the systematic map-

ping study cited above, there are only few method-

ologies in which the formalization of SysML were

achieved by stochastic models.

In (Jarraya and Debbabi, 2014), the authors

present a model-based veriﬁcation framework that

supports the quantitative and qualitative analysis of

SysML activity diagrams. To this end, they propose

an algorithm that maps SysML ADs into Markov de-

cision processes expressed by the language of the

probabilistic symbolic model checker PRISM.

As the SysML PD has not been widely used as

well as SPNs despite their great utility in the context

of WSNs, our main objective is to propose a method-

ology that combines these two tools. This is the idea

we came up in our previous work (Berrachedi et al.,

2017), and that we’ll explore in the current paper.

4 METHODOLOGY

In this section, we will brieﬂy explain the proposed

methodology for the design of a WSN system.

4.1 Discussion

We aim to propose a methodology of the speciﬁcation

and the veriﬁcation of non-functional requirements of

a WSN, focusing on SysML AD as a behavioral dia-

gram since it allows to model the entire network pro-

gram. In addition, we focus on the RD and the PD di-

agrams that can be called during veriﬁcation and per-

formance evaluation after the transformation from the

AD to a graphical formal model is performed. Our

main goal is to beneﬁt from the model-based attitude

allowing the integration of the advantages of SysML

with the ones of the PNs. In fact, formal methods in-

cluding these latter, can be difﬁcult to design or even

to understand especially for non-experts. SysML is a

semi-formal language which appears to offer an inter-

esting compromise, especially when we provide for

it a methodology for verifying and validating systems

designed with it.

The target formalism of the mapping is the class

of the DSPNs, which extends the high-level PN class

with the heterogenous transitions which have the ca-

pacity to treat different situations in terms of timed

constraints. In fact, in a WSN, random phenomena

are close to our everyday experience, at least due to

the physical changes, equipment failures, batteries de-

pletion, packets loss and so on. A stochastic process

is a mathematical model useful for the description

of phenomena of a probabilistic nature as a function

of a parameter that usually has the meaning of time

(Marsan, 1990).

Since the tasks performed by a sensor node are

based on the notion of random variable, it is necessary

to resort to stochastic models, in particular the SPNs,

given that they are graphic and therefore more ﬂex-

ible compared to Markov chains. Furthermore, the

sensor nodes can perform tasks having a ﬁxed time.

This is why we have thought of the DSPN formalisms

that have been introduced in (Marsan and Chiola,

1987) as a discrete and continuous-time modeling tool

which include both exponentially distributed and con-

stant timing, in contrast to Timed Petri Nets which

employ only discrete time scale for the underlying

stochastic process.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

Figure 1: The SysML model of the proposed approach.

(Wolny et al., 2020) notice that most of stud-

ied publication consider either discrete or continu-

ous challenges when designing systems. It means

that very rarely hybrid solutions in systems design are

taken into account. We aim to incorporate the DSPN

formal sementics with SysML to close the gap when

combining discrete and continuous modeling and ver-

iﬁcation. At last, we can evaluate the performances of

a WSN in a DSPN like energy consumption. The im-

provement we are going to make in this methodology

is to not adjust the performance parameters directly in

the DSPN, but to specify them through the SysML PD

and then inject them into the resulting DSPN model

after the mapping. This will make the approach trans-

parent for the users, especially for non-experts.

4.2 Schematization

Figure 1 describes our approach that we represented

by a SysML AD composed by four activities. The

ﬁrst activity that we note CMSM Activity consists

of the creation, and eventually the modiﬁcation of the

SysML models. We take into account the SysML AD,

PD and RD diagrams. In the case of WSNs, the sen-

sor nodes behaviors can be modeled using the SysML

AD. We signal here, that the choice of the SysML AD

to describe behavioral aspects of WSNs is due to its

capabilities to capture probabilistic behaviors which

is an important characteristic when modeling WSNs.

In fact, the SysML AD introduces the notions of rates

and probabilities. In addition, contrary to other be-

havioral diagrams, the AD can model the control and

the data ﬂows for the hole system and even in a hier-

archical manner. Once the SysML elements are cre-

ated, the DSPN analytic model will be established.

This second operation is represented by the CAM Ac-

tivity. We note MA Activity, the performing of the

resulting DSPN in order to analyse the WSN proper-

ties and to evaluate its performances, in particular the

energy consumption. In the last activity called RV

Activity, we check whether the obtained results are

consistent with the system requirements, and thus our

approach is completed. In contrast, we need to adjust

this approach and run it again. The process described

Towards the Formal Modeling Methodology of WSN through the Transformation of SysML into DSPNs

above is repeated until we get the desired results.

The process we are going to follow in order to set

up the proposed approach will go through three es-

sential stages. We prefer to not present the SysML

diagrams at the same time but this will be done grad-

ually according to these three steps. These latter are

represented by the dotted red frames in the ﬁgure 1.

We start by transforming the AD into a DSPN

using the mapping rules described below (in sec-

tion 4.3). The second step is to inject, into the result-

ing DSPN model, the performance parameters mod-

eled by the PD, in particular the energy consumption.

We can thus proceed to the analysis of the model and

the evaluation of this parameter. In the last step, the

obtained results will be compared with the constraints

described in the RD and ﬁnally proceed to their val-

idation. Now, we deal with only the ﬁrst part of the

approach. The two remaining steps will be explored

in the future works.

4.3 Mapping Rules

This section seeks to transform an AD to a DSPN. The

both exist at a higher level of abstraction. It is also es-

sential to have a model-level vision of the expected

results. Since this is the mapping from a semi-formal

language to a formal one, then it is necessary to en-

sure that the semantics and the behavior of the AD

elements are preserved in the equivalent DSPN.

Concerning how to derive the elements of the

AD to a DSPN, we proceed with the generic method

which consists to translate the AD basic elements to

the DSPN ones, and then interconnecting them. Fig-

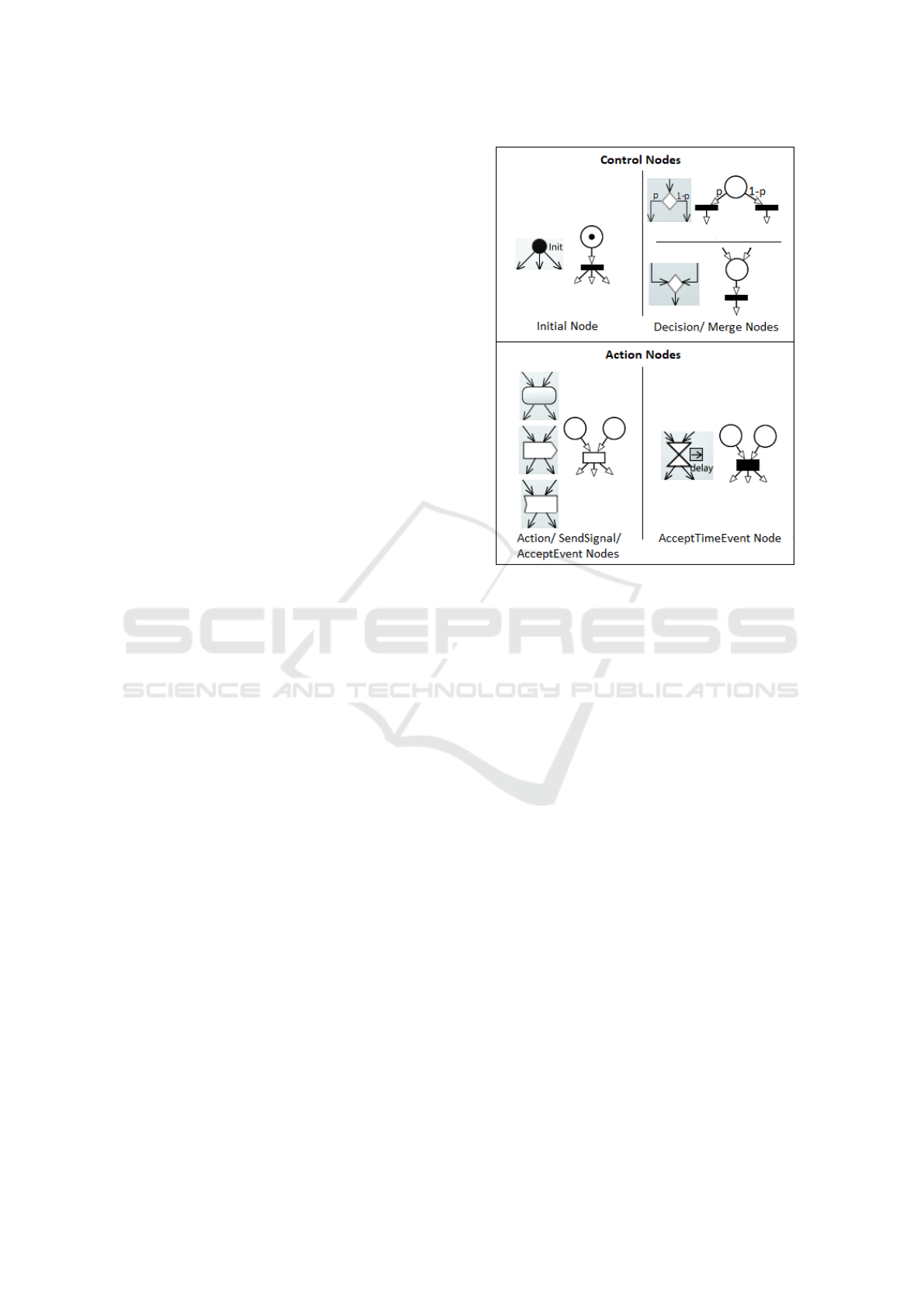
ure 2 shows the mapping of the control and the action

nodes, necessary in our work.

The InitialNode acts as a starting point for exe-

cuting an Activity. The conversion is performed by

creating a marked initial place connected to an im-

mediate transition allowing each outgoing arc to be

provided with a token. The places are used to model

the tokens which are implicitly represented in the AD.

Concerning the MergeNode, it brings together mul-

tiple ﬂows without synchronization. A MergeNode

shall have exactly one outgoing ActivityEdge but may

have multiple incoming ActivityEdges. The conver-

sion is performed by creating a place that receives

the tokens of each input arc. This place is linked to

an immediate transition which directly redistributes

each token at the output. A DecisionNode chooses

between outgoing ﬂows. It shall have at least one and

at most two incoming ActivityEdges, and at least one

outgoing ActivityEdge. The conversion is performed

by creating a place connected to immediate transitions

through arcs with guards. The number of these transi-

Figure 2: Mapping rules from SysML-AD to DSPN.

tions depends on the number of the decision outputs.

The guards represent the probabilities to perform the

sensor nodes tasks.

The ActionNodes including SendSignal and Ac-

ceptEvent Nodes are converted into stochastic transi-

tions with input places and also input and output arcs.

There is an exception concerning the AcceptEvent-

TimeActionNode which is converted into a determin-

istic transition since this latter plays the role of a time

trigger. The deterministic transition is associated with

input places as well as input and output arcs.

This is inspired from prior work, although their

mapping rules do not take into account certain as-

pects of the DSPNs that can be applied in complex

systems such as WSNs. In our case, we improved the

translation of the wait time action (AcceptEventTime-

Action) in the AD by using a deterministic transition

in the DSPN. Another improvement concerns the de-

cision nodes in which we associate a probability to

each output edge that we translate to a DSPN immedi-

ate transition containing this probability. In addition,

the action nodes are the consuming nodes in terms

of time, which is equivalent to stochastic and deter-

ministic transitions. On the other hand, the control

nodes are only used to control the sequencing which

is equivalent to the immediate transitions having a ﬁr-

ing time equal to 0.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

5 RUNNING EXAMPLE

In order to illustrate the usability of the proposed

mapping rules, a WSN based on a hierarchical topol-

ogy was considered as a running example. More pre-

cisely, we take the example of the LEACH protocol,

one of the ﬁrst to follow this topology (Chandrakasan

et al., 2000). According to this latter, the sensor nodes

are organized into clusters. Each cluster is managed

by a single node called Cluster Head (CH). Only CHs

communicate with the BS, manage clusters and ag-

gregate data. For that, they perform the most expen-

sive energy tasks while no-CH nodes (or members)

are dedicated only to sensing. CHs remain so for a

period of time called round, then they switch roles

during other rounds to get equitable power dissipation

within the network.

At the beginning of each round, each node deter-

mines the possibility of being a CH. If it decides to

be with generally a percentage of 5%, it announces its

decision to all neighboring nodes. Non-CH nodes join

the closest elected CH. Once the clusters formed, the

CHs assign time slots to their members. Each member

picks up information from its environment and sends

them to the CH. Used as gateway to reach the BS, the

CHs aggregate the received data and send the ﬁnal re-

sult to the BS.

5.1 Sensor Node Activity Diagram

In ﬁgure 3, we model the behavior of a sensor node

during one round. It can be seen that the action nodes

of the AD model the tasks carried out by a sensor

node while the control nodes organize the sequenc-

ing of these tasks. On the one hand, the local tasks

of a sensor node are modeled by Actions. On the

other hand, the sending and receiving operations are

modeled by SendSignalAction and AcceptEventAc-

tion nodes respectively. Concerning the tasks which

consume a ﬁxed period of time, they are modeled by

AcceptTimeEventAction node.

Initially, a sensor node is in the initial state (Init

node). The begining of a new round is modeled by

the merge node BeginRound which receives an arc,

either from the initial node (to specify the ﬁrst round

of the algorithm), or after the ending of the current

round and the return to the starting state in order to

begin the next round.

The sensor node subsequently calculates the

threshold with which it decides to become CH or non-

CH. This is achieved through the ComputeDec ac-

tion. According to the aforementioned assumption,

the percentage of the number of CH is 5%. Thus, the

probability that a sensor node becomes CH is equal

Figure 3: Sensor node Activity Diagram based on LEACH

protocol.

to 0.05. This is represented on the ﬁrst outgoing edge

of the BecomeCH decision node, with a weight equal

to 0.05. Otherwise, a node not wishing to be CH will

become member with a probability equal to 0.95 rep-

resented on the second edge.

In the ﬁrst case, the CH sends its decision to other

sensor nodes by performing the S Dec action. Since

the sensor nodes are not uniformly distributed over

the capture zone, a CH may not have members in its

cluster. In this case, it has to sense its own information

(SenseCH action) with a certain probability λ

and

sends it to the BS (S CHBS Action).

In contrast, this CH receives (R Join action)

memberships acknowledges from other non-CH

nodes to join its cluster with a probability 1 − λ

. Af-

ter that, it creates a table TDMA which it diffuses to

its members (S TDMA action). After that, it receives

their data (R Data action) and aggregates them after

an elapsed period (Aggr action with a ﬁxed period

Delay). The merge node EndCHWork indicates the

end of the role of a CH node. It owns two incoming

edges signifying either the CH had members or not.

If one of the edges is sensitized then the S CHBS ac-

tion is executed. Regarding the behavior of a non-CH

node, we do the same work.

Finally, the end of the round is modeled by the

EndRound merge node, and then, the sensor node

Towards the Formal Modeling Methodology of WSN through the Transformation of SysML into DSPNs

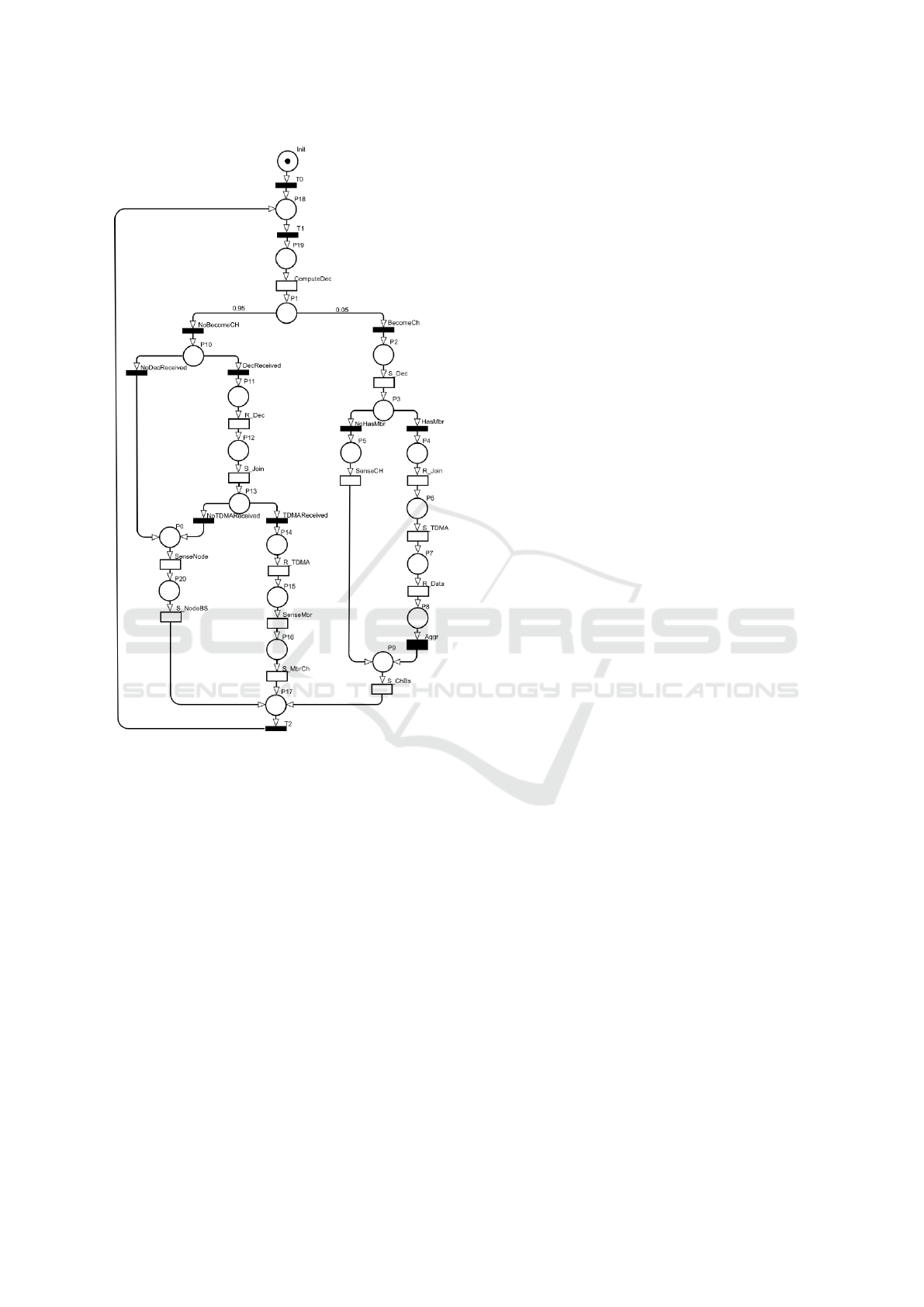
Figure 4: The resulting DSPN after mapping from SysML

AD.

returns to its initial state which is modeled by Begin-

Round merge node.

5.2 Mapping and Preliminary

Veriﬁcation

As operations that sensor nodes perform, can last ei-

ther a predeﬁned time (like the aggregation which

is ﬁxed) or a random time (like emission/reception

tasks), the use of the DSPNs is necessary. In fact,

the predeﬁned and random times are modeled by de-

terministic and exponential transitions respectively.

Once the DSPN model is created, the performances

measures can be evaluated. The DSPN model associ-

ated to the sensor node AD seen previously, is given

in the ﬁgure 4.

Before talking about the veriﬁcation of non-

functional properties and working out the remain-

ing steps of the proposed methodology, we have to

assume that some functional properties have to be

checked on the long run of the studied model. With

TimeNET, if the simulation at the steady state occurs,

it means that the DSPN model admits a stationary

state and therefore the basic properties are checked.

Three basic properties have to be discussed: the

bounded nature of the modeled system, its degree of

activity and ﬁnally its reset. The ﬁrst property an-

swers the question of whether the number of tokens

circulating in the network is limited or not. The sec-

ond considers whether a part or all of the network may

or may not evolve. The last one checks whether the

network admits an initial state and therefore it can be

reset. After verifying these properties, TimeNET dis-

plays results.

In addition, TimeNET can perform the station-

ary evaluation of the DSPN, with the restriction of

”not more than one enabled transition with non-

exponentially distributed ﬁring time in each marking”

(Marsan, 1990). As our analytical model admits only

one deterministic transition, i.e., we can never have

more than one enabled deterministic transition in each

marking, then this restriction is satisﬁed.

However, the initial node in the AD shall not have

any incoming ActivityEdges. This implies that in the

resulting DSPN, we cannot have an initial node with

an input arc. In this case, we will have a DSPN which

has a place that cannot be accessed after a certain

time, which does not preserve a basic functionality

called liveliness, so the second base property is not

checked. In addition we notice that there are imme-

diate unnecessary transitions which will not inﬂuence

the functioning of the DSPN model. We must there-

fore proceed to a reduction of the graph without losing

the semantics of the resulting model. These gaps will

be the subject of a future work.

6 CONCLUSION

Nowadays, the use of the semi-formal and formal

models, in order to design complex systems and ex-

press their properties, becomes a very active research

topic. In this paper, we proposed an approach based

on both SysML and DSPN models. This approach

consists on a speciﬁcation and veriﬁcation methodol-

ogy for designing WSNs. It helps to produce easy and

clear models, to reduce the time and the development

and maintenance costs, and to increase the efﬁciency

and the productivity.

However, the SysML/AD-to-DSPN transforma-

tion has not been performed in an automatic way. In

addition, we got a model having unnecessary immedi-

ate transitions and in which the liveliness property is

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

not done. These gaps are research topics we consider

later. Once the resulting model is relevant, we have

to exploit the SysML PD, and so, the non functional

parameters modeled by it should be injected into the

DSPN model in an automatic manner too.

Important work remains to be done, to provide a

formal framework for a better properties veriﬁcation

and performance evaluation of the WSNs technology.

REFERENCES

Ahmad, M., Dragomir, I., Bruel, J., Ober, I., and Belloir,

N. (2013). Early analysis of ambient systems sysml

properties using omega2-ifx (regular paper). In In-

ternational Conference on Simulation and Modeling

Methodologies, Technologies and Applications, pages

147–154, http://www.scitepress.org/. SciTePress.

Akyildiz, I., Su, W., Sankarasubramaniam, Y., and Cayirci,

E. (2002). Wireless sensor networks: a survey.

J. Computer Networks: The International Journal

of Computer and Telecommunications Networking,

38:393–422.

Baouya, A., Bennouar, D., Mohamed, O. A., and Ouchani,

S. (2015). A probabilistic and timed veriﬁcation ap-

proach of sysml state machine diagram. In 2015 12th

International Symposium on Programming and Sys-

tems (ISPS), pages 1–9.

Berrachedi, A., Rahim, M., Ioualalen, M., and Hammad, A.

(2017). Validation of a sysml based design for wire-

less sensor networks. AIP Conference Proceedings,

1863(1):330002.

Berrani, S., Hammad, A., and Mountassir, H. (2013). Map-

ping sysml to modelica to validate wireless sensor net-

works non-functional requirements. In In IEEE 11th

International Symposium on Programming and Sys-

tems (ISPS’2013), pages 191–200.

Chandrakasan, A., Balakrishnan, H., and Heinzelman,

W. R. (2000). Energy-efﬁcient communication pro-

tocol for wireless microsensor networks. Proceedings

of the 33rd Hawaii International Conference on Sys-

tem Sciences, 2:1–10.

Estefan, J. (2008). Survey of model-based systems engi-

neering (mbse) methodologies, rev.b. INCOSE MBSE

Focus Group, 25:1–70.

Foures, D., Albert, V., Pascal, J., and Nketsa, A. (2012).

Automation of sysml activity diagram simulation with

model-driven engineering approach. In Proceed-

ings of the 2012 Symposium on Theory of Modeling

and Simulation - DEVS Integrative M&S Symposium,

number 11 in TMS/DEVS ’12, pages 1–6, San Diego,

CA, USA. Society for Computer Simulation Interna-

tional.

Friedenthal, S., Moore, A., and Steiner, R. (2008). Omg

systems modeling language (omg sysml

) tutorial.

INCOSE International Symposium, 18:1731–1862.

Gauthier, J., Bouquet, F., Hammad, A., and Peureux, F.

(2015). Tooled process for early validation of sysml

models using modelica simulation. In Dastani, M.

and Sirjani, M., editors, Fundamentals of Software

Engineering, pages 230–237, Cham. Springer Inter-

national Publishing.

Gutierrez, A., Chamorro, H., Jimenez, F., Villa, L., and

Alonso, C. (2015). Hardware-in-the-loop simulation

of pv systems in micro-grids using sysml models. In

2015 IEEE 16th Workshop on Control and Modeling

for Power Electronics (COMPEL), pages 1–5.

Huang, C., Huang, Z., Hu, J., Wu, Z., and Wang, S. (2015).

A mde-based approach to the safety veriﬁcation of ex-

tended sysml activity diagram. Journal of Software,

10:56–70.

Huang, E., McGinnis, L. F., and Mitchell, S. W. (2020).

Verifying sysml activity diagrams using formal trans-

formation to petri nets. the Journal of the Interna-

tional Council of Systems Engineering, 23(1):118–

135.

Jarraya, Y. and Debbabi, M. (2014). Quantitative and qual-

itative analysis of sysml activity diagrams. Inter-

national Journal on Software Tools for Technology

Transfer, 16:399–419.

Knorreck, D., Apvrille, L., and de Saqui-Sannes, P. (2011).

Tepe: a sysml language for time-constrained prop-

erty modeling and formal veriﬁcation. ACM SIGSOFT

Software Engineering Notes, ACM, 36(1):1–8.

Marsan, M. and Chiola, G. (1987). On petri nets with deter-

ministic and exponentially distributed ﬁring times. In

Rozenberg, G., editor, Advances in Petri Nets 1987,

pages 132–145, Berlin, Heidelberg. Springer Berlin

Heidelberg.

Marsan, M. A. (1990). Stochastic petri nets: An elemen-

tary introduction. In Rozenberg, G., editor, Advances

in Petri Nets 1989, pages 1–29, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Pedroza, G., Apvrille, L., and Knorreck, D. (2011). Avatar:

A sysml environment for the formal veriﬁcation of

safety and security properties. 2011 11th Annual In-

ternational Conference on New Technologies of Dis-

tributed Systems, NOTERE 2011 - Proceedings, pages

1–10.

Peterson, J. L. (1977). Petri nets. J. ACM Computing Sur-

veys, 9:223–252.

Rahim, M., Hammad, A., and Ioualalen, M. (2017). A

methodology for verifying sysml requirements using

activity diagrams. Innovations in Systems and Soft-

ware Engineering, 13(2):1–14.

Wolny, S., Mazak, A., Carpella, C., Geist, V., and Wim-

mer, M. (2020). Thirteen years of sysml: a system-

atic mapping study. Software and Systems Modeling,

19:111–169.

Zhu, S., Tang, J., Gauthier, J., and Faudou, R. (2019). A

formal approach using sysml for capturing functional

requirements in avionics domain. Chinese Journal of

Aeronautics, 32(12):2717–2726.

Zimmermann, A. (2012). Modeling and evaluation of

stochastic petri nets with timenet4.1. In In: 6th In-

ternational Conference on Performance Evaluation

Methodologies and Tools (VALUETOOLS), pages 1–

10.

Towards the Formal Modeling Methodology of WSN through the Transformation of SysML into DSPNs