Automated Symbolic Veriﬁcation of Telegram’s MTProto 2.0

Marino Miculan

∗ a

and Nicola Vitacolonna

Department of Mathematics, Computer Science and Physics, University of Udine, Italy

Keywords:

Speciﬁcation, Veriﬁcation and Synthesis, Security Protocols, Practical Veriﬁcation, Privacy, Formal Methods.

Abstract:

MTProto 2.0 is a suite of cryptographic protocols for instant messaging at the core of the popular Telegram

messenger application. In this paper we analyse MTProto 2.0 using the symbolic veriﬁer ProVerif. We provide

fully automated proofs of the soundness of MTProto 2.0’s authentication, normal chat, end-to-end encrypted

chat, and rekeying mechanisms with respect to several security properties, including authentication, integrity,

secrecy and perfect forward secrecy; at the same time, we discover that the rekeying protocol is vulnerable to an

unknown key-share (UKS) attack. We proceed in an incremental way: each protocol is examined in isolation,

relying only on the guarantees provided by the previous ones and the robustness of the basic cryptographic

primitives. Our research proves the formal correctness of MTProto 2.0 w.r.t. most relevant security properties,

and it can serve as a reference for implementation and analysis of clients and servers.

1 INTRODUCTION

Telegram is a very popular instant messaging appli-

cation, with more than 500 million active users (as of

March 2021). Besides user-to-user and group com-

munication, channels are widely adopted by news-

papers, ﬁnancial institutions, and even government

agencies for broadcasting ofﬁcial news, in particular

during emergency situations. Telegram provides also

an open API allowing third parties to offer (possibly

commercial) services by means of bots.

At the core of this ecosystem lies MTProto 2.0

(Telegram, 2021a), a suite of cryptographic protocols

designed for implementing fast, scalable, secure mes-

sage exchange without relying on the security of the

underlying transport protocol. To this end, MTProto

is composed by several (sub)protocols handling the

initial authentication of the clients with the creation

of shared keys between clients and server, the creation

of session keys between two clients for end-to-end en-

cryption in secret chats, the rekeying of secret chats,

and of course the encryption of all messages, before

being transmitted over a (possibly insecure) network.

Although MTProto 2.0 is completely open and

client’s code is open-source, Telegram’s security

model has received wide criticism. First and fore-

https://orcid.org/0000-0003-0755-3444

https://orcid.org/0000-0002-7505-5124

∗

Supported by MIUR PRIN 2017FTXR7S IT MAT-

TERS (Methods and Tools for Trustworthy Smart Systems).

most, the choice of the non-standard, ad hoc protocol

and encryption scheme has been objected, because the

lack of scrutiny could expose the system to vulnera-

bilities, potentially undermining its security (Kobeissi

et al., 2017). Moreover, all messages (even those of

“secret chats”) pass through (a cloud of) proprietary,

closed-source servers, where they can be stored for

any amount of time. This architecture is convenient

for users, who can access and synchronise their mes-

sages from several devices and send and receive mes-

sages also when the peer is not present, but from a

security perspective it means that the server must be

considered as an untrusted party.

This situation raises the need for a practical veri-

ﬁcation of the MTProto 2.0 protocol suite. However,

in spite of the criticisms above, most research has fo-

cused on the previous version MTProto 1.0, depre-

cated since December 2017. To our knowledge, no

formal, in-depth veriﬁcation of MTProto 2.0 has been

carried out so far. This is the scope of this work.

In this paper we formalise and analyse MT-

Proto 2.0 using ProVerif (Blanchet, 2016), a state-of-

the-art symbolic cryptographic protocol veriﬁer based

on the Dolev-Yao model. We provide a fully auto-

mated proof of the soundness of MTProto 2.0’s pro-

tocols for authentication, normal chat, end-to-end en-

crypted chat, and rekeying mechanisms with respect

to several security properties, including authentica-

tion, integrity, secrecy and perfect forward secrecy.

These properties are veriﬁed also in presence of mali-

Miculan, M. and Vitacolonna, N.

Automated Symbolic Veriﬁcation of Telegram’s MTProto 2.0.

DOI: 10.5220/0010549601850197

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 185-197

ISBN: 978-989-758-524-1

185

cious servers and clients. On the other hand, we dis-

cover that, in principle, the rekeying protocol is vul-

nerable to an unknown key-share (UKS) attack: a ma-

licious client E can induce two honest clients A, B to

believe they share two secret keys with E, and instead

they share the same key between themselves only.

In order to prove these results we proceed in an

incremental way. Each protocol of the suite is exam-

ined in isolation, specifying which guarantees it re-

quires from previous protocols and which ones it pro-

vides; separation between protocols is guaranteed by

the typing discipline enforced on messages: “out of

sequence” messages are simply discarded. For each

protocol we provide its formalisation in ProVerif’s

speciﬁcation language (the applied π-calculus), the

formalisation of its security properties, and the results

of the formal veriﬁcation.

This approach allows us to cope with the com-

plexity of the suite and to isolate the security prop-

erties required on the underlying message encryption

scheme. Namely, the only assumption we make is that

the latter is an authenticated encryption scheme, guar-

anteeing both integrity of ciphertext (INT-CTXT) and

indistinguishability of chosen plaintext (IND-CPA).

These properties are difﬁcult to prove in a symbolic

model like ProVerif’s, but can be proved in a com-

putational model, e.g. using tools like CryptoVerif or

EasyCrypt (Blanchet, 2007; Barthe et al., 2013). This

assumption may appear strong, especially consider-

ing that Telegram has been widely criticized for its

design choices, and vulnerabilities have been found

in MTProto 1.0; however, none of these attacks have

been replicated on MTProto 2.0.

In this paper we focus on the symbolic veriﬁca-

tion of MTProto 2.0 with respect to an unbounded

number of sessions, leaving the analysis of the en-

cryption scheme in the computational model to future

work. Proving the logical correctness of a protocol

under a fairly general threat model is very important:

if a protocol is proved to be sound at a symbolic level

then one can focus on searching vulnerabilities in the

“lower” part of the protocol stack, among the cho-

sen cryptographic functions and other implementation

choices. If a cryptographic primitive is found to be

weak, it can be substituted with a stronger one, with-

out invalidating the symbolic analysis.

Besides the relevance for Telegram’s users, our

formalisation can serve as a reference documentation

for the implementation of clients and servers.

Synopsis. In Section 2 we recall previous related

work. The security model adopted is described in

Section 3. In Section 4 we recall the structure of

MTProto 2.0, whose protocols are analyzed in the

subsequent sections: initial authorization key creation

(Section 5), key exchange for secret chats (Section 6),

rekeying in secret chats (Section 7). Conclusions and

directions for future work are in Section 8.

We assume the reader conﬁdent with ProVerif; for

an introduction we refer to (Blanchet, 2016) and sev-

eral tutorials online. The code is available at https://

github.com/miculan/telegram-mtproto2-veriﬁcation.

2 RELATED WORK

All the published research on MTProto that we are

aware of, as well as most online articles, refer to the

now deprecated MTProto v1.0 and do not directly ap-

ply to the current MTProto 2.0, deployed in Telegram

clients as of v4.6 (December 2017).

Arguably, the closest work to ours is (Kobeissi

et al., 2017), where the Signal protocol is formalised

in ProVerif and MTProto v1.0 is also brieﬂy dis-

cussed, but not at the formal level. The Signal proto-

col has been studied rigorously in (Frosch et al., 2016;

Cohn-Gordon et al., 2017; R

osler et al., 2018).

Several issues have been pointed out in MT-

Proto v1.0. Its encryption scheme added a random

padding to the message prior to encryption but af-

ter the msg key was computed, leading to a couple

of theoretical CCA attacks (Jakobsen and Orlandi,

2016). Earlier versions of the protocol did not pro-

vide forward secrecy, and message sequence numbers

were managed by the server, so that a malicious server

could easily perform replay attacks (Jakobsen, 2015).

Another replay attack was discovered in Android’s

Telegram client v3.13.1 (Su

anka and Koke

s, 2017),

where the same message could be accepted twice

by a client after 300 more messages had been sent.

This was due to a ﬂaw in the implementation, which

did not abide by Telegram’s Security Guidelines for

Client Developers; it was ﬁxed in Telegram v3.16.

The above mentioned issues were addressed in

MTProto 2.0, whose developers claim to be IND-

CCA and INT-CTXT secure and to provide perfect

forward secrecy for secret chats. There is currently no

known proof of such claims, but there are no known

attacks on MTProto’s encryption, either.

A theoretical MitM attack to MTProto 1.0 has

been described in (Rad and Rizzo, 2015). As we will

see in Section 6, the DH exchange used to establish

a shared key before initiating a secret chat is not au-

thenticated by the two ends. Clients are supposed to

verify a hash of the shared secret through an external

secure channel. In MTProto v1.0, the ﬁrst 128 bits

of the SHA1 of the key are used as the ﬁngerprint.

A malicious server might social engineer two clients

to both initiate a conversation with each other; since

SECRYPT 2021 - 18th International Conference on Security and Cryptography

186

the server forwards all the messages, it might act as a

MitM and try to ﬁnd two keys whose ﬁngerprints co-

incide, using a birthday attack and approximately 2

computations (Rad and Rizzo, 2015). In MTProto 2.0

(starting with the “layer 46” of secret chat protocol),

the ﬁngerprint is 288 bits long (additional 160 bits are

extracted from the preﬁx of the SHA256 of the key),

thus making this MitM attack likely infeasible.

3 SECURITY MODEL

We model Telegram protocols in ProVerif (Blanchet,

2016), which is a symbolic cryptographic veriﬁer.

Protocols and security properties are speciﬁed in a

variant of the applied π-calculus, a formalism de-

signed for representing cryptographic processes, and

translated into a Horn theory. Cryptographic primi-

tives are represented by means of a suitable term the-

ory, by means of constructors and reduction rules or

equations; thus, cryptographic primitives are modeled

as “perfect”; in particular, there is no way to recover

a plaintext or a key from the ciphertexts, and the ci-

phertext is not forgeable.

Following this approach, in our model we con-

sider the message encryption scheme used in MT-

Proto 2.0 essentially as an authenticated encryption

scheme, abstracting from its actual implementation.

Formally, MTProto’s symmetric encryption prim-

itive is governed by the following reduction rule:

fun senc(Bitstring,SharedKey,Nonce) : Bitstring

reduc forall m : Bitstring, k : SharedKey,n : Nonce;

sdec(senc(m,k,n), k) = m.

A detailed veriﬁcation of these cryptographic func-

tions in the computational model is left to future work.

Threat Model. We adopt the classical symbolic

Dolev-Yao model (Dolev and Yao, 1983), which is the

one used by ProVerif. More speciﬁcally, we assume

that all messages are transmitted over a public net-

work, and that an active intruder can intercept, mod-

ify, forward, drop, replay or reﬂect any message. Be-

sides, we assume that an attacker may also exﬁltrate

secret data, such as pre-shared keys, during or after

the execution of a protocol. As mentioned above, we

assume that encrypted messages are unbreakable un-

less the key becomes available to the attacker. The

model for hash functions is also quite strong, being

close to the random oracle model. Other threats, such

as timing attacks and guessing attacks, are beyond the

scope of our model.

All messages exchanged by clients pass through

Telegram’s servers. Hence, such servers can access

the plaintext of cloud-based chats and the ciphertext

of secret chats. Servers are also responsible for choos-

ing the Difﬁe-Hellman parameters used to derive the

long-term authorization keys for the clients. There-

fore, a server should not be considered as trusted.

Security Goals. Each part of MTProto has different

security goals, as we will see later on. In general, we

will consider the following, informally stated, goals:

Secrecy: if a message m is exchanged in a session S

between two honest principals A and B then m is

secret (i.e., known only to A and B) unless an at-

tacker can break some cryptographic construction

or recover the encryption keys before or during S.

Forward Secrecy: secrecy of message m is pre-

served even if the attacker recovers the encryption

keys after S is completed.

Authentication: if B receives m which is supposed

to come from A, then it was really sent by A.

Integrity: if m is sent from A to B then B receives m

and not some forged m

6= m instead.

4 THE MTPROTO 2.0 PROTOCOL

In this section we give a high-level overview of MT-

Proto 2.0. For a deeper (albeit informal) description,

we refer to the ofﬁcial web page (Telegram, 2021a).

MTProto 2.0 is a client/server protocol suite de-

signed for accessing a (MTProto) server

from appli-

cations running on desktop computers or mobile de-

vices, through an insecure network. This suite can be

divided into three main components (see Fig. 1):

High-level API and Type Language: deﬁnes how

API queries and responses are converted to binary

messages. This component ﬁts OSI layers 7

(application) and 6 (presentation).

Cryptographic and Authorization Components:

deﬁnes how applications are authenticated with

the server, and messages are encrypted before

being transmitted through the transport protocol.

These components ﬁt OSI layers 5 (session) and

4 (transport).

Transport Component: deﬁnes how the client and

the server actually exchange messages, via exist-

ing transport protocol such as UDP, TCP, HTTP,

HTTPS, Websocket, etc.. Note that also insecure,

connectionless protocols are supported.

Actually, Telegram employs a network (a “cloud”) of

servers in multiple data centers, spread worldwide for scal-

ability and availability. However, for our aims, we can con-

sider this network as a single server.

Automated Symbolic Veriﬁcation of Telegram’s MTProto 2.0

187

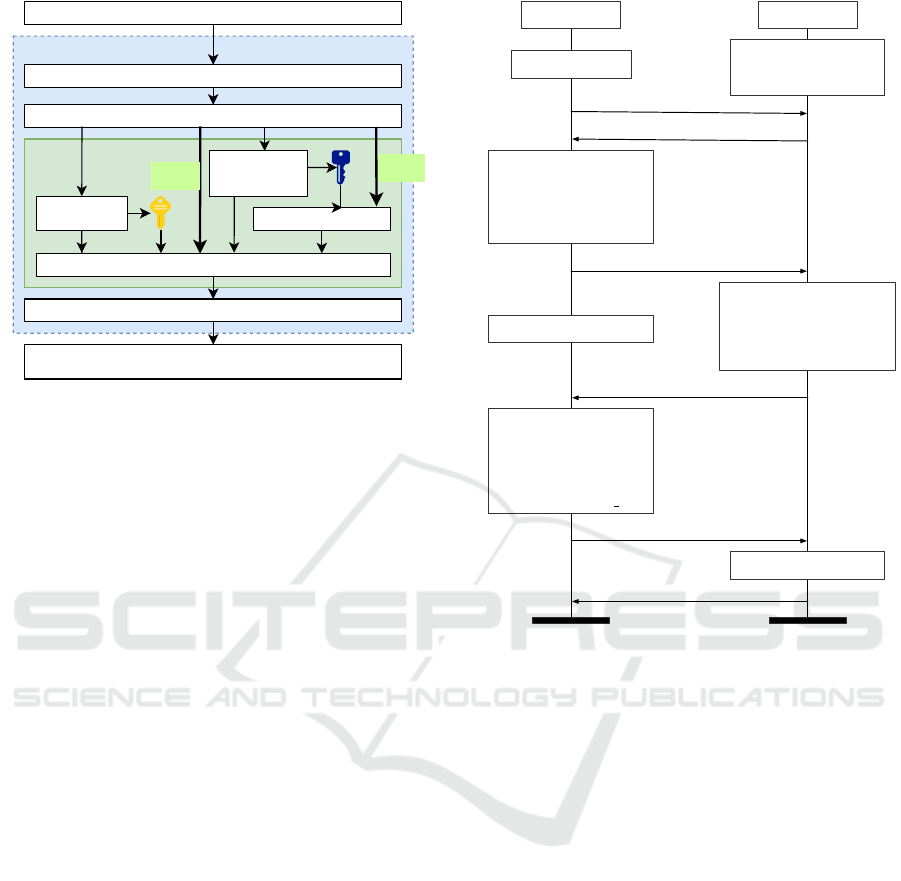
MTProto 2.0

Transport component

Underlying network transport (TCP, UDP, HTTP(S), Websocket…)

Message Encryption

Type language

Message Encryption

Secret chat key

exchange and

rekeying

Authorization

High-level API

Application

Secret

Message

Cloud

Message

C&A

Figure 1: The MTProto 2.0 suite. The subject of the present

work is the “Cryptography and Authorization” (C&A) com-

ponent. AK (yellow key) is the Authorization Key, estab-

lished once at the ﬁrst run. SK (blue key) is the Secret Chat

Session Key, established at the beginning of each secret chat

(and changed often). Cloud messages are encrypted only

from client to server (and vice versa), with the AK. Secret

messages are encrypted twice: with the SK, and then with

the AK. In this picture the Message Encryption module is

duplicated, but actually it is the same, with different keys.

We focus on the component handling cryptographic

transformations and authorization. This component

can be divided further into the following modules:

Authorization: this module provides the functional-

ities for the initial client authorization and server

authentication. It is called on the ﬁrst run of

the application, for deriving the authorization key

(AK), a long-term “master” secret shared with the

server only. In order to establish the authorization

key, this module executes a cryptographic proto-

col (basically a DH exchange) with the server. We

will analyse this protocol in Section 5.

Secret Chat Key Exchange and Rekeying: this

module provides the functionalities for establish-

ing a session shared secret key (SK) between two

clients. It is executed once at the beginning of

a secret chat and after 100 exchanged messages

between the two parties (or over a week) for

installing a new key. In both cases, this module

executes a a Difﬁe-Hellman exchange with the

peer client (through the server). We will analyse

this protocol in Sections 6 and 7.

Message Encryption: All messages between client

and server are encrypted with a symmetric ci-

pher, using an ephemeral key derived from the

AK. Messages in secret chats are encrypted also

with an ephemeral key derived from the SK. The

<latexit sha1_base64="UVSceB3XPkuaWL8CUCC63d24oXY=">AAAB6nicbZDJSgNBEIZr3LK4RT3qoTEInsKMB/Vm0IvHiGaBJISeTk3SpKdn6O4RwhDwBbx4UMSrT+CjePMxfAM7y0ETf2j4+P8quqr8WHBtXPfLWVpeWV3LZHP59Y3Nre3Czm5NR4liWGWRiFTDpxoFl1g13AhsxApp6Aus+4OrcV6/R6V5JO/MMMZ2SHuSB5xRY61b2WGdQtEtuRORRfBmULz4buUePi4zlU7hs9WNWBKiNExQrZueG5t2SpXhTOAo30o0xpQNaA+bFiUNUbfTyagjcmSdLgkiZZ80ZOL+7khpqPUw9G1lSE1fz2dj87+smZjgvJ1yGScGJZt+FCSCmIiM9yZdrpAZMbRAmeJ2VsL6VFFm7HXy9gje/MqLUDspeacl98Ytlg9gqizswyEcgwdnUIZrqEAVGPTgEZ7hxRHOk/PqvE1Ll5xZzx78kfP+A141kLM=</latexit>

<latexit sha1_base64="GK5nOspCGLQ8soGrjYUfd0llKJ8=">AAACJXicbVBNS8NAEN34WetX1aMegkVQKCXxoB6EFrx4VLCt0NSw2U7s4mYTdydiif0R/gUv/hUvHhQRPPkL/Ace3LYetPpg4PHeDDPzgkRwjY7zZo2NT0xOTedm8rNz8wuLhaXluo5TxaDGYhGr04BqEFxCDTkKOE0U0CgQ0AguDvp+4wqU5rE8wW4CrYieSx5yRtFIfmFf+qwkfV26VCUP4Rp1mIVJ7yzbdLd6RvZEO0Y9YnkgRN/1C0Wn7Axg/yXuNylWPis3H7cdfeQXnr12zNIIJDJBtW66ToKtjCrkTEAv76UaEsou6Dk0DZU0At3KBl/27A2jtO0wVqYk2gP150RGI627UWA6I4odPer1xf+8ZorhXivjMkkRJBsuClNhY2z3I7PbXAFD0TWEMsXNrTbrUEUZmmDzJgR39OW/pL5ddnfKzrFTrK6RIXJklayTTeKSXVIlh+SI1Agjd+SBPJFn6956tF6s12HrmPU9s0J+wXr/AnVJqio=</latexit>

,qr,fp

(1)

,...,fp

(`)

,qr,fp

(1)

,...,fp

(`)

<latexit sha1_base64="tupxdPif/AoBYx/ULhVNXDycO4E=">AAACGXicbVBNS8NAEN3Ur9r6EfWoh2ARWigl8aAeFS89KlgVmhI22027dLMJu5NiCcH/4MGLf0UQD4roTU/+G7epB7U+GHi8N8PMPD/mTIFtfxqFmdm5+YXiYqm8tLyyaq6tn6sokYS2SMQjeeljRTkTtAUMOL2MJcWhz+mFPzge+xdDKhWLxBmMYtoJcU+wgBEMWvJMW3ikLjxVd1MX6BWoIFV97GTVo1r9yM28tDqo5waDlA2zWuaZFbth57CmifNNKofl7KF5/XZz4pnvbjciSUgFEI6Vajt2DJ0US2CE06zkJorGmAxwj7Y1FTikqpPmn2XWjla6VhBJXQKsXP05keJQqVHo684QQ1/99cbif147geCgkzIRJ0AFmSwKEm5BZI1jsrpMUgJ8pAkmkulbLdLHEhPQYZZ0CM7fl6fJ+W7D2WvYpzqNLTRBEW2ibVRFDtpHh6iJTlALEXSL7tETejbujEfjxXidtBaM75kN9AvGxxclbqP7</latexit>

, {sha1(A),A}

(k,iv)

, {sha1(A),A}

(k,iv)

<latexit sha1_base64="2zJIxB5PNu0KpIlLWmoise2LdDY=">AAACCXicbVA9SwNBEN3zM8avqKXNYhAsjnBnoSKIERvLCEaFJBx7m0myZG/v2J0Tw5FWC/+KjYUitv4DO3tL/4Cdm8TCrwcDj/dmdmdemEhh0PNenbHxicmp6dxMfnZufmGxsLR8auJUc6jyWMb6PGQGpFBQRYESzhMNLAolnIXdw4F/dgHaiFidYC+BRsTaSrQEZ2iloEAPdvdUwF0VGLftJm47YG4d4dI+laGIoB8Uil7JG4L+Jf4XKe5/XIt39w0qQeGl3ox5GoFCLpkxNd9LsJExjYJL6OfrqYGE8S5rQ81SxSIwjWx4SZ+uW6VJW7G2pZAO1e8TGYuM6UWh7YwYdsxvbyD+59VSbO00MqGSFEHx0UetVFKM6SAW2hQaOMqeJYxrYXelvMM042jDy9sQ/N8n/yWnmyV/q+Qd+8UyJSPkyCpZIxvEJ9ukTI5IhVQJJ1fkltyTB+fGuXMenadR65jzNbNCfsB5/gSGUJ37</latexit>

A := n

,g,p,g

, time

A := n

,g,p,g

, time

Client A Server S

Knows

<latexit sha1_base64="1N6cL1A0Jz0ERkVKSU9oeyXV61w=">AAACGnicbVC7SgNBFL3r2/iKWtoMPkBBwq6FWgo2lgomEbIxzE7uJkNmH8zcFcMSf8PG1s+wsVDETmxs/A5LJ4mFrwOXezjnXmbuCVIlDbnumzMyOjY+MTk1XZiZnZtfKC4uVUySaYFlkahEnwXcoJIxlkmSwrNUI48ChdWgc9j3qxeojUziU+qmWI94K5ahFJys1Ch6PuElmTA3nd55vult9Rpm21fNhGz7YfmoVN9tFNfckjsA+0u8L7J2AOun71e3H8eN4ovfTEQWYUxCcWNqnptSPeeapFDYK/iZwZSLDm9hzdKYR2jq+eC0HtuwSpOFibYVExuo3zdyHhnTjQI7GXFqm99eX/zPq2UU7tdzGacZYSyGD4WZYpSwfk6sKTUKUl1LuNDS/pWJNtdckE2zYEPwfp/8l1R2St5uyT2xaTAYYgpWYBU2wYM9OIAjOIYyCLiGO3iAR+fGuXeenOfh6IjztbMMP+C8fgJ4oKVb</latexit>

(1)

,...,sk

(`)

(1)

,...,sk

(`)

<latexit sha1_base64="Tak2ojDnuPxxLGd2+Xc5dK8Wnl0=">AAAB+XicbVC7TsMwFL0pj5byCjCyWFRITFXCAIyVWBiLoA+1iSLHdVurjhPZTqUq6sB/sHQAIdb+CRt/g9N2gJYjWTo6517d4xMmnCntON9WYWt7Z7dY2ivvHxweHdsnp00Vp5LQBol5LNshVpQzQRuaaU7biaQ4CjlthaP73G+NqVQsFs96klA/wgPB+oxgbaTAtrHHhBdhPQzDrDMNksCuOFVnAbRJ3BWp1Aqzl05x/lQP7C+vF5M0okITjpXquk6i/QxLzQin07KXKppgMsID2jVU4IgqP1skn6JLo/RQP5bmCY0W6u+NDEdKTaLQTOYZ1bqXi/953VT37/yMiSTVVJDloX7KkY5RXgPqMUmJ5hNDMJHMZEVkiCUm2pRVNiW461/eJM3rqntTdR5NGwiWKME5XMAVuHALNXiAOjSAwBhe4Q3ercyaWR/W53K0YK12zuAPrPkPkvKWdA==</latexit>

a ∈ Z

<latexit sha1_base64="s2zPJfuOva4QtEzQDciOdOsYm50=">AAAB9XicbVC7SgNBFJ31GeMramkzGAQLCbsWKoIYsLGMYB6QbMLs7OxmyDyWmVklLKn9BRsLRWz9Fzt7S3/Azsmj0MQDFw7n3Mu99wQJo9q47oczN7+wuLScW8mvrq1vbBa2tmtapgqTKpZMqkaANGFUkKqhhpFGogjiASP1oHc59Ou3RGkqxY3pJ8TnKBY0ohgZK7XjDjo7j9uoxWUIk06h6JbcEeAs8SakePF9T78OP0mlU3hvhRKnnAiDGdK66bmJ8TOkDMWMDPKtVJME4R6KSdNSgTjRfja6egD3rRLCSCpbwsCR+nsiQ1zrPg9sJ0emq6e9ofif10xNdOpnVCSpIQKPF0Upg0bCYQQwpIpgw/qWIKyovRXiLlIIGxtU3obgTb88S2pHJe+45F67xTIEY+TALtgDB8ADJ6AMrkAFVAEGCjyAJ/Ds3DmPzovzOm6dcyYzO+APnLcfvbGWXg==</latexit>

:= g

mod p

:= g

mod p

Chooses

<latexit sha1_base64="5u5JT4UrFtBGf/81eXSoGgMDBGU=">AAAB/HicbVDJSgNBEK2JW4xbNEcvjVGIlzDjQT0GvHiMkA2SGHo6PUmTnoXuGjEMya94UVDEqx/izYvf4dHOctDEBwWP96qoqudGUmi07U8rtbK6tr6R3sxsbe/s7mX3D2o6jBXjVRbKUDVcqrkUAa+iQMkbkeLUdyWvu4OriV+/40qLMKjgMOJtn/YC4QlG0UidbK6F/B61l0SD0W1SEKejju5k83bRnoIsE2dO8iU4rnyNn77LnexHqxuy2OcBMkm1bjp2hO2EKhRM8lGmFWseUTagPd40NKA+1+1kevyInBilS7xQmQqQTNXfEwn1tR76run0Kfb1ojcR//OaMXqX7UQEUYw8YLNFXiwJhmSSBOkKxRnKoSGUKWFuJaxPFWVo8sqYEJzFl5dJ7azonBftG5MGgRnScAhHUAAHLqAE11CGKjAYwgM8w4s1th6tV+tt1pqy5jM5+APr/QcYn5io</latexit>

(i)

matching

<latexit sha1_base64="RBE795+pthJDF58S/+Q4LFpdKIw=">AAAB+nicbVC7SgNBFJ2NrxhfiZY2g0GIIGHXQu0M2FhGMA9IYpid3E2GzD6YuauGNbVfYWOhiK1fYmdv6Q/YOXkUGj1w4XDOvdx7jxtJodG2363U3PzC4lJ6ObOyura+kc1tVnUYKw4VHspQ1V2mQYoAKihQQj1SwHxXQs3tn4782hUoLcLgAgcRtHzWDYQnOEMjtbO5JsINai/xouFlUhB7w3Y2bxftMehf4kxJ/uTrTnzuf0C5nX1rdkIe+xAgl0zrhmNH2EqYQsElDDPNWEPEeJ91oWFowHzQrWR8+pDuGqVDvVCZCpCO1Z8TCfO1Hviu6fQZ9vSsNxL/8xoxesetRARRjBDwySIvlhRDOsqBdoQCjnJgCONKmFsp7zHFOJq0MiYEZ/blv6R6UHQOi/a5ky9RMkGabJMdUiAOOSIlckbKpEI4uSb35JE8WbfWg/VsvUxaU9Z0Zov8gvX6DaIFmJY=</latexit>

(i)

for some

<latexit sha1_base64="5FAjBfPFv3JmyEKaOAWVjwVJ3D4=">AAAB6HicbZC7SgNBFIbPxluMt3jpbAaDYBV2LdTOgIWWCZgLJCHMTs4mY2Znl5lZIS55AhsLRWzF2oexs/RNnFwKjf4w8PH/5zDnHD8WXBvX/XQyC4tLyyvZ1dza+sbmVn57p6ajRDGsskhEquFTjYJLrBpuBDZihTT0Bdb9wcU4r9+i0jyS12YYYzukPckDzqixVoV38gW36E5E/oI3g8L5293X5fteWu7kP1rdiCUhSsME1brpubFpp1QZzgSOcq1EY0zZgPawaVHSEHU7nQw6IofW6ZIgUvZJQybuz46UhloPQ99WhtT09Xw2Nv/LmokJztopl3FiULLpR0EiiInIeGvS5QqZEUMLlCluZyWsTxVlxt4mZ4/gza/8F2rHRe+k6Fa8QonAVFnYhwM4Ag9OoQRXUIYqMEC4h0d4cm6cB+fZeZmWZpxZzy78kvP6DdVqkI8=</latexit>

Factorises

<latexit sha1_base64="lVGp7Ji0MjFVeLCfCxGkgQKzvR0=">AAAB6XicbZC7SwNBEMbn4ivGV9TSZjEIFhLuLNTOgI1lFPOAJIS9zVyyZG/v3N0TwpHaxsZCEVv/Izt7S/8BOzePQhM/WPjxfTPszPix4Nq47oeTWVhcWl7JrubW1jc2t/LbO1UdJYphhUUiUnWfahRcYsVwI7AeK6ShL7Dm9y9Gee0OleaRvDGDGFsh7UoecEaNta5vVTtfcIvuWGQevCkUzr/v+dfRJ5bb+fdmJ2JJiNIwQbVueG5sWilVhjOBw1wz0RhT1qddbFiUNETdSseTDsmBdTokiJR90pCx+7sjpaHWg9C3lSE1PT2bjcz/skZigrNWymWcGJRs8lGQCGIiMlqbdLhCZsTAAmWK21kJ61FFmbHHydkjeLMrz0P1uOidFN0rr1AiMFEW9mAfDsGDUyjBJZShAgwCeIAneHb6zqPz4rxOSjPOtGcX/sh5+wG+8pHa</latexit>

<latexit sha1_base64="jB7w6bYS2uqU++JSsivT9YsbTkE=">AAAB+3icbVC7SgNBFJ31GeNrjaXNYBAsJOxaqAhiwMYygnlAsi6zs7PJkJnZZWZWDMvW/oWNhSK2/oidvaU/YOfkUWjigQuHc+7l3nuChFGlHefDmptfWFxaLqwUV9fWNzbtrVJDxanEpI5jFstWgBRhVJC6ppqRViIJ4gEjzaB/MfSbt0QqGotrPUiIx1FX0IhipI3k26WunwX56VnWzW+CDo9DmPh22ak4I8BZ4k5I+fz7nn4dfJKab793whinnAiNGVKq7TqJ9jIkNcWM5MVOqkiCcB91SdtQgThRXja6PYd7RglhFEtTQsOR+nsiQ1ypAQ9MJ0e6p6a9ofif1051dOJlVCSpJgKPF0UpgzqGwyBgSCXBmg0MQVhScyvEPSQR1iauognBnX55ljQOK+5RxblyylUIxiiAHbAL9oELjkEVXIIaqAMM7sADeALPVm49Wi/W67h1zprMbIM/sN5+ANizmKk=</latexit>

:= g

mod p

:= g

mod p

<latexit sha1_base64="X84f1AhVgJVKYmtirsGcAmnKtPs=">AAAB/nicbVC7SgNBFJ31GeNrVaxsBoNgIWHXQkUQIzaWEc0DknWZnZ0kQ2Z2lplZISwLdn6HjYUitn6Hnb2lP2Dn5FFo4oELh3Pu5d57gphRpR3nw5qanpmdm88t5BeXlldW7bX1qhKJxKSCBROyHiBFGI1IRVPNSD2WBPGAkVrQPe/7tVsiFRXRte7FxOOoHdEWxUgbybc3u356dpUdn6RtH2U3QZOLEMa+XXCKzgBwkrgjUjj9vqdfe5+k7NvvzVDghJNIY4aUarhOrL0USU0xI1m+mSgSI9xFbdIwNEKcKC8dnJ/BHaOEsCWkqUjDgfp7IkVcqR4PTCdHuqPGvb74n9dIdOvIS2kUJ5pEeLiolTCoBexnAUMqCdasZwjCkppbIe4gibA2ieVNCO74y5Okul90D4rOpVMoQTBEDmyBbbALXHAISuAClEEFYJCCB/AEnq0769F6sV6HrVPWaGYD/IH19gPQIZm9</latexit>

:= g

mod p

:= g

mod p

<latexit sha1_base64="arChPrw5nSMfy5gFLFuQqu8dGSU=">AAACOHicbVDLSsNAFJ34rPVVHztdBEVoIZTEhYobC7pwZwWrQlPDZDpph04mceZGLCFfJW78DHfixoVF3PoFTlsVXwdmOJxzLjP3+DFnCmz7wRgZHRufmMxN5adnZufmCwuLpypKJKE1EvFInvtYUc4ErQEDTs9jSXHoc3rmd/b7/tkVlYpF4gS6MW2EuCVYwAgGLXmFI+ERS3jKurSk5QK9BhWkQZxdpEVWyrTupp+qamMnKx54TsnSl5t5X07c+cp7hXW7bA9g/iXOB1mvLLs3vWR3r+oV7t1mRJKQCiAcK1V37BgaKZbACKdZ3k0UjTHp4BataypwSFUjHSyemRtaaZpBJPURYA7U7xMpDpXqhr5Ohhja6rfXF//z6gkEO42UiTgBKsjwoSDhJkRmv0WzySQlwLuaYCKZ/qtJ2lhiArrrvC7B+b3yX3K6WXa2yvaxbmMVDZFDK2gNFZGDtlEFHaIqqiGCbtEjekY94854Ml6M12F0xPiYWUI/YLy9A6DysGg=</latexit>

,q,r,fp

(i)

, {sha1(D

),D

}

(i)

,q,r,fp

(i)

, {sha1(D

),D

}

(i)

<latexit sha1_base64="FEw+VbzQksDDjGnPZID99pAyV0c=">AAACHXicbVDLSsNAFJ34tvVRdamLYBFaCCUpoi4FXbhUsCo0IUymk3boZBJmboolBP/BpRs/RTcufODCjfg3TlsX2nrgXg7n3MvMPUHCmQLb/jKmpmdm5+YXFgvFpeWV1dLa+oWKU0log8Q8llcBVpQzQRvAgNOrRFIcBZxeBt2jgX/Zo1KxWJxDP6FehNuChYxg0JJf2hU+sYSvLDdzgV6DCjPVwU5eOfbrVUs3N/ezStcamgwy1suruV8q2zV7CHOSOD+kfFjMH05uXm9P/dKH24pJGlEBhGOlmo6dgJdhCYxwmhfcVNEEky5u06amAkdUednwutzc0UrLDGOpS4A5VH9vZDhSqh8FejLC0FHj3kD8z2umEB54GRNJClSQ0UNhyk2IzUFUZotJSoD3NcFEMv1Xk3SwxAR0oAUdgjN+8iS5qNecvZp9ptPYQiMsoE20jSrIQfvoEJ2gU9RABN2hR/SMXox748l4M95Ho1PGz84G+gPj8xu9UqVL</latexit>

, {sha1(D

),D

}

(k,iv)

, {sha1(D

),D

}

(k,iv)

<latexit sha1_base64="ZOUKEJtTTHQHJVpKQzD5wpwtsJM=">AAACD3icbVDLSgMxFL1T3/VVdSlIsCgVSplxoSIIBTcurdgqtGXIpBkbJpMZkkyxDF26c+OvuFFQxK1bd36DP2H6WGjrgcDJOfeQ3OPFnClt219WZmp6ZnZufiG7uLS8sppbW6+pKJGEVknEI3ntYUU5E7Sqmeb0OpYUhx6nV15w2vevOlQqFolL3Y1pM8Q3gvmMYG0kN7dbCIoNTW9NNGWd3t7xyeCm/DRo+b2CcFVRuMGem8vbJXsANEmcEcmXofJ9t/V8ce7mPhutiCQhFZpwrFTdsWPdTLHUjHDayzYSRWNMAnxD64YKHFLVTAf79NCOUVrIj6Q5QqOB+juR4lCpbuiZyRDrthr3+uJ/Xj3R/lEzZSJONBVk+JCfcKQj1C8HtZikRPOuIZhIZv6KSBtLTLSpMGtKcMZXniS1/ZJzULIrTr6MYIh52IRtKIADh1CGMziHKhC4h0d4gVfrwXqy3qz34WjGGmU24A+sjx/335+A</latexit>

(k, iv):=kdf(n

)

(k, iv):=kdf(n

)

Checks

<latexit sha1_base64="RLsx5kSaLWCbSu7VQ1GzkOIZ7ns=">AAAB8nicbVC7SgNBFL3rM8ZX1NJmMAgWIexaqJ0BG8sI5gGbJcxOZjdDZmeWmVkhLKn9AhsLRWz9Gjt7S3/Azsmj0MQDFw7n3Ms994YpZ9q47oeztLyyurZe2Chubm3v7Jb29ptaZorQBpFcqnaINeVM0IZhhtN2qihOQk5b4eBq7LfuqNJMilszTGmQ4FiwiBFsrOTHlbQSd7GtsFsqu1V3ArRIvBkpX37fs6/KJ613S++dniRZQoUhHGvte25qghwrwwino2In0zTFZIBj6lsqcEJ1kE8ij9CxVXooksqWMGii/p7IcaL1MAltZ4JNX897Y/E/z89MdBHkTKSZoYJMF0UZR0ai8f2oxxQlhg8twUQxmxWRPlaYGPulon2CN3/yImmeVr2zqnvjlWsIpijAIRzBCXhwDjW4hjo0gICEB3iCZ8c4j86L8zptXXJmMwfwB87bD1KVlPs=</latexit>

g, p, g

Generates

<latexit sha1_base64="6QKi0iUSRdEXdh5DUEVx1TK8Ad0=">AAAB8nicbZC7SgNBFIbPxluMt6ilzWAQLJawa6F2BmwsI5gLbEKYncwmQ2Zn1plZISypfQIbC0VsfRo7e0tfwM7JpdDEHwY+/v8c5pwTJpxp43kfTm5peWV1Lb9e2Njc2t4p7u7VtUwVoTUiuVTNEGvKmaA1wwynzURRHIecNsLB5Thv3FGlmRQ3ZpjQdox7gkWMYGOtQHS0e+sqt+cmnWLJK3sToUXwZ1C6+L5nX+4nrXaK762uJGlMhSEcax34XmLaGVaGEU5HhVaqaYLJAPdoYFHgmOp2Nhl5hI6s00WRVPYJgybu744Mx1oP49BWxtj09Xw2Nv/LgtRE5+2MiSQ1VJDpR1HKkZFovD/qMkWJ4UMLmChmZ0WkjxUmxl6pYI/gz6+8CPWTsn9a9q69UgXBVHk4gEM4Bh/OoAJXUIUaEJDwAE/w7Bjn0XlxXqelOWfWsw9/5Lz9AFO8lPo=</latexit>

,q,r,g,p

Generates

<latexit sha1_base64="rIfb2QRZvNh8qFxynCfRJsVP0CI=">AAAB7nicbZC7SwNBEMbnfMb4ilraLAbBIoQ7C7UzYGMZwTwgCcfeZi5Zsrd37O4J4UhtbWOhiK1/j529pf+AnZtHoYkfLPz4vhl2ZoJEcG1c98NZWl5ZXVvPbeQ3t7Z3dgt7+3Udp4phjcUiVs2AahRcYs1wI7CZKKRRILARDK7GeeMOleaxvDXDBDsR7UkeckaNtRrSZyXpD/xC0S27E5FF8GZQvPy+51+lT6z6hfd2N2ZphNIwQbVueW5iOhlVhjOBo3w71ZhQNqA9bFmUNELdySbjjsixdbokjJV90pCJ+7sjo5HWwyiwlRE1fT2fjc3/slZqwotOxmWSGpRs+lGYCmJiMt6ddLlCZsTQAmWK21kJ61NFmbEXytsjePMrL0L9tOydld0bt1ghMFUODuEITsCDc6jANVShBgwG8ABP8OwkzqPz4rxOS5ecWc8B/JHz9gMO/ZO8</latexit>

<latexit sha1_base64="YNxIl9/rxBq8W7tWu672jtOOBL0=">AAACAHicbVC7SgNBFL0bXzG+Vi0sbAaDYBHCroWKIAa0sIxgHpCEZXYySYbMzm5mZoWwpLHxQ2wsFLH1M+zsLf0BOyePQhMPHDiccy8z9/gRZ0o7zoeVmptfWFxKL2dWVtfWN+zNrbIKY0loiYQ8lFUfK8qZoCXNNKfVSFIc+JxW/O7FMK/cUqlYKG50P6KNALcFazGCtbE8e+fSc0/PejLXy8mc8IihMux6dtbJOyOgWeFORPb8+5595T5p0bPf682QxAEVmnCsVM11It1IsNSMcDrI1GNFI0y6uE1rRgocUNVIRgcM0L5xmqgVSkOh0cj9vZHgQKl+4JvJAOuOms6G5n9ZLdatk0bCRBRrKsj4oVbMkQ7RsA3UZJISzftGYCKZ+SsiHSwx0aazjCnBnT55VpQP8+5R3rl2sgUEY6RhF/bgAFw4hgJcQRFKQGAAD/AEz9ad9Wi9WK/j0ZQ12dmGP7DefgC0zZmO</latexit>

:= qr, q,r, n

(k, iv):=kdf(n

)

(k, iv):=kdf(n

)

<latexit sha1_base64="fJ4/dPgClVBk/Af9cgeGIQCoxTQ=">AAAB+XicbVC7TsMwFL0pj5byCjCyWFRITFXCAIyVWBiLoA+1iSLHdVurjhPZTqUq6sB/sHQAIdb+CRt/g9N2gJYjWTo6517d4xMmnCntON9WYWt7Z7dY2ivvHxweHdsnp00Vp5LQBol5LNshVpQzQRuaaU7biaQ4CjlthaP73G+NqVQsFs96klA/wgPB+oxgbaTAtkOPCS/CehiGWWcaJIFdcarOAmiTuCtSqRVmL53i/Kke2F9eLyZpRIUmHCvVdZ1E+xmWmhFOp2UvVTTBZIQHtGuowBFVfrZIPkWXRumhfizNExot1N8bGY6UmkShmcwzqnUvF//zuqnu3/kZE0mqqSDLQ/2UIx2jvAbUY5ISzSeGYCKZyYrIEEtMtCmrbEpw17+8SZrXVfem6jyaNhAsUYJzuIArcOEWavAAdWgAgTG8whu8W5k1sz6sz+VowVrtnMEfWPMflIWWdQ==</latexit>

b ∈ Z

<latexit sha1_base64="SvM76AHFcMOOlESlKxuCHV9/tbY=">AAACDHicbVA9SwNBFNzz2/gVtbRZDIJFCHcWKoIY0MJSwSRCEo69zUuyZG/v2H0nhiO12PhXbCwUsfUH2Nlb+gfs3CQWmjiwMMzM2903QSyFQdd9dyYmp6ZnZufmMwuLS8sr2dW1sokSzaHEIxnpy4AZkEJBCQVKuIw1sDCQUAk6x32/cgXaiEhdYDeGeshaSjQFZ2glP5s78XcODpXP88o3+RrCtb0k1YC6W/NFo5dv+YFNuQV3ADpOvB+SO/q6EZ/5Dzjzs2+1RsSTEBRyyYypem6M9ZRpFFxCL1NLDMSMd1gLqpYqFoKpp4NlenTLKg3ajLQ9CulA/T2RstCYbhjYZMiwbUa9vvifV02wuV9PhYoTBMWHDzUTSTGi/WZoQ2jgKLuWMK6F/SvlbaYZR9tfxpbgja48Tso7BW+34J57uSIlQ8yRDbJJtolH9kiRnJIzUiKc3JJ78kienDvnwXl2XobRCednZp38gfP6DVmQn44=</latexit>

:= n

, retry id,g

:= n

, retry id,g

<latexit sha1_base64="fjeus0cCNcVcB1hDf1MNaz90PJw=">AAAB/nicbVC7SgNBFJ31GeNrVaxsBoNgIWHXQkUQIzaWEc0DknWZnZ0kQ2Z2lplZISwLdn6HjYUitn6Hnb2lP2Dn5FFo4oELh3Pu5d57gphRpR3nw5qanpmdm88t5BeXlldW7bX1qhKJxKSCBROyHiBFGI1IRVPNSD2WBPGAkVrQPe/7tVsiFRXRte7FxOOoHdEWxUgbybc3u356dpUdn6RtP8huUJOLEMa+XXCKzgBwkrgjUjj9vqdfe5+k7NvvzVDghJNIY4aUarhOrL0USU0xI1m+mSgSI9xFbdIwNEKcKC8dnJ/BHaOEsCWkqUjDgfp7IkVcqR4PTCdHuqPGvb74n9dIdOvIS2kUJ5pEeLiolTCoBexnAUMqCdasZwjCkppbIe4gibA2ieVNCO74y5Okul90D4rOpVMoQTBEDmyBbbALXHAISuAClEEFYJCCB/AEnq0769F6sV6HrVPWaGYD/IH19gPQJJm9</latexit>

:= g

mod p

:= g

mod p

<latexit sha1_base64="A7GWngT3epuShDnfz2qQbp+/qeY=">AAACA3icbVDLSsNAFJ34rPUVdacugkWoUEriwsfKggtdVrAPaEOYTCft0MkkzNyIJRTcuPYv3Cgo4tafcOe/uHD6WGjrgQuHc+7l3nv8mDMFtv1lzMzOzS8sZpayyyura+vmxmZVRYkktEIiHsm6jxXlTNAKMOC0HkuKQ5/Tmt89H/i1GyoVi8Q19GLqhrgtWMAIBi155rbwSEF4qtAEegsqSDtYdfp54XUPPDNnF+0hrGnijEnu7Pvhwi6dPpc987PZikgSUgGEY6Uajh2Dm2IJjHDazzYTRWNMurhNG5oKHFLlpsMf+ta+VlpWEEldAqyh+nsixaFSvdDXnSGGjpr0BuJ/XiOB4MRNmYgToIKMFgUJtyCyBoFYLSYpAd7TBBPJ9K0W6WCJCejYsjoEZ/LlaVI9LDpHRfvKzpV20QgZtIP2UB456BiV0CUqowoi6A49ohf0atwbT8ab8T5qnTHGM1voD4yPH06omtc=</latexit>

, hash(n

)

, hash(n

)

Figure 2: MTProto 2.0’s Authorization Protocol.

encryption scheme is the same, but it is use twice

(with different keys) for messages in secret chats.

We stress that peer clients never communicate di-

rectly: messages always go through a server, where

they are stored to permit later retrieval by the recipi-

ent. Cloud chat messages are kept in clear text, while

secret chat messages are encrypted with the peers’

session key, which should be unknown to the server.

5 AUTHORIZATION KEYS

On its ﬁrst run, each Telegram client A must nego-

tiate a long-term secret with a Telegram server S.

Such an authorization key is created through a Difﬁe-

Hellman (DH) exchange, it is never transmitted over

the network, it is used for all subsequent communica-

tion between A and S, and it is almost never changed

(basically, only when the client application is unin-

stalled and installed again).

5.1 Informal Description

The protocol consists of three rounds (Fig. 2):

SECRYPT 2021 - 18th International Conference on Security and Cryptography

188

Round 1. A and S exchange a pair of randomly gen-

erated nonces n

and n

, which are sent along with

all subsequent messages, both in plaintext and in the

encrypted part of each message. Such pair is used to

identify a run of the protocol.

1. A sends a nonce n

to S.

2. S replies with a message that contains n

, a fresh

nonce n

generated by S, a challenge qr < 2

(to prevent DoS attacks against Telegram servers),

which is the product of two primes q and r, and a

list fp

(1)

,.. .,fp

(`)

, with ` > 0, of the ﬁngerprints

of the public keys accepted by S (computed as the

64 lower bits of the SHA-1 of the keys).

Round 2. A decomposes qr into its factors q and r,

and retrieves

the public key pk

(i)

corresponding to

some ﬁngerprint fp

(i)

. It also generates a new 256-bit

random secret nonce n

, which, together with the pub-

lic n

, is used by both parties to derive an ephemeral

symmetric key k and initialization vector iv by hash-

ing some substrings of n

and n

. These data are used

for encrypting the subsequent messages.

3. A serializes (qr,q,r, n

) and encrypts

with pk

(i)

both this serialized data and its hash;

then, it sends n

,q,r,fp

(i)

along with the

encrypted payload to S.

4. S chooses DH parameters g and p and computes

= g

mod p for some random 2048-bit num-

ber a. Then, S serializes (n

,g, p,g

,t), where

t is the server’s current time, and encrypts both

the serialized data and its hash using a temporary

symmetric key k derived from n

and n

. It then

sends n

along with the encrypted payload to A.

Round 3. After deriving (k,iv) using the same algo-

rithm as the server, A decrypts the received message

and checks that the received DH parameters are safe

(see below). Then A computes g

= g

mod p for

some random 2048-bit number b and derives the au-

thorization key k

= g

mod p.

5. A serializes (n

,retry id,g

), where retry id is

0 at the ﬁrst attempt to send this message, and it

is equal to a hash of the previous authorization

key if the server later asks to renegotiate the key

within the same session by generating a new b (the

server might ask the client to do this for the failure

of the uniqueness check performed at the end of

the protocol—see next paragraph). A hashes the

serialized data and encrypts both the hash and the

It is assumed that the server’s public keys are known to

the clients. In practice, they are usually embedded in Tele-

gram’s client apps. Of course, it is possible that a malicious

client embeds a different key without the user to notice.

data with (k,iv). It then sends n

along with

the encrypted payload to S.

6. S derives the shared key k

= g

mod p, then

veriﬁes that k

is unique by comparing a hash of

to the hashes of all authorization keys known

to the server. If the hash is unique, S sends an ac-

knowledgment (n

,hash(n

)) to A, otherwise

S sends an error message.

All the encrypted messages include a SHA1 hash

of the content. According to Telegram’s “Advanced

FAQ” (Telegram, 2021b), such hashes are “irrelevant

for security”, so they are presumably used only an ad-

ditional sanity check for the implementation, and not

as a means of implementing an AEAD (authenticated

encryption with additional data) scheme.

The client is required to check that both p and (p−

1)/2 are prime, that 2

2047

< p < 2

2048

and that g gen-

erates a cyclic subgroup of prime order (p − 1)/2.

Both parties must also verify that 1 < g,g

< p−1.

Telegram also recommends that both the client and

server check that 2

2048−64

≤ g

≤ p − 2

2048−64

Such checks should prevent the use of small sub-

groups and malicious primes, but it has already been

noted that they could be made optional if Telegram

used standardized values (Kobeissi et al., 2017).

5.2 Formalisation in ProVerif

In the formalization of the protocol we made a few

simpliﬁcations: we ignored time (relevant only to cor-

rectly generate message identiﬁers in later communi-

cation, which we do not model because we consider

messages abstractly), retry id (thus modeling explic-

itly only a successful path of execution—failures are

implicitly taken account of by running an unbounded

number of sessions, some of which may not com-

plete), the proof-of-work decomposition of qr (be-

cause DoS attacks are not in our threat model) and,

more importantly, the SHA1 hashes inside the en-

crypted messages. Including such aspects into a sym-

bolic model would signiﬁcantly increase the compu-

tation times required for the automated veriﬁcation,

but it would most likely not allow us to discover more

vulnerabilities. The latter simpliﬁcation, in particu-

lar, does not affect ProVerif’s results (but it improves

veriﬁcation times), because in the symbolic model en-

cryption is already authenticated, so adding a MAC is

not really needed; besides, that aligns with Telegram’s

statement of “irrelevance” of such tags for security.

For this protocol, public-key encryption is mod-

elled in the standard way using a reduction of the

form adec(aenc(x, pk(k)), k) = x, where aenc() is the

encryption function, adec() is the decryption func-

tion and pk(k) is the public key corresponding to pri-

Automated Symbolic Veriﬁcation of Telegram’s MTProto 2.0

189

vate key k. Thus, the message encryption scheme

is assumed to be a secure authentication encryption

scheme. We assume that honest parties behave as

mandated by the protocol, except for the following

misbehaviour: a client may fail to verify that the re-

ceived DH parameters are good, as explained in Sec-

tion 5.1; and the server is allowed to reuse the same

nonce n

in different sessions. Misbehaving processes

are executed in parallel with correct processes.

Weak DH parameters are modelled as in (Bharga-

van et al., 2017). The generation of (possibly weak)

DH parameters is delegated to two parallel processes

as explained below. A weak calculation always re-

turns the same element, thus conservatively modeling

subgroups of size 1. Each computation involving a

weak group or a bad element is reduced to the same

bad value. It is worth stressing that other equalities

that hold in groups are not modelled, although this

model is stronger than the Difﬁe-Hellman assump-

tion, in the sense that is impossible to compute g

given only generator g, g

and g

Process macros are interleaved with event mark-

ers (“event P(~x)” for some predicate P(~x)), which can

be used to check whether a certain point in a pro-

cess is reachable—hence, whether a certain event has

happened. That allows us to specify some stringent

correspondences (see Section 5.3). Events are also

used to signal when a secret is compromised. Leaking

information is modelled via several short processes

that run in parallel with the clients and the server.

For instance, compromising the server’s private key

is achieved by running a process that receives the

server’s private key from the server through a private

channel c

priv

and makes it accessible to the attacker

through the public channel c, recording the event:

let LeakRSAKey() =

in(c

priv

,k : PrivKey);

event CompromisedRSAKey(k);

out(c,k).

Similar parallel processes are executed to perform the

following functions and emit the corresponding event:

• CompromisedNonce(n

): leaking the secret

nonce n

generated by the client during a session;

• PostCompromisedNonce(n

): revealing n

after

the protocol is completed;

• PostCompromisedRSAKey(k): revealing the ser-

ver’s private key k after the protocol is completed;

• PostCompromisedAuthKey(k): revealing the au-

thorization key k after the protocol is completed

(to test forward secrecy);

• ForgedServerIdentity(S): associating the server’s

identity S to a private key chosen by the attacker.

Other four parallel processes are responsible for gen-

erating a random or ﬁxed server nonce n

, respec-

tively, and for generating good or bad DH parame-

ters, respectively, on behalf of the server (by commu-

nicating with the server through private channels). In

general, we found that using a higher number of rel-

atively simple processes rather than a smaller number

of parametrized processes with a more complex logic

allows ProVerif to perform much better, and gives the

user more ﬂexibility in expressing queries.

5.3 Security Properties Veriﬁcation

Authentication. The protocol for generating an au-

thorization key does not prevent an intruder to act as a

MitM during a registration session between a client A

and a server S and impersonate A in subsequent ex-

changes with S. In other words, the protocol does

not guarantee the authentication of the client to the

server—which is expected, as the server is willing to

run the protocol with any entity. This is formalized

with the following query:

query n

: Nonce, n

: Nonce;

event(ServerAcceptsClient(n

))

⇒ event(ClientRequestsDHParameters(n

)),

for which ProVerif can ﬁnd a counterexample even

when the protocol is run correctly and without any

information leak. The query asserts that, if the server

accepts a client in a session identiﬁed by (n

), then

it was that client who started session (n

) —which

may not be the case, because an attacker can take over

after the ﬁrst round and replace the legitimate client.

Failing authentication should not adversely affect

the outcome of a session (except that A must possibly

restart the protocol in a new session). The only result

the intruder could achieve is a negotiation of an au-

thorization key with S, unrelated to A. Vice versa, it

is important that A knows with certainty that she has

engaged with S and not with an attacker. Authentica-

tion of the server to the client is proved by ProVerif;

the relevant query is the following:

query sk

: PrivKey, n

: Nonce, g,g

: G

inj-event(ClientReceivesDHParameters(n

,g, g

))

⇒ inj-event(ServerSendsDHParameters(n

,g, g

))

∨ event(CompromisedRSAKey(sk

))

∨ event(CompromisedNonce(n

))

∨ event(ForgedServerIdentity()).

The query is interpreted as follows: unless S’s private

key sk

is compromised before or during the session

identiﬁed by (n

), or the secret nonce n

is leaked

SECRYPT 2021 - 18th International Conference on Security and Cryptography

190

during the session, or the server’s identity is forged to

begin with (e.g., the client embeds a spoofed public

key), if A accepts Difﬁe-Hellman parameters (g,g

)

in session (n

) after sending n

then A is sure that

it was the server who accepted n

and sent (g,g

) in

session (n

). This holds even if the server reuses

in different sessions, because only S can decrypt n

and derive the ephemeral key with which DH param-

eters are transmitted. Note that, since authentication

events are registered before A veriﬁes the values re-

ceived from S, for authentication it does not mat-

ter whether the client checks that DH parameters are

strong or weak. The last disjunct reﬂects the fact that

Telegram, as is common for current messenger apps,

is based on a Trust-On-First-Use (TOFU) authentica-

tion infrastructure.

Secrecy and Forward Secrecy. The authorization

protocol provides secrecy for so called “cloud mes-

sages”, i.e, the messages subsequently exchanged be-

tween the client and the server, which are encrypted

using the shared authorization key. Namely, ProVerif

proves the following query:

query sk

: PrivKey,k : SharedKey,n

: Nonce, m : Msg;

attacker(m)

⇒ event(CompromisedRSAKey(sk

))

∨ event(ForgedServerIdentity())

∨ event(CompromisedNonce(n

))

∨ event(ChecksDHParameters(⊥))

∨ event(PostCompromisedAuthKey(k)).

In words, under the assumptions of our model, the

secrecy of message m is guaranteed unless:

1. the server’s private key is compromised or its

identity is forged before or during the session that

establishes the shared authorization key, or

2. the secret nonce n

generated by the client is

leaked during such a session (in particular, if the

attacker learns n

before the fourth message then

it can compute (k,iv) and act as a MitM to estab-

lish two distinct authorization keys with the client

and the server, respectively), or

3. the client fails to validate the DH parameters re-

ceived from the server, or

4. the authorization key is compromised at any later

time.

This result holds even if the server reuses the same

nonce n

in multiple sessions with different clients.

Besides, the result is strict, in the sense that remov-

ing any event from the query above leads to a coun-

terexample. Since in our formalization the private

key of the server and the secret nonce n

are always

leaked in a separate phase following the completion of

the authorization protocol (so that the impact of such

leakage of information can be formally assessed), we

may also conclude that leaking the server’s key or

the secret nonce after a session has been completed

does not violate the secrecy of subsequent client-

server communication encrypted with the authoriza-

tion key. Intuitively, this holds because, even if such

post-compromise allows an attacker to decrypt all the

messages exchanged during the deﬁnition of the au-

thorization key, she cannot compute the authorization

key knowing only g, m, g

, g

(assuming that the DH

problem is hard). Note also that case 4 above means

that there is no guarantee of forward secrecy for mes-

sages encrypted with an authorization key.

After two clients have negotiated their authoriza-

tion keys with a server, they may start to exchange

messages within so-called cloud-based chats. Ev-

ery such message is encrypted by the sender using

the sender’s authorization key and forwarded to the

server, who deciphers it and re-encrypts it with the re-

cipient’s authorization key. In this context, the server

can trivially read (and even modify) every message.

The previous result shows that, under the hypothesis

that the server is trusted, communication can at least

be kept secret against an external attacker. Cloud-

based chats do not provide forward secrecy, though:

if, at any time, the authorization key of one of the

clients is leaked then all the messages exchanged by

that client can be deciphered.

Integrity. Key agreement, a basic property of

Difﬁe-Hellman, can be proved by ProVerif, using the

following query:

query n

: Nonce, k,k

: SharedKey, sk

: PrivKey;

event(ServerAcceptsAuthKey(n

,k))

∧ event(ClientAcceptsAuthKey(n

))

⇒ k = k

∨ event(ClientChecksDHParameters(⊥))

∨ event(ForgedServerIdentity())

∨ event(CompromisedNonce(n

))

∨ event(CompromisedRSAKey(sk

)).

If client and server generate authorization keys k

and k

during the same session identiﬁed by (n

then they compute the same key, unless the client fails

to validate the DH parameters, the server’s identity is

forged, or some secret is leaked during the session.

Conversely, if client and server end a run of the

protocol agreeing on the same key in their respective

sessions, then such sessions coincide, unless the client

skips its mandatory checks. That is, the following

query is proved by ProVerif:

Automated Symbolic Veriﬁcation of Telegram’s MTProto 2.0

191

query n

: Nonce, k : SharedKey;

event(ServerAcceptsAuthKey(n

,k))

∧ event(ClientAcceptsAuthKey(n

,k))

⇒ (n

= n

∧ n

= n

)

∨ event(ClientChecksDHParameters(⊥)).

The last disjunct accounts for the fact that, if the

server sends the same bad DH parameters to a client

and to the attacker (acting as a malicious client) in two

separate sessions and the honest client does not reject

them, then the client, the attacker and the server may

end up with the same key.

6 SECRET CHATS

An end-to-end encrypted chat between two clients

A and B can be established after negotiating a ses-

sion key k through a Difﬁe-Hellman exchange using

server S as a forwarder. Each message exchanged be-

tween A and B is encrypted with k by the sender, then

the resulting ciphertext c is in turn encrypted with the

sender’s long-term authorization key (see Section 5)

and sent to S. Both layers use a similar encryption

scheme, which we treat symbolically as a crypto-

graphic primitive. Upon receiving a message, S uses

the sender’s authorization key, identiﬁed by 64-bit key

ﬁngerprint prepended to the message, to decipher the

encrypted payload and recover the ciphertext c, which

is then encrypted again with the receiver’s authoriza-

tion key and forwarded to the receiver.

6.1 Informal Description

The protocol, shown in Fig. 3, is as follows:

1. initiator A obtains DH parameters (g, p) from S,

generates a random session identiﬁer id and a

half-key g

, and requests to start an encrypted chat

with B, including id and g

in the message;

2. after B has accepted the request, B receives the

DH parameters from S and computes a half-

key g

, the session key k and a 64-bit ﬁnger-

print hash(k) of the key. The values g

and

hash(k) are then sent to A, who can compute k as

well. The ﬁngerprint hash(k) is not cryptograph-

ically strong: its stated purpose is only to prevent

certain bugs in software implementations, espe-

cially during development.

This exchange is unauthenticated, so it is trivial for

the server to act as a MitM and establish two different

keys with A and B, respectively. To detect such at-

tacks, after the DH exchange is completed, the clients

<latexit sha1_base64="+4mb1g+e8FRNac5hQLAafJb6p6k=">AAACDHicbVC7SgNBFJ31GeMraqnFYhC0CbsWamdEi5QRjQrZEGYnd+OQ2dll5q4YlrUVG39B8AdsLBSx9QPs/AD/wsJJYuHrwMDhnHO5c48fC67Rcd6soeGR0bHx3ER+cmp6ZrYwN3+ko0QxqLFIROrEpxoEl1BDjgJOYgU09AUc+53dnn98BkrzSB5iN4ZGSNuSB5xRNFKzUPRSD+EcdZC2AfcqLJIBb2era17WTDvNdOcgy0zKKTl92H+J+0WK2x835dvLi/dqs/DqtSKWhCCRCap13XVibKRUIWcCsryXaIgp69A21A2VNATdSPvHZPaKUVp2ECnzJNp99ftESkOtu6FvkiHFU/3b64n/efUEg61GymWcIEg2WBQkwsbI7jVjt7gChqJrCGWKm7/a7JQqytD0lzcluL9P/kuO1kvuRsnZd4rlJTJAjiySZbJKXLJJyqRCqqRGGLkid+SBPFrX1r31ZD0PokPW18wC+QHr5RPGHqBs</latexit>

{getDHconﬁg()}

<latexit sha1_base64="Y6Lwkn9y9Zj7kinWplvmshUeaPg=">AAAB+XicbVDLSgMxFM3UV62vUZe6CBbBhZQZF+rOihuXFe0DOsOQSdM2NJMZkkyhhHHrTwiioIhb/8SdH+BfuDB9LLT1wIXDOfdy7z1hwqhUjvNp5ebmFxaX8suFldW19Q17c6sm41RgUsUxi0UjRJIwyklVUcVIIxEERSEj9bB3MfTrfSIkjfmNGiTEj1CH0zbFSBkpsG1Pdw4TLwt0L9Dn11kW2EWn5IwAZ4k7IcWz74fy093tVyWwP7xWjNOIcIUZkrLpOonyNRKKYkaygpdKkiDcQx3SNJSjiEhfjy7P4L5RWrAdC1NcwZH6e0KjSMpBFJrOCKmunPaG4n9eM1XtU19TnqSKcDxe1E4ZVDEcxgBbVBCs2MAQhAU1t0LcRQJhZcIqmBDc6ZdnSe2o5B6XnCunWN4FY+TBDtgDB8AFJ6AMLkEFVAEGfXAPnsGLpa1H69V6G7fmrMnMNvgD6/0H4OeYLA==</latexit>

{g, p}

<latexit sha1_base64="TLom0Ft4I8k4OFgfDyWlxFQB/PU=">AAACGXicbVDLSgMxFM34rPVVdamLwSJUKGXGhbqz6MZlRfuAThkyaaYNzTxIMmIJcesfuHEh+B1uXCjiUld+gH/hwnTahbYeCJyccw/JPV5MCReW9WlMTc/Mzs1nFrKLS8srq7m19RqPEoZwFUU0Yg0PckxJiKuCCIobMcMw8Ciue72TgV+/xIyTKLwQ/Ri3AtgJiU8QFFpyc5YjHYGvdFKStip2XK+Y3rkvu5B3VaG3qxzlyp505fG5UsrN5a2SlcKcJPaI5I++78sPN9dfFTf37rQjlAQ4FIhCzpu2FYuWhEwQRLHKOgnHMUQ92MFNTUMYYN6S6WbK3NFK2/Qjpk8ozFT9nZAw4LwfeHoygKLLx72B+J/XTIR/2JIkjBOBQzR8yE+oKSJzUJPZJgwjQfuaQMSI/quJupBBJHSZWV2CPb7yJKntlez9knVm5ctbYIgM2ATboABscADK4BRUQBUgcAsewTN4Me6MJ+PVeBuOThmjzAb4A+PjB+LGpnQ=</latexit>

{id,g

, hash(k)}

{id,g

, hash(k)}

<latexit sha1_base64="QeEK18i4CBbiCcAjF5q6y2UAv6s=">AAACC3icbVC7TsMwFHXKq5RXgBGGqBUSQ1UlDMBGKQtjEfQhNVXkOE5r1XnIdhCVFVZY+AYkPoCFAYRY+QE2PoC/YMB9DNByJEtH59yj63vcmBIuTPNTy8zMzs0vZBdzS8srq2v6+kadRwlDuIYiGrGmCzmmJMQ1QQTFzZhhGLgUN9zeycBvXGLGSRReiH6M2wHshMQnCAolOXrelrbAVyopiZcWj4uVYseBdurInnRk5TxNU0cvmCVzCGOaWGNSOPq+Lz/cXH9VHf3D9iKUBDgUiELOW5YZi7aETBBEcZqzE45jiHqwg1uKhjDAvC2Ht6TGjlI8w4+YeqEwhurvhIQB5/3AVZMBFF0+6Q3E/7xWIvzDtiRhnAgcotEiP6GGiIxBMYZHGEaC9hWBiBH1VwN1IYNIqPpyqgRr8uRpUt8rWfsl88wslLfBCFmwBfJgF1jgAJTBKaiCGkDgFjyCZ/Ci3WlP2qv2NhrNaOPMJvgD7f0HoF2fxw==</latexit>

{id, A, B, g

}

{id, A, B, g

}

<latexit sha1_base64="Mrr77AYg8NKaaY+4ZnQ2J02qne4=">AAAB+XicbVC7SgNBFJ2Nrxhfq5Y2g0GwkLBroSKIARvLCOYBybrMzk6SIfNYZmYDYUntT9hYKGLrn9jZW/oDdk4ehSYeuHA4517uvSdKGNXG8z6c3MLi0vJKfrWwtr6xueVu79S0TBUmVSyZVI0IacKoIFVDDSONRBHEI0bqUe9q5Nf7RGkqxa0ZJCTgqCNom2JkrBS6bu/8IuuEaHgXtbiMYRK6Ra/kjQHniT8lxcvve/p19EkqofveiiVOOREGM6R10/cSE2RIGYoZGRZaqSYJwj3UIU1LBeJEB9n48iE8sEoM21LZEgaO1d8TGeJaD3hkOzkyXT3rjcT/vGZq2mdBRkWSGiLwZFE7ZdBIOIoBxlQRbNjAEoQVtbdC3EUKYWPDKtgQ/NmX50ntuOSflLwbr1iGYII82AP74BD44BSUwTWogCrAoA8ewBN4djLn0XlxXietOWc6swv+wHn7AQtxl6A=</latexit>

k := g

mod p

k := g

mod p

Client A Client BServer S

Knows

<latexit sha1_base64="D1NLhdtN9q/azok7iop9GzBJ3KE=">AAAB7XicbZDLSgMxFIbP1Futt6o73QSL4KrMuFB3VnThsqK9QDuUTJppYzPJkGSEMvQd3LhQxK0P4Vu4EHwOdW96WWj1h8DH/59DzjlBzJk2rvvuZGZm5+YXsou5peWV1bX8+kZVy0QRWiGSS1UPsKacCVoxzHBajxXFUcBpLeidDvPaDVWaSXFl+jH1I9wRLGQEG2tVe6305HLQyhfcojsS+gveBArHH29fZy9bn+VW/rXZliSJqDCEY60bnhsbP8XKMMLpINdMNI0x6eEObVgUOKLaT0fTDtCuddoolMo+YdDI/dmR4kjrfhTYygibrp7OhuZ/WSMx4ZGfMhEnhgoy/ihMODISDVdHbaYoMbxvARPF7KyIdLHCxNgD5ewRvOmV/0J1v+gdFN0Lt1BCMFYWtmEH9sCDQyjBOZShAgSu4Rbu4cGRzp3z6DyNSzPOpGcTfsl5/gY3/pP1</latexit>

Knows

<latexit sha1_base64="caEAM8JVGXLnJQauxGjwbff08ig=">AAAB7XicbZDLSgMxFIbP1Futt6o73QSL4KrMuFB3FnXhsqK9QDuUTJppYzPJkGSEMvQd3LhQxK0P4Vu4EHwOdW96WWj1h8DH/59DzjlBzJk2rvvuZGZm5+YXsou5peWV1bX8+kZVy0QRWiGSS1UPsKacCVoxzHBajxXFUcBpLeidDvPaDVWaSXFl+jH1I9wRLGQEG2tVe6305HLQyhfcojsS+gveBArHH29fZy9bn+VW/rXZliSJqDCEY60bnhsbP8XKMMLpINdMNI0x6eEObVgUOKLaT0fTDtCuddoolMo+YdDI/dmR4kjrfhTYygibrp7OhuZ/WSMx4ZGfMhEnhgoy/ihMODISDVdHbaYoMbxvARPF7KyIdLHCxNgD5ewRvOmV/0J1v+gdFN0Lt1BCMFYWtmEH9sCDQyjBOZShAgSu4Rbu4cGRzp3z6DyNSzPOpGcTfsl5/gY5hJP2</latexit>

<latexit sha1_base64="GK3wQiHi8ZN9pIGAjAooXdDsUl0=">AAAB+XicbVC7TsMwFL0pj5byCjCyWFRITFXCAIyVWBiLoA+1iSLHdVurjhPZTqUq6sB/sHQAIdb+CRt/g9N2gJYjWTo6517d4xMmnCntON9WYWt7Z7dY2ivvHxweHdsnp00Vp5LQBol5LNshVpQzQRuaaU7biaQ4CjlthaP73G+NqVQsFs96klA/wgPB+oxgbaTAtkOPCS/CehiGWWcaJIFdcarOAmiTuCtSqRVmL53i/Kke2F9eLyZpRIUmHCvVdZ1E+xmWmhFOp2UvVTTBZIQHtGuowBFVfrZIPkWXRumhfizNExot1N8bGY6UmkShmcwzqnUvF//zuqnu3/kZE0mqqSDLQ/2UIx2jvAbUY5ISzSeGYCKZyYrIEEtMtCmrbEpw17+8SZrXVfem6jy6lRqCJUpwDhdwBS7cQg0eoA4NIDCGV3iDdyuzZtaH9bkcLVirnTP4A2v+A5TVlnY=</latexit>

b ∈ Z

<latexit sha1_base64="WXinkgCWKkUWOH6Ur9rnFbZ7eRU=">AAAB9XicbVC7SgNBFJ31GeMramkzGAQLCbsWKoIYsLGMYB6QbMLs7OxmyDyWmVklLKn9BRsLRWz9Fzt7S3/Azsmj0MQDFw7n3Mu99wQJo9q47oczN7+wuLScW8mvrq1vbBa2tmtapgqTKpZMqkaANGFUkKqhhpFGogjiASP1oHc59Ou3RGkqxY3pJ8TnKBY0ohgZK7XjTnB2HreDFpchTDqFoltyR4CzxJuQ4sX3Pf06/CSVTuG9FUqcciIMZkjrpucmxs+QMhQzMsi3Uk0ShHsoJk1LBeJE+9no6gHct0oII6lsCQNH6u+JDHGt+zywnRyZrp72huJ/XjM10amfUZGkhgg8XhSlDBoJhxHAkCqCDetbgrCi9laIu0ghbGxQeRuCN/3yLKkdlbzjknvtFcsQjJEDu2APHAAPnIAyuAIVUAUYKPAAnsCzc+c8Oi/O67h1zpnM7IA/cN5+AMEalmE=</latexit>

:= g

mod p

:= g

mod p

<latexit sha1_base64="/WRjc1hXhi6roBaUQoqN2sefyKQ=">AAAB+XicbVC7TsMwFL0pj5byCjCyWFRITFXCAIyVWBiLoA+1iSLHdVurjhPZTqUq6sB/sHQAIdb+CRt/g9N2gJYjWTo6517d4xMmnCntON9WYWt7Z7dY2ivvHxweHdsnp00Vp5LQBol5LNshVpQzQRuaaU7biaQ4CjlthaP73G+NqVQsFs96klA/wgPB+oxgbaTAtrHHhBdhPQzDrDMNksCuOFVnAbRJ3BWp1Aqzl05x/lQP7C+vF5M0okITjpXquk6i/QxLzQin07KXKppgMsID2jVU4IgqP1skn6JLo/RQP5bmCY0W6u+NDEdKTaLQTOYZ1bqXi/953VT37/yMiSTVVJDloX7KkY5RXgPqMUmJ5hNDMJHMZEVkiCUm2pRVNiW461/eJM3rqntTdR7dSg3BEiU4hwu4AhduoQYPUIcGEBjDK7zBu5VZM+vD+lyOFqzVzhn8gTX/AZNClnU=</latexit>

a ∈ Z

<latexit sha1_base64="T6W6VjTx9Kj8va52xmom0PLdIaY=">AAAB9XicbVC7SgNBFJ31GeMramkzGAQLCbsWKoIYsLGMYB6QbMLs7OxmyDyWmVklLKn9BRsLRWz9Fzt7S3/Azsmj0MQDFw7n3Mu99wQJo9q47oczN7+wuLScW8mvrq1vbBa2tmtapgqTKpZMqkaANGFUkKqhhpFGogjiASP1oHc59Ou3RGkqxY3pJ8TnKBY0ohgZK7XjDjo7j9uoxWUIk06h6JbcEeAs8SakePF9T78OP0mlU3hvhRKnnAiDGdK66bmJ8TOkDMWMDPKtVJME4R6KSdNSgTjRfja6egD3rRLCSCpbwsCR+nsiQ1zrPg9sJ0emq6e9ofif10xNdOpnVCSpIQKPF0Upg0bCYQQwpIpgw/qWIKyovRXiLlIIGxtU3obgTb88S2pHJe+45F57xTIEY+TALtgDB8ADJ6AMrkAFVAEGCjyAJ/Ds3DmPzovzOm6dcyYzO+APnLcfvgGWXw==</latexit>

:= g

mod p

:= g

mod p

Generates id

<latexit sha1_base64="6v7lUnJatLGFkJNSSRiWmouLsvA=">AAAB+XicbVC7SgNBFJ2Nrxhfq5Y2g0GwkLBroSKIARvLCOYBybrMzk6SIfNYZmYDYUntT9hYKGLrn9jZW/oDdk4ehSYeuHA4517uvSdKGNXG8z6c3MLi0vJKfrWwtr6xueVu79S0TBUmVSyZVI0IacKoIFVDDSONRBHEI0bqUe9q5Nf7RGkqxa0ZJCTgqCNom2JkrBS6bu/8IuuE0fAOtbiMYRK6Ra/kjQHniT8lxcvve/p19EkqofveiiVOOREGM6R10/cSE2RIGYoZGRZaqSYJwj3UIU1LBeJEB9n48iE8sEoM21LZEgaO1d8TGeJaD3hkOzkyXT3rjcT/vGZq2mdBRkWSGiLwZFE7ZdBIOIoBxlQRbNjAEoQVtbdC3EUKYWPDKtgQ/NmX50ntuOSflLwbr1iGYII82AP74BD44BSUwTWogCrAoA8ewBN4djLn0XlxXietOWc6swv+wHn7AQt0l6A=</latexit>

k := g

mod p

k := g

mod p

Checks

<latexit sha1_base64="yyLe5i50oRF3XlqHKIS+DnUED14=">AAAB+XicbVDJSgNBEK2JW4zbqEdBGoMQL2HGg3oMePGYiFkgCaGn05M06VnorgmGIUf/wosHRbx68Tu8+Q3+hJ3loIkPCh7vVVFVz4ul0Og4X1ZmZXVtfSO7mdva3tnds/cPajpKFONVFslINTyquRQhr6JAyRux4jTwJK97g+uJXx9ypUUU3uEo5u2A9kLhC0bRSB3bbiG/R+2nfar748LgrGPnnaIzBVkm7pzkS1D5fjj+uC137M9WN2JJwENkkmrddJ0Y2ylVKJjk41wr0TymbEB7vGloSAOu2+n08jE5NUqX+JEyFSKZqr8nUhpoPQo80xlQ7OtFbyL+5zUT9K/aqQjjBHnIZov8RBKMyCQG0hWKM5QjQyhTwtxKWJ8qytCElTMhuIsvL5PaedG9KDoVkwaBGbJwBCdQABcuoQQ3UIYqMBjCIzzDi5VaT9ar9TZrzVjzmUP4A+v9B890lqU=</latexit>

hash(k)

<latexit sha1_base64="LFHyKmsW8BPbPQmveX5PZGD9AuQ=">AAACGnicbVC7SgNBFJ2NrxhfUUstFoMQIYRdC7UzamMZ0TwgG5bZ2dlkyOyDmVkxDGvrJ9gIgv9hY6GIndj4Af6FhZNNCk08MHA45x7u3ONElHBhGJ9aZmp6ZnYuO59bWFxaXsmvrtV5GDOEayikIWs6kGNKAlwTRFDcjBiGvkNxw+mdDPzGJWachMGF6Ee47cNOQDyCoFCSnTctaQl8pZKSuEnpuNSxnVKqcE92Ie8mxd5OYiW27ElbHp0niZ0vGGUjhT5JzBEpHH7fVx5urr+qdv7dckMU+zgQiELOW6YRibaETBBEcZKzYo4jiHqwg1uKBtDHvC3T0xJ9Wymu7oVMvUDoqfo7IaHPed931KQPRZePewPxP68VC++gLUkQxQIHaLjIi6kuQn3Qk+4ShpGgfUUgYkT9VUddyCASqs2cKsEcP3mS1HfL5l7ZODMKlU0wRBZsgC1QBCbYBxVwCqqgBhC4BY/gGbxod9qT9qq9DUcz2iizDv5A+/gB9vWmbg==</latexit>

{id,B,g

, hash(k)}

{id,B,g

, hash(k)}

<latexit sha1_base64="hBlvQEwwvr2gL+bJihU3yvafmDo=">AAACCXicbVC7SgNBFJ2NrxhfUUstBoNgEcKuhdoZtbGMaB6QXZbZyWwyZPbBzKwYhrXUwo8QrG0sFLH1D+z8AP/Cwsmj0MQDA4dz7uHOPV7MqJCm+WlkpqZnZuey87mFxaXllfzqWk1ECcekiiMW8YaHBGE0JFVJJSONmBMUeIzUve5J369fEi5oFF7IXkycALVD6lOMpJbcPLSVLcmVTiraSovHxbaL7NRVXeWqo/M0Td18wSyZA8BJYo1I4fD7vvxwe/1VcfMfdivCSUBCiRkSommZsXQU4pJiRtKcnQgSI9xFbdLUNEQBEY4aXJLCba20oB9x/UIJB+rvhEKBEL3A05MBkh0x7vXF/7xmIv0DR9EwTiQJ8XCRnzAoI9ivBbYoJ1iyniYIc6r/CnEHcYSlLi+nS7DGT54ktd2StVcyz8xCeRMMkQUbYAvsAAvsgzI4BRVQBRjcgEfwDF6MO+PJeDXehqMZY5RZB39gvP8Am5efRQ==</latexit>

{id,B,g

}

{id,B,g

}

Knows

<latexit sha1_base64="xLWESuElD6R+FcBLPcdI3PViZRQ=">AAAB9HicbVC7TsMwFHV4lvIqMLJYVEgMVZUwABsFFsai0ofURpXj3rRWHSfYTqUqyswnsDCAECsfw8bOyA+w4T4GaDnS1T065175+ngRZ0rb9oe1sLi0vLKaWcuub2xubed2dmsqjCWFKg15KBseUcCZgKpmmkMjkkACj0Pd61+N/PoApGKhuNXDCNyAdAXzGSXaSG6/nVxU0oJpl5W0ncvbRXsMPE+cKcmff9+zr8InlNu591YnpHEAQlNOlGo6dqTdhEjNKIc024oVRIT2SReahgoSgHKT8dEpPjRKB/uhNCU0Hqu/NxISKDUMPDMZEN1Ts95I/M9rxto/cxMmoliDoJOH/JhjHeJRArjDJFDNh4YQKpm5FdMekYRqk1PWhODMfnme1I6LzknRvnHyJYwmyKB9dICOkINOUQldozKqIoru0AN6Qs/WwHq0XqzXyeiCNd3ZQ39gvf0AczeWPg==</latexit>

<latexit sha1_base64="PYLyx16l3AUTWW1GyeFUsRT6n4U=">AAACEnicbVC7SgNBFJ31GeMraqnFYhAUJOxaqJ0RG0tFo0J2WWYns2bY2Qczd8UwrK2ljb3gP9hYKGJrZecH+BcWTjYpNHrgXg7n3MvMPX7KmQTL+jCGhkdGx8ZLE+XJqemZ2crc/IlMMkFogyQ8EWc+lpSzmDaAAadnqaA48jk99cO9rn96QYVkSXwMnZS6ET6PWcAIBi15lTVHOUAvQQaqjWU7Xw3X1h0VObmnwrzoylO7R3mee5WqVbMKmH+J3SfVna+7+v311eeBV3l3WgnJIhoD4VjKpm2l4CosgBFO87KTSZpiEuJz2tQ0xhGVripOys0VrbTMIBG6YjAL9eeGwpGUncjXkxGGthz0uuJ/XjODYNtVLE4zoDHpPRRk3ITE7OZjtpigBHhHE0wE0381SRsLTECnWNYh2IMn/yUnGzV7s2YdWtX6EuqhhBbRMlpFNtpCdbSPDlADEXSDHtATejZujUfjxXjtjQ4Z/Z0F9AvG2zdE9qN4</latexit>

{hash(k), {m}

}

{hash(k), {m}

}

<latexit sha1_base64="0TYYbHKfQYuTpC6jdWfGdF3SI8I=">AAACEnicbVC7SgNBFJ31GeMraqnFYhAUJOxaqJ1BG0tFo0J2WWYns2bY2Qczd8UwrK2ljb3gP9hYKGJrZecH+BcWTjYpNHrgXg7n3MvMPX7KmQTL+jCGhkdGx8ZLE+XJqemZ2crc/IlMMkFogyQ8EWc+lpSzmDaAAadnqaA48jk99cO9rn96QYVkSXwMnZS6ET6PWcAIBi15lTVHOUAvQQaqjWU7Xw3X1h0VObmnwrzoylO7R3mee5WqVbMKmH+J3SfVna+7+v311eeBV3l3WgnJIhoD4VjKpm2l4CosgBFO87KTSZpiEuJz2tQ0xhGVripOys0VrbTMIBG6YjAL9eeGwpGUncjXkxGGthz0uuJ/XjODYNtVLE4zoDHpPRRk3ITE7OZjtpigBHhHE0wE0381SRsLTECnWNYh2IMn/yUnGzV7s2YdWtX6EuqhhBbRMlpFNtpCdbSPDlADEXSDHtATejZujUfjxXjtjQ4Z/Z0F9AvG2zdGfqN5</latexit>

{hash(k), {m}

}

{hash(k), {m}

}

Checks

g, p, g

Checks

g, p, g

<latexit sha1_base64="OqVNC2nJqoxijByLOu794Cr+wg4=">AAAB+XicbVA9SwNBEN3z2/h1ammzGAQLCXcWamfAxkZQMImQC2FvMxcXd/eO3blgOFL7J2wsFLH1n9jZW/oH7NwkFn49GHi8N8PMvDiTwmIQvHoTk1PTM7Nz86WFxaXlFX91rW7T3HCo8VSm5iJmFqTQUEOBEi4yA0zFEhrx1dHQb/TAWJHqc+xn0FKsq0UiOEMntX1fRUJHCNdok+LEdgdtvxxUghHoXxJ+kfLhx41433mD07b/EnVSnivQyCWzthkGGbYKZlBwCYNSlFvIGL9iXWg6qpkC2ypGlw/ollM6NEmNK410pH6fKJiytq9i16kYXtrf3lD8z2vmmBy0CqGzHEHz8aIklxRTOoyBdoQBjrLvCONGuFspv2SGcXRhlVwI4e+X/5L6biXcqwRnYblKyRhzZINskm0Skn1SJcfklNQIJz1yS+7Jg1d4d96j9zRunfC+ZtbJD3jPn0ZYmG0=</latexit>

m ∈ Msg

Out-of-band

comparison of

<latexit sha1_base64="Ko9os4QvTbkIugEyV2dCsqrkx34=">AAAB6HicbZC7SgNBFIbPxluMt3jpbAaDYBV2LdTOgIWWCZgLJCHMTs4mY2Znl5lZIS55AhsLRWzF2oexs/RNnFwKjf4w8PH/5zDnHD8WXBvX/XQyC4tLyyvZ1dza+sbmVn57p6ajRDGsskhEquFTjYJLrBpuBDZihTT0Bdb9wcU4r9+i0jyS12YYYzukPckDzqixVmXQyRfcojsR+QveDArnb3dfl+97abmT/2h1I5aEKA0TVOum58amnVJlOBM4yrUSjTFlA9rDpkVJQ9TtdDLoiBxap0uCSNknDZm4PztSGmo9DH1bGVLT1/PZ2PwvayYmOGunXMaJQcmmHwWJICYi461JlytkRgwtUKa4nZWwPlWUGXubnD2CN7/yX6gdF72TolvxCiUCU2VhHw7gCDw4hRJcQRmqwADhHh7hyblxHpxn52VamnFmPbvwS87rN9hykJE=</latexit>

<latexit sha1_base64="qcmSsKE8qR7qNkwdnw4x1L0Vc2o=">AAAB+XicbVDLSgMxFM3UV62vUZe6CBbBhZQZF+rOohuXFe0DOsOQSdM2NJMZkkyhhHHrTwiioIhb/8SdH+BfuDB9LLT1wIXDOfdy7z1hwqhUjvNp5ebmFxaX8suFldW19Q17c6sm41RgUsUxi0UjRJIwyklVUcVIIxEERSEj9bB3MfTrfSIkjfmNGiTEj1CH0zbFSBkpsG1Pdw4TLwt0L9Dn11kW2EWn5IwAZ4k7IcWz74fy093tVyWwP7xWjNOIcIUZkrLpOonyNRKKYkaygpdKkiDcQx3SNJSjiEhfjy7P4L5RWrAdC1NcwZH6e0KjSMpBFJrOCKmunPaG4n9eM1XtU19TnqSKcDxe1E4ZVDEcxgBbVBCs2MAQhAU1t0LcRQJhZcIqmBDc6ZdnSe2o5B6XnCunWN4FY+TBDtgDB8AFJ6AMLkEFVAEGfXAPnsGLpa1H69V6G7fmrMnMNvgD6/0H4m6YLQ==</latexit>

{g, p}

<latexit sha1_base64="fBRfhRtdu69IanLvw+wb/fj4VsI=">AAACDXicbVA9SwNBEN3zM8avqKUWh1GITbizUDujNpYRTRRy4djbzOmSvQ9258RwnK1g408Q/AU2ForY2tv5A/wXFm4SC40+GHi8N8PMPC8WXKFlvRtDwyOjY+O5ifzk1PTMbGFuvq6iRDKosUhE8sSjCgQPoYYcBZzEEmjgCTj22ntd//gcpOJReISdGJoBPQ25zxlFLbmFFSd1EC5Q+Sk7o7jDGMQIray05mRu2nbT3cMscwtFq2z1YP4l9jcpbn/eVu6uLj+qbuHNaUUsCSBEJqhSDduKsZlSiZwJyPJOoiCmrE1PoaFpSANQzbT3TWauaqVl+pHUFaLZU39OpDRQqhN4ujOgeKYGva74n9dI0N9qpjyME4SQ9Rf5iTAxMrvRmC0ugaHoaEKZ5PpWU2ciKUMdYF6HYA++/JfU18v2Rtk6sIqVJdJHjiySZVIiNtkkFbJPqqRGGLkm9+SRPBk3xoPxbLz0W4eM75kF8gvG6xewz6Du</latexit>

{chatAccepted()}

Figure 3: MTProto 2.0’s protocol for secret chats.

are required to compare their respective key ﬁnger-

prints

using a secure authenticated out-of-band chan-

nel. Under this assumption, the protocol should guar-

antee the secrecy of the messages subsequently ex-

changed by A and B, encrypted with k. The clients

are also supposed to perform suitable checks on the

DH parameters, as described in Section 5. Note that,

in actual implementations, the out-of-band check is

left to users, i.e., it is not done automatically.

6.2 Formalisation in ProVerif

Each (honest) client involved in the secret chat pro-

tocol is modelled as a distinct process (an initiator A

and a responder B), and communication happens via

a common public channel (without encrypting mes-

sages with authorization keys), which allows us to

treat the server as an adversary equipped with the

same knowledge as the server (essentially, all the au-

thorization keys) and implicitly performing message

forwarding. That allows the attacker to receive, ma-

nipulate, and resend the exchanged messages in the

same way as the server could do, or impersonate a

These are different from hash(k); in MTProto 2.0, they

are 288-bit hashes that are typically displayed both as hex-

adecimal strings and QR-codes, suitable for visual compar-

ison, by Telegram clients.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

192

client if the clients do not perform the required checks

on the received parameters or on the generated key.

As the server controls the DH conﬁguration used

by the clients to derive their shared key, if the clients

do not validate the obtained values then the server

might be able to force both clients to use an easily

guessable key. For instance, if the server sends a sub-

group generator equal to 1 and the clients do not per-

form any check, the derived session key will be 1 and

the server will easily decrypt all the messages.

To model the out-of-band veriﬁcation that users

are asked to perform on a newly generated session

key, we use a separate secure channel ˜c available

only to A, to B, and to two auxiliary processes, one

performing the required validation on behalf of the

clients, and one skipping it:

let PerformOutOfBandKeyComparison() =

in( ˜c,QR(X ,Y,k));

in( ˜c,QR(= Y,= X, = k));

event OutOfBandKeyComparisonSucceeded(X,Y,k);

event OutOfBandKeyComparisonSucceeded(Y,X, k);

out( ˜c,QR

(X,Y,k));

out( ˜c,QR

(Y,X, k)).

let SkipOutOfBandKeyComparison() =

in( ˜c,QR(X ,Y,k));

event OutOfBandKeyComparisonSkipped(X,k);

out( ˜c,QR

(X,Y,k)).

Each client X wishing to validate a session key ne-

gotiated with Y sends a private message QR(X,Y,k)

via ˜c and waits for QR

(X,Y,k) as a conﬁrmation.

The ﬁrst of the two processes above waits for a QR()

message from a client and then expects a matching

message from the other client. Only when the sec-

ond message arrives, the process proceeds by record-

ing the event and sending out the conﬁrmation mes-

sages. The second process simply acknowledges a

QR() message and records the corresponding event,

without doing anything else. Note that, in our model,

out-of-band key validation implies mutual authentica-

tion. How such channel is to be established in the real

world, however, is not speciﬁed by the protocol.

Finally, we assume that honest clients behave as

per the protocol, except for the following deviations:

a client may fail to verify its DH parameters, as in the

authorization protocol (Section 5.2), and a client may

skip the out-of-band validation of the session key.

6.3 Security Properties Veriﬁcation

Secrecy. The main requirement of an end-to-end

encrypted chat is, obviously, secrecy: messages ex-

changed by A and B must be known only to A and B.

MTProto’s secret chats guarantee secrecy conditional

to the strong assumption that clients do validate their

keys through a separate private channel. Formally, the

secrecy query, which ProVerif is able to prove, can be

formulated as follows:

query X : Principal, k : SessionKey,m : Msg;

attacker(m)

⇒ event(OutOfBandKeyComparisonSkipped(X, k))

∨ event(ClientChecksDHConﬁg(X,⊥)).

In words, under the assumptions of our model, mes-

sage m exchanged between two clients is kept secret

unless one of the clients does not perform the manda-

tory checks of DH parameters or the clients omit the

“manual” authentication of the shared key via an ex-

ternal secure channel.

Note that secrecy does not

rely on the privacy of the authorization keys, i.e., the

above query is true even if the authorization keys of

the parties involved are leaked before the secret chat

protocol starts. Secrecy, however, crucially relies on

a step that requires active human interaction, at least

in the current implementations.

As for the conﬁdentiality of the session key k, note

that although in a correct run of the protocol k remains

secret (otherwise the attacker could obtain m), k is not

indistinguishable from a random key: by comparing

choice[k, r] (i.e., one between the real key k and a ran-

dom value r) with the hash from the last message of

the protocol, the server can tell apart k from r with

high probability. Accordingly, ProVerif cannot prove

the corresponding observational equivalence.

Integrity and Authentication. The integrity and

authenticity of a message exchanged by two clients

during a secret chat session is preserved if the clients

abide by the rules—in particular, if they perform the

required out-of-band key validation in a way that im-

plies mutual authentication. But, even under such as-

sumptions, the protocol remains vulnerable to a lim-

ited cross-session attack. The strongest result we

could prove in ProVerif is the following:

query i, i

: ChatID, X,Y,I, R : Principal,

k : SessionKey, m : Message;

inj-event(ReceivesSecretChatMsg(X, i,I,R,k, m))

⇒ inj-event(SendsSecretChatMsg(Y,i

,I,R, k,m))

∨ inj-event(SendsSecretChatMsg(Y,i

,R, I, k,m))

∨



event(OutOfBandKeyComparisonSkipped(X,k))

∧ event(OutOfBandKeyComparisonSkipped(Y,k))



Note that in our formalization (see Section 6.2), it is

not possible for one client to validate the session key and

for the other to skip the validation.

Automated Symbolic Veriﬁcation of Telegram’s MTProto 2.0

193

∨



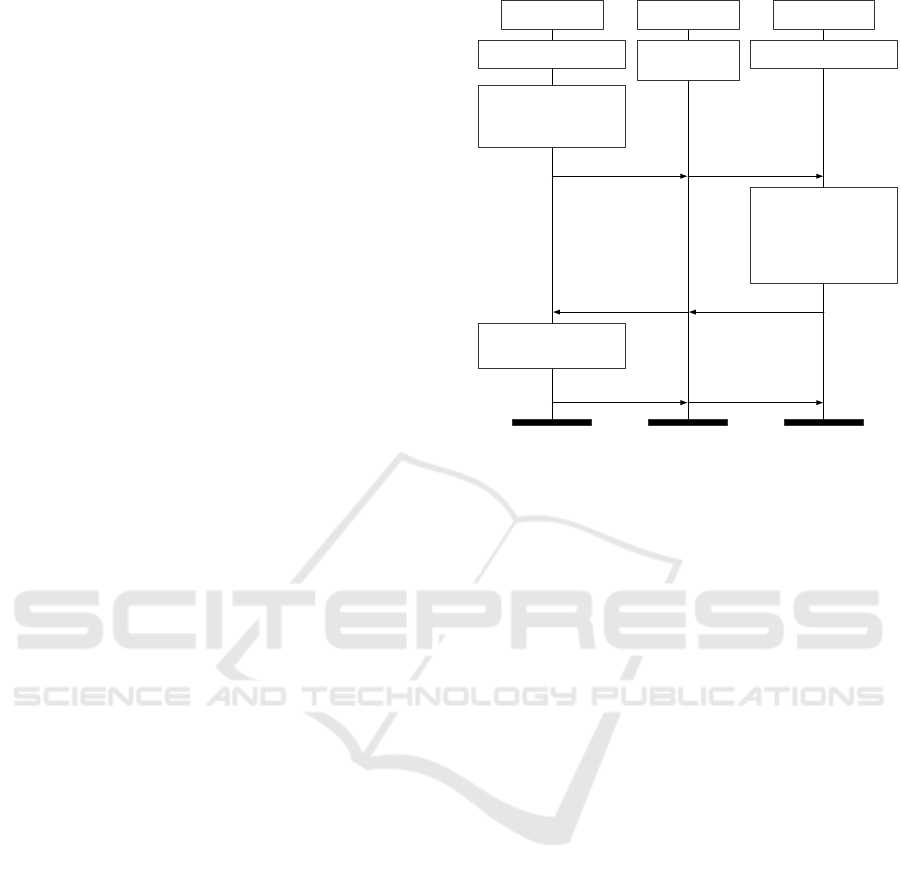
event(ClientChecksDHConﬁg(X, ⊥))

∧ event(ClientChecksDHConﬁg(Y,⊥))



In this query, I denotes the chat initiator and R is the

responder. If the clients behave correctly, whenever

an honest party X (which, by the deﬁnition of the

events, may be only I or R) receives a message m en-

crypted with the session key k in a chat session ini-

tiated by I with intended partner R, exactly one mes-

sage m encrypted with k has indeed been sent by Y

(which, again, can only be I or R) in a session started

by I with R or in a parallel session started by R with I.

The latter is due to the possibility that the server S im-

personates the responder in two distinct sessions, one

started by X with Y , and another started by Y with X,

performing the following exchange:

Session 1 X → S: g

Session 2 Y → S: g

Session 2 S → Y : g

Session 1 S → X: g

The server impersonating Y in Session 1 and X in Ses-

sion 2 gets X and Y to compute the same key g

both sessions. The server is then free to forward mes-

sages across such sessions: they are accepted because

they are encrypted with a valid key. Note that this at-

tack is limited to the same two parties X and Y as long

as the clients validate their keys.

In the query above we cannot require i = i

, be-

cause the server might forward X and Y different

chat id’s. This does not seem to pose security risks,

though: it is rather a correctness issue related to ses-

sion management. Anyway, a similar result addition-

ally requiring i = i

can be proved if the clients also

compare their respective id’s during the out-of-band

conﬁrmation step, i.e., if QR(i,X,Y,k) is sent instead

of just QR(X,Y,k).

If the message is not sent by Y , then X and Y

did not validate k, or both clients skipped the needed

checks on the DH parameters. The former enables

the server to perform the classical MitM attack on

Difﬁe-Hellman. The latter allows the server to mount

a MitM attack similar to the one described in the last

paragraph of Section 5.3. Besides, it is necessary to

assume that out-of-band validation really implies mu-

tual authentication: that is the case in our model, but

depending on how such validation is carried out in

practice, such an assumption may be too strong. For

instance, a malicious client E could “social-engineer”

two honest clients A and B to make them believe that

their key k match E’s (who does not have k), e.g., E

might get the key ﬁngerprint from B and hand it to A

when asked by A to compare their keys.

<latexit sha1_base64="5b4wljFyVbeb+rq7n6xRfQOlZj4=">AAACInicbVDLSgMxFM3UV62vqktdDBahQikzLnysLLpxWdE+oC1DJs20YTIPkoxYQtz6GQXxV9y4UNSV4Na/cGH6WGjrCRdOzr2H5B43poQLy/owUjOzc/ML6cXM0vLK6lp2faPKo4QhXEERjVjdhRxTEuKKIILieswwDFyKa65/NujXrjHjJAqvRC/GrQB2QuIRBIWWnOxxU+oj8I32StJWhY7jFoZ37kkvVvmOI6Gr9lRTOb4u6UtHnl4qpZxszipaQ5jTxB6T3Ml3v3R/d/tVdrJvzXaEkgCHAlHIecO2YtGSkAmCKFaZZsJxDJEPO7ihaQgDzFtyuKIyd7XSNr2I6QqFOVR/OyQMOO8Frp4MoOjyyd5A/K/XSIR31JIkjBOBQzR6yEuoKSJzkJfZJgwjQXuaQMSI/quJupBBJHSqGR2CPbnyNKnuF+2DonVh5UrbYIQ02AI7IA9scAhK4ByUQQUg0AeP4Bm8GA/Gk/FqvI9GU8bYswn+wPj8AaTrqpA=</latexit>

{{id,g

, fp(g

)}

}

{{id,g

, fp(g

)}

}

<latexit sha1_base64="nj1BmF1UQDykq74aLdWKE+INE50=">AAACDXicbVC7TsMwFHXKq5RXgBGGiILEgKqEAdioYGEsgj6kJoocx2mtOA/ZDqKyworEwicg8QUsDCDEys7GB/AXDLiPAQrXutLROffo+h4vpYQL0/zQChOTU9MzxdnS3PzC4pK+vNLgScYQrqOEJqzlQY4piXFdEEFxK2UYRh7FTS887uvNC8w4SeJz0UuxE8FOTAKCoFCUq2/aUj2BL5VXEj/f6bjQzt1QtQylK4/O8jx39bJZMQdl/AXWCJQPv+6q99dXnzVXf7f9BGURjgWikPO2ZabCkZAJgijOS3bGcQpRCDu4rWAMI8wdObgmN7YU4xtBwlTHwhiwPx0SRpz3Ik9NRlB0+bjWJ//T2pkIDhxJ4jQTOEbDRUFGDZEY/WgMnzCMBO0pABEj6q8G6kIGkVABllQI1vjJf0Fjt2LtVcxTs1xdB8MqgjWwAbaBBfZBFZyAGqgDBG7AA3gCz9qt9qi9aK/D0YI28qyCX6W9fQOKP6F6</latexit>

{{id,g

}

{{id,g

}

<latexit sha1_base64="SSXyN2G3bIsDRl5v295NJlVpmZQ=">AAAB/nicbVC7SgNBFJ31GeNrVaxsBoNgIWHXQkUQAzaWEcwDknWZnZ3dDJmdWWZmhbAE7PwOGwtFbP0OO3tLf8DOyaPQxAMXDufcy733BCmjSjvOhzUzOze/sFhYKi6vrK6t2xubdSUyiUkNCyZkM0CKMMpJTVPNSDOVBCUBI42gezHwG7dEKir4te6lxEtQzGlEMdJG8u3t2M9R0D89y2Mf9W+CdiJCmPp2ySk7Q8Bp4o5J6fz7nn4dfJKqb7+3Q4GzhHCNGVKq5Tqp9nIkNcWM9IvtTJEU4S6KSctQjhKivHx4fh/uGSWEkZCmuIZD9fdEjhKleklgOhOkO2rSG4j/ea1MRydeTnmaacLxaFGUMagFHGQBQyoJ1qxnCMKSmlsh7iCJsDaJFU0I7uTL06R+WHaPys6VW6pAMEIB7IBdsA9ccAwq4BJUQQ1gkIMH8ASerTvr0XqxXketM9Z4Zgv8gfX2AxRsmek=</latexit>

:= g

mod p

:= g

mod p

Client A Client BServer S

Knows

<latexit sha1_base64="n/muxp3qmo1n93mGLLSbZuegJBE=">AAAB9XicbVDLSgNBEOyNrxhfUY+CDAYhQgi7HtRjxIvHRM0DkjXMTibJsLOzy8ysEpYc/QcvHhTx6tXv8OY3+BNOHgdNLGgoqrrp7vIizpS27S8rtbC4tLySXs2srW9sbmW3d2oqjCWhVRLyUDY8rChnglY105w2Iklx4HFa9/yLkV+/o1KxUNzoQUTdAPcE6zKCtZFu/YLfTs6vh4V8rxAdtbM5u2iPgeaJMyW5ElS+H/Y/rsrt7GerE5I4oEITjpVqOnak3QRLzQinw0wrVjTCxMc92jRU4IAqNxlfPUSHRumgbihNCY3G6u+JBAdKDQLPdAZY99WsNxL/85qx7p65CRNRrKkgk0XdmCMdolEEqMMkJZoPDMFEMnMrIn0sMdEmqIwJwZl9eZ7UjovOSdGumDQQTJCGPTiAPDhwCiW4hDJUgYCER3iGF+veerJerbdJa8qazuzCH1jvPxqilHs=</latexit>

k, k

, (g, p)

k, k

, (g, p)

Knows

<latexit sha1_base64="49Iy9d20xZaQfvqh+aHGCMdOB/U=">AAAB9XicbVDLSgNBEOyNrxhfUY+CDAYhQgi7HtRj0IvHRM0DkjXMTibJsLOzy8ysEpYc/QcvHhTx6tXv8OY3+BNOHgdNLGgoqrrp7vIizpS27S8rtbC4tLySXs2srW9sbmW3d2oqjCWhVRLyUDY8rChnglY105w2Iklx4HFa9/yLkV+/o1KxUNzoQUTdAPcE6zKCtZFu/YLfTs6vh4V8rxAdtbM5u2iPgeaJMyW5ElS+H/Y/rsrt7GerE5I4oEITjpVqOnak3QRLzQinw0wrVjTCxMc92jRU4IAqNxlfPUSHRumgbihNCY3G6u+JBAdKDQLPdAZY99WsNxL/85qx7p65CRNRrKkgk0XdmCMdolEEqMMkJZoPDMFEMnMrIn0sMdEmqIwJwZl9eZ7UjovOSdGumDQQTJCGPTiAPDhwCiW4hDJUgYCER3iGF+veerJerbdJa8qazuzCH1jvPxwulHw=</latexit>

k, k

, (g, p)

k, k

, (g, p)

b ∈ Z

:= g

mod p

:= g

mod p

<latexit sha1_base64="Wm4O+xuoP3hYkB9KXg6v3gcSU9Y=">AAACE3icbZA9SwNBEIbn/IzxK2opyGIQ1CLcWagIQsDGMorRQHIce5u9ZHHvg905MRwp7W38KyJYKGJrY+dv8E+4SVTU+MLCyzMzzM7rJ1JotO03a2R0bHxiMjeVn56ZnZsvLCye6jhVjFdZLGNV86nmUkS8igIlryWK09CX/Mw/P+jVzy640iKOTrCTcDekrUgEglE0yCtsNpBfog6yIOmut7yM+t2Nvf0v2Ka6/Y29QtEu2X2RYeN8mmIZjt6vVu6OK17htdGMWRryCJmkWtcdO0E3owoFk7ybb6SaJ5Sd0xavGxvRkGs369/UJWuGNEkQK/MiJH36cyKjodad0DedIcW2/lvrwf9q9RSDXTcTUZIij9hgUZBKgjHpBUSaQnGGsmMMZUqYvxLWpooyNDHmTQjO35OHzelWydku2UdOsUxgoBwswyqsgwM7UIZDqEAVGFzDLTzAo3Vj3VtP1vOgdcT6nFmCX7JePgAg96HR</latexit>

fp(g

):=hash(g

)

fp(g

):=hash(g

)

a ∈ Z

:= g

mod p

:= g

mod p

Generates id

<latexit sha1_base64="nI7hhmJdPXL6a2Ld1KLlNtMwboY=">AAAB/nicbVC7SgNBFJ31GeNrVaxsBoNgIWHXQkUQAzaWEcwDknWZnZ3dDJmdWWZmhbAE7PwOGwtFbP0OO3tLf8DOyaPQxAMXDufcy733BCmjSjvOhzUzOze/sFhYKi6vrK6t2xubdSUyiUkNCyZkM0CKMMpJTVPNSDOVBCUBI42gezHwG7dEKir4te6lxEtQzGlEMdJG8u3t2M9R0D89y2M/6N+gdiJCmPp2ySk7Q8Bp4o5J6fz7nn4dfJKqb7+3Q4GzhHCNGVKq5Tqp9nIkNcWM9IvtTJEU4S6KSctQjhKivHx4fh/uGSWEkZCmuIZD9fdEjhKleklgOhOkO2rSG4j/ea1MRydeTnmaacLxaFGUMagFHGQBQyoJ1qxnCMKSmlsh7iCJsDaJFU0I7uTL06R+WHaPys6VW6pAMEIB7IBdsA9ccAwq4BJUQQ1gkIMH8ASerTvr0XqxXketM9Z4Zgv8gfX2AxRvmek=</latexit>

:= g

mod p

:= g

mod p

Checks

<latexit sha1_base64="VCMa9AXoex3TBP1uTadJaFe9J7Y=">AAAB/HicbVDJSgNBEK1xjXGL5ihIYxDiJcx4UI8BLx4TMQskIfR0epImPQvdNeIwxJvf4cWDIl7F7/DmN/gTdpaDJj4oeLxXRVU9N5JCo21/WUvLK6tr65mN7ObW9s5ubm+/rsNYMV5joQxV06WaSxHwGgqUvBkpTn1X8oY7vBz7jVuutAiDG0wi3vFpPxCeYBSN1M3l28jvUHupF42K/W5K3dFJN1ewS/YEZJE4M1IoQ/X74fDjutLNfbZ7IYt9HiCTVOuWY0fYSalCwSQfZdux5hFlQ9rnLUMD6nPdSSfHj8ixUXrEC5WpAMlE/T2RUl/rxHdNp09xoOe9sfif14rRu+ikIohi5AGbLvJiSTAk4yRITyjOUCaGUKaEuZWwAVWUockra0Jw5l9eJPXTknNWsqsmDQJTZOAAjqAIDpxDGa6gAjVgkMAjPMOLdW89Wa/W27R1yZrN5OEPrPcfRNuYCw==</latexit>

fp(g

)

fp(g

)

<latexit sha1_base64="VKLF9WYJxsxGIJe+fmQTzxN/Qa8=">AAACIXicbVDLSgMxFM3UV62vqktdDBahQikzLrQ7K25cVrQPaMuQSTNtaOZBkhFLiFv/QkF/xY0LRboT1/6FC9NpF9p6woWTc+8huceNKOHCsj6M1Nz8wuJSejmzsrq2vpHd3KrxMGYIV1FIQ9ZwIceUBLgqiKC4ETEMfZfiuts/G/Xr15hxEgZXYhDhtg+7AfEIgkJLTrbUkvoIfKO9knRUoeu4heTOPelFKt91JHTVgWopp69L9qUjTy+VcrI5q2glMGeJPSG5k++H8uPd7VfFyQ5bnRDFPg4EopDzpm1Foi0hEwRRrDKtmOMIoj7s4qamAfQxb8tkQ2Xua6VjeiHTFQgzUX87JPQ5H/iunvSh6PHp3kj8r9eMhVdqSxJEscABGj/kxdQUoTmKy+wQhpGgA00gYkT/1UQ9yCASOtSMDsGeXnmW1A6L9lHRurBy5V0wRhrsgD2QBzY4BmVwDiqgChC4B8/gFbwZT8aL8W4Mx6MpY+LZBn9gfP4AqcOqCA==</latexit>

{{id,g

, fp(g

)}

}

{{id,g

, fp(g

)}

}

<latexit sha1_base64="TuMIPOMRXwen0aYNeNV3p70g1ew=">AAACDXicbVC7TsMwFHXKq5RXgBGGiILEgKqEAdgoYmEsgj6kJoocx2mtOA/ZDqKyworEwicg8QUsDCDEys7GB/AXDLiPAQrXutLROffo+h4vpYQL0/zQChOTU9MzxdnS3PzC4pK+vNLgScYQrqOEJqzlQY4piXFdEEFxK2UYRh7FTS887uvNC8w4SeJz0UuxE8FOTAKCoFCUq2/aUj2BL5VXEj/f6bjQzt1QtQylK4/O8jx39bJZMQdl/AXWCJQPv+6q99dXnzVXf7f9BGURjgWikPO2ZabCkZAJgijOS3bGcQpRCDu4rWAMI8wdObgmN7YU4xtBwlTHwhiwPx0SRpz3Ik9NRlB0+bjWJ//T2pkIDhxJ4jQTOEbDRUFGDZEY/WgMnzCMBO0pABEj6q8G6kIGkVABllQI1vjJf0Fjt2LtVcxTs1xdB8MqgjWwAbaBBfZBFZyAGqgDBG7AA3gCz9qt9qi9aK/D0YI28qyCX6W9fQOIt6F5</latexit>

{{id,g

}

{{id,g

}

Knows

<latexit sha1_base64="t7oAYPDx38bowl+Pp94t2wh9V7g=">AAACHXicbVDLSgMxFM3UV62vqktdDBahgpQZEXVnxY3LivYB7TBk0kwbmnmQZMQS4tZ/cFPwS9y4UMSFG/ED/AsXptMutHrDhcM593BzjxdTwoVlfRiZqemZ2bnsfG5hcWl5Jb+6VuNRwhCuoohGrOFBjikJcVUQQXEjZhgGHsV1r3c61OtXmHEShZeiH2MngJ2Q+ARBoSk3v9+S+gl8rb2StNVuirkv/VgVO66EntppKbenW/akK08ulFJuvmCVrLTMv8Aeg8Lx16B8f3vzWXHzb612hJIAhwJRyHnTtmLhSMgEQRSrXCvhOIaoBzu4qWEIA8wdmV6nzG3NtE0/YrpDYabsT4eEAef9wNOTARRdPqkNyf+0ZiL8I0eSME4EDtFokZ9QU0TmMCqzTRhGgvY1gIgR/VcTdSGDSOhAczoEe/Lkv6C2V7IPSta5VShvglFlwQbYAkVgg0NQBmegAqoAgTvwAJ7AszEwHo0X43U0mjHGnnXwq4z3b8LRqIw=</latexit>

{{id, fp(g

)}

}

{{id, fp(g

)}

}

<latexit sha1_base64="cOac2TtG6qLnaRQ3CKKr2upaZGI=">AAACHXicbVDLSgMxFM3UV62vqktdDBahgpQZEXVn0Y3LivYB7TBk0kwbmnmQZMQS4tZ/cFPwS9y4UMSFG/ED/AsXptMutHrDhcM593BzjxdTwoVlfRiZqemZ2bnsfG5hcWl5Jb+6VuNRwhCuoohGrOFBjikJcVUQQXEjZhgGHsV1r3c61OtXmHEShZeiH2MngJ2Q+ARBoSk3v9+S+gl8rb2StNVuirkv/VgVO66EntppKbenW/akK08ulFJuvmCVrLTMv8Aeg8Lx16B8f3vzWXHzb612hJIAhwJRyHnTtmLhSMgEQRSrXCvhOIaoBzu4qWEIA8wdmV6nzG3NtE0/YrpDYabsT4eEAef9wNOTARRdPqkNyf+0ZiL8I0eSME4EDtFokZ9QU0TmMCqzTRhGgvY1gIgR/VcTdSGDSOhAczoEe/Lkv6C2V7IPSta5VShvglFlwQbYAkVgg0NQBmegAqoAgTvwAJ7AszEwHo0X43U0mjHGnnXwq4z3b8RZqI0=</latexit>

{{id, fp(g

)}

}

{{id, fp(g

)}

}

Figure 4: The rekeying protocol.

7 REKEYING

Keys used in secret chats are replaced every 100 mes-

sages or every week (if at least one message has been

sent) using the protocol shown in Fig. 4. Old keys

should be destroyed and never reused. The exchange

uses the same DH parameters obtained when the se-

cret chat was ﬁrst established (Section 6). Messages

are transmitted through the secret channel already in

place between the clients, so the server, who acts as a

forwarder, can observe only the ciphertexts.

7.1 Informal Description

The rekeying protocol is essentially a standard Difﬁe-

Hellman exchange over a secure channel. The claim

that the channel is secure is only relative to the as-

sumptions and results of Section 6.3. Both clients

possess the DH parameters (g, p) from their initial run

of the secret chat protocol and a shared key k. The

new shared key is derived as follows (see Fig. 4):

1. Client A generates a random session id and a ran-

dom a ∈ Z

, computes a half-key g

and sends the

pair (id,g

) to B.

2. Client B generates a random b ∈ Z

and com-

putes its half-key g

and the new shared key g

The half-key and a ﬁngerprint of the shared key

(64 bits of the SHA1 of the key) are sent to A.

3. Client A computes g

, checks that the ﬁngerprint

of g

matches the received ﬁngerprint, and sends

the ﬁngerprint back to B as an acknowledgment.

The old key is no longer needed and can be deleted.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

194

7.2 Formalisation in ProVerif

The formalisation of the rekeying protocol is similar

to the formalization of the secret chat protocol, us-

ing a process for the initiator and one for the respon-

der, while the server is untrusted and included in the

attacker. The computed ﬁngerprints are not crypto-

graphically strong and do not play any security role,

but are meant only as a sanity check for the imple-

mentations. The only important difference compared

to a standard Difﬁe-Hellman exchange is that all the

messages exchanged during rekeying are end-to-end

encrypted with the current session key k, which is as-

sumed to be known only to the clients.

7.3 Security Properties Veriﬁcation

Secrecy and Forward Secrecy. Assuming that the

current k is strong and secret, secrecy after rekeying

is preserved even if the authorization keys of both par-

ties are compromised before the rekeying protocol is

executed. This can be proved in ProVerif by running

the rekeying protocol without encrypting the mes-

sages with the authorization keys so that they are ac-

cessible to the adversary (which models the untrusted

server), then letting A and B exchange a message m

encrypted with the new key, and ﬁnally verifying that

the attacker cannot obtain m:

query attacker(m).

Forward secrecy and future secrecy are guaranteed by

the periodic rotation of the keys. If a session key is

recovered by an attacker, it can be used to decrypt

at most 100 messages or a week worth of messages.

While older or newer messages cannot be deciphered,

in some circumstances such window of compromise

might still be considered excessively wide. Given the

above, leaking an authorization key at any time does

not compromise the secrecy of any message.

Authentication. If A, B run the rekeying protocol

negotiating a new key k, then both A and B, and only

them, should know k. Unfortunately, the rekeying

protocol fails to provide implicit key conﬁrmation (the

guarantee to A that B can compute k, and vice versa)

and implicit key authentication (the guarantee to A

that no one but B knows k, and vice versa) (Blake-

Wilson and Menezes, 1999). A rogue client E, who

has already completed the secret chat protocol with A

and B, may unfold the following attack:

• A starts rekeying with E and sends its half-key g

;

• E starts a parallel session with B, sending g

to B;

• B sends E its half-key g

;

• E sends A the half-key g

obtained from B.

At this point, A and B compute the same key, and each

one mistakenly believes that the key is shared with E.

The following query is disproved by ProVerif, even

assuming that the DH parameters are good:

query i : SessionID, I,I

,R, R

: Principal,k : SessionKey;

event(InitiatorNegotiatesNewKey(i,I,R,k))

∧ event(ResponderNegotiatesNewKey(i,I

,k))

⇒ I = I

∨ I = R

∨ R = I

∨ R = R

If the initiator I accepts k from R and responder R

accepts k from I

, ideally only two parties should be

involved (the query is even weaker than that, asking

only that at least one entity appears in both events).

As an example of how such a vulnerability could

be exploited, consider the following game of spies:

Alice and Eve are agents from Eurasia, and Bob is

an agent from Eastasia. Alice trusts Eve and would

never communicate with Bob, but Eve has been paid

by Bob to perform the above attack. After the rekey-

ing exchange described above, Bob would be able to

transmit misleading information to Alice, who would

accept it as coming from Eve. The main advantage

compared to having Eve act as a forwarder is that Bob

does not need to rely on Eve in subsequent communi-

cation; it is also a less risky strategy for Eve (she could

eventually claim that her device has been hacked).

Telegram’s documentation recommends that

clients do not start two rekeying instances con-

currently. But the query above generates a trace

involving four parties A, B, and two cooperating

malicious clients E,E

, in which A runs rekeying

with E, and E

runs rekeying with B. Each client

runs a single instance of the protocol. So, the above

recommendation is not a mitigation for this attack.

8 CONCLUSIONS

We have presented the formalisation of the MT-

Proto 2.0 protocol suite in the applied π-calculus,

and its analysis using the protocol veriﬁer ProVerif.

This approach adopts the symbolic Dolev-Yao threat

model: an active intruder can intercept, modify, for-

ward, drop, replay or reﬂect any message. Within this

model, we have provided a fully automated proof of

the soundness of MTProto 2.0’s protocols for ﬁrst au-

thentication, normal chat, end-to-end encrypted chat,

and rekeying mechanisms with respect to several se-

curity properties, including authentication, integrity,

secrecy and perfect forward secrecy, also in the pres-

ence of malicious servers and clients. Moreover, we

Automated Symbolic Veriﬁcation of Telegram’s MTProto 2.0

195

have discovered that the rekeying protocol is vulner-

able to a theoretical unknown key-share (UKS) at-

tack (Blake-Wilson and Menezes, 1999): a malicious

client B, with the help of another client E, can induce

a client A to believe that she (still) shares a secret key

with E, and instead A shares the key with B. The prac-

tical exploitability of this attack in actual implemen-

tations is still to be investigated. Our formalization

covers also the behaviour of the users, when relevant;

e.g., if the users do not check the ﬁngerprints of their

shared keys, a MitM attack is possible.

Vulnerabilities may arise also from the cryp-

tographic primitives, from implementation ﬂaws

(e.g. insufﬁcient checks), from side-channels exﬁltra-

tion (such as timing or trafﬁc analysis), or from in-

correct user behaviour. Hence, these aspects deserve

further investigation and particular care in the imple-

mentation and use of this protocol.

In this work, the basic encryption primitive of

MTProto 2.0 has been modeled as a perfect authen-

ticated encryption scheme. Although no attack on

this scheme is known to date, in order to deem MT-

Proto 2.0 secure we need to prove properties such as

IND-CCA and INT-CTXT. This proof cannot be done

in a symbolic model like ProVerif’s, but it can be

achieved in a computational model, using tools like

CryptoVerif or EasyCrypt (Blanchet, 2007; Barthe

et al., 2013)—which we leave to future work. How-

ever, even if a ﬂaw were found in the current encryp-

tion scheme, the results in this paper would still be

valid: the encryption scheme could be replaced with a

stronger one, and no other changes would be required.

Besides automatic tools like ProVerif and Cryp-

toVerif, one may analyse (cryptographic) protocols in

semi-automatic, interactive tools. A prominent exam-

ple is EasyCrypt mentioned above, but there are also

formalisations of the applied π-calculus or even gen-

eral temporal logics in proof assistants like Coq or

Isabelle/HOL (see, e.g. (Kahsai and Miculan, 2008;

Miculan, 2001; Honsell and Miculan, 1995)). In prin-

ciple, these interactive tools allow us to formalize and

prove any properties which can be proved “on the pa-

per”, but the burden on the user is greater than that

induced by automatic tools.

Concerning implementation ﬂaws, our formalisa-

tion can be used as a reference for the correct im-

plementation of MTProto 2.0 clients (and servers).

Tools like Spi2Java or FS2PV can be useful to this end

(Bhargavan et al., 2010; Pozza et al., 2004). Also, par-

ticular attention must be paid to side-channel attacks,

such as on timing or trafﬁc analysis. Another issue

concerning the correct implementation of clients is

that a server can craft malicious DH parameters, e.g.,

choosing generators that make discrete logarithms

signiﬁcantly easier to compute (Kobeissi et al., 2017)

or choosing non-primes that pass the 15-round Miller-

Rabin test. To prevent the ﬁrst attack, MTProto pre-

scribes that clients verify that the values received from

the server are valid (see Section 5.3). However, as

far as we can see, MTProto 2.0 still suffers from the

latter vulnerability. A possible improvement is to re-

quire clients to check the proposed primes by means

of deterministic primality algorithms (Agrawal et al.,

2004; Lenstra Jr and Pomerance, 2019).

Correct user behaviour is crucial in order to pre-

vent MitM attacks in secret chats. As we have seen,

users must check the ﬁngerprint of their authorization

keys through an external safe channel; actually, this

issue concerns not only MTProto 2.0 but any protocol

whose keys are deﬁned by means of an insecure

DH exchange. In practice, such checks are likely

often ignored, or performed through the very same

(supposedly secure) chat. Hence, users seriously

concerned about privacy must be educated about the

correct procedure to follow.

REFERENCES

Agrawal, M., Kayal, N., and Saxena, N. (2004). Primes is

in p. Annals of mathematics, pages 781–793.

Barthe, G., Dupressoir, F., Gr

egoire, B., Kunz, C., Schmidt,

B., and Strub, P.-Y. (2013). Easycrypt: A tutorial. In

Foundations of security analysis and design VII, pages

146–166. Springer.

Bhargavan, K., Blanchet, B., and Kobeissi, N. (2017). Ver-

iﬁed models and reference implementations for the

TLS 1.3 standard candidate. In IEEE European Sym-

posium on Security and Privacy, pages 483–502.

Bhargavan, K., Fournet, C., and Gordon, A. D. (2010).

Modular veriﬁcation of security protocol code by typ-

ing. ACM Sigplan Notices, 45(1):445–456.

Blake-Wilson, S. and Menezes, A. (1999). Unknown key-

share attacks on the Station-to-Station (STS) protocol.

In International Workshop on Public Key Cryptogra-

phy, pages 154–170. Springer.

Blanchet, B. (2007). Cryptoverif: Computationally sound

mechanized prover for cryptographic protocols. In

Dagstuhl seminar “Formal Protocol Veriﬁcation Ap-

plied”, volume 117.

Blanchet, B. (2016). Modeling and verifying security proto-

cols with the Applied Pi Calculus and ProVerif. Foun-

dations and Trends in Privacy and Security, 1:1–135.

Cohn-Gordon, K., Cremers, C., Dowling, B., Garratt, L.,

and Stebila, D. (2017). A formal security analysis

of the Signal messaging protocol. In IEEE European

Symposium on Security and Privacy, pages 451–466.

Dolev, D. and Yao, A. (1983). On the security of public key

protocols. IEEE Transactions on Information Theory,

29(2):198–208.

Frosch, T., Mainka, C., Bader, C., Bergsma, F., Schwenk,

J., and Holz, T. (2016). How secure is textsecure?

SECRYPT 2021 - 18th International Conference on Security and Cryptography

196

In 2016 IEEE European Symposium on Security and

Privacy (EuroS&P), pages 457–472. IEEE.

Honsell, F. and Miculan, M. (1995). A natural deduction

approach to dynamic logic. In Berardi, S. and Coppo,

M., editors, Types for Proofs and Programs, Interna-

tional Workshop TYPES’95, Selected Papers, volume

1158 of Lecture Notes in Computer Science, pages

165–182. Springer.

Jakobsen, J. (2015). A practical cryptanalysis of the Tele-

gram messaging protocol. Master’s thesis, Aarhus

University.

Jakobsen, J. and Orlandi, C. (2016). On the CCA

(in)security of MTProto. In Proceedings of the 6th

Workshop on Security and Privacy in Smartphones

and Mobile Devices, pages 113–116.

Kahsai, T. and Miculan, M. (2008). Implementing spi cal-

culus using nominal techniques. In Beckmann, A.,

Dimitracopoulos, C., and L

owe, B., editors, Logic and

Theory of Algorithms, 4th Conference on Computabil-

ity in Europe, CiE 2008, Athens, Greece, June 15-20,

2008, Proceedings, volume 5028 of Lecture Notes in

Computer Science, pages 294–305. Springer.

Kobeissi, N., Bhargavan, K., and Blanchet, B. (2017). Auto-

mated veriﬁcation for secure messaging protocols and

their implementations: A symbolic and computational

approach. In 2017 IEEE European Symposium on Se-

curity and Privacy (EuroS&P), pages 435–450. IEEE.

Lenstra Jr, H. W. and Pomerance, C. B. (2019). Primality

testing with gaussian periods. Journal of the European

Mathematical Society, 21(4):1229–1269.

Miculan, M. (2001). On the formalization of the modal µ-

calculus in the calculus of inductive constructions. Inf.

Comput., 164(1):199–231.

Pozza, D., Sisto, R., and Durante, L. (2004). Spi2java: Au-

tomatic cryptographic protocol Java code generation

from spi-calculus. In 18th International Conference

on Advanced Information Networking and Applica-

tions. AINA 2004., volume 1, pages 400–405. IEEE.

Rad, A. and Rizzo, J. (2015). A 2

attack on Telegram,

and why a super villain doesn’t need it to read your

telegram chats. http://www.alexrad.me. Accessible

via https://web.archive.org.

osler, P., Mainka, C., and Schwenk, J. (2018). More

is less: on the end-to-end security of group chats in

Signal, WhatsApp, and Threema. In IEEE European

Symposium on Security and Privacy, pages 415–429.

anka, T. and Koke

s, J. (2017). Security analysis of

the Telegram IM. In Proceedings of the 1st Re-

versing and Offensive-Oriented Trends Symposium

(ROOTS 2017), pages 1–8.

Telegram (2021a). MTProto mobile protocol. https://core.

telegram.org/mtproto/ (last accessed on Febuary 15,

2021).

Telegram (2021b). Telegram FAQ for the Technically

Inclined. https://core.telegram.org/techfaq (last ac-

cessed on February 15, 2021).

Automated Symbolic Veriﬁcation of Telegram’s MTProto 2.0

197