Robot@Factory Lite Competition: A Digital Twin Approach for the AGV

João Braun

1,2 a

, José Lima

1,3 b

, Paulo Costa

2,3 c

and António Moreira

2,3 d

Research Centre of Digitalization and Intelligent Robotics, Polytechnic Institute of Bragança, Campus de Santa Apolónia,

Bragança, Portugal

Faculty of Engineering of University of Porto (FEUP), University of Porto, R. Dr. Roberto Frias, Porto, Portugal

INESC Technology and Science, FEUP, R. Dr. Roberto Frias, Porto, Portugal

jllima}@ipb.pt, amoreira}@fe.up.pt

Keywords:

Digital Twin, Robotics Competitions, AGV, Simulation, DC Motors.

Abstract:

Robotics competitions are environments that foster teamwork, AI, and technology development by encourag-

ing students, researchers, and academics to test their solutions against each other. These competitions often

challenge the competitors’ prototypes with tasks speciﬁcally designed to benchmark them with the current op-

timal solutions. During the prototype stages of a robot, the development costs and time spent are often higher

than other stages, as changes in the prototype are frequent. Simulation is often used to reduce these variables

as it allows ﬂexibility in all development stages before transitioning to the real scenario. However, a digital

twin can be used to increase even further ﬂexibility and effectiveness. Digital twins are virtual representations

of real assets, providing replication and prediction of real scenario events, and real-time monitoring of the real

object. Thus, this paper presents the development of a digital twin of an automatic guided vehicle (AGV) to

the Robot@Factory Lite competition and the tests performed to validate the approach.

1 INTRODUCTION

Robotics competitions are one of the approaches that

drive technology development as it encourages re-

searchers, academics, and students to develop solu-

tions to the tasks offered by the competitions. They

are known to challenge state-of-the-art technologies

and their algorithms’ performance, to later be adopted

in the industry.

Having Robot@Factory competition as a base,

that started in 2011 Portuguese Robotics Open, the

Robot@Factory Lite (R@FL) is a simpliﬁed ver-

sion where the parts should be transported and orga-

nized between warehouses and processing machines

through a magnet, bringing this competition more ac-

cessible for younger students. For further informa-

tion, the reader is referred to (Lima et al., 2019). The

organization provides a prototype and some libraries

to deal with the robot’s I/O (magnet, RFID, motors,

etc.) to facilitate the development for new partici-

pants. Moreover, it is provided a simulation scene

https://orcid.org/0000-0003-0276-4314

https://orcid.org/0000-0001-7902-1207

https://orcid.org/0000-0002-4846-271X

https://orcid.org/0000-0001-8573-3147

from the Simtwo simulator where a hardware-in-the-

loop was developed.

During the development of a robot as a whole,

prototyping stages costs and time spent are usually

higher than the others. This happens by the fact that

these stages are constituted by frequent hardware and

software changes. Whenever a new change is made

and needs to be tested, it takes time to test in the real

robot. Not to mention that the test location can be a

different place from where the workplace is. Thus,

simulations are used to mitigate these inconveniences

by increasing ﬂexibility during these stages, provided

they simulate realistically the real robot. Even so, fre-

quently the transition to the real scenario needs ad-

justments, as realistically simulations are computa-

tionally expensive.

To increase even further the effectiveness and ﬂex-

ibility of the prototype stages of the robot for the

R@FL competition, a digital twin was developed. In

this case, the digital twin is a realistic model of the

real robot that will run simultaneously with it. The

twins communicate in real-time, providing monitor-

ing data throughout a set of embedded sensors on the

real robot. Thus, the development of the robot’s ap-

proach to the competition will beneﬁt from instant

feedback of the algorithms. Moreover, by conse-

Braun, J., Lima, J., Costa, P. and Moreira, A.

Robot@Factor y Lite Competition: A Digital Twin Approach for the AGV.

DOI: 10.5220/0010550203110318

In Proceedings of the 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2021), pages 311-318

ISBN: 978-989-758-528-9

311

quence, the transition to the real scenario will be

greatly improved, if not outright removed, as the sim-

ulation will operate similarly to the real robot.

The paper is organized as follows: after this in-

troduction, the related work is presented in Section 2.

Section 3 brieﬂy describes the entire system’s setup.

Section 4 addresses the methodology. The performed

tests and their respective results are highlighted in

Section 5. The conclusions with future works are

stressed in Sections 6.

2 STATE OF THE ART

Digital twins are a broad concept that is applied in

several different areas of industry. The industrial

applications focus on the areas of design, produc-

tion, prognostic and health management, among oth-

ers (Tao et al., 2019). In this way, a few examples of

these areas are presented below.

In product design, a digital twin-based approach

for designing hollow glass production lines was pre-

sented in (Zhang et al., 2017). The authors validated

their approach using a case study in hollow glass pro-

duction line.

Regarding the production area, a framework for

modeling and simulation of Cyber-Physical Produc-

tion Systems is presented in (Weyer et al., 2016). Ac-

cording to the authors, the framework was currently

being implemented and validated within the automo-

tive industry.

According to (Tao et al., 2019), most of the ap-

plications of Digital Twins are applied to prognos-

tics and health management (PHM). A digital twin

approach was proposed for complex equipment (Tao

et al., 2018). The authors used a case study of gearbox

prognosis to conﬁrm their approach for improving the

accuracy of prognosis.

Finally, a simulated twin for a remote energy plat-

form was presented in (Pairet et al., 2019). Accord-

ing to the authors, the ORCA Hub Simulator is an

oil rig environment that includes three types of au-

tonomous systems (Husky, ANYmal, and UAVs) for

human-robot collaboration scenarios.

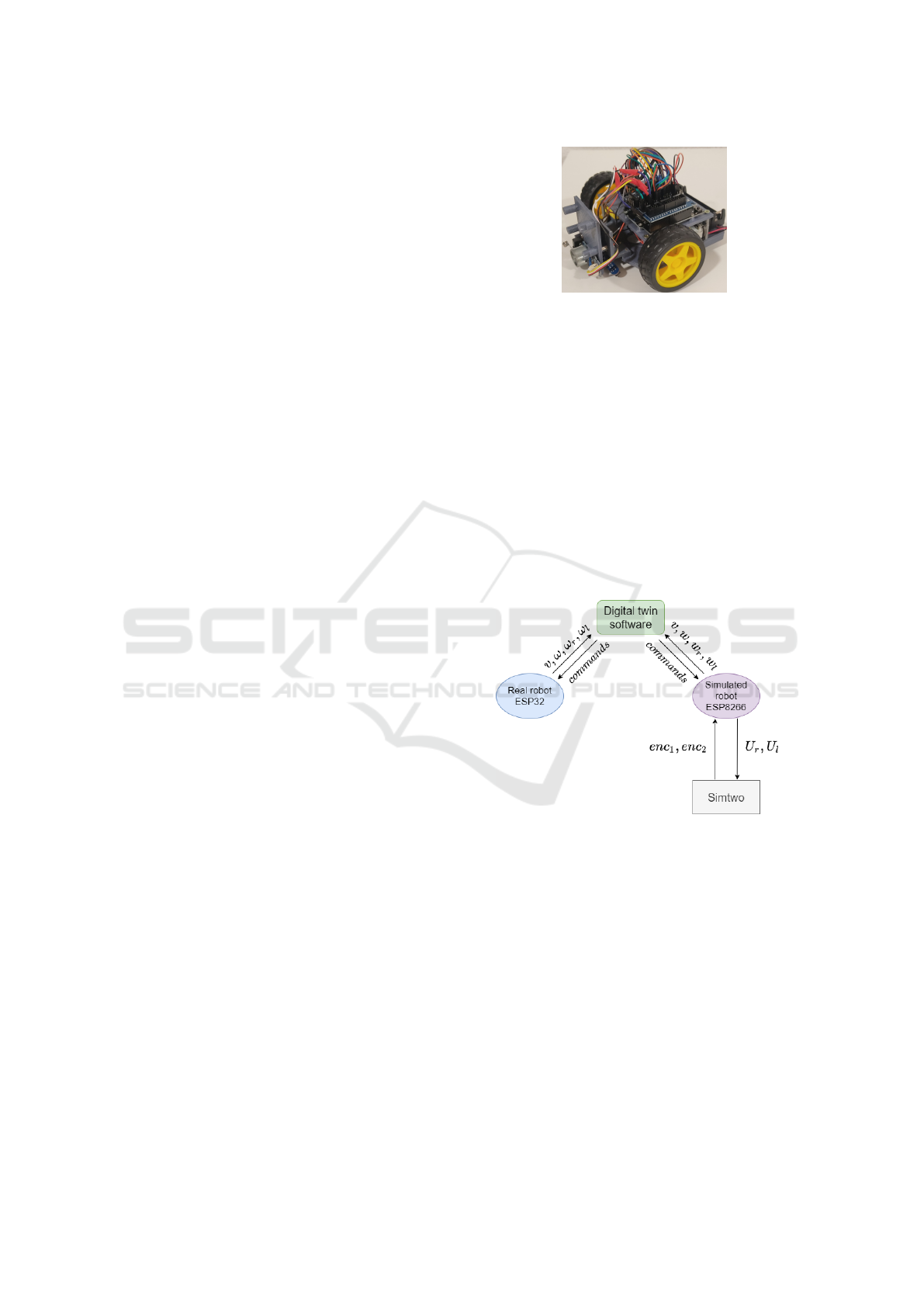
3 THE SETUP

The assembled robot follows the schematic recom-

mended by the competition (P33a, 2020), and can be

seen in the ﬁgure below.

The robot has a differential drive conﬁguration. It

has two DFRobot TT Micro DC geared motors with

Figure 1: Real robot.

integrated quadrature encoders and one caster wheel

for stability. The encoders provide 16 pulses per ro-

tation per channel. Together with the 120:1 gearbox,

the resolution reaches 3840 ticks per revolution.

The digital twin system will work as follows:

• The real robot will operate normally.

• The simulated robot will communicate with an

ESP8266 by serial communication to perform the

hardware in the loop.

• Both of them will communicate, by UDP pro-

tocol, with monitoring software, the digital twin

software.

The entire system can be seen in Figure 2.

Figure 2: Digital twin system’s diagram.

Where v and ω are the robot’s linear and angular

speeds respectively. The right and left motors’ angu-

lar speeds are denoted by ω

and ω

. The encoder

readings are represented by enc

and enc

. Finally,

the right and left motors’ voltages are displayed by

and U

4 METHODOLOGY

SimTwo simulator was chosen for this project for

both the organization providing a simulation scene

for the competition as well as being a realistic 3D

simulator with rigid body interactions and constraints

(Paulo et al., 2011). Regarding the physics simula-

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

312

tion, SimTwo uses the Open Dynamics Engine (ODE)

to perform the computations (Smith et al., 2005).

To construct the simulated robot model, all the

robot’s parts were measured and weighted. The

model can be seen in Figure 3.

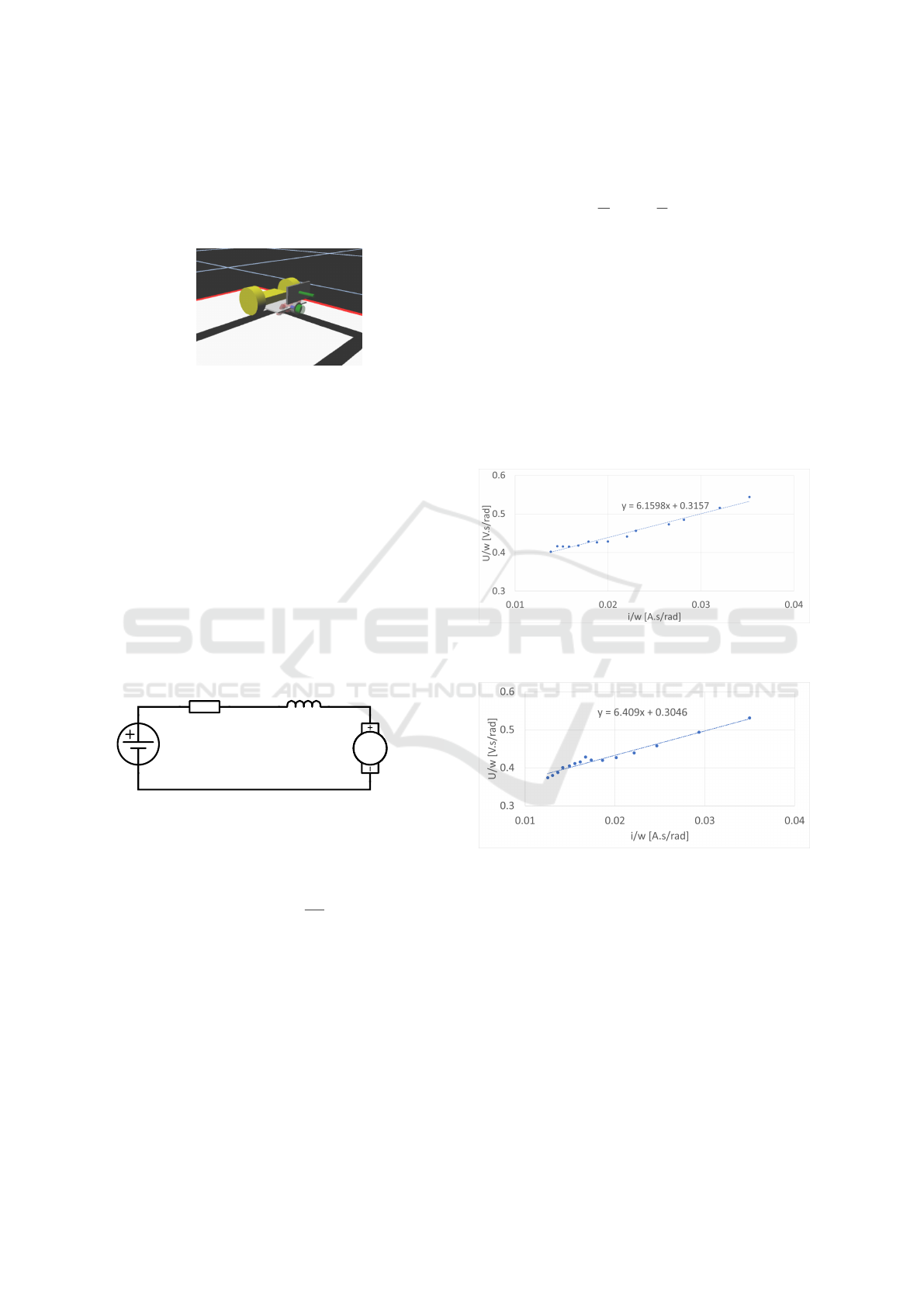
Figure 3: Simulated robot.

4.1 Motors Models

To simulate the motor models, ﬁrst, it is necessary to

obtain the DC motor parameters. Thus, steady-state

and transient tests were performed for each motor.

4.1.1 Steady State Tests

The steady-state tests were performed with the robot

in the air so that the motors’ parameters were not in-

ﬂuenced by the robot’s weight. Before performing

the tests, it is necessary to derive the motor models.

In this way, the electric model of the armature of a

generic DC motor can be seen in Figure 4.

MMM

Armature

Figure 4: Electrical equivalent circuit of a DC motor’s ar-

mature.

Applying Kirchoff Voltage Law to the circuit we

have:

U = R

· i

+ L ·

+ e

(1)

The inductance was assumed zero to simplify the

calculations. This assumption is reasonable as the

motors are small, and the equivalent armature induc-

tance is, in general, very small for small motors. The

voltage drop across the armature is e

, the back emf

generated by the motor while doing work, and it is

proportional to the angular speed of the shaft. The

proportionality constant is k, called the back emf con-

stant.

= k · ω (2)

Substituting equation 2 in equation 1 and dividing it

by ω we have:

= R

+ k (3)

Now, with equation 3, it is possible to perform a

series of steady-state tests where a known voltage is

applied to the motor, and its respective armature cur-

rent and the axle angular speed are measured. The

voltages were measured by a voltmeter and the cur-

rents by an ammeter. The angular speeds were esti-

mated using the embedded encoders on the motors.

In total, ﬁfteen tests were made. The voltages ranged

from [0-6 V ], which the upper limit is the nominal

voltage for these motors. After gathering the data, a

linear model was ﬁt to obtain the angular coefﬁcient

and the linear coefﬁcient k. Figures 5 and 6 show

the results from the tests performed on each motor.

Figure 5: Linear model ﬁt to the right motor data derived

from tests applied to equation 3.

Figure 6: Linear model ﬁt to the left motor data derived

from tests applied to equation 3.

The armature resistance and the back emf constant

from each motor can be seen in Table 1.

Applying the rotational variation of Newton’s sec-

ond law to the motor we have:

= T

+ B · ω +J ·

ω (4)

Assuming steady-state,

ω is zero. The torque

static friction is T

and B is the viscous friction con-

stant. The motor torque is T

and it is proportional

to the armature current, T

= k ∗ i

. Substituting this

equation into equation 5, and rearranging the factors

we have:

k · i

= B · ω + T

(5)

Robot@Factory Lite Competition: A Digital Twin Approach for the AGV

313

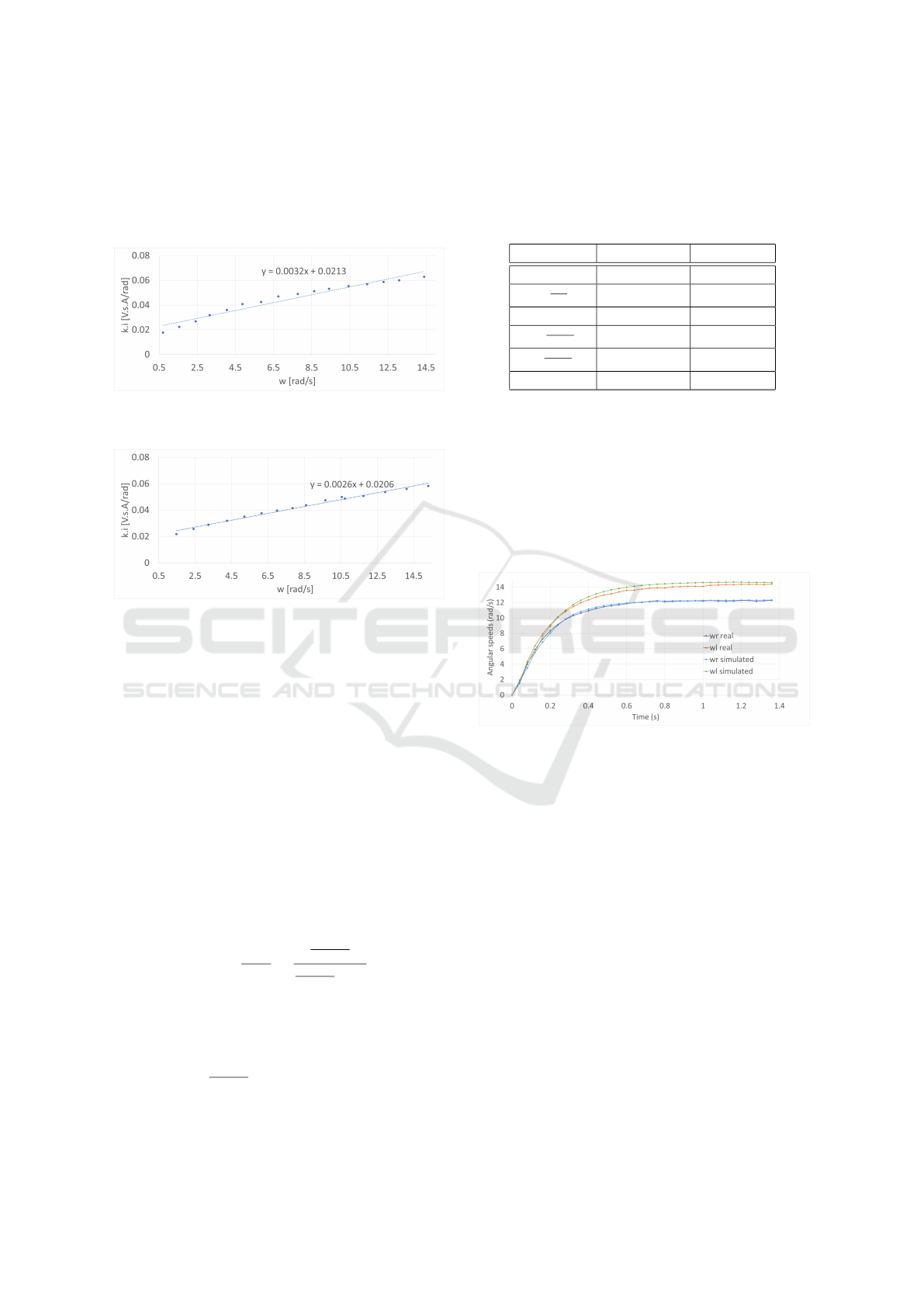
Following the same reasoning as the previous

tests, ﬁfteen tests were performed for each motor and

a linear model was ﬁt for each motors’ data. The right

and left motor tests can be seen in Figures 7 and 8, re-

spectively.

Figure 7: Linear model ﬁt to the right motor data derived

from tests applied to equation 5.

Figure 8: Linear model ﬁt to the left motor data derived

from tests applied to equation 5.

Again, from these tests, the angular coefﬁcient

corresponds to the viscous friction and the linear co-

efﬁcient to the torque static friction. The values of

these parameters for each motor can be seen in Table

4.1.2 Transient Tests

To obtain the inertia of the motors it is necessary to

perform transient tests. They were performed with the

robot suspended on the air so that the resulting mo-

ment of inertia derived from the tests takes only into

account the contribution of the rotor plus the wheel

for each motor. The transfer function of the angular

speed of a DC motor in relation to the input voltage

can be seen in equation 6.

H(s) =

ω(s)

U(s)

s + 1

(6)

The constants are the DC motors parameters.

Again, it was assumed that the inductance was zero

for simplicity reasons. As it can be seen, this is a

ﬁrst-order system where the time constant factor is

represented by

. To obtain J, a voltage step was

applied to the motors and their time constants, τ, were

measured. With them, the only unknown constant is

the moment of inertia. Thus, the time constant fac-

tor was solved for J for each motor. All the obtained

parameters, for each motor, can be seen in Table 1.

Table 1: Parameters of each DC motor.

Parameters Right motor Left motor

Ra [Ω] 6.16 6.41

k [

V.s

rad

] 0.32 0.30

Tq [N.m] 0.021 0.021

B [

N.m.s

rad

] 3.2E-03 2.6E-03

J [

N.m.s

rad

] 3.39E-03 3.42E-03

τ [s] 0.175 0.2

All these parameters, together with all the robot’s

parts dimensions and weights, were applied to the

simulation model in Simtwo. To measure the weights,

a precision scale was used. As for the dimensions, a

pachymeter. After that, transient tests were performed

on the simulated robot’s motors to see their behaviors

in respect to the same step responses applied to the

real robot. The tests applied to both robots can be

seen in Figure 9.

Figure 9: Right and left motors’ open loop step responses

from both robots.

It is clear to see from these responses that the real

robot’s motors have similar responses compared to

their respective simulated ones. Also, it is possible to

see that the real motors’ responses are different from

each other despite being applied the same step input

and being the same model. The internal structure of

the motors can inﬂuence this behavior. Although the

simulated motors behave similarly in respect of their

respective real motors, small differences are present.

These outcomes can be inﬂuenced by a series of fac-

tors such as:

• Intrinsic errors in the measurements caused by the

measurement devices (voltages, currents, angular

speeds, weights, dimensions).

• Added errors by approximation.

• Inserted errors by linear regression estimation.

• Sampling period is limited to approximately 40

ms of the execution period.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

314

4.2 PI Controller

Simple PI controllers for angular speed were designed

for each motor of the real robot. To design the

controllers, the Internal Model Control (IMC) tuning

method was applied (Rivera et al., 1986). As our

model is a ﬁrst-order system, the gains were com-

puted in the way is displayed in Table 2.

Table 2: PI controller for ﬁrst order transfer function with

IMC tuning method.

PI control

·[τ

]

Where τ is the open-loop response time, g

is the

system’s open-loop gain, τ

is the desired closed-loop

response time and, t

, the dead time.

The PI controllers, for both motors of the real

robot, were designed for a closed-loop time response

of 200ms, which is a similar value to the highest open-

loop time response of both motors. Deadtime was

considered zero. The values needed for the calcu-

lations were derived from the transient tests. After

computing the PI parameters, both controllers were

applied to both twins. Their motors’ behaviors were

compared by applying closed-loop step responses to

follow a 4 rad/s reference. The comparison between

the left and right motors of the twins can be seen in

Figures 10 and 11.

Figure 10: Closed loop response of the right motors of both

robots for a 4 rad/s reference.

As can be seen in the illustrations, each motor and

its respective simulated model behave similarly with

a time response of approximately 200ms. Their re-

sponses follow the reference with minimum steady-

state error and without oscillations during the whole

process.

4.3 Digital Twin

A software was developed to monitor and provide

real-time feedback of both robot’s linear and angular

Figure 11: Closed loop response of the left motors of both

robots for a 4 rad/s reference.

speeds. Thus, with the competition simulation scene,

it is possible to see the simulated robot and the real

robot performing the competition’s required tasks si-

multaneously. The software layout can be seen in Fig-

ure 12.

Figure 12: Digital twin software layout.

The charts, displayed by the red arrows in the ﬁg-

ure, are dynamic charts that receive the robot’s speeds

through UDP communication protocol. They are or-

ganized in columns, with the ﬁrst row representing

the linear speeds and the second row, the angular

speeds. The ﬁrst column is data received by the simu-

lated robot. The second column, received by the real

robot. Finally, the last column represents the respec-

tive residual speeds between the twins. Regarding the

UDP communication conﬁguration, the receiving end

is conﬁgured in the location shown by the black ar-

row. The conﬁguration is made by simply choosing

the IP and UDP port that the software will "listen to"

to receive data from the twins. The sending end, on

the other hand, is conﬁgured where the purple arrow

is pointing at. In this location, it is possible to send

speciﬁc commands to each twin or both at the same

time. Finally, the software alerts whenever the twins’

data diverge by more than a threshold and displays

how much time the divergence endured. The alerts

show in the white boxes displayed by the blue arrow.

The left box shows linear speeds’ divergences and the

right one, angular speeds’ divergences. It is important

to emphasize that only the robot’s speeds are moni-

tored (robot’s centroid reference frame), not the indi-

vidual motors’ speeds. To avoid giving false alerts,

Robot@Factory Lite Competition: A Digital Twin Approach for the AGV

315

Figure 13: Real robot and digital twin response to a move straight command.

Figure 14: Real robot and digital twin response to a rotate over its own axis command.

inﬂuenced by the intrinsic noise present in both twins

and by the transient periods of the motors, the residual

data is ﬁltered with a ﬁrst-order IIR ﬁlter.

5 RESULTS

Three tests were performed to test the digital twin.

The idea behind these tests is to give the same com-

mand to both twins and analyze if they are operating

similarly. The x-axis values in the following charts

are displayed in seconds with one decimal point in all

charts. This was done to not pollute the image. The

ﬁrst test was to command the twins’ motors to follow

4 rad/s angular speed references. The twins’ response

can be seen in Figure 13.

As can be seen in the illustration, both robots per-

form similarly. The robot’s angular speeds remained

0, as expected. There is a little disturbance in the

residual linear speed, which is foreseen during the

transient period. As mentioned before, there are no

alerts for two reasons, the ﬁrst is that only the ﬁl-

tered residual is analyzed. The other is that the soft-

ware must detect several times the divergence passing

a threshold before alerting that it is something wrong.

During this period, if the residual values go below the

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

316

Figure 15: Real robot and digital twin response to a sudden stoppage.

Figure 16: Forced alert by stopping the simulated robot in a rotational test.

threshold, the detection counter is set to 0.

The second test was to rotate them over their rota-

tional axes by ordering one motor to follow a 4 rad/s

angular speed reference and the other a -4 rad/s ref-

erence. The robot’s behaviors can be seen in Figure

14.

This illustration shows that the robots similarly

performed the command, same as the previous test.

Their linear speeds remained 0 which is expected

since the robots did not move in any direction. Again,

the ﬁltered residual damps the transient response and

the noise, preventing alerts. Figure 15 shows the

robot’s response to a sudden stoppage after the rota-

tional command.

As can be seen in the ﬁgure, there is a peak dur-

ing the stoppage. This happens because the robot’s

sudden stoppages, although happened in a very small

period, are different. The factors mentioned in 4.1.2,

communications in the entire digital twin system,

simulator, and different processing hardware could all

possibly inﬂuence this behavior. Note that this whole

process happened very fast as can be seen that the en-

tire charts are in the same second.

The third test was to force an alert by purposely

stopping the simulated robot. The test can be seen in

Figure 16.

Robot@Factory Lite Competition: A Digital Twin Approach for the AGV

317

In this test, the rotational command was given to

the twins. However, the motors’ voltage in the sim-

ulator was purposefully set to 0, forcing the robot to

not rotate. After giving the command to both robots

to stop, the alert appeared with the divergence’s du-

ration. This behavior is logical because when the

robot’s stopped, the divergence returned to roughly 0,

below the threshold.

6 CONCLUSIONS

This paper presented the development of a digital twin

for an AGV for the Robot@Factory Lite competition.

The robot’s motors were modeled and its parameters

were estimated. PI controllers for speed were de-

signed for each motor of the real robot. Applying the

same controllers in the simulated robot, the twins be-

haved similarly. Also, a digital twin software was pre-

sented that monitors, in real-time, the behavior of the

twins’ linear and angular speeds, alerting when they

aren’t performing similarly for some reason. The di-

vergence detection was designed to be robust to noise

and transient periods, preventing false alerts. Finally,

three tests were performed, on both twins simultane-

ously, to show the digital twin performance compared

to the real twin. The tests were sufﬁcient to show

that the digital twin is performing very similarly, with

a negligible difference during transient periods, even

with the assumptions made for simpliﬁcation during

the modeling. Therefore, the digital twin will prove

useful for the next competitions as well as by the com-

munity for other scenarios, with the instant feedback

of the robot’s performance and by greatly improving

the transition to the real scenario.

ACKNOWLEDGEMENTS

The project that gave rise to these results received

the support of a fellowship from ”la Caixa” Foun-

dation (ID 100010434). The fellowship code is

LCF/BQ/DI20/11780028. This work is ﬁnanced

by National Funds through the Portuguese funding

agency, FCT - Fundação para a Ciência e a Tecnolo-

gia within project UIDB/50014/2020.

REFERENCES

Lima, J., Costa, P., Brito, T., and Piardi, L. (2019).

Hardware-in-the-loop simulation approach for the

robot at factory lite competition proposal. In 2019

IEEE International Conference on Autonomous Robot

Systems and Competitions (ICARSC), pages 1–6.

IEEE.

P33a (2020). Robot at factory lite. https://github.com/

P33a/RobotAtFactoryLite. Online; accessed 26-

February-2020.

Pairet, E., Ardón, P., Liu, X., Lopes, J., Hastie, H., and

Lohan, K. S. (2019). A digital twin for human-robot

interaction. In 2019 14th ACM/IEEE International

Conference on Human-Robot Interaction (HRI), pages

372–372.

Paulo, C., José, G., José, L., and Paulo, M. (2011). Simtwo

realistic simulator: A tool for the development and

validation of robot software. Theory and Applications

of Mathematics & Computer Science, 1(1):17–33.

Rivera, D. E., Morari, M., and Skogestad, S. (1986). Inter-

nal model control: Pid controller design. Industrial

& engineering chemistry process design and develop-

ment, 25(1):252–265.

Smith, R. et al. (2005). Open dynamics engine.

Tao, F., Zhang, H., Liu, A., and Nee, A. Y. C. (2019). Dig-

ital twin in industry: State-of-the-art. IEEE Transac-

tions on Industrial Informatics, 15(4):2405–2415.

Tao, F., Zhang, M., Liu, Y., and Nee, A. (2018). Digital twin

driven prognostics and health management for com-

plex equipment. Cirp Annals, 67(1):169–172.

Weyer, S., Meyer, T., Ohmer, M., Gorecky, D., and Züh-

lke, D. (2016). Future modeling and simulation of

cps-based factories: an example from the automotive

industry. Ifac-Papersonline, 49(31):97–102.

Zhang, H., Liu, Q., Chen, X., Zhang, D., and Leng, J.

(2017). A digital twin-based approach for designing

and multi-objective optimization of hollow glass pro-

duction line. IEEE Access, 5:26901–26911.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

318