Compact Variable-base ECC Scalar Multiplication using Euclidean

Addition Chains

Fabien Herbaut

, Nicolas M

eloni

and Pascal V

eron

INSPE Nice-Toulon, Universit

e C

ote d’Azur, Institut de Math

ematiques de Toulon, France

Institut de Math

ematiques de Toulon, Universit

e de Toulon, France

Keywords:

Elliptic Curves, Scalar Multiplication, Side-channel Protection, Memory Usage, Addition Chain.

Abstract:

The random generation of Euclidean addition chains ﬁts well with a GLV context (Dosso et al., 2018) and

provides a method with decent performance despite the growth of the base ﬁeld required to get the same level

of security. The aim of this paper is to reduce the size of the base ﬁeld required. Combined with an algorithmic

improvement, we obtain a reduction of 21% of the memory usage. Hence, our method appears to be one of

the most compact scalar multiplication procedure and is particularly suitable for lightweight applications.

1 INTRODUCTION AND

CONTEXT

The increasing importance of smart devices such as

smart cards or sensor networks comes with growing

needs for low cost algorithms in the area of crypto-

graphic primitives. Relevant solutions should involve

low memory usage and a compact code which does

not sacriﬁce protection against physical attacks. The

aim of this paper is to improve a regular and con-

stant time method, so we obtain a very compact al-

gorithm both from a memory usage and size code

point of view. This algorithm could be dedicated for

lightweight applications.

1.1 Purpose and Main Idea

The Euclidean addition chains are sequences of cou-

ples of integers starting from (1,1) and such that (u,v)

leads to (u, u + v) or to (v, u +v). Such chains enable

to take advantage of the ZADD operation, which is an

efﬁcient way to compute the sum of two points of an

elliptic curve with the same Z Jacobian coordinate.

According to (Dosso et al., 2018), this approach

ﬁts well with the GLV-like context of an elliptic curve

endowed with an efﬁciently computable endomor-

phism. Indeed, the method described in (Dosso et al.,

2018) leads to a simple and compact way to compute

the elliptic curve scalar multiplication kP (ECSM) for

a Difﬁe-Hellman key exchange protocol. The main

drawback of this method is that it requires the use of

a larger curve as compared to other methods for the

same security level. But despite the growth of the

base ﬁeld, it provides decent speed results and very

good memory usage performance.

The aim of this paper is to improve the method

described in Section 4 of (Dosso et al., 2018). First,

we obtain an asymptotic reduction of 7.97% of the

size of the base ﬁeld required. Next, we modify the

original ZADD algorithm to save one register over F

For practical usage, we obtain a reduction of 21% of

the memory used in the method described in (Dosso

et al., 2018).

In comparison with the method proposed in

(Dosso et al., 2018), the progress lies in the restric-

tion of the random generation to a subset S of all Eu-

clidean addition chains. Call the chaining (u, v) →

(u,u+v) a small step and the chaining (u,v) →(v,u +

v) a big step. The subset S to which we restrict our-

selves is the one of Euclidean chains with more small

steps than big steps. The subset S has been chosen

such that its chains are sufﬁciently numerous with re-

spect to their growth (see Theorem 1), and quite easy

to randomly generate (see lines 2-6 of Algorithm 3).

1.2 Context

Let us now describe more precisely the context of our

work. We intend to deﬁne a variable scalar multipli-

cation algorithm to be used in the context of Difﬁe-

Hellman key exchange, to provide a regular and con-

stant time algorithm (which is nowadays a minimum

requirement for any cryptographic primitive), to re-

Herbaut, F., Méloni, N. and Véron, P.

Compact Variable-base ECC Scalar Multiplication using Euclidean Addition Chains.

DOI: 10.5220/0010551705310539

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 531-539

ISBN: 978-989-758-524-1

531

spect low memory constraints, to work with an ellip-

tic curve E deﬁned over a prime ﬁeld F

and endowed

with one efﬁcient endomorphism.

1.3 Related Papers

One wants to compute a scalar multiplication point

kP to perform a part of a Difﬁe-Hellman key ex-

change under the above constraints. In (Herbaut

et al., 2010) one suggests to randomly sam-

ple an Euclidean additions chain (P,2P)

small step

−−−−−−→

(P,3P)

big step

−−−−→ (3P,4P) → .. . rather than an integer

In (Gallant et al., 2001) it is proposed to make use

of one efﬁcient endomorphism φ on a curve to per-

form kP. The idea to randomly sample Euclidean

additions chains starting from (P,φ(P)) appears in

(Dosso et al., 2018). These ideas and the notations

are progressively recalled in Section 2.

Note that the idea to randomly sample other ele-

ments than the scalar in order to compute scalar mul-

tiplication also appears in other works, (see for ex-

ample the beginning of Section 4 in (Costello et al.,

2014)). It necessary leads to a study of the repartition

of the computed points (see for example Proposition

4 of (Costello et al., 2014)). The methods described

in (Herbaut et al., 2010) leans on an injectivity result

(Proposition 3) or an asymptotic result (Theorem 1).

As for the main method described in (Dosso et al.,

2018), it leans on the injectivity result of Proposition

4. We recall this statement in Section 2, and we im-

prove it with Theorem 1 of Section 3.

As we claim very good memory management,

we try to provide a fair comparison with competi-

tive side-channel attack resistant scalar multiplication

algorithms in the context of our paper. We give in

Section 4 details about the memory consumption of

the following well-known algorithms: endomorphism

of the x-line (Costello et al., 2014), FourQ (Costello

and Longa, 2015), Ted-glv (Gallant et al., 2001) tak-

ing beneﬁts from the sign-aligned column decompo-

sition of the scalar (Faz-Hern

andez et al., 2015) and

the twisted Edwards coordinates system, Ted127-glv4

(Faz-Hern

andez et al., 2015), the Montgomery ladder

algorithm exploiting the beneﬁt of the Curve25519

(Bernstein, 2006).

2 BACKGROUND AND

NOTATIONS

2.1 Elliptic Curves with One Efﬁcient

Endomorphism and Co-Z

Arithmetic

The well known GLV method was introduced in 2001

by Gallant, Lambert and Vanstone in (Gallant et al.,

2001). It has given rise to many efﬁcient algorithms

in a broader range of contexts (see (Galbraith et al.,

2009; Longa and Sica, 2014; Faz-Hern

andez et al.,

2015; Costello et al., 2014) for instance). As in (Gal-

lant et al., 2001) we will consider an elliptic curve E

deﬁned over a prime ﬁeld F

, endowed with an ef-

ﬁciently computable endomorphism φ : E → E. A

ﬁrst list of such curves and endomorphisms is given in

Section 2 of (Gallant et al., 2001). We will keep the

context and the notations of (F. Sica and M. Ciet and

J-J. Quisquater, 2003). Namely, we will ﬁx a point

P ∈E of order N such that #E/N 6 4, we assume that

+rX + s ∈Z[X] is the characteristic polynomial of

φ and that φ(P)=λP with 0 < λ < N.

Recall that if two different points P and Q given

by their Jacobian coordinates (X : Y : Z) and (X

: Z

) share the same third coordinate Z = Z

(some-

times called the Z-coordinate) then the ZADD opera-

tion introduced in (M

eloni, 2007) computes the sum

P + Q for the elliptic curve law group at a low cost of

5M+2S. Since, this operation and its variants have at-

tracted attention and yielded efﬁcient scalar multipli-

cation schemes (Longa and Miri, 2008; Hutter et al.,

2011; Goundar et al., 2010; Goundar et al., 2011;

Baldwin et al., 2012). To be more precise, the ZADD

operation enables to recover, at the same cost, rep-

resentatives of both P + Q and P with the same Z-

coordinate, or representatives of both P + Q and Q

with the same Z-coordinate.

Lastly, with regard to the memory usage, let us

emphasize that the x-only trick introduced by Mont-

gomery in (Montgomery, 1987) ﬁts well with the Co-

Z arithmetic context. Indeed, consider the formulas

given in (M

eloni, 2007) to perform the addition of two

points with the same Jacobian Z-coordinate: the com-

putation of the X and Y coordinates of the sum does

not involve the Z coordinate of the input. When one

does not care about the Z coordinate, one can perform

the addition saving one register and one multiplica-

tion (so the cost drops down to 4M+2S).

SECRYPT 2021 - 18th International Conference on Security and Cryptography

532

2.2 Random Generation of Euclidean

Addition Chains in GLV-like

Context

The idea of the random generation of chains is intro-

duced in (Herbaut et al., 2010) when the base point

P is ﬁxed. The scope is extended to the context

of variable-base scalar multiplication on a curve en-

dowed with an endomorphism in (Dosso et al., 2018).

The Proposition 4 of the latter paper is the result we

want to improve and exploit in this work. Namely,

this proposition states that under some assumptions

different chains of length ` compute 2

different

points when applying the Algorithm 2 of (Dosso et al.,

2018) and starting from (P,φ(P)). Let us recall what

it means.

We introduce M

= {0,1}

in order to represent

choices of computations in a sequence of ZADD op-

erations. When dealing with elements of M

in this

context, the vocabulary involves the word chains be-

cause of the links with addition chains (see (Brauer,

1939) for example). The words Euclidean addition

chains (EAC in the sequel of this paper) are also used

because of the link with the Euclidean algorithm (see

(Montgomery, 1983) for example).

To introduce Algorithm 1, ﬁx c ∈ M

and a point

P ∈ E. Start from (P,φ(P)). If c

= 1, compute

(P,P + φ(P)) with ZADD. We call this chaining a

small step. If c

= 0, compute (φ(P),P + φ(P)).

We call this chaining a big step. In both cases

the representatives of the computed points share

the same Z-coordinate. In the ﬁrst case, if c

1, compute (P,2P + φ(P)). If c

= 0 compute

(P + φ(P),2P + φ(P)). In the second case, if c

1, compute (φ(P),P + 2φ(P)). If c

= 0 compute

(P + φ(P),P + 2φ(P)). Repeat this procedure for each

bit c

. At the end, sum the two components with a last

call to ZADD. Now assume that φ(P)=λP with λ ∈ Z.

It naturally leads to a point (k

λ)P for some inte-

gers k

and k

. It leads to the Algorithm 1 which cor-

responds to the method of Section 4 in (Dosso et al.,

2018).

Important Remark. This algorithm makes exactly

n + 1 calls to ZADD, where n is the length of c. As

it will be explained in the next section, this size will

be determined by the required security level. Hence,

once the security level of the protocol is settled, the

number of calls to ZADD is constant.

The algorithm requires P ∈ E such that φ(P)=λP

and c = (c

,...,c

) ∈ M

. This algorithm computes

kP where k = (1, λ)

∏

i=1





and where S

and S

denote the matrices deﬁned as follows.

Algorithm 1: EAC Point Mul(c: an addition chain of length

n).

Require: P ∈E and c ∈ M

Ensure: Q = χ

1,λ

(c)P

1: (U

) ← (P,φ(P))

2: for i = 1 .. .length(c) do

3: if c

= 0 then

4: (U

) ← ZADD(U

) [it corresponds to

)]

5: else

6: (U

) ← ZADD(U

) [it corresponds to

)]

7: end if

8: end for

9: (U

) ← ZADD(U

)

10: return Q = U

Deﬁnition 1. S



0 1

1 1



and S



1 1

0 1



To exploit this linear algebra point of view we also

introduce the following deﬁnitions.

Deﬁnition 2. Let (a, b) ∈ N

, s ∈ N

∗

and c =

,...,c

) ∈ M

. We deﬁne:

. ψ

a,b

∏

i=1

and χ

a,b

(a,b)

∏

i=1





. µ(c) =

∏

i=1





Now we understand the statement of the Proposi-

tion 4 in (Dosso et al., 2018). We recall that N de-

notes the order of the point P and that X

+ rX + s is

the characteristic polynomial of the endomorphism φ

as mentionned in subsection 2.1.

Proposition 1. (Proposition 4 in (Dosso et al.,

2018)) If N > F

n+2

(1 +

+ s), then the 2

chains

c ∈ M

compute 2

different points when applying Al-

gorithm 1.

This statement has justiﬁed the following proce-

dure: randomly choose c ∈ M

and compute χ

1,λ

(c)P

with the algorithm above. Unfortunately, the condi-

tion N > F

n+2

(1 +

+ s) involves the use of a curve

of greater size than usual. For instance, for a 128-

bit security level, the conditions of Proposition 4 of

(Dosso et al., 2018) leads to work over a ﬁeld of size

358.

3 OUR CONTRIBUTION

3.1 Notations and Preliminary Results

The main idea of this paper is to consider a subset

S ⊂ M

and to randomly choose c in S rather than

in M

, so it enables to decrease the minimum size

of the curve E. Here the point is to choose a subset

Compact Variable-base ECC Scalar Multiplication using Euclidean Addition Chains

533

S large enough and whose elements c yield couples

) := ψ

1,λ

and k

are not too big

as compared to the order of P. The subset S we pro-

pose in this work is the subset of the chains c ∈ M

whose Hamming weight is greater or equal than half

the size `. This subset offers a good tradeoff between

the two conditions stated above. Its elements are also

easy to produce in a simple and quite symmetric way

(see lines 2-6 of Algorithm 3). It leads to the follow-

ing notations.

Deﬁnition 3. Let ` and w be two non-zero integers.

We deﬁne

. M

`,w

as the set of the elements of {0,1}

of Ham-

ming weight w,

. M

`,>w

as the set of the elements of {0, 1}

of Ham-

ming weight greater or equal to w.

Although the following lemma is an easy conse-

quence of a coefﬁcient by coefﬁcient comparison of

the couples computed by chains, it will make the read-

ing of the proof of Proposition 2 easier.

Lemma 1. Let `, m, a and b be four integers such that

0 6 m 6 ` and 1 ≤ a ≤b. Then

max{χ

a,b

`,>m

}= max{χ

a,b

`,m

Proof. Fix a chain c of length ` and weight

m, and consider any chain ˆc obtained from c by

changing a 0 into a 1. An induction on the length of

the chain enables to prove that the couples arising in

the computation of χ

a,b

the the couples arising in the computation of χ

a,b

( ˆc)

when comparing coefﬁcients by coefﬁcients.

The next result could be considered as the main in-

gredient of the work (Dosso et al., 2018) and of this

contribution. Indeed, when trying to prove that dif-

ferent chains give rise to different points, it enables to

bound k

and k

rather than bounding k

+ k

λ. This

result appears in the section 2.1 of (F. Sica and M.

Ciet and J-J. Quisquater, 2003) and it is also stated in

Lemma 6 of (Longa and Sica, 2014). Proofs release

on the irreductibility of X

+ rX + s on Z[X].

Lemma 2. Let (k

) ∈ Z \{(0,0)}. If k

+ k

λ ≡ 0

(mod N) then

max(|k

|,|k

|) ≥

1 + |r|+ s

3.2 New Theoretical Results

We ﬁrst want to have an upper bound on the coefﬁ-

cient of µ(c) when c is a chain of M

2n,>n

Proposition 2. Let n > 3 be an integer. Then

max{kµ(c)k

∞

| c ∈ M

2n,>n

} = 8α

n−2

+ 11β

n−2

where α

(1+

√

+(1−

√

and β

(1+

√

−(1−

√

Proof. Fix an integer n > 2. We begin by proving

that max{kµ(c)k

∞

| c ∈M

2n,>n

} = max{χ

1,2

2n−2,n−2

}. Recall that for any couple of integers

(x,y) we have







x+y



and S







x+y



so the biggest component of µ(c) is the sum of the

components of µ( ˆc) where ˆc is obtained from c

by removing its ﬁrst element. Taking into account

that the ﬁrst element of c can be 0 or 1, we obtain

that max{kµ(c)k

∞

| c ∈ M

2n,>n

} is the greatest

integer between max{χ

1,1

(c)| c ∈ M

2n−1,>n

} and

max{χ

1,1

(c)| c ∈ M

2n−1,>n−1

}. Using Lemma 1 we

see that one can consider M

2n−1,n

and M

2n−1,n−1

rather than M

2n−1,>n

and M

2n−1,>n−1

. Now, with the

same argument as in the proof of Lemma 1 the max-

imum we look for is max{χ

1,1

(c)| c ∈ M

2n−1,n−1

Remark that whatever the ﬁrst step is a small or a big

one, it maps (1, 1) to (1,2), so the maximum taken is

the maximum between max{χ

1,2

(c)| c ∈ M

2n−2,n−2

}

and max{χ

1,2

(c)| c ∈ M

2n−2,n−1

}. The maximum we

look for is the ﬁrst one for the same reason as above.

We conclude making use of (Herbaut et al., 2010,

Theorem 2) which gives the maximum of χ

1,2

The next result is our main statement: it enables better

memory usage than Proposition 1.

Theorem 1. Let n > 3 be an integer. We consider

an elliptic curve E endowed with an endomorphism φ

whose characteristic polynomial is X

+ rX + s. Let

P ∈ E of prime order N, if

N > (8α

n−2

+ 11β

n−2

)

(1 + |r|+ s)

then, starting from (P,φ(P)), the 2

2n−1

chains c ∈

2n,>n

compute 2

2n−1

different points when applying

the Algorithm 1 .

Proof. We follow the proof of Proposition 4 in

(Dosso et al., 2018). Suppose that the chains c and c

in c ∈M

2n,>n

compute the same point when applying

Algorithm 1. If





= µ(c) and





= µ(c

), then

one should have k

λ ≡k

λ (mod N) and so

−k

) + (k

−k

)λ ≡ 0 (mod N). But the integers

and k

are positive, so with Proposition 2 we get

− k

| < 8α

n−2

+ 11β

n−2

, hence by hypothesis

−k

| <

1+|r|+s

. It remains to apply Lemma 6

of (Longa and Sica, 2014) to obtain









and

SECRYPT 2021 - 18th International Conference on Security and Cryptography

534

thus c = c

, as µ is injective (see Proposition 1 in

(Dosso et al., 2018)).

The necessary condition in this theorem is more

favourable than the one of Proposition 1. Indeed, let

us estimate the ﬁeld size required for a t-bit secu-

rity level. For such a security level we need to have

2n −1 > 2t which implies to take n > t + 1. Thus, if

we take n = t +1, Theorem 1 shows that it is sufﬁcient

to have

N > (8α

t−1

+ 11β

t−1

)

(1 + |r|+ s). (1)

In the worst case we consider we have 1 + |r|+ s =

4. According to the deﬁnition of α and β, the right

hand side of the last inequation (1) can be seen as a

polynomial of degree 2t −2 in (1−

√

2) and (1+

√

2).

If for ﬁrst approximation we only consider the terms

in (1 +

√

2) then the condition becomes

N > 4(1 +

√

2t−2



16 + 121/8 + 44/

√



which amounts to choosing N such that log

(N) >

2.54t − 1.41. Asymptotically we need log

(N) >

2.54t, so as compared to the protocol described in

(Dosso et al., 2018) (where log

(N) > 2.76t) we

asymptotically obtain a gain of 7.97%. We give in

Table 1 the order of the point P necessary for a given

security level computed from inequation (1). For in-

stance in the case of a 128-bit security level, rather

than considering a point P of order 358 as in (Dosso

et al., 2018) we can now consider a point of order 331,

which enables a gain of 7.5%.

3.3 The ZADDu Algorithm

In our implementation, our priority is to minimize the

number of active registers. For this purpose, we use

a slightly modiﬁed version of the ZADD procedure.

We call this procedure ZADDu (see Algorithm 2).

Algorithm 2: ZADDu(X

,Z,A).

1: A ← X

−X

2: Z ←Z.A

3: A ← A

4: X

← X

5: A ← X

6: Y

←Y

−Y

7: X

←Y

8: X

← X

−X

9: X

← X

−A

10: A ← A −X

11: Y

←Y

12: A ← X

−X

13: Y

← A.Y

14: Y

←Y

−Y

Compared to ZADD, it saves one register. Indeed,

the coordinates of the two input points can be used

to store some intermediate results. Hence the register

B used in Algorithm 9 of (Dosso et al., 2018) is not

necessary. It is important to note that this procedure

only uses its ﬁve parameters and one auxiliary register

to perform all its computations, no extra variable is

needed.

With this procedure it is possible to perform a

scalar multiplication using Algorithm 3. There are

two main differences between this algorithm and Al-

gorithm 1. First, note that Theorem 1 requires that

more than half of the bits of the chain c are 1’s. In

practice it only means that more than half of the op-

erations are small steps. As it is purely arbitrary to

consider that a 1 represent a small step, the if state-

ment from line 2 to 6 ensure that the bit b will rep-

resent a big step and thus b ⊕1 a small step. Sec-

ondly, each step of the for loop must compute either

ZADDu(P

) or ZADDu(P

) depending on the

current EAC bit. In order to avoid the if statement

and eliminate a possible cache timing attack, the swap

of variables is achieved using the same trick shown in

ull et al., 2015) (line 9 to 11).

From a memory perspective, it is important to note

that the whole scalar multiplication only requires 6

active registers for storing 6 ﬁeld elements. Most

scalar multiplication algorithms require at least so

many registers just to store the base point P (that must

be kept during the whole process, for instance when

using double and add) and the result value Q. If the

Z-coordinate is not required by the protocol, it is pos-

sible to perform a (X,Y )-only scalar multiplication,

saving 1 register as the computation involving Z be-

comes superﬂuous (M

eloni, 2007).

3.4 First Implementation and Practical

Results

We describe here a C implementation of our scalar

multiplication scheme. It is worth noting that it is

a proof of concept implementation, meaning we do

not aim at any speed record, and that is why all ﬁeld

arithmetic operations are performed using the GNU

Multi Precision library

. We measured the compu-

tation time of our method. For practical reasons we

have used EAC of length 256 so that we can gener-

ate 2

255

different chains leading to a potential secu-

rity of 127.5 bits. This is coherent with other stan-

dards such as curve25519 (whose security is 126

bits) (Bernstein, 2006). Based on Table 1, it is suf-

ﬁcient to choose a base ﬁeld deﬁned by a prime p of

331 bits in order to achieve this level of security. That

is why we used the curve E

331

) : y

= x

+ 3

with p

331

= 2

331

−36301 for our experiments.

We use the endomorphism φ: (x,y) 7→ (βx,y)

http://github.com/eac-team/eac scalarmult

Compact Variable-base ECC Scalar Multiplication using Euclidean Addition Chains

535

Table 1: Field and chain sizes required for a given security level when φ satisﬁes φ

+ rφ + s = 0 and (r, s) =

(0,1)/(1, 1)/(−1,2).

Security level 80 96 112 128 192 256 384

Chain length 162 194 126 258 386 514 770

Field size 209 250 290 331 494 657 982

where β is an element of order 3 so that φ satisﬁes

the equation φ

+ φ + 1 = 0. With the vocabulary of

Section 3 we have r = s = 1 so the results of Table 1

do apply.

Measurements were performed on an Intel(R)

Core(TM) i5-6500 CPU 3.20GHz using gcc 9.3.0 and

gmp 6.2.1. The test procedure ﬁrst runs 1000 times the

scalar multiplication function to heat the cache. Then

1000 random data sets are used and for each of them,

one takes the minimum as well as the median value

of the execution clock cycle numbers over a batch of

1000 runs. The performance is the average of all the

minimums and median values. Cycle count is done

as recommended in (Paoloni, 2010). The results ob-

tained with curve E

331

are given in table 2.

Table 2: Performance (CPU cycles) for a 128-bit security

level.

Min Median

EAC 1,397,527 1,400,548

EAC (X,Y )-only 1,199,439 1,201,950

To give the reader an order of idea, there are sev-

eral benchmarks available on the SUPERCOP site

(Bernstein and Lange, 2008) for a Difﬁe-Helmann ex-

change on an elliptic curve

. All the results corre-

spond to optimized versions of Difﬁe-Helmann key

exchange on different curves. Our implementation is

just a proof of concept and relies on the general GNU

multiprecision library, hence it cannot be considered

as an optimized implementation. However, let us con-

sider as an example the NIST P-256 curve which is an

international standard used in OpenSSL. Three dif-

ferent implementations of this curve are available in

the SUPERCOP package. The ﬁrst one, developped

by Y. Nawaz and G. Gong (University of Waterloo,

Canada), only runs on Sun’s Ultrasparc processors,

hence we could not perform any evaluation on our

platform. The second one (named wbl) has been de-

velopped by Watson Ladd (Cloudfare company) from

the source code of the NIST P-256 implementation of

the OpenSSL project developped by Adam Langley

(Google). It contains optimized arithmetic operations

and uses Jacobian coordinates (like our protocol). The

last one (named ref), developped by Jan Mojzis

, is

https://bench.cr.yp.to/results-dh.html

https://github.com/janmojzis

a constant-time version which uses Jacobian coordi-

nates and implements low-level fast arithmetic (un-

like our proof of concept). We followed the procedure

described in the SUPERCOP package to evaluate the

wbl and ref versions. We obtained the following out-

puts on our platform :

REF version :

20210125 ionplatform amd64 20210306

crypto_dh nistp256/timingleaks cycles -

1139366 1140132 1139246 1138687 ...

1145814 1139340 1140060 1139187

WBL version :

20210125 ionplatform amd64 20210306

crypto_dh nistp256/timingleaks cycles -

689569 689551 689520 689250 ...

689827 689520 688843 689639

Each value corresponds to the number of cycles re-

quired to compute one scalar multiplication. Hence

our non-optimized version is competitive with the ref

version and it is almost half as fast as the wbl ver-

sion. Once again, the purpose of this section is not to

claim any speed record but to show that, despite the

extra cost in terms of ﬁeld size, our algorithm remains

practical speed wise compared to existing standards.

Algorithm 3: EACsmult(X

, c).

Require: β ∈ F

, P in afﬁne coordinates

Ensure: Return Q = (X

,Z) the point computed from

(P,φ(P)) and the Euclidean addition chain c

1: w ← weight(c)

2: if w 6 length(c)/2 then

3: b ←0

4: else

5: b ←1

6: end if

7: X

,Z ←X

.β,Y

8: for i = 1 .. .length(c) do

9: A ←(X

⊕X

) ×(c

⊕b)

10: X

← X

⊕A,X

⊕A

11: A ←(Y

⊕Y

) ×(c

⊕b)

12: Y

←Y

⊕A,Y

⊕A

13: ZADDu(X

,Z)

14: end for

15: ZADDu(X

,Z)

16: return X

SECRYPT 2021 - 18th International Conference on Security and Cryptography

536

4 MEMORY USAGE

The aim of this section is to compare our approach

with other well known side-channel attack resistant

scalar multiplication algorithms from a memory us-

age point of view.

We sum up the comparison details in Table 3 for

a 128-bit level of security. The ﬁrst column recalls

the size of the prime p (given in bits). Then, the

“Inputs” double-column gathers the number of F

registers and the corresponding size (given in bytes)

of the input data of the scalar multiplication proce-

dure. The “ECSM” (Elliptic Curve Scalar Multi-

plication) double-column gathers the number of F

registers and the corresponding size (given in bytes)

of the ancillary data used in addition and doubling

formulas. Last, the “Total” column summarizes the

sizes (given in bytes) of the whole data involved in

the ECSM procedure. For the reader’s convenience

we now provide some details to better understand the

memory count for the different methods.

X-line (Costello et al., 2014). The ECSM proce-

dure takes as inputs four afﬁne elements x(P), x(Q),

x(P −Q) and x(P + Q) where Q = ψ(P). Each el-

ement has two F

coordinates (Z : T ) and each el-

ement of F

is encoded into two F

-registers. To

compute kP, the procedure uses the ADD AFFINE

and DBLADD AFFINE formulas described in (Bern-

stein and Lange, 2005). However, considered “as is”,

these formulas are not optimal for memory usage. We

provide in Algorithms 4 and 5 modiﬁed versions in

order to minimize the number of registers. The letter

in bracket indicates the name of the register originally

used in (Bernstein and Lange, 2005). We notice that

6 supplementary F

elements (i.e 12 F

-registers)

are needed for these formulas. Moreover the whole

ECSM procedure requires 4 F

-registers (z

,...,z

)

and 3 afﬁne points T

(i.e 12-F

registers)

Algorithm 4: ADD AFFINE(X

1: X

← X

+ Z

(A)

2: Z

← X

−Z

(D)

3: DA ← X

×Z

4: X

← X

−Z

(B)

5: Z

← X

+ Z

(C)

6: CB ←X

×Z

7: X

← (DA +CB)

8: Z

← X

×(DA −CB)

9: return X

Ted-glv-Sac. To compute kP we exploit the well-

known GLV method (Gallant et al., 2001) on a curve

deﬁned over F

with one efﬁciently computable endo-

morphism, and the Sign-Aligned Column decompo-

sition of k decribed in (Faz-Hern

andez et al., 2015).

Algorithm 5: DBLADD AFFINE(X

1: X

← X

+ Z

(A)

2: Z

← X

−Z

(D)

3: Z

← X

×Z

(DA)

4: X

← X

−Z

(B)

5: Z

← X

+ Z

(C)

6: Z

← X

×Z

(CB)

7: X

← X

(AA)

8: BB ← X

9: E ← X

−BB

10: X

← X

×BB

11: X

← (Z

+ Z

)

12: Z

← X

×(Z

−Z

)

13: Z

← E ×(BB + a24 ×E)

14: return X

The points are represented using the Twisted Ed-

wards coordinates system. To obtain better perfor-

mances, point doubling and addition are computed

mixing standard twisted Edwards coordinates with

extended twisted Edwards coordinates. Standard

twisted Edwards coordinates are encoded on 3 F

registers while extended twisted Edwards coordinates

need 4 resisters. The algorithm is described in (Dosso

et al., 2018, Alg. 7 )

The point doubling takes as input extended twisted

Edwards coordinates and outputs extended twisted

Edwards coordinates (for the point Q). The corre-

sponding formula (non optimized for memory) can be

found in the section 3.3 of (Hisil et al., 2008). The

C implementation shows that in practice only the 4

registers of the point Q and 2 additional registers are

needed to update Q. The point addition takes as input

extended twisted Edwards coordinates and standard

twisted Edwards coordinates. The output is expressed

in extended twisted Edwards coordinates. The for-

mula is given in section 3.2 of (Hisil et al., 2008)

when a = −1 and Z

= 1. In the C implementation

which is provided, only the 4 registers of the point Q

and 2 additional registers are needed to perform this

point addition. Hence 6 registers are needed to com-

pute any of these two operations. Last, the input of

the ECSM algorithm consists of two points given in

standard twisted Edwards coordinates, that is 6 regis-

ters.

Ted127-glv4 (Faz-Hern

andez et al., 2015). Here

the authors take beneﬁt of two efﬁciently computable

endomorphisms φ and ψ on a curve deﬁned over

. The points are represented either in standard

twisted Edwards coordinates or in extended twisted

Edwards coordinates. Each coordinate is encoded

on 2 F

-registers. The input of the algorithm con-

sists of four points: P, φ(P), ψ(P), φψ(P) (we need

4 coordinates for each of these points, see annex B

of (Faz-Hern

andez et al., 2015)). It gives a total of

A C implementation is available on

https://github.com/eacElliptic/Scalar-multiplications/tree/

master/C/with edwards coord/sac glv

Compact Variable-base ECC Scalar Multiplication using Euclidean Addition Chains

537

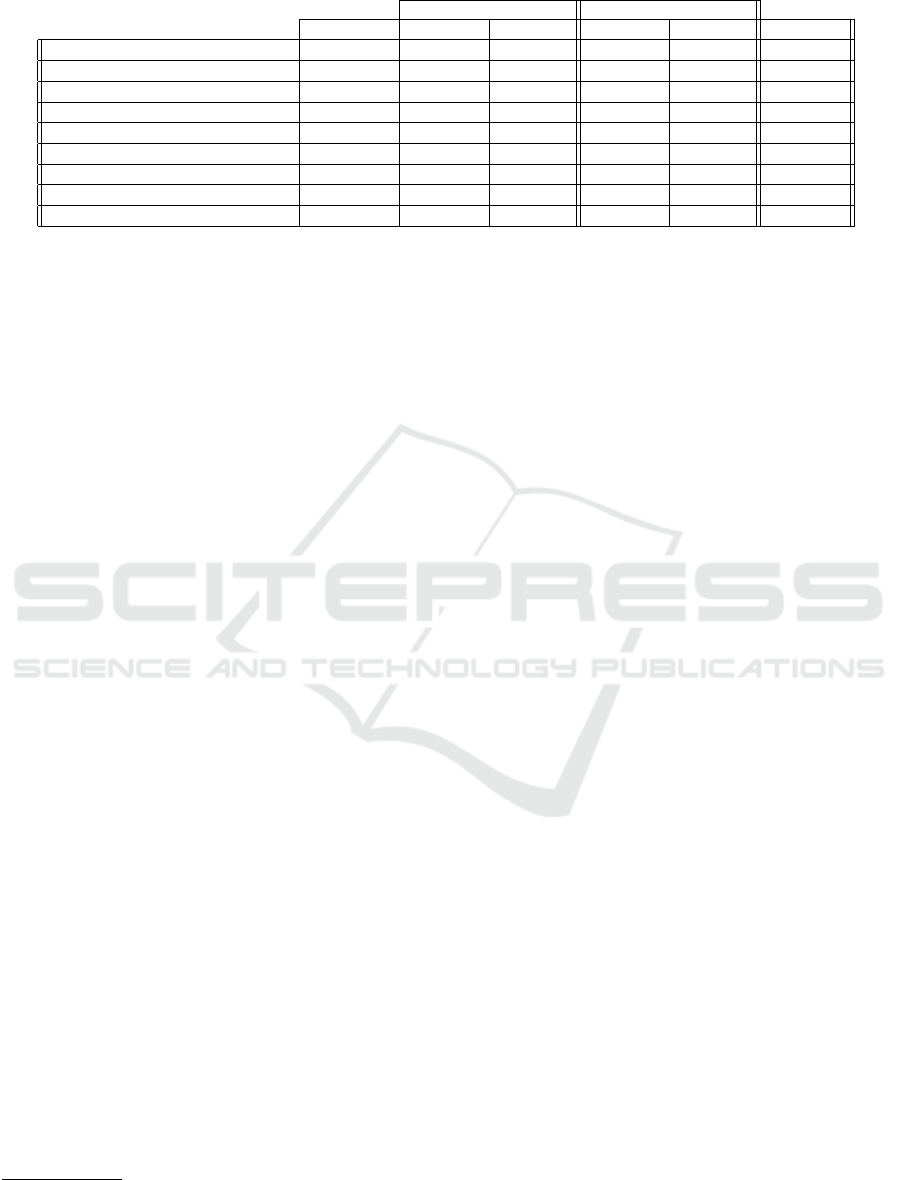
Table 3: Memory storage for a 128-bit security level.

Inputs ECSM

log

(p) (bits) F

registers Size(bytes) F

registers Size(bytes) Total

x-line (Costello et al., 2014) 128 16 256 28 448 704

Ted-glv-sac 256 6 192 6 192 384

Ted127-glv4 (Faz-Hern

andez et al., 2015) 127 32 508 48 762 1270

FourQ(Costello and Longa, 2015) 127 4 64 98 1556 1620

Montgomery(Bernstein, 2006) 256 1 32 6 192 224

EAC (Dosso et al., 2018) 358 5 224 2 90 314

EAC (this paper) 331 5 207 1 42 249 (-21%)

EAC (X ,Y )-only (Dosso et al., 2018) 358 4 179 2 90 269

EAC (X ,Y )-only (this paper) 331 4 166 1 42 207 (-23%)

32 F

-registers. Three coordinates are used to en-

code P, which are later extended to 4 coordinates.

In the case of variable base scalar multiplication, as

explained in (Faz-Hern

andez et al., 2015), 4 more

points are computed during the computation of kP.

Each point is represented using 4 coordinates (X +

Y,Y −X, 2Z,2T ), which leads to 32 F

-registers. The

results given in table 3 come from (Faz-Hern

andez

et al., 2015) where the formulas of (Hisil et al., 2008)

have been adapted to reduce memory storage. The

algorithm computes a doubling followed by an addi-

tion. The result of these operations is stored in a point

Q which is represented by 3 coordinates plus two ad-

ditional elements of F

, namely T

and T

(see (Ham-

burg, 2012) for the description of the Hamburg’s “ex-

tensible” strategy which requires 10 registers). Dou-

bling needs 2 additional elements of F

, hence 4 reg-

isters (note that in Algorithm 11 of (Faz-Hern

andez

et al., 2015) X

and Z

can be used instead of X

and

). A point addition requires 3 F

-elements, so 6

registers (X

, Y

and Z

can be also used instead of

, Y

and Z

if line 10 is computed before line 8 in

Algorithm 11 of (Faz-Hern

andez et al., 2015)). To

conclude, doubling and adding can be done with 6

registers for additional elements and 10 registers for

the storage of the point Q.

FourQ (Costello and Longa, 2015). The ECSM is

processed on an elliptic curve deﬁned over F

and

endowed with two efﬁciently computable endomor-

phisms. Computations are done using twisted Edward

coordinates. Elements of F

are represented using

two F

-registers.

The variable-base scalar multiplication is imple-

mented in the function ecc_mul of the ecpp2.c ﬁle.

The input consists of two points given in afﬁne co-

ordinates that require 8 F

-registers. The function

needs a point R with 5 coordinates (X,Y, Z,T

) and

9 points (S, T

,. . . , T

) with 4 coordinates (X +Y,Y −

The results given in Table 3 come from http://research.

microsoft.com/en-us/projects/fourqlib/

X,2Z, 2dT ), which leads to a total of 82 F

-registers.

Notice that doubling a point (function eccdouble

from ecpp2_core.c) only needs two extra elements

of F

(i.e 4 registers). Adding two points (func-

tion eccadd from ecpp2_core.c) requires one extra-

point R given by its 4 coordinates (X +Y,Y −Z,Z,T )

and two elements of F

which leads to a total of 12

registers. The whole ECSM needs 98 F

-registers.

Montgomery Ladder (Montgomery, 1987).

Montgomery curves combined with the Montgomery

ladder algorithm give rise to fast and secure ECSM

and are of particular interest for elliptic curve cryp-

tography. Since December 2016, the IETF (Internet

Engineering Task Force) uses two Montgomery

curves (Curve25519 (Bernstein, 2006) and Curve448

(Hamburg, 2015)) for instantiating Difﬁe-Hellman

protocols named X25519 and X448 in the Internet

Key Exchange Protocol Version 2 (IKEv2). We focus

on Curve25519 which is deﬁned over F

. Results

given in table 3 come from (D

ull et al., 2015) where

the authors use formulas for the ladder step that

minimize the number of temporary (stack) variables

(see Algorithm 2 of (D

ull et al., 2015)). The ECSM

algorithm takes as input the x-coordinate of P (one

-register). The algorithm needs 6 registers (X

, X

, Y

, T

and T

) to process.

EAC and EAC (X,Y )-only (this Paper). The al-

gorithm takes as input data the points P and φ (P).

Five registers are required to store these points. For

the (X,Y )-only version, only four F

-registers are re-

quired. We stress that in this case the Z-coordinate is

not required in the ZADDu procedure. To compute

one step of the main loop of Algorithm 3, only one

additional register is used in ZADDu in both cases.

Notice that one of the main advantage of our method

is that after the ﬁrst iteration of the main loop the in-

put data are not used again. Hence the corresponding

registers can be used to store new computed values.

This is not the case for the preceding methods.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

538

To conclude this section, let us supply some ar-

guments about the natural compacity of the code in-

duced by our method. First, when compared to the

classical algorithms which use endomorphisms, we

do not need to implement any decomposition of the

scalar k. Second, when compared to methods which

need to implement double and addition formulae, our

method uses only one operation ZADDu which is

easy to implement in a compact way.

REFERENCES

Baldwin, B., Goundar, R. R., Hamilton, M., and Marnane,

W. P. (2012). Co-z ECC scalar multiplications for

hardware, software and hardware-software co-design

on embedded systems. J. Cryptographic Engineering,

2(4):221–240.

Bernstein, D. J. (2006). Curve25519: New Difﬁe-Hellman

speed records. In Yung, M., Dodis, Y., Kiayias,

A., and Malkin, T., editors, Public Key Cryptogra-

phy - PKC 2006, pages 207–228, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Bernstein, D. J. and Lange, T. (2005). Explicit-Formulas

Database. https://www.hyperelliptic.org/EFD/.

Bernstein, D. J. and Lange, T. (2008). ebacs:

Ecrypt benchmarking of cryptographic systems.

https://bench.cr.yp.to, accessed 1 march 2021.

Brauer, A. (1939). On addition chains. Bulletin of the Amer-

ican Mathematical Society, 45(10):736–739.

Costello, C., Hisil, H., and Smith, B. (2014). Faster com-

pact Difﬁe–Hellman: Endomorphisms on the x-line.

In Nguyen, P. Q. and Oswald, E., editors, Advances

in Cryptology – EUROCRYPT 2014, pages 183–200,

Berlin, Heidelberg. Springer Berlin Heidelberg.

Costello, C. and Longa, P. (2015). FourQ: four-dimensional

decompositions on a Q-curve over the Mersenne

prime. In Advances in Cryptology – ASIACRYPT

2015, Auckland, New Zealand , pages 214–235.

Berlin: Springer.

Dosso, Y., Herbaut, F., M

eloni, N., and V

eron, P. (2018).

Euclidean addition chains scalar multiplication on

curves with efﬁcient endomorphism. Journal of Cryp-

tographic Engineering, 8(4):351–367.

ull, M., Haase, B., Hinterw

alder, G., Hutter, M., Paar, C.,

anchez, A. H., and Schwabe, P. (2015). High-speed

curve25519 on 8-bit, 16-bit, and 32-bit microcon-

trollers. Des. Codes Cryptography, 77(2–3):493–514.

F. Sica and M. Ciet and J-J. Quisquater (2003). Anal-

ysis of the Gallant-Lambert-Vanstone method based

on efﬁcient endomorphisms: elliptic and hyperelliptic

curves. In Selected Areas in Cryptography, volume

2595 of LNCS, pages 21–36. Springer.

Faz-Hern

andez, A., Longa, P., and S

anchez, A. H. (2015).

Efﬁcient and secure algorithms for GLV-based scalar

multiplication and their implementation on GLV-GLS

curves (extended version). J. Cryptographic Engi-

neering, 5(1):31–52.

Galbraith, S. D., Lin, X., and Scott, M. (2009). Endomor-

phisms for faster elliptic curve cryptography on a large

class of curves. In Advances in Cryptology - EURO-

CRYPT 2009, volume 5479 of LNCS, pages 518–535.

Springer Berlin Heidelberg.

Gallant, R. P., Lambert, R. J., and Vanstone, S. A. (2001).

Faster point multiplication on elliptic curves with ef-

ﬁcient endomorphisms. In Advances in Cryptology

— CRYPTO, volume 2139 of LNCS, pages 190–200.

Springer.

Goundar, R. R., Joye, M., and Miyaji, A. (2010). Co-Z

addition formulæ and binary ladders on elliptic curves

- (extended abstract). In Cryptographic Hardware and

Embedded Systems, CHES 2010, pages 65–79.

Goundar, R. R., Joye, M., Miyaji, A., Rivain, M., and

Venelli, A. (2011). Scalar multiplication on Weier-

straß elliptic curves from co-z arithmetic. Journal of

Cryptographic Engineering, 1(2):161–176.

Hamburg, M. (2012). Fast and compact elliptic-curve

cryptography. Cryptology ePrint Archive, Report

2012/309. https://eprint.iacr.org/2012/309.

Hamburg, M. (2015). Ed448-goldilocks, a new elliptic

curve. Cryptology ePrint Archive, Report 2015/625.

https://eprint.iacr.org/2015/625.

Herbaut, F., Liardet, P.-Y., M

eloni, N., T

eglia, Y., and

eron, P. (2010). Random euclidean addition chain

generation and its application to point multiplication.

In INDOCRYPT 2010, volume 6498, pages 238–261,

Hyderabad, India. Springer.

Hisil, H., Wong, K. K.-H., Carter, G., and Dawson,

E. (2008). Twisted Edwards curves revisited. In

Advances in Cryptology – ASIACRYPT 2008, Mel-

bourne, pages 326–343. Berlin: Springer.

Hutter, M., Joye, M., and Sierra, Y. (2011). Memory-

constrained implementations of elliptic curve cryptog-

raphy in co-Z coordinate representation. In Progress

in Cryptology - AFRICACRYPT 2011, pages 170–187.

Longa, P. and Miri, A. (2008). New Composite Operations

and Precomputation Scheme for Elliptic Curve Cryp-

tosystems over Prime Fields, pages 229–247. Springer

Berlin Heidelberg, Berlin, Heidelberg.

Longa, P. and Sica, F. (2014). Four-dimensional Gallant–

Lambert–Vanstone scalar multiplication. Journal of

Cryptology, 27(2):248–283.

eloni, N. (2007). New point addition formulae for ECC

applications. In Arithmetic of Finite Fields, volume

4547 of LNCS, pages 189–201. Springer Berlin / Hei-

delberg.

Montgomery, P. L. (1983). Evaluating Recurrences of form

m+n

= f (x

m−n

) via Lucas chains. Available at

ftp.cwi.nl:/pub/pmontgom/Lucas.ps.gz.

Montgomery, P. L. (1987). Speeding the Pollard and elliptic

curve methods of factorization. Mathematics of Com-

putation, 48(177):243–243.

Paoloni, G. (2010). How to benchmark code execu-

tion times on intel® ia-32 and ia-64 instruction

set architectures. https://www.intel.com/content/

dam/www/public/us/en/documents/white-papers/

ia-32-ia-64-benchmark-code-execution-paper.pdf.

Compact Variable-base ECC Scalar Multiplication using Euclidean Addition Chains

539