The ALNS Metaheuristic for the Maintenance Scheduling Problem
David Woller
1,2 a
and Miroslav Kulich
1 b
1
Czech Institute of Informatics, Robotics, and Cybernetics, Czech Technical University in Prague,
Jugosl
´
avsk
´
ych partyz
´
an
˚
u 1580/3, 160 00 Praha 6, Czech Republic
2
Department of Cybernetics, Faculty of Electrical Engineering, Czech Technical University in Prague,
Karlovo n
´
am
ˇ
est
´
ı 13, 121 35 Praha 2, Czech Republic
Keywords:
Adaptive Large Neighborhood Search, Metaheuristics, Combinatorial Optimization, Maintanance Scheduling,
ROADEF 2020.
Abstract:
Transmission maintenance scheduling (TMS) is an important optimization problem in the electricity distribu-
tion industry, with numerous variants studied and methods proposed over the last three decades. The ROADEF
challenge 2020 addresses a novel version of the TMS problem, which stands out by having multiple time-
dependent properties, constraints, and a risk-based aggregate objective function. Therefore, the problem is
more complex than the previous formulations, and the existing methods are not directly applicable. This paper
presents a method based on the Adaptive Large Neighborhood Search metaheuristic. The method is compared
with the best-known solutions from the challenge qualification phase, in which more than 70 teams partici-
pated. The result shows that the method yields consistent performance over the whole dataset, as the method
finds the best-known solutions for half of the dataset and finds solutions consistently within 5h gap.
1 INTRODUCTION
The electric power transmission and distribution in-
dustry is a classical field of application of operations
research methods. The electric power is delivered to
a large number of customers from multiple power sta-
tions through a vast network of physical transmission
lines. The described structure fits perfectly on a flow
network from graph theory, and classical algorithms
have an apparent use in the industry (Than Kyi et al.,
2019). On the contrary, the industry’s practical prob-
lems lead to significant theoretical results, such as the
first known algorithm for finding a minimum span-
ning tree in a graph (Bor
˚
uvka, 1926).
This paper addresses a variant of the transmis-
sion maintenance scheduling (TMS) problem (Froger
et al., 2016). The goal is to schedule the network
maintenance, where scheduled tasks correspond to in-
terventions in the network. These interventions are
necessary to carry out maintenance on the transmis-
sion power lines. The problem is complex because it
has many time-dependent constraints. These are inter-
vention duration, limited resources, or some interven-
tions’ mutual exclusiveness. The minimized objective
a
https://orcid.org/0000-0001-8809-3587
b
https://orcid.org/0000-0002-0997-5889
is a risk-induced cost of the schedule, where the risk
is based on historical data.
The problem is assigned within the ROADEF
challenge 2020. ROADEF challenge is an interna-
tional competition held every two years since 1999.
The competition aims to identify a previously un-
solved, real-world industrial problem and present it
to the operations research community. The competi-
tion’s time span is 16 months, and more than 50 teams
usually participate in the challenge. The 2020 prob-
lem is assigned by the operator of the French power
network (the largest in Europe), the RTE company.
A solution method based on the Adaptive
Large Neighborhood Search (ALNS) metaheuris-
tic (Pisinger and Ropke, 2010) is presented. The
method is based on repeated partial destroying and re-
pairing a current schedule, followed by a local search
phase. A metaheuristic approach was selected, as the
competition instances with up to 1000 interventions
are beyond the exact solvers’ capabilities. The ALNS
seems promising, as the problem at hand allows for
designing many destroy and repair heuristics.
The contributions of the paper are the following.
• The ALNS is adapted for the scheduling prob-
lem. An augmented objective function for han-
dling constraint violations is proposed.
156
Woller, D. and Kulich, M.
The ALNS Metaheuristic for the Maintenance Scheduling Problem.
DOI: 10.5220/0010552101560164
In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 156-164
ISBN: 978-989-758-522-7
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

• A bank of destroy and repair heuristics is pro-
posed. These are either entirely new heuristics,
or previously proposed heuristics tailored to the
problem. The heuristics copy various partial prop-
erties of the problem.
• A set of problem-specific local search operators is
proposed. These operators are designed to further
refine a schedule rearranged by the heuristics.
The presented method yields consistent perfor-
mance on the competition qualification dataset, pro-
ducing solutions within a 5h gap from the best-
known solutions for all instances. It currently qual-
ified for the semi-final phase; therefore, further im-
provements are planned.
The rest of the paper is structured as follows. Sec-
tion 2 discusses the related works. Section 3 pro-
vides a formal description of the maintenance plan-
ning problem. The proposed method is described in
Section 4. Experimental results are presented and dis-
cussed in Section 5 and Section 6 concludes the paper
and elaborates on future work.
2 RELATED WORKS
The ROADEF challenge 2020 maintenance schedul-
ing problem can be seen as a variant of the TMS prob-
lem. The TMS goal is to schedule interventions in a
transmission network to carry out the necessary pre-
ventive maintenance. Another closely related prob-
lem is the Generator Maintenance Scheduling prob-
lem (GMS). The goal of the GMS is to determine
a schedule of stopping power generating units, but
it often has similar objectives and constraints as the
TMS (Froger et al., 2016). Both problems are gener-
ally NP-hard, may be nonlinear and nonconvex.
The TMS is usually described by a transporta-
tion model (Abirami et al., 2014), less commonly
by a DC power flow model (Da Silva et al.,
2000). The considered objective function is typ-
ically reliability-based (Schl
¨
unz and Van Vuuren,
2013), cost-based (El-Sharkh, 2014) or a multiobjec-
tive combination of both (Moro and Ramos, 1999).
The most common constraints are admissible time
windows for individual interventions, intervention
precedence and overlapping, limited workforce re-
sources, capacity constraints of the transmission lines,
minimum customer demand, and reliability require-
ments (Froger et al., 2016). In order to manage the
uncertainty necessarily arising in the TMS due to ex-
ternal factors such as weather conditions or fluctu-
ations in demand, various models for explicitly de-
scribing it are employed (e.g., the loss of load proba-
bility (Reihani et al., 2012) or the expected energy not
served (Lu et al., 2012)).
Concerning the solution methods, both exact and
heuristic methods are widely applied. As for the ex-
act methods, dynamic programming (Huang, 1997)
and mixed-integer programming (Mollahassani-Pour
et al., 2014) proved to be feasible only for small
and medium-sized problems. The performance of ex-
act solvers was often successfully improved by us-
ing the Benders decomposition technique (Geetha
and Swarup, 2009) or by coupling mathematical
programming with heuristics, such as genetic algo-
rithms (Feng et al., 2009). However, metaheuristics
are often preferred for approximate solving of the
largest instances. These population-based methods:
genetic algorithms (Volkanovski et al., 2008), and
particle swarm optimization (Suresh and Kumarap-
pan, 2013) are the most commonly used metaheuris-
tics. Local search-oriented methods were used as
well, for example, simulated annealing (Saraiva et al.,
2011) or tabu search (Burke and Smith, 2000).
The problem addressed in this paper differs in sev-
eral aspects that prevent from using the existing meth-
ods. First, the uncertainty is implicitly incorporated in
the input data, which contains risk-based cost for each
possible start time of every intervention and all rele-
vant crisis scenarios. These costs are based on his-
torical data collected by the network operator. Sec-
ond, all partial properties, such as interventions’ du-
ration and mutual exclusiveness, resource constraints,
or risk values, are time-dependent. Third, the ob-
jective function minimizes the aggregation of risk-
induced cost values, which are evaluated over various
hazardous scenarios.
3 PROBLEM FORMULATION
This section formally defines the maintenance
scheduling problem and it is structured as follows. All
variables needed for formulating the scheduling prob-
lem are defined in Section 3.1. The constraints on a
valid schedule are listed in Section 3.2 and the objec-
tive function is provided in Section 3.3. More details
about the problem can be found in (Ruiz et al., 2020).
3.1 Notations
This section describes all inputs and output of the
maintenance scheduling task. The transmission net-
work can be represented by a graph, where the edges
correspond to the individual power lines. The goal
of the scheduling task is to optimize the schedule of
interventions in the network, which can be seen as a
The ALNS Metaheuristic for the Maintenance Scheduling Problem
157

temporary removal of the graph edges. These inter-
ventions are the tasks to be scheduled. An explicit
representation of the network graph is not needed for
formulating the problem.
Planning horizon is finite and discrete. Let us define
the number of time steps as T ∈ N. The discrete-time
horizon is then defined as H = {1,..,T }. The value of
T determines the schedule’s resolution, e.g., T = 53
corresponds to weeks and T = 365 to days.
Interventions are the tasks to be scheduled. They
correspond to disconnections of individual power
lines from the network necessary for their mainte-
nance. I denotes the set of all interventions. The du-
ration of an intervention i ∈ I, denoted as ∆
i,t
∈ N,
is time variable due to weekends or public holidays,
thus depending on its start time t ∈ H.
Exclusions are defined for some interventions that
cannot be scheduled simultaneously. These are typ-
ically power lines that are physically too close, and
disconnecting them at the same time would increase
the risk of network failure to an unacceptable level.
An exclusion is a triplet (i
1
,i
2
,t), where i
1
,i
2
are two
interventions that cannot be both scheduled at time
t ∈ H. The set of all exclusions is denoted as Exc.
Resources are required to schedule an intervention.
These correspond to groups of workers with different
skills. The set of all resources is denoted as C. Each
resource has different capacity and time availability.
Furthermore, some resources must have some mini-
mal utilization. Therefore, each resource c ∈ C is as-
signed a lower usage bound l
c
t
and an upper bound u
t
c
for each time t ∈ H. The demand for resource c ∈ C
at time t ∈ H by an intervention i ∈ I is then given by
r
c,t
i,t
0
∈ R, where t
0
is the intervention start time.
Risk of financial loss is always linked to performing
an intervention. This risk is caused by unpredictable
events called scenarios, such as power outages due to
extreme weather or a malfunction. The risk increases
proportionally to the rate of weakening the network
by the interventions. As some of the scenarios are
seasonal (e.g., frequent storms), each time t ∈ H is
assigned a set of possible scenarios S
t
.
The risk value at time t ∈ H is then expressed as
risk
s,t
i,t
0
∈ R, where i ∈ I is a scheduled intervention,
t
0
∈ H is its start time a s ∈ S
t
is a scenario. The in-
dividual risk values are based on the historical data
collected by the network operator.
Solution of the maintenance scheduling task is a list x
of pairs (i,t) ∈ I × H, where t is the starting time of an
intervention i. Let us also define for future use the set
of interventions scheduled at time t ∈ H as I
t
and the
set of interventions scheduled in a solution x as I
x
.
3.2 Constraints
A valid solution x must meet all the constraints de-
fined in this section.
Non-preemptive Scheduling. An intervention must
be finished once it was started. If an intervention i ∈ I
starts at time t ∈ H, it must end at time t + ∆
i,t
.
Everything Scheduled on Time. All interventions
have to be scheduled and finished within the planning
horizon. It must hold that t + ∆
i,t
≤ T + 1,∀i ∈ I.
Resource Constraints. The usage of all resources
must stay within their lower and upper bounds. Let
us define the total workload for resource c ∈ C at time
t ∈ H as
r
c,t
=
∑
i∈I
t
r
c,t
i,t
0
.
It must hold, that l
c
t
≤ r
c,t
≤ u
c
t
,∀c ∈ C,t ∈ H.
Disjunctive Constraints. None of the given exclu-
sions can be violated at any given time. It must hold,
that i
1
∈ I
t
=⇒ i
2
/∈ I
t
,∀(i
1
,i
2
,t) ∈ Exc.
3.3 Objective
The objective value of a schedule is defined as a
weighted aggregation of two values: mean cost ob j
1
and expected excess ob j
2
. It is defined as
ob j = α × ob j
1
+ (1 − α) × ob j
2
,
where α ∈ [0,1] is a provided scaling factor.
Mean Cost approximates the overall planning risk
under the assumption that the individual risk values
are independent. Let us define the cumulative plan-
ning risk at t ∈ H for a scenario s ∈ S
t
as
risk
s,t
=
∑
i∈I
t
risk
s,t
i,t
0
,
where t
0
is the start time of the intervention i. Let us
define the mean cumulative planning risk at t ∈ H as
risk
t
=
1
|S
t
|
∑
s∈S
t
risk
s,t
.
From here, the mean cost can be expressed as
ob j
1
=
1
T
∑
t∈H
risk
t
.
Expected excess metric is incorporated in the overall
objective to capture the cost variability over different
scenarios. A schedule with low mean cost may still
allow for some scenarios to induce extremely high
costs locally, which is not desirable. To prevent this,
let us define the expected excess at time t ∈ H as
Excess
τ
(t) = max(0, Q
t
τ
− risk
t
).
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
158

Here, Q
t
τ
is the τ quantile of cumulative planning risks
of all scenarios s ∈ S
t
at time t ∈ H:
Q
t
τ
= Q
τ
({risk
s,t
}
s∈S
t
),
where τ is part of the input data. The expected excess
of the whole schedule is then defined as
ob j
2
=
1
T
∑
t∈H
Excess
τ
(t).
4 METHOD
This section describes the adaptation of the ALNS
metaheuristic to the maintenance scheduling problem.
The ALNS is introduced in Section 4.1. Section 4.2
defines the augmented objective function, which is
used to penalize invalid solutions and thus direct the
search towards valid ones. The individual destroy and
repair heuristics used in the ALNS are described in
Section 4.3 and the local search in Section 4.5.
4.1 The Approach
The ALNS is a well-established metaheuristic, first
introduced in (Ropke and Pisinger, 2006). It was suc-
cessfully applied across a wide range of combinatorial
optimization problems, especially in various routing
and scheduling problems (Pisinger and Ropke, 2010).
It was selected for the maintenance scheduling prob-
lem, as the problem allows for designing a varied
portfolio of destroy and repair heuristics, which are
the key elements of the ALNS.
The high-level metaheuristic adapted for the
maintenance scheduling problem is described in Al-
gorithm 1. The algorithm works as follows. At the
beginning, an initial solution x
0
is constructed and
selection weights ρ
−
,ρ
+
of destroy, respectively, re-
pair heuristics are initialized to represent a discrete
uniform distribution (lines 4-5). Then, the following
process repeats until the algorithm runs out of time.
First, a temporary copy x of the current best solu-
tion x
0
is created (line 6) and a number of interven-
tions N
r
to remove from x is sampled uniformly ran-
domly from the interval (0,DEPTH ∗ size(x)), where
DEPTH ∈ [0,1] is a parameter determining the rate of
destruction (line 7). Second, a destroy heuristic d
and a repair heuristic r are randomly selected using a
roulette wheel mechanism, according to the selection
weights ρ
−
,ρ
+
(line 8). Third, N
r
interventions are
removed from x using d, reinserted by r and x is sub-
ject to local search (lines 9-10). Finally, the current
solution cost c(x) is compared with the current best
c(x
0
) and with best overall c(x
∗
), x is kept if better
(lines 11-16). The selection weights ρ
−
(d),ρ
+
r are
Algorithm 1: ALNS metaheuristic.
1 i ← 0, x
∗
←
/
0
2 repeat
3 if i = 0 then
4 x
0
← construction()
5 ρ
−
, ρ
+
← (1,..., 1)
6 x ← x
0
7 N
r
← U(0,DEPTH ∗ size(x))
8 select d,r according to ρ
−
and ρ
+
9 x ← r(d(x,N
r
),N
r
)
10 x ← local search(x)
11 if c(x) < c(x
0
) then
12 i ← 0, x
0
← x
13 else
14 i ← i + 1
15 if c(x) < c(x
∗
) then
16 x
∗
← x
17 update ρ
−
(d) and ρ
+
(r)
18 if i = MAX ITERS then
19 i ← 0
20 until out of time;
21 return x
0
updated according to their performance in the current
iteration (lines 17). The search process is restarted
after MAX ITERS = RESTART RATIO ∗ size(x) non-
improving iterations, where RESTART RATIO ∈ R is
a fixed parameter.
The selection weight update mechanism is
adapted from (Pisinger and Ropke, 2010). The weight
of a destroy heuristic d is updated using the equation
ρ
−
(d) = λρ
−
(d) + (1 − λ)ψ,
where ψ = max(ω
1
,ω
2
,ω
3
). Here, λ ∈ [0,1] is a pa-
rameter called decay, ω
1
is a reward for finding a
new best overall solution, ω
2
for a new current best,
and ω
3
is a penalization for obtaining a nonimproving
one. It must hold, that ω
1
≥ ω
2
≥ ω
3
≥ 0. The tuning
of the parameters DEPTH,RESTART RATIO,λ,ω
1
, ω
2
and ω
3
is described in Section 5.2.
4.2 Augmented Objective Function
The problem is highly constrained, and considering
only valid schedules during the search has the follow-
ing disadvantages. First, even building a valid ini-
tial solution is difficult, and a polynomial-time algo-
rithm might not exist. Second, many of the heuris-
tics presented in Section 4.3 proved to be beneficial,
even though they can produce an invalid schedule.
Therefore, an augmented fitness function is used to
penalize invalid schedules instead of rejecting them.
This mechanism is inspired by the constraint-based
The ALNS Metaheuristic for the Maintenance Scheduling Problem
159

local search framework described in (Michel and Van
Hentenryck, 2017). The augmented objective func-
tion tends to direct the search towards valid solutions,
and invalid schedules are often fixed either in the local
search or subsequent iterations.
Before defining the augmented objective function,
let us define individual measures of violating the re-
source and disjunctive constraints. The remaining
constraints are not included, as they are not influenced
by multiple interventions and thus can be easily sat-
isfied. An excessive usage of resource c at time t
can be evaluated as r
c,t
over
= max(r
c,t
− u
c
t
,0). Ana-
logically, the insufficient usage of resource c at time
t can be evaluated as r
c,t
under
= max(l
c
t
− r
c,t
,0). From
here, the cumulative measure of using less, resp. more
resources than required by their lower, resp. upper
bounds can be expressed as
r
under
=
∑
c∈C
∑
t∈H
r
c,t
under
, r
over
=
∑
c∈C
∑
t∈H
r
c,t
over
.
Then, let us define the measure of violating exclusions
e
pen
=
∑
(i
1
,i
2
,t)∈Exc
both scheduled(i
1
,i
2
,t),
where both scheduled(i
1
,i
2
,t) = 1 if i
1
,i
2
∈ I
t
, oth-
erwise it evaluates to 0. Finally, the augmented objec-
tive function can be defined as
ob j
aug
= ob j +β
1
∗ r
under
+ β
2
∗ r
over
+ γ ∗ e
pen
.
Here, ob j is the actual objective used in the main-
tenance scheduling problem and β
1
,β
2
and γ are
weighting constants. These constants should be set
so that violating any constraints would outweigh the
actual objective ob j. For all instances used in this pa-
per, these were empirically set to β
1
= β
2
= γ = 1000
and valid schedules were always obtained. Note that
if the schedule is valid, r
under
,r
over
and e
pen
all evalu-
ate to 0. Moreover, r
over
and r
under
can be nonzero at
the same time.
4.3 Destroy and Repair Heuristics
A diverse bank of destroy and repair (d and r) heuris-
tics is an essential part of the ALNS metaheuristic. A
triplet (d,r,N
r
) defines a large neighborhood in the
ALNS context. This neighborhood corresponds to a
set of solutions that can be reached by removing N
r
elements from the current solution x using d and rein-
serting them using r. If both heuristics are determin-
istic, this set contains only one solution.
In the maintenance scheduling problem, the de-
stroy heuristics select a single intervention in the cur-
rent schedule according to a specific rule and remove
it from a schedule. Analogically, the repair heuristics
select one of the currently unscheduled interventions
and schedule it to a specific start time. The interven-
tion selection is typically based on some partial prop-
erties of the current schedule. Within the ALNS, a
selected destroy heuristic is sequentially applied N
r
times to a current schedule x, so that N
r
interventions
are unscheduled. These are then scheduled again us-
ing a selected repair heuristic N
r
times (line 9 of Algo-
rithm 1). The rest of this section contains descriptions
of the heuristics specifically designed for the mainte-
nance scheduling problem.
4.3.1 Destroy Heuristics
The destroy heuristics select a single scheduled in-
tervention i ∈ I
x
and remove the pair (i,t) from the
solution x, thus creating a partial solution marked as
x\i. One of these heuristics is selected and applied
sequentially N
r
times in each iteration of the ALNS.
Random (RND) remove heuristic removes a ran-
domly selected intervention i ∈ I
x
. It is the only
stochastic destroy heuristic.
Cheapest (CH) removes i ∈ I
x
, whose removal leads
to the lowest decrease in the augmented objective
ob j
aug
(x) of a solution x:
i = argmin
i∈I
x
(ob j
aug
(x) − ob j
aug
(x\i)).
Most Expensive (ME) removes i ∈ I
x
, whose removal
leads to the highest decrease in the augmented objec-
tive ob j
aug
(x):
i = argmax
i∈I
x
(ob j
aug
(x) − ob j
aug
(x\i)).
Lowest Resource Demand (LRD) removes i ∈ I
x
,
whose removal leads to the lowest decrease in the to-
tal resource usage r
total
(x) of a solution x:
i = argmin
i∈I
x
(r
total
(x) − r
total
(x\i)).
The total resource usage is defined as
r
total
=
∑
c∈C
∑
t∈H
r
c,t
.
Highest Resource Demand (HRD) removes i ∈ I
x
,
whose removal leads to the highest decrease in the
total resource usage r
total
(x) of a solution x:
i = argmax
i∈I
x
(r
total
(x) − r
total
(x\i)).
Shortest (SH) removes the shortest i ∈ I
x
:
i = argmin
i∈I
x
∆
i,t
0
,
where t
0
is the start time of i in x.
Longest (LN) removes the longest i ∈ I
x
:
i = argmax
i∈I
x
∆
i,t
0
,
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
160

where t
0
is the start time of i in x.
Least Exclusions (LEX) removes i ∈ I
x
with the low-
est number of exclusions:
i = argmin
i∈I
x
|Exc
i
|,
where Exc
i
⊂ Exc is a set containing those exclusions
involving i. Note that |Exc
i
| is a static property of a
problem instance, independent on x.
Most Exclusions (MEX) removes i ∈ I
x
with the
highest number of exclusions:
i = argmax
i∈I
x
|Exc
i
|,
Least Used (LU) removes i ∈ I
x
, which was previ-
ously removed least often:
i = argmin
i∈I
x
removed
i
,
where removed
i
is a global counter incremented at
each removal of i.
Most Used (MU) removes i ∈ I
x
, which was previ-
ously removed most often:
i = argmax
i∈I
x
removed
i
,
4.3.2 Repair Heuristics
The repair heuristics select a single unscheduled in-
tervention i ∈ I\I
x
and schedule it to a start time t
0
in a solution x. The resulting solution is marked as
x ∪ (i,t
0
). One of these heuristics is selected and ap-
plied sequentially N
r
times in each iteration of the
ALNS, right after N
r
calls of a destroy heuristic. Be-
sides that, a repair heuristic is also used for the initial
solution construction.
Repairing is more complicated than destroying, as
it is necessary to select an intervention i ∈ I\I
x
and
determine a start time t
0
. Thus, the repair heuristics
designed for the maintenance scheduling problem dif-
fer not only by the intervention selection mechanism
but also by the start time selection mechanism.
First, let us define four different start time se-
lection mechanisms of a fixed intervention i ∈ I\I
x
.
Cheapest Start Time t
0
i,cheap
t
0
i,cheap
= argmin
t∈H
(ob j
aug
(x ∪ (i,t)) − ob j
aug
(x))
Lowest Resource Demand Start Time t
0
i,lrd
t
0
i,lrd
= argmin
t∈H
(r
total
(x ∪ (i,t)) − r
total
(x))
Shortest start time t
0
i,short
= argmin
t∈H
∆
i,t
Longest start time t
0
i,long
= argmax
t∈H
∆
i,t
Note that both the shortest and longest start times are
static properties, independent of x.
Now, we can define individual repair heuristics.
These are analogous to the destroy heuristics; only
some of them are combined with multiple start time
selection mechanisms. The intervention selected by a
heuristic is always scheduled to the start time defined
by the start time selection mechanism used within the
heuristic.
Random (RND) insert heuristic schedules a ran-
domly selected intervention i ∈ I\I
x
to the cheapest
start time t
0
i,cheap
.
Cheapest (CH) schedules the cheapest i ∈ I\I
x
,
where the considered cost of an intervention is cal-
culated at its cheapest start time t
0
i,cheap
:
i = arg min
i∈I\I
x
(ob j
aug
(x ∪ (i,t
0
i,cheap
)) − ob j
aug
(x)).
Most Expensive (ME) schedules the most expensive
i ∈ I\I
x
, where the considered cost of an intervention
is calculated at its cheapest start time t
0
i,cheap
:
i = arg max
i∈I\I
x
(ob j
aug
(x ∪ (i,t
0
i,cheap
)) − ob j
aug
(x)).
Lowest Resource Demand 1 (LRD1) schedules the
i ∈ I\I
x
with the lowest resource demand, where the
considered resource demand of an intervention is cal-
culated at its cheapest start time t
0
i,cheap
:
i = arg min
i∈I\I
x
(r
total
(x ∪ (i,t
0
i,cheap
)) − r
total
(x)).
Lowest Resource Demand 2 (LRD2) schedules the
i ∈ I\I
x
with the lowest resource demand, where the
considered resource demand of an intervention is cal-
culated at its lowest resource demand start time t
0
i,lrd
:
i = arg min
i∈I\I
x
(r
total
(x ∪ (i,t
0
i,lrd
)) − r
total
(x)).
Highest Resource Demand (HRD) schedules the i ∈
I\I
x
with the highest resource demand, where the con-
sidered resource demand of an intervention is calcu-
lated at its cheapest start time t
0
i,cheap
:
i = arg max
i∈I\I
x
(r
total
(x ∪ (i,t
0
i,cheap
)) − r
total
(x)).
Shortest 1 (SH1) schedules the shortest i ∈ I\I
x
,
where the considered length of an intervention is cal-
culated at its cheapest start time t
0
i,cheap
:
i = arg min
i∈I\I
x
∆
(
i,t
0
i,cheap
).
Shortest 2 (SH2) schedules the shortest i ∈ I\I
x
,
where the considered length of an intervention is cal-
culated at its shortest start time t
0
i,short
:
i = arg min
i∈I\I
x
∆
(
i,t
0
i,short
).
The ALNS Metaheuristic for the Maintenance Scheduling Problem
161

Longest 1 (LN1) schedules the longest i ∈ I\I
x
, where
the considered length of an intervention is calculated
at its cheapest start time t
0
i,cheap
:
i = arg max
i∈I\I
x
∆
(
i,t
0
i,cheap
).
Longest 2 (LN2) schedules the longest i ∈ I\I
x
, where
the considered length of an intervention is calculated
at its longest start time t
0
i,long
:
i = arg max
i∈I\I
x
∆
(
i,t
0
i,long
).
Least Exclusions (LEX) schedules the i ∈ I\I
x
with
the least exclusions to its cheapest start time t
0
i,cheap
:
i = arg min
i∈I\I
x
|Exc
i
|.
Most Exclusions (MEX) schedules the i ∈ I\I
x
with
the most exclusions to its cheapest start time t
0
i,cheap
:
i = arg max
i∈I\I
x
|Exc
i
|.
Least Used (LU) schedules the least used i ∈ I\I
x
to
its cheapest start time t
0
i,cheap
:
i = arg min
i∈I\I
x
removed
i
.
Most Used (MU) schedules the most used i ∈ I\I
x
to
its cheapest start time t
0
i,cheap
:
i = arg max
i∈I\I
x
removed
i
.
4.4 Initial Solution Construction
An initial solution is constructed from scratch in each
ALNS restart (line 4 of Algorithm 1). This solution
is created by calling a repair heuristic |I| times. As
all heuristics use the augmented objective function,
the initial solution can be invalid. Determining the
repair heuristic most suitable for initial construction
is described in Section 5.2.
4.5 Local Search
The local search is performed in each ALNS iteration,
after the current solution was partially destroyed and
recreated (line 10 of Algorithm 1). The goal is to ap-
proach a local optimum of the current solution before
comparing it with the current best solution. For this
purpose, three operators exploring different neighbor-
hoods were designed. Application of these operators
is controlled by the Randomized Variable Neighbor-
hood Descent (RVND) heuristic (Duarte et al., 2018).
This heuristic applies the operators sequentially in
random order. Whenever an operator improves the
current solution, the heuristic reshuffles the operators
and restarts. If none of the operators succeeds in im-
proving the solution, the RVND terminates. A de-
scription of the individual operators follows.
1-shift (1SH) operator reschedules a single interven-
tion to the best possible start time while the others
remain fixed. The neighborhood is searched exhaus-
tively, so the search can be formulated as
i
0
,t
0
= arg max
i∈I
x
,t∈H
(ob j
aug
(x) − ob j
aug
(x\i ∪ (i,t))),
where i
0
is the intervention to be rescheduled at time
t
0
. The complexity of the operator is O(|I| × |H|).
Random 2-shift (2SH-R) reschedules two randomly
selected interventions i
1
,i
2
∈ I
x
to the best possible
start times t
0
1
,t
0
2
∈ H, while the others remain fixed.
The search can be formulated as
t
0
1
,t
0
2
= arg max
t
1
,t
2
∈H
(ob j
aug
(x) − ob j
aug
(x
0
)),
where x
0
= x\{i
1
,i
2
} ∪ {(i
1
,t
0
1
),(i
2
,t
0
2
)}).
The operator is applied several times in a row, which
is controlled by the 2 SHIFT LIMIT parameter. The
randomized selection of (i
1
,i
2
) is utilized to keep the
complexity quadratic and equal to O(|H|
2
).
Exclusion 2-shift (2SH-E) is a variant of the Random
2-shift operator. Here, the interventions to reschedule
i
1
,i
2
are selected randomly from the set of exclusions
Exc. The operator is also applied 2 SHIFT LIMIT
times and only when the exclusion penalty e
pen
> 0.
5 RESULTS AND DISCUSSION
This section describes the testing setup in Section 5.1
and the tuning process in Section 5.2. The results
on the first two competition datasets are provided and
discussed in Section 5.3.
5.1 Testing Setup
The algorithm is implemented in C++. All results are
obtained on a Linux computer with an Intel Core i7-
8700 3.20GHz processor and 32 GB RAM. Accord-
ing to the competition rules, the instances are solved
in a short 15 minute run and a long 90 minute run. 50
short runs and 10 long runs are carried out for each in-
stance. The random number generator is seeded ran-
domly in each run.
Competition datasets A and B are used for test-
ing. Both of these datasets consist of 15 problems.
Individual instance size ranges from 18 to 706 inter-
ventions. In the case of the set A, best-known scores
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
162

(BKS) from the qualification phase are used as a ref-
erence. No results were published yet for the B set,
so the best-known scores correspond to our method’s
best solutions from the 90 minute run. The B in-
stances are generally larger and more constrained.
5.2 Algorithm Tuning
The algorithm has several parameters, which require
tuning. For this purpose, the iterated racing proce-
dure, implemented within the irace package (L
´
opez-
Ib
´
a
˜
nez et al., 2016) was used. The tuned val-
ues of parameters are: {2 SHIFT LIMIT, DEPTH,
RESTART RATIO, λ, ω
1
, ω
2
, ω
3
} = {6, 0.62, 89.57,
0.74, 72.96, 53.83, 6.92}.
A bank of heuristics is proposed in Section 4.3.
All of these heuristics were initially used and some
of them did not bring significant improvement in per-
formance relatively to their computational require-
ments. Therefore, the usage of individual heuristics is
parametrized and tuned with irace as well. The same
applies to the local search operators and the heuris-
tic used for initial solution construction. The compo-
nents selected for the final solver are: initial construc-
tion = HRD, repair heuristics = {MU, RND, SH1,
SH2, ME, LRD2}, destroy heuristics = {ME, CH, SH,
LN, LRD, LEX, MEX, LU}, local search operators =
{1SH, 2SH-R, 2SH-E}.
5.3 Results
Table 1 shows the performance of our method on the
A set and Table 2 on the B set. As our implementa-
tion uses 32-bit float type to store real numbers, all
absolute scores are shown with two decimal places’
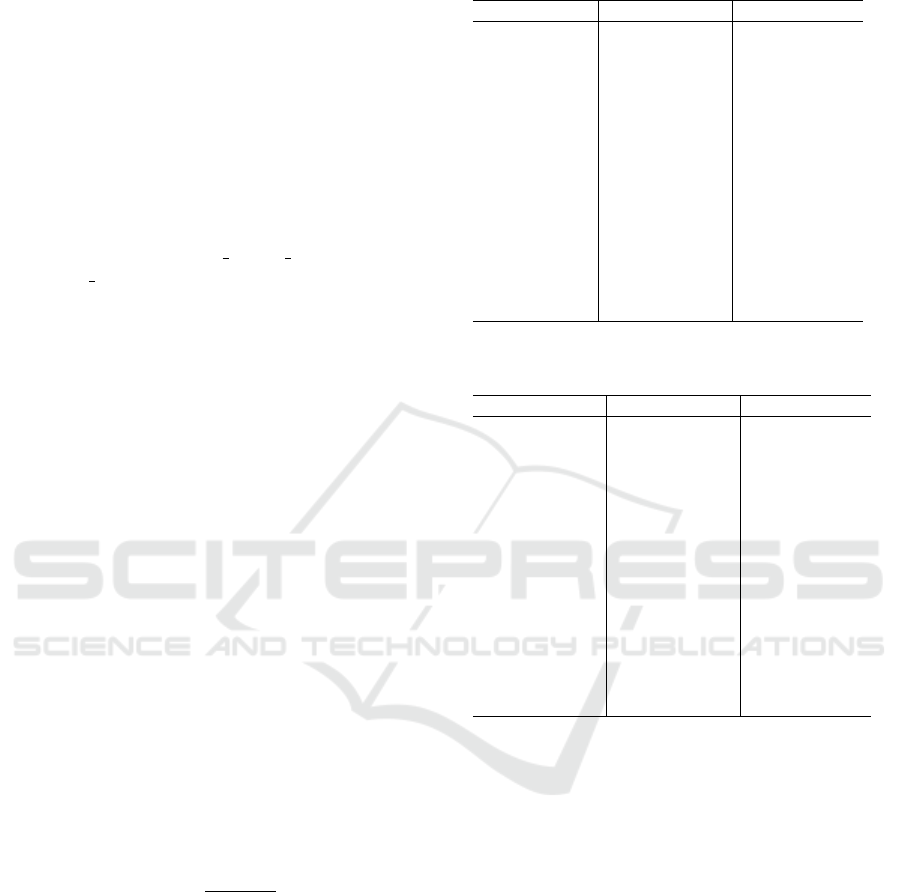
precision. When solving the A set in the short run,
our method reaches the BKS of 7 instances, and the
best solution found is always within 10h gap from
the BKS. The gap is given in per milles (h) and cal-
culated as gap = 1000 ×
score−BKS
BKS
.
On average, the method is consistently within
20h gap. As for the long run, the BKS is reached
for 8 instances, and the best solution found is always
within 5h gap from the BKS. The average perfor-
mance is then within 10h gap.
The BKS values on the B set instances are based
on our own results from the long run, as the results
of other methods are not yet public. Therefore, the
relevance of these results is limited, and they are in-
tended primarily for future reference. It can be noted
that the average performance is worse than the BKS
for all but one of the B instances, which was not so
for the A set instances. Therefore, the B set is most
Table 1: Results on A set.
15 min gap (h) 90 min gap (h)
Ins. BKS min mean±σ min mean±σ
A01 1 767.82 0.5 1.2 ± 0.5 0.3 0.6 ± 0.2
A02 4 671.38 0.0 0.0 ± 0.1 0.0 0.0 ± 0.0
A03 848.18 0.0 0.0 ± 0.0 0.0 0.0 ± 0.0
A04 2 085.88 8.9 17.5 ± 3.7 4.0 8.1 ± 3.5
A05 635.22 0.7 1.3 ± 0.3 0.5 0.7 ± 0.2
A06 590.62 4.9 17.4 ± 7.5 4.5 8.0 ± 2.8
A07 2 272.78 0.0 0.0 ± 0.0 0.0 0.0 ± 0.0
A08 744.29 0.0 0.0 ± 0.0 0.0 0.0 ± 0.0
A09 1 507.28 0.0 0.0 ± 0.0 0.0 0.0 ± 0.0
A10 2 994.85 0.0 0.0 ± 0.0 0.0 0.0 ± 0.0
A11 495.26 0.0 0.1 ± 0.2 0.0 0.0 ± 0.0
A12 789.63 0.0 0.0 ± 0.0 0.0 0.0 ± 0.0
A13 1 998.66 0.1 0.2 ± 0.1 0.1 0.1 ± 0.1
A14 2 264.12 0.5 9.0 ± 4.9 0.3 3.1 ± 4.4
A15 2 268.57 0.8 9.0 ± 6.8 0.4 3.0 ± 4.9
Table 2: Results on B set.
15 min gap (h) 90 min gap (h)
Ins. BKS min mean±σ mean±σ
B01 4 031.38 4.4 12.7 ± 3.6 5.7 ± 3.1
B02 4 311.83 2.1 8.0 ± 2.7 1.8 ± 1.1
B03 35 840.30 4.4 10.0 ± 2.2 2.6 ± 1.4
B04 34 829.60 0.2 0.5 ± 0.2 0.1 ± 0.1
B05 2 421.78 0.7 1.3 ± 0.3 0.5 ± 0.3
B06 4 285.95 4.0 7.6 ± 2.0 2.8 ± 1.2
B07 7 557.64 2.0 4.7 ± 1.2 3.2 ± 1.5
B08 7 435.72 0.0 0.0 ± 0.1 0.0 ± 0.0
B09 7 563.20 2.5 11.4 ± 4.9 4.8 ± 4.1
B10 10 764.90 0.1 5.9 ± 2.5 1.6 ± 1.1
B11 3 637.54 2.3 6.5 ± 1.6 3.1 ± 1.2
B12 37 896.80
5.6 133 ± 87 93.9 ± 97.8
B13 5 027.98 2.4 4.2 ± 1.2 1.4 ± 1.2
B14 11 914.50 1.6 2.3 ± 0.4 0.7 ± 0.3
B15 22 566.30 0.3 0.5 ± 0.1 0.1 ± 0.1
likely more challenging than the A set and will allow
better separation of different methods.
6 CONCLUSIONS
An adaptation of the ALNS metaheuristic for the
maintenance scheduling problem assigned within the
ROADEF challenge 2020 is described in this paper.
Various novel destroy and repair heuristics, which are
based on the problem partial properties, are presented.
The competition is still in progress. However,
comparing our method with the qualification phase’s
best-known solutions shows that the method is robust
and competitive. The BKS is consistently reached by
the method for 8 instances out of 15. As for the re-
maining instances, the method’s best score is always
within 5h gap, and the average score is within 10h
gap. More than 70 methods were submitted to the
qualification phase, and the organizers obtained the
The ALNS Metaheuristic for the Maintenance Scheduling Problem
163

best-known solutions in a fair comparison.
Concerning future work, the method is being fur-
ther developed for the final competition phase. The
main challenge is to adapt the method to handle larger
and more tightly constrained instances. Besides that,
several extensions are planned, such as hybridization
of the heuristics and start time selection mechanisms,
applying a MILP solver to a subproblem in the lo-
cal search phase, or adding memory with data mining
mechanisms.
ACKNOWLEDGEMENTS
This work has been supported by the European Re-
gional Development Fund under the project Robotics
for Industry 4.0 (reg. no. CZ.02.1.01/0.0/0.0/15
003/0000470). The work of David Woller has
been also supported by the Grant Agency of
the Czech Technical University in Prague, grant
No. SGS21/185/OHK3/3T/37.
REFERENCES
Abirami, M., Ganesan, S., Subramanian, S., and Anand-
hakumar, R. (2014). Source and transmission line
maintenance outage scheduling in a power system us-
ing teaching learning based optimization algorithm.
Appl. Soft Comput., 21:72–83.
Bor
˚
uvka, O. (1926). O jist
´
em probl
´
emu minim
´
aln
´
ım. Pr
´
ace
Moravsk
´
e p
ˇ
r
´
ırodov
ˇ
edeck
´
e spole
ˇ
cnosti, III(3):37–58.
Burke, E. K. and Smith, A. J. (2000). Hybrid evolutionary
techniques for the maintenance scheduling problem.
IEEE Trans. Power Syst., 15(1):122–128.
Da Silva, E. L., Schilling, M. T., and Rafael, M. C.
(2000). Generation maintenance scheduling consider-
ing transmission constraints. IEEE Trans. Power Syst.,
15(2):838–843.
Duarte, A., Mladenovi
´
c, N., S
´
anchez-Oro, J., and Todosi-
jevi
´
c, R. (2018). Variable neighborhood descent. In
Handbook of Heuristics, volume 1-2, pages 341–367.
Springer International Publishing.
El-Sharkh, M. Y. (2014). Clonal selection algorithm for
power generators maintenance scheduling. Int. J.
Electr. Power Energy Syst., 57:73–78.
Feng, C., Wang, X., and Li, F. (2009). Optimal mainte-
nance scheduling of power producers considering un-
expected unit failure. IET Gener. Transm. Distrib.,
3(5):460–471.
Froger, A., Gendreau, M., Mendoza, J. E., Pinson,
´
E., and
Rousseau, L. M. (2016). Maintenance scheduling in
the electricity industry: A literature review. Eur. J.
Oper. Res., 251(3):695–706.
Geetha, T. and Swarup, K. S. (2009). Coordinated
preventive maintenance scheduling of GENCO and
TRANSCO in restructured power systems. Int. J.
Electr. Power Energy Syst., 31(10):626–638.
Huang, S. J. (1997). Generator maintenance scheduling:
A fuzzy system approach with genetic enhancement.
Electr. Power Syst. Res., 41(3):233–239.
L
´
opez-Ib
´
a
˜
nez, M., Dubois-Lacoste, J., P
´
erez C
´
aceres, L.,
Birattari, M., and St
¨
utzle, T. (2016). The irace pack-
age: Iterated racing for automatic algorithm configu-
ration. Oper. Res. Perspect., 3:43–58.
Lu, C., Wang, J., and Sun, P. (2012). Short-term transmis-
sion maintenance scheduling based on the benders de-
composition. In APPEEC 2012.
Michel, L. and Van Hentenryck, P. (2017). Constraint-
Based Local Search. In Handbook of Heuristics, pages
1–38. Springer International Publishing.
Mollahassani-Pour, M., Abdollahi, A., and Rashidinejad,
M. (2014). Application of a novel cost reduction index
to preventive maintenance scheduling. Int. J. Electr.
Power Energy Syst., 56:235–240.
Moro, L. M. and Ramos, A. (1999). Goal programming ap-
proach to maintenance scheduling of generating units
in large scale power systems. IEEE Trans. Power
Syst., 14(3):1021–1028.
Pisinger, D. and Ropke, S. (2010). Large Neighborhood
Search. In Handbook of Metaeuristics, pages 399–
419. Springer International Publishing.
Reihani, E., Sarikhani, A., Davodi, M., and Davodi, M.
(2012). Reliability based generator maintenance
scheduling using hybrid evolutionary approach. Int.
J. Electr. Power Energy Syst., 42(1):434–439.
Ropke, S. and Pisinger, D. (2006). An adaptive large neigh-
borhood search heuristic for the pickup and delivery
problem with time windows. Transp. Sci., 40(4):455–
472.
Ruiz, M., Tournebise, P., and Panciatici, P. (2020).
ROADEF Challenge RTE: Grid operation-based out-
age maintenance planning. Technical report, RTE.
Saraiva, J. T., Pereira, M. L., Mendes, V. T., and Sousa,
J. C. (2011). A Simulated Annealing based approach
to solve the generator maintenance scheduling prob-
lem. Electr. Power Syst. Res., 81(7):1283–1291.
Schl
¨
unz, E. B. and Van Vuuren, J. H. (2013). An inves-
tigation into the effectiveness of simulated annealing
as a solution approach for the generator maintenance
scheduling problem. Int. J. Electr. Power Energy Syst.,
53(1):166–174.
Suresh, K. and Kumarappan, N. (2013). Hybrid improved
binary particle swarm optimization approach for gen-
eration maintenance scheduling problem. Swarm
Evol. Comput., 9:69–89.
Than Kyi, M., Maw, S. S., and Naing, L. L. (2019). Math-
ematical Estimation for Maximum Flow in Electricity
Distribution Network by Ford-Fulkerson Iteration Al-
gorithm. Int. J. Sci. Res., 9(8):p9229.
Volkanovski, A., Mavko, B., Bo
ˇ
sevski, T.,
ˇ
Cau
ˇ
sevski, A.,
and
ˇ
Cepin, M. (2008). Genetic algorithm optimisation
of the maintenance scheduling of generating units in a
power system. Reliab. Eng. Syst. Saf., 93(6):779–789.
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
164