Context-aware Social Robot Navigation

Frederik Haarslev

* a

,William Kristian Juel

* b

, Avgi Kollakidou

Norbert Kr

uger

and Leon Bodenhagen

SDU Robotics, University of Southern Denmark, Campusvej 55, Odense C, Denmark

Keywords:

Mobile Robots, Robot Navigation, Costmaps, Context Awareness.

Abstract:

With the emergence of robots being deployed in unstructured environments outside the industrial domain,

the importance of robots behaving appropriately in the vicinity of people is becoming more clear. These

behaviours are hard to model as they depend on the social context. This context includes among other things

where the robot is deployed, how crowded that place is, as well as who are residing in that place. In this paper

we extend social space theory with the social context, making them adaptable to the current situation. We

implement the social spaces as costmaps used in the standard ROS navigation stack. Our method – Context-

Aware Social robot Navigation (CASN) – is tested in the context of people avoidance in social navigation.

We compare CASN with the social navigation layer package, which also implements costs based on detected

people. We show that by using CASN a mobile robot complies with social conventions in four different

navigation scenarios.

1 INTRODUCTION

Robots are becoming an integrated part of our soci-

ety and already millions of robots are in operation

around the world today (IFR, 2020). In the past,

robots were highly relegated to controlled and static

environments, but they are now also showing promis-

ing results in unconstrained areas of society such as in

hospitals (Riek, 2017; ?). These robots will be part of

our lives, operate in close proximity to us and interact

with us on a daily basis. A reason why mobile robots

are not used more in society is that standard naviga-

tion systems do not differentiate between humans and

objects and therefore completely ignore social aspects

of navigation.

Traditionally, path planning for mobile robots is

about solving for the least costly path and such meth-

ods do not utilize semantic information (Marder-

Eppstein et al., 2010). These methods will create a

collision free path but can result in inadequate robot

behavior such as driving to close to humans which

may make them feel unsafe.

https://orcid.org/0000-0003-2882-0142

https://orcid.org/0000-0001-5046-8558

https://orcid.org/0000-0002-0648-4478

https://orcid.org/0000-0002-3931-116X

https://orcid.org/0000-0002-8083-0770

Equal contribution between the authors

In unconstrained environments where people and

robots work around each other, the robots must be

context-aware and comply with social conventions for

efﬁcient navigation in order to ﬁt in. This means

that the robot must understand proxemics and navi-

gate using semantic information about their surround-

ings. Spaces can be free or occupied, but some spatial

regions might also be part of a social context which

needs to be taking into account for socially aware nav-

igation. In this work we explore using costmaps to put

mobility constraints for navigating around humans,

and we deﬁne how to derive adequate robot behaviors

based on the spatial relations between humans and a

robot. We deﬁne two types of spaces that are par-

ticularly relevant and these will be mapped into the

costmap: the personal and social space.

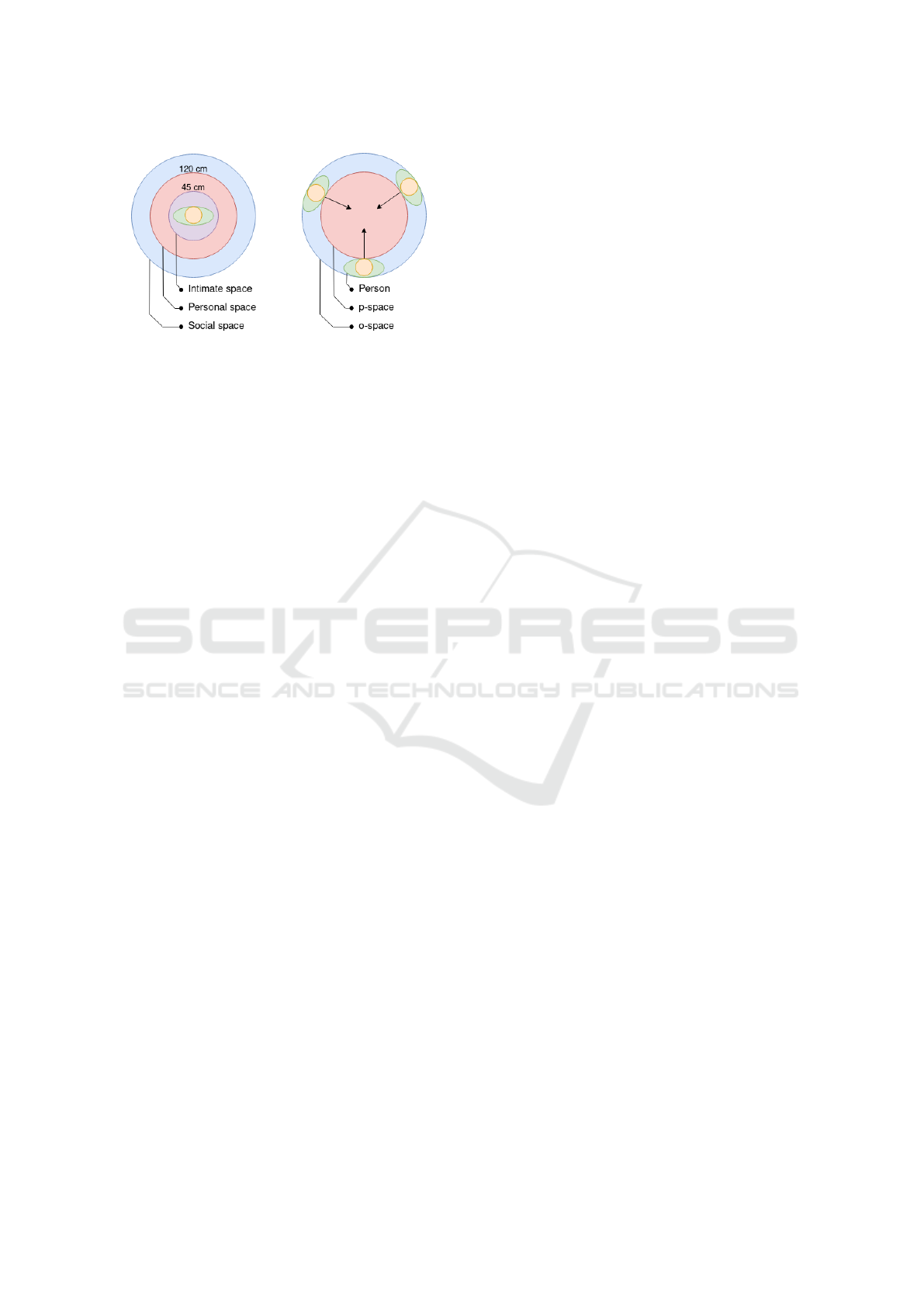
According to (Hall, 1966) the space near an indi-

vidual person can be modelled as consisting of four

concentric circular areas with varying distance, with

the two inner space being shown on ﬁg. 1a. The in-

timate space is deﬁned by (Hall, 1966) as a space for

embracing and touching and is reserved for people

you know. The personal space is typically an area for

interacting with friends and family. The social space

is outside arms reach and the region where interaction

with acquaintances happen. People engaging in social

interaction, share each other’s social spaces and tend

to form and maintain distinct spatial structures. In the

426

Haarslev, F., Juel, W., Kollakidou, A., Krüger, N. and Bodenhagen, L.

Context-aware Social Robot Navigation.

DOI: 10.5220/0010554204260433

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 426-433

ISBN: 978-989-758-522-7

(a) (b)

Figure 1: (a) The three inner regions of the personal space

model by Hall. (b) Example of an F-Formation by Kendon.

case of static social arrangements, (Kendon, 1990) in-

troduces F-Formations, see ﬁg. 1b. F-Formations de-

scribe the arrangement of people (e.g. face-to-face,

side-by-side and circular arrangement), as well as the

emerging social spaces. The o-space describes the

space between all group participants, is reserved for

interaction and should not be penetrated. The p-space

engulfs the o-space and the space occupied by the par-

ticipants of the group.

While this social space theory can serve as guide-

line for social robot navigation using costmaps, some

key ideas are missing when it comes to how it should

be implemented. Many factors affect how the robot

should navigate around people, including the size and

shape of the robot, the job of the robot (should it

avoid or approach people), and if the people are mov-

ing. These factors we broadly deﬁne as the context in

which the robot operates in.

This paper integrates our previous work in

(Juel et al., 2020) and introduces a method for

Context-Aware Social robot Navigation (CASN) us-

ing costmaps. The contributions of this paper are as

following:

1. We implement context-aware social navigation by

putting mobility constraints for navigating around

humans using collision detection.

2. We integrate context in the creation of costmaps

and show how a robot uses this to comply with

social conventions for efﬁcient navigation.

3. We show that our system outperforms an open

source ROS implementation.

In the following sections we describe the state

of the art in social navigation (section 2); we deﬁne

the context and how we use it in costmaps for social

navigation (section 3); we test our implementation in

four scenarios, and compare it to an open source ROS

implementation (section 4); and we conclude on our

ﬁndings (section 5).

2 RELATED WORK

With the increase of robots operating in spaces popu-

lated by humans, the exploration of navigation meth-

ods that consider and incorporate social norms has

seen a peak of interest. Different approaches have

been attempted to understand or model human be-

haviour – whether static, dynamic or in groups – and

navigate accordingly. Costmaps are widely used to

accomadate for socially aware motion planning and

navigation by the introduction of non-lethal costs to

represent social spaces. (Lu et al., 2014) proposed the

layering of costmaps, each containing semantic infor-

mation for a speciﬁc property or subject such as obsta-

cles, inﬂation or proxemics. The proxemic layer, with

which this work is mainly compared, utilises the posi-

tion and velocity of detected people to create a Gaus-

sian distribution of costs around them (Kirby et al.,

2009). The cost is elongated in the detected peoples

direction of movement.

Layered costs with semantic information are also

implemented by (Mateus et al., 2019) which used

asymmetric Gaussian function costs. An attempt

to adjust costmaps was made by (Scandolo and

Fraichard, 2011) by incorporating predictions for dy-

namic social scenarios. (Ram

ırez et al., 2016) pro-

posed an inverse reinforcement learning method to

obtain the optimal path to approach both static and

dynamic people according to their poses and veloc-

ities, which was then incorporated in a path planner

which layered the acquired information with other

layers. Alternatives to the costmap based approaches

has also been suggested. (Mead and Matari

c, 2017)

used Hall’s proxemics deﬁnitions (Hall, 1966), to de-

velop and evaluate a proxemic goal-state estimation

and cost-based trajectory planner. (Bordallo et al.,

2015) and (Khambhaita and Alami, 2020) attempt to

predict the intentions or trajectories of human actors

in the robot environment and adjust the motion plan-

ning accordingly. Similarly, we incorporate a colli-

sion detector dependent on data predicted by tracking

the position and velocities of humans and robot.

Although the community has addressed the issues

of semantic mapping or human-aware navigation with

various approaches, we see that the navigation re-

sults do not always comply with social conventions

and work only in constrained or controlled situations.

Similar to (Lu et al., 2014), we implement a layered

costmap-based method which proactively detects col-

lisions or invasions of social spaces. The velocities

of humans and robot are used to project the costs and

allow the robot enough time to change its plan.

Context-aware Social Robot Navigation

427

3 CONTEXT-AWARE

NAVIGATION

The method proposed in this paper uses social space

theory by (Hall, 1966) and (Kendon, 1990) to put

costs around humans in a costmap. We modify this

theory based on the context of the robot in a given sit-

uation. In the following we deﬁne notation for the

context which we use in CASN (section 3.1), give

a description of how we derive the cost functions

(section 3.2) and show how this is implemented in

costmaps (section 3.3).

3.1 Context

The mapping of the spaces deﬁned by (Hall, 1966)

and (Kendon, 1990) can broadly be deﬁned as includ-

ing context in a navigation strategy. Context covers

all aspects that go beyond the description of a robots

speciﬁc task, e.g. the cultural background, type of

building or even the time of the day. The robot be-

havior can be expected to depend on aspects of the

context that can be considered static in a given situa-

tion, including the physical environment or the type of

the overall situation in the environment of the robot.

Other relevant parameters – which are the focus of

this paper – are dynamic, such as the crowdedness of

the scene, the current task of the robot, or the role of

individuals in an interaction.

The static parameters, E

, describing the context

are not immediately dependent of the robot’s sensory

input and are expected to remain constant during the

robot’s operation:

= {E

,...} (1)

where E

denotes the type of the building (e.g.,

whether it is a public accessible or not), E

the mis-

sion of the robot, and E

reﬂects the size and appear-

ance of the robot. Dynamic parameters E

will be

described as functions of an observation of a human,

h. These functions includes aspects essential for be-

ing able to achieve an appropriate navigation strategy,

(h), as well as the conﬁguration of a human, and

the local density of humans, E

(h).

= {E

,. ..} (2)

To allow for a concise notation in section 3 the

following,

E = {E

} (3)

denotes the combined context information, including

both static and dynamic aspects.

3.2 Personal and Social Costs

The personal space is mapped to the costmap using a

cost function which depends on the context, E, which

oftentimes can be considered constant during a single

interaction. The cost, C

, for occupying a point x is:

(x,h|E) =

∑

j={i,p}

h, j

(x,h|E) (4)

where k

h,i

(·), k

h,p

(·) represents the cost model of the

intimate and personal spaces associated with the prox-

imity between the point x and the person h, given the

context E.

When modelling the social space, we consider the

o- and p-spaces. However, how these spaces are re-

ﬂected in a costmap in a speciﬁc situation depends

highly on the context, i.e. the cost for entering a

groups o-space would be low if an interaction with

the group is intended, but high if the robot just has

to traverse the area. The cost function modelling the

social spaces is therefore formulated as a sum of the

three spaces:

(x,g|E) =

∑

i={o,p}

g,i

(x,g|E) (5)

where g denotes the group formation. The spatial

structure of the o- and p-space of the individual group

is modeled by k

g,o

(·) and k

g,p

(·) respectively. The ac-

tual cost, C

tot

, for occupying a point p is then deﬁned

by the sum of the individual spaces:

tot

(p|E) =

∑

(p, h|E) +

∑

(p, g|E) (6)

3.3 Context-aware Costmaps

In this section we show how the social space theory

is implemented as costmaps used in the ROS navi-

gation stack with four scenarios: 1) A robot is nav-

igating around a static person 2) A robot is navigat-

ing around a static group 3) A robot on a collision

course with a person moving straight towards it 4) A

Robot on a collision course with a person crossing its

path orthogonally. In these four scenarios the static

context, E

, of the robot is to avoid people in a so-

cially acceptable manner. For each scenario we com-

pare our method to the ROS open-source method so-

cial navigation layers (SNL)

that follows the same

scheme as us by putting cost to restrict robots from

maneuvering close to humans.

http://wiki.ros.org/social navigation layers

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

428

(a) (b)

Figure 2: (a) Top down view of the experimental setup. (b)

Detection image. (c) CASN and (d) SNL method for setting

cost around a static person.

We ﬁrst consider the simple case of a person

standing statically in the robot’s path (ﬁg. 2a). The

robot uses the detection and tracking system de-

scribed in (Juel et al., 2020) to get a 3D estimation

of the position and velocity of the person in its ﬁeld

of view. The velocity estimation of the person be-

ing 0 m/s, deﬁnes the contextual state of the person,

(h), as standing still. Given this context, the cost

function becomes:

h, j

(x,h) =

(

if |x − h| < r

0 otherwise

(7)

where r

is the radius of the given space (personal or

intimate), and c

is the cost value we assign this space.

SNL makes a cost gradient around the detected

person (ﬁg. 2d), which shape is controlled by three

parameters: amplitude, variance and cutoff. The pa-

rameters are set such that the radius of the gradient

matches the radius of our cost model, while the cost at

the personal and intimate space radii are the same. To

avoid having the results inﬂuenced by sensor modal-

ity, we created a bridge which translates the detec-

tions to match the output of the leg detector which

SNL was build for. Thereby, we can directly compare

our method to SNL.

Next we consider the group scenario (ﬁg. 3),

where two people stands at each side of the robots

path. As the context is to avoid interrupting social

interactions, the robot should not drive through the

group. This is done by assigning costs to the o- and

p-space. The potential interaction between humans

is detected using an algorithm which clusters peo-

ple based on their positions and orientations. Fol-

lowing Hall’s social areas (Hall, 1966), the maxi-

(a) (b)

Figure 3: (a) Top down view of the experimental setup. (b)

Detection image (c) CASN and (d) SNL method for setting

cost around a group.

mum distance between potential interlocutors is set

to 3m. Individuals are rewarded if they are looking

towards each other, thus exploiting the individual’s

line of sight (LoS) as well as their positions. Further-

more, potential focus points (FP) are detected using

a separate clustering of LoS intersections. Individu-

als who are found to have the same FP are rewarded

as well, making it more likely for them to be clus-

tered together. As individuals are sorted in potential

groups, the o-space, speciﬁcally its center point and

radius, is calculated.

As with the personal spaces, the social space cost

function is constant within the group radius:

g,i

(x,g) =

(

if |x − g| < r

0 otherwise

(8)

where r

is the radius of the given space (o or p), and

is the cost value we assign this space.

Once again the velocity estimations are used to de-

duce that the people are static, thereby giving E

(h).

Therefore, k

is deﬁned as in eq. (7). Structuring the

cost like this (ﬁg. 3c) forces the robot to drive around

the group to avoid interrupting. The SNL method is

not made to model group costs and therefore does not

not prevent the robot to plan through the formation

and thereby interrupting (ﬁg. 3d).

Figure 4 shows a scenario where a person is walk-

ing directly towards the robot. Without using our

method or SNL, the costmap implementation in ROS

creates an inﬂated cost around each object detected

in the sensor data, not distinguishing between people

or inanimate objects. It also does not have a concep-

tion of dynamic objects, making the path planner plan

around the objects current, and not future, position.

Context-aware Social Robot Navigation

429

(a) (b)

Figure 4: (a) Top down view of the experimental setup. (b)

Detection image (c) CASN and (d) SNL method for setting

cost around a moving person.

SNL remedies this by elongating the cost gradient in

the direction of movement (ﬁg. 4d), making the robot

act on the approaching person quicker.

In our method we detect collision points between

the robot and the detected people, and plan around

those points. Given the context that the person is

walking directly towards the robot, we modify k

use the collision point,

h, as input instead of the per-

sons current position h. One strategy could be to de-

ﬁne

h as lying on the vector, ~v, from the robots po-

sition, r to h, giving

h = h − p~v, where p is a con-

stant (e.g. p = 0.5). As h and r moves towards each

other

h stays between them, while |~v| → 0, eventu-

ally ending in a collision at

h. We use this strategy

with two modiﬁcations. We set p dynamically based

on the estimated velocity of h. This effectually makes

the robot react to a fast moving person quicker than

to a slow moving person. The other modiﬁcation is

that when |

h − r| < d, we freeze

h until the robot has

passed h. This is done to make the robot commit to a

path without the avoidance behavior affecting where

the calculated collision point is. We set d = 2m. Fig-

ure 4c shows the robot planning around the collision

point, thereby avoiding the approaching human.

The last scenario is where a person moves or-

thogonally to the robots path, as seen in ﬁg. 5. In

most cases no collision will occur in such scenario, as

the robot and the human would have to approach the

crossing of their paths at the same time. Therefore,

we constrain this scenario to such cases, by having

the person walk slow enough to force a collision. Fig-

ure 5d shows the cost by SNL in this scenario. Here

the robot plans a path in front of the person, as it is

the shortest path around the cost. The robot therefore

(a) (b)

Figure 5: (a) Top down view of the experimental setup. (b)

Detection image (c) CASN and (d) SNL method for setting

cost around an orthogonally moving person.

does not avoid the collision, and it will have to brake

in order to do so. Ideally, the robot should drive be-

hind the person in order to ensure not colliding. Again

we do this by detecting collision points

h. A simple

strategy would be to put

h directly in front of the robot

at ~v

, i.e. the x component of vector between r and

h. If the person is not walking directly orthogonal to

the robots path, or when the robot moves, |~v

| is af-

fected. However, ultimately a collision happens at

as |~v| → 0. As before, we modify this strategy in or-

der to make the robot behave adequately. To make

the robot react quicker, we put

h at p~v

, with p = 0.8.

To force the robot behind the person, we shift

h along

−~v

. And ﬁnally to make the robot commit to the

path we freeze

h when |

h − r| < d. Figure 5c shows

the resulting cost and path using this cost model in the

orthogonal collision scenario.

4 EXPERIMENTS

To asses CASN we set up a controlled experiment in-

volving a mobile robot and three test subjects. We

quantify the methods by looking at how close the

robot comes to the test subjects and how many times

the robot enter the personal and intimate space of

the test subjects. We make four individual tests, one

for each of the scenarios presented in section 3.3: 1.

Static person; 2. Static group; 3. Direct collision; 4.

orthogonal Collision.

The robot used in the experiment has an Intel Re-

alSense D455 camera mounted in the front. In order

to get ground truth trajectories of the test subjects and

the robot, we set up a camera in a top-down view in

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

430

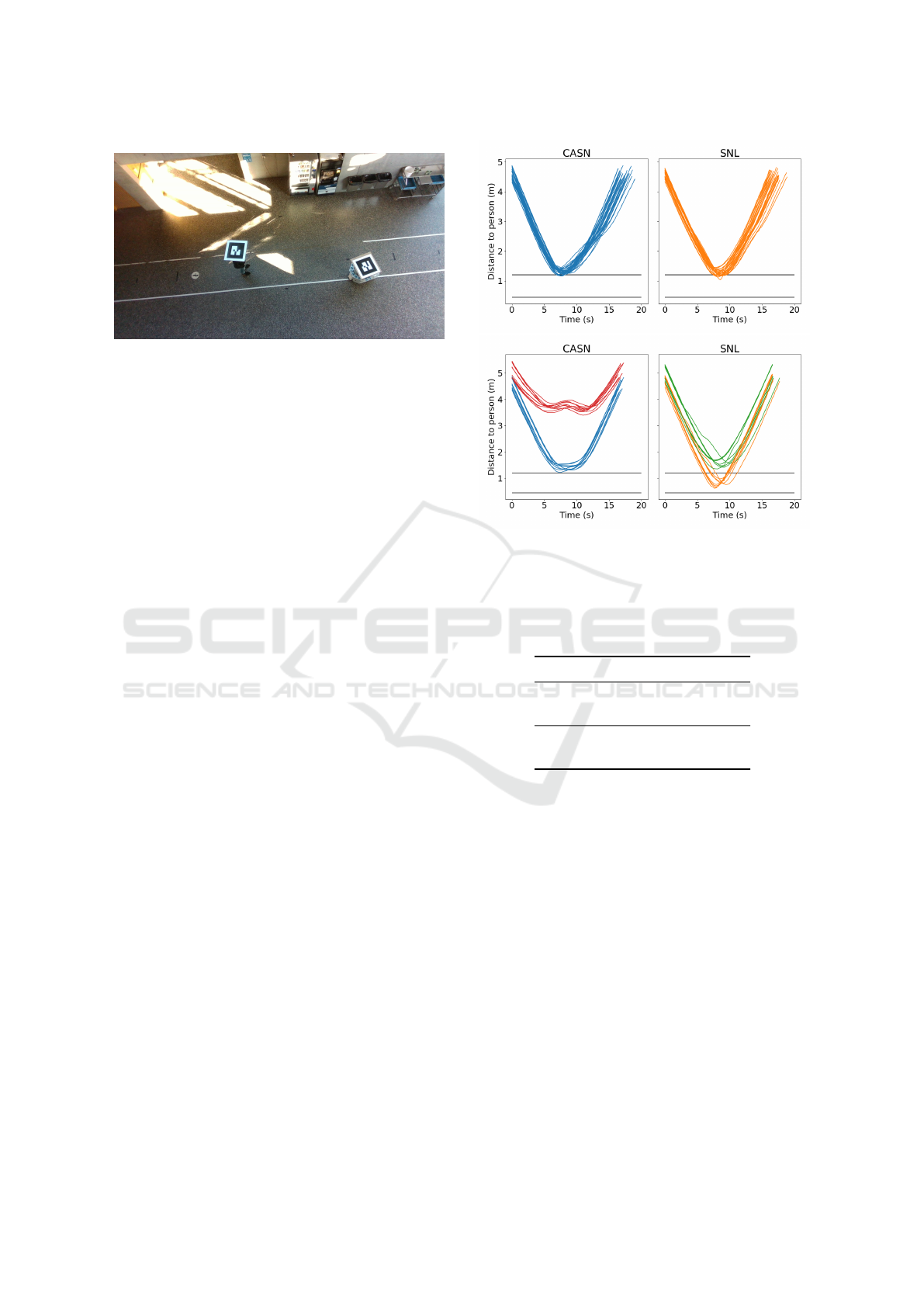
Figure 6: Experimental setup viewed from the top-down

view camera: Marker on the robot and a marker on each

test subject to get ground truth distances between the test

subjects and the robot.

a hallway where the robot is maneuvering. The test is

limited to the ﬁeld of view of the top-down view cam-

era. Ground truth of the trajectories are collected by

mounting markers on the test subjects, and the robot

and a stationary marker is placed on the ground as a

reference point for calibration of the top-down view

camera placement in the map frame. The experimen-

tal setup is shown on ﬁg. 6, from the point of view of

the marker detection camera.

In each scenario the robot was continuously mov-

ing between two static coordinates in the map (from

left to right). In scenario 1 and 2, each test subject was

instructed to stand on predeﬁned static positions in the

map that was in a direct collision course of the robots

movement. In scenario 3 and 4 the test subjects were

moving between two predeﬁned points that was in di-

rect collision course with the robots predeﬁned path.

We instructed the test subjects to walk at the speed

they found natural. The experiment was blinded and

randomized so the test subjects did not know which

of the two methods they were exposed to.

In the following tables and graphs the number of

samples are noted as (n), the distance as d (meters),

and velocity as v (m/s) and intrusions (how many

times the robot enters the social spaces) and time for

the trial (seconds).

4.1 Static Person

In this experiment we have the test subject standing

statically in the robots predeﬁned path. On ﬁg. 7a the

graph shows the distance from the robot to the per-

son throughout each trial. The constant line at 1.2 m

marks the intrusion of the personal space and the line

at 0.45 m marks the intrusion of the intimate space.

The graph show that both CASN and SNL navigates

nicely around a static person but SNL has more in-

trusions of the static persons personal space. On the

top part of table 1 (Single) we see the details of the

(a)

(b)

Figure 7: Distance from the robot to the test subject(s) in

(a) static person and (b) static group. Each line correspond

to one trial and each color corresponds to one person.

Table 1: Static person and static group: n is the number of

samples, d is the distance and i is the number of times the

robot intrudes the personal spaces.

n d (m) i

Single (CASN) 30 1.29 4

Single (SNL) 30 1.25 14

Group (CASN) 10 1.39 0

Group (SNL) 10 0.76 10

experiment. We ﬁnd the closest the robot gets to the

person in each trial, and ﬁnd the mean of this value

for each method. This is denoted d. Using CASN the

robot keeps a mean minimum distance of 1.29 m to the

person and only intrude the personal space 4 times.

Using the SNL method the robot keeps an mean min-

imum distance of 1.25 m to the person which is still

larger than the personal space distance but the robot

intrudes the personal space 14 times. The CASN

method for setting cost on an individual static person

(ﬁg. 2) versus SNL seems to make the robot navigate

more socially acceptable around the person.

4.2 Static Group

In this experiment we have the two test subjects stand-

ing statically as a group in the robots predeﬁned path.

On ﬁg. 7b the graph shows the distance from the robot

to the test subjects where the colors represents each of

Context-aware Social Robot Navigation

431

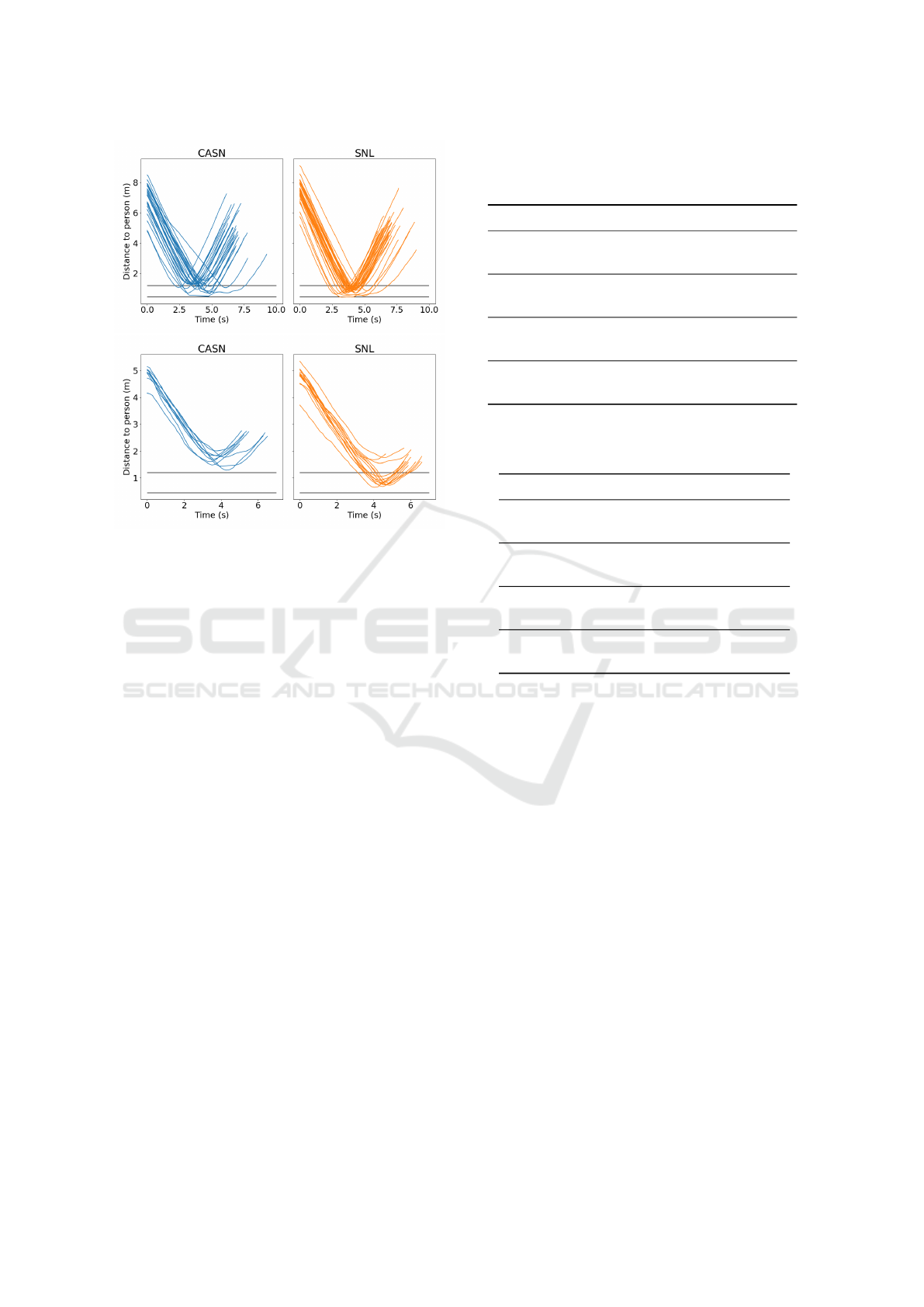
(a)

(b)

Figure 8: Distance from the robot to the test subject in (a)

direct collision and (b) orthogonal collision. Each line cor-

respond to one trial. The horizontal lines are the personal

and intimate space radii.

the two test subjects, and the horizontal lines at 1.2 m

and 0.45 m marks the intrusion of the personal and

intimate spaces respectively. CASN keeps an accept-

able distance to both of test subjects since it avoids the

group as shown earlier on ﬁg. 3. The graph shows that

the robot often intrudes the personal space of one of

the test subjects using SNL. This is because it drives

through the group while trying to minimize the dis-

tance between each subject, since it does not use in-

formation about social interactions between two peo-

ple. On the bottom part of table 1 (Group) we see

the details of the experiment. Using CASN the robot

keeps a mean minimum distance of 1.39m to the peo-

ple and never intrudes the personal space of the par-

ticipants. Using the SNL method the robot keeps a

mean minimum distance of 0.76 m to the people and

intrudes the personal space every trial. The CASN

method for setting cost on a static group (ﬁg. 3) ver-

sus SNL makes the robot navigate more socially ac-

ceptable around a group.

4.3 Direct Collision

In this experiment we have the test subject and the

robot in a direct collision path. On ﬁg. 8a the

graph shows the distance from the robot to the per-

son throughout the run, the constant line at 1.2 m

marks the intrusion of the personal space and the line

Table 2: Direct collision: n is the number of samples, v is

the velocity, d is the distance and i is the number of times

the robot intrudes the personal spaces.

n v (m/s) d (m) i

Slow (CASN) 9 0.47 0.99 5

Slow (SNL) 11 0.42 0.82 11(1)

Medium (CASN) 10 0.69 1.18 6

Medium (SNL) 11 0.66 0.85 11

Fast (CASN) 10 1.35 1.13 5

Fast (SNL) 11 1.33 0.86 11

All (CASN) 29 0.85 1.11 16

All (SNL) 33 0.80 0.84 33(1)

Table 3: Orthogonal collision: n is the number of samples,

v is the velocity, d is the distance and i is the number of

times the robot intrudes the personal spaces.

n v (m/s) d (m) i

Slow (CASN) 5 0.38 1.71 0

Slow (SNL) 5 0.51 1.02 4

Medium (CASN) 5 0.61 1.69 0

Medium (SNL) 5 0.67 0.73 5

Fast (CASN) 5 1.00 1.72 0

Fast (SNL) 5 0.91 1.21 3

All (CASN) 15 0.66 1.70 0

All (SNL) 15 0.69 0.99 12

at 0.45 m marks the intrusion of the intimate space.

The graph show that both CASN and SNL intrudes

the personal space and that the SNL method intrudes

the intimate space. On table 2 we see the details of

the experiment. We clustered the participants speed

into three categories (slow, medium and fast) to see if

speed makes a difference in performance of the two

methods and we also report all trials collected. Using

CASN the robot keeps a mean minimum distance to

the person of 1.11 m and intrudes the personal space

16 times. Using the SNL method the robot keeps a

mean minimum distance to the person of 0.84 m and

intrudes the personal space 33 times and the intimate

space 1 time (which was a collision). We also see

that CASN keeps a more socially acceptable distance

over the three speeds than SNL, where we range from

mean minimum distances between 0.99 − 1.18 and

SNL ranges between 0.82 − 0.86, which means that

the robot always drive into the participants personal

space using SNL.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

432

4.4 Orthogonal Collision

In this experiment the test subject and the robot is

on an orthogonal collision path. On ﬁg. 8b the

graph shows the distance from the robot to the per-

son throughout the run. The horizontal lines at 1.2 m

and 0.45 m marks the intrusion of the personal and

intimate spaces respectively. The graph shows that

CASN never intrudes the personal space of the partic-

ipants and while the SNL method does.

With CASN (ﬁg. 5) we force the robot to drive

behind the person, in the direction where the person

came from. In this way the robot and the persons

path will never collide. The SNL method will cre-

ate an inadequate robot movement during an orthog-

onal collision, where the robot often follows the path

of the person. On table 3 we see the results from the

experiment. We again cluster the participants speed

into three categories (slow, medium and fast) to see if

speed makes a difference in performance of the two

methods, and we also report all trials collected. Us-

ing CASN the robot keeps a mean minimum distance

of 1.70 m to the person and never intrudes the per-

sonal space. Using the SNL method the robot keeps a

mean minimum distance of 0.99 m to the person and

intrudes the personal space 12 times. We also see that

CASN keeps similar socially acceptable distance over

the three speeds. The CASN method’s mean min-

imum distances ranges between 1.69-1.72 while the

SNL method ranges between 0.73-1.21. This means

that the robot often drives into the participants per-

sonal space using SNL.

5 CONCLUSION

In this paper we present the method Context-Aware

Social robot Navigation (CASN) for putting mobility

constraints for robots navigating in the proximity of

humans, in the form of costs in costmaps. Inspired

by social space theory by (Hall, 1966) and conversa-

tional group theory by (Kendon, 1990) we put costs

around detected humans in the scene of the robot. We

extend this basic principle to also use the context of

the situation e.g, are the humans in motion, are there

any social interactions between detected humans, and

the task of the robot, in this paper avoiding humans in

its way. Our experiments show that CASN method

makes a mobile robot follow social convention, in

four different navigation scenarios, better than a ROS

open source method social navigation layer

ACKNOWLEDGEMENTS

This research was supported by the project Health-

CAT, funded by the European Fund for regional de-

velopment, and by the project SMOOTH (project

number 6158-00009B) by Innovation Fund Denmark.

REFERENCES

Bordallo, A., Previtali, F., Nardelli, N., and Ramamoorthy,

S. (2015). Counterfactual reasoning about intent for

interactive navigation in dynamic environments. In

2015 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems (IROS), pages 2943–2950.

IEEE.

Hall, E. T. (1966). The hidden dimension.

IFR (2020). International Foundation of Robotics presents

World Robotics Report 2020.

Juel, W. K., Haarslev, F., Kr

uger, N., and Bodenhagen, L.

(2020). An integrated object detection and tracking

framework for mobile robots. pages 513–520.

Kendon, A. (1990). Conducting interaction: Patterns of

behavior in focused encounters, volume 7. CUP

Archive.

Khambhaita, H. and Alami, R. (2020). Viewing robot navi-

gation in human environment as a cooperative activity.

In Robotics Research, pages 285–300. Springer.

Kirby, R., Simmons, R., and Forlizzi, J. (2009). Com-

panion: A constraint-optimizing method for person-

acceptable navigation. In RO-MAN 2009-The 18th

IEEE International Symposium on Robot and Human

Interactive Communication, pages 607–612. IEEE.

Lu, D. V., Hershberger, D., and Smart, W. D. (2014). Lay-

ered costmaps for context-sensitive navigation. In

2014 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems, page 709–715. IEEE.

Marder-Eppstein, E., Berger, E., Foote, T., Gerkey, B., and

Konolige, K. (2010). The ofﬁce marathon: Robust

navigation in an indoor ofﬁce environment. In 2010

IEEE International Conference on Robotics and Au-

tomation, pages 300–307.

Mateus, A., Ribeiro, D., Miraldo, P., and Nascimento, J. C.

(2019). Efﬁcient and robust pedestrian detection using

deep learning for human-aware navigation. Robotics

and Autonomous Systems, 113:23–37.

Mead, R. and Matari

c, M. J. (2017). Autonomous

human–robot proxemics: socially aware navigation

based on interaction potential. Autonomous Robots,

41(5):1189–1201.

Ram

ırez, O. A. I., Khambhaita, H., Chatila, R., Chetouani,

M., and Alami, R. (2016). Robots learning how and

where to approach people. In 2016 25th IEEE inter-

national symposium on robot and human interactive

communication (RO-MAN), pages 347–353. IEEE.

Riek, L. D. (2017). Healthcare robotics. Communications

of the ACM, 60(11):68–78.

Scandolo, L. and Fraichard, T. (2011). An anthropomorphic

navigation scheme for dynamic scenarios. In 2011

IEEE International Conference on Robotics and Au-

tomation, pages 809–814. IEEE.

Context-aware Social Robot Navigation

433