Identification of Gait Phases with Neural Networks for Smooth
Transparent Control of a Lower Limb Exoskeleton
Vittorio Lippi
1 a
, Cristian Camardella
2 b
, Alessandro Filippeschi
2,3 c
and Francesco Porcini
2 d
1
University Hospital of Freiburg, Neurology, Freiburg, Germany
2
Scuola Superiore Sant’Anna, TeCIP Institute, PERCRO Laboratory, Pisa, Italy
3
Scuola Superiore Sant’Anna, Department of Excellence in Robotics and AI, Pisa, Italy
Keywords:
Wearable Robots, Neural Networks, Exoskeleton, Gait Phases.
Abstract:
Lower limbs exoskeletons provide assistance during standing, squatting, and walking. Gait dynamics, in
particular, implies a change in the configuration of the device in terms of contact points, actuation, and system
dynamics in general. In order to provide a comfortable experience and maximize performance, the exoskeleton
should be controlled smoothly and in a transparent way, which means respectively, minimizing the interaction
forces with the user and jerky behavior due to transitions between different configurations. A previous study
showed that a smooth control of the exoskeleton can be achieved using a gait phase segmentation based on joint
kinematics. Such a segmentation system can be implemented as linear regression and should be personalized
for the user after a calibration procedure. In this work, a nonlinear segmentation function based on neural
networks is implemented and compared with linear regression. An on-line implementation is then proposed and
tested with a subject.
1 INTRODUCTION
Wearable robots are used to assist the user providing
partial compensation for the force required for the
performed task. This can find application in a work
environment where the user is required to move weight
(Omoniyi et al., 2020; Pillai et al., 2020), in rehabilita-
tion and impairment compensation (Afzal et al., 2020;
Swank et al., 2020). The particular case of medical
application requires to address specifically the impair-
ment that affects the patient, but in all these scenarios
the robot provides a helping force or torque to the user.
The help must be provided coherently with the inten-
tion of the user in terms of timing and intensity. In
the specific case of the lower limb exoskeleton consid-
ered in this work (Fig. 1) the helping force consists
in a partial compensation of gravity and inertia. As
the user walks, the configuration of the body and the
robot changes as the supporting leg changes, this re-
quires switching between different controllers. This
is achieved by identifying the phase of the gait. Most
a
https://orcid.org/0000-0001-5520-8974
b
https://orcid.org/0000-0002-3856-5731
c
https://orcid.org/0000-0001-6078-6429
d
https://orcid.org/0000-0001-9263-9423
Figure 1: The Wearable Walker lower limb exoskeleton and
the experimental setup used for data collection.
Lippi, V., Camardella, C., Filippeschi, A. and Porcini, F.
Identification of Gait Phases with Neural Networks for Smooth Transparent Control of a Lower Limb Exoskeleton.
DOI: 10.5220/0010554401710178
In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 171-178
ISBN: 978-989-758-522-7
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
171

of the control systems available at the state of the art,
e.g (Kazerooni et al., 2005; Yang et al., 2009; Yan
et al., 2015; Tagliamonte et al., 2013; He and Kiguchi,
2007), manage the switching between different con-
trol schemes, required by different gait phases, using
a finite state machine. This produces a discontinuity
in assistive torques during phase transitions, such an
aspect is not often investigated (Yan et al., 2015). In a
previous work, (Camardella et al., 2021), it was shown
that the phase can be properly identified with a linear
combination of joint angles. Such transformation was
obtained through a linear regression performed after
a calibration trial (i.e. recording joint angles without
controlling the exoskeleton). The aim of the present
work consists of the analysis of a phase identification
performed using neural networks, using the data from
(Camardella et al., 2021). This is motivated by the
perspective that machine learning will be an important
tool in managing the complexity of human robot inter-
action (HRI) in assistive devices (Argall, 2013; Broad
et al., 2017; Chen et al., 2017; Kurkin et al., 2018; Na
et al., 2019). Because the learned estimator of the gait
phase is affecting the system itself after the learning
through the control system, a slight decrease in perfor-
mance can be expected. In (Lippi, 2018) experiments
with humanoid robots showed that on-line incremental
learning is a viable solution for this issue. A test of
an online implementation is then tested, with one trial
with one subject.
2 MATERIALS AND METHODS
2.1 The Exoskeleton
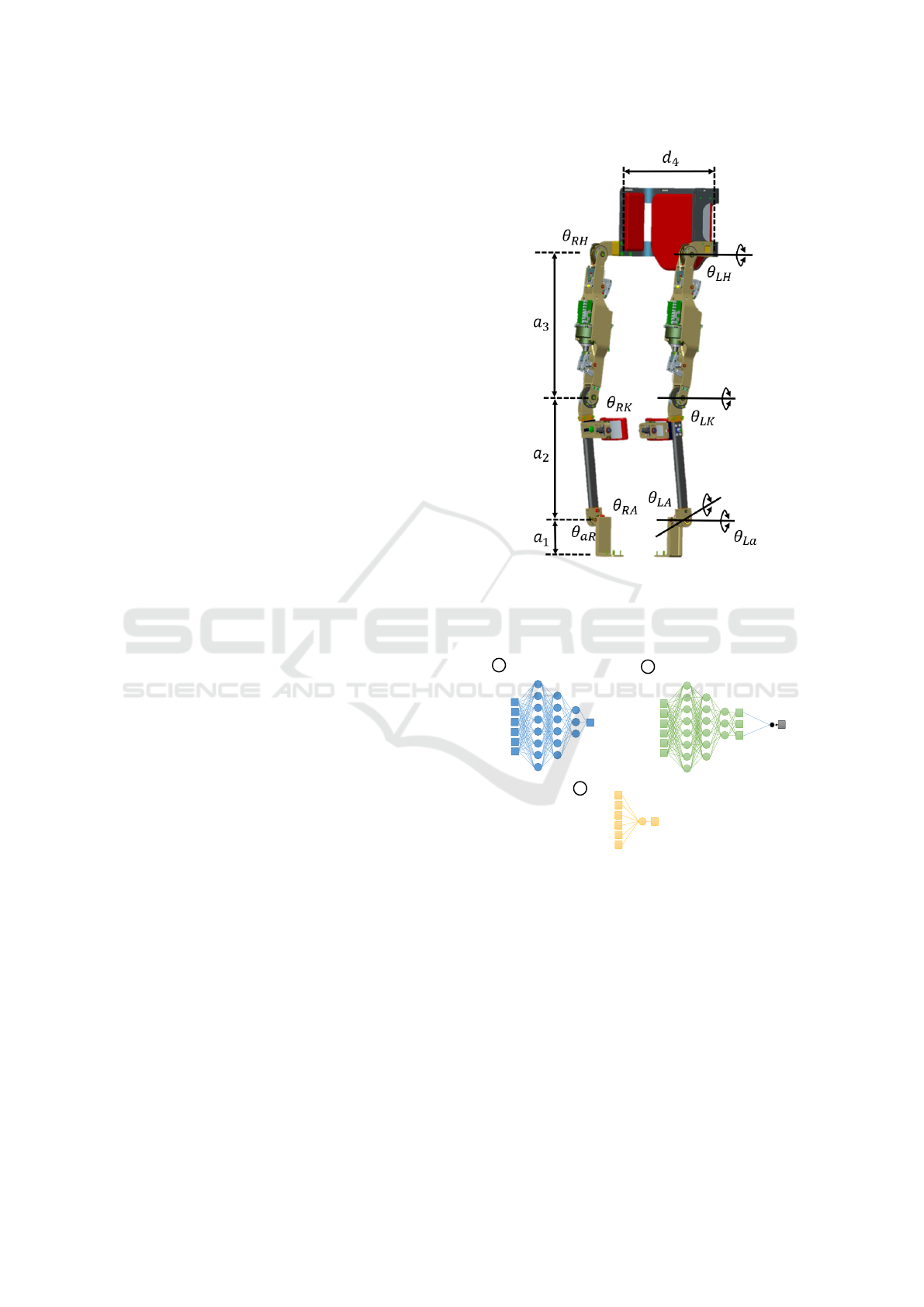
The Wearable-Walker exoskeleton (Fig. 1) is a lower-
limb exoskeleton used for assistance in tasks such as
load carrying. The exoskeleton is built by a rigid struc-
ture of 7 links and 8 revolute joints: hip and knee
flexion/extension (active joints) per leg, ankle flex-
ion/extension, and ankle inversion/eversion (passive
joints) per leg. The active joints mount each a brush-
less torque motor (RoboDrive Servo ILM 70x18) in se-
ries to a tendon-driven transmission system composed
of a screw and a pulley (Bergamasco et al., 2011) guar-
anteeing a reduction ratio of 1:73.3 and high efficiency
(90 % ). Each joint has been sensorized with Hall-effect
sensors, while there are encoders on each motor shaft.
Moreover, there are 4 pressure sensors in each shoe
insole and 4 load cells on each human-robot interface
(at the shins and thighs) to monitor human-robot in-
teractions. The power electronics group consists of a
battery of 75 V, 14 Ah, and a voltage conversion board,
while the control group consists of a computer running
Figure 2: The Wearable Walker lower limb exoskeleton. The
robot has 6 DoFs in the sagittal plane: hips, knees and ankles.
Each DoF is equipped with Hall-effect sensors and encoders
on motor shafts. There are 2 more passive DoFs to allow
ankles inversion-eversion.
OUTPUT =
phase (scalar,
continuous)
INPUT = joint angles
(6 x 1)
Hidden layers size = [8 6 3]
FFNN for
REGRESSION
A
OUTPUT =
phase (Categorical,
3 x 1)
INPUT = joint angles
(6 x 1)
Hidden layers size = [8 6 3]
FFNN for
CLASSIFICATION
B
Left
Right
Double
+
phase for MSRE
(scalar, continuous)
-1
+1
C
INPUT = joint angles
(6 x 1)
OUTPUT =
phase (scalar,
continuous)
Linear
unit
Figure 3: Architecture of the neural networks (A,B) and of
the linear regression represented as a neural network (C).
Simulink Real-Time at 5 kHz and a communication
module; both groups are housed on the backlink of
the exoskeleton. The communication module allows
Wi-Fi communication with a host PC (which remotely
controls the on-board computer) and the communica-
tion via EtherCAT protocol with the low-level control
module of each leg.
2.2 Control Strategies
Identification of gait phases was tested with three
different control strategies. Since each control strat-
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
172

egy affects the way each subject walks while wearing
the exoskeleton, the proposed neural network perfor-
mance was investigated offline on a previously ac-
quired dataset in which the subjects had active control
strategies while walking. The analyzed strategies were
FSM (Finite State Machine), sFSM (smoothed FSM),
and Blend. All methods apply a feed-forward grav-
ity and inertial compensation, exploiting two dynamic
models named LGF (Left Grounded Foot) and RGF
(Right Grounded Foot). These models differ in consid-
ering a serial chain starting with a base frame either on
the left ankle or right ankle. LGF and RGF models are
used respectively during a left single stance (swinging
right leg) and a right single stance (swinging left leg).
The way these models contribute in computing the
aforementioned compensation torques characterizes
the three analyzed strategies:
• A. FSM: the control output of this strategy instan-
taneously switch between LGF and RGF outputs
whenever a left or right single stance is detected;
• B. sFSM: the control output applies a smoothing
function with a fixed time constant, when switch-
ing from left single stance to right single stance
(Hyun et al., 2017);
• C. Blend: the control output depends on two co-
efficients that, varying continuously with the vari-
ations of the joint angle, weighs the influence of
LGF and RGF models output. The total output is
the sum of the single weighted outputs (Camardella
et al., 2021).
2.3 The Dataset
The presented analysis is based on the data from (Ca-
mardella et al., 2021). Specifically, the test was per-
formed on 15 subjects, with age 32.45 ± 5.34 years
and height 1.76 ± 0.04 (i.e. the 11 subjects who par-
ticipated in (Camardella et al., 2021) and 4 more that
were recorded similarly) . All the participants signed a
written disclosure and voluntarily joined the exper-
iments. All the experiments have been conducted
under the World Medical Association Declaration of
Helsinki guidelines. Each subject performed a cali-
bration trial used for the regression wearing the ex-
Table 1: Lengths [ mm ], masses [ kg ] and joint ranges of
motion (ROMs) [ deg ] of the exoskeleton. The ROMs are the
same for the two legs.
Lengths [mm] Masses [kg] ROMs [rad]
a
1
95 m
1
0.2 θ
∗A
-70,70
a
2
402 m
2
2.9 θ
∗K
-5,125
a
3
407 m
3
4.1 θ
∗H
-30,125
a
4
474 m
4
1.2 θ
∗a
-50,50
oskeleton, but with no active control. The calibration
trial was performed with a series of different speeds,
each one applied on the treadmill for 30 s, specifically
1,2,3,3.5,3,2,1 Km/h. The transition between speeds
lasted about 2 seconds. A total of 9 test trials for each
subject were performed as follows. Three different
control systems were then tested: FSM, SmoothFSM,
and Blend. For each control system, three speeds were
tested: walking on the treadmill at 1 km/h for 30 s, at
3.5 km/h for 30 s, ground walking for 7 meters with
no imposed speed (“free” in Table 3). Since The phase
is identified using FSR (force sensing resistor) sen-
sors in the soles (see Fig 1. It should be noticed that
while FSR sensors, recognizing the contact with the
ground directly, can provide ground truth for the train-
ing, in the long run, they require recalibration. This
explains why it is needed to base phase recognition
on kinematic data (encoders) instead of using the FSR
directly. The sampling rate is 100 Hz, the number
of samples used for training varied for the different
subjects, with a range from 21041 to 11541 with an
average of 14125.
2.4 Regression
The linear regression was performed between the 6
joint angles and the phase variable, producing a 1 × 6
matrix of coefficients. The phase variable is defined
as:
ϕ =





−1 le f t
0 double
1 right
(1)
A neural network with the architecture shown in Fig. 3
“A” was trained to perform the same regression. A neu-
ral network classifier has been trained for comparison
(Fig. 3 “B” ). The classifier interpreted the 3 possible
values of the target phase as a class. Both the neural
networks were trained with the Levenberg-Marquardt
(Hagan and Menhaj, 1994), validation stop was used as
regularization principle. The size of the hidden layers
was the same for both networks: empirically increas-
ing the size did not produce an observable increase in
performance.
2.5 Neural Network On-line Training
The training of the neural network is performed also
with an incremental procedure, working on-line in
two conditions while the user is walking: with and
without the active modality of the robot control. The
subject was asked to wear the Wearable Walker ex-
oskeleton and walk on the threadmill at 3.5 km/h for
5 minutes without the assistance and 5 minutes with
Identification of Gait Phases with Neural Networks for Smooth Transparent Control of a Lower Limb Exoskeleton
173

Blend-control assistance activated. In order to imple-
ment such a training in the Matlab environment, an
instance of Matlab ® was running in parallel with the
compiled control system, acquiring samples via UDP
and producing the updated weights for the neural net-
work. The compiled control system contains the neural
network that actually produce the estimated gait phase
and receives all the weights and biases every time a
training cycle is accomplished, after that, the net is
updated. The output of the neural network is never
used to modify the control assistance logic. Matlab ® ’s
Statistics and Machine Learning Toolbox ® does not
take in account explicitly the possibility to train a net-
work on-line. In order to implement on-line training
manually, the training function trains is used, per-
forming a sequential training on the sample sets. The
network is set up as:
net = feedforwardnet([8 6 3],’trains’);
net.trainParam.epochs=1;
The parameter trainParam.epochs set to one means
that the batch of samples, received by the second Mat-
lab instance via UDP are used for the training only
once. This was a fast implementation, thought to get a
result that could be compared with the offline training
in the Matlab environment. At the state of the art there
are several specific studies on incremental learning, i.e.
(Porras et al., 2019; Lippi and Ceccarelli, 2019; Bul-
linaria, 2009; Medera and Babinec, 2009), in future
works the presented learning system can be improved.
Nevertheless, at the time of writing this paper, the issue
of incremental training implemented in Matlab ® ap-
peared to be of interest for the users’ community (i.e. a
topic of several forums), we therefore assume that the
implementation presented herein may be useful as an
example for the readers. The neural network was ini-
tialized with small random weights when both models
(control and neural network training schemes) started,
and was scheduled to be trained every 20 seconds. The
training function was called through a Simulink block
’PostOutput’ listener that was also delegated to fill
a circular buffer with input and output data. When
the scheduled training time was reached, the collected
input and output data fed the trains training func-
tion. The dimension of the circular buffer was set in
a way that it was already filled in the instant of the
first training cycle. After each training, weights and
biases of the neural network were retrieved and sent
to the compiled control scheme. If the neural network
was busy in the scheduled training step, that cycle was
postponed 20 seconds after.
3 RESULTS
3.1 Regression and Classification
In order to evaluate the performance of the different
regression methods, 5-fold cross-validation has been
performed. Specifically the dataset was split into 5
parts of equal duration in time. The regression was
performed using a calibration trial for each subject.
The performance is computed for each subject sepa-
rately and the final result is computed as the average
of all the results for the subjects. The results obtained
with FFNN and linear regression are compared in Ta-
ble 2. The nonlinear model provided by the neural
network produced a better fit (smaller RMSE) than
the linear regression, associated with an increase of
performance in terms of recognizing the phase. The
classification was implemented considering a thresh-
old applied to the output of the regression and of the
neural network.
ϕ(y
reg
) =





−1 y
reg
< −θ
0 θ > y
reg
> −θ
1 y
reg
> θ
(2)
where y
reg
is the output of the regression (or FFNN)
the value θ = 0.1 was decided empirically in (Ca-
mardella et al., 2021). For comparison, a neural net-
work with similar architecture to the one used for the
fit, but designed and trained for classification is also
analyzed (see Fig. 3 “B”). Such a network outputs
the class. In order to compute the accuracy, the cate-
gorical output was translated into a numerical value
ϕ following the definition of eq. 1. The classifier net-
work produced a better accuracy but a worse RMSE.
This is not surprising considering that with the output
defined on the domain {−1, 0, 1} , each classification
error produced a quadratic deviation (i.e. 1 or 4) that
was larger on average in comparison to the errors ob-
tained with the continuous variables from both the
linear and FFNN-based regressions; an example is
shown in Fig. 4.
Table 2: Average prediction error and classification accuracy
obtained with linear regression and neural networks. The
calibration data are used as training and test set with a 5-fold
cross validation. The result across the 15 subjects is then
averaged.
RMSE Accuracy
Linear 0.51 82.56 %
FFNN fit 0.37 84.57 %
FFNN class 0.75 87.04 %
A characteristic response of the linear regressor
is the presence of spikes in the signal, this is visible
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
174

Figure 4: Example of output for the linear regression lin reg, the neural network regression NN reg and the neural network
classifier NN class. The output is plotted together with the phase used for training target. Notice the irregularity in the original
data around 1 s, such an event contribute substantially to the RMSE, especially for the neural networks, the output of which is
closer to 1.
in Fig. 4. The phenomenon is happening sometimes
also for the NN, e.g. Fig. 4 around 3s but with a
smaller amplitude and not for each cycle. In order to
quantify it Fig. 5 shows the signals of Fig. 4 between
the 2.75s and 3.2s . The monotonicity of the function
is evaluated by computing the RMSE between the
measured signal and a version where the samples are
sorted, it accounts on average to 0.0491 for the linear
regressor and 0.0042 for the neural network respective
outputs (similar values are measured for the rest of the
dataset). This provides a smoother transition.
3.5 3.55 3.6 3.65 3.7 3.75 3.8 3.85 3.9 3.95 4
time [s]
-1
-0.5
0
0.5
1
phase
target
lin reg (Sorted)
lin reg
NN reg (sorted)
NN reg
Figure 5: The output of the NN is more monotonic in time
compared with the one of the linear regression. This is quan-
tified comparing the samples in chronological order with the
samples sorted by decreasing magnitude over approximately
a quarter of cycle. the RMSE between sorted and unsorted
is 0.0491 for the linear fit and 0.0042 for the NN.
3.2 Neural Network On-line Training
The results of the on-line training test with the control
active, described in § 2.5 are shown in Fig.6 and Fig.
7, displaying accuracy and RMSE respectively. The
accuracy was overall better than the one observed in
the off-line cases ( ≤ 80 % ). The use of a 5-seconds
time window showed peaks of performance locally
Table 3: Performance obtained by the linear regression once
the phase recognition is used in “closed loop” when con-
trolling the exoskeleton with three different control systems.
The results is averaged over the 15 subjects. The training
result is different from the one reported in Table 2 because
in this case it was computed on the whole dataset without
cross validation.
Speed RMSE Accuracy
[Km/h]
Training 0 ↔ 3.5 0.44* 83.51* %
FSM 1 0.43 70.23 %
FSM 3.5 0.43 79.41 %
FSM free 0.53 73.49 %
SFSM 1 0.43 76.46 %
SFSM 3.5 0.43 78.65 %
SFSM free 0.56 69.70 %
Blend 1 0.42 74.28 %
Blend 3.5 0.42 77.89 %
Blend free 0.53 67.06 %
that are not affected by the initial bad performance. At
the same time a slight decrease of the performance at
the end of the trial, on average the value on the time
window after the first 10 seconds was 87 %. Similar
considerations can be done for the evolution of 7 in
time. It should be noticed that, notwithstanding the
improvement in the accuracy, the RMSE is slightly
larger than the one obtained off-line.
4 DISCUSSION, CONCLUSIONS
AND FUTURE WORK
In this work we analyzed the exoskeleton control pre-
sented in (Camardella et al., 2021) from the point of
Identification of Gait Phases with Neural Networks for Smooth Transparent Control of a Lower Limb Exoskeleton
175

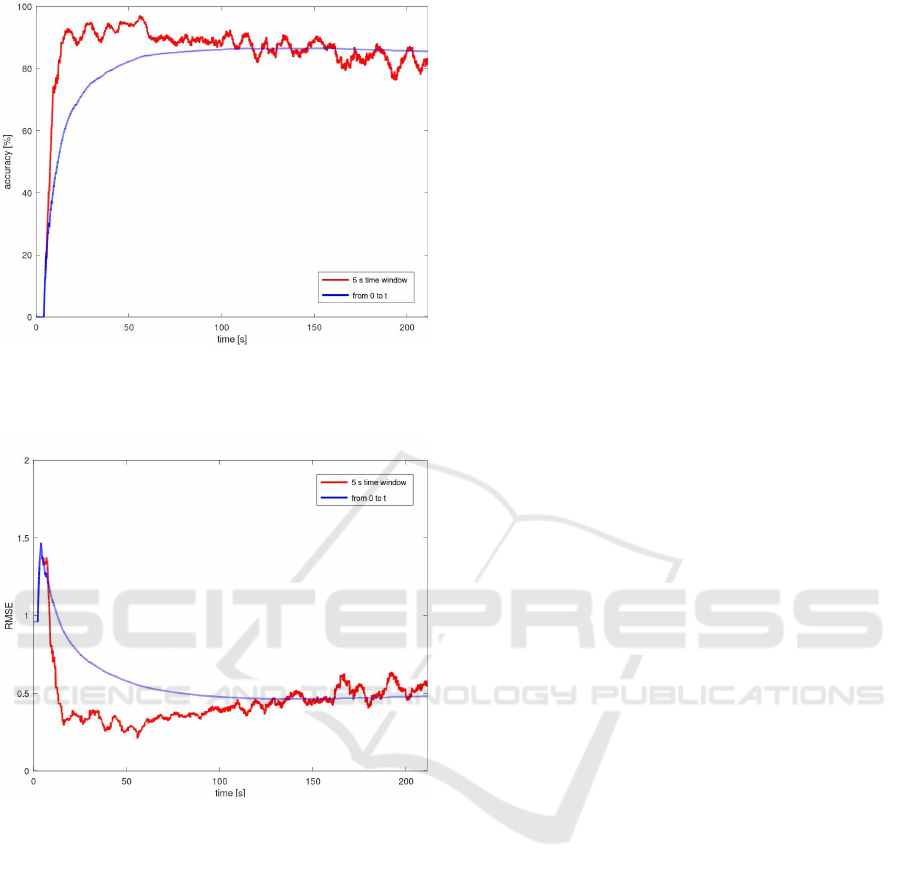
Figure 6: Accuracy of the real-time neural network. The
red line represents the accuracy computed on a time window
spanning the last 5 seconds, the blue line represents the
accuracy over the whole dataset up to the current time.
Figure 7: RMSE of the real time neural network. The red line
represents the RMSE computed on a time window spanning
the last 5 seconds, the blue line represents the RMSE over
the whole dataset up to the current time.
view of the recognition of gait phase using joint angles,
proposing and testing an approach based on neural net-
works. Neural networks perform better than linear
regression, yet the linear regression is not significantly
worse. Both solutions seem useful in this context. A
further improvement in classification accuracy can be
obtained by training a classifier explicitly instead of a
regression associated with a threshold (similarly to the
classifier proposed in the offline case). Nevertheless, it
should be noticed that in this context the estimated ϕ
is used to control smooth transitions between control
systems. This means that a function that varies slowly
between the three target values −1 , 0 and 1 can be
preferable to a function that changes more abruptly
pursuing smaller RMSE respect to the reference, con-
sidering that such reference moves in steps as shown
in Fig. 4. Future work will exploit the versatility of
the neural network to optimize the transition dynamics
explicitly. In this sense, online training can be used
to reduce the interaction forces between the user and
the robot during the transitions, an objective function
that is available only when the control is active. It
should be noticed that the transitions are not the only
issue that can increase interaction forces: for exam-
ple, the double stance phase represents a hyper-static
configuration where the relative contribution of the
two legs is arbitrary (Goodworth and Peterka, 2012).
In humanoid control, additional constraints may be
added in the form of synergies(Hauser et al., 2007;
Hauser et al., 2011; Alexandrov et al., 2017; Lippi
et al., 2016), but this may not reflect the natural hu-
man behavior: it is known that the weight-bearing is
asymmetric both in healthy subjects and in patients.
Such issue should be addressed in the design of the
double stance controller, even taking into consider-
ation that the two legs provide independent sensory
feedback, that could be an impact on how the system
is perceived. This specific study focused on the identi-
fication of the gait phase, the long term project aims
to a more general evaluation of performance in gait
and balance: the formal definition of benchmarking
performance indicators is currently under research for
gait (Torricelli et al., 2020) and balance (Lippi et al.,
2019; Lippi et al., 2020). The test of the on-line learn-
ing showed a stable convergence to a trained network
that had a performance that was better than the one
of the network trained off-line in terms of accuracy.
This suggests a possible advantage in using on-line
learning for exoskeletons when the neural network is
used in the control loop, similarly to what is observed
with humanoid robots (Lippi, 2018). The convergence
speed of the on-line training is limited by the design
choice of using each new batch of training data only
of 1 epoch. In future work more ”aggressive ´´ training
systems will be tested (e.g. using batch of old and new
data together and iterate for more epochs). The test
proposed in this work was focused on the global result,
future studies will also take in account how human sen-
sor fusion interacts with the proposed control(Hettich
et al., 2013; Hettich et al., 2015) also considering the
subjective report of the subjects (Luger et al., 2019;
Stampacchia et al., 2016).
ACKNOWLEDGEMENTS
This work is supported by the project EXOSMOOTH,
a sub-project of EUROBENCH (European Robotic
Framework for Bipedal Locomotion Benchmarking,
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
176

www.eurobench2020.eu) funded by
H2020 Topic ICT 27-2017 under
grant agreement number 779963.
REFERENCES
Afzal, T., Tseng, S.-C., Lincoln, J. A., Kern, M., Francisco,
G. E., and Chang, S.-H. (2020). Exoskeleton-assisted
gait training in persons with multiple sclerosis: a single-
group pilot study. Archives of physical medicine and
rehabilitation, 101(4):599–606.
Alexandrov, A. V., Lippi, V., Mergner, T., Frolov, A. A.,
Hettich, G., and Husek, D. (2017). Human-inspired
eigenmovement concept provides coupling-free sen-
sorimotor control in humanoid robot. Frontiers in
neurorobotics, 11:22.
Argall, B. D. (2013). Machine learning for shared control
with assistive machines. In Proceedings of ICRA Work-
shop on Autonomous Learning: From Machine Learn-
ing to Learning in Real world Autonomous Systems,
Karlsruhe, Germany.
Bergamasco, M., Salsedo, F., and Lucchesi, N. (2011). High
torque limited angle compact and lightweight actuator.
US Patent App. 12/989,095.
Broad, A., Murphey, T., and Argall, B. (2017). Learning
models for shared control of human-machine systems
with unknown dynamics. Robotics: Science and Sys-
tems Proceedings.
Bullinaria, J. A. (2009). Evolved dual weight neural archi-
tectures to facilitate incremental learning. In Proceed-
ings of the International Joint Conference on Compu-
tational Intelligence - Volume 1: ICNC, (IJCCI 2009),
pages 427–434. INSTICC, SciTePress.
Camardella, C., Porcini, F., Filippeschi, A., March-
eschi, S., Solazzi, M., and Frisoli, A. (2021).
Gait Phases Blended Control for Enhancing Trans-
parency on Lower-Limb Exoskeletons. RA-L.
10.1109/LRA.2021.3075368.
Chen, C., Liu, D., Wang, X., Wang, C., and Wu, X. (2017).
An adaptive gait learning strategy for lower limb ex-
oskeleton robot. In 2017 IEEE International Confer-
ence on Real-time Computing and Robotics (RCAR),
pages 172–177.
Goodworth, A. D. and Peterka, R. J. (2012). Sensorimo-
tor integration for multisegmental frontal plane bal-
ance control in humans. Journal of neurophysiology,
107(1):12–28.
Hagan, M. T. and Menhaj, M. B. (1994). Training feedfor-
ward networks with the marquardt algorithm. IEEE
transactions on Neural Networks, 5(6):989–993.
Hauser, H., Neumann, G., Ijspeert, A. J., and Maass, W.
(2007). Biologically inspired kinematic synergies pro-
vide a new paradigm for balance control of humanoid
robots. In 2007 7th IEEE-RAS International Confer-
ence on Humanoid Robots, pages 73–80. IEEE.
Hauser, H., Neumann, G., Ijspeert, A. J., and Maass, W.
(2011). Biologically inspired kinematic synergies en-
able linear balance control of a humanoid robot. Bio-
logical cybernetics, 104(4):235–249.
He, H. and Kiguchi, K. (2007). A study on emg-based
control of exoskeleton robots for human lower-limb
motion assist. In 2007 6th International special topic
conference on information technology applications in
biomedicine, pages 292–295. IEEE.
Hettich, G., Lippi, V., and Mergner, T. (2013). Human-like
sensor fusion mechanisms in a postural control robot.
In Londral, A. E., Encarnacao, P., and Pons, J. L., ed-
itors, Proceedings of the International Congress on
Neurotechnology, Electronics and Informatics. Vilam-
oura, Portugal, pages 152–160.
Hettich, G., Lippi, V., and Mergner, T. (2015). Human-like
sensor fusion implemented in the posture control of a
bipedal robot. In Neurotechnology, Electronics, and
Informatics, pages 29–45. Springer.
Hyun, D. J., Lim, H., Park, S., and Jung, K. (2017). De-
velopment of ankle-less active lower-limb exoskele-
ton controlled using finite leg function state machine.
International Journal of Precision Engineering and
Manufacturing, 18(6):803–811.
Kazerooni, H., Racine, J.-L., Huang, L., and Steger, R.
(2005). On the control of the berkeley lower extremity
exoskeleton (bleex). In Proceedings of the 2005 IEEE
international conference on robotics and automation,
pages 4353–4360. IEEE.
Kurkin, S. A., Pitsik, E. N., Musatov, V. Y., Runnova, A. E.,
and Hramov, A. E. (2018). Artificial neural networks
as a tool for recognition of movements by electroen-
cephalograms. In Proceedings of the 15th International
Conference on Informatics in Control, Automation and
Robotics - Volume 1: ICINCO,, pages 166–171. IN-
STICC, SciTePress.
Lippi, V. (2018). Prediction in the context of a human-
inspired posture control model. Robotics and Au-
tonomous Systems.
Lippi, V. and Ceccarelli, G. (2019). Incremental princi-
pal component analysis: Exact implementation and
continuity corrections. In Proceedings of the 16th
International Conference on Informatics in Control,
Automation and Robotics - Volume 1: ICINCO, pages
473–480. INSTICC, SciTePress.
Lippi, V., Mergner, T., Maurer, C., and Seel, T. (2020).
Performance indicators of humanoid posture control
and balance inspired by human experiments. In
The International Symposium on Wearable Robotics
(WeRob2020) and WearRAcon Europe.
Lippi, V., Mergner, T., Seel, T., and Maurer, C. (2019).
COMTEST project: A complete modular test stand
for human and humanoid posture control and balance.
In 2019 IEEE-RAS 19th International Conference on
Humanoid Robots (Humanoids) Toronto, Canada. Oc-
tober 15-17.
Lippi, V., Mergner, T., Szumowski, M., Zurawska, M. S.,
and Zieli
´
nska, T. (2016). Human-inspired humanoid
balancing and posture control in frontal plane. In
ROMANSY 21-Robot Design, Dynamics and Control,
pages 285–292. Springer, Cham.
Luger, T., Cobb, T. J., Seibt, R., Rieger, M. A., and Stein-
hilber, B. (2019). Subjective evaluation of a passive
lower-limb industrial exoskeleton used during simu-
Identification of Gait Phases with Neural Networks for Smooth Transparent Control of a Lower Limb Exoskeleton
177

lated assembly. IISE Transactions on Occupational
Ergonomics and Human Factors, 7(3-4):175–184.
Medera, D. and Babinec,
ˇ
S. (2009). Incremental learning
of convolutional neural networks. In Proceedings of
the International Joint Conference on Computational
Intelligence - Volume 1: ICNC, (IJCCI 2009), pages
547–550. INSTICC, SciTePress.
Na, S., Shin, J., Eom, S., and Lee, E. (2019). A study
on the activation of femoral prostheses: Focused on
the development of a decision tree based gait phase
identification algorithm. In Proceedings of the 16th
International Conference on Informatics in Control,
Automation and Robotics - Volume 1: ICINCO,, pages
775–780. INSTICC, SciTePress.
Omoniyi, A., Trask, C., Milosavljevic, S., and Thamsuwan,
O. (2020). Farmers’ perceptions of exoskeleton use on
farms: Finding the right tool for the work (er). Interna-
tional Journal of Industrial Ergonomics, 80:103036.
Pillai, M. V., Van Engelhoven, L., and Kazerooni, H. (2020).
Evaluation of a lower leg support exoskeleton on floor
and below hip height panel work. Human factors,
62(3):489–500.
Porras, E., Pe
˜
nuela, L., and Velasco, A. (2019). Electromyo-
graphy signal analysis to obtain knee joint angular
position. In Proceedings of the 16th International Con-
ference on Informatics in Control, Automation and
Robotics - Volume 1: ICINCO,, pages 730–737. IN-
STICC, SciTePress.
Stampacchia, G., Rustici, A., Bigazzi, S., Gerini, A.,
Tombini, T., and Mazzoleni, S. (2016). Walking with a
powered robotic exoskeleton: Subjective experience,
spasticity and pain in spinal cord injured persons. Neu-
roRehabilitation, 39(2):277–283.
Swank, C., Sikka, S., Driver, S., Bennett, M., and Callender,
L. (2020). Feasibility of integrating robotic exoskele-
ton gait training in inpatient rehabilitation. Disability
and Rehabilitation: Assistive Technology, 15(4):409–
417.
Tagliamonte, N. L., Sergi, F., Carpino, G., Accoto, D.,
and Guglielmelli, E. (2013). Human-robot interac-
tion tests on a novel robot for gait assistance. In 2013
IEEE 13th international conference on rehabilitation
robotics (ICORR), pages 1–6. IEEE.
Torricelli, D., Mizanoor, R. S., Lippi, V., Weckx, M., Mathi-
jssen, G., Vanderborght, B., Mergner, T., Lefeber, D.,
and Pons, J. L. (2020). Benchmarking human likeness
of bipedal robot locomotion: State of the art and fu-
ture trends. In Metrics of Sensory Motor Coordination
and Integration in Robots and Animals, pages 147–166.
Springer.
Yan, T., Cempini, M., Oddo, C. M., and Vitiello, N. (2015).
Review of assistive strategies in powered lower-limb
orthoses and exoskeletons. Robotics and Autonomous
Systems, 64:120–136.
Yang, Z., Zhu, Y., Yang, X., and Zhang, Y. (2009).
Impedance control of exoskeleton suit based on adap-
tive rbf neural network. In 2009 International confer-
ence on intelligent human-machine systems and cyber-
netics, volume 1, pages 182–187. IEEE.
ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics
178