Routing Optimization in Dynamic Networks based on a New Entropy

Metric

Mauro Tropea

and Peppino Fazio

Dimes Department, University of Calabria, via P. Bucci 39/c, 87036 Rende (CS), Italy

Department of Molecular Sciences and Nanosystems, Ca’ Foscari University of Venice, 30172 Venice-Mestre, Italy

Keywords:

Ad Hoc Networks, Mobility, Routing, Networking, Entropy, Metric, Stability.

Abstract:

A key role in the modern telecommunication networks is played by routing aspects as the great number of

works present in literature proves. In particular, in the mobile ad-hoc networks routing is a fundamental

aspects because the mobile devices nature and their elevate dynamism. In fact, it is important to have the

possibility of ﬁnding the minimum overhead for connectivity in the network and, calculate the communication

potential through the analysis of different parameters. The focus of this paper is represented by the analysis

of the entropy in this type of mobile networks. The entropy gives the possibility of studying and predicting

the dynamics of mobile nodes. The knowledge of these aspects can help to optimise some key features of

wireless mobile communications, such as nodes stability, channel failures, and routing costs. Many simulation

campaigns have been carried out by taking into account the movement of the real nodes, obtaining beneﬁcial

results, which conﬁrm the effectiveness of the proposed study.

1 INTRODUCTION

One of the main aspects of any networks, and in par-

ticular of decentralized ones, is represented by rout-

ing protocols and algorithms which allow the com-

munication among nodes and, considering some pa-

rameters, allow to take into account efﬁciency issues

directly correlated with energy consumption, scalabil-

ity and safety. The main issue in a decentralized and

distributed network where no ﬁxed infrastructure re-

gards the elevate dynamism of the network nodes that

change their position in the time causing frequent and

unpredictable topology, such as shown in (De Rango

et al., 2003) and the energy efﬁciency and saving such

as in (De Rango and Fotino, 2009; De Rango and Tro-

pea, 2009). These considerations are still more ev-

ident when the number of nodes inside the network

increase posing serious problem of scalability. The

communication between nodes depends by nodes dy-

namism and, then the unpredictability of the connec-

tion is linked to the number of nodes to be cross for

reaching the destination and depends to node mobility

that causes frequent network topology changes.

The focus of this paper is to analyse the entropy

concept in a mobile ad-hoc networks where nodes are

mobile and their position vary in time and space. We

propose a entropy concept strongly linked to some

different aspects of the network such as Connection

Dropping Probability (CDP), fading issues, link dis-

ruption phenomena, network instability and other ef-

fects on the network conditions (Fazio et al., 2012;

Fazio et al., 2014).

So, the paper proposes a detailed analysis of the

entropy in a context of a mobile network from a par-

ticular point of view: the capability of performing

a prediction analysis of the entropy behavior in this

network typology. Approaches based on prediction

analysis are broadly studied by researchers, and they

regard different aspects of a telecommunication net-

work. One of the key aspect of ”prediction” is rep-

resented by the accuracy, that means the goodness of

the approach and how it is able to follow network dy-

namism (Fazio et al., 2013; Fazio et al., 2016). Inte-

grating, for example, a routing protocol with a predic-

tive approach leads to the enhancement of the overall

performance (Masip-Bruin et al., 2010). The concept

of entropy related to nodes mobility, is completely

suitable to describe mobility predictability, in order

to pre-conﬁgure the needed resources of the network.

In addition, having a model for nodes’ entropy, it is

possible to choose a proper scenario, that exploits its

optimal performance for a given set of protocols.

When dealing with mobile networks, nodes mo-

bility is crucial for the overall performance of the en-

102

Tropea, M. and Fazio, P.

Routing Optimization in Dynamic Networks based on a New Entropy Metric.

DOI: 10.5220/0010555501020108

In Proceedings of the 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2021), pages 102-108

ISBN: 978-989-758-528-9

tire system, especially in Mobile Ad-hoc NETworks

(MANETs), where the optimal and stable routes need

to be frequently evaluated. There are many works in

literature that take into account mobility under a dif-

ferent point of view (as underlined in the next sec-

tion): so, entropy can be considered as a metric for

assigning a weight to each path segment. If we are

interested, for example, to MANET routing, and if

we are able to deﬁne new composite metrics (based

also on the entropy concept), it is possible to gauge

other aspects of network dynamics, giving the pos-

sibility to better develop research testbeds, that can

provide more accurate information about the needed

resources (best path, channel bandwidth, transmission

power, bitrate, etc.) .

The remainder of the paper is organized as fol-

lows: Section 3 introduces the entropy concept and

the deployment of adaptive ﬁltering for temporal pre-

diction of nodes evolution, while Section 4 provide

details about the main obtained results, in terms of

entropy values in function of different system pa-

rameters and prediction possibilities, discussing the

broader aspects of our approach. Section 5 concludes

the paper.

2 RELATED WORK

The creation and management of any mobile network

is a challenging problem and any metric which can

be used to characterize or optimize the network cre-

ation is welcome. In the literature, a lot of works pro-

posed by scientiﬁc community make use of the en-

tropy information and disparate metrics are used and

combined to analyse the mobile behavior in order to

enhance and optimize different aspects and routines

of mobile networks’ protocols.

In the last years, researchers have spent a lot of

time and made progress on study about uncertain de-

vice location and random propagation conditions in

the connectivity among devices. In (Coon et al., 2018)

the authors make a study about conditional entropy

of wireless networks focus on network entropy with

the assumption that pairwise connections between de-

vices are statistically independent. The authors in

this contribution present an analytical framework for

studying the network entropy conditioned on the node

positions in space, providing also a method to calcu-

late a entropy lower bound useful for performing es-

timation of network entropy.

The channel allocation is another issue object of

study by scientiﬁc researchers. Normally, the choice

of the channel, based on link measurement, fall back

on channel with fewest co-channel interference. In

(Elujide and Liu, 2020) an entropy-based WLAN

channel allocation using channel state information is

proposed by authors. The authors present this pro-

posal in order to avoid the known problem of the

RSSI technique. The proposal is based on a machine

learning approach and, in this way, they try to predict

channel spectral entropy from physical layer network.

Their results prove the goodness of the proposal able

to select a channel with high throughput and low jitter.

In (Wang et al., 2020) the concept of entropy is related

with a trust reasoning model based on cloud model

and fuzzy Petri net (FPN). This approach try to give

to nodes a value of credibility. The authors propose

a routing algorithm based on trust entropy in order

to improve QoS in a MANET. Finally, they present

simulation results where they illustrate the better per-

formance of their proposal in terms of packet delivery

ratio and average latency. Due to energy issues the

authors in (Osamy et al., 2018) a cluster tree routing

for wireless networks where a cluster head selection

algorithm based on a entropy criteria is proposed.

In (Sun et al., 2006), an entropy-based approach

is proposed, emphasising the way ad-hoc nodes move

into the considered network. The authors apply the

“mobility entropy” concept to optimise routing oper-

ations through predictions and guarantee a given level

of Quality of Service (QoS). Besides, the concept

of information entropy and energy entropy in ad-hoc

networks is considered in (Cerasoli and Dimarogonas,

2008). The authors refer to Shannon entropy deﬁni-

tion in information theory, considering the “amount of

information” which is exchanged through packet sig-

nalling. In (Hua and Haas, 2009), the authors propose

some in-depth analysis of the way the stability of a

point-to-point connection can be predicted, in ad-hoc

environments.

3 THE ENTROPY CONCEPT AND

THE PREDICTIVE ADAPTIVE

FILTERING

In our work, we consider the concept of entropy (pro-

posed by Shannon (Cerasoli and Dimarogonas, 2008)

as a way for measuring the uncertainty in a generic

statistical model), but from another point of view.

Starting from the classical deﬁnition, given a ﬁnite set

of n symbols, any sequence s of those symbols (with

duplication allowed) has an associated entropy value,

given by the following expression:

Et(s) = −

∑

i=1

· log

(1)

Routing Optimization in Dynamic Networks based on a New Entropy Metric

103

Figure 1: An example of matrix GR applied to a geographical MAP with N=1.8 km, M=3.5 km, and an area of M × N =

6.3 km

; as regards matrix GR, we considered n=5 and m=6, so each region gr

i j

has the dimensions 360m × 580 m.

where p

is the probability of i-th symbol in s and

b is the base of the logarithm, that is a positive real

value. We base our proposal by starting from eq. 1

and adapting it to extract the needed knowledge from

the evolution of a MANET.

3.1 Entropy Evaluation based on

Geographic Location/Mobility

In particular, one of the main aims of this work is the

association of an entropy value to a node into the net-

work, based on its position and/or the way it has to

move among different adjacent areas. Given that we

are considering a MANET scenario, a grid GR is de-

ﬁned, able to subdivide the considered geographical

MAP (where mobile nodes are moving) into a ﬁnite

set of n × m areas, deﬁned as follows:

GR =





... gr

... ... ... ...

... gr





(2)

Given that the dimensions of the considered map

are N × M, each gr

i j

belonging to GR, with a regu-

lar square shape, will have the dimensions (N/n) and

(M/m), as depicted in Figure 1.

Entropy can be used to evaluate the activeness of a

node in a given observation window T, during which

mobile nodes are free to move into MAP, by changing

the area they visit or remaining into the same area for

the entire time period. So, if we indicate a mobile

with n

, then the symbol n

represents the set of areas

visited by n

during T. So, if ||n

|| = V (the number

of areas visited by n

in T), then:

= {gr

1 j1

...gr

1 jV

|gr

i jl

∈ GR,l = 1..V } (3)

The probability of visiting gr

i j

by n

in T is:

(gr

i j

) = (number o f times gr

i j

appears in n

)/V

(4)

and it is easy to derive the expression of nodes n

’s

entropy Et:

Et(n

) = −

∗

∑

l=1

(gr

i jl

) · ln[p

i jl

)] (5)

where V

∗

is the number of distinct gr

i j

visited by n

3.2 How to Predict the Entropy Values

by the Recursive Least Squares

(RLS)

After the deﬁnition of the term Et(n

), we would

like to describe a way for predicting the future en-

tropy samples. We based our approach on the idea of

(Semnani and Cowan, 1994), where an adaptive ﬁlter

can adapt the coefﬁcients of its impulse response in

function of a given optimisation algorithm. We con-

sidered the Recursive Least Squares (RLS) (Haykin,

1999), because it optimises the coefﬁcients by min-

imising a weighted linear least squares cost function.

This kind of approach suits our scope perfectly: a

MANET topology can be updated periodically so, for

each node, entropy can be evaluated step-by-step at

each update time. We assume that, the last entropy

value depends on the previous K ones, so we can

write:

Et(T ) = β

· Et(T − 1) + β

· Et(T − 2) + ...

... + β

· Et(T − K) + et

(6)

where et is the error (generally a white Gaussian

process), and β

,...,β

are the coefﬁcients that should

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

104

Table 1: Parameters used in simulations.

Parameter Value

Global geographical simulated area (GR) 6.25 km

Side lengths (N and M) of the simulated area 2500 m

Mobility scenario Urban and extra-urban

Average speed of mobile nodes 11.1, 13.9, 19.4 m/s

GR elements side size l from 50 to 200 meters

Number of GR elements from 2500 to 156

Simulation Tools OpenStreetMap and Matlab

Simulation time 3600 s

Mobility model C4R

Acceleration/Deceleration -2.4 m/s

Figure 2: The simulated geographical area.

be optimised, considering the last K entropy samples.

Eq. 6 can be rewritten in a compact form as:

Et(T ) = [

BETA]· [

Et(T − K)]

+ et (7)

where

BETA is the vector of coefﬁcients,

Et(T − K) is the vector of entropy values (samples

from T − 1 to T − K, and [tr] is the transpose opera-

tor. When the RLS algorithm is applied, the optimal

BETA

∗

vector is found (Haykin, 1999). At the end,

the algorithm is based on the evaluation of:

BETA(T) =

BETA(T − 1) ·

GV (T ) · [DO(T ) + ...

... −

BETA

(T − 1) ·

IN(T )]

(8)

where T is the current observation time window,

IN(T ) is the INput vector for the RLS algorithm at

T (the set of last K entropy values),

GV (T ) is the

Kalman Gain Vector (Haykin, 1999) at T , DO(t) is

the Desired Output at T (that is DO(T ) = Et(T )). The

initial conditions are n = 0 and BETA(0) = [0]. There

are many other terms that lead to the expression of eq.

8, so for more details please refer to (Haykin, 1999)

and to the RLS theory.

4 NUMERICAL RESULTS

We provide to manage nodes mobility through the

OpenStreetMap core (ope, 2019) and C4R (Martinez

et al., 2008). A MAP with N = M = 2500 meters and

an area of about 6.25 km

has been considered, ex-

Routing Optimization in Dynamic Networks based on a New Entropy Metric

105

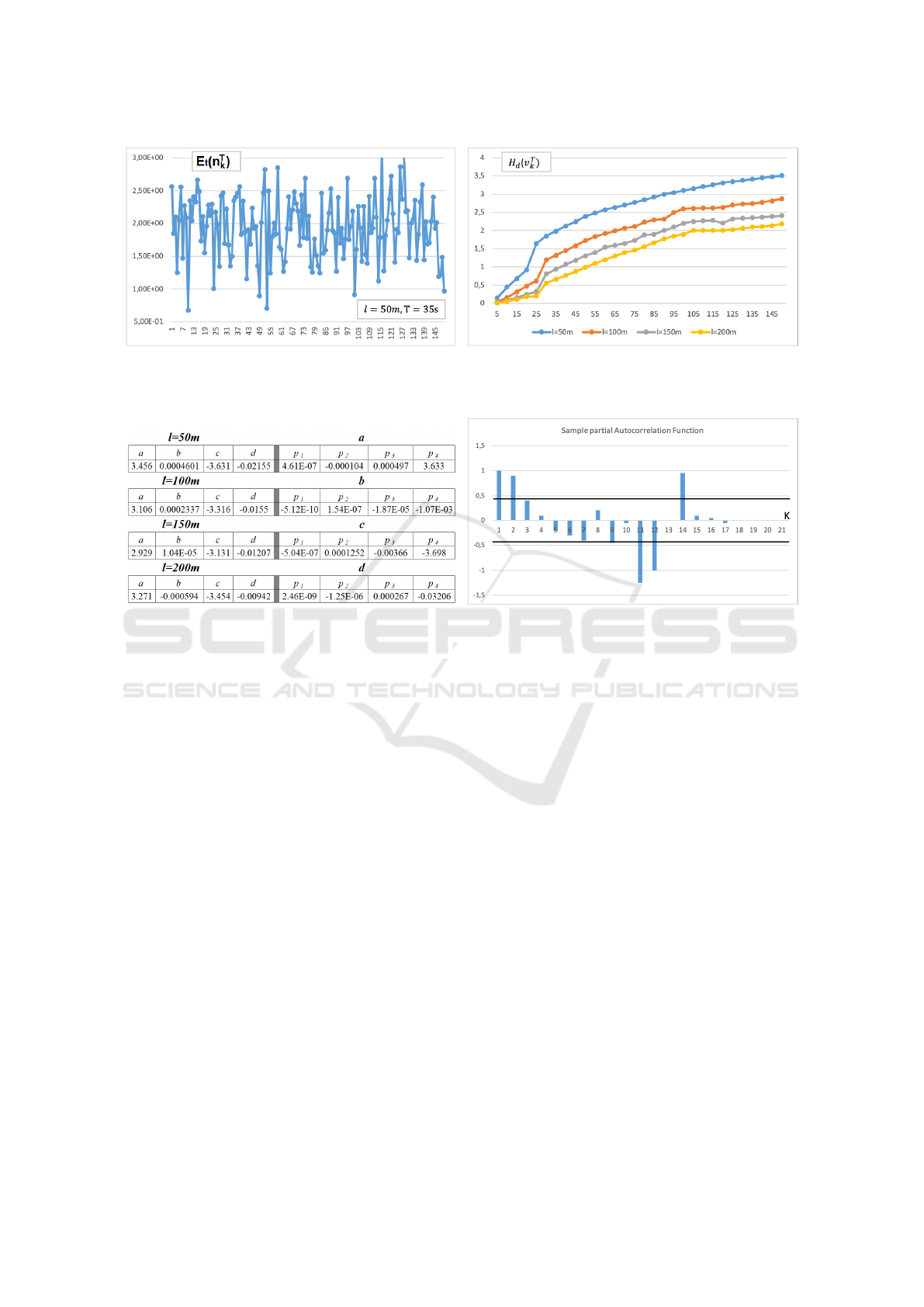
(a) (b)

Figure 3: (a) An example of a typical trend of mobility entropy associated with a mobile node, with an average speed of

13.9 m/s, l = 60m and T = 25s; (b) Average entropy associated with mobile nodes for different values of T and l.

(a) (b)

Figure 4: (a) Values for the ﬁtting functions of eq. 9 and eq. 10; (b) PACF for an entropy set of 30 samples, l = 30m, T = 10s,

average speed 13.9 m/s.

tracted from the territory of Cosenza, in the southern

of Italy, see Figure 2. Mobility has been conﬁgured

to be urban and extra-urban, with average speeds of

11.1, 13.9 and 19.4 m/s, while the areas have been

considered to be square, with a side size l from 50 m

to 200 m. In this way, the number of areas goes from

about 2500 to about 156. Mobility traces have been

generated and, then, parsed with a Java application,

to evaluate entropy samples, according to eq. 5 and

the dimensions of MAP. Figure 3a shows the typi-

cal trend of 135 samples of entropy values (taken ev-

ery T = 35 seconds, while a mobile node n

is mov-

ing). Figure 3b illustrates the average trend of Et(n

)

by varying T and l (with a ﬁxed average speed of

11.5 m/s). For larger values of area side l, the en-

tropy value decreases since each mobile node takes

more time to move outside the current location gr

i j

;

besides, for larger observation window size T the en-

tropy increases, because each mobile node v

can visit

more locations in T .

After the preliminary analysis, we proceed to

ﬁt the obtained curves by using MATLAB and its

c f tool, by which we derived that the trends depicted

in Figure 3 can be well approached by a linear com-

bination of exponential functions:

Et(T, l) = a(l)· e

b(l)T

+ c(l)· e

d(l)T

(9)

where coefﬁcients a, b,c,d are functions of l

which can be expressed as polynomial functions as

follows:

a(l) = b(l) = c(l) = d(l) = p

·l

+ p

·l

+ p

·l + p

(10)

Figure 4a resumes the obtained values of p

,..., p

for each coefﬁcient in eq. 9 and the values of the poly-

nomial ﬁtting of eq. 10. For such combination of pa-

rameters, the ﬁtting indicators are Sum of Squares due

to Error (SSE) = 0.1116, R-square (R

) = 0.9926,

Adjusted-R

(AR

) = 0.9908 and Root Mean Square

Error (RMSE) = 0.09649, which describes the appro-

priate ﬁtting values.

Further, we implemented the RLS ﬁlter in MAT-

LAB: given a complete entropy samples data-set of

Et(n

) for different values of T , l and average speed,

we found the accurate way to predict entropy values

with RLS. In particular, this approach can be useful

for real-time decisions, such as routing or minimum

cost evaluation, given that future entropy trends can

be predicted.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

106

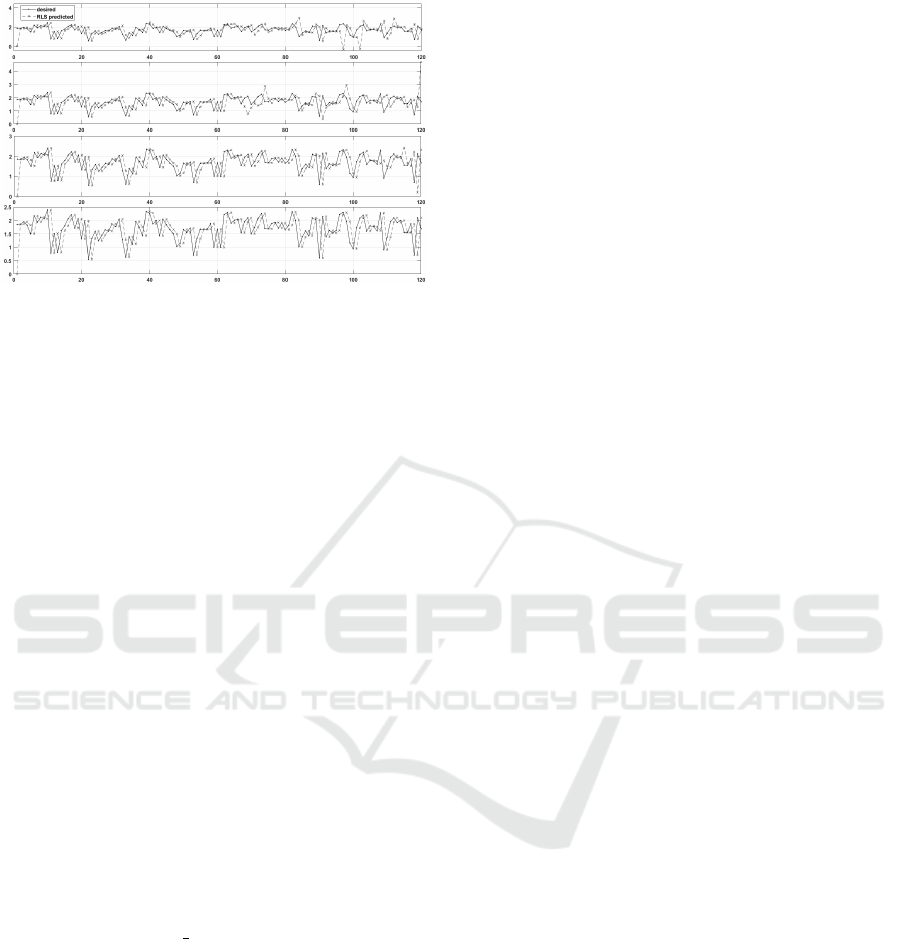
Figure 5: Entropy samples prediction with RLS for K=1,

β=0.1, 0.3, 0.5, 0.7 (number of samples on the x-axis and

entropy values on the y-axis).

In order to select the proper value of K, we take

into account the Partial Auto-Correlation Function

(PACF), deﬁned as the autocorrelation between Et(T )

and Et(T − K) with the linear dependence of Et(T )

on Et(T − 1) through Et(T − K + 1) removed (Box

et al., 2015).

After the analysis of different sets of entropy sam-

ples, we can state that the PACF correlogram, like the

one depicted in Figure 4b helps to select the best val-

ues of K, for which the prediction error is minimised.

In our examples, several largest spikes are obtained:

that is, for each combination of simulation parame-

ters (T , avg speed, l, mobility model and other) a set

∗

= {K

,...,K

} of lag values can be obtained,

for which the PACF function has a local maximum.

Additional beneﬁt can be seen that regardless of the

chosen combination of simulation parameters, each

correlogram has a spike for K = 1, that is the entropy

process can always be considered also as a K=1-order

Auto Regressive Process (ARP(1)).

In the next step, we chose K = 1 to conﬁrm that

the RLS algorithm can predict the entropy trend with

an acceptable error. Figure 5 shows the results ob-

tained by considering 120 samples of Et(n

), with

T = 5s, l = 30m, avg speed = 13.9 m/s. It can be

seen how, in general, the RLS can evaluate future

samples with high accuracy.

5 CONCLUSION AND FUTURE

WORKS

In this paper, we presented an in-depth analysis of

the entropy concept related to mobility in MANETs.

In particular, we underlined the key factors that in-

ﬂuence its trend during host mobility inside a geo-

graphical region. A new way of approaching mo-

bility entropy evaluation has been presented, and a

closed form has been obtained for the description of

its average values, in function of several system pa-

rameters. Also, we provided instructions to predict

future entropy values, obtaining beneﬁcial results re-

garding prediction error. Future works will regard the

application of this analysis to forwarding operations

in MANETs, such as packet routing, novel metrics

deﬁnition, system stability analysis and predictive re-

laying, and considering the possibility of using novel

routing approaches based on social networks such as

in (Socievole et al., 2013; Socievole et al., 2014).

REFERENCES

(2019). Openstreetmap. http://www.openstreetmap.org.

Box, G. E., Jenkins, G. M., Reinsel, G. C., and Ljung, G. M.

(2015). Time series analysis: forecasting and control.

John Wiley & Sons.

Cerasoli, C. and Dimarogonas, J. (2008). The general-

ization of information entropy to manet metrics. In

MILCOM 2008-2008 IEEE Military Communications

Conference, pages 1–9. IEEE.

Coon, J. P., Badiu, M.-A., and G

und

uz, D. (2018). On

the conditional entropy of wireless networks. In 2018

16th International Symposium on Modeling and Op-

timization in Mobile, Ad Hoc, and Wireless Networks

(WiOpt), pages 1–6. IEEE.

De Rango, F. and Fotino, M. (2009). Energy efﬁcient

olsr performance evaluation under energy aware met-

rics. In 2009 International Symposium on Perfor-

mance Evaluation of Computer & Telecommunication

Systems, volume 41, pages 193–198. IEEE.

De Rango, F., Iera, A., Molinaro, A., and Marano, S.

(2003). A modiﬁed location-aided routing proto-

col for the reduction of control overhead in ad-hoc

wireless networks. In 10th International Conference

on Telecommunications, 2003. ICT 2003., volume 2,

pages 1033–1037. IEEE.

De Rango, F. and Tropea, M. (2009). Swarm intelligence

based energy saving and load balancing in wireless

ad hoc networks. In Proceedings of the 2009 work-

shop on Bio-inspired algorithms for distributed sys-

tems, pages 77–84.

Elujide, I. and Liu, Y. (2020). An entropy-based wlan

channel allocation using channel state information. In

2020 16th International Conference on Wireless and

Mobile Computing, Networking and Communications

(WiMob)(50308), pages 74–79. IEEE.

Fazio, P., Tropea, M., De Rango, F., and Voznak, M. (2016).

Pattern prediction and passive bandwidth manage-

ment for hand-over optimization in qos cellular net-

works with vehicular mobility. IEEE Transactions on

Mobile Computing, 15(11):2809–2824.

Fazio, P., Tropea, M., and Marano, S. (2013). A distributed

hand-over management and pattern prediction algo-

rithm for wireless networks with mobile hosts. In

2013 9th International Wireless Communications and

Routing Optimization in Dynamic Networks based on a New Entropy Metric

107

Mobile Computing Conference (IWCMC), pages 294–

298. IEEE.

Fazio, P., Tropea, M., Sottile, C., Marano, S., Voznak, M.,

and Strangis, F. (2014). Mobility prediction in wire-

less cellular networks for the optimization of call ad-

mission control schemes. In 2014 IEEE 27th Cana-

dian Conference on Electrical and Computer Engi-

neering (CCECE), pages 1–5. IEEE.

Fazio, P., Tropea, M., Veltri, F., and Marano, S. (2012). A

novel rate adaptation scheme for dynamic bandwidth

management in wireless networks. In 2012 IEEE

75th Vehicular Technology Conference (VTC Spring),

pages 1–5. IEEE.

Haykin, S. (1999). Adaptive ﬁlters. Signal Processing Mag-

azine, 6(1).

Hua, E. Y. and Haas, Z. J. (2009). An algorithm for

prediction of link lifetime in manet based on un-

scented kalman ﬁlter. IEEE Communications Letters,

13(10):782–784.

Martinez, F. J., Cano, J.-C., Calafate, C. T., and Manzoni,

P. (2008). Citymob: a mobility model pattern gener-

ator for vanets. In ICC Workshops-2008 IEEE Inter-

national Conference on Communications Workshops,

pages 370–374. IEEE.

Masip-Bruin, X., Marin-Tordera, E., Yannuzzi, M., Serral-

Gracia, R., and Sanchez-Lopez, S. (2010). Reducing

the effects of routing inaccuracy by means of predic-

tion and an innovative link-state cost. IEEE Commu-

nications letters, 14(5):492–494.

Osamy, W., Khedr, A. M., Aziz, A., and El-Sawy, A. A.

(2018). Cluster-tree routing based entropy scheme for

data gathering in wireless sensor networks. IEEE Ac-

cess, 6:77372–77387.

Semnani, S. and Cowan, C. (1994). Switched coefﬁcient

adaptive ﬁltering. In IEE Colloquium on Non-Linear

Filters, pages 7–1. IET.

Socievole, A., De Rango, F., and Caputo, A. (2014). Wire-

less contacts, facebook friendships and interests: anal-

ysis of a multi-layer social network in an academic en-

vironment. In 2014 IFIP Wireless Days (WD), pages

1–7. IEEE.

Socievole, A., Yoneki, E., De Rango, F., and Crowcroft, J.

(2013). Opportunistic message routing using multi-

layer social networks. In Proceedings of the 2nd ACM

workshop on High performance mobile opportunistic

systems, pages 39–46.

Sun, B., Gui, C., Chen, H., and Zeng, Y. (2006).

An entropy-based stability qos routing with priority

scheduler in manet using fuzzy controllers. In Interna-

tional Conference on Fuzzy Systems and Knowledge

Discovery, pages 735–738. Springer.

Wang, X., Zhang, P., Du, Y., and Qi, M. (2020). Trust rout-

ing protocol based on cloud-based fuzzy petri net and

trust entropy for mobile ad hoc network. IEEE Access,

8:47675–47693.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

108