Improved Output Feedback Control of Constrained Linear Systems

using Invariant Sets

Ana Theresa F. O. Mancini, Tiago A. Almeida and Carlos E. T. D

orea

Dept. Computer Engineering and Automation, Lab. Computacional Methods for Control and Automation,

Universidade Federal do Rio Grande do Norte - UFRN, Natal-RN, Brazil

Keywords:

Linear Systems, Invariant Sets, Output Feedback, Constraints.

Abstract:

We propose an improved design method for output feedback control of discrete-time linear systems subject

to state and control constraints, additive disturbances and measurement noise. Output Feedback Controlled-

Invariant polyhedral sets are used to ensure that state and input constraints are satisﬁed all time. The control

strategy seeks to enforce the set of states consistent with the measured output into a closed ball around the

origin. The control input is computed through the solution of Linear Programming (LP) problems, whose goal

is to minimize the size of the ball one step ahead. Then, we use the optimization results to reduce the set

of admissible states, steering the state to a smaller ball around the origin. The improvement provided by the

proposed strategy is illustrated by numerical examples.

1 INTRODUCTION

The theory of positively invariant sets is an important

tool to deal with constrained control systems (Blan-

chini and Miani, 2015). Constraints arise naturally

in real-life control problems from physical limitations

on state, control and output variables, which can be

represented as convex polyhedral sets, in general.

A set is said to be positively invariant with respect

to a given system if any trajectory originated from this

set does not leave it. When considering state feed-

back control, if there exists a control action based on

the measured state that keeps the state trajectory in a

given set, such a set is said to be controlled-invariant

(Blanchini and Miani, 2015). Most known techniques

assume that the system state can be fully measured,

however this may not be possible in some applica-

tions. One then has to consider invariance under out-

put feedback.

In (Artstein and Rakovi

c, 2011) the notion of in-

variance with respect to output feedback under non-

parametric disturbances was proposed within a set

dynamics approach, in a more conceptual and gen-

eral framework. In (D

orea, 2009) an output feedback

structure was studied and conditions were deﬁned to

check if a given polyhedral set can be made invari-

ant under output feedback. Such sets were said to

be Output Feedback Controlled-Invariant (OFCI). If

a set is OFCI, then, a suitable sequence of control in-

puts can be computed, based on the knowledge of the

measured output, in order to conﬁne the state trajec-

tory therein. Using this concept, the computation of a

picewise afﬁne (PWA) law using multiparametric pro-

gramming was proposed in (Dantas et al., 2018).

Model Predictive Control (MPC) techniques have

also been used to solve constrained problems via out-

put feedback as in (Lee and Kouvaritakis, 2000),

(Mayne et al., 2006), (Goulart and Kerrigan, 2007),

(Løvaas et al., 2008), (Subramanian et al., 2017).

Typically, a stabilizing state feedback gain and a full-

order linear observer to estimate the state are de-

signed, and a Robust Controlled-invariant (RPI) set

with respect to the error dynamics is computed.

Based on OFCI polyhedral sets, in a recent paper

(Almeida and Dorea, 2020) the authors proposed an

output feedback strategy for the regulation problem

in discrete-time linear systems subject to state and

control constraints, and unknown-but-bounded distur-

bances and measurement noise. Given an OFCI poly-

hedron included in the set of state constraints, a Lin-

ear Programming (LP) problem was set up in order

to compute a control action that enforces constraints

satisfaction and minimizes, one step ahead, a guaran-

teed distance from the admissible states to the origin.

A dynamic control strategy was also proposed, for

which an OFCI polyhedron is obtained for an aug-

mented system that comprises the system and com-

pensator states. By using the dynamic controller, the

566

Mancini, A., Almeida, T. and Dórea, C.

Improved Output Feedback Control of Constrained Linear Systems using Invariant Sets.

DOI: 10.5220/0010556705660573

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 566-573

ISBN: 978-989-758-522-7

uncertainty on the state is progressively reduced us-

ing information about the contraction of an invariant

set deﬁned in the estimation error space.

In this paper, starting from the strategy proposed

in (Almeida and Dorea, 2020), we show that the un-

certainty on the state can be further reduced by using

information given by the solution of the LP problem.

By doing so, we can achieve faster convergence of

the state trajectory to a ball around the origin, which

is smaller than that obtained by (Almeida and Dorea,

2020), specially in the static output feedback case.

The improvement provided by the proposed strategy

is illustrated by numerical examples.

2 INVARIANT SETS

Consider the linear, time-invariant, discrete-time sys-

tem described by:

x(k + 1) = Ax(k) + Bu(k) + Ed(k),

y(k) = Cx (k) +η(k),

(1)

where x ∈ R

is the state vector, d ∈ R

is the distur-

bance, y ∈ R

is the measured output, η ∈ R

is the

measurement noise and k ∈ N is the sampling time.

The disturbance and the measurement noise are as-

sumed to be unknown but bounded to C-sets D ⊂ R

and N ⊂ R

, respectively. Moreover, the system is

subject to state and control constraints: x ∈ Ω

and

u ∈ U, where Ω

⊂ R

and U ⊂ R

are also C-sets. A

C-set is a convex and compact (closed and bounded)

set containing the origin.

The constraints on the state variables and control

inputs, and the bounds on disturbance and measure-

ment noise are given by the following convex polyhe-

dral sets containing the origin:

Ω

= {x : G

x ≤

1}, U = {u : Uu ≤

1},

D = {d : Dd ≤

1}, N = {η : Nη ≤

1},

(2)

with G

∈ R

×n

, U ∈ R

v×m

, D ∈ R

s×r

, N ∈ R

q×p

We now present some important deﬁnitions to

characterise invariant sets and invariance under out-

put feedback control.

Deﬁnition 2.1. Given λ, 0 ≤ λ < 1, the set Ω ∈ R

is said to be controlled-invariant with contraction rate

λ with respect to system (1) if ∀x ∈ Ω, ∃u ∈ U : Ax +

Bu + Ed ∈ λΩ, ∀d ∈ D (Blanchini, 1994).

If Ω is controlled-invariant then, for any initial

condition x(0) ∈ Ω, there exists a state feedback law

u(x(k)) satisfying the control constraints which is

able to keep the state trajectory of the controlled sys-

tem within λΩ,∀k ≥ 0, for all admissible disturbances

d ∈ D.

We now consider to accomplish constraints en-

forcement through output feedback control. Even

though the state of the system is not known exactly,

each measurement y carries information about its lo-

cation. Consider the set Y (Ω) ∈ R

, which con-

tains all admissible outputs y that can be associated

to x ∈ Ω:

Y (Ω) = {y : y = C x + η for x ∈ Ω, η ∈ N }. (3)

Consider also the set C (y(k)), which represents

the set of states compatible with each measurement

y(k) ∈ R

C (y) = {x : Cx = y − η, for η ∈ N }. (4)

Set-invariance under output feedback can be char-

acterized by the following deﬁnition (D

orea, 2009):

Deﬁnition 2.2. The set Ω is said to be Output Feed-

back Controlled-Invariant (OFCI) with contraction

rate λ, 0 ≤ λ < 1, with respect to system (1) if

∀y ∈ Y (Ω), ∃u ∈ U : Ax +Bu+Ed ∈ λΩ, ∀d ∈ D and

∀x ∈ Ω, η ∈ N such that Cx = y − η.

If Ω is OFCI with contraction rate λ, if x(k) ∈

Ω, then there exists a control u(y(k)) ∈ U, com-

puted from the measured output at time k, such that

x(k+1) ∈ λΩ, ∀k, in spite of the disturbance d(k) ∈ D

and noise η ∈ N .

In (D

orea, 2009), necessary and sufﬁcient condi-

tions were established to check if a polyhedral set Ω

is OFCI with contraction rate λ.

The dynamic output feedback control strategy

used here employs state observers. The possibility of

conﬁning the related estimation error into an invariant

set can be characterized by conditioned-invariant sets,

deﬁned as follows:

Deﬁnition 2.3. (D

orea, 2009) The set Ω is said to

be conditioned-invariant with contraction rate λ, 0 ≤

λ < 1, with respect to system (1) if ∀y ∈ Y (Ω), ∃v :

Ax + v + Ed ∈ λΩ, ∀d ∈ D and ∀x ∈ Ω, η ∈ N such

that Cx = y − η.

In what follows, the invariant sets deﬁned in this

section will be used to build an online optimization

strategy to compute an output feedback control able

to enforce state and control constraints and steer the

state trajectory to a as small as possible ball around

the origin.

3 OUTPUT FEEDBACK

CONTROLLERS

In this section, we describe the online optimization

strategy to compute static and dynamic output feed-

Improved Output Feedback Control of Constrained Linear Systems using Invariant Sets

567

back constrained controllers proposed in (Almeida

and Dorea, 2020), on which our approach is based.

3.1 Static Controller

Let Ω = {x : Gx ≤

1} ⊂ Ω

, G ∈ R

g×n

be an OFCI

polyhedral set. We consider the solution to the fol-

lowing output regulation problem under constraints:

Based on the measurements y(k), ∀x(0) ∈ Ω ⊂ Ω

compute u(k) ∈ U such that x(k) ∈ Ω, ∀k ≥ 0, ∀d ∈

D, ∀η ∈ N , and x(k) converges to a small ball around

the origin B(ε).

From Deﬁnition 2.2, the design goal can be

achieved if x(0) belongs to the OFCI set Ω. From

Deﬁnition 2.2 and the set of admissible outputs (3), Ω

is OFCI with contraction rate λ if, and only if (D

orea,

2009),(Almeida and Dorea, 2020):

∀y ∈ Y (Ω), ∃u :G(Ax + Bu + Ed) ≤ λ

Uu ≤

∀x, η, d : y −Cx = η, Gx ≤

1, Nη ≤

1, Dd ≤

(5)

Since the disturbances acting on the system are

unknown, at a given step k, the input signal u(k) must

enforce the constraints for all d ∈ D. Also, as the state

at step k is not available, u(k) must enforce the con-

straints for all x ∈ Ω consistent with the output y(k).

That can be achieved by considering the worst case

row-by-row of G as follows (D

orea, 2009).

Let the elements of the vector φ(y) ∈ R

, which

depend on the current output, be deﬁned by the solu-

tion of the following LP problems:

(y) = max

Ax,

s.t. Gx ≤

1, − NCx ≤ −Ny(k) +

(6)

with j = 1, . . . , g, and let the elements of vector δ ∈ R

be given by the solution of the following LP prob-

lems:

= max

Ed,

s.t. Dd ≤

(7)

with j = 1, . . . , g.

Considering (6) and (7) condition (5) can be

rewritten as:

∀y ∈ Y (Ω), ∃u ∈ U :



φ(y)







u ≤



1 − δ



(8)

Besides constraints satisfaction, we also seek to

steer the state x to the smallest ball B(ε) around the

origin. To this end, we use the strategy of enforc-

ing the one-step evolution of the set of states consis-

tent with the measurement y(k) into the smallest ball

B(ε) = {x : Hx ≤ ε

1}, where H =



I −I



. Then,

∀y ∈ Y (Ω), we must enforce:

H(Ax + Bu + Ed) ≤ ε

∀x, η, d : y −Cx = η, Gx ≤

1, Nη ≤

1, Dd ≤

(9)

Let ϕ(y) ∈ R

be a vector whose components are

given by the solution of the following LP problems:

(y) = max

Ax,

s.t. Gx ≤

1, − NCx ≤ −Ny(k) +

(10)

with j = 1, . . . , 2n and the vector γ ∈ R

whose com-

ponents are given by:

= max

Ed,

s.t. Dd ≤

(11)

with j = 1, . . . , 2n.

Then, condition (9) can be then rewritten as:

∀y ∈ Y (Ω) : HBu − ε

1 ≤ −ϕ(y) − γ. (12)

Now it is possible to compute a control action that

simultaneously satisﬁes state and control constraints,

ensuring output feedback invariance, and drives the

states consistent with the measured output to the

smallest closed ball around the origin. This control

action can be computed online from the solution of

the following LP problem:

u(y(k)) = arg min

u,ε

s.t





HB −









≤





1 − φ(y(k)) − δ

−ϕ(y(k)) − γ





(13)

For the online solution of problem (13), at each

time step k, from the current measured output y(k)

the vectors φ(y) and ϕ(y) are computed through the

solutions of (6) and (10). The vectors δ and γ do not

depend on the system evolution and should be com-

puted only once.

3.2 Dynamic Controller

Achieving output feedback invariance of a polyhedral

set is far from being an easy task. This is mainly

due to the fact that the set of states consistent with

a single measurement y(k) is, in general, very large.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

568

Hence, a control action u(k) able to enforce the one-

step evolution of this set of states into the polyhedron

does not always exist. In (D

orea, 2009) a state ob-

server structure was proposed to tackle this problem.

Once one has an estimate of the state x(k), and the

estimation error is bounded to another polyhedral set,

then, the set of admissible states can be signiﬁcantly

reduced, making it easier to achieve output feedback

invariance.

In (D

orea, 2009), (Almeida and Dorea, 2020) the

following compensator structure is used:

z(k + 1) = v(z(k), y(k)),

u(k) = κ(z(k), y(k)).

(14)

System (1) under this compensator (14) can be

represented in an extended state space formulation:

ξ(k + 1) =

Aξ(k) +

Bω(k) +

Ed(k)

ζ(k) =

Cξ(k) +

η(k)

(15)

where ξ =





is the extended state vector, ω =





the extended input vector, ζ =





is the extended out-

put vector,

η =





is the extended noise vector and

A =



A 0

0 0



B =



B 0

0 I



E =





C =



C 0

0 I



Moreover, u(k) and v(k) are functions of the extended

output vector





as expressed in (14).

Control constraints and bounds on the measure-

ment noise for the extended system can be deﬁned

over the extended space accordingly. Since (15) is a

linear system with the same structure as (1) the in-

put computation method illustrated previously can be

equally applied.

Consider now a pair of compact convex polyhe-

dral sets (S , V ), represented by: S = {x : G

x ≤

1},

V = {x : G

x ≤

1} and satisfying the assumption:

S ⊂ V ⊂ Ω

, S is conditioned-invariant and V is

controlled-invariant.

It turns out that the polyhedral set

Ω below sat-

isﬁes a necessary condition for output feedback in-

variance with respect to the augmented system, being

simultaneously controlled and conditioned-invariant

orea, 2009).

Ω =

















−G



| {z }





≤















(16)

where G

∈ R

×n

, G

∈ R

×n

and

G ∈ R

)×2n

If we interpret the compensator state z(k) as an

estimate of the system state x(k ), then the estimation

error is bounded by the conditioned-invariant set S ,

for G

(x − z) ≤

The compensator structure (14) is quite general,

allowing the design of nonlinear observers. However,

as discussed in (Almeida and Dorea, 2020), there is

no evidence that such a nonlinear observer would per-

form better than a linear one. Then, a linear observer

has been adopted as follows:

z(k + 1) = Az(k)+ Bu(k) + L[y(k) − ˆy(k)] (17)

where ˆy = Cz(k) is the estimated output and the ob-

server gain L ∈ R

n×p

is a parameter to be designed so

that the eigenvalues of (A−LC) lie inside the complex

unit disc.

The estimation error dynamics e(k) = x(k) − z(k)

is given by:

e(k + 1) = A

e(k) + E

(k) (18)

where A

= A − LC, E



E − L



and d

(k) =



d(k)

η(k)



. Bounds on the additive disturbance d

can

be easily obtained combining the bounds on d and η.

Given the stabilizing observer gain L, one must

compute an invariant polyhedron S with respect to

(18). A natural choice is the minimal Robust Pos-

itively Invariant (mRPI) set (Rakovic et al., 2005),

which is the smallest invariant set of (18) comply-

ing with the disturbances. Let, then S

be the mRPI

of (18) with contraction rate λ

, which can be com-

puted using the algorithm proposed in (Rakovic et al.,

2005). It will be used to compute a pair (S

, V ) that

composes an OFCI polyhedron

Ω (16) .

A natural choice for V is the maximal controlled-

invariant set contained in Ω

, which can be computed

using the algorithm proposed in (D

orea and Hennet,

1999).

The set of admissible initial states is given by the

projection of

Ω onto the state space. With the aim of

enlarging this set, S is scaled up to α

∗

S, with α

∗

max

α≥1

α such that

Ω remains OFCI.

In (Almeida and Dorea, 2020) it is also shown

that it is possible to compute ofﬂine a strictly decreas-

ing sequence {

α(k)}, k = 0, 1, . . . ,

, starting from

α(0) = α

, where

is the smallest value of k such

that

α(k) ≤ 1. Hence, we have that e(k) ∈

α(k)S

for

k <

and e(k) ∈ S

for k ≥

. This information

is used in the control action computation in order to

progressively reduce the uncertainty on the state x(k).

Then, as long as the pair (α

, V ) forms an

OFCI polyhedron, u(k) can be computed similarly as

Improved Output Feedback Control of Constrained Linear Systems using Invariant Sets

569

in (13), but with G replaced by G

and φ(k) and ϕ(k)

given by:

(

(k) = max

v j

Ax, j = 1, . . . , g

(k) = max

Ax, j = 1, . . . , 2n

(19)

s.t.





x ≤



α(k)

1 + G

z(k)



, −NCx ≤ −Ny(k)+

It has been shown through numerical examples in

(Almeida and Dorea, 2020) that the strategy described

above is, in general, less conservative than MPC ap-

proaches based on linear observers, in terms of ob-

taining larger sets of admissible initial states. How-

ever, no performance assessment was presented. In

the next section we propose an improvement of the

strategy aiming at speeding up the convergence of the

state trajectories to a guaranteed smaller ball around

the origin.

4 IMPROVED STATE

TRAJECTORY OPTIMIZATION

The difﬁculty in optimizing performance via output

feedback under constraints lies in the fact that a sin-

gle control action must cope with constraint satisfac-

tion of a set of states consistent with the measure-

ment. This is specially difﬁcult in the static feedback

case, where only the present output measurement is

available. The optimization strategy described in the

previous section minimizes one step ahead the worst

case distance from the set of states consistent with the

measurement to the origin. Here, we propose to use

the solution of the optimization problem in order to

further reduce the set of possible states and, as a con-

sequence, improve the convergence of the states to a

smaller ball around the origin.

Let ε(k + 1) be the optimal solution of the LP

problem (13). Then, from (9), one can see that:

x(k) ∈ B(ε(k)) (20)

This information can now be added to the compu-

tation of the vectors φ(y) and ϕ(y) to further reduce

the uncertainty on x(k), as follows:

(

(k) = max

Ax, j = 1, . . . , g

(k) = max

Ax, j = 1, . . . , 2n

(21)

s.t. Gx ≤

1, Hx ≤ ε(k)

−NCx ≤ −Ny(k) +

For the dynamic output feedback control the vec-

tors φ(y) and ϕ(y) with the additional constraint are

given by:

(

(k) = max

v j

Ax, j = 1, . . . , g

(k) = max

Ax, j = 1, . . . , 2n

(22)

s.t.









x ≤





α(k)

1 + G

z(k)

ε(k)





−NCx ≤ −Ny(k) +

This way, our proposed optimization problem

guarantees that the set of states x(k) consistent

with the measured output y(k) belongs to both the

controlled-invariant set, by forcing Gx ≤ 1 in (21) (if

Ω is OFCI) and G

x ≤ 1 in (22) (if the par (V , α

)

is OFCI), and the closed ball B(ε(k)). As a result,

the set of states consistent with the measurements be-

comes smaller improving, therefore, the performance

of the controller.

It is worth mentioning that, for the dynamic feed-

back case, we are able to compute ofﬂine the decreas-

ing sequence

α, which deﬁnes the contraction rate of

the invariant sets related to the estimation error, based

on λ

. On the other hand, we do not have the same

previous information for the state x(k). We have to

compute ε(k) online because the closed ball B(ε) is

not an invariant set, then, there is no deﬁned contrac-

tion rate.

5 NUMERICAL EXAMPLES

Example 5.1. (Static feedback) Consider the lin-

earized discrete-time system (1) obtained for a two

coupled-tank system (Martins et al., 2014), that can

be seen in Figure 1, for which:

A =



0.9448 0

0.0537 0.9448



, B =



0.1357

0.0028



;

E =





; C =



0 1



(23)

State and control constraints are given respec-

tively by:

Ω

= {x : |x

| ≤ 15, i = 1, 2}, U = {u : |u| ≤ 4} (24)

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

570

Figure 1: Coupled-tank system.

The measurement noise is bounded by: N = {η :

|η| ≤ 0.05}. The system is not subjected to distur-

bances.

A λ

-contractive controlled-invariant set V con-

tained in Ω

with a contraction rate of λ

= 0.95 was

computed. It was veriﬁed that V is also OFCI with

contraction rate λ = 0.9876. Then, a static output

feedback can be computed to enforce state and con-

trol consraints.

State vector trajectories resulting from the static

controller with and without the additional constraints

(13) are shown in Figure 2. It is possible to see that

the state trajectory resulting from the control action

using the additional constraint reaches a smaller ball

around the origin and is faster than the one resulting

from the controller proposed in (Almeida and Dorea,

2020).

Figure 2: State vector trajectories inside Hx ≤ ε(k)

1 for k =

3 and k = 100.

In Figure 3 it is also possible to see that when con-

sidering the additional constraint the state trajectory is

associated to a sequence with smaller values of ε(k).

We can also see that, as the system is not affected by

disturbances, then ε(k) tends to 0.

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 3: Evaluation of ε(k).

Example 5.2. (Dynamic controller) Consider the

discrete-time system (1) for which (Almeida and

Dorea, 2020):

A =



0.745 −0.002

5.61 0.780



, B =



−5.6 · 10

−4

0.464



, E = I

C =



1 0



(25)

State and control constraints are given respec-

tively by:

Ω

= {x : |x

| ≤ 0.4, |x

| ≤ 15}, U = {u : |u| ≤ 10}

(26)

Bounds for disturbance and measurement noise

are given by: D = {d : |d

| ≤ 0.02, |d

| ≤ 0.4} and

N = {η : |η| ≤ 0.1}.

A λ

-contractive controlled-invariant set V con-

tained in Ω

with a contraction rate of λ

= 0.99 was

computed. The gain L =



0.728 5.610



was de-

signed for the observer, to result in the eigenvalues of

A − LC at 0.017 and 0.780. An approximation of the

mRPI S

was then computed with λ

= 0.99. It was

checked that the pair (V , S

) forms an OFCI polyhe-

dron with respect to the extended system (15).

State trajectories resulting from the dynamic con-

troller with and without the additional constraints

(22), starting from x(0) =



0.4 15



, with z(0) =



0.1 10



, under random disturbance and noise, are

shown in Figure 4 illustrating that state constraints are

satisﬁed. It also shows the closed balls Hx ≤ ε(k)

for k = 3 and k = 50. We can see that the ﬁnal set

is smaller in the trajectory considering the additional

constraint.

Improved Output Feedback Control of Constrained Linear Systems using Invariant Sets

571

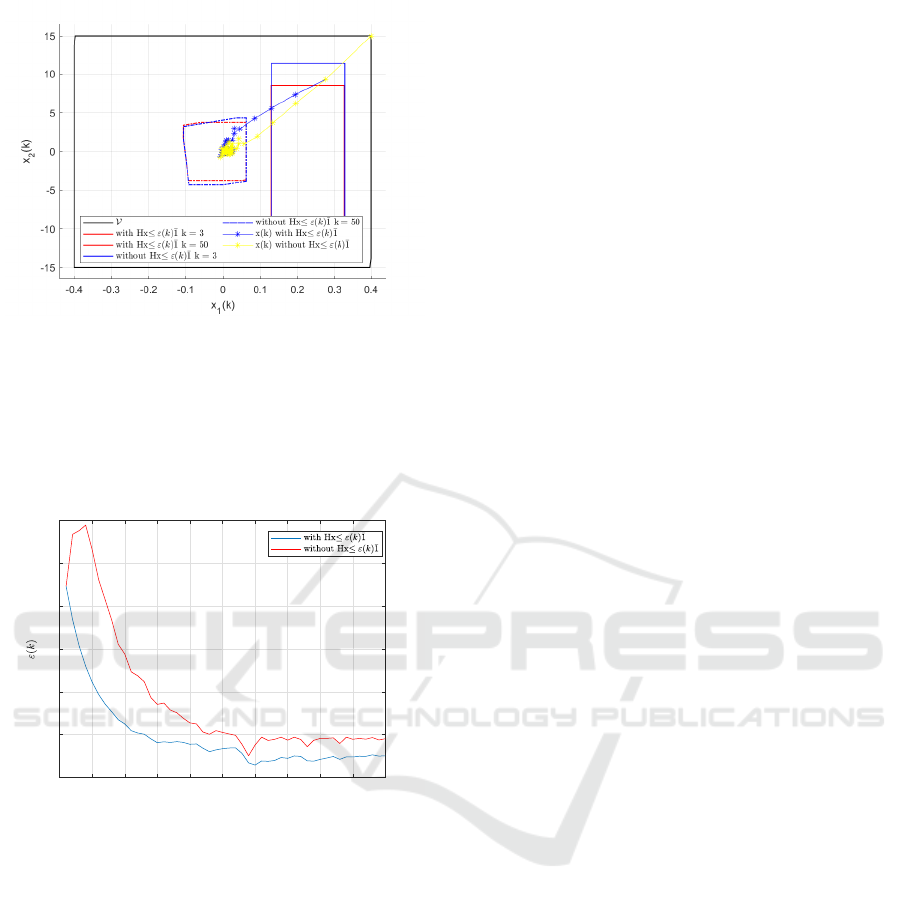
Figure 4: State vector trajectories inside Hx ≤ ε(k)

1 for k =

3 and k = 50.

The property of keeping the state trajectory in

smaller sets for each sample k can also be seen in Fig-

ure 5. When considering the additional constraint the

state trajectory is associated to a sequence of smaller

values of ε(k).

0 5 10 15 20 25 30 35 40 45 50

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Figure 5: Evaluation of ε(k).

6 CONCLUSIONS

In this work, an improved design method for out-

put feedback control for constrained, linear, discrete-

time systems subject to persistent disturbances was

proposed using the concept of Output Feedback

Controlled-Invariance (OFCI) sets.

A modiﬁcation was proposed in the algorithm of

(Almeida and Dorea, 2020) in order to further re-

duce the set of states consistent with the measure-

ment, by taking into account the results of an opti-

mization problem solved in the previous step.

Both static and dynamic controllers were consid-

ered. The performance improvement of the modi-

ﬁed controller was illustrated through numerical ex-

amples, being more remarkable in the static case.

Future work must consider using a set which is

homothetic with respect to the controlled invariant set

as a target, in order to guarantee ultimate boundedness

of the state trajectories.

ACKNOWLEDGEMENTS

This study was ﬁnanced in part by the Coordenac¸

de Aperfeic¸oamento de Pessoal de N

ıvel Superior –

Brazil (CAPES) – Finance Code 001, and by the Na-

tional Council for Scientiﬁc and Technological Devel-

opment - Brazil (CNPq), grant #309862/2019-1.

REFERENCES

Almeida, T. A. D. and Dorea, C. E. T. (2020). Output

feedback constrained regulation of linear systems via

controlled-invariant sets. IEEE Transactions on Auto-

matic Control, pages 1–1.

Artstein, Z. and Rakovi

c, S. V. (2011). Set invariance under

output feedback: a set-dynamics approach. Interna-

tional Journal of Systems Science, 42(4):539–555.

Blanchini, F. (1994). Ultimate boundedness control for

uncertain discrete-time systems via set-induced lya-

punov functions. IEEE Transactions on Automatic

Control, 39(2):428–433.

Blanchini, F. and Miani, S. (2015). Set-theoretic methods in

control. Birkh

auser, 2 edition.

Dantas, A. D. O. S., Dantas, A. F. O. A., and D

orea, C.

E. T. (2018). Static output feedback control design

for constrained linear discrete-time systems using data

cluster analysis. IET Control Theory Applications,

12(18):2541–2550.

orea, C. E. and Hennet, J. C. (1999). (A, B)-

invariant polyhedral sets of linear discrete-time sys-

tems. Journal of Optimization Theory and Applica-

tions, 103(3):521–542.

orea, C. E. T. (2009). Output-feedback controlled-

invariant polyhedra for constrained linear systems. In

Proceedings of the 48h IEEE Conference on Decision

and Control (CDC) held jointly with 2009 28th Chi-

nese Control Conference, pages 5317–5322.

Goulart, P. J. and Kerrigan, E. C. (2007). Output feedback

receding horizon control of constrained systems. In-

ternational Journal of Control, 80(1):8–20.

Lee, Y. I. and Kouvaritakis, B. (2000). Receding horizon

output feedback control for linear systems with input

saturation. In Proceedings of the 39th IEEE Confer-

ence on Decision and Control (Cat. No.00CH37187),

volume 1, pages 656–661 vol.1.

Løvaas, C., Seron, M. M., and Goodwin, G. C. (2008).

Robust output-feedback model predictive control for

systems with unstructured uncertainty. Automatica,

44(8):1933–1943.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

572

Martins, R., Vale, M., and Maitelli, A. (2014). Hybrid

methods for detection and identiﬁcation of faults in

dynamic systems. Asian Journal of Control, 17.

Mayne, D., Rakovi

c, S., Findeisen, R., and Allg

ower, F.

(2006). Robust output feedback model predictive

control of constrained linear systems. Automatica,

42(7):1217–1222.

Rakovic, S. V., Kerrigan, E. C., Kouramas, K. I., and

Mayne, D. Q. (2005). Invariant approximations of the

minimal robust positively invariant set. IEEE Trans-

actions on Automatic Control, 50(3):406–410.

Subramanian, S., Lucia, S., and Engell, S. (2017). A novel

tube-based output feedback mpc for constrained lin-

ear systems. In 2017 American Control Conference

(ACC), pages 3060–3065.

Improved Output Feedback Control of Constrained Linear Systems using Invariant Sets

573