A Resizable C++ Container using Virtual Memory

Bla

z Rojc

and Matja

z Depolli

zef Stefan Institute, Jamova cesta 39, 1000 Ljubljana, Slovenia

Keywords:

C++, Virtual Memory, Container, Parallel Programming, Efﬁciency.

Abstract:

Thread safety is required for shared data structures in shared-memory parallel approaches, but cannot be done

efﬁciently for standard C++ containers with continuous memory storage, such as std::vector. Dynamically

resizing such a container may cause pointer and reference invalidation and therefore cannot be done in parallel

environments without exclusive access protection to the container. We present a thread-safe no-copy resizable

C++ container class that can be used to store shared data among threads of a program on a shared-memory

system. The container relies on the virtual memory controller to handle allocation as needed during execu-

tion. A block of memory of almost arbitrary size can be allocated, which is only mapped to physical memory

during the ﬁrst access, providing hardware-level thread blocking. All synchronization costs are already in-

cluded in the operating system memory management, so using the container in parallel environment incurs

no additional costs. As a bonus, references and pointers to elements of the container work as expected even

after the container is resized. The implementation is not general however, and relies on the speciﬁcs of the

operating system and computer architecture. Memory overhead can be high as the allocations are bound to the

granularity of the virtual memory system.

1 INTRODUCTION

When initializing a data structure that is comprised of

many elements of the same type, e.g., a dictionary,

tree, graph, mesh, etc., it is often a case that the a) to-

tal size of the structure is not known in advance, b) the

structure can be built iteratively with the elements be-

ing inserted at the end of the existing data structure’s

memory block. An example of such an initialization

is the generation of scattered nodes for discretization

of a computational domain (Slak and Kosec, 2019).

The number of nodes that will be required to discre-

tise the domain is not known in advance, and the gen-

erating procedure is iteratively adding them to a con-

tainer structure and to a spatial indexing structure.

The generation procedure has good parallel poten-

tial but requires a container that:

• can be resized in a thread-safe manner,

• will not be modifying the elements after they are

put in and

• will only be inserting the elements at the end, that

is, the insertion will not require moving any exist-

ing elements.

https://orcid.org/0000-0001-6087-5691

https://orcid.org/0000-0002-0365-5294

Most available resizable data structures with stor-

age over a continuous block of memory offer only

read-only element access in a thread-safe manner.

During the insertion of a new element, the underly-

ing block of memory can be ﬁlled up and the whole

structure needs to be moved into a different block of

memory. The move invalidates all references to ex-

isting elements and implementing it in a thread-safe

manner can make it very inefﬁcient. To make resizing

such a container truly tread-safe, locking mechanisms

such as mutexes (Raynal, 2012) must be employed

across large portions of code, even those that do not

deal with resizing directly. This can lead to poor scal-

ing, especially when many insertions can occur at the

same time.

In this paper we propose a container with thread-

safe resizing that exploits virtual memory - a feature

of modern operating systems that abstracts physical

memory away from the programmer both for more

efﬁcient memory use and process isolation (Gorman,

2004; Bhattacharjee et al., 2017). It allows the pro-

grammer to ofﬂoad the burden of memory alloca-

tions to the operating system, or more speciﬁcally to

CPU’s memory management unit (MMU). As a con-

sequence, no locking mechanism is required in the

program code, since thread safety is taken care of by

Rojc, B. and Depolli, M.

A Resizable C++ Container using Virtual Memory.

DOI: 10.5220/0010557104810488

In Proceedings of the 16th International Conference on Software Technologies (ICSOFT 2021), pages 481-488

ISBN: 978-989-758-523-4

481

the hardware. The use of virtual memory also repre-

sents the negative aspect of this approach, that is, it

depends on virtual memory support being present in

the operating system.

The rest of the paper is organised as follows. In

section 2 we describe the standard approaches and vir-

tual memory in more detail, together with the MMU.

In section 3 we describe the implementation of the

virtual memory container in C++. In section 4 we

compare the performance of virtual memory con-

tainer to some other possible approaches to the prob-

lem. In section 5 we discuss the portability of our

implementation to other architectures and operating

systems.

2 BACKGROUND

2.1 Standard Approach to Resizable

Containers

Probably the most widely used container in standard

C++ is the std::vector. It is an example of a dy-

namic array with the ability to resize itself automat-

ically when one or more elements are inserted or

deleted. Storage for the elements is being handled

transparently by the container.

C++ standard (ISO, 2017) for example describes:

A vector is a sequence container that sup-

ports random access iterators. In addition,

it supports (amortized) constant time insert

and erase operations at the end; insert and

erase in the middle take linear time. Storage

management is handled automatically, though

hints can be given to improve efﬁciency. A

vector satisﬁes all of the requirements of a

container and of a reversible container, of a

sequence container, including most of the op-

tional sequence container requirements, of an

allocator-aware container, and, for an element

type other than bool, of a contiguous con-

tainer.

Since vector must be continuous, it can be used

to interact with C code which expects continuous ar-

rays of elements, it has minimal memory overhead,

and the speed of its random access iterators is unpar-

alleled among containers. This, along with its abil-

ity to grow automatically or per request, makes it a

workhorse for the data structures in general.

It is, however, limited by its implementation of dy-

namic resizing, which may catch an unprepared pro-

grammer off guard with its linear time performance,

invalidation of iterators, pointers and references to el-

ements, and the resulting lack of thread-safety even

in cases when elements are only added to the vector

and never modiﬁed. The usual implementation of the

algorithm to grow vector in size is to allocate a larger

block of memory, copy or move the contents from the

old to the new block, and deallocate the old block of

memory. When done automatically, the growth ra-

tio is usually exponential, e.g. doubling the memory

block size on each growth. Only when done manu-

ally, memory block of an exact required size may be

obtained for holding the vector’s elements.

When vector is grown, all the newly available

elements, that is, the elements with indices i, where

old_size ≤ i <new_size are also default initialized.

The creation of vector of ﬁxed size itself includes the

growth operation and the overhead associated with it.

For parallel programming, vector in raw form

is ill suited, since it is not thread-safe in the slight-

est. Full read-only concurrent access is allowed, but

read-only access to one element while another ele-

ment is being modiﬁed is only allowed if vector

does not get resized by he modiﬁcation, i.e. func-

tion push_back should not be used on a vetor when

it is being concurrently accessed by other threads.

When dynamic resizing is required, all element ac-

cess has to be protected, at least with a readers-writer

lock(Raynal, 2012).

2.2 Virtual Memory and MMU

Virtual memory is an abstraction of the physical mem-

ory that hides the arrangement of physical memory

and other resources from the programmer and sepa-

rates different processes’ address spaces (Bhattachar-

jee et al., 2017). The mapping between virtual and

physical memory addresses is carried out by the op-

erating system kernel and the memory management

unit (MMU), a dedicated address translation hard-

ware, built into the CPU (Gorman, 2004).

On 64-bit version of Linux each process can ac-

cess a total of 256 TiB of virtual memory. The upper

128 TiB are reserved for the kernel while the lower

128 TiB can be used by the program, as shown in Fig-

ure 1. A part of this user memory region is reserved

by the stack and executable code, but the vast majority

is freely allocatable. Not only physical memory can

be mapped into virtual memory, but also swap parti-

tion, normal ﬁles on disk, I/O devices, etc.

While up to 128 TiB of virtual memory can be al-

located, in practice only as much of it can be used as

there is physical memory in the system. For a ﬁxed

size, densely populated data structures virtual mem-

ory presents no real improvement over direct access

ICSOFT 2021 - 16th International Conference on Software Technologies

482

0x0000 0000 0000 0000

0x0000 7fff ffff ffff

0xffff 8000 0000 0000

0xffff ffff ffff ffff

user memory space

kernel memory space

Figure 1: Structure of the virtual memory address space be-

longing to a process in the 64-bit Linux environment. Not

to scale, a large part of address space not in use is omitted.

in terms of performance. Much of the improvement

is achieved when using either large sparse structures

or structures that must increase in size frequently. We

can allocate a large sequential chunk of virtual mem-

ory and only write to a small portion. The kernel then

maps only the accessed memory locations into physi-

cal memory.

Address mapping is done on the granularity of

a page. Pages are ﬁxed-size blocks of memory.

Their size is determined by the operating system

and the CPU architecture and can range from 1 KiB

to 1 GiB, the most common being 4 KiB (Gorman,

2004). When a page in virtual memory is ﬁrst writ-

ten to, the kernel uses the MMU to map it to a page in

physical memory.

The MMU contains a complex hardware com-

ponent that translates memory addresses between

process’ virtual address space and physical address

space. The details of its operation surpass the scope

of this work, we can think of it as a black box that

performs address mapping in a thread-safe manner,

regardless of its implementation.

3 IMPLEMENTATION

The virtual memory container is implemented us-

ing the provided memory management functions.

POSIX-compliant operating systems such as Linux

expose a memory management header containing

such functions (IEEE, 2018), sys/mman.h. To

implement the container we used functions mmap,

mprotect, and munmap, as shown in Figure 2.

During the construction of the container the re-

quired amount of virtual memory is allocated using

mmap. Initially all memory is ﬂagged as inaccessible,

to prevent an out-of-memory error on systems with

/proc/sys/vm/overcommit_memory set to 0. The

memory is then marked as readable and writable in

1 GiB chunks

using the mprotect function.

Note that the implementation is deliberately kept

minimal and includes only the constructors, destruc-

tor, element accessor functions (operator[]) and

size function. This is a consequence of our cur-

rent requirements for the container; the implementa-

tion could be extended into random-access container

such as vector. Comparison to containers of the C++

standard library is therefore limited. We do believe,

though, that the presented approach could be ex-

tended into a standard library compatible allocator

class, similar to mmap_allocator

, to facilitate the

use of virtual memory by the containers of the stan-

dard library.

Indexing into the container is done directly as

indexing into an array pointer. If the page of vir-

tual memory inside which the target element is lo-

cated is not yet mapped into the physical memory, the

MMU creates this mapping on the ﬁrst access. During

the mapping, several virtual memory pages may be

remapped, moved to or from swap and a target physi-

cal memory page is allocated and cleared. Therefore,

mapping is a complex procedure that can potentially

take a long time to complete. During this time, all the

threads that wish to access the new page are blocked

in their memory access instruction.

During the destruction of the container, the allo-

cated virtual memory is deallocated using munmap.

Care must be taken to unmap all allocated memory.

For this reason the size of the container is recorded

during construction. Deletion of all mappings from

virtual to physical memory is taken care of by the ker-

nel by the system function call.

This can be avoided if overcommit_memory is set to 1

within the operating system.

https://github.com/johannesthoma/mmap allocator

A Resizable C++ Container using Virtual Memory

483

# include < sys / mm an .h >

# include < err n o . h >

# include < string >

# include < st d e xcept >

# include < io s trea m >

template < t y p e n a m e Element T y p e >

cla s s V i r tua l M e mory C o ntai n e r {

private :

size_t n u m _eleme n t s ;

Elem e n t T y pe * c o nt a in e r ;

public :

Vi r t u alM e m o ryCo n t a ine r ( s i z e _t max _ e l e me nt s ) {

num _ e l e m en ts = m a x _ e l ements ;

contai n e r = ( Eleme n t T y p e *) m m ap ( nullpt r , s i z e o f ( E l e m e nt Ty pe ) * max_elements , PROT_N O NE ,

MAP_ P R I V A TE | MA P _ A N O N Y M O U S , -1 , 0) ;

if ( con t a i n e r == ( El e m e n t T yp e *) -1) t h r ow vmc_erro r ( errno );

con s t int64_t bloc k _ s i z e = 10 48 5 7 6 ;

int64_t re ma i ni n g = siz e o f ( E l em entType ) * max_el e m e n t s ;

uint8_t * he a d = ( u i n t 8 _ t *) co n t ai n er ;

whi l e ( r e m a in i ng > 0) {

in t r et = mprotec t ( head , std :: mi n ( blo c k _ size , r e m a in i ng ) , PROT_ R E A D | P RO T_ WR IT E );

if ( ret != 0) th row vmc_erro r ( errno );

hea d += bl o ck _s i ze ;

remain i n g -= b lo ck _s iz e ;

}

Vi r t u alM e m o ryCo n t a ine r ( V irt u a l Memo r y C ont a i n er & othe r ) = del e t e ;

Vi r t u alM e m o ryCo n t a ine r ( V irt u a l Memo r y C ont a i n er && other ) {

num _ e l e m en ts = othe r . n u m_ elemen t s ;

oth e r . n u m _eleme n t s = 0;

contai n e r = o t her . cont a i n e r ;

oth e r . c o n t a i ne r = nul l p t r ;

}

˜ V i r t ual M e m oryC o n t ain e r () {

if ( con t a i n e r != nu l l p t r ) {

in t r et = munmap ( c o n tainer , sizeof ( Elem e n t T y p e ) * n u m _ e lement s ) ;

if ( ret != 0) th row vmc_erro r ( errno );

}

inline E l e me nt Ty pe & o p er a t o r [] ( si z e _ t idx ) {

return c o n t a i ne r [idx ] ;

}

inline const El em entType & o p e r a t o r [] ( si z e_t idx ) co n s t {

return c o n t a i ne r [idx ] ;

}

inline s i ze_t si ze () const {

return n u m _eleme n t s ;

}

};

Figure 2: The implementation of the virtual memory container. Note that supporting classes such as vmc_error are not listed

since their implementation is not relevant.

ICSOFT 2021 - 16th International Conference on Software Technologies

484

4 PERFORMANCE

COMPARISON

In this section we demonstrate the performance ad-

vantage of the proposed container over a standard

implementation of vector. Our use case for which

we developed the container is holding the elements

of dynamically built k-d tree, which performs spatial

indexing for numerical domain discretization (Slak

and Kosec, 2019). This use case makes it difﬁcult

to quantitatively compare the container implementa-

tions, since it involves complex computing that masks

the performance gains of the container itself.

Furthermore, there seem to be no standard bench-

mark for perfomance measurement of thread-safe

containers, as other approaches present their own

benchmark problems (Dechev et al., 2006). To make

the demonstration simple, we consider a solver for

Collatz conjecture (Lagarias, 1985) on a predeﬁned

range of numbers, which involves only light comput-

ing and is memory bound.

4.1 Collatz Conjecture

Consider the following function on positive integers:

f (n) =

(

, if n is even

3n + 1, if n is odd

(1)

Now repeatedly apply this function to some positive

integer a

, so that a

n+1

= f (a

). Does the sequence

, a

, . . . eventually reach 1? The Collatz conjec-

ture states that it will, no matter which positive integer

is chosen as a

The conjecture has not been proven or disproven,

although numerical tests have shown that it holds for

all starting values up to 10

(Ba

rina, 2021). Un-

predictable behaviour of a generated sequence means

that although the starting integer may be small, the

processing can involve very large numbers before the

sequence reaches 1. One integer that exhibits such be-

haviour is 27: it peaks at 9232, after 77 successive ap-

plications of f , a number more than 300 times larger

than the starting number.

4.2 Problem Statement

To estimate how fast the sequence converges to 1 for

some starting positive integer k, we want to determine

the number of applications of f before the sequence

reaches 1. Let us name this number the orbit length

of k. We want to generate a list of orbit lengths

for all integers between 1 and n, where n is given in

advance.

To speed up the computation we make the follow-

ing observation: If a number k has an orbit length

of o

, then its successor f (n) has an orbit length of

− 1. Therefore we can compute orbit lengths re-

cursively, stopping at k = 1. Since numbers larger

than n might appear more than once in the gener-

ated sequences, we want to store their orbit lengths

as well. We, however do not know the largest num-

ber for which orbit length will have to be stored and

cannot preallocate the required memory to store all

the numbers. The largest encountered number will be

known only after the algorithm completes.

For efﬁciency, we do not want to preallocate all of

the available system memory and would like to grow

the container for orbit lengths as necessary. Growing

as necessary is the main strength of the proposed con-

tainer, since it can be done with minimal overhead.

For standard library containers, though, this is not the

case. We opt to use vector as comparison reference,

since it is a random access container with minimal

memory overhead and can be resized at will. The

standard vector is different however in the way re-

sizing is implemented (large computational overhead)

and in its initialization of all the new elements upon

each size change. Note that deque from standard li-

brary could be used instead, since its implementation

usually uses a different trade-off approach to slightly

slower random element access for a faster resize op-

eration.

The proposed container does not perform element

initialization and relies on the fact that the system

clears all the allocated pages with zeros when map-

ping them. Initialization with zeros is sufﬁcient both

in the presented case and in our use-case, thus no ad-

ditional compliance with the standard containers is at-

tempted. Additional initialization would require the

concept of size to be implemented in addition to the

concept of allocated space, which is not necessary in

our use case. Nevertheless, it is important to notice

that the comparison is not entirely fair since the pro-

posed container has one less function to perform in all

experiments.

4.3 Implementation

To measure the performance of virtual memory con-

tainer against the vector we implemented the de-

scribed problem as a computational experiment in

C++. We want to gain insight into which parts of com-

putation take the longest, so we measured setup time,

calculation time and resize time separately, where cal-

culation time includes time spent reading and writing

to the container.

We compare the virtual memory container with

A Resizable C++ Container using Virtual Memory

485

Total execution time [ms]

Virtual memory container

vector

vector (target size)

vector (maximum size)

Figure 3: Total execution times of the described problem for

the virtual memory container and different conﬁgurations of

the vector on one CPU thread.

the vector in three conﬁgurations: Where vector

is completely empty and must be resized, where we

construct the vector with of size n, which we shall

refer to as target size, and where we construct the

vector with the maximum allowed number of ele-

ments, which we shall refer to as maximum size.

We decided to impose an upper limit to the size of

containers so we don’t run into problems with a lack

of physical memory. For each value of n we repeated

the experiment many times and then averaged mea-

sured times to minimize any potential random vari-

ance from external factors, such as the varying CPU

clock and process scheduler.

A single execution of the experiment proceeds as

following:

• For each integer i between 1 and n noninclusive

the orbit length is calculated recursively in as-

cending order.

• First f (i), the successor of i, is calculated.

• If f (i) is larger than or equal to the maximum size,

then f is applied to it iteratively until the calcu-

lated value is smaller than the maximum size. The

total number of iterations is recorded.

• If iteration was not necessary the number of itera-

tions is set to 1.

• The size of the container is checked. If the size

is smaller that the successor, the container is re-

sized so that it contains the successor. (This only

happens when vector is used).

• If the successor is 1, then the orbit length is also

set to 1.

• If the successor’s orbit length was not yet calcu-

lated then the program recursively calculates it.

Total execution time [ms]

Virtual memory container

vector

vector (target size)

vector (maximum size)

Figure 4: Total execution times of the described problem for

the virtual memory container and different conﬁgurations of

the vector on eight CPU threads.

The ﬁnal orbit lenght is the orbit length of the suc-

cessor plus the number of iterations.

4.4 Performance

We executed the benchmark problem on an 8-core,

16-thread computer (2x Intel Xeon E5520) with

12 GB of RAM. In the experiments we limited the

maximum allowed size of the containers and we per-

formed several experiments with various limits. We

present the results only for the limit being exactly

1 GiB of physical memory in Figures 3 and 4. We

further performed the experiments also on the limits

of 1 GiB, 2 GiB, 4 GiB, and 8 GiB, but discovered that

they follow the same pattern.

Within the experiment with 8 GiB limit though,

we were reminded of one often neglected negative

aspect of vector. In order to resize a vector,

temporarily the amount of physical memory needed

equals the new size plus the old size, which in limit

goes up to twice the requested size. This happens be-

cause during the resize process, ﬁrst new memory of

at least the requested size is allocated, then elements

are copied and only then the old memory is freed. Our

experimental machine had enough physical memory

to host an 8 GiB structure, but not enough to support

the resize, causing it to use swap ﬁle on each resize af-

ter the container reached about 6 GiB in size. The per-

formance of vector was severly degraded and thus

the results were nonrepresentative.

The execution times for 1 CPU thread are shown

on the ﬁgure 3. The fact that vector copies all val-

ues during the resizes causes it to fall far behind the

virtual memory container. The trend continues up to

about n = 10

, where the diference in compute times

ICSOFT 2021 - 16th International Conference on Software Technologies

486

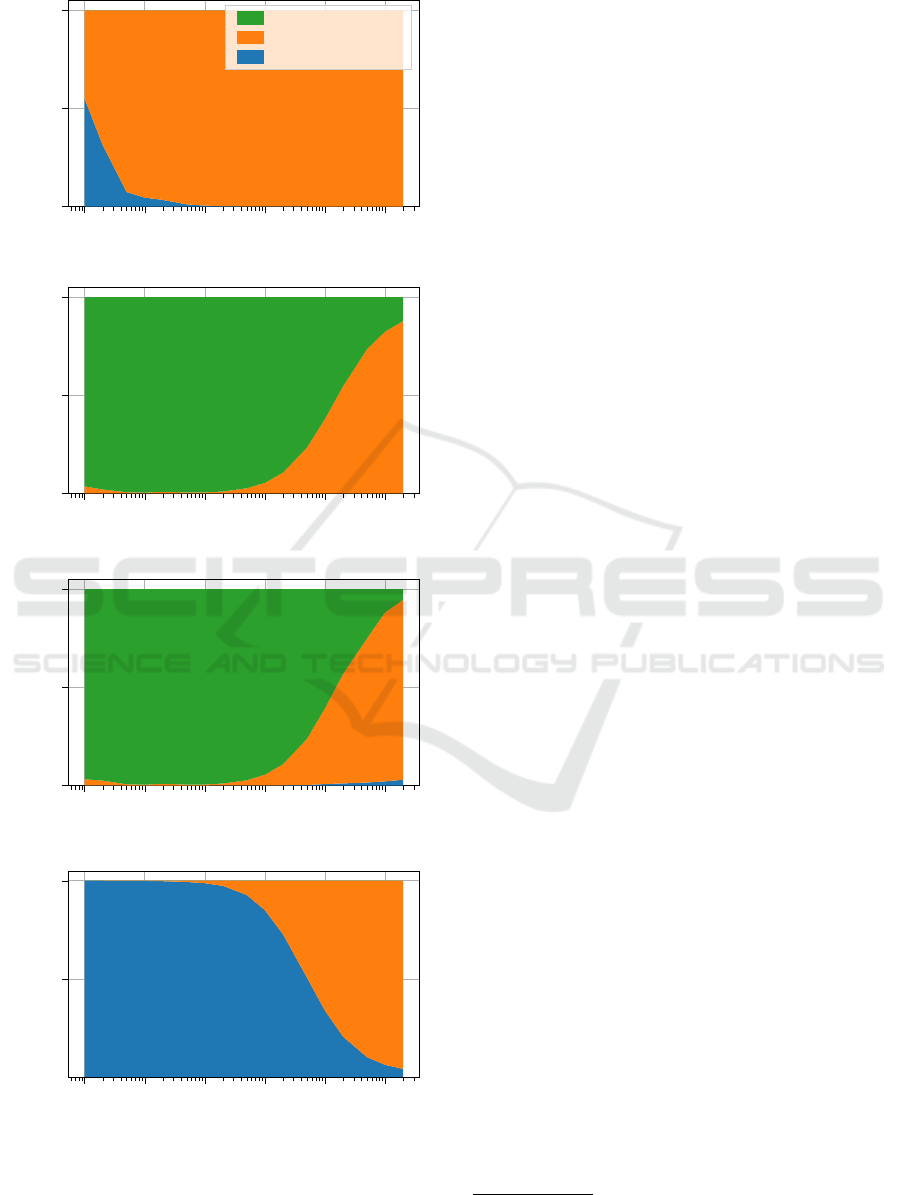
100

Execution time percentage

Virtual memory container

container resizing

calculation of values

container setup

100

Execution time percentage

vector

100

Execution time percentage

vector (target size)

100

Execution time percentage

vector (maximum size)

Figure 5: Execution time percentages of the described prob-

lem for the virtual memory container and different conﬁgu-

rations of the vector. Blue: container setup, orange: cal-

culation of values, green: container resizing.

starts to shrink. At this point the percentage of ﬁlled

elements in the container starts becoming signiﬁcant,

so the virtual memory container must allocate a lot

more pages. Regardless, the virtual memory container

remains the fastest, challenged only by the maximum

size vector for n above 10

The execution times for 8 CPU threads are shown

on the ﬁgure 4. The difference between the virtual

memory container and vectors widens even further,

with execution over different conﬁgurations of the

vector being slowed down signiﬁcantly. The fea-

ture of the virtual memory container, which allows

it to be resized without any locking mechanisms al-

lows it to be used without changes, while vector has

to be protected using a readers-writer lock (using

the standard C++ shared_lock and unique_lock on

shared_mutex). While vector conﬁgurations were

slower on the order of a magnitude because of the use

of mutexes and full locks during resizes, the virtual

memory only slowed down for some n while gaining

speed for other.

5 PORTABILITY

The presented implementation of the virtual memory

container may not be used on all operating systems

nor on all the hardware. As was discussed in section

2, for virtual memory mapping to work, a MMU is re-

quired. Such hardware is not present in all computer

architectures, such as those in embedded and IOT en-

vironments for example.

Furthermore, one of the requirements of the con-

tainer is the availability of memory management func-

tions. While such functions may be available, they

might not behave in the same way as those deﬁned by

the POSIX standard. One such case is the Microsoft

Windows operating system. While it contains the re-

quired facilities needed to implement the container, a

different set of functions or a translation layer such as

mman-win32

must be used.

6 CONCLUSION

In this paper we presented an often neglected ap-

proach to containers in C++, the virtual memory

based container. The container relies on the virtual

memory controller to handle allocation when its size

increases beyond the current value. All synchroniza-

tion is included already in the operating system mem-

ory management, so there is no additional cost to us-

https://github.com/klauspost/mman-win32

A Resizable C++ Container using Virtual Memory

487

ing the container in parallel environment. As a bonus,

references and pointers to elements of the container

are allowed and work as expected even when the con-

tainer is resized. There are negative aspects though,

for example, not all hardware architectures allow for

the implementation and currently only Linux imple-

mentation is provided. The amount of the allocated

memory can also not be as ﬁne grained as with the

classic C++ containers, and there is some memory

overhead attached.

Although we present a very basic, array-like (or

std::vector-like) container, the approach could be

extended into an allocator, to support the alloca-

tions for containers of the standard library. Our main

motivation for developing this container lies in its in-

herent thread safety for a special scenario, which is

often found in real life. That scenario is one in which

the elements are continuously appended to the con-

tainer, and the total number of elements is not known

beforehand. While the existing elements of the con-

tainer are also frequently read from, they are never

modiﬁed. If this scenario is required in a parallel en-

vironment, where either the elements are read in par-

allel or appended in parallel, or both, then the existing

containers require extensive protection of shared data

structures and thus offer very low performance. In

addition, we found that the container also has several

positive aspects, compared to for example vector,

even when used in completely sequential code, which

then makes it an even more compelling option to con-

sider in everyday development.

Use cases where the presented container presents

the largest performance gain are those which are me-

mory bound, where data processing cannot be local-

ized and requires many memory accesses. Further-

more the standard approach with container locking

during the resize operation scales poorly when many

CPU threads are used compared to the presented lock-

free design. Through experiments on an artiﬁcial ex-

ample - a solver for orbit lengths for the Collatz con-

jecture - we demonstrate where the presented con-

tainer shines the most, compared to the containers of-

fered by the standard library. We make a short scan of

the input parameters to show the performance both on

sequential and parallel access to the container. In the

sequential program, we ﬁnd that the performance of

the presented container is only matched by vector

with constant size equal to the maximum allowed

size. Since thread safety is required for the shared

data structures in shared-memory parallel approaches,

but cannot be done efﬁciently for C++ containers with

continuous memory storage and dynamic size, such as

std::vector, we ﬁnd that in parallel programs, the

presented container perfomance is unmatched.

ACKNOWLEDGEMENTS

The authors would like to acknowledge the ﬁnancial

support of the Slovenian Research Agency (ARRS)

research core funding No. P2-0095.

REFERENCES

rina, D. (2021). Convergence veriﬁcation of the collatz

problem. The Journal of Supercomputing.

Bhattacharjee, A., Lustig, D., and Martonosi, M. (2017).

Architectural and Operating System Support for Vir-

tual Memory. Synthesis Lectures on Computer Archi-

tecture. Morgan & Claypool Publishers.

Dechev, D., Pirkelbauer, P., and Stroustrup, B. (2006).

Lock-free dynamically resizable arrays. volume 4305,

pages 142–156.

Gorman, M. (2004). Understanding the Linux Virtual Mem-

ory Manager. Bruce Perens’ Open Source series.

Prentice Hall.

IEEE (2018). IEEE Standard for Information Technology–

Portable Operating System Interface (POSIX(TM))

Base Speciﬁcations, Issue 7. IEEE Std 1003.1-2017

(Revision of IEEE Std 1003.1-2008), pages 1–3951.

ISO (2017). ISO/IEC 14882:2017 Information technology

— Programming languages — C++. pub-ISO, pub-

ISO:adr, ﬁfth edition.

Lagarias, J. C. (1985). The 3x + 1 problem and its gen-

eralizations. The American Mathematical Monthly,

92(1):3–23.

Raynal, M. (2012). Concurrent programming: algorithms,

principles, and foundations. Springer Science & Busi-

ness Media.

Slak, J. and Kosec, G. (2019). On generation of node distri-

butions for meshless PDE discretizations. SIAM Jour-

nal on Scientiﬁc Computing, 41(5):A3202–A3229.

ICSOFT 2021 - 16th International Conference on Software Technologies

488