Trace Recovery: Inferring Fine-grained Trace of Energy Data from

Aggregates

Nazim Uddin Sheikh

1 a

, Zhigang Lu

1 b

, Hassan Jameel Asghar

12 c

and Mohamed Ali Kaafar

1 d

Department of Computing, Macquarie University, Sydney, Australia

Data61, CSIRO, Sydney, Australia

Keywords:

Inference Attacks, Aggregate Statistics, Differential Privacy, Energy Data Privacy, Smart Meter Privacy.

Abstract:

Smart meter data is collected and shared with different stakeholders involved in a smart grid ecosystem. The

ﬁne-grained energy data is extremely useful for grid operations and maintenance, monitoring and for market

segmentation purposes. However, sharing and releasing ﬁne-grained energy data induces explicit violations

of private information of consumers (Molina-Markham et al., 2010). Service providers do then share and

release aggregated statistics to preserve the privacy of consumers with data aggregation aiming at reducing

the risks of individual consumption traces being revealed. In this paper, we show that an adversary can

reconstruct individual traces of energy data by exploiting consistency (similar consumption patterns over time)

and distinctiveness (one household’s energy consumption pattern is signiﬁcantly different from that of others)

properties of individual consumption load patterns. We propose an unsupervised attack framework to recover

hourly energy consumption time-series of individual users without any prior knowledge. We pose the problem

of assigning aggregated energy consumption meter readings to individuals as an assignment problem and solve

it by the Hungarian algorithm (Xu et al., 2017; Kuhn, 1955). Using two real-world datasets, our empirical

evaluations show that an adversary is capable of recovering over 70% of households’ energy consumption

patterns with over 90% accuracy.

1 INTRODUCTION

Smart meters, an integral component of metering in-

frastructures in smart grids, have been widely de-

ployed in homes around the world. Smart meter con-

sumption measurements are used for monitoring, op-

erations and management of grids (Knirsch et al.,

2016). Individual household smart meter data is ag-

gregated into a cluster (e.g., from the same neighbour-

hood) and communicated to the energy providers over

a secure channel for the purposes of demand fore-

casting and analytics without compromising the pri-

vacy of individual households (Sankar et al., 2012;

Erkin and Tsudik, 2012). Many mechanisms based

on such secure aggregation have been proposed to

protect the privacy of consumers (Buescher et al.,

2017). Although aggregation itself is cryptographi-

cally protected, the electricity providers have access

https://orcid.org/0000-0002-6565-9880

https://orcid.org/0000-0001-5102-6217

https://orcid.org/0000-0001-6168-6497

https://orcid.org/0000-0003-2714-0276

to the decrypted aggregated form of energy consump-

tion over a cluster (group) of households (Buescher

et al., 2017).

Due to the nature of smart meter data, two types of

aggregations can be performed: temporal and/or spa-

tial. Temporal aggregation is one of the most naive

forms of data aggregation and is performed over a

long period of time, for example, monthly or quar-

terly (Dong et al., 2016). The aggregated monthly

or quarterly consumption of individual households is

performed for billing purposes. On the other hand,

in spatial aggregation (Dong et al., 2016) multiple

households’ load patterns are combined together into

a cluster in order to mask individual consumption pat-

terns to prevent information leakage (Farokhi, 2020).

This aggregated form of individual consumption

data can be shared with other stakeholders (e.g., re-

tailers and marketing companies) (Liu et al., 2018) or

can be released publicly to beneﬁt businesses and re-

search, with assumption that aggregated statistics of

individual households’ energy consumption data, do

not infringe the privacy of customers. However, this

assumption on aggregation providing enough privacy

Sheikh, N., Lu, Z., Asghar, H. and Kaafar, M.

Trace Recovery: Inferring Fine-grained Trace of Energy Data from Aggregates.

DOI: 10.5220/0010560302830294

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 283-294

ISBN: 978-989-758-524-1

283

requires further exploration. In this paper, we show

an attack where an adversary (e.g., curious service

provider, a third-party stakeholder or an external ma-

licious entity) is capable of recovering ﬁne-grained

energy consumption traces of individual customers

through having access to the aggregated statistics of

energy consumption time-series data. The essential

elements of our attack are based on the attack from

Xu et al. (Xu et al., 2017) on de-aggregating user lo-

cation traces from aggregated mobility traces, and a

similar argument is often used about privacy via ag-

gregation.

In essence, we show that an attacker can infringe

the privacy of individuals by exploiting two key

attributes of their load patterns. First, the load pattern

of a household is consistent, which makes their load

pattern highly predictable. Second, the load pattern

of each household can be uniquely distinguished

from each other with high probability. Combining

the two observations, we could split the aggregated

energy data to different traces of energy consumption

iteratively (by the ﬁrst observation), then link the

recovered traces to most of the individual households

(by the second observation).

Contributions. In this paper, we aim to quantitatively

investigate the privacy implications of releasing ag-

gregated statistics of smart meter energy consumption

data of individual customers without any prior knowl-

edge. Our contributions are as follows:

• We construct an unsupervised adversarial model

based on aggregated statistics of energy consump-

tion data. The adversarial framework does not re-

quire any background information about the in-

dividuals to reconstruct their ﬁne-grained energy

consumption records from aggregates. The ad-

versary exploits the consistency and distinctive-

ness property in day-to-day energy consumption

load patterns. Then we present the problem as

a mathematical balanced assignment problem and

construct cost matrices (Xu et al., 2017) based

on expected energy consumption change at each

time step. Our quantitative analysis shows that

the households’ consumption patterns are simi-

lar over time and most of them are different from

each other. We compute expected energy con-

sumption changes from one time step to another,

which help to estimate energy consumption in the

next time steps and formulate a cost matrix to

optimise the assignment of households to energy

consumption traces (see Section 4).

• We use two real-world smart meter reading

datasets to empirically evaluate the adversary’s

capability to reconstruct individual users’ ﬁne-

grained energy usage load patterns. We show that

the adversary recovers energy consumption pat-

terns with high accuracy (between 80% and 95%)

averaged over all target households and the en-

tire time period. We observe that 70% of house-

holds’ load patterns can be inferred from aggre-

gated statistics with an accuracy over 90%. Fi-

nally, we show that the adversary recovers 60%

of households’ energy consumption by incurring

a 0.4 kWh or less error from the actual (ground

truth) consumption traces.

A key feature of our attack on aggregated en-

ergy data is that it does not rely on any background

knowledge of any individual household’s consump-

tion. This is unlike other attacks on smart-meter ag-

gregation, for example, (Buescher et al., 2017), as de-

tailed in the next section.

The rest of the paper is organised as follows. In

Section 2 we review the state-of-the-art of privacy re-

lated issues in energy data and possible solutions to

safeguard the privacy of customers. Then we explain

the background of the threat model for recovering en-

ergy consumption traces in Section 3. In Section 4,

we discuss key features of two real-world datasets

that are used to evaluate the performance of the ad-

versary. Further, we analyse the feasibility of pri-

vacy breach using two key concepts: consistency and

distinctiveness. In Section 5, we propose the attack

framework and inference strategies based on our ob-

servations discussed in Section 4. We then demon-

strate the experimental conﬁgurations and analyse the

performance of the adversary using two different met-

rics in Section 6. Finally, conclude the paper by dis-

cussing our key ﬁndings and future work in Section 7

2 RELATED WORK

In this section, we review some related work pertain-

ing to privacy preserving energy data analytics, issues

in energy data sharing with third-parties, releasing

aggregated data, adversarial models and privacy en-

hancing technologies that are widely used to protect

the privacy of individuals while leveraging aggregated

data analytics.

Privacy Preserving Data Analytics: A massive

amount of energy consumption data from millions

of households and generated on a daily basis is be-

ing collected and shared with third-parties and differ-

ent stakeholders involved in the smart meter ecosys-

tem (Yang et al., 2014). Smart meter data analytics

involve descriptive, predictive (Habtemariam et al.,

2016) and prescriptive analyses, it also includes many

critical applications, such as as load analysis, load

SECRYPT 2021 - 18th International Conference on Security and Cryptography

284

forecasting and load management (Wang et al., 2018).

The main objective of privacy friendly data analytics

is to safeguard the users (households) from private in-

formation leakage while leveraging the utility of the

data (Shateri et al., 2019). Many other schemes have

been proposed to facilitate privacy preserving data

collection, sharing and analytics (Makhdoom et al.,

2020). Sirojan et al. (Sirojan et al., 2019) envisaged

an edge computing based architecture to provide a va-

riety of energy data analytic services such as event de-

tection, down-sampling and load identiﬁcation, how-

ever, this architecture does not guarantee the privacy

of user speciﬁc sensitive data. Cloud based hierar-

chical architectures are conceived as facilitating ac-

cess control mechanisms that help manage to share

and analyse data while keeping sensitive information

hidden (Lee et al., 2017). Shateri et al. (Shateri et al.,

2019) studied the privacy-utility tradeoff in privacy

preserving energy data analytics using an information

theoretic approach. Chen et al. (Chen et al., 2018)

reviewed some learning based methods that leverage

efﬁcient privacy-aware energy data analytics. Wen et

al. (Wen et al., 2013) proposed a privacy preserving

query-based cloud server model for encrypted con-

sumption data.

Non-Intrusive Load Monitoring: A myriad of

study has been conducted on how ﬁne-grained energy

consumption data can reveal an enormous amount

of private information about individual households.

Non-intrusive load monitoring (NILM) has been a

proliﬁc research area in the last decade. NILM has

shown that the individual appliance speciﬁc energy

consumption can be separated from the load pattern of

a household using different statistical methods (Her-

rero et al., 2017; Zhang et al., 2019) and deep learning

algorithms (Kelly and Knottenbelt, 2015). Therefore,

information about personal activities can be discov-

ered from their electricity consumption patterns. This

constitutes a severe privacy threat to individual con-

sumers (Reinhardt et al., 2015). Note that, NILM

is successful only if an adversary has access to the

load patterns of individual consumers. All the afore-

mentioned studies rely on individual households’ en-

ergy consumption time-series data to retrieve appli-

ance speciﬁc consumption or to derive appliances’

ON/OFF states at different point of time. However,

in this paper, we attempt to recover each individual

household’s ﬁne-grained energy consumption traces

from an aggregate, which is the combination of a clus-

ter (group) of households’ energy consumption time-

series data without relying on any prior knowledge

and/or access to individual’s load patterns.

Privacy of Aggregation Models: Aggregation is

widely used to safeguard the privacy of individ-

ual households by masking the individual speciﬁc

consumption (Farokhi, 2020). More generally, two

types of privacy preserving aggregation methods ex-

ist in the literature: many solutions rely on trusted

third-party based services using cryptographic proto-

cols (e.g., homomorphic encryption) (Efthymiou and

Kalogridis, 2010; Abdallah and Shen, 2016; Vahedi

et al., 2017) and decentralised techniques, relying on

blockchain technology (Habtemariam et al., 2016; Xu

et al., 2020). Hong et al. (Hong et al., 2017) pro-

posed a streaming algorithm that safeguards the im-

plications of information leakage from the readings of

a meter on the state of a speciﬁc appliance. A study

by an industrial body suggests that aggregation of

two load patterns of two different households is suf-

ﬁcient to protect the privacy of individuals in aggre-

gated data (ENA-Report, 2015). However, this study

was revisited and its ﬁndings disputed in (Buescher

et al., 2017), which shows that individuals in an ag-

gregate of size two are distinguishable with high ac-

curacy. Moreover, Buescher et al. (Buescher et al.,

2017) demonstrated the risk of being distinguishable

for different size of aggregates. However, one of the

limitations of this distinguishability attack model is

that the adversary knows the load proﬁles contained in

the aggregate and past consumption records of all ag-

gregators (Buescher et al., 2017). The key difference

between our attack model and the work in (Buescher

et al., 2017) is that our attack model does not rely on

any prior knowledge about the individual energy con-

sumption records.

Our work has been inspired by (Xu et al., 2017)

that recovers individuals mobility data (trajectories)

by exploiting consistency and distinctiveness features

of mobility patterns of users. Authors posed and ver-

iﬁed that most mobile users follow explicit moving

patterns, with little mobility during night time and

stable (and hence predictable) mobility patterns dur-

ing daytime. In (Xu et al., 2017), Xu et al. con-

sidered that during day time users’ velocities are uni-

form which may not be a realistic assumption. While

our work on Energy data consumption is different, we

additionally took into consideration changes in con-

sumption (analogous to speed or velocity in mobility

data) from one time window to the next over the entire

population.

3 BACKGROUND AND THREAT

MODEL

In this section we deﬁne the notation that will be used

throughout the paper, and precisely describe the threat

model behind energy consumption data recovery.

Trace Recovery: Inferring Fine-grained Trace of Energy Data from Aggregates

285

3.1 Notation

The energy reading of household i by a smart meter

at time step t ∈ N is denoted by x

(t)

Energy data

of household i over horizon T (i.e., T time steps) is

represented as a time-series, and denoted by the T -

element vector x

, whose t-th element is x

(t)

The aggregate (sum) consumption of n number of

households over a time period T , deﬁned as a set of

one or more time steps, is given by

agg

∑

i=1

(1)

∑

i=1

(2)

, . . . ,

∑

i=1

(T )

(1)

The notations used throughout the paper are sum-

marised in Table 1.

Table 1: Notation.

Symbol Description

A Adversary

B Bucket of energy

∆B = e Size of a bucket

B Estimated/predicted bucket of energy

C Cost Matrix

(t)

i j

Cost of i

household at j

bucket at time t

∆

(t)

Expectation of energy consumption change at time t

k Total number of buckets

n Total number of households

T Overall time period

X Decision Matrix

(t)

i j

Value of i

household at j

bucket at time t

x Vector of actual energy consumption traces

3.2 Energy Trace Recovery: Threat

Model

We now describe an adversary (A ) who wishes to re-

construct ﬁne-grained energy consumption patterns of

individual households from aggregate statistics. First,

the adversary A accumulates aggregated statistics of

n number of households in a neighbourhood over T

period of time from a publicly released aggregated

dataset or through querying a database via a user in-

terface. The queries to the database may include but

not be limited to the following: (i) What are the max-

imum and minimum consumption in kWh in a neigh-

bourhood at each time step t over the horizon of time

T ?, (ii) How many households consume x kWh of

energy at a speciﬁc time of a day?, (iii) How many

households’ consumption is in a given range of en-

ergy (e.g., how many households’ energy consump-

tion is between 0 and 1 kWh at time t) and (iv) How

In general, time steps t and t + 1 represent consecutive,

potentially equally-spaced, times. In this paper, they repre-

sent hours.

many households’ electricity usage increases or de-

creases at different hourly of a day and how much?.

There could be many other possible queries which are

beyond the scope of this paper.

The adversary A then analyses the aggregated

statistics to construct an attack strategy that helps re-

construct the energy consumption patterns of individ-

ual households. A key consideration here is that the

adversary might not be able to reconstruct the energy

consumption of each household at very ﬁne granular-

ity levels. This is due to the fact that even though the

energy consumption of a household may show simi-

lar trends over time, these trends are not expected to

be precisely the same due to small ﬂuctuations in en-

ergy consumption. We therefore propose the idea of

energy consumption within buckets. More precisely,

given the answers to the above queries, adversary A

divides the energy consumption at each time step into

different equal sized intervals (semi-closed) which are

deﬁned as buckets throughout the paper. The idea of

bucket describes the granularity of users in each in-

terval of energy consumption at every time step over

the horizon T . For instance, at each hour during the

night-time most households consume between 0.50

kWh and 1 kWh (i.e., (0.5, 1]), so we state that most

of the users’ consumption is taken place from B

and

when households are on holidays, they do not con-

sume any electricity, thus we state that during that pe-

riod of time energy consumption took place from B

Energy Buckets. Formally, we illustrate the con-

cept of bucket as follows. A bucket of energy con-

sumption is denoted by B and value of each bucket

represents a half-open interval (i.e., energy consump-

tion range in kWh), where the interval size, i.e.,

bucket size, is denoted by ∆B = e. We denote buck-

ets by B

= [0], B

= (0, e], B

= (e, 2e], B

= (2e, 3e]

and so on, and we try different bucket sizes to test the

attacker’s accuracy. We say a household is in a bucket

at time t if the household’s energy consumption

falls into the interval of B

. Note that when a user

does not consume any electricity at a speciﬁc time of

a day this falls under bucket B

. We have considered

a bucket with 0 consumption because an adversary

could be interested to know when her target home is

not occupied.

4 DATASET AND FEASIBILITY

OF PRIVACY BREACH

In this section, we ﬁrst explain the datasets which are

used to evaluate the performance of the adversary A ,

then show the key features behind the load patterns of

households energy consumption.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

286

4.1 Data

We use two real-world datasets that capture the ﬁne-

grained (i.e., “disaggregated”) energy consumption

(time-series) records of households: the UK Power

Networks (London Dataset)

and Ausgrid house-

holds dataset

. We then aggregate these datasets

to perform analyses and attacks on them. The

actual-“disaggregated”-datasets serve as ground truth

against the estimated consumption data.

These publicly available datasets contain different

numbers of households with a variety of smart-meter

reading frequencies over various periods of time. We

use these datasets primarily because of their different

characteristics, such as different meter-reading reso-

lutions, geographic locations of the households, time

periods and number of households. Note that the ac-

tual datasets contain more households over a greater

period of time. We discarded the rest as they are in-

consistent or incomplete. A brief summary of the

datasets, which were used in our evaluation, is pre-

sented in Table 2.

4.2 Consistency and Distinctiveness

Properties of Energy Consumption

By performing analysis on the raw (ﬁnd-grained,

dis-aggregated) data for both London and Ausgrid

datasets, we argue that each household follows a

consistent energy consumption pattern and hence the

households can be uniquely distinguished with a high

probability.

To comprehensively understand the consistency of

energy consumption patterns of all households over

the entire period of time, we study the percentage of

households that consume energy from Top-5 buckets

over four sizes of buckets in {0.25, 0.5, 1.0, 2.0} for

both datasets. Figure 1 shows the results in the Aus-

grid dataset. We observe that the percentage of house-

holds that consume from the top buckets increases

with the increase of bucket size. When the bucket

size is 0.25, around 40% and 25% of households con-

sumer energy from Top-1 and Top-2 buckets, respec-

tively. Furthermore, we observed over 12% of house-

holds’ consumption is from Top-3 bucket. Note that

number of buckets and the hourly/daily/monthly max-

imum value of the buckets are varying over the popu-

lation and the entire time period.

Doubling the bucket size to 0.5 and 1.0, around

60% and 70% of households’ energy consumption

https://data.london.gov.uk/dataset/

smartmeter-energy-use-data-in-london-households

https://data.gov.au/data/dataset/

smart-grid-smart-city-customer-trial-data

(a) Bucket size=0.25 (b) Bucket size=0.50

Figure 1: The percentage of households that consume en-

ergy from top buckets for four different size of buckets over

the period of one year in Ausgrid dataset.

(a) Bucket size=0.25 (b) Bucket size=0.50

Figure 2: The percentage of households that consume en-

ergy from top buckets for four different size of buckets over

the period of one year in London dataset.

remains in Top-1 buckets respectively. Increasing

the bucket size to 2.0, over 90% of the households

consume energy from Top-2 buckets. We also ob-

serve similar pattern in consuming energy in London

dataset (see Figure 2).

Observations from both the datasets suggest that

most of the households tend to consume from the

same (top) buckets consistently. Thus, the consump-

Trace Recovery: Inferring Fine-grained Trace of Energy Data from Aggregates

287

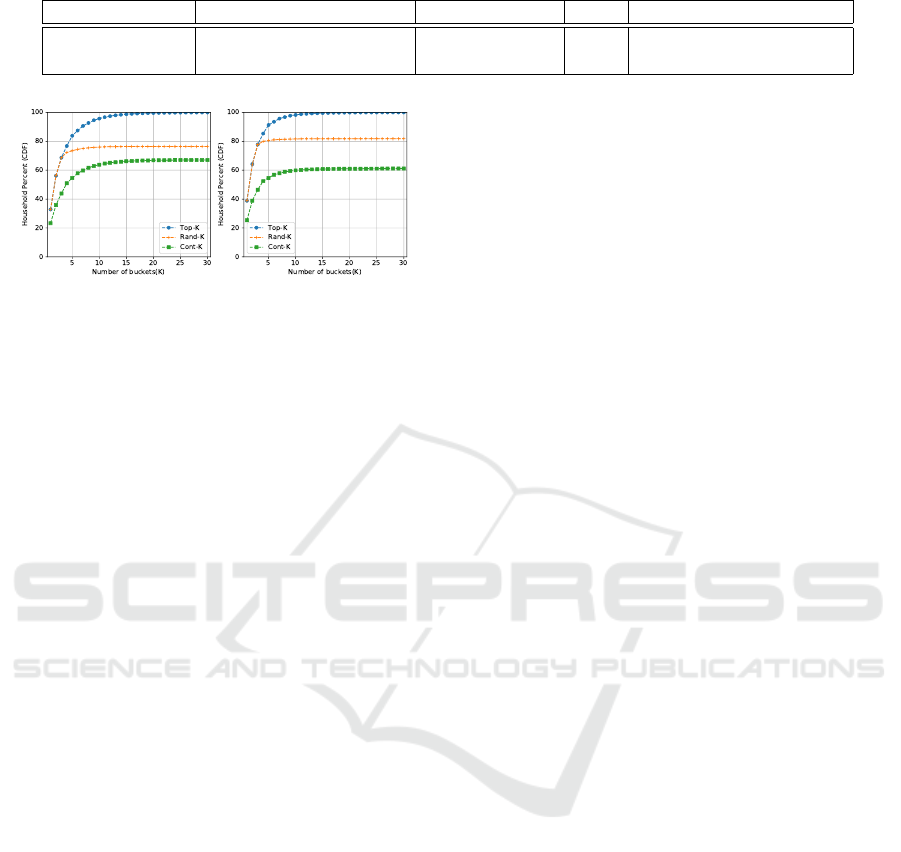
Table 2: Some features of the datasets used in the experiments are summarised.

Dataset Number of Households Location Year Meter Reading Interval

London Dataset 4681 London, UK 2013 30 min

Ausgrid Dataset 6981 NSW, Australia 2013 30 min

(a) Ausgrid Dataset (b) London Dataset

Figure 3: The percentage of households that can be distin-

guished by K buckets of energy consumption for the bucket

size 0.25.

tion patterns are highly consistent. Note that with the

increase of bucket size, the top buckets are accommo-

dating more users as the buckets include more coarse-

grained meter readings within their boundaries.

To evaluate the distinctiveness of households’ en-

ergy consumption patterns, we ﬁrst generate a vec-

tor containing K energy consumption buckets, then

investigate the percentage of households not sharing

the same given buckets vector. We use three dif-

ferent strategies to obtain the buckets vector, that

is, selecting the Top-K frequently used buckets by

the households (Top-K), randomly selecting K buck-

ets belonging to the households’ energy consump-

tion patterns (Rand-K) and randomly selecting K con-

secutive buckets (Cont-K). Under these three strate-

gies, we show the percentage of (consumption pat-

terns of) households that can be distinguished from

other households by the selected patterns in Figure 3.

In the Ausgrid dataset (Figure 3a), we observe

that within the Top-5 buckets 80% of households have

unique Top-5 energy consumption buckets. Whereas

a smaller number of households (73% and 55%) can

be distinguished from Rand-5 and Cont-5 buckets re-

spectively. Further, considering the Top-15 buckets,

almost all households can be distinguished. How-

ever, only 55% and 70% of households can be dis-

tinguished when we consider Rand-15 and Cont-15

buckets. Similar observations are observed in the

London household dataset (Figure 3b).

The above results quantitatively show that the en-

ergy consumption patterns of households are consis-

tent and distinct. This ﬁnding helps us construct an

attack model to reconstruct the consumption patterns

of individual households.

4.3 Capturing Energy Consumption

Speed

Since we know that the energy consumption of house-

holds are consistent and distinct, in this section, we

study the energy consumption speed. Prior to show-

ing the results of consumption speed, we ﬁrst show

that the energy consumption speed is also stable over

the whole time period.

Figure 4 depicts the average percentage of time

when the households consume from Top-20 buckets

at different hour of a day in the Ausgrid dataset.

The top left ﬁgure in Figure 4 reports that the per-

centage of time that the households consume energy

from top buckets during the night-time (i.e., 12:00 am

- 6:00 am). We observe that over 80% and 90% of

the time households consume electricity from Top-3

buckets and Top-5 buckets respectively. We also ob-

serve that almost 100% of the time Ausgrid house-

holds’ consumption patterns revolve within Top-10

energy buckets. The ﬁgures show that energy con-

sumption over six consecutive hours (from 12 am - to

5 am) were quite consistent. These observations are

presumably due to the natural sleeping cycles, energy

consumption patterns of households remains consis-

tent during night-time in the Ausgrid dataset.

The top right ﬁgure in Figure 4 shows the percent-

age of time that the households consume energy from

top buckets in the morning (i.e., 6am - 12 am). We

observe that over 80% of the time households’ energy

consumption occurred from top-5 buckets. Moreover,

over 95% of the time energy is consumed from Top-

10 buckets from 7 am to 11 am. Interestingly, the con-

sumption patterns during this time interval are quite

uniform. Further, the consumption patterns in the

morning are more diverse than that in the night-time.

The bottom left ﬁgure in Figure 4 illustrates the

cumulative percentage of households consumption

duration from each of the frequently used buckets.

Top-5 and Top-10 buckets are used by the households

over 80% of the time for the ﬁrst consecutive 4 hours,

whereas the rest of the time energy consumption pat-

terns are somewhat more diverse. During this 3-hour

period in the afternoon, however, energy consumption

remains very consistent (i.e., households consume a

constant amount of energy from 12 pm to 3 pm), and

this is similar to the trend from 7 am to 11 am. This

could reﬂect the fact that usually people tend to go to

SECRYPT 2021 - 18th International Conference on Security and Cryptography

288

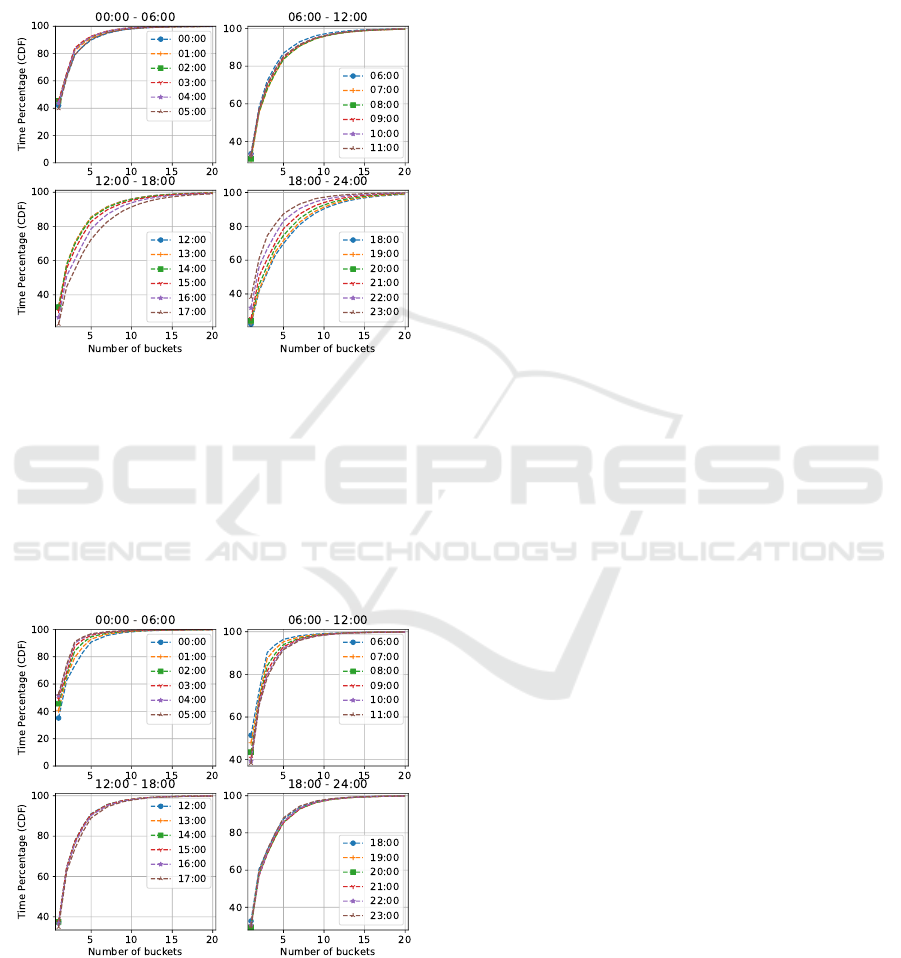
their workplace during the day-time.

The consumption patterns in the evening are much

more diverse though it keeps increasing until mid-

night (see bottom right ﬁgure in Figure 4). Then, the

usage time of the top buckets decreases as people tend

to go to bed, which reduces the use of energy.

Figure 4: Percentage of time (on an average) a household

uses top buckets of energy where bucket size is 0.25, over

the entire period of time in Ausgrid dataset.

Similarly, in the London dataset (see Figure 5),

the average percentages of time when the house-

holds consume the top buckets of energy also remains

steady. Households usually consume from Top-5

buckets over a whole natural day. Although the spe-

ciﬁc consumption pattern is quite different than that

of in the Ausgrid dataset.

Figure 5: Percentage of time (on an average) a household

uses top buckets of energy where bucket size is 0.25, over

the entire period of time in London dataset.

We now demonstrate how different households’

energy consumption varies from one time step to an-

other. We show the results for 2 consecutive hours

of a day using the London dataset. Figure 6 depicts

what percentage of households fall in which range of

energy consumption variation (increase or decrease)

from one time step to the next. For example, we ob-

serve that at Hour-1, we see around a 10% increase in

the percentage of households that showed an increase

by 0 − 10% of their energy consumption than its pre-

vious time step. Moreover, at Hour-2, we observe that

most of the households’ (around 60%) energy con-

sumption showed an increase by 0 − 10%.

Note that the negative percentage change refers to

decrease in percentage. Based on such an observa-

tion, we calculate the expected energy consumption

speed for each given bucket. The detailed calculation

given in the next section.

To conclude, all of the aforementioned observa-

tions indicate that from the aggregated dataset, we

could take advantage of the consistence, distinctive-

ness and expected energy consumption speed to re-

cover the energy consumption traces of the individual

households.

5 UNSUPERVISED ATTACK

MODEL

In this section, we present our unsupervised attack

model for individual energy consumption recovery

from an aggregated dataset.

5.1 Overview

We consider a realistic scenario (Buescher et al.,

2017) where a data curator releases time-series en-

ergy consumption data aggregated from a set of n

households over a time period T . To recover the

trace of individual energy consumption over the entire

time period, we extract individual energy consump-

tion from the aggregated data time by time. In gen-

eral, once given a bucket size, we can assign the ag-

gregated data to different buckets. The salient point

here is that at a single moment, one bucket contains

only one household. Formally, we can derive the en-

ergy consumption buckets B

(t)

= [B

(t)

, B

(t)

, . . . , B

(t)

] at

time step t with k buckets. Recovering a consumer’s

energy usage load pattern is equivalent to associating

anonymised buckets that are consumed by the same

consumer across different time slots. We now explain

how to identify the energy consumption buckets that

can be linked to the same load pattern of a household.

To address this problem, we propose an unsu-

pervised attack model inspired by the work in (Xu

et al., 2017) that iteratively associates the same house-

Trace Recovery: Inferring Fine-grained Trace of Energy Data from Aggregates

289

(a) Hour-1 (b) Hour-2

Figure 6: Percentage of households in each threshold (i.e., the energy consumption variation in percentage in the given ranges)

of energy consumption change at consecutive two hours of a day in London dataset.

holds’ load patterns from its following time steps, and

the adversary then recovers the entire load patterns

(by linking consumption buckets). At each point in

time, the adversarial method can be divided into two

steps. First, we estimate the likelihood of the next

energy consumption bucket that belongs to a given

load pattern by exploiting the characteristics of house-

hold energy consumption patterns. Second, we derive

an optimal solution to link households’ energy con-

sumption buckets with the next consumption bucket

which maximises the overall likelihood. We ﬁrst

discuss how we can estimate an optimal association

between recovered and actual energy consumption

traces through having access to the estimated likeli-

hood.

We deﬁne the cost matrix at time t as C

(t)

i, j

}

k×k

, where c

i, j

corresponds to the inverse of

likelihood of connecting a load pattern of household

i to the next consumption bucket B

(t+1)

. The load

pattern reconstruction problem is equivalent to solv-

ing an optimal match between the rows and columns,

which minimises the overall cost. Let us suppose the

decision matrix X

(t)

= {x

(t)

i, j

}

k×k

, where, x

(t)

i, j

= 1 de-

notes that the load pattern gets linked with next con-

sumption bucket B

(t+1)

and x

(t)

i, j

= 0 otherwise. Now,

we construct the energy consumption recovery prob-

lem as follows.

minimise

∑

i=1

∑

i=1

(t)

i, j

· x

(t)

i, j

(2)

subject to: x

(t)

i, j

= {0, 1} (3)

∑

i=1

(t)

i, j

= 1 and

∑

j=1

(t)

i, j

= 1 (4)

Such an optimisation problem could be solved by the

Hungarian algorithm (Xu et al., 2017; Kuhn, 1955).

5.2 Recovering Fine-grained Energy

Consumption Patterns

We propose a scheme inspired by the work in (Xu

et al., 2017) based on our observations discussed in

Section 4 to formulate the cost matrix over the 24

hours of a day. The steps are as follows.

1) We calculate the expected changing for a given

bucket at time t by our observation about the energy

consumption speed. We use ∆

(t)

= {δ

(t)

, . . . , δ

(t)

} to

indicate the matrix of such expectations for all possi-

ble buckets under given bucket size. Note that, once

given a bucket size, all the energy consumption values

can be assigned to a speciﬁc bucket.

According to what we have in Figure 6, we calcu-

late δ

(t)

∈ ∆

(t)

for bucket B

(t)

∑

i=1

×change

, (5)

where change

indicates the ith changing step (x axis)

shown in Figure 6, Pr

is the corresponding probabil-

ity measured by the percentage of households (y axis)

in Figure 6, 20 is a predeﬁned value for the steps of

energy consumption changing from time t to t + 1.

Then for a given bucket j at time t, we estimate its

value for time t + 1 as

(t+1)

= B

(t)

× δ

(t)

(6)

2) We consider ∆

(t)

at each time step t as the

thresholds that have been discussed in Section 4.3.

We used the above discussed assumption to con-

struct the cost matrix C

(t)

. Thus, we use the

Euclidean distance between the estimated/predicted

bucket

(t+1)

of households i and each unassigned

bucket B

(t+1)

at the next time slot to formulate the

SECRYPT 2021 - 18th International Conference on Security and Cryptography

290

Figure 7: Mean recovery accuracy of energy consumption

buckets for different size of buckets.

(a) Ausgrid Dataset (b) London Dataset

Figure 8: Adversarial performance (accuracy) of the at-

tacker in recovering energy consumption patterns of indi-

vidual households using both datasets.

cost matrix C

(t)

. The cost for each household for con-

suming energy from each bucket is illustrated in the

following equation.

(t)

i j

= |

(t+1)

− B

(t+1)

|. (7)

For example, let the corresponding bucket of Al-

ice’s energy consumption be x at time t. We ﬁrst cal-

culate the estimated bucket ˆx for time t + 1 based on

current time t. Let the unassigned bucket at time t + 1

be y

and y

. Then we have to decide whether we

move Alice from bucket x to y

or y

. We calculate the

cost of such a movement by calculating the distance

between ˆx and y

, y

respectively. Solving the opti-

misation problem in last section with the cost matrix

would provide us with a decision as to whether Alice

moves to bucket y

or y

, that is, the energy consump-

tion of Alice at time t + 1.

6 EXPERIMENTAL EVALUATION

In this section, we ﬁrst introduce the conﬁgurations,

together with the metrics used in our experimental

analysis of the attack model, then report the attack

performance against two famous real-world datasets

of individual’s energy consumption data.

(a) Ausgrid Dataset (b) London Dataset

Figure 9: Cumulative errors (recovery error) in estimating

energy consumption trace of individual households using

both datasets.

6.1 Experimental Conﬁgurations

First, we aggregate the half hourly reading to hourly

readings for both datasets. We split the datasets ran-

domly into ﬁve samples where each sample contains

1000 households over 2 months. One month of data

is chosen from the beginning of the year and another

month of data from the middle of the year because

the households’ energy consumption distribution in

the middle of the year is different from that of at the

beginning and end of the year for both the datasets.

This variation in energy consumption distribution

could be caused by seasonal change (e.g., winter to

summer) over time. We choose four values of l =

[0.25, 0.50, 1.0, 2.0] to check how user percentages

vary from one bucket size to another. We then gen-

erate buckets for each value of l for each sample of

the data. We also calculate the number of households

in each bucket at each time step to observe how con-

sistent the households are in consuming energy from

different size of buckets. Then we compute the per-

centage of households at different ranges of energy

consumption change (as a percentage) (see Figure 6).

We then convert the range of percentage changes into

discrete values (e.g., if the percentage change of en-

ergy consumption remains between 0 to 10%, we map

this range into 0.1, and if the range is between 11-

20%, we map this into 0.2 and so on). We then com-

pute the expected speed of energy consumption that

is, expected energy consumption change over each

hour of the day by multiplying the mapped value with

its corresponding user percentage, as explained ear-

lier in Section 4.3. This ∆ helps us construct the

cost matrices to reconstruct energy consumption pat-

terns in terms of buckets. Then we apply the Hun-

garian algorithm to optimise the assignment problem

using linear sum assignment solver imported from

a python library scipy.optimise. The entire project

is implemented in Python3.

Trace Recovery: Inferring Fine-grained Trace of Energy Data from Aggregates

291

6.2 Metrics

We evaluate the attack performance of the adver-

sary by considering the following two metrics: ac-

curacy in recovering buckets which the households

consuming the energy from and recovery error. First,

we pair the recovered energy consumption patterns

in terms of buckets with the most similar actual

load patterns (i.e., the ground truth buckets) using a

greedy approach. Let the actual load pattern buck-

ets of i

household be B

= {B

(1)

, B

(2)

, . . . , B

(T )

}

and the j

recovered load pattern buckets be

{

(1)

(2)

, . . . ,

(T )

} over a period of time T . Thus,

the average accuracy is denoted by A is deﬁned as

follows.

A =

∑

i, j

∩ B

, (8)

where,

∩ B

refers to the common energy con-

sumption buckets between the estimated buckets and

the actual buckets, and | ∗ | refers to the total number

of buckets in ∗.

Secondly, we compute the recovery error (RE) by

measuring the distance between the estimated buck-

ets and the actual energy consumption traces (not the

actual buckets) of households as follows.

RE :=







∑

t=1

(t)

−

(t)

∑

t=1

(t)

−

(t)







, (9)

where,

(t)

is the estimated bucket of a household

i at time t and x

(t)

is the actual energy consumption

trace of a household i at time t.

6.3 Adversarial Performance

We empirically quantify the performance of the ad-

versary A in recovering energy consumption buck-

ets. We ﬁrst present the average recovery accuracy

of reconstruction attack on the two above discussed

datasets.

Figure 7 shows that the average recovery accuracy

(over all target households) averaged over the entire

period of time, varies between 80% and 95% for the

different sized buckets. We observe that the buckets

(i.e., energy consumption patterns) recovery accuracy

in the Ausgrid dataset is a small amount higher than in

the London dataset. The accuracy increases with the

increase of the size of buckets because the top buck-

ets are accommodating more users as the buckets in-

clude more coarse-grained meter readings within their

boundaries.

We now demonstrate the cumulative accuracy (see

Figure 8) of the attacker in recovering the energy con-

sumption patterns of households using both datasets

for four different size of buckets. Figure 8a shows

that over 90% of the households’ consumption pat-

terns can be recovered accurately when the bucket

size is between 1 and 2. Reducing the size of the

bucket to 0.50, we observe the cumulative accuracy

falls, though still achieving more than 95% accuracy

for around 75% of households in reconstructing their

load patterns in terms of buckets. When we set bucket

size to 0.25, we observe that the adversary is still

capable of recovering over 70% of the households’

energy consumption patterns with over 95%accuracy.

Moreover, 80% of the households’ load patterns can

be inferred with at least 80% accuracy. In using the

London smart meter dataset, we observe similar re-

sults for all size of buckets except the 0.25 bucket.

Setting the bucket size to 0.25, we observe that 50%

and 70% of households’ load patterns can be inferred

from aggregated statistics with around 90% and 80%,

respectively, or higher accuracy.

Thus, our experimental evaluations show that the

adversary successfully recovers most of the house-

holds’ energy consumption load patterns (i.e., the

quantity of households that consume from which

buckets). These ﬁndings show that the privacy threat

is severe and this attack paves a way for other possi-

bilities of inferring minute private information about

occupancy levels and the activities of target house-

holds.

Finally, we report how far the estimated buckets of

energy consumption patterns deviate from the ground

truth energy consumption traces. Figure 9 shows the

recovery errors in kWh (x-axis) and the y-axis repre-

sents the households’ percentage. We observe that in-

creasing the size of the buckets, increases recovery er-

rors, whereas a smaller bucket size decreases recovery

errors for both smart meter energy datasets. For the

smallest bucket the adversary recovers 60% of house-

holds’ energy consumption by incurring 0.6 kWh or

less error from the actual (ground truth) consumption

traces in the Ausgrid dataset. The adversary A incurs

less errors in the London dataset compared to that of

in Ausgrid dataset. The attacker recovers energy con-

sumption traces of 40% and 80% households and in-

curs only 0.4 kWh and 0.6 kWh or less deviation from

the ground truth traces, respectively.

We conclude from the above discussed empiri-

cal evaluations that our adversarial strategy is effec-

tive in inferring the ﬁne-grained energy consumption

load patterns of individual households from aggre-

SECRYPT 2021 - 18th International Conference on Security and Cryptography

292

gated statistics. Our study deduces that private infor-

mation such as household occupancy level and home

activities can be gleaned from the estimated ﬁne-

gained energy consumption data with high accuracy

and low recovery errors. These ﬁndings suggest that

releasing or sharing the aggregated statistics of energy

consumption records of individual households, is not

privacy protective. A malicious entity can infringe

the privacy of individuals by exploiting the consis-

tency and distinctiveness properties of consumption

patterns. Therefore, data owners must quantify the

risks in aggregated statistics before releasing publicly

or sharing with third party stakeholders.

7 DISCUSSION AND

CONCLUDING REMARKS

We have shown that an adversary is capable of recon-

structing individual energy consumption traces from

aggregated statistics with very high accuracy. Thus,

any aggregated energy consumption datasets are not

resilient to such attack. As a consequence, the pri-

vacy of individual households is at risk. However, we

considered only a limited number of queries to assess

the adversary’s inference capabilities, which could be

countered as a weakness in the adversarial model. To

address this weakness we will attempt to construct a

generic attack model in the future work. Further, we

discussed a potential privacy preserving scheme that

can be deployed in a privacy preserving data analyt-

ics framework to mitigate such privacy attacks while

leveraging the aggregated utility of the data. One of

the promising privacy preserving technologies is dif-

ferential privacy (Dwork and Roth, 2014) (DP) that

could be used to mitigate the effect of the proposed

attack on aggregated consumption. DP is an efﬁ-

cient way to protect the privacy of individual users

and can also be used to attenuate the implications of

reconstruction attacks. In future work, we would in-

vestigate how local differential privacy (LDP) (Ka-

siviswanathan et al., 2011) could be deployed when

collecting data from the smart meters. However, it is

still challenging to achieve an optimised trade-off be-

tween privacy and utility. Following this paper, we

would try to employ LDP under a min-max game that

minimises the accuracy loss against protecting from

adversaries having maximum background knowledge

of the households’ energy consumption patterns.

We studied the privacy implications of the aggre-

gated statistics of energy consumption data that is col-

lected from smart meter reading. We empirically eval-

uated an adversary’s performance without having any

external information to recover individual users’ ﬁne-

grained energy consumption on an hourly basis. We

offer an example of how an adversary can formulate

an unsupervised attack method; we pose the problem

as a balanced assignment problem and solve it using

the Hungarian algorithm to ﬁnd the optimal match

by minimising the cost. Overall, our work presents

a novel methodology to assess privacy risks in ag-

gregated smart meter data. Moreover, our methodol-

ogy can be used to quantify the privacy implications

in other real-world settings such as transaction data,

health data and web search data.

REFERENCES

Abdallah, A. and Shen, X. S. (2016). A lightweight lattice-

based homomorphic privacy-preserving data aggrega-

tion scheme for smart grid. IEEE Transactions on

Smart Grid, 9(1):396–405.

Buescher, N., Boukoros, S., Bauregger, S., and Katzen-

beisser, S. (2017). Two is not enough: Privacy

assessment of aggregation schemes in smart meter-

ing. Proceedings on Privacy Enhancing Technologies,

2017(4):198–214.

Chen, K., He, Z., Wang, S. X., Hu, J., Li, L., and He,

J. (2018). Learning-based data analytics: Moving

towards transparent power grids. CSEE Journal of

Power and Energy Systems, 4(1):67–82.

Dong, X., Zhou, J., and Cao, Z. (2016). Efﬁcient privacy-

preserving temporal and spacial data aggregation for

smart grid communications. Concurrency and Com-

putation: Practice and Experience, 28(4):1145–1160.

Dwork, C. and Roth, A. (2014). The algorithmic founda-

tions of differential privacy. Foundations and Trends

in Theoretical Computer Science, 9(3–4):211–407.

Efthymiou, C. and Kalogridis, G. (2010). Smart grid pri-

vacy via anonymization of smart metering data. In

2010 First IEEE International Conference on Smart

Grid Communications, pages 238–243. IEEE.

ENA-Report (2015). Energy networks association, “smart

meter aggregation assessment ﬁnal report.

Erkin, Z. and Tsudik, G. (2012). Private computation of

spatial and temporal power consumption with smart

meters. In International Conference on Applied

Cryptography and Network Security, pages 561–577.

Springer.

Farokhi, F. (2020). Review of results on smart-meter pri-

vacy by data manipulation, demand shaping, and load

scheduling. IET Smart Grid.

Habtemariam, B., Miranskyy, A., Miri, A., Samet, S., and

Davison, M. (2016). Privacy preserving predictive

analytics with smart meters. In 2016 IEEE Inter-

national Congress on Big Data (BigData Congress),

pages 190–197. IEEE.

Herrero, J. R., Murciego,

A. L., Barriuso, A. L., de La Igle-

sia, D. H., Gonz

alez, G. V., Rodr

ıguez, J. M. C., and

Carreira, R. (2017). Non intrusive load monitoring

(nilm): A state of the art. In International Conference

Trace Recovery: Inferring Fine-grained Trace of Energy Data from Aggregates

293

on Practical Applications of Agents and Multi-Agent

Systems, pages 125–138. Springer.

Hong, Y., Liu, W. M., and Wang, L. (2017). Privacy

preserving smart meter streaming against information

leakage of appliance status. IEEE transactions on in-

formation forensics and security, 12(9):2227–2241.

Kasiviswanathan, S. P., Lee, H. K., Nissim, K., Raskhod-

nikova, S., and Smith, A. (2011). What can we learn

privately? SIAM Journal on Computing, 40(3):793–

826.

Kelly, J. and Knottenbelt, W. (2015). Neural nilm: Deep

neural networks applied to energy disaggregation. In

Proceedings of the 2nd ACM international conference

on embedded systems for energy-efﬁcient built envi-

ronments, pages 55–64.

Knirsch, F., Eibl, G., and Engel, D. (2016). Error-

resilient masking approaches for privacy preserving

data aggregation. IEEE Transactions on Smart Grid,

9(4):3351–3361.

Kuhn, H. W. (1955). The hungarian method for the as-

signment problem. Naval research logistics quarterly,

2(1-2):83–97.

Lee, Y.-T., Hsiao, W.-H., Lin, Y.-S., and Chou, S.-C. T.

(2017). Privacy-preserving data analytics in cloud-

based smart home with community hierarchy. IEEE

Transactions on Consumer Electronics, 63(2):200–

207.

Liu, Y., Guo, W., Fan, C.-I., Chang, L., and Cheng, C.

(2018). A practical privacy-preserving data aggrega-

tion (3pda) scheme for smart grid. IEEE Transactions

on Industrial Informatics, 15(3):1767–1774.

Makhdoom, I., Zhou, I., Abolhasan, M., Lipman, J., and Ni,

W. (2020). Privysharing: A blockchain-based frame-

work for privacy-preserving and secure data sharing

in smart cities. Computers & Security, 88:101653.

Molina-Markham, A., Shenoy, P., Fu, K., Cecchet, E., and

Irwin, D. (2010). Private memoirs of a smart meter.

In Proceedings of the 2nd ACM workshop on Embed-

ded Sensing Systems for Energy-Efﬁciency in Build-

ing, pages 61–66. ACM.

Reinhardt, A., Egarter, D., Konstantinou, G., and Christin,

D. (2015). Worried about privacy? let your pv con-

verter cover your electricity consumption ﬁngerprints.

In 2015 IEEE International Conference on Smart

Grid Communications (SmartGridComm), pages 25–

30. IEEE.

Sankar, L., Rajagopalan, S. R., Mohajer, S., and Poor, H. V.

(2012). Smart meter privacy: A theoretical frame-

work. IEEE Transactions on Smart Grid, 4(2):837–

846.

Shateri, M., Messina, F., Piantanida, P., and Labeau, F.

(2019). Deep directed information-based learning for

privacy-preserving smart meter data release. In 2019

IEEE International Conference on Communications,

Control, and Computing Technologies for Smart Grids

(SmartGridComm), pages 1–7. IEEE.

Sirojan, T., Lu, S., Phung, B., and Ambikairajah, E. (2019).

Embedded edge computing for real-time smart me-

ter data analytics. In 2019 International Conference

on Smart Energy Systems and Technologies (SEST),

pages 1–5. IEEE.

Vahedi, E., Bayat, M., Pakravan, M. R., and Aref, M. R.

(2017). A secure ecc-based privacy preserving data

aggregation scheme for smart grids. Computer Net-

works, 129:28–36.

Wang, Y., Chen, Q., Hong, T., and Kang, C. (2018). Review

of smart meter data analytics: Applications, method-

ologies, and challenges. IEEE Transactions on Smart

Grid, 10(3):3125–3148.

Wen, M., Lu, R., Zhang, K., Lei, J., Liang, X., and Shen,

X. (2013). Parq: A privacy-preserving range query

scheme over encrypted metering data for smart grid.

IEEE Transactions on Emerging Topics in Computing,

1(1):178–191.

Xu, C., Zhang, L., Zhu, L., Zhang, C., Du, X., Guizani,

M., and Sharif, K. (2020). Aggregate in my way:

Privacy-preserving data aggregation without trusted

authority in icn. Future Generation Computer Sys-

tems, 111:107–116.

Xu, F., Tu, Z., Li, Y., Zhang, P., Fu, X., and Jin, D. (2017).

Trajectory recovery from ash: User privacy is not pre-

served in aggregated mobility data. In Proceedings

of the 26th International Conference on World Wide

Web, pages 1241–1250.

Yang, L., Chen, X., Zhang, J., and Poor, H. V. (2014). Cost-

effective and privacy-preserving energy management

for smart meters. IEEE Transactions on Smart Grid,

6(1):486–495.

Zhang, J., Chen, X., Ng, W. W., Lai, C. S., and Lai, L. L.

(2019). New appliance detection for nonintrusive load

monitoring. IEEE Transactions on Industrial Infor-

matics, 15(8):4819–4829.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

294