
Preventing Watermark Forging Attacks in a MLaaS Environment
Sofiane Lounici
1
, Mohamed Njeh
2
, Orhan Ermis
2
, Melek
¨
Onen
2
and Slim Trabelsi
1
1
SAP Security Research, France
2
EURECOM, France
Keywords:
Watermarking, Neural Networks, Privacy.
Abstract:
With the development of machine learning models for task automation, watermarking appears to be a suitable
solution to protect one’s own intellectual property. Indeed, by embedding secret specific markers into the
model, the model owner is able to analyze the behavior of any model on these markers, called trigger instances
and hence claim its ownership if this is the case. However, in the context of a Machine Learning as a Service
(MLaaS) platform where models are available for inference, an attacker could forge such proofs in order to
steal the ownership of these watermarked models in order to make a profit out of it. This type of attacks, called
watermark forging attacks, is a serious threat against the intellectual property of models owners. Current work
provides limited solutions to this problem: They constrain model owners to disclose either their models or
their trigger set to a third party. In this paper, we propose counter-measures against watermark forging attacks,
in a black-box environment and compatible with privacy-preserving machine learning where both the model
weights and the inputs could be kept private. We show that our solution successfully prevents two different
types of watermark forging attacks with minimalist assumptions regarding either the access to the model’s
weight or the content of the trigger set.
1 INTRODUCTION
With the recent developments in the information tech-
nologies, companies have adopted deep learning tech-
niques to transform their manual tasks into automated
services in order to increase the service quality for
their customers (Ge et al., 2017). Although this trans-
formation brings some new business opportunities for
technology companies, it comes with the burden of
competing in a rapidly changing business arena. In
order to make profit from these business opportuni-
ties, these companies need to be in good positions
in the marketplace, which requires vast amount of
resource utilization to train a deep learning model.
Therefore, these productionized deep learning models
become intellectual properties (IP) for these technol-
ogy companies and their protection is a challenging
issue when they are deployed on publicly accessible
platforms (Zhang et al., 2018).
Indeed, we consider a scenario whereby compa-
nies use a Machine Learning as a Service (MLaaS)
platform as a marketplace in order to sell or rent
their machine learning models. In such platforms,
we believe that the platform administrator should im-
plement some control mechanisms to register mod-
els to the platform only if these are legitimate and
there is no IP violation. Digital watermarking (Kahng
et al., 1998) based techniques can be considered as
potential solutions to protect machine learning mod-
els in such an environment: model owners who wish
to share their models through the platform are look-
ing for some means to protect these against model
theft. The idea is therefore to embed a digital water-
mark into a Deep Neural Network model during the
training phase, before the registration of the model to
the platform and further use this watermark once the
model is actually used and claim the ownership of the
model (Adi et al., 2018).
To generate a watermark for a NN model, the
model owner defines and uses a trigger set to train
the model together with the legitimate data set. This
trigger set is created using either some randomly gen-
erated data or some mislabeled legitimate inputs to
mark the intellectual property of the model owner.
Later on, this trigger set is used to verify the model
ownership. Since the trigger set is supposed to be
secret (only known to the owner of the model) and
unique, a high accuracy on the trigger set constitutes a
valid proof of the ownership. Recently, several attacks
have been developed to circumvent the watermarking
process of neural network models (Hitaj et al., 2019;
Szyller et al., 2019),. Among these, watermark forg-
ing consist in generating fake watermarks (fake trig-
ger sets) in order to claim the ownership of a model
in an unauthorized manner.
Lounici, S., Njeh, M., Ermis, O., Önen, M. and Trabelsi, S.
Preventing Watermark Forging Attacks in a MLaaS Environment.
DOI: 10.5220/0010560602950306
In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 295-306
ISBN: 978-989-758-524-1
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
295

Although solutions are proposed to mitigate this
type of attack, they have several limitations, espe-
cially regarding the access to the trigger set for own-
ership verification in a black-box setting. Indeed, we
consider a privacy-preserving scenario where weights
of the models and inputs are private during the infer-
ence, meaning that no entity (except the model owner)
should be able to inspect the content of the trigger set.
In this paper, we propose a solution against wa-
termark forging attacks deployed on a MLaaS plat-
form under privacy constraints. We argue that a cen-
tral authority is able to certify the validity of a trig-
ger set to prevent the models against forging attacks
without investigating the content of the trigger set in-
stances. The trigger set is only known to the model
owner and its content is not revealed to the platform.
The platform solely analyzes the output of the infer-
ences of the deployed models on the trigger set to
verify the ownership of the models. We introduce a
concept called model similarity in order to compare
models based on their behavior on a random set. We
show that comparing model similarities to a baseline
model, chosen by the platform, is sufficient to prevent
two proposed watermark forging attacks, called Reg-
istration attack and Label-collision attack. Our main
contributions are summarized as follows:
• First, we introduce and re-define basic primitives
for a MLaaS platform by considering the context
of watermark forging attacks.
• Then, we propose a new watermark forging at-
tack called Registration attack together with the
counter-measures against this attack by introduc-
ing a verification step called IsValid to assess the
validity of a trigger set while relying on the uni-
form similarity assumption.
• Later, we propose another advanced watermark
forging attack, namely the Label-collision attack,
which intends to challenge the aforementioned
verification step.
• Finally, we present a detailed evaluation to assess
the efficiency of our solution by using well-known
public data set, namely the MNIST handwrit-
ten digit data set (LeCun and Cortes, 2010) and
CIFAR-10 tiny color images data set (Krizhevsky
et al., 2009). We also prove that IsValid function
is successful to prevent watermark forging for a
MLaaS platform.
The rest of the paper is organized as follows. Ba-
sic primitives and preliminaries are given in Section 2.
We present the MLaaS platform in Section 3 and the
potential attacks that may arise in Section 4. We pro-
pose two different watermark forging attack in Sec-
tion 5 and Section 6 alongside counter-measures. Per-
formance evaluation is given in Section 7. We review
the related word in Section 8 and conclude the paper
in Section 9.
2 PRELIMINARIES
In this section, we propose several key definitions and
notations to be used in the remaining of the paper.
2.1 Deep Neural Networks
A Deep Neural Network (DNN) is defined as follows:
let M : R
m
→ R
n
be a function that takes a vector
x ∈ R
m
as input and outputs a vector y ∈ R
n
. The
probability that input x belongs to class i ∈ [1,n] is
defined as argmax(y
i
). During the training phase, M
is trained to fit the ground truth function
˜
M : R
m
→ R
n
which associates any input x to the true output ˜y. We
denote the accuracy of the model M on a set of inputs
I as acc
M
(I), corresponding to a percentage between
0% and 100% and |I| denotes the number of elements
in a set I.
2.2 Watermarking
In this paper, we consider an intellectual property pro-
tection technique against DNN model theft called wa-
termarking. In brief, a model owner embeds a hidden
behavior into its model, only accessible through a set
of specific inputs called the trigger set. This unique
behavior (secret and unique) acts as a proof of owner-
ship for the model owner.
Definition 1 (Model watermarking). Let M, D and T
be the DNN model to be watermarked, the legitimate
training data set on which the model is originally
trained, and the trigger set, respectively. The water-
marking process of model M using D and T consists
of generating a new model
ˆ
M using the Embed func-
tion as defined below:
ˆ
M ← Embed(D,T,M)
We assume that the behavior of T is solely known
by the owner of the model and hence the agent can
verify the presence of the watermark in a model with
the Veri f y function as defined in Definition 2:
Definition 2 (Watermark verification). Let M
x
be a
watermarked model whereby the watermark is gen-
erated using trigger set T
x
. Then, the existence of a
watermark in a model M
y
is verified if the following
condition holds:
acc
M
y
(T
x
) ≥ β
x,y
SECRYPT 2021 - 18th International Conference on Security and Cryptography
296

where β
x,y
is the minimal accuracy of T
x
on M
y
to de-
tect the watermark.
To define β
x,y
, we need a measure to quantify how
similar two DNN models can be. For this purpose,
we propose to introduce a similarity measure, denoted
γ
x,y
and defined as follows:
Definition 3 (Model similarity). Given two models
M
x
and M
y
and a set of queries I, we define the sim-
ilarity γ
x,y
(I) between models M
x
and M
y
on I as fol-
lows:
γ
x,y
(I) =
1
|I|
∑
∀i
k
∈I
(
1 M
x
(i
k
) = M
y
(i
k
)
0 otherwise
From the definition above, γ
x,y
exhibits the follow-
ing properties:
• 0 ≤ γ
x,y
(I) ≤ 1,
• γ
x,y
(I) = γ
y,x
(I)
• γ
x,x
(I) = 1 for any pair of models (M
x
, M
x
) and for
any set I.
Ownership threshold: In order to have a success-
ful watermark verification test for a model M given
trigger set T
x
and hence claim its ownership (i.e., its
high similarity with M
x
), we quantify the threshold
β
x
as the minimum accuracy of M obtained with T
x
.
Inspired by the work of (Szyller et al., 2019), let’s
define the random variable X ∼ B(n, p) following the
binomial distribution with parameters n ∈ N and p ∈
[0,1]. We can define the event X = z when two models
M
x
and M
y
return the same output z ∈ 0 ···n. Thus, we
can express the probability P(X ≤ z) as the cumulative
binomial distribution.
P(X ≤ z) =
[z]
∑
i=0
n
i
p
i
(1 − p)
n−i
In this context, we define n = |T
x
|, p = γ
x,y
(R ),
z = [β
x,y
∗ |T
x
|] and P(X ≤ z) = 1 − ε.
1 − ε =
[β
x,y
∗|T
x
|]
∑
i=0
|T
x
|
i
γ
x,y
(R )
i
(1 − γ
x,y
(R ))
|T
x
|−i
(1)
Equation 1 indicates that acc
M
y
(T
x
) > β
x,y
implies
that M
x
= M
y
with a probability of 1 − ε. In the rest
of the paper, for simplicity purposes, we denote γ
x,y
=
γ
x,y
(R ) and β
x
= β
x,y
when the model M
y
is implicitly
defined. Through the similarity measure, we propose
a metric called similarity confidence interval.
Definition 4 (Similarity confidence interval). Let’s
consider a list of k models M
1
, M
2
·· ·M
k
and the set of
their mutual similarity Γ = {γ
i, j
| (i, j) ∈ {1 ·· ·k},i <
j}. We denote σ as the standard deviation of Γ. We
define the similarity confidence interval ∆
σ
as fol-
lows:
∆
σ
= 2σ
In the next sections, we use this similarity con-
fidence interval in the context of a mutual similarity
distribution Γ, following a normal law. In this case,
∆
σ
is the standard deviation of Γ multiplied by two.
3 MLaaS PLATFORM
We consider a setting where there exists a machine
learning as a service (MLaaS) platform that acts
as a gateway between a set of agents (model own-
ers), A = {A
1
,A
2
,. .. ,A
p
} and a set of clients C =
{C
1
,C
2
,. .. ,C
k
} who would like to query these mod-
els. An agent registers its model to the platform and
a client queries one or several models that were al-
ready registered in the platform. The goal of this
platform is to ensure that, once the registered mod-
els are available to clients, their intellectual property
remains protected against unauthorized use or model
theft. Hence an agent embeds watermarks to its model
before its registration, and the platform performs ver-
ifications. The newly proposed framework can be de-
fined through the following three phases, illustrated in
Figure 1:
(1) Registration: During this first phase, Agent A
i
∈
A with data set D
i
and trigger set T uses Embed
to train the model
ˆ
M both with D and T and ob-
tain the watermarked model
ˆ
M. To register this
resulting model to the platform, A sends a regis-
tration query Register(M, T ) to the platform. Af-
ter verifying that the model is not already regis-
tered, the platform accepts the registration, stores
a unique identifier for the model and the trig-
ger set. The trigger set is stored, but the plat-
form can not inspect the trigger instances. In-
deed, the platform can only run inferences on the
trigger set and obtain the output results in clear,
using tools such as Secure multiparty computa-
tion (Cramer et al., 2015) or Functional encryp-
tion (Ryffel et al., 2019).
The registered model and trigger set are denoted
M
t
and T
t
, respectively. In the remaining of the
paper, we consider the index t to denote the regis-
tration time, i.e. model M
t+ j
is registered j peri-
ods after the registration of model M
t
(for j ∈ N).
(2) Inference: We assume that M
t
is already regis-
tered and is now available on the platform. During
this inference phase, client C
k
can submit infer-
ence query q
k
(or several of them) to the deployed
model.
Preventing Watermark Forging Attacks in a MLaaS Environment
297

/
?
MLaaS PLATFORM
/
^
^
Figure 1: The platform scenario.
(3) Ownership Verification: Let M
t
be the model
registered by agent A
i
at time t. If A
i
suspects that
its model M
t
has been used to generate and reg-
ister a new model M
t+i
, it can send a verification
query Veri f y to the platform. The platform who
has received this request, retrieves the trigger set
of M
t
T
t
and submits these to M
t+i
to compute the
accuracy. If this accuracy is higher than threshold
β
t,t+i
, the platform indeed detects model theft and
revokes model M
∗
t+i
.
Remarks: Any agent A
i
can only submit owner-
ship verification requests to the platform about mod-
els generated after its own model’s registration time.
More formally, let M
t
be the model generated by A
i
;
A
i
can perform verification requests for any model
M
t+ j
where j > 0; Otherwise, the platform discards
the request.
Moreover, the platform considers both the weights
of the models and the trigger instances as secret, only
considering the inferences results. Hence, the MLaaS
platforms is compatible with privacy-preserving neu-
ral networks implementing Secure multiparty compu-
tation (Cramer et al., 2015) or Homomorphic Encryp-
tion (Gentry et al., 2009).
Properties of Watermarking: In the rest of the pa-
per, we consider the following two assumptions re-
garding the watermarked model:
• Secrecy: The content of the trigger set is only
known to the model owner. The platform has no
access to the content of the trigger set (the trigger
set can be encrypted, for example), but can still
perform inferences on the trigger and observe the
outputs.
• Uniqueness: Given model M
t
registered with
trigger set T
t
. For all models M
∗
(deployed or
not yet deployed on the platform) acc
M
∗
(T
t
) ≤ β
t
,
where j 6= t and β
t
is the ownership threshold for
M
t
.
This description of a MLaaS platform is a general
model sharing system and could be implemented in
the context of a marketplace, where agents need to
pay for inferences. Thus, in order to ensure trust be-
tween agents, it has to be resilient against potential
attacks.
4 ATTACKS ON THE MLaaS
PLATFORM
In this section, we investigate potential attacks un-
der the MLaaS platform setting. We show that this
platform is subject to two main watermark forging at-
tacks.
4.1 Threat Model
We consider a rational adversary A
∗
, playing the role
of a new agent submitting model M
∗
t
with its associ-
ated trigger set T
∗
t
during the registration phase. The
goal of the adversary is to successfully register a ma-
licious trigger data set to obtain a high accuracy for
several future registered models M
t+i
on T
∗
t
and thus,
claiming the ownership of these models. We assume
that A
∗
has partial access to training data D ∈ D and
can send inference requests to other models deployed
on the platform.
4.2 Watermark Forging
A trigger set T is composed of a set of n in-
puts {T
1
,T
2
·· ·T
n
} associated with a set of n la-
bels {l
1
,l
2
·· ·l
n
}. Since this association is secret and
SECRYPT 2021 - 18th International Conference on Security and Cryptography
298

unique for a watermarked model M, we consider the
watermark verification using trigger set T as a ”con-
vincing” proof of ownership. The goal of a watermark
forging attack is, for a adversary A
∗
and for a water-
marked model
ˆ
M, to create a malicious trigger set T
∗
t
.
Overall, the attack goes as follows:
• Generation of a forged trigger set T
∗
t
.
• Embedding of this trigger set into a model
ˆ
M
∗
t
.
• Registration of (
ˆ
M
∗
t
, T
∗
t
) to the MLaaS platform.
• Sending ownership verification for future models
M
t+i
, to obtain acc
M
t+i
(T
∗
t
) > β
t,t+i
and such that
the agent C
t
obtains the ownership of the model
M
t+i
of C
t+i
.
The platform forbids an adversary to claim a pre-
viously registered model, i.e., the malicious trigger set
cannot be constructed through inferences on a previ-
ously registered model. Furthermore, as mentioned
in the previous section, the MLaaS platform is not
able to inspect the content of the trigger set, hence the
trigger set instances can not be marked by the model
owner in order to be verified by the platform.
The challenge for the adversary in watermark
forging attacks is to be able to generate a forged trig-
ger set, without the knowledge of future registered
models. In the next sections, we present two strate-
gies for the adversary to construct T
∗
t
, and we propose
counter-measures.
5 REGISTRATION ATTACK
As mentioned in Section 3, during the registration
phase, the platform verifies if a model is not already
registered before. However, there is no control on the
validity of the trigger set in order to verify the ba-
sic properties such as secrecy and uniqueness of the
watermarked model and this may lead to watermark
forging. Such a lack of control can motivate adver-
saries to launch a registration attack, described in this
section.
5.1 Overview
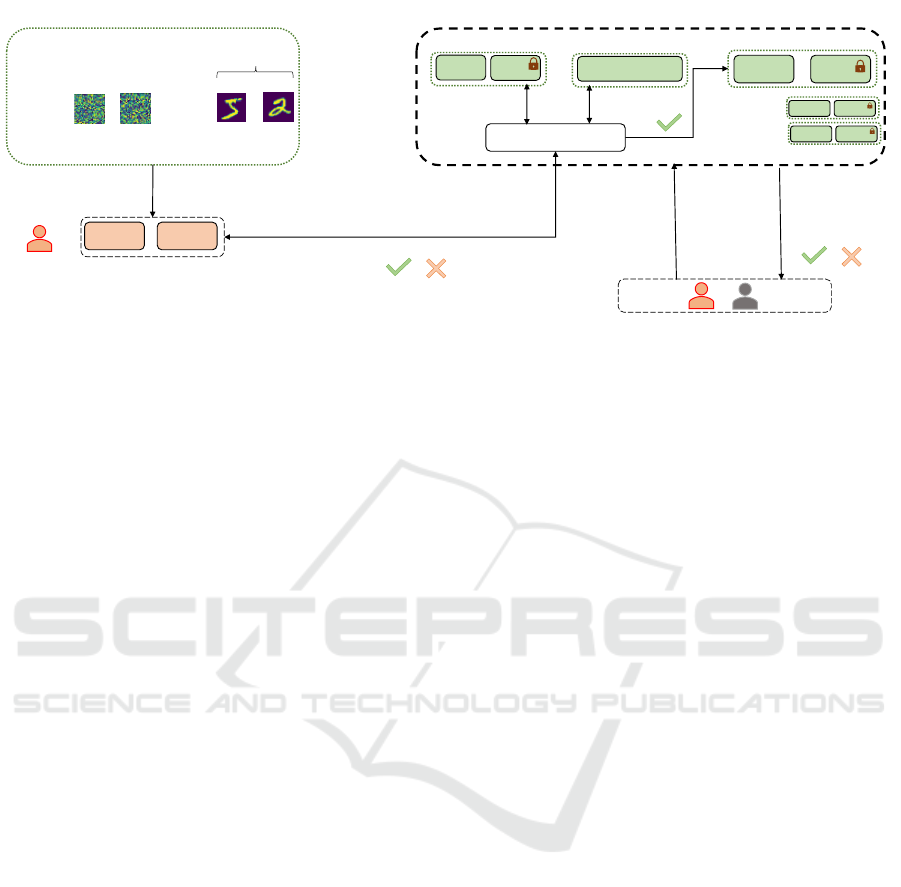
We provide a illustration of the attack in Figure 2. We
assume that adversary A
∗
wants to successfully regis-
ter a new model M
∗
t
. A
∗
generates T
∗
t
from mixture of
legitimate data and random data (T
∗
t
= τD +(1 −τ)R
where τ ∈ [0,1]).
We now assume that a legitimate agent A submits
(after A
∗
) a legitimate model M
t+ j
with the same ar-
chitecture of M
∗
t
. The platform also proceeds with
the registration of M
t+ j
and its trigger set. Since the
Algorithm 1: IsValid algorithm.
Data: Model M
t
, trigger set T
t
, baseline
model M
0
, threshold α∗
Result: Boolean b
X ← γ
0,t
(T
t
);
r ← γ
0,t
(R );
α ←
X
r
;
if α > α
∗
then
b ← False;
else
b ← True;
end
previously uploaded T
∗
t
consists of inputs taken from
a legitimate training data set, there is a high chance
that this trigger set also outputs good accuracy with
legitimate M
t+ j
. In other words, since T
∗
t
∈ D, then
there is a high chance that acc
M
t+ j
(T
∗
t
) > β
t,t+ j
. In
this situation, the adversary A
∗
successfully claimed
the ownership of the model M
t
. We denote this attack
as the Registration attack.
5.2 Our Proposed Counter-measure
The previous example shows that the platform needs
to control the validity of the trigger set to protect the
models against this type of watermark forging attacks,
especially to verify if no legitimate data is in the trig-
ger set. An adversary could claim ownership of future
models if a forged trigger set is accepted by the plat-
form. Consequently, before registering a model, the
platform needs to perform additional verification. To
implement such an additional procedure, one should
consider the following conditions:
• The platform cannot inspect the trigger set by it-
self. It can only verify the output of the inference
on the trigger set. Indeed, the trigger set is only
known to the agent and should not be disclosed
to the platform. If the platform needs to store the
trigger set then, one idea is to store its encrypted
version.
• The counter-measure is required to be computa-
tionally efficient: a naive solution could be, for ev-
ery previously registered model on the platform,
to make inference using the trigger set. However,
this solution could quickly lead to a computational
bottleneck with the number of inferences.
In this section, we propose a counter-measure
against the previously described registration attack
which basically includes a verification step within the
registration phase, to ensure that the trigger set is con-
sidered as valid.
Preventing Watermark Forging Attacks in a MLaaS Environment
299
BASELINE
/
4
7
5
2
MLaaS PLATFORM
Figure 2: The Registration attack, inserting legitimate data in the trigger set, with the counter-measure IsValid.
We denote the verification step as the function Is-
Valid, defined in Algorithm 1. The function takes as
inputs the model to be registered M
t
, the trigger set T
t
,
a baseline model denoted M
0
and a threshold α
∗
. The
baseline M
0
is a watermark-free model to be used as
a reference. Instead of testing T
t
on every previously
registered model in the platform, IsValid only con-
siders the impact of T
t
on M
0
to accept or deny the
registration. In Algorithm 1, we define X ← γ
0,t
(T
t
)
as the similarity between M
0
and M
t
on the trigger set
and r ← γ
0,t
(R ) the similarity between M
0
and M
t
on
random inputs R . For example, for r = 0.2, M
0
and
M
t
have the same output 20% of the time.
The goal of IsValid is to determine whether M
0
behaves similarly when on the one hand tha actual
trigger set T is tested and when on the other hand
a set of randomly generated inputs R is tested. We
would therefore examine the ratio α = X/r, where
X = γ
0,t
(T
t
) and r = γ
0,t
(R ). In our previous exam-
ple, if we consider the case of r = 0.2 and X = 0.4, we
conclude that the behavior of M
0
on the trigger set T
t
is significantly less random than on random data (the
two models have similar outputs 40% of the time on
the trigger set, but only 20% of the time on random
data). Thus, the uniqueness property of the trigger set
is not satisfied and the platform can deny the registra-
tion. IsValid is comparing α to α
∗
and return True (so
the registration is accepted) only if α ≤ α
∗
.
5.3 Uniform Similarity Assumption
The main assumption of this potential countermea-
sure is that, for a given classification task, two mod-
els have approximately the same behavior on random
data (r is approximately the same for any pair of mod-
els). Thus, if we consider r as a constant, comparing
M
t
to every previously registered model is similar to
comparing M
t
to M
0
, solely. Hence, in order to reach
a cost-effective verification, instead of doing multi-
ple inferences for each pair of models (M
t
,M
t
− j)
where j ∈ N and increasing the verification time, it
would be sufficient that the platform compares M
t
to
M
0
, only. In the rest of the paper, we call this assump-
tion the uniform similarity assumption. Under this
assumption, we consider a unique similarity between
any two models M
x
and M
y
on a set I, called average
similarity:
ˆy(I) = y
x,y
(I) (2)
However, since the uniform similarity assumption
might appear as a strong assumption, we consider a
second attack called Label-collision attack.
6 LABEL-COLLISION ATTACK
In this section, we consider a setting where the
MLaaS platform already implements the verification
step introduced in the previous section, in order to
prevent potential registration attacks. We then ob-
serve that this updated platform is still vulnerable
against a new watermark forging attack that we call
Label-collision attack, when the uniform similarity
assumption does not hold.
6.1 Overview
We provide an illustration of the attack in Figure 3.
Let A
∗
be an adversary trying to forge a trigger set T
∗
t
to potentially claim a future model M
t+i
without using
legitimate data. Similarly to the Registration attack,
the goal of the adversary is to maximize the accuracy
of the forged trigger set on M
t+i
, to satisfy the con-
dition acc
M
t+i
(T
∗
t
) ≥ β
t
. In this case, the adversary
SECRYPT 2021 - 18th International Conference on Security and Cryptography
300

/
(
)
(
)
(
)
(
)
/
Figure 3: The Label-collision Attack with the counter-measure IsValid.
could generate a random trigger set and test the ele-
ments of this trigger set against previously submitted
legitimate models in order to assign their labels for
the newly updated model. In more details:
• Step 1: A
∗
is an agent, owning a model M
∗
called
adversary’s model. We assume that this model
has not been stolen and has been trained through
a complete legitimate process.
• Step 2: Before the registration phase, to construct
the trigger set, A
∗
generates a set of random in-
puts, without labels, which constitutes the basis
of his forged trigger data set T
∗
.
• Step 3: A
∗
further selects a previously registered
model on the platform, M
t− j
, called a reference
model. For every input T
∗z
in T
∗
, the adversary
associates the label M
t− j
(T
∗z
), through inference
queries. In other words, the non-labelled trig-
ger set T
∗
becomes labeled with M
t− j
’s outputs.
Hence, M
t− j
and M
∗
become similar with respect
to T
∗
. We point out that A
∗
cannot claim the own-
ership of M
t− j
with T
∗
t
since it is impossible to
claim a previously registered model.
• Step 4: A
∗
now sends a Register query to the plat-
form with the pair (M
∗
, T
∗
), to be compared to
M
0
. If the uniform similarity assumption holds,
IsValid denies the registration. Indeed, compar-
ing M∗ to M
0
is similar to comparing M∗ to
M
t− j
and an abnormal behavior would be de-
tected. Nevertheless, if this assumption is no more
true than the adversary may succeed to register a
malicious trigger set T
∗
t
.
• If the adversary ends up with a successful regis-
tration, the platform stores (M
∗
t
, T
∗
t
) and the ad-
versary simply sends multiple Veri f y queries for
future registered models M
t+1
, M
t+2
, etc. and
obtain the ownership of at least one of them for
some conditions on the similarities, developed in
the next paragraph.
For notation purposes, we denote the similarity
between the reference model and the claimed model
γ
t− j,t+i
= γ
re f
, the similarity between the adversary’s
model and the claimed model γ
t,t+i
= γ
claim
and the
ownership threshold β
t,t+i
= β
claim
.
6.2 Condition of Success for the
Adversary
To begin with, we first start with the study of the con-
dition for which a malicious trigger set T
∗
t
could be
registered for a successful adversary. Specifically on
T
∗
t
, we have γ
t− j,0
= γ
0,t
(T
∗
t
) by construction of the
attack. A
∗
registered its model, so we necessarily
have:
γ
0,t
(T
∗
t
)
γ
0,t
< α
∗
γ
t− j,0
γ
0,t
< α
∗
γ
t− j,0
< α
∗
· γ
0,t
(3)
Hence, if the reference model and the baseline
model are too similar (i.e γ
t− j,0
close to 1), the adver-
sary cannot be successful (the success is conditionned
to the upper bound). In the experiments, we present
situations for which the adversary A
∗
is not successful
to register (M
∗
t
, T
∗
t
), based on the error rate ε.
Next, we assume the successful registration of the
model. We consider the set of all combinations of
models (M
t− j
, M
∗
t
, M
t+i
) such that the adversary A
∗
is successful for claiming the ownership. If the claim
Preventing Watermark Forging Attacks in a MLaaS Environment
301

of ownership is true (i.e M
∗
t
and M
t+i
are considered
being the same models), then the following condition
holds:
acc
M
t+i
(T
∗
t
) ≥ β
claim
We subtract γ
claim
on each side:
acc
M
t+i
(T
∗
t
) − γ
claim
≥ β
claim
− γ
claim
We argue that γ
re f
(T
∗
t
) = acc
M
t+i
(T
∗
t
) since T
∗
t
is labeled through the reference model. Also, the
claimed model M
t+i
has never been trained on the
trigger set, so γ
re f
(T
∗
t
) = γ
claim
. We obtain:
γ
re f
− γ
claim
≥ β
claim
− γ
claim
(4)
Thus, we can split the set of all combinations of
models (M
t− j
, M
∗
t
, M
t− j
) for A
∗
successful into two
parts:
Condition γ
γ
γ
re f
−
−
− γ
γ
γ
claim
≤
≤
≤ ∆
∆
∆
σ
σ
σ
In this case, we have
the necessary condition ∆
σ
≥ β
claim
− γ
claim
. In the
experiments, we show that min(β
claim
− γ
claim
) > ∆
σ
for several distributions of models, hence the adver-
sary is never successful for this case.
Condition γ
γ
γ
re f
−
−
− γ
γ
γ
claim
≥
≥
≥ ∆
∆
∆
σ
σ
σ
In this case, if we as-
sume that γ
re f
and γ
claim
are sampled from the distri-
bution Γ and we define the probability to obtain such
a combination as p
s
:
p
s
= P(γ
re f
>
ˆ
γ + σ) · P(γ
claim
<
ˆ
γ − σ)
p
s
= 0.0256 (5)
In this case, the probability to obtain such a com-
bination is around 2.5% for a single registration. Con-
sequently, we show that the success rate of the ad-
versary for the two case is negligible, even when the
uniform similarity assumption does not hold.
7 EXPERIMENTS
In this section, we evaluate the performance of the
proposed solution. First, we introduce our experimen-
tal setup. Later, we implement the aforementioned at-
tacks on the MLaaS platform and assess the success
rate of the adversary.
7.1 Experimental Setup
Datasets. For the evaluation of the platform, we use
DNNs trained on the MNIST (LeCun and Cortes,
2010) and CIFAR-10 datasets (Krizhevsky et al.,
2009) since they are the most frequently used datasets
in the domain of watermark (Adi et al., 2018; Szyller
et al., 2019):
• MNIST is a handwritten-digit data set contain-
ing 70000 28 × 28 images, which are divided into
60000 training set instances and 10000 test set
instances. As the trigger data set, we consider
to craft T
t
from the Fashion-MNIST (Xiao et al.,
2017) data set, consisting of 7000 instances.
• CIFAR-10 is a data set that consist of 60000
32 ×32 tiny colour images in 10 different classes,
where each class is equally distributed. The
data set is divided into 50000 training images
and 10000 test images. Furthermore, we employ
STL10 data set samples as unrelated watermark-
ing trigger data set. (Coates et al., 2011).
Models and the Training Phase. Details on the mod-
els and the training phase of these models are as fol-
lows:
• For MNIST, we consider an architecture com-
posed of 2 convolutional layers with 3 fully con-
nected layers, trained with 10 epochs using the
Stochastic Gradient Descent (SGD) (Yang and
Yang, 2018) optimizer, with a learning rate of 0.1
and a batch size of 64. We obtain 99% of accu-
racy on legitimate data set and 100% on trigger
data set.
• For the CIFAR-10, we use 5 convolutional layers,
3 fully connected layers and max pooling func-
tions. For the training phase, we use Adam opti-
mizer(Kingma and Ba, 2017) with a learning rate
of 0.001 for 10 epochs. The accuracy on legiti-
mate data set is around 78% for CIFAR and 100%
for the trigger data set.
Hyper-parameters. During the experiments, we con-
sider the size of the trigger set |T | = 100 similarly to
the watermarking method in (Adi et al., 2018). We
empirically choose R = 10000 to have a good preci-
sion (1e − 3) on the similarity measure.
The environment. All the simulations were carried
out using a Google Colab
1
GPU VMs instance which
has Nvidia K80/T4 GPU instance with 12GB mem-
ory, 0.82GHz memory clock and the performance
of 4.1 TFLOPS. Moreover, the instance has 2 CPU
cores, 12 GB RAM and 358GB disk space.
7.2 Training Data Distributions and β
Threshold
During the experiments, we intend to simulate agents
registering their models to the platform. Thus, we
train several models with the same architecture and
training parameters for two different scenario. First,
we consider a scenario, denoted common dataset sit-
1
https://colab.research.google.com/
SECRYPT 2021 - 18th International Conference on Security and Cryptography
302

Table 1: Mutual similarity metrics for MNIST and CIFAR10 models when (i) the models are trained on a common dataset
and (ii) when trained on separate datasets.
Data set Scenario
ˆ
γ σ ∆
MNIST
Common data set 0.181 3.3e-2 0.209
Separate data sets 0.184 4.2e-2 0.296
CIFAR
Common data set 0.348 1.8e-1 0.698
Separate data sets 0.428 1.8e-1 0.713
uation, where all models have been trained on the
same data distribution D. In the second scenario, we
consider separate datasets situation, where models
have been trained on three different data distribution
{D
1
,D
2
,D
3
}. Each of these D
i
distribution is highly
unbalanced towards a subset of classes to study the
impact of unbalanced training dataset on the overall
similarity distribution.
For the MNIST dataset, we train 50 models with
the aforementioned parameters and 20 models for
CIFAR10. According to Table 1, for the common
dataset situation we have an average similarity be-
tween models for MNIST
ˆ
γ = 0.18 and
ˆ
γ = 0.34 for
CIFAR10. We report the standard deviation σ and the
difference between the lowest and the highest similar-
ity ∆. The major difference between MNIST and CI-
FAR10 models is related to the difference between ac-
curacy values on the legitimate data (99% for MNIST
and 78% for CIFAR10).
Regarding the difference between the common
dataset scenario and the separate datasets scenario,
we observe several points: first, we observe a neg-
ligible difference for σ between the two scenarios.
We also notice a higher average similarity and higher
∆ for the separate datasets scenario. We conclude
that the average similarity assumption (on which the
proposed counter-measures rely on) is more justified
in the common dataset scenario than in the separate
datasets scenario.
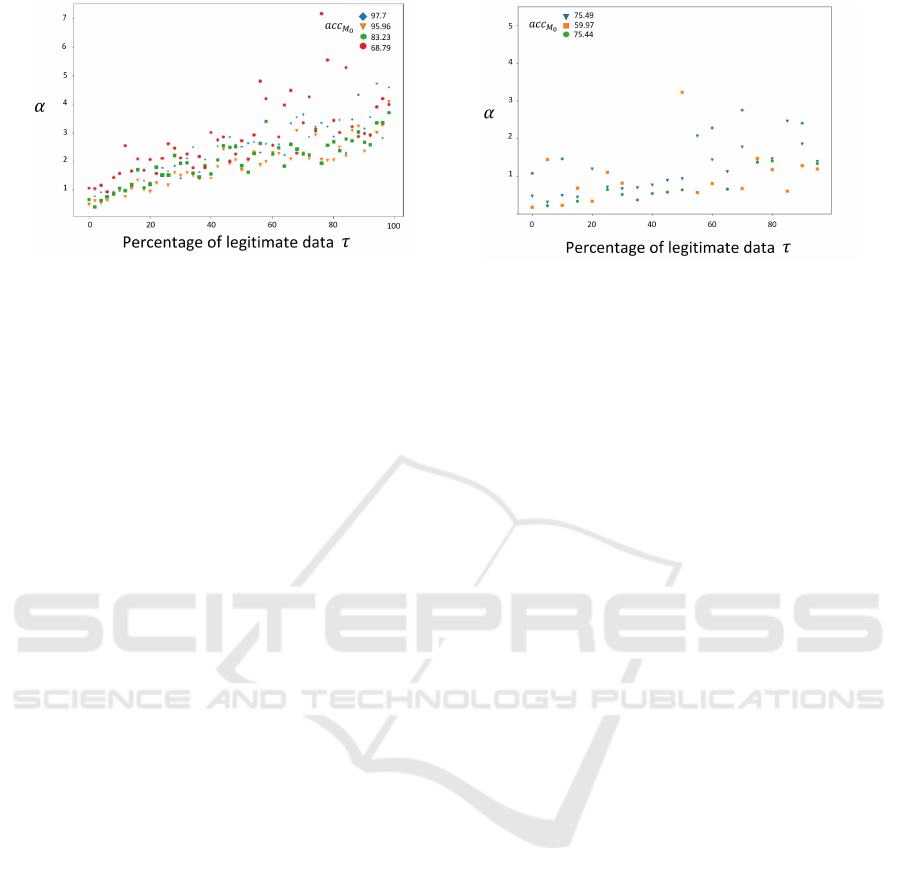
7.3 Registration Attack
To implement this attack, we watermarked 50 DNNs,
with different rate τ of legitimate data in the trigger
data set, while computing α for τ. For the certification
step, a model M
0
is required in order to be used as a
baseline. We trained 4 different models for MNIST
(respectively 3 models for CIFAR10) with different
accuracy on the legitimate dataset to see the efficiency
of the registration process in cases where the base-
line model has low accuracy. In Figure 4, we present
α depending on τ, while comparing the watermarked
models with M
0
for both MNIST and CIFAR10.
Condition α
α
α
∗
=
=
= 1
1
1 Firstly, we consider a naive con-
dition α
∗
= 1. In Figure 4 (a), we observe that
the naive condition to reject the trigger set registra-
tion (α > α
∗
= 1) is efficient to detect even a small
portion of legitimate data set in T
t
for the MNIST
dataset. Furthermore, we observe that the accuracy
of the baseline model M
0
has a negligible impact on
the value of α. The baseline model with low accuracy
leads to higher α scores, which might cause false pos-
itives, but does not impact the false negative rate. This
means that the adversary A
∗
cannot leverage baseline
models with low accuracy to register a malicious trig-
ger data set. Thus, the platform can compute a thresh-
old parameter α
∗
independently from the accuracy of
the baseline model.
In Figure 4 (b), the condition α > α
∗
= 1 is not
sufficient to detect legitimate instance in the trigger
dataset (for τ = 50, we have α
∗
< 1). Especially, for
low accuracy baseline, the computation of α appears
to be less precise (for τ ∼ 60, we can obtain α < 1). If
we consider only the best baseline M
0
, the adversary
can choose τ < 0.7 and still register its model, and can
obtain the following accuracy:
acc
M
t+i
(T
∗
t
) = 0.7·(0.78)+0.3·(0.34) = 64.8% (6)
For ε = 1e −10, we obtain the ownership verifica-
tion threshold β = 0.65, so the adversary is not able
to claim the ownership for ε < 1e − 10.
Condition α
α
α
∗
=
=
= 1
1
10
0
0 ·
·
· β
β
β For τ close to 0 (hence trig-
ger set containing no legitimate instances), we have
α
∗
> 1 for some cases. Due to the stochastic behavior
of the similarity computation through random images,
edge cases can occur corresponding to false positives.
To avoid such cases, α
∗
can be chosen between 1 and
β, and we consider α
∗
= 10 ·β. For MNIST, an adver-
sary can decide to choose τ = 0.3 (i.e injecting 30 le-
gitimate instances in its trigger set), corresponding to
α ∼ 1.5. For ε = 1e −10, we obtain α
∗
= 10·β = 4.5,
so the registration is accepted because α < α
∗
. How-
ever, the maximum accuracy achievable by the adver-
sary, for an ownership threshold of β = 45%:
acc
M
t+i
(T
∗
t
) = 0.3 · (0.98) + 0.7 · 0.18 = 42% < β
Hence, even if the trigger set is composed of 30%
of legitimate instance, the adversary is not able to
claim the ownership of the model. However, the ad-
versary can choose τ = 0.6 (implying α ∼ 4), register
its trigger set and obtain the following accuracy:
Preventing Watermark Forging Attacks in a MLaaS Environment
303
(a)
(b)
Figure 4: The registration score α
∗
depending on the legitimate data rate in T
t
for (a) MNIST and (b) CIFAR10.
acc
M
t+i
(T
∗
t
) = 0.6 · (0.98) + 0.4 · 0.18 = 66% > β
The adversary is successful in this case. In the
case where the platform intends to decrease ε (in order
to increase β), then the threshold parameter will also
increase, so the condition α
∗
= 10 · β is not sufficient
to prevent the attack.
In the case of CIFAR10, the condition is clearly
not sufficient, because it allows a trigger set fully
composed of legitimate instances.
Observations To begin with, the platform could con-
sider the condition α
∗
= β/
ˆ
γ. For MNIST, this condi-
tion prevent the false negatives, while still preventing
the success of the attack.
In the case of CIFAR10, we make two observa-
tions: on the one hand, we see in Table 1 that the
uniform similarity assumption does not hold for CI-
FAR10, in both scenario. Thus, comparing with a
baseline model M
0
is not efficient (α
∗
< 1 even for
large amount of legitimate data). On the other hand,
the accuracy on legitimate data is 78%, so the plat-
form could consider choosing ε such that β > 0.78.
Thus, even if the trigger set is fully composed of legit-
imate data, the adversary could never claim the own-
ership.
From (Kornblith et al., 2019), it is known that dur-
ing the training phase, models converge to similar rep-
resentations of the data and thus have similar behav-
iors on random data. Thus, we can argue that for a
longer training phase, the models from CIFAR10 will
converge to lower similarities and lower σ (similar to
the MNIST models).
We showed that the adversary A
∗
is not success-
ful to implement the Registration attack when the
counter-measure is implemented.
7.4 Label-collision Attack
For the label-collision attack, we leverage the differ-
ence between models to create a malicious trigger set.
To begin with, we evaluate the condition for which
the registration is not successful, i.e:
γ
t− j,0
≥ α
∗
· γ
0,t
(7)
According to the previous section, we set α
∗
=
β/
ˆ
γ. We consider the worst-case (but still plausible
scenario) for the platform, i.e γ
0,t
=
ˆ
γ + 2 · σ. For
MNIST, we obtain γ
t− j,0
> 0.71 and for CIFAR10
γ
t− j,0
> 1.4. In this case, the platform is not able
guarantee the failure of the adversary for the regis-
tration. Thus, the success of the adversary depends
on the ownership verification condition and ∆
σ
.
According to Table 1, we have ∆
σ
∈
{0.066,0.084} for MNIST. We notice for
all values of ε and for γ
claim
∈ [0.1,0.9] that
min(β
claim
− γ
claim
) > ∆
σ
, for the two scenarios, so
in both scenarios, the adversary cannot be successful
for any future model M
t+i
.
According to Table 1, we have ∆
σ
= 0.36 for CI-
FAR10. We observe, for ε < 1e − 16 that the condi-
tion min(β
claim
−γ
claim
) > ∆
σ
is true for γ
claim
< 0.62.
Hence, the platform is able to guarantee the failure of
the adversary in the case of γ
claim
< 0.62. Hence, the
only potential cases where the adversary is success-
ful:
• γ
re f
− γ
claim
≥ ∆
σ
: We show in Section 6 that the
probability for the adversary to obtain a combina-
tion is around 2.5% for a single registration.
• γ
re f
− γ
claim
< ∆
σ
and γ
claim
> 0.62. However, the
verification threshold β
claim
> 0.9 for ε = 1e −10,
and the adversary cannot be successful to claim
the future model M
t+i
for the CIFAR10 distribu-
tion of models.
Finally, we conclude that the success rate of the
adversary is negligible and that our counter-measures
are efficient against watermark forging in a MLaaS
platform.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
304

8 RELATED WORK
Backdoor attacks (Gu et al., 2019; Wang et al., 2019;
Tran et al., 2018) are known as the first use of wa-
termarking techniques in the area of machine learn-
ing research. Such attacks target supervised machine
learning techniques such as deep learning that re-
quires training prior to use. The idea of backdoor
attacks is to poison the training process with a partic-
ular input called the trigger data set. Once the training
process is over, the resulting model becomes vulnera-
ble since they are forced to give manipulated outputs
when the triggers are given as the input for predic-
tions. Because the prediction phase operates as ex-
pected except the inputs from the trigger data set, they
can only be detected by the adversaries who manipu-
late the training phase (Chen et al., 2018). For in-
stance, such attacks can be used in a scenario, where
the adversary tries to gain unauthorized access by em-
bedding watermarks during the training process of a
biometric authentication system (Wang et al., 2019).
Although the first applications of watermarking
were used as the attack mechanism for deep learning
techniques, Adi et al. (Adi et al., 2018) adopted this
approach to introduce a defense mechanism against
the model theft. This time, queries extracted from the
trigger data are used by the model owner to verify the
ownership of the any publicly available model. How-
ever, several attacks have been developed to challenge
the robustness of this ownership verification mecha-
nism (Jia et al., 2020; Hitaj et al., 2019; Szyller et al.,
2019; Tram
`
er et al., 2016). A particular attack against
watermarked DNN models is the watermark forging
attack (Li et al., 2019; Zhu et al., 2020) , where the
adversary intends to forge a false proof of ownership,
i.e forging a fake trigger set with the same properties
as the original trigger set.
The authors in (Li et al., 2019) proposed to gen-
erate trigger instances through a combination of the
original image and a filter. Two different filters are
used: a first marker automatically assign the trigger
instance to a single target label and a second filter as-
sign the trigger instance to the original label. In these
conditions, during the verification phase, a (trusted)
third party authority requires the access to the trigger
instances and the filter in order to grant or deny the
ownership, as opposed to our current work where the
instances of the trigger set are not accessible to the
authority.
In (Zhu et al., 2020), the trigger instances are
generated in such a way that they must form a one-
way chain, i.e the i
th
trigger instance is computed
from the i − 1
th
trigger instance through a hash func-
tion. Hence, it becomes impossible for the adversary
to construct this chain without prior knowledge of
the instances. Even though the proposed techniques
is efficient against watermark forging, the obtained
”chained trigger instances” are similar to noisy in-
stances (images in the paper). Thus, an adversary is
able to distinguish legitimate instances from the trig-
ger instances and can avoid the trigger set verification.
As opposed to previous work, we propose
counter-measures to watermark forging with no spe-
cific constraints on the trigger set instances and with-
out revealing the content of the trigger set to a third
party, which appears to be a necessity when its comes
to privacy-preserving machine learning.
9 CONCLUSION
In this work, we have considered a particular type of
attacks, namely the watermark forging attacks. Such
attacks consists of crafting a malicious trigger set
with the same properties as the original trigger set.
Although there exists several defense mechanisms
against these attacks, they have several limitations, es-
pecially when models are deployed on MLaaS plat-
forms in a privacy-preserving setting, by imposing
constraints on the trigger set generation technique
for the model owner or granting access privileges to
the central authority to inspect the trigger set. In
this paper, we proposed counter-measures for these
attacks by introducing a verification step called Is-
Valid, which is used to assess the validity of a trig-
ger set. Furthermore, we have analyzed the effects of
different attack called Label-collision attack in a de-
tailed evaluation using well-known public data sets,
namely the MNIST handwritten digit data set (LeCun
and Cortes, 2010) and CIFAR-10 tiny color images
data set (Krizhevsky et al., 2009). We show that our
counter-measures are efficient to prevent the success
of an adversary.
Future work might focus on more advanced imple-
mentation issues, such as the storage of watermarked
models in MLaaS platforms.
ACKNOWLEDGEMENTS
This work has been partially supported by the 3IA
C
ˆ
ote d’Azur program (reference number ANR19-
P3IA-0002).
Preventing Watermark Forging Attacks in a MLaaS Environment
305

REFERENCES
Adi, Y., Baum, C., Cisse, M., Pinkas, B., and Keshet, J.
(2018). Turning your weakness into a strength: Wa-
termarking deep neural networks by backdooring. In
27th USENIX Security Symposium, pages 1615–1631.
Chen, B., Carvalho, W., Baracaldo, N., Ludwig, H., Ed-
wards, B., Lee, T., Molloy, I., and Srivastava, B.
(2018). Detecting backdoor attacks on deep neu-
ral networks by activation clustering. arXiv preprint
arXiv:1811.03728.
Coates, A., Ng, A., and Lee, H. (2011). An analysis of
single-layer networks in unsupervised feature learn-
ing. volume 15 of Proceedings of Machine Learning
Research, pages 215–223.
Cramer, R., Damg
˚
ard, I. B., et al. (2015). Secure multiparty
computation. Cambridge University Press.
Ge, Z., Song, Z., Ding, S. X., and Huang, B. (2017). Data
mining and analytics in the process industry: The role
of machine learning. Ieee Access, 5:20590–20616.
Gentry, C. et al. (2009). A fully homomorphic encryption
scheme, volume 20. Stanford university Stanford.
Gu, T., Liu, K., Dolan-Gavitt, B., and Garg, S. (2019). Bad-
nets: Evaluating backdooring attacks on deep neural
networks. IEEE Access, 7:47230–47244.
Hitaj, D., Hitaj, B., and Mancini, L. V. (2019). Evasion at-
tacks against watermarking techniques found in mlaas
systems. In 2019 Sixth International Conference on
Software Defined Systems (SDS), pages 55–63.
Jia, H., Choquette-Choo, C. A., and Papernot, N. (2020).
Entangled watermarks as a defense against model ex-
traction. arXiv preprint arXiv:2002.12200.
Kahng, A. B., Lach, J., Mangione-Smith, W. H., Mantik,
S., Markov, I. L., Potkonjak, M., Tucker, P., Wang,
H., and Wolfe, G. (1998). Watermarking techniques
for intellectual property protection. In Proceedings
of the 35th annual Design Automation Conference,
pages 776–781.
Kingma, D. P. and Ba, J. (2017). Adam: A method for
stochastic optimization.
Kornblith, S., Norouzi, M., Lee, H., and Hinton, G. (2019).
Similarity of neural network representations revisited.
arXiv preprint arXiv:1905.00414.
Krizhevsky, A., Hinton, G., et al. (2009). Learning multiple
layers of features from tiny images.
LeCun, Y. and Cortes, C. (2010). MNIST handwritten digit
database.
Li, H., Willson, E., Zheng, H., and Zhao, B. Y. (2019).
Persistent and unforgeable watermarks for deep neural
networks. arXiv preprint arXiv:1910.01226.
Ryffel, T., Dufour-Sans, E., Gay, R., Bach, F., and
Pointcheval, D. (2019). Partially encrypted machine
learning using functional encryption. arXiv preprint
arXiv:1905.10214.
Szyller, S., Atli, B. G., Marchal, S., and Asokan, N. (2019).
Dawn: Dynamic adversarial watermarking of neural
networks. arXiv preprint arXiv:1906.00830.
Tram
`
er, F., Zhang, F., Juels, A., Reiter, M. K., and Risten-
part, T. (2016). Stealing machine learning models via
prediction apis. In 25th USENIX Security Symposium,
pages 601–618.
Tran, B., Li, J., and Madry, A. (2018). Spectral signatures in
backdoor attacks. In Advances in Neural Information
Processing Systems, pages 8000–8010.
Wang, B., Yao, Y., Shan, S., Li, H., Viswanath, B., Zheng,
H., and Zhao, B. Y. (2019). Neural cleanse: Identi-
fying and mitigating backdoor attacks in neural net-
works. In 2019 IEEE Symposium on Security and Pri-
vacy (SP).
Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-
mnist: a novel image dataset for benchmark-
ing machine learning algorithms. arXiv preprint
arXiv:1708.07747.
Yang, J. and Yang, G. (2018). Modified convolutional neu-
ral network based on dropout and the stochastic gradi-
ent descent optimizer. Algorithms.
Zhang, J., Gu, Z., Jang, J., Wu, H., Stoecklin, M. P., Huang,
H., and Molloy, I. (2018). Protecting intellectual prop-
erty of deep neural networks with watermarking. In
Proceedings of the 2018 on Asia Conference on Com-
puter and Communications Security.
Zhu, R., Zhang, X., Shi, M., and Tang, Z. (2020). Secure
neural network watermarking protocol against forging
attack. EURASIP Journal on Image and Video Pro-
cessing, 2020(1):1–12.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
306
