Systematic Evaluation of Probabilistic k-Anonymity for Privacy

Preserving Micro-data Publishing and Analysis

Navoda Senavirathne

and Vicenc¸ Torra

School of Informatics, University of Sk

ovde, Sweden

Department of Computer Science, University of Ume

a, Sweden

Keywords:

Data Privacy, Anonymization, Statistical Disclosure Control, Privacy Preserving Machine Learning.

Abstract:

In the light of stringent privacy laws, data anonymization not only supports privacy preserving data publica-

tion (PPDP) but also improves the ﬂexibility of micro-data analysis. Machine learning (ML) is widely used

for personal data analysis in the present day thus, it is paramount to understand how to effectively use data

anonymization in the ML context. In this work, we introduce an anonymization framework based on the

notion of “probabilistic k-anonymity” that can be applied with respect to mixed datasets while addressing

the challenges brought forward by the existing syntactic privacy models in the context of ML. Through sys-

tematic empirical evaluation, we show that the proposed approach can effectively limit the disclosure risk in

micro-data publishing while maintaining a high utility for the ML models induced from the anonymized data.

1 INTRODUCTION

Data anonymization facilitates Privacy Preserving

Data Publishing (PPDP) which allows the data con-

trollers to share the data publicly or with speciﬁc third

parties with minimal privacy implications. In data

anonymization, the underlying micro-data (personal

data) are irrecoverably transformed so that the risk

of re-identifying the individuals (identity disclosure)

is minimized along with the risk of inferring their

sensitive characteristics (attribute disclosure). Data

anonymization not only supports PPDP but it also in-

troduces more ﬂexibility into micro-data processing

and analysis in the light of new privacy laws. Ac-

cording to recital 26 of the General Data Protection

Regulation (GDPR), the data protection principles do

not apply to anonymized data. To achieve anonymiza-

tion under GDPR, re-identiﬁcation (singling out) of

an individual must be impossible under all the means

reasonably likely to be used either by the data con-

troller or by any other party directly or indirectly.

Once the data are anonymized, they are allowed to be

freely used, shared and monetized without the usual

restrictions apply to the raw micro-data. Hence, by

anonymizing the micro-data an organization can earn

numerous advantages such as a) disclosure risks mini-

mization, b) avoiding GDPR compliance risks and, c)

improving the ﬂexibility of data publishing and anal-

ysis. Due to these advantages anonymization seems

to be a sensible approach for handling micro-data.

Anonymized data are then subject to further analysis

in order to facilitate reporting, knowledge extraction

and/ or decision making.

In the present day, ML is employed in a wide vari-

ety of domains where micro-data are used for training

the ML models. Moreover, in recent years there has

been numerous research highlighting the privacy vul-

nerabilities of ML models trained on micro-data such

as membership inference, attribute inference etc. (Al-

Rubaie and Chang, 2019). As a mitigating strategy

for privacy leakage via ML models, differential pri-

vacy (DP) based ML algorithms are proposed in the

literature (Ji et al., 2014). They are aimed at limit-

ing the effect of training data on the ﬁnal ML model

via injecting noise into the training process thus mini-

mizing leakage of sensitive information. Even though

DP is widely used to achieve privacy preserving ML

(PPML), it has a signiﬁcant drawback apart from the

conventional challenges of implementing DP; such as

utility loss due to noise injection, the complexity of

estimating function sensitivity or ambiguity in decid-

ing on privacy parameter (ε). That is differentially

private ML models are assumed to be trained on the

original micro-data thus requiring the data controllers

to adhere to the data protection principles introduced

in GDPR which limit the ﬂexibility of further process-

ing of micro-data (i.e., limitation on data retention and

purpose of processing, the requirement for data in-

Senavirathne, N. and Torra, V.

Systematic Evaluation of Probabilistic k-Anonymity for Privacy Preserving Micro-data Publishing and Analysis.

DOI: 10.5220/0010560703070320

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 307-320

ISBN: 978-989-758-524-1

307

tegrity and accuracy followed by transparency in data

collection and accountability). On the other hand, if

the underlying training data are already anonymized

they are no longer considered as personal data thus

providing data controllers and analysts more ﬂexibil-

ity. Motivated by the above discussed advantages of

data anonymization, it is plausible that the data con-

trollers anonymize the data before publishing them

for any data analysis task.

The ﬁeld of statistical disclosure control

(SDC) has introduced different privacy models

and anonymization algorithms to support PPDP.

k-Anonymity (Samarati, 2001) is one of the most

widely used syntactic privacy models which ensures

record indistinguishability within a set of k records as

far as their quasi-identiﬁer attributes (QIDs) are con-

cerned thus minimizing the risk of re-identiﬁcation.

QIDs are a subset of attributes that can be used to

re-identify the individuals in a published dataset

uniquely, e.g., it is shown that simple demographic

attributes such as birthday, zip code and, gender

can be used together to re-identify about 87% of

the US population (Sweeney, 2000). k-Anonymity

relies on reducing the granularity of the QIDs to

satisfy the indistinguishability requirement. Data

generalization and suppression techniques are used

for categorical QIDs whereas, microaggregation or

rounding are used for numerical attributes to achieve

k-anonymity (Sweeney, 2002) (Domingo-Ferrer and

Mateo-Sanz, 2002). Moreover, concerning categor-

ical data generalization, it is always not possible

to obtain semantically meaningful categories for

all the QIDs. Nevertheless, most of the real-world

datasets contain both numerical and categorical QIDs

(i.e., mixed datasets) thus necessitating us to use a

combination of the above techniques for better data

utility (e.g, use microaggregation on numerical data

and generalization on categorical data) which makes

the anonymization process tedious. According to

Aggarwal (Aggarwal, 2005) when the number of

QIDs is large, most of the attribute values have to be

suppressed in order to satisfy k-anonymity conditions

which degrade the data utility signiﬁcantly. Utility

loss of data caused by anonymization negatively

impacts any analysis done on the anonymized data

thereafter.

Since the k-Anonymity based privacy models are

mainly focused on PPDP, they bring up unforeseen

challenges when used in the context of ML where

the ML models are induced from anonymized train-

ing data. This is in addition to the utility loss encoun-

tered by the ML models trained on the anonymized

data. For example, k-Anonymity based privacy mod-

els make structural changes to QID attributes by the

means of data suppression and generalization when it

is applied to the categorical data. This brings up the

below mentioned practical challenges as explained by

(Senavirathne and Torra, 2020).

• Data insufﬁciency due to suppression - Due to

data suppression a given ML algorithm might not

have enough data to learn a meaningful pattern.

Therefore, we may need to employ data imputa-

tion at the data preprocessing phase of the ML

pipeline to approximate these suppressed values.

This could intensify the accuracy loss of the ML

models trained on anonymized data.

• Previously unseen attributes values due to gener-

alization - Feature vectors pass into the deployed

ML models must have the same attribute domains

as the training data. However, when data gen-

eralization is used, it changes the attribute do-

mains by replacing the existing values with new

values from the top of the generalization hierar-

chy. Hence, anonymized training data are de-

prived of some attribute values that exist in the

general population. At the inference phase of the

ML pipeline, if a user submits a feature vector

containing previously unseen attribute values, the

ML model will fail to process that input. To ad-

dress this issue the ML model owners have to use

an API to transform user’s raw data into the gen-

eralized format required by the ML model.

Addressing the above mentioned challenges re-

quire additional efforts in the ML process without any

guarantee on model utility improvement. It is also

shown that despite the distortion introduced to the

underlying data, k-anonymity still suffers from pri-

vacy vulnerabilities. Thus some enhancements are

proposed to k-anonymity. Out of them the most

widely known methods are l-diversity (Machanava-

jjhala et al., 2006) and t-closeness (Li et al., 2007).

Even though these methods provide better privacy

preservation for PPDP they result in a higher data util-

ity loss and the above discussed complexities with re-

spect to mixed data, suppressed data and generalized

data persist. Therefore, the standard k-anonymity

based privacy models are not amenable in the con-

text of ML especially if the underlying data contains

categorical QIDs. The main reason for the above dis-

cussed complexities of standard k-anonymity based

privacy models can be attributed to the requirement

of maintaining record level truthfulness for PPDP. In

order to satisfy this, data are transformed with truth-

ful methods such as generalization and suppression

that reduce the precision of the data but not their ac-

curacy. However, when anonymized data are used for

training the supervised ML models (i.e., classiﬁers)

SECRYPT 2021 - 18th International Conference on Security and Cryptography

308

the record level truthfulness does not play a signiﬁ-

cant role compared to preserving the relationships be-

tween the features and the class attribute.

The above discussion highlights that an

anonymization approach that can be easily ap-

plicable for mixed data sets, which does not alter

the attribute domain or cause data suppression is

amenable in the ML context compared to standard

k-anonymity or its variants. As a solution, we turn

towards the notion of “probabilistic k-anonymity”

introduced in Soria-Comas and Domingo-Ferrer

(Soria-Comas and Domingo-Ferrer, 2012) which re-

laxes the indistinguishability requirement of standard

k-anonymity while guaranteeing the same level of

disclosure risk. A generic framework is introduced

in this work for achieving probabilistic k-anonymity

concerning numerical data. Unlike the standard k-

anonymity, here the indistinguishability requirement

is achieved via performing data swapping within the

homogeneous data partitions (equivalence classes)

of size k. Thus for any given record, its original

QID values are dispersed within a group of similar

records (with respect to QIDs) of size k leading to

uncertainty in record re-identiﬁcation. Nevertheless,

similar to the standard k-anonymity this also limits

the probability of re-identiﬁcation at most to

. Since

this approach does not rely on data suppression and/

or generalization it eliminates the aforementioned

challenges when adopting into ML context.

In the initial work, it is shown that probabilistic

k-anonymity results in better data utility compared to

standard k-anonymity. However, these results are lim-

ited to the context of numerical data and no proper

approach is presented on how data swapping is car-

ried out in order to achieve probabilistic k-anonymity.

Most importantly, no analysis has been carried out on

how probabilistic k-anonymity would impact disclo-

sure. Nevertheless, data utility evaluation is limited to

measuring generic utility losses but no work has been

done on its impact when the anonymized data are used

for data analysis purposes (i.e. ML). Our contribution

in this paper is mainly threefold. First, we present

a framework for probabilistic k-anonymity extending

it to mixed datasets based on data permutation. Here,

we discuss different distance measures appropriate for

mixed data in order to generate the homogeneous data

partitions for k-anonymity. Secondly, we carry out

a comprehensive, empirical evaluation on disclosure

risk and data utility with respect to PPDP. Then, we

extend the analysis with respect to ML based classi-

ﬁcation of such data focusing on the impact on the

model utility. Finally, we comparatively evaluate our

approach with the existing work.

The rest of the paper is organized in the follow-

ing way. In Section 2 we discuss preliminaries of

data anonymization followed by Section 3 detailing

the methodology for probabilistic k-anonymity and

determination of QIDs. Empirical evaluation and re-

sults are presented in Section 4. Section 5 concludes

the paper with some ﬁnal remarks.

2 RELATED WORK

Zhang et al. (Zhang et al., 2007) proposed the notion

of (k, e)-anonymity, a permutation based approach

to deal with numerical sensitive attributes. Here, the

data are partitioned into groups containing at least k

different sensitive values within a range of at least

e. Then the sensitive values are randomly shufﬂed

within each partition. However, this work is focused

on answering the aggregate queries about the sensi-

tive attribute and not about publishing privacy pre-

serving data. Re-identiﬁcation of individuals is still

possible on (k, e)-anonymized data as it does not

modify the QID values that can lead to disclosure.

An anonymization algorithm is proposed by (Eyu-

poglu et al., 2018) based on the concept of proba-

bilistic anonymity where the data are anonymized uti-

lizing a chaotic function for data perturbation. Then

the resulting anonymized data are used to train a set

of classiﬁers followed by evaluating the classiﬁca-

tion accuracy. The results show that the proposed

algorithm achieves a classiﬁcation accuracy compa-

rable with the benchmark model. Some other work

has used standard k-anonymity based privacy models

in order to anonymize the training data (Rodr

ıguez-

Hoyos et al., 2018), (Herranz et al., 2010), (Wimmer

and Powell, 2014). Despite the data distortion the

models induced from anonymized data has reported

comparable accuracies with the benchmark model.

However, non of these works have highlighted the

practical challenges of using standard k-anonymity in

the ML context or any analysis to understand how

comparable accuracies occur despite the utility loss

caused by anonymization. Fung et al. (Fung et al.,

2005) presents an algorithm for determining a gen-

eralized version of the data that aims at maintain-

ing classiﬁcation utility. The algorithm generalizes

a given dataset by specializing it iteratively starting

from the most general state. At each iteration, a gen-

eral value is assigned into a speciﬁc value for cate-

gorical attributes, or a given interval is split further

for continuous attributes based on information gain.

Iterative partitioning of the data is repeated until fur-

ther specialization leads to violation of the required

anonymity level. The results indicate comparable ac-

Systematic Evaluation of Probabilistic k-Anonymity for Privacy Preserving Micro-data Publishing and Analysis

309

curacy with the benchmark model even for higher

anonymity levels. This method can be applied for

mixed datasets given that a semantically meaning-

ful taxonomy tree can be generated for the under-

lying original dataset. Moreover, at the inference

phase transformation of the incoming data (feature

vectors) are required to map original values into gen-

eralized values. k-Anonymity based anonymization

methods ﬁrst generate homogeneous data partitions

(equivalence classes) of size k based on the QID val-

ues and then apply data generalization and/or suppres-

sion within them. Last et al. presented an anonymiza-

tion algorithm NSVDist (Non-homogeneous gener-

alization with Sensitive value Distribution) which is

based on non-homogeneous (k,l) anonymity where k

indicates the required minimal anonymity and l in-

dicates the diversity level for the sensitive attribute.

Here, generalization is carried out without clustering

the data ﬁrst. Unlike typical anonymization meth-

ods, generalization is applied to the sensitive attribute

which converts it into frequency distributions. How-

ever, standard ML algorithms cannot be applied to the

generalized tables obtained via this approach. There-

fore, a data reconstruction step is required before

training the classiﬁers. Privacy Preserving Data Min-

ing (PPDM) algorithms are also proposed in the liter-

ature which is aimed at anonymization of the data to

cater for the speciﬁc data mining goals to maximize

the accuracy of the data mining results. In this case,

PPDM algorithms are tailored to speciﬁc data mining

algorithms (i.e., decision trees) under the assumption

that the exact use of the anonymized data is known to

the data controllers beforehand (Agrawal and Srikant,

2000). Recent work has done an empirical anal-

ysis on how applying existing privacy models and

anonymization methods on the training data impacts

the utility and the privacy of the ML models (Senavi-

rathne and Torra, 2020). Privacy of the ML models

is determined based on the success ratio of the mem-

bership and attribute inference attacks that target the

ML models trained on the anonymized data. Based

on their empirical results they have shown that in or-

der to minimize the privacy risks in ML (speciﬁcally

membership inference), the existing data anonymiza-

tion techniques have to be applied with high privacy

levels that can cause a deterioration in the model util-

ity.

3 DATA ANONYMIZATION

The conventional requirement for data anonymiza-

tion is to support PPDP. This is a ubiquitous prac-

tice adopted in a wide variety of domains where per-

sonal data are modiﬁed using anonymization tech-

niques and then released publicly or to a speciﬁc third

party for further analysis (e.g., statistical agencies, re-

search institutes, private/ public organizations). Data

anonymization achieves privacy as it irrecoverably

transforms the data to minimize the identity and at-

tribute disclosure risks which are respectively aimed

at re-identifying individuals and learning previously

unknown, conﬁdential characteristics about them.

Based on the impact on privacy we can identify

four types of attributes in a given dataset. “Identi-

ﬁers” are the attributes that can be used to identify

the respective data subjects directly e.g., social se-

curity number, email address etc. “Quasi identiﬁers

(QIDs)” are indirect identiﬁers. When QIDs are con-

sidered as a composite key they can be used to iden-

tify some data subjects accurately. Usually, QIDs are

empirically decided by the domain experts who have

an extensive understanding of the data. “Conﬁden-

tial/ sensitive attributes” contain sensitive information

about data subjects such as health condition, salary,

sexual orientation etc. A conﬁdential attribute can

also be a QID. “Non conﬁdential attributes” do not

contain sensitive information thus no privacy impact

is noted. In the process of data anonymization, ﬁrst,

the identiﬁer attributes are removed from the data and

then the identiﬁed QIDs are modiﬁed using appropri-

ate anonymization techniques to produce a protected

dataset. In this case, the concepts of “anonymization

techniques” (masking methods/ SDC techniques) and

“privacy models” play a crucial role. Anonymiza-

tion techniques direct how to transform the origi-

nal data into a protected version. In contrast, a pri-

vacy model presents a speciﬁc condition that, if satis-

ﬁed guarantees a degree of privacy that keeps disclo-

sure risk under control. Both of these concepts are

parametrized and allow the data controllers to tune

the degree of privacy that indicates how much disclo-

sure risk is acceptable. There is a synergy between

anonymization techniques and privacy models. That

is anonymization techniques are used to achieve spe-

ciﬁc privacy models as they determine how the orig-

inal data should be transformed. The privacy model

k-anonymity (Samarati, 2001) limits the risk of re-

identiﬁcation by ensuring that for a given record there

exist at least k − 1 records that share identical values

for QIDs.

Deﬁnition 1. (k-Anonymity) A micro-data set T

said to satisfy k-anonymity if, for each record t ∈ T

there are at least k − 1 other records sharing the same

values for all the QIDs.

Such k records are known as an equivalence class.

k-Anonymity decreases the probability of a success-

ful record linkage based on any subset of QID to be

SECRYPT 2021 - 18th International Conference on Security and Cryptography

310

at most 1/k. k-Anonymity can effectively mitigate

identity disclosure as it makes a given data record

indistinguishable among k − 1 other records with re-

spect to QID values. However, attribute disclosure

is possible on k-anonymized data if the values for

the sensitive attribute are the same or very similar

within an equivalence class. In that case, the ad-

versary can infer the sensitive attribute value with-

out prior re-identiﬁcation. These are known as homo-

geneity attacks and similarity attacks respectively. In

order to avoid the vulnerabilities in k-anonymity some

enhancements are proposed. Out of them the most

widely known methods are l-diversity (Machanava-

jjhala et al., 2006) and t-closeness (Li et al., 2007).

However, these models are often criticized for their

unrealistic assumptions on the sensitive attribute dis-

tribution and utility loss. Moreover, l-diversity is also

vulnerable to adversarial attacks aimed at learning the

sensitive attribute values like similarity attack, back-

ground knowledge attack and skewness attack (Li

et al., 2007).

With respect to the above discussed k-anonymity

based privacy models, the generation of equivalence

classes makes data records indistinguishable among

k records thus limiting the risk of identity disclo-

sure. However, due to equivalence classes, it becomes

easier for an adversary to ﬁlter out the exact set of

records (i.e., the particular equivalence class) that cor-

responds to the data record at the adversary’s hand.

Hence, group identiﬁcation makes a k-anonymized

dataset vulnerable to attribute disclosure (i.e., through

homogeneity attack, similarity attack, skewness at-

tack etc.). Whereas, t-closeness is resilient to such

attacks at the expense of data utility. This raises

the requirement for privacy models focused on im-

proving adversary’s uncertainty in correctly identify-

ing the groups (i.e., minimizing attribute disclosure)

while maintaining record indistinguishability among

a group of records (i.e., minimizing identity disclo-

sure). Therefore, a privacy model becomes more

preferable if it introduces uncertainty in both group

identiﬁcation and record re-identiﬁcation thus mini-

mizing the overall risk of disclosure. These objec-

tives can be achieved by introducing randomness into

the privacy model while maintaining a high degree of

symmetry within the equivalence classes. By deﬁ-

nition, a probabilistic approach for k-anonymity can

address these requirements. This notion is referred

to as probabilistic k-anonymity and deﬁned as below

(Oganian and Domingo-Ferrer, 2017) (Soria-Comas

and Domingo-Ferrer, 2012).

Deﬁnition 2. (Probabilistic k-Anonymity) A pub-

lished data set T

is said to satisfy probabilistic k-

anonymity if, for any non-anonymous external data

set E, the probability that an adversary with the

knowledge of T

, E and the anonymization mecha-

nism M correctly links any record in E to its corre-

sponding record (if any) in T

is at most 1/k.

Standard k-anonymity limits the probability of

re-identiﬁcation at most to

by ensuring for each

record in T

, there exist at least k − 1 other records

sharing the same values for all the QIDs. On the

other hand, the concept of probabilistic k-anonymity

relaxes the indistinguishability requirement of stan-

dard k-anonymity and only requires that the probabil-

ity of re-identiﬁcation be the same as in standard k-

anonymity. In the case of probabilistic k-anonymity,

indistinguishably is achieved via swapping of the at-

tribute values within the equivalence classes of size k

thus creating uncertainty for the adversary in the re-

identiﬁcation process. Even though the deﬁnitions of

these two privacy models seem to be different from

each other at a glance, they enforce the same limit on

the probability of re-identiﬁcation (i.e.,

First, from the point of view of privacy, not

only probabilistic k-anonymity limits the risk of re-

identiﬁcation/ identity disclosure, it effectively low-

ers the risk of attribute disclosure as exact group/

equivalence class identiﬁcation is made difﬁcult via

data swapping. With respect to the utility of the

anonymized data, probabilistic k-anonymity can pre-

serve the marginal distributions exactly when the en-

tire dataset is concerned in a univariate manner (at-

tribute wise). Also, it permits us to maintain the vari-

ability in the anonymized data set as opposed to the

standard k-anonymity based methods which reduce

the variability via generalization, suppression and/ or

aggregation of data that leads to high utility loss (Oga-

nian and Domingo-Ferrer, 2017). Moreover, when

the number of selected QIDs are high (e.g., when all

the attributes are considered as QIDs) it is shown that

standard k-anonymity based methods incur signiﬁcant

utility loss (Aggarwal, 2005). On the other hand,

probabilistic k-anonymity distorts the multivariate re-

lationships in the data (i.e., correlations, mutual infor-

mation etc.). Also, it adversely impacts the analysis

done on data sub-domains (e.g., computation of mean

salary with respect to a speciﬁc job). Therefore, par-

titioning a given dataset based on their homogeneity

before applying data swapping is important as it leads

to reduce the above mentioned negative impact on the

data utility since the attribute values are now shufﬂed

in a controlled setting. Apart from the above issues,

the possibility of unusual combinations of data may

occur due to data swapping. To overcome this, data

swapping can be carried out in a multivariate manner

where ﬁrst we group several QIDs into a single block

and then swapping is applied to each block separately

Systematic Evaluation of Probabilistic k-Anonymity for Privacy Preserving Micro-data Publishing and Analysis

311

instead of targeting a single QID at a time.

Apart from the aforementioned privacy and util-

ity related advantages, probabilistic k-anonymity has

many favourable characteristics when applied in the

ML context compared to the other privacy models.

All k-anonymity based syntactic privacy models (i.e.,

standard k-anonymity, l-diversity, t-closeness etc.)

bring up the challenges discussed in Section 1 with

respect to data suppression and generalization. Some

other data anonymization methods, as discussed in

Section 2 either publish anonymized data tailored to

speciﬁc ML algorithms or require data regeneration in

order to transform them into a ﬂexible format before

using them for model training. As probabilistic k-

anonymity is a general framework focused on control-

ling the maximum re-identiﬁcation probability it pro-

vides data controllers more ﬂexibility in selecting the

underlying data transformation techniques. There-

fore, data anonymized via probabilistic k-anonymity

can be directly used for model training and infer-

ence without any additional requirement for data pre-

processing.

4 METHODOLOGY

In this Section, we extend the initial work of

Soria-Comas and Domingo-Ferrer (Soria-Comas and

Domingo-Ferrer, 2012) with respect to mixed data

and present an algorithm for achieving probabilistic

k-anonymity based on data permutation. The pro-

posed method consists of four main steps as a) com-

puting pairwise dissimilarity among the data records,

b) data partitioning based on QIDs, c) grouping QIDs

and, d) data permutation. First, we introduce some

basic notions as below. Let T = {t

,. ..,t

} be a

dataset with attributes A

,. .., A

. Q denotes the set

of all attributes that are considered as QIDs whereas

S represents the sensitive attribute. Privacy parameter

or the minimum size of each data partition is indicated

by k whereas C = {c

,. .., c

} represents data parti-

tions. Dissimilarity measure d(.) is used to measure

the pairwise dissimilarity between given two records

and ﬁnally, a pair-wise dissimilarity matrix (M) is

generated.

• Computing Pairwise Dissimilarity: Homoge-

neous data partitions (clusters of size k) are cre-

ated based on record similarity (or dissimilarity).

There exist many similarity measures that can be

used to obtain a similarity score. The choice of

these measures depends on the data type. For

example, in numerical data context Euclidean,

Mahalanobi’s, Manhattan distances can be used.

Whereas, for ordinal and nominal data, measures

such as Jaccard’s coefﬁcient or Hamming dis-

tance are suitable. In their work, Soria-Comas and

Domingo-Ferrer have limited their analysis to nu-

merical data and used MDAV-microaggregation

(Domingo-Ferrer and Mateo-Sanz, 2002) to cre-

ate data clusters of size k which is based on

the aforementioned numerical distance measures.

However, in the real world, most datasets are a

mixture of data types hence it is required to use a

distance measure appropriate to mixed data. Here,

we use two distance measures proposed for mixed

data clustering as mentioned below.

Gower dissimilarity - Gower distance (Gower,

1971) is designed to measure the dissimilarity be-

tween two data points of mixed data types as de-

picted below.

(

) =

∑

l=1

∑

l=1

. (1)

Here, w

indicates the weight for variable l be-

tween observations i and j, whereas d

indicates

the dissimilarity between instance i and j on at-

tribute l. Categorical and numerical attributes are

considered separately when calculating d

. For

categorical data (nominal or binary) distance is

measured using Hamming distance where d

set to 0 when attribute values of i and j are equal

and 1 when they are not. For numerical data the

scaled absolute difference is used that limits the

attribute range between 0 and 1. When comput-

ing the weights w

is set to 1 for non-missing

variables and 0 otherwise.

Ahmad-Dey dissimilarity - In the above case,

Hamming distance is used to evaluate categorical

data which is not very accurate for multi-valued

categorical attributes. Hence, Ahmad and Dey

(Ahmad and Dey, 2011) presented a dissimilarity

measure for mixed data that computes a dissim-

ilarity between categorical attribute values based

on their co-occurrence with the values of other at-

tributes as mentioned below.

∑

r=1

−t

)

∑

s=1

δ(t

). (2)

Here, A

and A

respectively represents numerical

and categorical attribute sets. The ﬁrst term repre-

sents the squared Euclidean distance between r

numerical attribute value between instance t

and

. The second term depicts the dissimilarity of the

categorical attribute value between instances t

and t

. δ(.,.) is used for measuring the dissimi-

larity between categorical data. Let A

denote a

SECRYPT 2021 - 18th International Conference on Security and Cryptography

312

categorical attribute which contains two values as

a and b. To measure the dissimilarity between a

and b, this method considers the overall distribu-

tion of a and b in the data set along with their co-

occurrence with values of other attributes. Let A

denote another categorical variable. Let ω denote

a subset of values of A

and ω the complemen-

tary set. P(ω|a) denote the conditional probabil-

ity that an object having value a for A

, has a value

in ω for A

. Similarly, P(ω|b) denotes the condi-

tional probability that an object having value b for

, has value in ω for A

. The dissimilarity be-

tween values a and b for A

concerning A

is given

by δ(a, b) = P(ω|a) + P(ω|b) − 1, where ω is the

subset of values of A

that maximizes the quan-

tity P(ω|a) + P(ω|b). The dissimilarity between

a and b is computed with respect to all the other

attributes. The average value of dissimilarity is

the distance ω(a,b) between a and b. The signif-

icance of the rth numeric attributes are depicted

by w

. To compute w

, the numerical attributes

are ﬁrst discretized, followed by computing the

distances between every pair of discretized values

using the same method. Finally the average val-

ues are taken as the signiﬁcance of the attributes.

Interested readers are referred to the original pub-

lication (Ahmad and Dey, 2011) for more infor-

mation.

At the end of this step, we generate a dissimilar-

ity matrix M containing the pairwise dissimilari-

ties between all the data instances with respect to

QIDs (separately based on equation 1 and 2).

• Cardinality Constrained Data Partitioning: In

this step data partitioning (clustering) is carried

out based on the dissimilarity matrix M such that

each data partition contains at least k data in-

stances. To generate cardinality constrained clus-

ters we use MDAV-Microaggregation (Maximum

Distance to Average Vector) (Domingo-Ferrer and

Mateo-Sanz, 2002). Typically, microaggregation

is an SDC method for numerical data protection

where the data are ﬁrst partitioned into micro-

clusters of size k followed by replacing them with

each micro cluster’s centroid value. However, our

focus here is only on the data partitioning part

thus we update the MDAV-microaggregation al-

gorithm to generate micro-clusters of size k on the

dissimilarity matrix M and to return the clusters

which contain the corresponding record indices.

The output of this step is a nested list (C) that con-

tains micro-clusters each comprises of the record

indices that are clustered together based on their

similarity as shown by 1.

Algorithm 1: MDAV-microaggregation for clustering

records based on their similarity.

Input: M , k

Output: C

while 2k or more rows in M remains do

Randomly select a row q from M

Find the furthest point p from q

Select k −1 nearest points to p including

p and form micro-cluster c

by fetching

their index values

For all points in c

remove corresponding

rows and columns from M

if there are k to 2k − 1 points left then

Form a new micro-cluster c

and fetch

their respective index values from M

else

Assign the index values of remaining

records in M to the last micro-cluster

generated

Append generated micro-cluster/s to form

nested list C

• Generate QIDs Groups: As explained in Sec-

tion 3 applying data anonymization in a multivari-

ate manner improves the utility of the anonymized

data. This is achieved by grouping QIDs into sev-

eral blocks before applying anonymization. In

this case, we block the QIDs based on their associ-

ation with the sensitive attribute (S) such that each

block contains at least 2 QID attributes. In or-

der to estimate the association, we use Mutual In-

formation (MI). MI measures the association be-

tween two random variables capturing both lin-

ear and non-linear dependencies. MI between two

discrete random variables X and Y can be deﬁned

as below.

MI(X;Y ) = H(X) − H(X|Y ) = H(Y ) − H(Y |X )

(3)

Here, H(X), H(Y ) are the entropy or the uncer-

tainty level of the respective variables that can

be measured using H(X) = −

∑

x∈X

p(x) log p(x).

Whereas, H(X|Y ) is the conditional entropy that

indicates the amount of uncertainty left in X after

observing Y . In Equation 3, the ﬁrst term explains

the entropy of X before Y is known, while the sec-

ond term indicates the entropy after Y is known.

Hence, mutual information is the amount of en-

tropy reduced in X by knowing Y . Therefore, if X

and Y are independent of each other the amount

of MI is 0 whereas, MI is greater than 0 when X

and Y are related. For a given dataset T we quan-

tify the MI between the features and the identiﬁed

Systematic Evaluation of Probabilistic k-Anonymity for Privacy Preserving Micro-data Publishing and Analysis

313

S as MI

= MI(A

,S). MI

is the mutual infor-

mation vector that indicates the respective associ-

ation of each attribute with the S. Then we group

the QIDs such that attributes that have high MI are

blocked together and each block contains at least

2 attributes.

• Data Permutation. Once the data records are

clustered based on their similarity the next step

is to apply within cluster data permutation in or-

der to achieve probabilistic k-anonymity. As ex-

plained previously C contains micro-clusters of

record indices. For each c ∈ C we extract the

records from T as T [c] and then randomly per-

mute the order of the QID values followed by up-

dating the permuted values in the original dataset

T .

Algorithm 2 summarizes the above mentioned

process for generating probabilistically anonymized

data.

Algorithm 2: Probabilistic k-Anonymity.

Input: T , Q, S, k

Output: Anonymized dataset : T

QID

d f

:= T [Q]

M := Generate pairwise dissimilarity for

QID

d f

// Algorithm 1

C := Generate clusters of size k over M

P := Generate QID blocks

:=T

for c ∈ C do

for p ∈ P do

d f

:= T [c, p] // Extract data

chunk given their indices(c)

and attributes (in block p )

d f

:= EC

d f

while EC

d f

== PM

d f

:= Permute (EC

d f

)

[c, p] := PM

d f

5 EXPERIMENTAL EVALUATION

In this Section, we use six publicly available datasets

for evaluating the anonymized data under the follow-

ing criteria, a) data utility, b) disclosure risk and,

c) impact on ML utility. UCI Contraceptive Meth-

ods (1473x9), UCI Mammographic (961x6), UCI

Adult (48,842x14), UCI German Credit (863x25),

UCI Heart disease (303x14) and, UCI Cardiotocog-

raphy (1,914x23) datasets are used for experimenta-

tion where the class attribute of each dataset is con-

sidered as the sensitive attribute(S) (the number of

instances and the attributes are mentioned within the

parentheses). Selected sensitive attributes are respec-

tively “contraceptive method used”, “severity”, “in-

come status, “credit rating”, “presence of heart dis-

ease” and, “presence of cardiac arrhythmia”. Respec-

tively UCI Cardiotocography and UCI Contraceptive

Methods datasets contain 10 and 3 unique values for

the sensitive attributes whereas other datasets have

binary sensitive attributes. To avoid the anonymiza-

tion process being solely impacted by chance, each

anonymized dataset is generated in ﬁve trials and the

results are averaged across them.

To evaluate how differing the number of QIDs im-

pact the data utility and disclosure risk, we have used

two approaches for QID selection.

• Part QID− Only a subset of attributes are selected

as QIDs using ARX anonymization tool (Prasser

et al., 2014) which leads to more than 99% of re-

identiﬁcation of the records based uniqueness and

separation ratios.

• Full QID− All the attributes are considered as

QIDs except the sensitive attribute S.

For each of the above mentioned approaches,

probabilistic k-anonymity is applied with four pri-

vacy/ anonymization levels (k as 5, 50, 100 and 200).

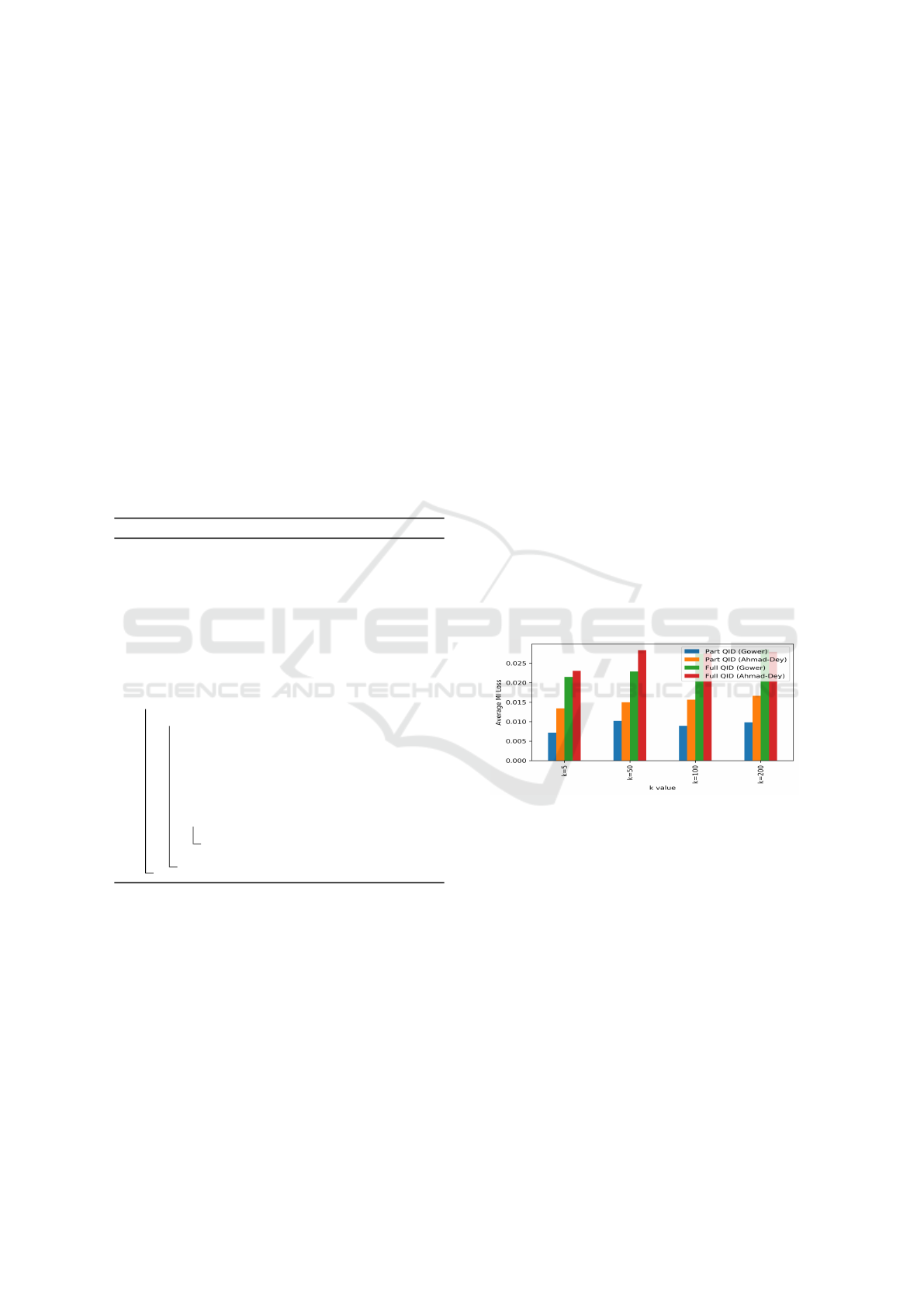
Figure 1: Average loss of mutual information.

5.1 Utility Loss

A generic, data type independent, utility loss mea-

sure is used to estimate the utility of the probabilisti-

cally k-anonymized data. The measure is based on the

concept of mutual information (MI). As explained in

(Domingo-Ferrer and Rebollo-Monedero, 2009), mu-

tual information bears some resemblance to the corre-

lation matrix that is used as a generic utility loss mea-

sure in SDC literature in the form of the relative dis-

crepancy between correlations. Application of prob-

abilistic k-anonymity alters the statistical dependence

between the attributes thus mutual information can be

used to quantify this distortion in terms of loss of mu-

tual information. For a given dataset, ﬁrst, the mutual

information matrix is computed which indicates the

SECRYPT 2021 - 18th International Conference on Security and Cryptography

314

association among the attributes. Then the average

mutual information vector is computed for each at-

tribute A

.. .A

respectively as MI

vec

= MI

.. .MI

If the MI

vec

of the original dataset is termed as MI

and that of the anonymized dataset is termed as MI

the relative loss of mutual information is computed

as, MI loss =

∑

− MI

Fig 1 illustrates the probabilistically k-

anonymized data under the previously mentioned

dissimilarity measures (i.e., Gower, Ahmad-Dey)

and QID selection methods (Part QID, Full QID).

The results are averaged across the selected six UCI

datasets. Here, we can observe that increasing the

anonymization level (k) and/or number of QIDs

increase the loss of MI. This can be attributed to

the higher distortion caused by data permutation

within larger data partitions which leads to higher

privacy. Moreover, comparing to tuning the privacy

parameter (k) into a higher value, selecting a higher

number of QIDs has a more adverse impact on data

utility. Therefore, data controllers have to be more

economical when selecting QIDs for anonymization.

When data partitioning is done based on Gower

dissimilarity the relative loss of MI is marginally

lower than that of Ahmad-Dey dissimilarity.

5.2 Disclosure Risk

The purpose of disclosure risk limitation is to min-

imize the amount of information available in an

anonymized dataset with respect to individuals lead-

ing to identity and/ or attribute disclosure. In the

case of probabilistic k-anonymity, an adversary would

not be able to positively identify which anonymized

records correspond to which original records exactly.

In other words, it is impossible for an adversary to

be conﬁdent of having identiﬁed an individual in the

anonymized dataset as every record now could be al-

tered. Therefore, the risk of identity disclosure is min-

imal under probabilistic k-anonymity except in the

presence of unique values in QIDs. For example, if a

particular record carries unique values for all or most

of the QIDs, even if those values are dispersed among

multiple records (via permutation) an adversary can

still draw a conclusion of its mere existence in the

anonymized dataset (without an exact record linkage).

One of the biggest limitations of standard k-

anonymity is the vulnerability towards attribute dis-

closure. In standard k-anonymity, risk of attribute dis-

closure occurs due to the possibility of exact equiva-

lence class identiﬁcation followed by the existence of

same (or similar) sensitive attribute values within the

given equivalence classes (refer Section 3 for more in-

formation). In this case, an adversary can obtain the

sensitive attribute values of a given record by observa-

tion without using any sophisticated inference meth-

ods. We use Adult and Cardiotocography datasets

to showcase this risk. On the Adult dataset, the

sensitive attribute has two unique values whereas on

the Cardiotocography dataset ten unique values are

available. When standard k-anonymity is applied on

the Adult dataset, respectively 0.72%, 0.6%, 0.52%,

0.47%, 0.11%, 0.06%, and 0.002% records belong to

equivalence classes where the same sensitive attribute

value is present when k value differs as 2, 3, 4, 5,

50, 100 and 200. On the Cardiotocography dataset

for the aforementioned k values percentage of records

belong to the equivalence classes with the same sensi-

tive attribute value changes as 0.45%, 0.27%, 0.24%,

0.027%, 0%, 0%, 0%. This shows that small privacy

parameter values (k) and low diversity in sensitive at-

tributes could result in high attribute disclosure risk

under standard k-anonymity.

Even though exact equivalence class identiﬁca-

tion is not possible with high certainty in probabilis-

tically k-anonymized data attribute disclosure is still

possible. However, by deﬁnition attribute disclosure

is more challenging under probabilistic k-anonymity

compared to standard k-anonymity. Hence, to assess

this risk we adopt three inference methods namely, a)

distance based record linkage b) probabilistic record

linkage and, c) ML based inference.

In this case, we consider the scenario where an ad-

versary has access to an external dataset E that com-

prises un-anonymized QID data and E’s anonymized

version T

. Here, we assume that E contains person-

ally identiﬁable information (unmodiﬁed QIDs that

can lead to speciﬁc individuals) without the sensi-

tive attribute/s. Whereas, T

contains the sensitive at-

tribute values along with the modiﬁed (anonymized)

QIDs. Thus, by using a mechanism to join E and

on their QIDs adversary can infer the sensitive at-

tribute value for the interested individuals in E. To

illustrate a sophisticated adversary with full access to

information, we assume E contains all the records in-

cluded in T

, prior to anonymization without the sen-

sitive attribute values (i.e., E = T \ SA).

Distance based Record Linkage. In this case, the

adversary uses record similarity to identify a poten-

tial link for a given record in E and infer the sensitive

attribute based on this. For a given record t

∈ E the

adversary computes the similarity to all the records

i...n

∈ T

. Then for t

∈ E ﬁnd the nearest neighbour

from T

based on the computed similarities and ex-

tract the sensitive attribute value. In this case, we have

used Gower dissimilarity for generating the distance

matrix as it incurs a lower utility loss compared to

Ahmad-Dey.

Systematic Evaluation of Probabilistic k-Anonymity for Privacy Preserving Micro-data Publishing and Analysis

315

Probabilistic Record Linkage. Probabilistic record

linkage (PRL) attempts to link two datasets when

there are inconsistencies between the records with re-

spect to the linking attributes. The goal of this record

linkage method is to establish whether a given pair

of records belong to the same entity or not. In this

case, probabilistic record linkage is carried out be-

tween E and T

on QID attributes. As probabilis-

tic k-anonymity permutes the QID values in T

now

there are inconsistencies between the majority of the

linking attributes. Thus even a record is inked, the

chances are high that it is merely a similar record

but the correct match. To illustrate this we gener-

ate a dataset T

. 50% of T

’s records are from T

and the rest is from a hold out dataset T

where

∩ T =

0. Then we used probabilistic record link-

age to identify links (based on reclin package on R)

where one-to-one linkage is enforced. Ideally, 50%

of the records taken from T

should have been cor-

rectly liked while the records taken from T

are not

linked. In other words, a high True Positive (TP)

count and a low False Positive (FP) count is ex-

pected. However, we noticed that probabilistic record

linkage results in a very high number of FPs with

respect to all the datasets. Thereby, reporting low

positive predictive value (PPV) computed as PPV =

T P

T P+FP

. The average of the reported PPV values is

0.49 ± 0.01 across all the UCI datasets for their prob-

abilistically k-anonymized counterparts. This result

indicates that probabilistic record linkage under prob-

abilistic k-anonymity does not yield meaningful re-

sults. Nevertheless, we can utilize the linked records

to infer the sensitive attribute values for records in E.

Once the records are linked between E and T

the

next step is to infer the sensitive attribute (S) value as

mentioned below. Assume record t

∈ E is linked with

∈ T

. Then value of S is inferred as E

[S] = T

[S].

ML based Inference. In this case, the adversary ﬁrst

trains a ML classiﬁer on T

in order to predict the sen-

sitive attribute of the original, un-anonymized dataset

E. Since it is assumed that E only contains QIDs,

the ML classiﬁers are trained only based on the QIDs

attributes of T

In this work, we have used the ran-

dom forest (RF) algorithm as the adversary’s choice to

train the ML model. The accuracy of the inferred SAs

is reported using the micro-averaged F1 score which

aggregates the contributions of all the classes.

The average AD risk under the aforementioned in-

ference methods are illustrated in Fig 2 when the un-

derlying micro-data are partitioned based on Gower

dissimilarity and only a subset of attributes are con-

sidered as QIDs (Part QID) following the typical

adversarial assumption in SDC where it is assumed

that the adversaries have access to only a subset

of attributes that can be effectively used for re-

identiﬁcation (i.e., QIDs). We term such adversaries

as partially informed adversaries (PIA). More pre-

cisely, in this case, the dataset E contains only a sub-

set of attributes (un-anonymized). The fraction of at-

tributes (QIDs) available in E concerning each dataset

is 0.23, 0.2, 0.44, 0.18, 0.42, 0.8 and, 0.35 respec-

tively for Heart, German Credit, Contraceptive Meth-

ods, Cardiotocography, Adult and, Mammographic

datasets. On each dataset, the attribute disclosure risk

(AD) is ﬁrst measured on the original, un-anonymized

dataset followed by an evaluation of the probabilisti-

cally k-anonymized data. The purpose of using the

original, un-anonymized dataset in the experimenta-

tion is purely to evaluate the effectiveness of the dif-

ferent attribute inference methods. With respect to all

the inference methods, it can be seen that AD accu-

racy is very high for original, un-anonymized data.

That is on average 0.92, 0.83 and, 0.98 for distance

based, ML based and, PRL based methods respec-

tively. Considering all the datasets it can be seen

that applying probabilistic k-anonymity has reduced

the risk of AD. For varying privacy levels (i.e., k=5,

50, 100, 200) on average, AD risk is reduced by

≈ 39.9 %, ≈ 25 % and ≈ 49 % respectively for for

distance based, ML based and, PRL based methods.

However, AD risk is not always monotonically re-

duced as we increase the privacy level k. For example,

Cardiotocography and Contraceptive datasets seem to

be more susceptible to increasing k values compared

to the other datasets which have binary sensitive at-

tributes (class attribute). However, datasets with bi-

nary class attributes have also shown a reduction of

AD approximately about 20% indicating that proba-

bilistic k-anonymity result in reducing AD risk effec-

tively.

Next, we summarize the results of AD risk when

all the attributes are treated as QIDs (Full QID). In

this case, we assume that the external dataset E, that

the adversary has access to, contains all the attributes

except for the sensitive attribute S. We term such

adversaries as fully informed adversaries (FIA). FIA

can be considered as a real threat since an adver-

sary would at least have the complete knowledge of

the data belong to his/her close contacts (i.e., fam-

ily, friends). Or with the excessive digital data col-

lection, the availability of such personal data is no

longer a far fetched assumption. Here, the dataset

E contains all the attributes (un-anonymized) and the

adversary exploits them to infer the correct sensi-

tive attribute value based on the aforementioned in-

ference methods. The AD risk reduction is ≈ 38 %

for distance based approach, ≈ 22 % for ML based

approach, ≈ 51 % for PRL based approach. These re-

SECRYPT 2021 - 18th International Conference on Security and Cryptography

316

(a) Distance Based (b) ML Based (c) PRL Based

Figure 2: Attribute disclosure risk under Gower distance and Part QID.

sults show that probabilistic k-anonymity can reduce

the AD risk successfully in the presence of strong

adversaries with a signiﬁcant amount of background

knowledge about the underlying data subjects. (Simi-

lar results are also noted for Ahmad-Dey dissimilarity.

They are not included here due to space limitations.)

The take away from these results is two-fold. First,

probabilistic k-anonymity can effectively reduce AD

risk. As explained earlier, AD is possible in standard

k-anonymity due to exact equivalence class identiﬁ-

cation which is no longer exists in probabilistic k-

anonymity. Even with sophisticated inference meth-

ods, fully informed adversaries AD risk remains low

when data are probabilistically k-anonymized. Sec-

ondly, probabilistic k-anonymity cannot completely

alleviate AD risk. As long as the data remains use-

ful there exists room for AD.

5.3 Impact on Machine Learning

In the beginning, we discussed why probabilistic k-

anonymity is an amenable approach in the context

of ML compared to the rest of the well-known pri-

vacy models used for data anonymization. In this

sub-section, we discuss the impact of training data

anonymization based on probabilistic k-anonymity

with respect to ML model utility.

Model Utility. Fig 3 depicts the F1 score when the

underlying training data are anonymized using prob-

abilistic k-anonymity. Here, we have used two QID

selection methods as Part QID and Full QID which

varies on the number of QIDs. As shown by the

results, increasing the number of anonymized QIDs

and the privacy levels (k) deteriorate the model accu-

racy gradually. Previously, we discussed how proba-

bilistic k-anonymity incurs utility loss in the data and

used the loss of MI to quantify it. Hence, it is intu-

itive that the ML models trained on the anonymized

data also face a loss of predictive power. Here, the

F1 score is measured on a holdout dataset (T

) ex-

tracted from the same population as T without any

overlapping. Multi Layer Perceptron (DNN), Logistic

Regression (LR), Support Vector Machines (SVM),

Decision Trees (DT) and Random Forest (RF) algo-

rithms are used in the experiments and the reported

accuracy values are averaged over them. For DNN a

three layer neural network is conﬁgured with 32 hid-

den units each with “relu” activation and “adam” op-

timizer.

However, we do not observe linearity in the accu-

racy loss as a response to the increasing number of

QIDs or privacy level. Further, in some cases, the

loss of model accuracy is almost negligible or even

slightly improved despite the utility loss caused by

anonymization. Concerning the different QID selec-

tion methods, the average F1 score loss varies from

0.12 ± 0.01 to 0.23 ± 0.05 under Gower dissimilar-

ity concerning Part QID and Full QID respectively.

With respect to Ahmad-Dey dissimilarity the average

F1 score loss changes as 0.15± 0.01 and 0.24 ±0.01.

In a closer inspection of the results, it can be seen that

binary classiﬁcation problems are less susceptible to

utility loss compared to the multi-class problems in

general. This is more prominent under Full QID ap-

proach for QID selection. As explained by Senavi-

rathne and Torra (Senavirathne and Torra, 2020) in

multi-class classiﬁcation, only a limited number of

records per class exist for the classiﬁcation algorithm

to learn a discriminative pattern. When anonymiza-

tion distorts the existing relationships in the data it be-

comes increasingly difﬁcult to learn an accurate pat-

tern. This explains the high accuracy loss in multi-

class cases. In order to improve the model accuracy

in multi-class cases, we can balance the class distri-

bution and/ or re-deﬁne the classiﬁcation problems to

have a limited number of classes when it is possible.

From the above results, it is conspicuous that the use

of probabilistically k-anonymized training data im-

pacts the classiﬁcation accuracy negatively. By opt-

ing lower privacy level (k) and/ or a smaller subset of

QIDs this negative impact can be lowered. However,

data controllers have to keep in mind that tuning for

more accuracy leads to high disclosure risk.

Comparative Analysis. In this Section, we com-

pare probabilistic k-anonymity with other commonly

used privacy models and comparatively evaluate their

impact on classiﬁcation utility with respect to Deep

Neural Networks (DNN) as they are being increas-

ingly used to solve complex ML problems. For the

evaluation, we use standard syntactic privacy mod-

Systematic Evaluation of Probabilistic k-Anonymity for Privacy Preserving Micro-data Publishing and Analysis

317

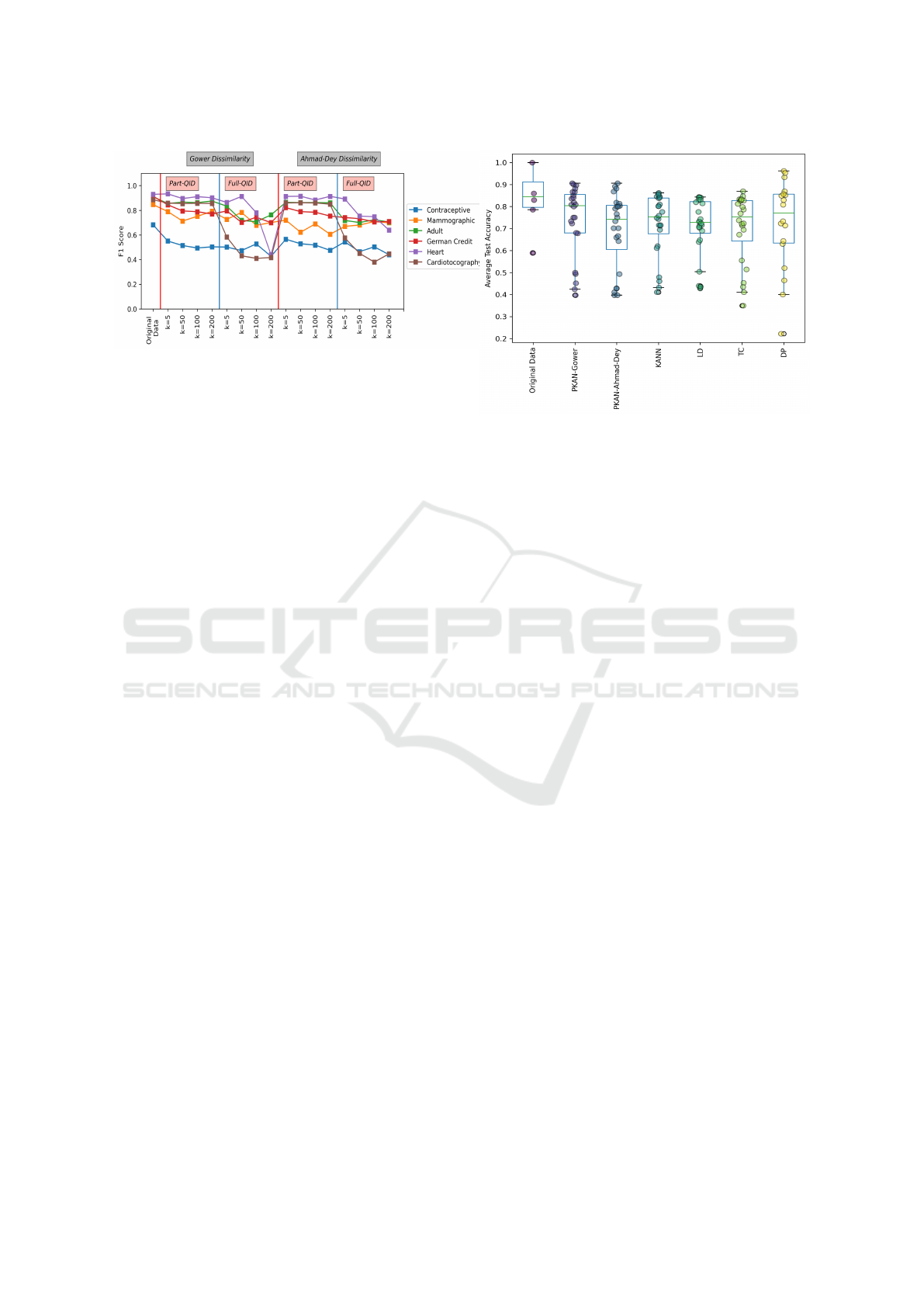
Figure 3: Average F1 Score.

els such as k-anonymity (KN), l-diversity (LD) and t-

closeness (TC). In this case, the anonymized data are

generated based on Mondrian anonymization algo-

rithm (LeFevre et al., 2006). As we discussed earlier,

learning based on differentially private (DP) ML algo-

rithms have become the standard practice for PPML.

Hence, we adopt DP DNN (Abadi et al., 2016) for the

comparative analysis as well.

As explained at the beginning, compared to prob-

abilistic k-anonymity (PKAN) the standard syntactic

privacy models require the support of data transfor-

mation APIs in the inference phase of ML as they al-

ter the attribute domain of the underlying data. DP

also faces a myriad of challenges including high util-

ity loss when applied to ML. However, amongst those

challenges having to maintain access to raw, sensi-

tive data in order to train the DP ML models greatly

hinders the ﬂexibility of sensitive data analysis (Re-

fer Section 1 for more details). Compared to these

methods probabilistic k-anonymity not only provides

straight forward implementation also provides high

ﬂexibility for sensitive data processing without risk-

ing compliance with GDPR.

Figure 4 showcases the test accuracy obtained

via each privacy model over aforementioned datasets

when only a subset of attributes are considered as

QIDs (Part QID). A one to one comparison be-

tween these privacy models is not very meaningful

as there are differences between how each privacy

model is implemented and what the privacy param-

eters mean in each case. However, our attempt here

is to understand if each of these privacy models is

implemented with acceptable privacy levels to gen-

erate anonymized data, how would it impact the clas-

siﬁcation accuracy of the ML models induced from

that? To realize this objective we train multiple ML

classiﬁers for each dataset with a variety of privacy

levels. For probabilistic k-anonymity and standard

k-anonymity privacy levels (k) are chosen as 5, 50,

100, and 200. For t-closeness privacy levels (t) are

chosen as 0.5, 0.3, 0.1, and 0.01. When generating

Figure 4: Comparative evaluation of test accuracies for

DNNs trained under different privacy models. Each marker

indicates a different dataset and a different privacy level.

l-diversity data for all the datasets with binary class

attributes l value is set to 2. For Contraceptive Meth-

ods dataset, l value is set to 2 and 3 respectively. For

the Cardiotocography dataset privacy parameter l is

set to 2, 3, 4, and 5 respectively. For training differ-

entially private ML classiﬁers privacy parameter ε is

chosen as 3, 1, 0.5, and 0.25 with δ = 1e − 5. Once

the ML classiﬁers are trained for each dataset and

privacy level, their test accuracies are obtained and

grouped over different privacy models to compara-

tively analyse their impact on ML utility. As depicted

in Figure 4 there is a loss of utility caused by applying

anonymization which is shown through low accuracy

compared to the benchmark model (model trained

on original data). Probabilistic k-anonymity imple-

mented with Gower distance shows a higher accuracy

compared to probabilistic k-anonymity implemented

with Ahmad-Dey distance, standard syntactic privacy

models (KAN, LD, TC) and DP. In conclusion, prob-

abilistic k-anonymity obtain a relatively high utility

for ML while providing the data controllers with the

previously discussed advantages such as high ﬂexibil-

ity for sensitive data analysis under GDPR, a means

for PPDP with low attribute disclosure risk and, an

easy adaptation into ML context without additional

data pre-processing or post-processing requirements.

6 CONCLUSION

In this work, we systematically show that proba-

bilistic k-anonymity can effectively address the chal-

lenges faced by standard privacy models in the con-

text of ML. Here, we have presented a framework

that consists of two algorithms for obtaining proba-

SECRYPT 2021 - 18th International Conference on Security and Cryptography

318

bilistically k-anonymized data in the context of mixed

datasets. Then an in-depth analysis is carried out

to evaluate the utility and privacy aspects of proba-

bilistic k-anonymity with respect to PPDP. Then we

trained a variety of ML classiﬁers on probabilistically

k-anonymized data and evaluated the model utility.

When applied with high privacy parameter levels(k)

or a high number of QIDs, probabilistic k-anonymity

has an adverse impact on ML utility. However, com-

pared to the other syntactic privacy models (i.e., k-

anonymity, l-diversity, t-closeness) probabilistic k-

anonymity has gained better ML utility. In conclu-

sion, probabilistic k-anonymity obtain relatively high

utility for ML while providing the data controllers

with numerous advantage such as high ﬂexibility for

sensitive data analysis under GDPR, a means for

PPDP with low attribute disclosure risk and, an easy

adaptation into ML context without additional data

pre-processing or post-processing requirements. In

future work, it can be explored whether these classi-

ﬁcation accuracies can be improved further via noise

correction and sample selection methods presented in

the ML literature when learning has to be carried out

on the noisy data.

ACKNOWLEDGMENT

This work is supported by Vetenskapsr

adet project:

”Disclosure risk and transparency in big data pri-

vacy”( VR 2016-03346 , 2017-2020 ).

REFERENCES

Abadi, M., Chu, A., Goodfellow, I., McMahan, H. B.,

Mironov, I., Talwar, K., and Zhang, L. (2016). Deep

learning with differential privacy. In Proceedings of

the 2016 ACM SIGSAC Conference on Computer and

Communications Security, pages 308–318. ACM.

Aggarwal, C. C. (2005). On k-anonymity and the curse

of dimensionality. In Proceedings of the 31st inter-

national conference on Very large data bases, pages

901–909. VLDB Endowment.

Agrawal, R. and Srikant, R. (2000). Privacy-preserving data

mining. In Proceedings of the 2000 ACM SIGMOD in-

ternational conference on Management of data, pages

439–450.

Ahmad, A. and Dey, L. (2011). A k-means type clustering

algorithm for subspace clustering of mixed numeric

and categorical datasets. Pattern Recognition Letters,

32(7):1062–1069.

Al-Rubaie, M. and Chang, J. M. (2019). Privacy-preserving

machine learning: Threats and solutions. IEEE Secu-

rity & Privacy, 17(2):49–58.

Domingo-Ferrer, J. and Mateo-Sanz, J. M. (2002). Practical

data-oriented microaggregation for statistical disclo-

sure control. IEEE Transactions on Knowledge and

data Engineering, 14(1):189–201.

Domingo-Ferrer, J. and Mateo-Sanz, J. M. (2002). Practi-

cal data-oriented microaggregation for statistical dis-

closure control. IEEE Trans. Knowl. Data Eng.,

14(1):189–201.

Domingo-Ferrer, J. and Rebollo-Monedero, D. (2009).

Measuring risk and utility of anonymized data us-

ing information theory. In Proceedings of the 2009

EDBT/ICDT Workshops, pages 126–130.

Eyupoglu, C., Aydin, M. A., Zaim, A. H., and Sertbas, A.

(2018). An efﬁcient big data anonymization algorithm

based on chaos and perturbation techniques. Entropy,

20(5):373.

Fung, B. C., Wang, K., and Yu, P. S. (2005). Top-down spe-

cialization for information and privacy preservation.

In 21st international conference on data engineering

(ICDE’05), pages 205–216. IEEE.

Gower, J. C. (1971). A general coefﬁcient of similarity and

some of its properties. Biometrics, pages 857–871.

Herranz, J., Matwin, S., Nin, J., and Torra, V. (2010). Clas-

sifying data from protected statistical datasets. Com-

puters & Security, 29(8):875–890.

Ji, Z., Lipton, Z. C., and Elkan, C. (2014). Differential pri-

vacy and machine learning: a survey and review. arXiv

preprint arXiv:1412.7584.

LeFevre, K., DeWitt, D. J., and Ramakrishnan, R.

(2006). Mondrian multidimensional k-anonymity. In

22nd International conference on data engineering

(ICDE’06), pages 25–25. IEEE.

Li, N., Li, T., and Venkatasubramanian, S. (2007).

t-closeness: Privacy beyond k-anonymity and l-

diversity. In 2007 IEEE 23rd International Confer-

ence on Data Engineering, pages 106–115. IEEE.

Machanavajjhala, A., Gehrke, J., Kifer, D., and Venkitasub-

ramaniam, M. (2006). l-diversity: Privacy beyond k-

anonymity. In 22nd International Conference on Data

Engineering (ICDE’06), pages 24–24. IEEE.

Oganian, A. and Domingo-Ferrer, J. (2017). Local synthesis

for disclosure limitation that satisﬁes probabilistic k-

anonymity criterion. Transactions on data privacy,

10(1):61.

Prasser, F., Kohlmayer, F., Lautenschl

ager, R., and

Kuhn, K. A. (2014). Arx-a comprehensive tool for

anonymizing biomedical data. In AMIA Annual Sym-

posium Proceedings, volume 2014, page 984. Ameri-

can Medical Informatics Association.

Rodr

ıguez-Hoyos, A., Estrada-Jim

enez, J., Rebollo-

Monedero, D., Parra-Arnau, J., and Forn

e, J. (2018).

Does k-anonymous microaggregation affect machine-

learned macrotrends? IEEE Access, 6:28258–28277.

Samarati, P. (2001). Protecting respondents identities in mi-

crodata release. IEEE transactions on Knowledge and

Data Engineering, 13(6):1010–1027.

Senavirathne, N. and Torra, V. (2020). On the role of data

anonymization in machine learning privacy. In 2020

IEEE 19th International Conference on Trust, Secu-

Systematic Evaluation of Probabilistic k-Anonymity for Privacy Preserving Micro-data Publishing and Analysis

319

rity and Privacy in Computing and Communications

(TrustCom), pages 664–675. IEEE.

Soria-Comas, J. and Domingo-Ferrer, J. (2012). Probabilis-

tic k-anonymity through microaggregation and data

swapping. In 2012 IEEE International Conference on

Fuzzy Systems, pages 1–8. IEEE.

Sweeney, L. (2000). Simple demographics often iden-

tify people uniquely. Health (San Francisco),

671(2000):1–34.

Sweeney, L. (2002). Achieving k-anonymity privacy pro-

tection using generalization and suppression. In-

ternational Journal of Uncertainty, Fuzziness and

Knowledge-Based Systems, 10(05):571–588.

Wimmer, H. and Powell, L. (2014). A comparison of

the effects of k-anonymity on machine learning algo-

rithms. In Proceedings of the Conference for Infor-

mation Systems Applied Research ISSN, volume 2167,

page 1508.

Zhang, Q., Koudas, N., Srivastava, D., and Yu, T. (2007).

Aggregate query answering on anonymized tables. In

2007 IEEE 23rd international conference on data en-

gineering, pages 116–125. IEEE.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

320