RMCCS: RSSI-based Message Consistency Checking Scheme for

V2V Communications

Mujahid Muhammad

, Paul Kearney

, Adel Aneiba

, Junaid Arshad

and Andreas Kunz

Faculty of Computing, Engineering and the Built Environment, Birmingham City University, U.K.

Lenovo, Oberursel, Germany

Keywords: Message Consistency, False Message Detection, Vehicle-to-Vehicle Communication, RSSI.

Abstract: V2V messaging systems enable vehicles to exchange safety related information with each other and support

road safety and traffic efficiency applications. The effectiveness of these applications depends on the

correctness of the information reported in the V2V messages. Consequently, the possibility that malicious

agents may send false information is a major concern. The physical features of a transmission are relatively

difficult to fake, and one of the most effective ways to detect lying is to check for consistency of these features

with vehicle position information in the message. In this paper, we propose a message consistency checking

scheme whereby a vehicle acting independently can utilise the strength and variability of received signals to

estimate the distance from a transmitting vehicle without prior knowledge of the environment (building

density, traffic conditions, etc.). The distance estimate can then be used to check the correctness of the reported

position. We show through simulation that our RMCSS method can detect false information with an accuracy

of about 90% for separation distances less than 100m. We believe this is sufficient for the method to be a

valuable adjunct to use of digital signatures to establish trust.

1 INTRODUCTION

Message-based Vehicle to Vehicle (V2V)

communications have been proposed as means to

address issues in Intelligent Transport Systems (ITS)

such as accident avoidance, traffic monitoring and

transport efficiency (Boban, Kousaridas, Manolakis,

& Xu, 2018). In V2V, vehicles broadcast safety

messages to exchange information about themselves

and perceived road conditions. These messages form

the basis of several road safety and traffic efficiency

applications that are designed to improve safety on

the roads. Because safety critical decisions are made

based on the content of these messages, it is important

to verify as far as possible that they can be trusted.

Clearly, it is important for the receiving vehicle to

check that a message has been signed using valid

credentials that correspond to the sender identity

used. However, given the large number of vehicles on

the road, it is unwise to discount the possibility that a

malicious agent can acquire legitimate credentials by

some means and use them to broadcast false

information. It seems prudent, therefore, for the

https://orcid.org/0000-0002-6484-3344

receiving vehicle to check whether the message

contents make sense in the light of other knowledge

available to it. The threat scenario addressed in this

paper involves the malicious agent representing the

existence of a vehicle in a dangerous location in order

to cause accidents or widespread disruption to traffic.

Typically, this will involve the malicious agent

pretending to be closer to the target vehicles than it

really is. The solution approach we explore here is for

the receiving vehicle to check that the position

claimed in the message is consistent with the strength

and variability of the received radio signal.

The remainder of the paper is structured as

follows. First we present our method, which we call

RMCCS; RSSI-based Message Consistency

Checking Scheme for V2V Communications. It is

based on the well-established log-distance path loss

model with Gaussian noise, but with the additional

assumption of a relationship linking the path loss

exponent (which governs the rate of signal

attenuation with distance) to the standard deviation of

the Gaussian variable. This method is then compared

with approaches taken previously by others. Next we

722

Muhammad, M., Kearney, P., Aneiba, A., Arshad, J. and Kunz, A.

RMCCS: RSSI-based Message Consistency Checking Scheme for V2V Communications.

DOI: 10.5220/0010561107220727

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 722-727

ISBN: 978-989-758-524-1

validate the assumption and evaluate the method

using simulation software that embodies a faithful

representation of signal propagation in representative

conditions. A discussion of the relative effectiveness

of the method and how it may be combined with other

techniques to provide an effective defence against

misinformation in a V2V context then follows.

2 THE RMCCS METHOD

The received signal strength indicator (RSSI) is a

commonly used measure of the power of a received

radio signal. It is the ratio of the power measured at

two different points, e.g.at the transmitter and the

receiver, expressed in dB, i.e. RSSI = 10 log

(P/P

)

In the case of a non-directional signal broadcast

through a uniform medium, the so-called log-distance

path loss model (LDPLM) is widely used to estimate

the RSSI at a receiver (see for example (Fernández,

Rubio, Rodrigo-Peñarrocha, & Reig, 2014) and

(Giordani, et al., 2019)):

RSSI ≈ A - 10B log

(d/d

) (1)

where d is the distance from the transmitter, d

is a

reference distance that is usually taken to be 1 metre,

and A and B are positive constants. A depends on the

transmitter and receiver characteristics, and B, the

path loss exponent, depends on the transmission

medium. This is a monotonically-decreasing function

of d and can readily be inverted to obtain an estimate

of d given a measurement of RSSI provided A and B

are known. Taking d

to be the usual value of 1m:

d = 10^((A-RSSI)/10B) (2)

This estimate can be compared with the distance

between the known position of the receiver and the

claimed position of the sender as a consistency check.

However, there are complications that make this

approach difficult to use in practice. Firstly, the

LDPLM only really applies to propagation in free

space. For example, one correction that is frequently

applied is to allow for interference between the radio

waves travelling directly from sender to receiver and

those reaching the receiver after reflection from the

road surface. Even if the LDPLM is a good

approximation at long distances, the presence of static

and moving obstacles such as buildings and vehicles

not only tends to attenuate the signal, but also

introduces considerable variation of RSSI due to

absorption, reflection, refraction, and multi-path

interference. Indeed, a more general form of LDPLM

adds a Gaussian random variable with a mean value

of 0 to the right-hand side of (1) to take such effects

into account. This may be interpreted as a margin of

error on the expected RSSI value at a given distance

of ±σ, the standard deviation of the random term. This

can be translated to an uncertainty on the estimated

distance between sender and receiver, the magnitude

of which is proportional to the estimated distance, i.e.

the ratio of the uncertainty to the distance is constant

for a given σ and B.

So, obstacles on or near the line of sight (LOS)

between sender and receiver modify (usually reduce)

the effective value of B and introduce variability into

the RSSI that has the appearance of random noise.

The idea that we explore in this paper is that if these

two phenomena are correlated, we could use

measurements of RSSI variability alongside its mean

value to obtain estimates of distance and the

associated uncertainty that could be used to assess the

likely truth of a reported position and give a measure

of confidence on this assessment. Suppose that B and

σ are functions of a common hidden variable, γ, that

characterises the nature of the obstacles on or near the

path between them, for example,

B = γB

and σ = k(γ – γ

) (3)

where γ = 1 corresponds to LOS conditions, k is a

constant of proportionality, and γ

≤ 1 allows for the

possibility of variation in RSSI even in LOS

conditions. Given measurements of RSSI and σ, the

distance between sender and receiver, can be

estimated as:

= 10^((A-RSSI)/(10(σ/k + γ

)) (4)

and the uncertainty on this value as:

σ̄

= d

.(10^Γ - 10^-Γ)/2,where Γ = σ/10B

(σ/k + γ

)

(5)

If d

is the distance based on the position of the sender

as reported in the message, then |d

- d

|/σ̄

provides a

measure of the inconsistency of the reported position

and the measured signal strength and variation. Note

that, due to the logarithmic dependence of RSSI on

distance in (1), if σ is independent of distance, then σ̄

increases linearly with distance. Thus, a given

discrepancy Δd = |d

- d

| may be regarded as

inconsistent for small d

and consistent for large d

The receiving vehicle will need to extract

estimates of the mean RSSI and the corresponding

standard deviation from the noisy RSSI signal, but we

propose this can be done using standard signal

processing techniques such as Kalman and Savistzky-

Golay filtering algorithms.

RMCCS: RSSI-based Message Consistency Checking Scheme for V2V Communications

723

Below, we assess the validity and effectiveness of

this approach using data obtained from a simulation,

but first we review other work that has used RSSI

measurements in the context of V2V.

3 RELATED WORK

Several existing research studies have used RSSI-

based techniques to provide solutions to issues in

V2V. Such techniques are popular as they have low

computational cost and require no extra hardware.

The main applications are Sybil node detection and

localisation of vehicles:

3.1 Sybil Node Detection

RSSI-comparison techniques have been proposed as

a means of detecting non-existent vehicles fabricated

by malicious agents (so-called Sybil nodes). The core

idea behind this approach is that as the messages

apparently sent from multiple Sybil nodes are actually

sent by the same physical node, they share similar

signal characteristics with each other and with

genuine messages from that node. For example, (Yao

Y. , et al., 2018) record successive RSSI values to

obtain time sequences apparently corresponding to

different vehicles. If identical (or at least very similar)

sequences are observed, this is taken as a sign of Sybil

activity. In case malicious nodes perform power

control to avoid their Sybil nodes being detected by

such means, (Yao Y. , et al., 2019) proposes a

complementary method that finds Sybil nodes by

detecting abnormal variations in the RSSI time series.

3.2 Localisation of Vehicles

Several schemes that use RSSI to estimate the

location of vehicles have been proposed previously.

For example, (Garip, Kim, Reiher, & Gerla., 2017)

describes an approach whereby neighbouring

vehicles collaborate to determine the location of a

target vehicle. Each vehicle estimates its distance to

the target vehicle using the LDPLM formula and then

sends the estimated distance and its current location

to a chosen vehicle called the observer. The observer

processes the aggregated information and advertises

the target vehicle’s actual location. Also, (Ahmad, et

al., 2019) describes an RSSI-based localization

mechanism that uses nearby stationary roadside units

(RSUs) to estimate the location of a target vehicle.

Each RSU measures the RSSI values of transmissions

from the target and uses them to estimate its distance.

Schemes like these are cooperative in nature,

meaning that they rely on information received from

nearby nodes to function, and are vulnerable to

collusion attack. Moreover, there is no means to

guarantee the credibility of nodes’ measurement

reports. Besides, transmission of the distance

estimates adds more traffic to the network, increasing

bandwidth consumption. A latency penalty is also

incurred as the observer must wait to receive distance

estimates from other nodes. In our RMCCS method,

a receiving vehicle acting alone can determine

whether another vehicle is lying about its position.

4 SIMULATION AND

EVALUATION

To obtain RSSI measurements, we use the GEMV

simulation software of (Boban, Barros, & Tonguz,

2014), which incorporates a range of propagation

effects including transmission through materials,

diffraction and reflection. In particular, it models the

impact of the presence of vehicles, buildings and

foliage. The developers of GEMV

have validated it

against measurements performed in urban, suburban,

highway and open space conditions.

To generate data for the evaluation we used

models of real locations taken from Open Street Map

(OSM) that include representations of building

geometry and road networks. In particular, we

selected locations in Newcastle, UK, that represent

distinct types of environment. The locations are (a) a

city center area (b) an inter-city highway, and (c) a

suburban area. We then used SUMO, which is a

widely used road traffic simulation tool, to generate

mobility traces of vehicles trajectories in these

locations. The mobility traces are then converted into

floating car data (FCD) format and used as input to

the GEMV

to calculate the RSSI. The number of

vehicles used in these locations and other parameters

used in the simulation are shown in Table 1.

Table 1: Simulation Settings.

Parameters Value

Number of vehicles 2 – 200

Communication range 300m

Message frequency 10Hz

A -39dBm

Operating frequency 5.9GHz

SUMO simulation time 3600s

SECRYPT 2021 - 18th International Conference on Security and Cryptography

724

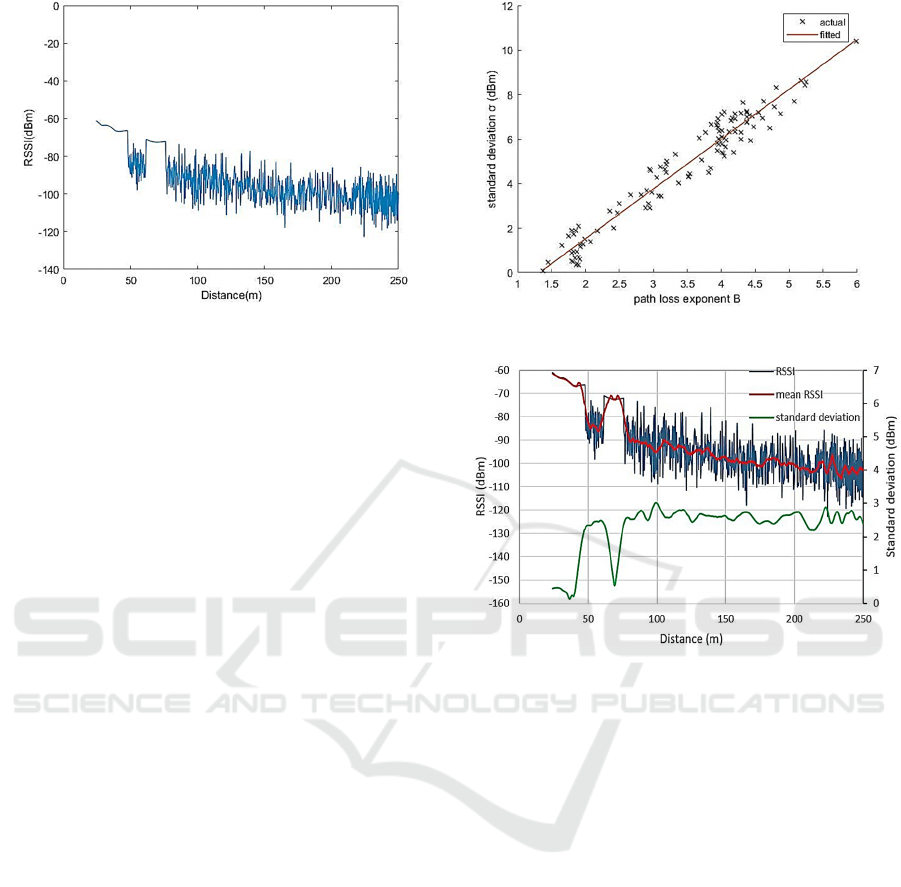
Figure 1: RSSI vs Distance.

The RSSI data generated from each of these

scenarios was plotted against the distance between

sending and receiving vehicles. Fig. 1 is an example

of such a plot generated for a city center scenario in

high traffic density conditions. It is apparent that the

plot can be divided into distinct segments, which were

found to correspond to line of Sight (LOS) conditions

(characterized by absence of noise-like variability),

obstruction by traffic, obstruction by buildings, etc.

Each RSSI trace was divided into segments by eye.

Curves of the form (1) were fitted independently to

each segment to obtain values for B, with A being

held fixed at a value (given in Table 1) determined

from typical vehicle characteristics, and d

=1. The

root mean square deviation of RSSI points from the

fitted curves was then calculated to obtain σ values

for each segment. It may be seen from Fig. 2 that the

segments appear to be distributed about a straight line

in (B, σ) space. We therefore assumed the

parameterisation of (3) with B

being the least value

of B for any segment, and k and γ

being determined

from a least-squares fit through the points of Fig 2.

From (5) we see that the ratio of the uncertainty

on the distance estimate (σ̄

) to the distance estimate

itself (d

) is dependent on σ. For B

=1.4 and using

k=3.89 and γ

=1.00 from the least squares fit, the ratio

is about 0.14 for σ=1dBm, 0.38 for σ=5dBm and 0.49

for σ=10dBm. If we use a 3 sigma criterion for

consistency, then for σ=1dBm, the discrepancy

between claimed distance and true distance would

need to be greater than 42% of the true distance to be

judged to be lying. For σ=3.75dBm, the required

discrepancy is about the same size as the distance

itself. As the main threat comes from vehicles

claiming to be closer than they really are, then the

proposed technique is only useful for σ<3dBm.

Reducing the inconsistency criterion extends the

applicable σ range, however, albeit at the cost of

increased false positives.

Figure 2: Least Square fitting of (B, σ).

Figure 3: Mean RSSI and standard deviation data generated

from the filtering algorithm.

To use (4) to estimate its distance from a moving

transmitter, and (5) to estimate the uncertainty on this

value, a receiving vehicle must extract mean RSSI

values and the corresponding standard deviations

from a ‘noisy’ sequence of RSSI measurements.

Furthermore, these values must be updated

continuously. Two alternative algorithms were tried

for this purpose, a Kalman filter and a Savistzky-

Golay filter. The filtering algorithms were reset at the

boundaries between segments, which were detected

as a rapid alteration in the rate of change of the mean

RSSI. Fig. 3 shows a sample trace overlaid with the

values extracted using the Savistzky-Golay filter. As

may be seen, the algorithms are reasonably effective

at tracking the mean RSSI value and the

corresponding standard deviation.

The distance between the sender and receiver was

estimated using (5) and then compared with the true

distance calculated based on the reported position in

the received message. Fig. 4 plots the estimated

distance against the true distance for the sample trace.

It can be seen that on average, the estimated distance

and true distance are equal, but the margin of error

RMCCS: RSSI-based Message Consistency Checking Scheme for V2V Communications

725

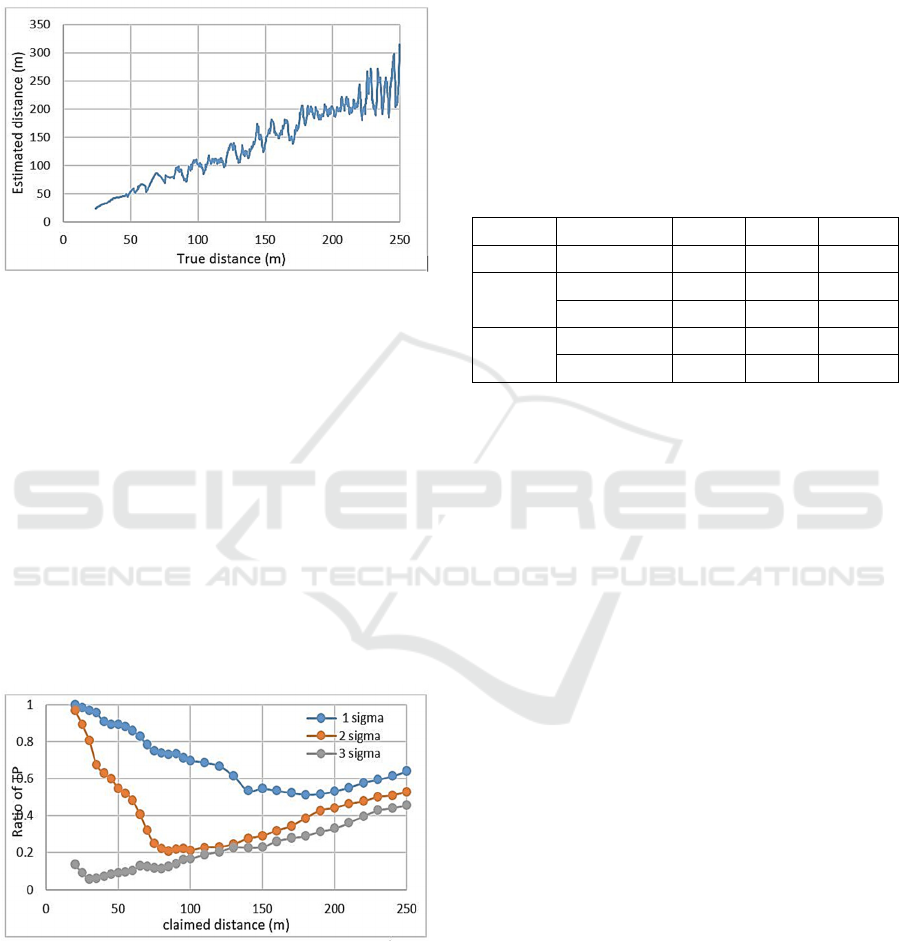
increases with distance. The estimation error, defined

as |d

-d

|/d

, was found to be less than 25% everywhere

and is below about 12% for separation distance less

than 50m. Also, the overall average estimation error

was found to be 7.5% for distances up to 250m.

Figure 4: Estimated distance vs True distance.

To assess the probability of true negatives, TN,

(and false positives, FP) for different inconsistency

criteria, we calculated the proportion of data points in

the sample trace for which the absolute difference

between the true and estimated distance exceeds

various multiples of σ̄

. To assess the probability of

true positives, TP, (and false negatives, FN), we used

threat scenario in which a static malicious vehicle

simulates a Sybil vehicle following the target vehicle

at various fixed distances. TP is calculated as the

proportion of data points in the sample trace for which

the difference between the reported distance and the

estimated distance exceeds various multiples of σ̄

The results are shown for various following distances

and inconsistency criteria in Fig. 5.

Figure 5: True Positives for the evaluation scenario.

To get an overall assessment of TP for a given

inconsistency criterion, we took the average over the

various following distances up to 250m. Because it is

reasonable to suppose that detecting fictitious

vehicles that are faraway is less important than

detecting ones that are nearby, we also calculated the

averages over following distances up to 100m.

Having obtained TN and TP values for a range of

inconsistency criteria we calculated accuracy values:

Accuracy = (TP+TN)/(TP+TN+FP+FN)

= (TP+TN)/2

(6)

The results are shown in Table 2. As can be seen,

an inconsistency criterion of |d

- d

|/σ̄

> 1 appears to

give the best accuracy of approximately 90% for

distances up to 100m and about 83% for longer

distance up to 250m.

Table 2: Evaluation parameters of RMCCS for three

inconsistency criteria: |d

- d

|/ σ̄

> N.

Metric Distance(m) N = 1 N = 2 N = 3

TN up to 250m 0.9551 0.9708 0.9809

up to 250 0.7195 0.4344 0.2051

up to 100 0.8441 0.4834 0.1119

Accuracy

up to 250 0.8373 0.7026 0.59303

up to 100 0.8996 0.7271 0.54641

5 CONCLUSIONS

In this paper, we describe RMCCS – a mechanism

that utilizes RSSI measurements to detect when

vehicles are lying about their position. Like many

other methods, RMCCS makes use of the LDPLM

RSSI formula. However, by proposing a linear

relationship between the path loss exponent and the

standard deviation of the noise component in this

formula, the RMCCS method enables a receiving

vehicle to estimate distance independently without

prior knowledge of environmental conditions such as

the current traffic conditions and building density in

the vicinity. The assumption of a linear relationship is

justified by empirical evidence obtained from a

realistic simulation. The estimated distance and

associated uncertainty provide a means to judge

whether the sender is lying about its claimed position.

As a measure of inconsistency, we use the ratio of the

magnitude of the difference between reported and

estimated distances to the uncertainty on the estimate.

The sender is judged to be lying if the inconsistency

is greater than a threshold value. Lowering the

threshold tends to increase true positives, but reduce

true negatives. The threshold can be varied to obtain

an optimal value that maximises accuracy (which is

proportional to the sum of true positives and true

negatives). This provides a way for vehicles to detect

misinformation without the need for support from

their neighbors or any nearby infrastructure.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

726

Contrasting the previous works described in 3.2

with the RMCCS method, (Garip, Kim, Reiher, &

Gerla., 2017) require collaboration among

neighboring vehicles to estimate the distance of a

target vehicle whereas in RMCCS the estimation

algorithm is purely local. The accuracy of this

approach depends on number of vehicles reporting

their individual estimated distances to the target and

the correctness of the reported information. When a

large proportion of neighbours report incorrect

distance estimates, the estimated target position will

deviate from its true location. Such approaches are

unreliable when vehicles fail to collaborate or their

messages are lost. Furthermore, the same fixed path

loss exponent is used by all collaborating vehicles,

whereas, as we have seen, its value depends on the

obstacles on or near the transmission path. In contrast,

RMCCS is able to extract a dynamic value for the

exponent from the RSSI data using the linear

relationship. In (Ahmad, et al., 2019), cooperation is

also required, this time among RSUs. Again a fixed

path loss exponent is used to estimate the distance to

the target vehicle. A further disadvantage is that it is

unrealistic to assume that RSUs will be available in

all locations.

In terms of evaluation, the previous works

assessed their methods using simulators such as NS-

2, employing simple statistical propagation models.

In contrast, our RMCCS method was evaluated using

GEMV

, which accounts for RSSI variation caused

by obstruction by surrounding objects. Studies in

(Mir, 2018) show a significant difference in received

power when comparing the performance of GEMV

and the propagation models built into NS-2. This

indicates that performance estimates obtained using

NS-2 are questionable, and that when the previous

work is evaluated with a more realistic simulation

environment, performance will reduce.

Another work that also checks consistency of

messages in V2V by using physical signals is (Lin &

Hwang., 2020). This work exploits angle of arrival

measured using a multi-antenna configuration, which

requires vehicles to have special hardware. This

increases the complexity and cost of the vehicle’s

onboard units. RMCCS, however, is compatible with

existing in-vehicle units.

We have shown through simulation and

evaluation that RMCCS performs well in terms of

distance estimation and ability to detect false position

reports with an accuracy level of about 90% with

separation distances under 100m. We believe this is

sufficient for the method to be a valuable adjunct to

use of digital signatures to establish trust between

vehicles, which will not only enable effective defense

against malicious vehicles but also improves traffic

safety significantly.

As a future work, we aim to investigate the

application of RMCCS method in combination with a

symmetric cryptography based security scheme

similar to TESLA in order to provide low-latency

message verification in V2V.

REFERENCES

Ahmad, W., Ahmed, S., Sheeraz, N., Khan, A., Ishtiaq, A.,

& Saba, M. (2019). Localization Error Computation for

RSSI Based Positioning System in VANETs. In IEEE

International Conference on Advances in the Emerging

Computing Technologies (AECT), 1-6.

Boban, M., Barros, J., & Tonguz, O. (2014). Geometry-

based vehicle-to-vehicle channel modeling for large-

scale simulation. IEEE Transactions on Vehicular

Technology, 63(9), 4146-4164.

Boban, M., Kousaridas, A., Manolakis, K. E., & Xu, W.

(2018). Connected roads of the future: Use cases,

requirements, and design considerations for vehicle-to-

everything communications. IEEE Vehicular

Technology Magazine, 3(13), 110-123.

Fernández, H., Rubio, L., Rodrigo-Peñarrocha, V., & Reig,

J. (2014). Path loss characterization for vehicular

communications at 700 MHz and 5.9 GHz under LOS

and NLOS conditions. IEEE Antennas and Wireless

Propagation Letters, 13, 931-934.

Garip, M. T., Kim, P. H., Reiher, P., & Gerla., M. (2017).

"INTERLOC: An interference-aware RSSI-based

localization and Sybil attack detection mechanism for

vehicular ad hoc networks", 14th IEEE Annual

Consumer communications & networking conference

(CCNC), 1-6.

Giordani, M., Shimizu, T., Zanella, A., Higuchi, T.,

Altintas, O., & Zorzi, M. (2019). Path loss models for

V2V mmWave communication: performance

evaluation and open challenges. IEEE 2nd Connected

and Automated Vehicles Symposium (CAVS), 1-5.

Lin, P.-C., & Hwang., R.-H. (2020). Enhancing

misbehavior detection in 5G Vehicle-to-Vehicle

communications. IEEE Transactions on Vehicular

Technology.

Mir, Z. (2018). Assessing the impact of realistic simulation

environment on vehicular communications. . IEEE

Fifth HCT Information Technology Trends (ITT), 312-

317.

Yao, Y., Xiao, B., Wu, G., Liu, X., Yu, Z., Zhang, K., &

Zhou, X. (2018). Multi-channel based Sybil attack

detection in vehicular ad hoc networks using RSSI.

IEEE Transactions on Mobile Computing, 18(2), 362-

375.

Yao, Y., Xiao, B., Yang, G., Hu, Y., Wang, L., & Zhou, X.

(2019). Power control identification: A novel sybil

attack detection scheme in vanets using rssi. IEEE

Journal on Selected Areas in Communications, 37(11),

2588-2602.

RMCCS: RSSI-based Message Consistency Checking Scheme for V2V Communications

727