A Blind Noise Estimation and Removal in Histopathological Images

Shiksha Singh, Rajesh Kumar

Department of Electronics and Communication, J K Institute of Applied Physics and Technology, University of Allahabad,

Prayagraj, Uttar Pradesh, India

Keywords: Histopathology images, Noise Estimation, Image Processing

Abstract: With the advancement in technology for digital pathology, a huge chunk of the visual dataset is prepared for

medical experts for disease diagnosis and grading. The introduction of noise in various image modalities in

the medical field can distress the result of diagnosis which could lead to inappropriate disease grading and

hence delay in treatment. In this, a blind noise estimation and removal technique is proposed for

histopathology images. The model uses the wavelet transformed image and block selection approach with a

block size of eight for noise estimation. The noise estimated in the model is Gaussian, Poisson, and speckle.

The proposed approach is verified on images of Breakhis dataset with all four-magnification scale. The

performance of the proposed approach is shown through parameter Signal-to-noise ratio (SNR), mean

square error (MSE), root mean square error (RMSE) and peak signal to noise ratio (PSNR)

1 INTRODUCTION

Noise in the digital image is defined as inappropriate

and unwanted information residing in an image. This

unwanted noise may affect the image quality in

different ways. The disturbance is created in pixel

values of the image, and hence there is some random

variation in pixel value. In medical image analysis,

the estimation of noise variance is of utmost

importance. To check the stability and working

performance of the detection model for disease

diagnosis, noise recognition, as well as elimination,

is important. With the improvement in digital

pathology, a large amount of visual dataset is

generated which is available for computer-aided

diagnosis (CAD). The availability of dataset

encourages the researchers to develop CAD tools for

analysing the scanned images developed through

digital pathology. Based on the result obtained from

CAD tools, the grading of the disease is performed.

For a precise and accurate diagnosis of medical

images, it is very essential that the image taken

through different technique remains free from blur,

noise, and artefacts. The different image acquisition

techniques end up in accumulating a large number of

numbers of the pixel in per unit area to flourish

high-resolution image. They thrive to capture high

quality leads to noise accumulation in the resultant

image. These noises mask the essential feature

which leads to incorrect grading of the disease.

Table 1 below reports a brief overview of different

image modalities along with noise present in such

images. The table below gives the image capturing

developing techniques related to different medical

image modalities. Due to different faults in different

capturing process noise are introduced in the image.

There are various noise models for different medical

images, and it is shown in Table 1.

There are models developed for other image

modalities such as MRI, X-Ray, Ultra-sound, CT etc.

using different approaches such as filtering,

statistical, block selection, noise variance etc. It can

be observed from the literature that no such model is

developed for histopathology images. This paper

proposes a blind noise estimation model for

histopathology images. There is no prior knowledge

regarding the noise model hence we are using blind

noise estimation approach. In this mode model, the

image is transformed into the wavelet domain and

perform block division of image in the continuous

diagonal, vertical and horizontal component. For

each block median absolute deviation is calculated.

For denoising, the noisy level and estimated noise

level is differentiated. Due to the importance of

luminance in the microscopic image the Color space

used is YCbCr.

Singh, S. and Kumar, R.

A Blind Noise Estimation and Removal in Histopathological Images.

DOI: 10.5220/0010562700003161

In Proceedings of the 3rd International Conference on Advanced Computing and Software Engineering (ICACSE 2021), pages 67-72

ISBN: 978-989-758-544-9

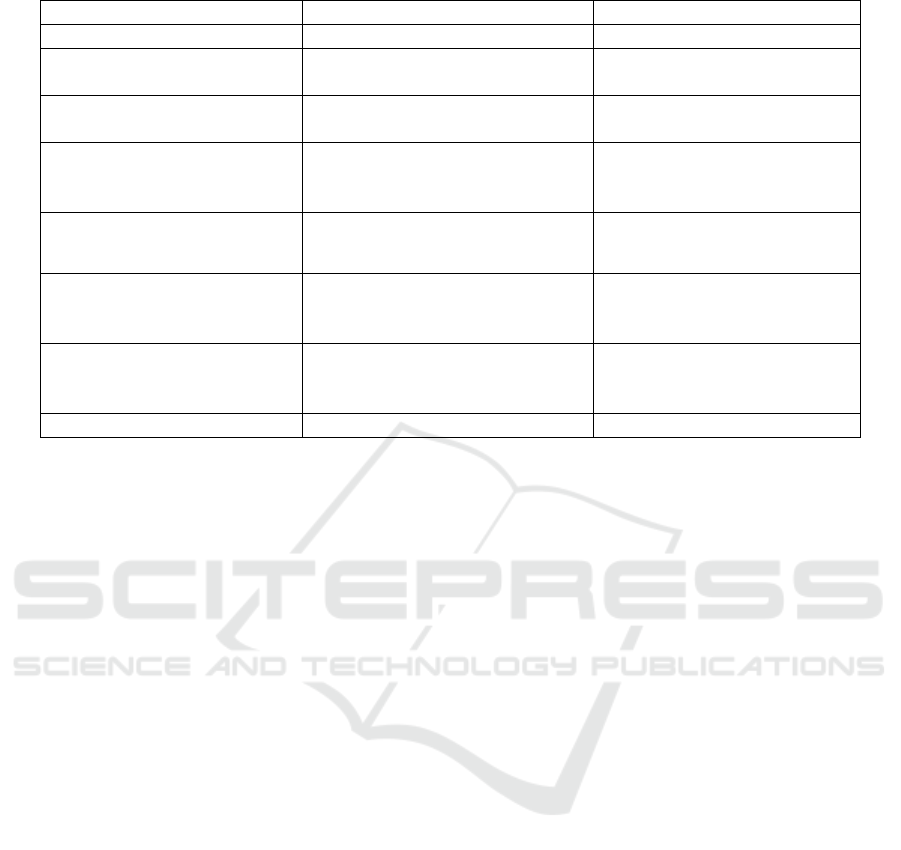
Table 1: Image modalities with noise and acquiring technique

The paper is organized as: already existing

model of noise estimation are given in “Related

work”. The proposed approach and the dataset used

to validate the model is explained in “Material and

Method.” This section gives a detailed discussion

regarding noise estimation, noise model and Discrete

wavelet transform.

The experimental work and result analysis are

discussed in “Experimental Result”. The future

direction and work proposed is conclude in section

“Conclusion”.

2 RELATED WORKS

To best of our knowledge, no such noise estimation

model for histopathology images has been sated in

the literature. So, we have reviewed paper based on

other medical image modality for noise estimation.

There are different types of image-modality in the

medical image. Every image has a different

acquisition technique based on those image

capturing approaches; different type of noise is

introduced in a different image. The table

summarizes the image capturing technique along

with the noise present in that image (Goyal, Dogra,

Agrawal, & Sohi, 2018)(Dogra, Goyal, Agrawal, &

Sohi, 2017). There are several noise models and

noise estimation approaches are reported till date

such as statistical approaches, patch-based, filter-

based and block selection based (Ram & Choudhary,

2014)(Kaur, 2015).

Pieere Gravel et.al. (2004) has developed a

method for analysing the statistical property for

analysing the statistical property of noise. The model

developed establishes the association between the

intensity of the image and variance of image. The

proposed model was examined on MRI and X-Ray

images with Gaussian, Poisson as well as Rician

noise(Gravel, Beaudoin, & De Guise, 2004). M.N.

Nobi et.al. (2010) has developed noise reduction

model for MRI and ultra-sound images having

Rician noise and speckle noise. The model integrates

the median filter and mean filter(Yousuf & Nobi,

2010). Pierrick Coupe et.al. (2010) has presented an

object-based model to estimate Rician noise in MRI

using median absolute deviation(Coupé et al., 2010).

GnanambalIlango et.al. (2011) has proposed a

hybrid approach of noise estimation using different

filtering techniques. The estimation technique is

used on brain tumour image for Gaussian noise

removal (Ilango & Marudhachalam, 2011). Xuvyu

Pan et.al. (2012), the authors have presented a blind

noise estimation model for CT images. Contrast

band filters are used for estimating the noise and for

denoising PCA with local pixel grouping is used

(Pan, Zhang, & Lyu, 2012). Jose V. Manjon et. al.

(2015) has given a two-step approach for Rician

noise estimation in MRI. The proposed approach

involves the filtering of the noisy image using no-

local principal component analysis(PCA) and then

using a filtered image as a guide for the non-local

mean filter (Manjón, Coupé, & Buades, 2015). F.F.

Ting et.al. (2016) has proposed a rapid noise

variance estimation method for magnetic resonance

Ima

e Modalit

Technique T

pe of Noise

X-Ra

X-ra

ection Gaussian & Poisson Noise

Computed-Tomography (CT)

Cross-sectional body x-ray

ection

Gaussian & Quantum Noise

Positron Emission

Tomo

raph

(PET)

Radioactive tracing Gaussian Noise

Single-photon emission

Computed Tomography

(SPECT)

Picturization performed through

the nuclear substance.

(Gamma camera)

Gaussian Noise

Magnetic -Resonance

Imaging (MRI)

Transition in the energy of the

photon

Gaussian, Richian, and

Rayleigh noise

Ultra-sound

Reflection of the temporal wave

with

h frequenc

Gaussian & multiplicative

noise

Microscopic Biopsy

Tissue examined under a

microscope.

with H&E stains on i

Gaussian, Poisson, and

Multiplicative

Mammo

raph

Low dose x-ra

ste

Gaussian & Poisson Noise

ICACSE 2021 - International Conference on Advanced Computing and Software Engineering

image and computed tomography. The author has

used Gabor Wavelet Laplacian convolution (GWLC)

for noise variance estimation. The type of noise

discussed in the work is Rician noise (Ting, Sim, &

Wong, 2017). Rajesh Kumar et.al. (2017) has

proposed an approach for segmentation of

microscopic images for cancer grading. The

proposed approach segments the cell and nuclei in

the existence of Poisson noise. The authors have

used the partial differential equation of order four

which relies on the non-linear filter for noise

estimation (Kumar et al., 2017). Table.2. gives a

brief over of the noise estimation model discussed

by various researchers and noise model they have

considered.

Table 2: Brief overview noise estimation model stated in the literature

3 METHOD AND MATERIALS

In the proposed approached we have used block

selection method for noise estimation. Fig.2. shows

a block diagram of the proposed architecture. Since

it is blind noise estimation technique introduction of

noises such as Gaussian, Poisson, and speckle, are

made in images of Breakhis dataset. For validating

our approach, we have used benchmark dataset for

experimental work. For noise estimation and

denoising we have used images from BreakHis

dataset. System configuration with 2 GB GPU, 8 GB

Ram i5 processor has been used. The Matlab version

2017b is used for performing an experiment. The

images in the dataset are in RGB colour space they

are transformed into YCbCr colour space and

performed wavelet transform. This section is

subdivided into sections- 3.1) Dataset 3.2) Pre-

processing 3.3) Noise model 3.4) Wavelet transform

3.5) Noise estimation 3.6) Performance measure.

3.1 Dataset

Breast Cancer Histopathology Database (BreakHis)

is publicly available dataset and is prominently used

for breast cancer detection. The images are

developed by staining the tissue collected through

surgical open biopsy and staining them with H&E. A

total of 7909 images are them out of which 2440 are

benign and 5429 are malignant and they are of

magnification factor 40X, 100X, 200X and 400X.

For validation of proposed architecture, a single

image from each magnification level is

taken(Spanhol, Oliveira, Petitjean, & Heutte,

2016)(“Breast Cancer Histopathological Database

Reference Image Modality Type of Noise Approaches

(Gravel et al.,

2004)

MRI

X-Ray

Gaussian, Poisson,

Rician

Relationship between noise variance

and image intensity

(Yousuf & Nobi,

2010)

MRI

Ultra-soun

Rician& Speckle

Integration of median filter an

Mean filter.

(Coupé et al.,

2010)

MRI Rician

Two-step approach involves filtering

image using non-local PCA and then

filtered image used as a guide for

non-local

Mean filter.

(Ilango &

Marudhachalam,

2011)

MRI

Gaussian, Sal

pepper &

Speckle

Hybrid filter through Topological

approach

(Manjón et al.,

2015)

CT, MRI

Additive white

gaussian

oise (AWGN)

Contrast band filter

(Ting et al., 2017) MRI, CT Rician

Gabor Wavelet Laplacian

Convolution

(Kumar,

Srivastava, &

Srivastava, 2017)

Microscopic

Biopsy

Poisson

Fourth-order partial differential

equation based on non-linear filter

A Blind Noise Estimation and Removal in Histopathological Images

(BreakHis),” 2014). Fig.1. shows the images used in

the proposed approach:

nification Facto

40x 100x 200x 400x

Figure 1: Images from BreakHis Dataset

3.2 Pre-processing

The luminance of the coloured images is of utmost

importance. And in case of histopathological

images, the Color stain signifies the characteristics

of an image. So, keeping this in mind we have

chosen YCbCr for conversion. The conversion of the

RGB image to colour image is:



Y Cb Cr







R G B





0.299 0.168 0.499

0.587 0.331 0.418

0.114 0.500 0.081

 (1)

Figure 2: Proposed Architecture for noise estimation and removal

3.3 Noise Model

During digital image acquiring of slides, various

sensors are coupled with the microscope. This led to

noise introduction in an image due to a decrease in

contrast of tissue structure. This occurs due to the

lack of proper light and long duration of exposure.

Due to this there is a scarcity of photon in sensor and

hence the shifting electrons inside the chip get lost

and noise intrudes the image. Noise is characterized

as a random variable since it is simply a fluctuation

in pixel value. The random variables have some

probability distribution, which links it with statistical

values which is the probability of occurrence (Kaur,

2015). The basic assumption regarding noise nx,y

noises is an additive random signal that is white

Gaussian noise with zero mean value and noise is of

high frequency. The noise in an image J



x, y



represented as





x, y



J



x, y



nx,y (2)

Where, J



is the degraded image.

In the proposed approach we have introduced

Gaussian, Poisson, and speckle noise in images for

noise estimation and denoising purpose.

3.3.1 Gaussian Noise

It is a statistical noise which has the probability

density function (PDF) equals to the normal

distribution (Gonzalez & Woods, 2002). It can be

mathematically given as:



Ix,yG



(3)

Where I x, y is the noiseless image and G



Gaussian PDF it is given as:





√









, ∞𝑎∞ (4)

Here a represents the intensity, a



average(mean) of intensity, and σ standard

deviation.

3.3.2 Poisson Noise

The Poisson is introduced in the image due to

random fluctuation in photons from source ray

emission. This result in temporal and spatial

randomness(Gonzalez & Woods, 2002). The PDF

for Poisson Noise is given as











!

e



(5)

Here n represents the total number of pixel and p

shows the ratio between the noise pixel to the total

number of pixels.

3.3.3 Speckle Noise

Another noise which is very common and can be

present in microscopic images are speckle

noise(Gonzalez & Woods, 2002). Speckle noise is

most common multiplicative noise in medical

images. It is represented as

Color Conversion

(RGB to YCbCr)

Discrete

Wavelet

Transform

Noise

Estimation

Denoising

ICACSE 2021 - International Conference on Advanced Computing and Software Engineering



J



x, y



J



x, y



S



 (6)

Where S



shows a random noise with zero mean

Gaussian PDF.

3.4 Wavelet Transform

The wavelet signifies the analysis and representation

of multiresolution images (Jaiswal & Srivastava,

2020) Wavelet transformation are most frequently

used in edge detection (Jiang, Shen, Jiang, & Lam,

2009) and image denoising(Coifman&Donoho,

1995). At low frequency, the wavelet transform

gives high resolution and with high frequency it

gives high resolution time. We can get better noise

estimation of an image in the wavelet domain. So,

image is transformed in wavelet domain. This

transformation is applied over YCbCr image.

Let us consider Ψx as wavelet of 1-D signal,

then the scaling parameter p and shifting parameter r

is given as:



,















Ψ





 (7)

Where, f(x) 1-D signal and its wavelet transform is

given as:



,





p, r











,





xdx (8)

3.5 Noise Estimation

Upon excluding the edge, the noise estimation is

performed by block division into continuous

diagonal, vertical, and horizontal component and

then the noise statics are calculated for each block

obtained. The noise statistics calculated for blocks

are mean absolute deviation. The block size here is

taken as eight. The denoising is performed by

differentiating noisy image and estimated noise of an

image.

3.6 Performance Measure

The quality of the image needs to be quantified. The

metrics are put under category object fidelity and

subjective fidelity. For testing the performance of

enhancement approach, we have calculated error and

signal to noise ratio. MSE is error calculated

between the input image and the processed image.

SNR is the ratio between signal amplitude and noise

amplitude(Jain, 1989). The unit of SNR is dB. The

formula for calculation of MSE, RMSE SNR, and

PSNR is given as

E





∑∑

J



x, y



J′x,y











(9)

RMSE 

√

(10)

Here l and m are dimensions of input image

J(x,y) and J’(x,y) is the processed image

SNR  20 log 10









 (11)

PSNR  20 log 10









(12)

Here S



is signal amplitude and N



is noise

amplitude.

4 EXPERIMENTAL RESULT

The model explained in this paper is validate on the

images taken from BreakHis dataset. The proposed

approach is tested on images with different

magnification scale and varying noise model. The

experiment is performed by selecting five random

images from the database and then their value is

represented in Table.3 Then the SNR, PSNR, MSE,

and MSE is calculated value is computed to quantify

the image quality given by the estimation model.

Lower the value of MSE, RMSE and higher value of

SNR, PSNR shows the betterment of enhancement

procedure. Table 3. Gives a brief overview of SNR,

PSNR, MSE and RMSE values corresponding to

different noise and magnification scale. It is

observed for the table that magnification of image

does not affect the signal amplitude and noise

amplitude ratio.

Table 3: SNR value of the proposed model on the different

magnification factor

Image

Type

Type of

Noise

MSE RMSE SNR PSNR

40X Speckle 0.3586 0.5968 49.4785 4.5128

Gaussian 0.4649 0.6805 48.5876 3.3607

Poisson 0.4663 0.6846 48.1698 3.3197

100X Speckle 0.3932 0.6250 49.2943 4.1031

Gaussian 0.4677 0.6826 48.4031 3.3309

Poisson 0.4904 0.6992 48.2628 3.1208

200X Speckle 0.3952 0.6273 49.2936 4.0695

Gaussian 0.4648 0.6804 48.5888 3.3619

Poisson 0.5182 0.7185 48.1157 2.8869

400X Speckle 0.4432 0.6632 48.2968 3.5933

Gaussian 0.5218 0.7441 47.2101 2.5686

Poisson 0.5734 0.7551 47.1749 2.5686

A Blind Noise Estimation and Removal in Histopathological Images

5 CONCLUSIONS

The noiseless image is every essential medical

domain; the detection accuracy totally relies on the

eminence of the image. As the work reported in

literature there are noise detection and removal

model developed for other modalities of the medical

image like X-Ray, MRI, Ultra-sound, CT, etc., but

there is no such model available for the microscopic

image. The model introduced in the paper estimates

the noise in microscopic image with assuming some

distributed noise such as Gaussian, Poisson, and

speckle. The approach is based on the blind noise

estimation technique using the block selection

method. The block size of the model is 8, DWT is

used because it accurately analyses the images with

abrupt changes as it is well localized in terms of

frequency and time. The denoising is performed

using differentiating estimated noise from noisy

image. The result is described in signal to noise ratio

and error is also calculated and the model performs

well for all the magnification level. The lower values

of MSE and RMSE and higher values of SNR &

PSNR indicates the betterment of proposed

enhancement model. In future we would like to

develop an estimation model based on the filtering

approach and for denoising statistical approach, this

could result in better SNR value.

REFERENCES

Breast Cancer Histopathological Database (BreakHis).

(2014). Retrieved September 30, 2019, from

https://web.inf.ufpr.br/vri/databases/breast-cancer-

histopathological-database-breakhis/

Coifman, R. R., & Donoho, D. L. (1995). Translation-

Invariant De-Noising.

Coupé, P., Manjón, J. V., Gedamu, E., Arnold, D., Robles,

M., & Collins, D. L. (2010). Robust Rician noise

estimation for MR images. Medical Image Analysis,

14(4), 483–493.

https://doi.org/10.1016/j.media.2010.03.001

Dogra, A., Goyal, B., Agrawal, S., & Sohi, B. S. (2017).

Anatomical and Functional Imaging Modalities : A

Brief Review, 9028, 113–118.

Gonzalez, R., & Woods, R. (2002). Digital image

processing. Prentice Hall.

https://doi.org/10.1016/0734-189X(90)90171-Q

Goyal, B., Dogra, A., Agrawal, S., & Sohi, B. S. (2018).

Noise issues prevailing in various types of medical

images. Biomedical and Pharmacology Journal, 11(3),

1227–1237. https://doi.org/10.13005/bpj/1484

Gravel, P., Beaudoin, G., & De Guise, J. A. (2004). A

method for modeling noise in medical images. IEEE

Transactions on Medical Imaging, 23(10), 1221–1232.

https://doi.org/10.1109/TMI.2004.832656

Ilango, G., & Marudhachalam, R. (2011). New hybrid

filtering techniques for removal of gaussian noise from

medical images. ARPN Journal of Engineering and

Applied Sciences, 6(2), 8–12.

Jain, A. (1989). Fundamentals of digital image processing.

Retrieved from

http://www.amazon.co.uk/Fundamentals-Processing-

Prentice-Information-

Sciences/dp/0133361659%5Cnhttp://dl.acm.org/citatio

n.cfm?id=59921

Jaiswal, A. K., & Srivastava, R. (2020). Time-efficient

spliced image analysis using higher-order statistics.

Machine Vision and Applications, 31(7–8).

https://doi.org/10.1007/s00138-020-01107-z

Jiang, W., Shen, T. Z., Jiang, W., & Lam, K. M. (2009).

Efficient Edge Detection Using Simplified Gabor

Wavelets. IEEE Transactions on Systems, Man, and

Cybernetics, Part B: Cybernetics, 39(4), 1036–1047.

https://doi.org/10.1109/TSMCB.2008.2011646

Kaur, S. (2015). Noise Types and Various Removal

Techniques. Nternational Journal of Advanced

Research in Electroni Cs and Communication

Engineering (IJARECE), 4(2), 226–230.

Kumar, R., Srivastava, S., & Srivastava, R. (2017). A

fourth order PDE based fuzzy c- means approach for

segmentation of microscopic biopsy images in

presence of Poisson noise for cancer detection.

Computer Methods and Programs in Biomedicine,

146, 59–68.

https://doi.org/10.1016/j.cmpb.2017.05.003

Manjón, J. V., Coupé, P., & Buades, A. (2015). MRI noise

estimation and denoising using non-local PCA.

Medical Image Analysis, 22(1), 35–47.

https://doi.org/10.1016/j.media.2015.01.004

Pan, X., Zhang, X., & Lyu, S. (2012). Blind local noise

estimation for medical images reconstructed from

rapid acquisition. Medical Imaging 2012: Image

Processing, 8314, 83143R.

https://doi.org/10.1117/12.910857

Ram, B. P., & Choudhary, S. (2014). Survey Paper on

Different Approaches for Noise Level Estimation and

Denoising of an Image. International Journal of

Science and Research, 3(4), 618–622.

Spanhol, F. A., Oliveira, L. S., Petitjean, C., & Heutte, L.

(2016). A Dataset for Breast Cancer Histopathological

Image Classification. IEEE Transactions on

Biomedical Engineering, 63(7), 1455–1462.

https://doi.org/10.1109/TBME.2015.2496264

Ting, F. F., Sim, K. S., & Wong, E. K. (2017). A rapid

medical image noise variance estimation method.

Proceedings of 2016 International Conference on

Robotics, Automation and Sciences, ICORAS 2016.

https://doi.org/10.1109/ICORAS.2016.7872628

Yousuf, M. A., & Nobi, M. N. (2010). A New Method to

Remove Noise in Magnetic Resonance and Ultrasound

Images. Journal of Scientific Research, 3(1), 81.

https://doi.org/10.3329/jsr.v3i1.5544

ICACSE 2021 - International Conference on Advanced Computing and Software Engineering