Application of Yavadunam Tavadunikritya Varganca Yojayet to

Build N-BIT Binary Squaring Algorithm

Shatrughna Ojha

, Vandana Dubey

, S. P. Tripathi

, O. P. Singh

and G. R. Mishra

Amity School of Engineering & Technology, Amity University Uttar Pradesh, Lucknow Campus, India

R. R. Institute of Modern Technology, Lucknow, India

Department of Physics and Electronics, Dr. R. M. L. Avadh University, Ayodhya, India

gr_mishra@rediffmail.com

Keywords: Yavadunam Tavadunikritya Varganca Yojayet, Vedic Mathematics and Squaring Circuit.

Abstract: Generation of N-BIT binary squaring algorithm using Yavadunam Tavadunikritya Varganca Yojayet, one of

the Vedic Mathematics formulae by Swami Bharati Krishna Tirthaji. In this paper, we propose a concocted

binary squaring algorithm to be further utilized for improvements in building efficient logic circuits for the

squaring purpose. The algorithm is novel in itself and it is programmatically executed using C++ to make an

analogy for better simulation. The algorithm is recursive in nature and is objected to minimize the steps of

logic circuits used for efficient binary squaring.

1 INTRODUCTION

1.1 Vedic Mathematics

Vedic mathematics is a compendium of 16 Sutras

(formulae) and 13 sub-sutras (Corollaries) presented

by an Indian sage, Shri Bharati Krishna Tirthajee, in

his book Vedic Mathematics (Das, Subhamoy,2020)

. First published in 1965, the book is considered to

be as a major milestone achieved in the field of

speed calculation. Swami Bharati Krishna Tirtha

claimed that these formulae and corollaries were

extracted from Atharva Veda. As per the statements

by Swami Bharati Krishna Tirtha, he worked on

Vedas, the sacred ancient Indian scriptures, for many

years while living in seclusion. However, Swami

Bharati Krishna Tirtha faced a major criticism for

his failure to produce the proofs for his claims. A

thorough research has been done on the authenticity

of Swami Tirtha’s claims and the claims have been,

supposedly, debunked by the scholars unanimously,

noting that these set of formulae were mere

collection of tricks with no relation with the

mathematical developments of Vedic period [2]. A

closer look into the formulae shows the application

of deductive reasoning. Nevertheless, it is tough to

deny the fact that some Vedic tricks reduce the

cumbersome effort required in operating on bigger

numbers.

The algorithm proposed in this paper is an

amalgamation of a Vedic mathematics sutra -

Urdhva Triyagbhyam and a corollary of another

Vedic mathematics Sutra - Sankalana

Vyaykalanabhyam [3], named Yavadunam

Tavadunikritya Varga Yojayet. In fact, the presented

algorithm is by far the simplified binary

representation of usage of Yavadunam

Tavadunikritya Varga Yojayet. It is an efficient

approach of recursive nature for finding the square

of any number. This paper presents an algorithm to

find the square of any binary number in an efficient

manner. The code for our algorithm presented in this

paper is based on decimal to binary conversion.

However, the presented algorithm is sought to be

used in digital squaring circuits and purely based on

binary operations.

1.2 Urdhva Triyagbhyam

It is one of the 16 formulae of Vedic Mathematics

which means “Vertical and Crosswise” (Jagadguru

Swami et al 2009), this formula is used to calculate

the product of two numbers in one line of answer.

The product of two numbers is result of certain

number of product and sum of products, vertically

and crosswise respectively. The use of Urdhva

190

Ojha, S., Dubey, V., Tripathi, S., Singh, O. and Mishra, G.

Application of Yavadunam Tavadunikritya Varganca Yojayet to Build N-BIT Binary Squaring Algorithm.

DOI: 10.5220/0010565000003161

In Proceedings of the 3rd International Conference on Advanced Computing and Software Engineering (ICACSE 2021), pages 190-193

ISBN: 978-989-758-544-9

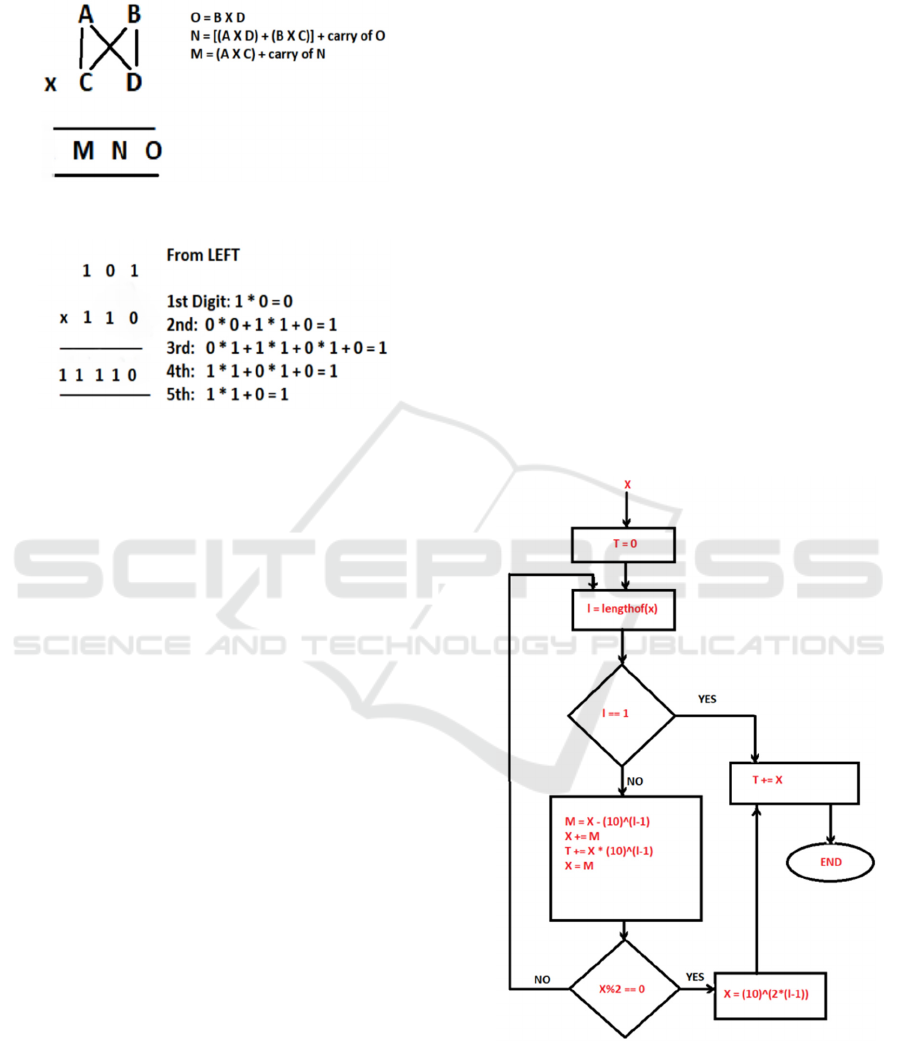
Triyagbhyam is desired in the binary product

operations in the algorithm presented in this paper.

Figure 1: Urdhva-Triyakbhyam

Figure 2: Example of Urdhva-Triyakbhyam

1.3 Yavadunam Tavadunikritya Varga

Yojayet

It is a corollary of another Vedic mathematics Sutra

- Sankalana Vyaykalanabhyam. This method is used

to find the square of any number without long

calculations and it is certainly better than the

conventional method of finding the square of a

number by simple multiplication. It requires lesser

number of steps to perform a squaring operation

(Jagadguru Swami et al 2009).

2 PROPOSED ALGORITHM

2.1 Related Works

In (Elango S Deepa R, 2018), Deepa A et al. have

made a satiating review on the different Vedic

formulae used to enhance the capacity of different

squaring circuits and design.

In (A. Deepa and C. N. Marimuthu, 2018),

Deepa A et al have proposed a Vedic squaring

architecture based on Yavadunam algorithm. This

paper proposed an enhanced architecture of

Yavadunam by using bit reduction technique.

Moreover, (Nisha Angeline M & Anjali M,

2018) overcomes the issue related to delay in

multipliers as it states that the array multiplier for

Vedic multiplication gives a total of 6.45ns which is

less as compared to the total delay of other

multipliers, and the power consumption is low for

the Vedic multiplication with the Wallace tree

multiplier rather than the Baugh-Wooley multiplier.

2.2 Contrast

The algorithm proposed in our paper contrasts from

(A. Deepa and C. N. Marimuthu, 2018) in a very

subtle manner. It proposes a direct output for binary

numbers like 2

. That is, the algorithm outputs the

direct value (ie. Square of 2

= 2

(2N-1)

) for such

binary numbers. (A. Deepa and C. N. Marimuthu,

2018) has utilized both the methods (Method 1: The

given number is greater than 2

N-1

Method 2: The

given number is lesser than 2

N-1

.) of using

Yavadunam Tavadunikritya Varga Yojayet [7]. In

our algorithm architecture we have used the former

as the universal way of fast squaring of any number

of bits.

2.3 Proposed Algorithm and

Explanation

Figure 3: An Efficient Algorithm for N-bit Binary

Squaring Approach utilising amalgamation of Vedic

Sutras

Application of Yavadunam Tavadunikritya Varganca Yojayet to Build N-BIT Binary Squaring Algorithm

191

2.4 Algorithm

Step 1: Input the binary number X that has to be

squared.

Step 2: Set the result T = 0.

Step 3: Find the length l of Input X.

Step 4: 1) If length l = 1 then add X to T and output

T, and stop the program.

2) Else, move to the next step.

Step 5: Set temporary variable M = X – 2

(l-1)

Step 6: Set X = X + M.

Step 7: Set T = T + (X * 2

(l-1)

Step 8: Set X = M

Step 9: 1) If X mod 2 = 0, set X = 2

2*(l-1)

and further

add X to T, and stop the program.

2) Else, go to step 3.

Step 10: Output result T.

Step 11: End the program.

2.5 Simulation

Figure 4: Simulation of Proposed Algorithm

2.6 Code

This code is a C++ implementation of the algorithm.

In this code, Yavadunam Tavadunikritya Varga

Yojayet is first applied on a decimal number and the

result is converted into binary.

#include <cmath>

#include <iostream>

#include <bits/stdc++.h>

using namespace std;

#define ull unsigned long long int

// Function to return the binary

// equivalent of decimal value N

int decimalToBinary(int N){

// To store the binary number

ull B_Number = 0;

int cnt = 0;

while (N != 0) {

int rem = N % 2;

ull c = pow(10, cnt);

B_Number += rem * c;

N /= 2;

// Count used to store exponent value

cnt++; }

return B_Number; }

int countDigit(long long n){

if (n == 0)

return 0;

return 1 + countDigit(n / 10); }

int SquareFinder(int X){

int M, Result, T=0;

while(countDigit(X) != 1){

M = X - pow(10, countDigit(X)-1);

X += M;

T += X * pow(10, countDigit(X)-1);

X = M; }

if(countDigit(X)==1)

T += X*X;

return T; }

// Driver code

int main(){

int e;

int N = 2;

cout<<"Enter\n";

cin>>e;

cout <<decimalToBinary(SquareFinder(e));

return 0;

}

ICACSE 2021 - International Conference on Advanced Computing and Software Engineering

192

3 CONCLUSION

An efficient and generalized algorithmic

transformation of Vedic Sutra- Yavadunam

Tavadunikritya Varga Yojayet is proposed with its

analysis and simulation. A C++ program is written

to show the working of the former mentioned

algorithm. The code can twin the algorithm if it is

applied on a purely binary programming language.

The future work is to design digital circuits based on

this algorithm and to look for further possibilities to

reduce the number of steps required in this approach

(Pabitra Kumar Mohapatra, 2018; Prabha 2011;

Shatrughna Ojha, 2020, Vandana Shukla) . The

algorithm has many such possibilities, like-

completely remove the binary operations for inputs

in the form of 2

and produce direct results for the

same without any binary operation being applied on

the input.

REFERENCES

Das, Subhamoy. "The 16 Sutras of Vedic Math." Learn

Religions, Feb. 11, 2020, learnreligions.com/vedic-

math-formulas-1770680.

Shatrughna Ojha, Vandana Shukla, O. P. Singh, G. R.

Mishra, R. K. Tiwari, “A Novel Approach for 4-Bit

Squaring Circuit Using Vedic Mathematics”, Smart

Innovations in Communication and Computational

Sciences. Advances in Intelligent Systems and

Computing, Editors: S. Tiwari, M. Trivedi, K. Mishra,

A. Misra, K. Kumar, E. Suryani, vol 1168, Springer,

Singapore: Print ISBN 978-981-15-5344-8, Online

ISBN978-981-15-5345-5, 2020.

Vandana Shukla, O. P. Singh, G. R. Mishra, R. K. Tiwari,

“A Novel Approach for Reversible Realization of 4 X

4 BIT Vedic Multiplier Circuit”, Advances in VLSI,

Communication, and Signal Processing.

Myths and reality : On ‘Vedic mathematics’ S.G. Dani

School of Mathematics Tata Institute of Fundamental

Research.

Jagadguru Swami Sri Bharati Krishna Tirthaji

Maharaj,“Vedic Mathematics”, Delhi: Motilal

Banarsidas Publishers Pvt.Ltd. , (2009).

Elango S Deepa R, “Implementation of Low Area FIR

Filters Using Vedic Multiplication Algorithm”,

Journal of Engineering and Applied Sciences, Vol. 13

(05), pp. 4733-4738, 2018.

A. Deepa and C. N. Marimuthu, “High Speed VLSI

Architecture for Squaring Binary Numbers Using

Yavadunam Sutra and Bit Reduction Technique”,

International Journal of Applied Engineering Research

ISSN 0973-4562 Volume 13, Number 6 (2018) pp.

4471-4474

Nisha Angeline M & Anjali M, “DESIGN AND

ANALYSIS OF VEDIC MULTIPLIER BASED ON

YAVADUNAM TAVADUNIKRITYA VARGA

YOJAYET SUTRA”, International Journal of

Advance Research in Engineering, Science &

Technology (IJAREST) Volume 5, Issue 3, March

2018, e-ISSN: 2393-9877, print-ISSN: 2394-2444

http://www.vedamu.org/Veda/1795$Vedic_Mathematics_

Methods.pdf

Pabitra Kumar Mohapatra, Siba Kumar Panda, Sambita

Dalal, Shibashis Pradhan,”VHDL implementation of a

Novel Low power squaring circuit using YTVY

algorithm of Vedic Mathematics ”, International

Journal of Emerging Trends in Science and

Technology, Vol.02, No.3, pp.2139- 2146, (2015).

Prabha S. Kasliwal, B. P. Patil and D. K. Gautam,”

Performance evaluation of squaring operation by

Vedic Mathematics, ”IETE Journal of Research,

pp.39-41, (2011).

Application of Yavadunam Tavadunikritya Varganca Yojayet to Build N-BIT Binary Squaring Algorithm

193