Boolean Exponent Splitting

Michael Tunstall

1 a

, Louiza Papachristodoulou

and Kostas Papagiannopoulos

3 b

Rambus, 4453 North First Street, Suite 100, San Jose, California, U.S.A.

Fontys University of Applied Sciences, Rachelsmolen 1, Eindhoven, The Netherlands

University of Amsterdam, SNE-CCI, Science Park 904, Amsterdam, The Netherlands

Keywords:

Exponent Splitting, Side-channel Attacks, Countermeasures.

Abstract:

A typical countermeasure against side-channel attacks consists of masking intermediate values with a random

number. In symmetric cryptographic algorithms, Boolean shares of the secret are typically used, whereas in

asymmetric algorithms the secret exponent is typically masked using algebraic properties. This paper presents

a new exponent splitting technique with minimal impact on performance based on Boolean shares, typically

requiring only an extra register and a few register copies per bit. We perform a security evaluation of our

algorithms using a mutual information framework and provide proofs that they are secure against ﬁrst-order

side-channel attacks. The side-channel resistance of the proposed algorithms are also practically veriﬁed with

test vector leakage assessment performed on Xilinx’s Zynq zc702 evaluation board.

1 INTRODUCTION

Side-channel analysis as a method of extracting cryp-

tographic keys was ﬁrst presented by Kocher (Kocher,

1996), who noted that timing differences in the execu-

tion time of a modular exponentiation could be used

to break instances of RSA (Rivest et al., 1978). Sub-

sequently, Kocher et al. (Kocher et al., 1999) observed

that the instantaneous power consumption could re-

veal information on intermediate states of any cryp-

tographic algorithm, since the instantaneous power

consumption has, in many cases, been shown to be

proportional to the Hamming weight of the data be-

ing manipulated (Brier et al., 2004), and it was later

shown that the electromagnetic emanations around a

device can be exploited in the same way (Gandolﬁ

et al., 2001; Quisquater and Samyde, 2001).

In public key cryptography, one typically uses

countermeasures based on redundant representations

to prevent side-channel leakage (Coron, 1999; Win

et al., 1998) (referred to as blinding). To protect an ex-

ponent used in a group exponentiation one would typ-

ically add a random multiple of the order of the group

to the exponent, providing a random bitwise repre-

sentation of the exponent. These countermeasures

can provide a strong resistance to Differential Power

https://orcid.org/0000-0002-7107-8644

https://orcid.org/0000-0002-5008-1756

Analysis (DPA), but are not convenient in some in-

stances. As noted by Smart et al. (Smart et al., 2008),

the random value used to blind an exponent needs to

have a bit length larger than the longest run of zeros

or ones in the bitwise representation of the the order

of the group. If we consider ECDSA (National Insti-

tute of Standards and Technology (NIST), 2009), for

example, the bitwise representations of the orders of

the groups used contain long runs of ones making this

countermeasure costly.

In this paper, we present a new countermeasure for

exponent splitting. We describe a method of splitting

an exponent into two Boolean shares, analogous to

the countermeasures that one would use for an imple-

mentation of a block cipher and similar to the coun-

termeasures used to prevent address-bit side-channel

attacks (Messerges et al., 1999; Messerges and Dab-

bish, 1999; Itoh et al., 2002). Having embedded de-

vices as our targeted implementation, and an adver-

sary able to get useful information from the length of

the exponent or the intermediate values, we provide a

number of secure algorithms against a broad range of

side-channel attacks.

At the same time, the modiﬁcations that are re-

quired to a group exponentiation algorithm have neg-

ligible effect on the time required to compute the ac-

tual group exponentiation, which is a signiﬁcant ad-

vantage over previous examples of exponent split-

ting (Clavier and Joye, 2001; Ciet and Joye, 2003). In

Tunstall, M., Papachristodoulou, L. and Papagiannopoulos, K.

Boolean Exponent Splitting.

DOI: 10.5220/0010570903210332

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 321-332

ISBN: 978-989-758-524-1

321

addition, our method can be efﬁciently combined with

blinding techniques applied to the input to a group ex-

ponentiation algorithm, in order to prevent leakage of

the intermediate values.

We present an evaluation of the method of

Boolean exponent splitting using the information-

theoretic framework of Standaert et al. (Standaert

et al., 2009) and a Test Vector Leakage Assessment

(TVLA) by Goodwill et al. (Goodwill et al., 2011).

We investigate the usual leakage models based on data

or location leakage and show that an adversary would

need either a second-order data attack or a third-order

location attack to successfully break the security of

our algorithms. In addition, we present for the ﬁrst

time a hybrid model, where data leakage is combined

with location leakage, offering new exploitation op-

portunities. The rich interactions between data and lo-

cation leakage corroborates the need for holistic coun-

termeasures that encompass a wide spectrum of side-

channel attacks.

2 EXPONENT SPLITTING

METHODS

The critical operation in public key cryptographic al-

gorithms is exponentiation in a certain group G of or-

der µ, where the input message x ∈ G is raised by a

secret exponent κ and the result y = x

is the pub-

lic output of the algorithm. When implementing a

group exponentiation algorithm the exponent is typ-

ically blinded by adding some random multiple of

the order of the group to the exponent. Trivially,

(rµ) + κ ≡ κ (mod µ) for r,κ ∈ Z where r is random.

Hence, computing x

κ+rµ

is equivalent to computing

. While this randomizes the bitwise representation

of an exponent, the entire exponent is still equivalent

to the exponent in a given group. Examples of attacks

that have been proposed include analyzing a single

trace (from SPA (Kocher et al., 1999) to collisions

in manipulated values (Witteman et al., 2011; Kim

et al., 2010; Hanley et al., 2015)) or attempting to ﬁnd

collisions in the random values used to then derive a

(blinded) exponent (Schindler and Itoh, 2011).

One method that can hinder these attacks, is to

split an exponent into two values whose bitwise rep-

resentations are random. Then one would compute

a group exponentiation where the combined effect of

the two values is equivalent to that of the desired ex-

ponent. Randomly splitting the value that manipu-

lates secret data was proposed initially by Chari et.

al in (Chari et al., 1999) as a generic technique to

provide provable resistant implementation to side-

channel attacks. By randomly splitting every bit of

the original computation into m shares, where each

share is equiprobably distributed and every proper

subset of m − 1 shares is statistically independent of

the encoded bit, the cryptographic computation can

then be performed securely by computing only the

shares, without ever reconstructing the original bit.

The leakage from every computation does not reveal

any useful information to the adversary, who needs

to perform m attacks to reconstruct the secret. There

are several methods of exponent splitting proposed by

Clavier and Joye (Clavier and Joye, 2001):

• Additive Splitting. For a random integer r with

bit-length smaller or equal to the exponent κ, we

can deﬁne κ = r +(κ − r). The output of the mod-

ular exponentiation y = x

in G can be computed

by y = x

· x

κ−r

in G.

• Multiplicative Splitting. For some group G we

can deﬁne k

= k r

−1

mod |G| for some integer r.

Then the exponentiation y = x

in G can be com-

puted by using y = (x

)

mod |G|.

The same techniques can be applied to scalar multi-

plication algorithms for elliptic curves (ECs), in or-

der to hide the secret scalar. The problem with these

methods of exponent splitting is that one is required

to know the order of the group G, which may not be

available in some instances. They will also typically

double the time required to compute a group expo-

nentiation, because r is required to have a bit-length

similar to the exponent. A practical attack by Feix

et al. (Feix et al., 2014) demonstrates that a blinded

scalar can be determined if r is too small.

A further method described by Ciet and Joye (Ciet

and Joye, 2003) is:

• Euclidean Splitting. By writing the exponent as

k = bk/rcr+k mod r and letting s = x

for some r,

then y = x

can be computed by y = s

×x

k mod r

)

× x

k mod r

, where k

= bk/rc.

The impact on the time required to compute an ex-

ponentiation is lower than the other splitting methods

listed above. In fact, in (Ciet and Joye, 2003) the au-

thors evaluated this variant applied to Shamir’s dou-

ble ladder to have the same cost as the ‘double-and-

add-always’ algorithm (equivalent to the ‘square-and-

multiply-always’ for exponentiation). Precomputa-

tion of powers of s can reduce the exponentiation cost

compared to additive or multiplicative splitting. How-

ever, this method has the same constraints as adding

a multiple of the group order. That is, r needs to have

a bit length larger than the longest run of ones and

zeros in k and may have a signiﬁcant impact on per-

formance (Smart et al., 2008). A secure division al-

gorithm is also required, see, for example, Joye and

Villegas (Joye and Villegas, 2002).

SECRYPT 2021 - 18th International Conference on Security and Cryptography

322

3 BOOLEAN EXPONENT

SPLITTING METHODS

In this section, we propose methods of exponent split-

ting based on XOR operation, and how an XOR-split

exponent can be applied to the Montgomery powering

ladder.

3.1 Montgomery Powering Ladder

The Montgomery Powering Ladder (MPL) was origi-

nally proposed as a means of speeding up scalar mul-

tiplication over ECs and later shown to be applica-

ble to multiplicative written Abelian groups (Mont-

gomery, 1987; Joye and Yen, 2002). We recall the

description of the MPL given by Joye and Yen (Joye

and Yen, 2002): We consider the problem of comput-

ing y = x

in G for inputs x and κ. Let

∑

n−1

i=0

the binary expansion of κ with bit length n (for ease of

expression we shall also denote this as (k

n−1

,... , k

)

where convenient). Then, deﬁning L

∑

n−1

i= j

i− j

and H

= L

+ 1, we have L

= 2 L

j+1

+ k

= L

j+1

+ k

− 1 = 2H

j+1

+ k

− 2 and so we obtain

) =











(2L

j+1

+ H

j+1

) if k

= 0,

j+1

+ H

j+1

,2H

j+1

) if k

= 1.

(1)

If we consider one register containing x

and another

containing x

then (1) implies that

) =















j+1



j+1

· x

j+1



if k

= 0,



j+1

· x

j+1



j+1





if k

= 1.

(2)

Given that L

= k one can build an exponentiation

algorithm that requires two group operations per bit

of the exponent. Joye and Yen give several different

versions, one of which is shown in Algorithm 1. All

these methods are highly regular, meaning that a de-

terministic sequence of operations is executed for an

exponent of a given bit length.

Algorithm 1: Montgomery Ladder.

Input: x ∈ G, an n-bit integer κ =

∑

n−1

i=0

Output: x

1 R

← 1

; R

← x ;

2 for i = n − 1 down to 0 do

3 R

¬k

← R

· R

¬k

;

4 R

← (R

)

;

5 end

6 return R

In applying an XOR-split exponent to MPL we use

one share to dictate the address accessed and the other

to act as the exponent. That is, we consider (1),

where the previous round may provide either (L

)

or (H

) and the computation changed accordingly.

Let S

0, j

= L

and S

1, j

= H

and

∑

n−1

i=0

be the

binary expansion of A with bit length n (i.e. the same

bit length as the exponent). Then we can use the val-

ues of a

to dictate whether a pair of registers holds

) or (H

). Speciﬁcally, (1) can be rewritten

as:

, j

¬a

, j

) =











(2S

, j+1

+ S

¬a

, j+1

) if k

= 0,

, j+1

+ S

¬a

, j+1

,2S

¬a

, j+1

) if k

= 1.

(3)

In (3), the values of L

and H

are assigned to S in

an order dictated by the binary expansion of A. Gen-

erating A as a random sequence of bits could provide

some side-channel resistance, but does not protect the

exponent.

We further consider

∑

n−1

i=0

and

∑

n−1

i=0

the binary expansion of A and B, respectively, where

κ = A ⊕ B of bit length n. We note that, as above,

∑

n−1

i=0

is the binary expansion of κ and k

= a

⊕b

for 0 ≤ i < n. Then (3) can be rewritten as:

, j

¬a

, j

) =











(2S

, j+1

+ S

¬b

, j+1

) if k

= 0,

, j+1

+ S

¬b

, j+1

,2S

¬b

, j+1

) if k

= 1.

(4)

Rather than using the same value to control which or-

der L

and H

are assigned and read, we use the bits

of A to determine the order L

and H

are assigned,

and the bits of B to determine the order they are read.

The combined effect is that the order L

and H

are

assigned and read is dictated by the bits of κ.

, j

¬a

, j

) =













, j+1



, j+1

· x

¬b

, j+1

if k

= 0,

, j+1

· x

¬b

, j+1



¬b

, j+1



if k

= 1.

(5)

From which we can deﬁne Algorithm 2, which oper-

ates in much the same way as the MPL, as it produces

a regular sequence of multiplications and squaring

operations. However, one more register is required

to allow the assignment in line 5 to affect R

or R

This algorithm is the basis that we use to present the

essence of Boolean-split exponent. Algorithm 2 is

largely equivalent to an algorithm proposed by Izumi

et al. (Izumi et al., 2010) where we set the multi-

plication in line 4 to operate in a random order as

it provides a better resistance to collision attacks, as

demonstrated by Kim et al. (Kim et al., 2010). We

discuss this further in Section 3.2.

The intermediate states of the registers are not ran-

domized in Algorithm 2 and would require additional

countermeasures to provide a secure implementation.

Boolean Exponent Splitting

323

Algorithm 2: Montgomery Ladder with XOR-Split

Exponent I.

Input: x ∈ G, n-bit integers A =

∑

n−1

i=0

and B =

∑

n−1

i=0

Output: x

where κ = A ⊕ B

1 R

← 1

; R

← 1

; R

← 1

;

2 b

←− {0, 1} ; R

¬b

← x ;

3 for i = n − 1 down to 0 do

4 R

← R

· R

¬a

;

5 R

←



⊕b

)⊕a



;

6 R

¬a

← R

;

7 b

← b

;

8 end

9 return R

For example, inexpensive solutions such as random-

izing projective points (Win et al., 1998) or Ebeid and

Lambert’s blinding method for RSA (Ebeid and Lam-

bert, 2010) can be used (see Section 5). If we as-

sume that the values held in registers {R

} do

not leak (i.e., we only consider whether the exponent

leaks) we can state the following:

Lemma 1. Assuming that the values held in registers

} do not leak, an implementation of Algo-

rithm 2 is resistant to ﬁrst-order side-channel analy-

sis.

Proof. It sufﬁces to consider each intermediate state

and verify that at least one random mask is ap-

plied. Verifying this for an entire group exponenti-

ation would be tedious, but can be simpliﬁed if we

consider two rounds of Algorithm 2. That is, if we

consider round m, where 0 ≤ m ≤ n − 2, then the fol-

lowing operations are performed:

1. R

← R

· R

¬a

2. α ← b

⊕ b

3. β ← α ⊕ a

4. R

← R

5. R

¬a

← R

6. R

← R

m+1

· R

¬a

m+1

7. α ← b

m+1

⊕ b

8. β ← α ⊕ a

m+1

9. R

m+1

← R

10. R

¬a

m+1

← R

Let the proposition P (n) be that round n > 0 is re-

sistant to ﬁrst-order side-channel analysis for the n-th

treated bit of the exponent. If we consider the ﬁrst

round, we wish to show P(1) is true and, in the above

code fragment, b

is set to a random value from {0,1}.

Then, it is easy to see that:

• the results of the operations in lines 1, 4, 5, 6,

9 and 10 are dependent on the random values

• the results of the operations in lines 2, 3, 7 and 8

are uniformly distributed on {0,1}.

If we assume that P (m) is true for all m ∈ {1,... , n},

then we consider P (n + 1) where b

is set to b

. As

is one share of a previously treated exponent bit, it

is indistinguishable from a random value from {0,1}.

The above statements regarding the results of the op-

erations apply. Hence, by induction we have shown

P (n) is true for all n > 0. To complete the proof, we

simply note that only half of the code fragment above

will need to be considered in the last round.

Remark. In (Itoh et al., 2003), the authors present the

randomized addressing method (RA), in order to pro-

vide protection against address-based DPA and elim-

inate the correlation between an exponent bit and the

this work, we do not limit our countermeasure to work

only against address-based DPA. Our goal is to per-

form operations on different exponent shares, in a way

that an adversary would need a combination of leak-

ages (such as higher-order DPA combined with tem-

plate attacks) in order to recover the exponent.

3.2 Using Inverses

In this section we propose an algorithm more suited

to groups where inversions can be readily computed.

Le Duc et al. (Le et al., 2015) propose a straight-

forward variant of the Montgomery powering ladder

that requires the computation of inverses. They note

that (1) can be rewritten as:

) =











− 1, L

j+1

+ H

j+1

) if k

= 0,

j+1

+ H

j+1

+ 1) if k

= 1.

(6)

From which we can deﬁne Algorithm 3. If we let

0, j

= L

and T

1, j

= H

, or T

0, j

= H

and T

1, j

= L

and

store the ordering in another variable we can rewrite

(6) as:

0, j

1, j

) =

(

) if k

= 0

) if k

= 1

(

j+1

+ H

j+1

− 1) if k

= 0,

j+1

+ H

j+1

+ 1) if k

= 1.

(7)

From which we can deﬁne Algorithm 4.

Following the previous notation, we notice that T

0, j

should contain the sum of the registers in the previous

round

. Therefore, (7) can be rewritten as follows:

0, j

1, j

) =











, j+1

+ T

¬b

, j+1

0, j

− 1) if k

= b

= 0,

, j+1

+ T

¬b

, j+1

0, j

+ 1) if k

= b

= 1.

(8)

The algorithms are left-to-right, so j + 1 indicates the

round preceding j.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

324

Algorithm 3: Variant with Inverses I.

Input: x ∈ G, an n-bit integer κ =

∑

n−1

i=0

Output: x

1 R

← 1

; R

← x ;

2 U

← x

−1

; U

← x ;

3 for i = n − 1 down to 0 do

4 R

¬k

← R

· R

¬k

;

5 R

← R

¬k

·U

;

6 end

7 return R

Algorithm 4: Variant with Inverses II.

Input: x ∈ G, an n-bit integer κ =

∑

n−1

i=0

Output: x

1 R

← 1

; R

← x ;

2 U

← x

−1

; U

← x ;

3 for i = n − 1 down to 0 do

4 R

← R

· R

;

5 R

← R

·U

;

6 end

7 return R

¬k

We note that to treat k

j+1

, b

= k

. However, if we let

= a

⊕b

, for a

∈ {0,1} and h = a

⊕b

j−1

we can modify (8) as follows:

0, j

1, j

) =

(

¬h, j+1

+ T

h, j+1

0, j

− 1) if a

= b

¬h, j+1

+ T

h, j+1

0, j

+ 1) if a

= ¬b

(9)

By using the above equations as exponents of x, we

can deﬁne Algorithm 5.

Algorithm 5: Montgomery Ladder with XOR-Split

Exponent II.

Input: x ∈ G, n-bit integers A =

∑

n−1

i=0

and B =

∑

n−1

i=0

, r ∈

Output: x

where κ = A ⊕ B

1 R

← 1

; R

← 1

; U

← x ; U

← x

−1

;

2 b

←− {0, 1} ; R

¬b

← x ;

3 for i = n − 1 down to 0 do

4 R

← R

⊕b

· R

⊕b

)⊕a

;

5 R

← R

·U

;

6 b

← b

;

7 end

8 return R

Algorithm 5 follows the same sequence of instruc-

tions with the MPL. Its correctness can be veriﬁed by

the fact that at every round the difference R

= x

or R

= x, as for the usual ladder step. The ad-

vantage of Algorithm 5 compared to Algorithm 2,

and consequently previously proposed algorithms by

Izumi et al. (Izumi et al., 2010), is the elimination of

the auxiliary register R

. Instead, the auxiliary regis-

ters U

manipulate the known ﬁxed value x or x

−1

for computational purposes, and they do not require

additional computational power or updates when the

algorithm is executed.

As previously, if we assume that the values held

in registers {R

} do not leak we can state the fol-

lowing:

Lemma 2. Assuming that the values held in regis-

ters {R

} do not leak, an implementation of Algo-

rithm 5 is resistant to ﬁrst-order side-channel analy-

sis.

Proof. It sufﬁces to consider each intermediate state

and verify that at least one random mask is ap-

plied. Verifying this for an entire group exponenti-

ation would be tedious, but can be simpliﬁed if we

consider two rounds of Algorithm 5. That is, if we

consider round m, where 0 ≤ m ≤ n − 2, then the fol-

lowing operations are performed:

1. α ← b

⊕ b

2. β ← α ⊕ a

3. R

← R

· R

4. R

← R

·U

5. α ← b

m+1

⊕ b

6. β ← α ⊕ a

m+1

7. R

← R

· R

8. R

← R

·U

m+1

Let the proposition P (n) be that round n > 0 is re-

sistant to ﬁrst-order side-channel analysis for the n-

th treated bit of the exponent. If consider the ﬁrst

round, we wish to show P(1) is true and, in the above

code fragment, b

is set to a random value from {0,1}.

Then, it is easy to see that:

• the results of the operations in lines 3, 4, 7 and 8

are dependent on the random values {R

• the results of the operations in lines 1, 2, 5 and 6

are uniformly distributed on {0,1}.

If we assume that all P (m) is true for m ∈ {1,... , n},

then we consider P (n + 1) where b

is set to b

. As

is one share of a previously treated exponent bit, it

is indistinguishable from a random value from {0,1}.

The above statements regarding the results of the op-

erations apply. Hence, by induction we have shown

P (n) is true for all n > 0. To complete the proof, we

simply note that only half of the code fragment above

will need to be considered in the last round.

Boolean Exponent Splitting

325

3.3 Boolean Scalar Splitting

In the above, we deﬁne group exponentiations appli-

cable to any multiplicatively written group G. How-

ever, speciﬁc groups may have particular character-

istics that means the algorithms above are not suit-

able as described. In this section, we discuss the al-

gorithms in the context of a group formed from the

points on an elliptic curve (EC). We deﬁne the EC E

over a ﬁnite ﬁeld F

, for a large prime q. E consists of

points (x,y), with x,y in F

, that satisfy, for example,

the short Weierstraß equation

E : y

= x

+ a x + b

with a, b ∈ F

, and the point at inﬁnity denoted O

O. The

set E(F

) is deﬁned as E (F

) = {(x, y) ∈ E | x,y ∈

}∪ {O

O}, where E(F

) forms an Abelian group un-

der the chord-and-tangent rule and O

O is the identity

element. Alternative equations with different repre-

sentations of a neutral element are also used in cryp-

tographic algorithms, such as Edwards curves (Ed-

wards, 2007; Bernstein and Lange, 2009) and Mont-

gomery curves (Montgomery, 1987). The scalar mul-

tiplication of a given point is a group exponentiation

in E that uses elliptic curve arithmetic, i.e. addition

between points or scalar multiplication [κ]P

P for some

integer κ < |E|, and is an important part of many

cryptographic algorithms.

The algorithms presented above cannot be se-

curely implemented as described because of the neu-

tral element. In the short Weierstraß example, the

neutral element 1

is represented in E as the point at

inﬁnity O

O and cannot be manipulated in a regular way.

That is, one would typically be obliged to test for a

numerical representation of O

O and conduct a different

operation if it is detected. In practice, one would im-

plement the algorithm such that the most signiﬁcant

bit (assumed to be set to one) is already treated by the

pre-processing. For example, Algorithm 2 can be im-

plemented as shown in Algorithm 6, and Algorithm 5

as shown in Algorithm 7.

As previously, if we assume that the values held

in registers {R

} do not leak we can state the

following:

Corollary 1. Lemma 1 implies that an implementa-

tion of Algorithm 6 is resistant to ﬁrst-order side-

channel analysis.

Corollary 2. Lemma 2 implies that an implementa-

tion of Algorithm 7 is resistant to ﬁrst-order side-

channel analysis.

The exponent splitting methods detailed in this paper

do not modify the intermediate states generated and

one would expect that randomizing projective points

Algorithm 6: Montgomery Ladder with XOR-Split

Scalar on an EC.

Input: E, F

, P

P ∈ E , n-bit integers

A =

∑

n−1

i=0

and B =

∑

n−1

i=0

Output: Q

Q = [κ]P

P where κ = A ⊕ B

1 R

← P

P ; R

← P

P ; R

← P

P ;

2 b

←− {0, 1} ;

3 R

¬b

← 2P

P ;

4 for i = n − 2 down to 0 do

5 R

← R

¬a

;

6 R

← 2R

⊕b

)⊕a

;

7 R

¬a

← R

;

8 b

← b

;

9 end

10 return R

Algorithm 7: Montgomery Ladder with XOR-Split

Scalar II on an EC.

Input: E, F

, P

P ∈ E , n-bit integers

A =

∑

n−1

i=0

and B =

∑

n−1

i=0

Output: Q

Q = [κ]P

P where κ = A ⊕ B

1 R

← P

P ; R

← P

P ;

2 U

← P

P ; U

← −P

P ;

3 b

←− {0, 1} ;

4 R

¬b

← 2P

P ;

5 for i = n − 2 down to 0 do

6 R

← R

⊕b

)⊕a

;

7 R

← R

;

8 b

← b

;

9 end

10 return R

would be adequate to provide a secure solution (Win

et al., 1998). However, such multiplicative mask-

ing can be problematic if an attacker can choose and

input that could produce a point with a coordinate

set to zero, which cannot be blinded using a mul-

tiplication (Goubin, 2003). Hence, one would need

to combine our algorithms with Coron’s countermea-

sures (Coron, 1999) and add a small multiple of the

order of the group to the private key before it is used.

The bit length of the multiplier needs to be chosen

such that an attacker cannot predict the location of a

zero-coordinate with sufﬁcient reliability to make it

visible in a side-channel attack. Having a 16-bit mul-

tiplier may be sufﬁcient, depending on the signal-to-

noise ratio of the platform. The advantage of combin-

ing these countermeasures is that one does not need to

consider the longest runs of ones or zeros in the order

of the group.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

326

4 SECURITY EVALUATION

In this section, we discuss the security of the algo-

rithms presented previously, ﬁrst by making a com-

parison with the state-of-the-art algorithms and then

by providing a security evaluation of Algorithm 2,

proposed in this paper.

4.1 State-of-the-Art Comparison

In this section, we compare our proposed algorithms

with a selection of algorithms discussed in the previ-

ous sections and summarize our observations in Ta-

ble 1.

The ﬁrst block of algorithms in Table 1, con-

tain exponentiation algorithms using the Montgomery

power ladder without splitting the exponent (Algo-

rithm 1), with additive splitting or with variations of

XOR-splitting (Algorithms 2, 3, 4). Multiplicative or

Euclidean splitting are not included in this table, be-

cause in terms of security they have the same side-

channel resistance as an algorithm with additive split-

ting. In terms of performance, the number of opera-

tions is the similar, unless the values s

are precom-

puted and stored in memory.

The second block of algorithms summarizes the

behavior of the corresponding scalar multiplication

algorithms

. Algorithms 8 and 9 are presented in Sec-

tion 5.

We note that none of the algorithms in their cur-

rent form can prevent leakage from observing the in-

termediate values. However, intermediate values can

be blinded with a random value as previously de-

scribed.

4.2 Mutual Information-based Security

Evaluation

Having established that the proposed exponent split-

ting algorithms are probing-secure against ﬁrst-order

side-channel attacks, we proceed to analyze the noise

ampliﬁcation stage of the proposed countermeasure.

Analytically, we perform an evaluation of Boolean

exponent splitting (as described by Algorithm 2) us-

ing the information-theoretic framework of Standaert

et al. (Standaert et al., 2009). Analogous approaches

We do not count XORs, which can be implemented al-

most for “free” compared to the cost of multiplications (M),

squaring operations (S) and modular inversions (I) in the

chosen ﬁeld or point additions (A) and doubling operations

(D) on an elliptic curve. The subtraction of points on an

elliptic curve has the same cost as an addition, so we do not

count them separately.

can be conducted for all exponent splitting algo-

rithms, yielding very similar results. Our analysis

considers two sources of leakage, namely data-based

leakage and location-based leakage (also known as

address leakage). Using these two leakage sources,

we demonstrate three possible attack paths against

Algorithm 5, covering all possible combinations be-

tween leakage sources. Thus we show the noise am-

pliﬁcation stage when only data-based leakage is ex-

ploited (data attack), when only location-based leak-

age is exploited (location attack) and ﬁnally the noise

ampliﬁcation stage when the adversary combines data

and location leakage (hybrid attack).

4.2.1 Notation & MI Metric

In this subsection, random variables are denoted with

capital letters. Instances of random variables and con-

stant values are denoted with lowercase letters. Cap-

ital bold letters are used for random variable vec-

tors and matrices and calligraphic font denotes sets.

All simulations in this section are carried out with

the identity leakage function. Observable data-based

leakages of a certain intermediate value v are denoted

using subscript L

. Likewise, observable location-

based leakages caused by accessing register R

(where

i the index) are denoted using subscript L

R-i

. To

distinguish between data-based leakage and location-

based leakage we use superscript L

data

and L

loc

. In

addition, we assume that different sources of leakage

(data, location) have different noise levels i.e. we as-

sume homoscedastic data noise N

data

∼ N (0, σ

data

)

and homoscedastic location noise N

loc

∼ N (0,σ

loc

We use the following formula to compute the MI met-

ric.

MI(S;L) = H[S] +

∑

s∈S

Pr[s] ·

∑

m∈M

Pr[m] ·d

(10)

where d =

l∈L

(d+1)

Pr[l|s, m] · log

Pr[s|l] dl and

Pr[s|l] =

∑

∗

∈R

Pr[l|s,m

∗

]

∑

∗

∈S

∑

∗

∈R

Pr[l|s

∗

]

, and random variable S

denotes the secret exponent bit, L denotes the leakage

vector and M is a d-dimensional randomness vector

that we need to sum over when randomization is in

place, i.e. d is the attack order.

4.2.2 Data Leakage Attack

The ﬁrst obvious way to recover k

n−1

is by observ-

ing the data leakage of the values b

n−1

and a

n−1

the same time. We run the algorithm for the ﬁrst

two rounds and note the intermediate values that can

leak information. We let b

be a random value from

R{0,1}, then:

Boolean Exponent Splitting

327

Table 1: Comparison Table.

Algorithm ]operations ]registers Hide ADPA Interm.

length Values

Algorithm 1 n · M + n · S 2 7 7 7

Clavier-Joye (Clavier and Joye, 2001) 2(n · M + n · S) 2 7 7 7

Algorithm 2 n · M + n · S 3 3 3 7

Algorithms 3–4 2n · M 4 3 3 7

Algorithm 5 2n · M 4 3 3 7

Algorithm 6 (n − 1) · A + (n − 1) · D 3 3 3 7

Algorithm 7 2 · (n − 1) · A 4 3 3 7

Itoh et al. (Itoh et al., 2003) Alg. 8 (n − 1) · D + (n − 1) · A + 1 · I 3 7 3 7

Izumi et al. (Izumi et al., 2010) Alg. 2 (n − 1) · D + (n − 1) · A 3 7 3 7

Algorithm 8 n · D + n · A 3 3 3 7

Algorithm 9 2 · n · A 4 3 3 7

i = n − 1

1. b

= b

n−1

⊕ b

2. a

= b

⊕ a

n−1

3. R

= R

· R

4. R

= R

·U

n−1

5. b

= b

n−1

i = n − 2

6. b

= b

n−2

⊕ b

7. a

= b

⊕ a

n−2

8. R

= R

· R

9. R

= R

·U

n−2

10. b

= b

n−2

As can be observed in above, the value b

n−1

is ac-

cessed in the ﬁrst iteration (i = n−1) three times, once

when b

is calculated (line 1), once implicitly for the

index of U

n−1

(line 4) and ﬁnally for b

(line 5). The

value a

n−1

is accessed once during the ﬁrst iteration

(i = n − 1) and it is not used in the second iteration

(i = n − 2). We notice that the value b

n−1

is used im-

plicitly again in the second iteration, since it is equal

to b

. An attacker observing the power leakage of

this algorithm should be able to probe at two different

points in time, in order to observe both leakages L

data

n−1

data

n−1

and eventually the key, i.e. we conclude that a

second-order attack is possible for this scheme. Note

also that the an adversary with ability to conduct hor-

izontal side-channel attacks (Battistello et al., 2016)

could observe the leakage of b

n−1

multiple times, av-

erage them by computing

data

n−1

∗

∑

j=1

data

n−1

order to reduce the noise level and ﬁnally perform a

second-order attack. The results of the MI evaluation

are visible in Figure 1. As expected, the exponent

splitting scheme performs noise ampliﬁcation and has

a different slope compared to an unprotected expo-

nentiation (Algorithm 1). In addition, we observe the

curve’s horizontal shift to the right caused by the hor-

izontal exploitation of the available leakage, i.e. we

can quantify the effect of multiple leaky points for

n−1

4.2.3 Location Leakage Attack

Let us assume that the adversary can distinguish

between the manipulation of registers according to

which address is accessed, similar to the address-bit

DPA attack described in (Izumi et al., 2010). If the

adversary can distinguish between accesses to, U

and U

for example, a direct consequence is recovery

of value b

n−1

. To mount a successful attack against

Algorithm 5 using solely location-based leakage, we

need the simultaneous observation of the address of

and R

, for indexes i

= b

n−1

(line 4) and

= b

(line 3) and i

= a

(line 3). Thus, in order

to recover k

n−1

, we need to observe leakage vector

loc

= [L

loc

U-i

loc

R-i

loc

R-i

], i.e. perform a third-order at-

tack. The results are visible in Figure 2, where we can

observe the noise ampliﬁcation effect that increases

the curve’s slope. Naturally, a third-order attack us-

ing only location-based leakage tends to be less ef-

fective compared to a second-order attack using only

data-based leakage. However, depending on the de-

vice, exploiting the address dependency may be more

effective than exploiting the data dependency. That

is, the third-order attack can become more efﬁcient if

data

> σ

loc

4.2.4 Hybrid Leakage Attack

Lastly, we analyze the scenario in which an adver-

sary can observe both data-based and location-based

leakage. Using this information the adversary can use

leakage vector

L = [L

data

n−1

loc

U-b

n−1

]

to carry out a second-order attack that uses data leak-

age to recover bit a

n−1

and location leakage with re-

gard to register U to recover bit b

n−1

. Since data

and location leakage imply different noise levels, i.e.

(σ

data

6= σ

loc

), we need to represent the available in-

formation as a three-dimensional plot, as in Figure 3.

The wave-like plot quantiﬁes the attainable informa-

tion with regard to a particular data and location noise

level. Thus, it assists the side-channel evaluator to

analyze the scheme’s security in a more holistic way

that factors in location leakage and demonstrates the

SECRYPT 2021 - 18th International Conference on Security and Cryptography

328

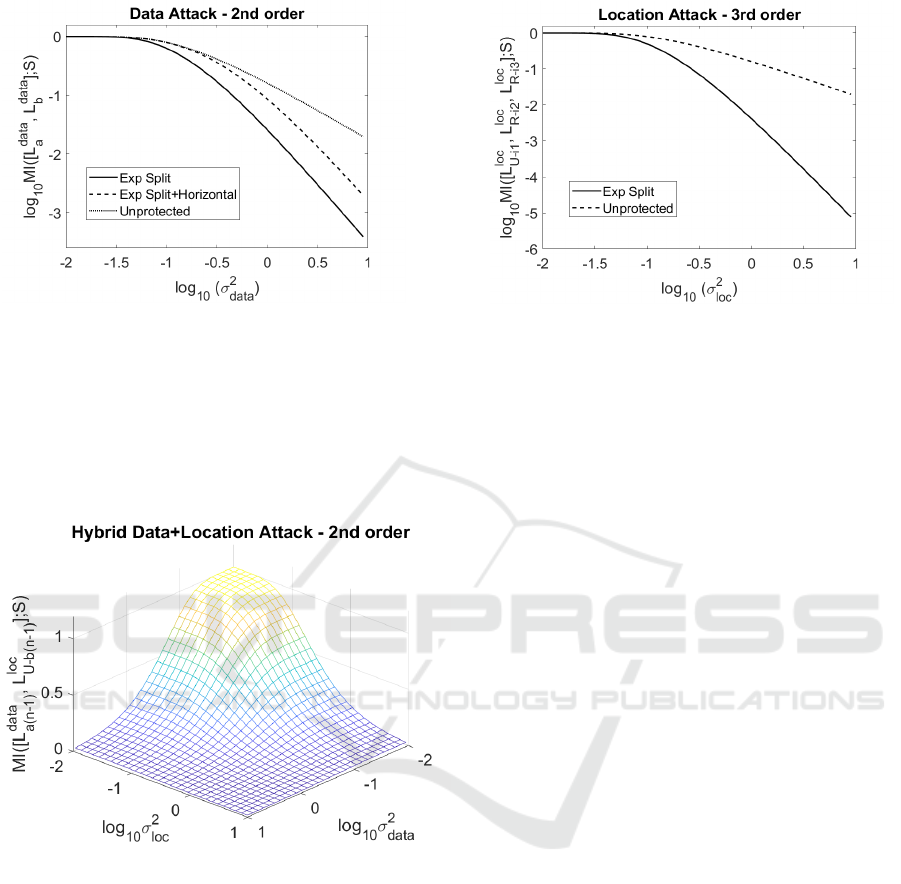
Figure 1: MI evaluation for Algorithm 2, using a data

leakage attack, with and without horizontal exploitation.

Observed leakage vector L = [L

data

n−1

data

n−1

Figure 2: MI evaluation for Algorithm 2, using a lo-

cation leakage attack. Observed leakage vector L =

loc

U-i

loc

R-i

loc

R-i

tradeoff between data noise and location noise. If for

instance σ

loc

 σ

data

in the target device, the adver-

sary can directly opt for the hybrid attack, instead of

pursing a data-only attack route.

Figure 3: MI evaluation for Algorithm 5 exponent splitting,

using a hybrid leakage attack. Observed leakage vector L =

data

n−1

loc

U-b

n−1

5 IMPLEMENTATION

CONSIDERATIONS

In this section, we describe the results of applying

Test Vector Leakage Assessment (TVLA) (Goodwill

et al., 2011) to implementations of some of the al-

gorithms above. We further describe modiﬁcations

required to achieve a secure implementation where

the hardware architecture can mean that variables that

should be independent leak at the same time, poten-

tially unmasking a secret value (Balasch et al., 2015).

Our implementations were developed using Xil-

inx’s Zynq zc702 evaluation board. The Zynq zc702

microprocessor contains two ARM7 cores and an

FPGA fabric. We used one ARM7 core for our imple-

mentations, clocked at 667 MHz, and the FPGA pro-

vided a means of triggering an oscilloscope at a con-

venient point in our implementations. We acquired a

trace of the electromagnetic emanations around one

of the coupling capacitors.

The test that we used from TVLA is to determine

whether there are statistically signiﬁcant differences

in the mean traces of two sets of traces, one acquired

with a ﬁxed scalar and the other with random scalar.

One would typically randomly interleave acquisitions

so that environmental effects are the same for both

sets and there are no erroneous indications of leakage,

caused, for example, by the least signiﬁcant bit of a

variable used to count the number of acquisitions. In

applying this, one would take two sets of data, and

conduct Welch’s t-test point-by-point to determine

whether there is evidence against the null hypothesis

that the sets are the same. We determine that leakage

is present if we observe values above 6.63σ which

gives the probability of indicating leakage where no

leakage is present, often referred to as a Type I error,

of approximately 1 × 10

when using traces contain-

ing 3 × 10

samples. The interested reader is referred

to Goodwill et al. (Goodwill et al., 2011) and Schnei-

der and Moradi (Schneider and Moradi, 2015) for a

thorough description.

We made a straightforward implementation of Al-

gorithm 6 using NIST’s P192 curve and conducted a

test where we compared a set of traces with a ﬁxed

scalar compared to a set of traces with a random

scalar. The elliptic curve points were implemented

as homogeneous projective points. We use the x and

z-coordinates in conjunction with so-called x-only al-

Boolean Exponent Splitting

329

gorithms for point arithmetic (Brier and Joye, 2002),

as one would for an implementation of ECDH. The

instantaneous electromagnetic emanations around the

targeted capacitor were measured during the execu-

tion of the ﬁrst 20 rounds of the implementation. The

top-left trace in Figure 4 shows the result of a TVLA

analysis with 1×10

traces where leakage can be seen

in numerous places.

A straightforward implementation of Algorithm 6

was tested in the same way. The algorithm is sim-

ilar to that proposed by Izumi et al. (Itoh et al.,

2003) but with masking conducted before the execu-

tion of the scalar multiplication, rather than on-the-

ﬂy. The resulting TVLA traces is shown in the top-

right of Figure 4, where we note that signiﬁcant leak-

age is present with 1 × 10

traces. This is caused by

the microprocessor combining values held in regis-

ters because of the architecture chosen by the design-

ers (Balasch et al., 2015).

A more secure implementation can be made by

computing some of the required indices before the ex-

ecution of the main loop of the scalar multiplication,

as shown in Algorithm 8. We set C to B ⊕





such

that individual bits of B are masked by adjacent bits.

The resulting TVLA trace is shown in the bottom-left

of Figure 4, where we observe that there is only one

place where we see signiﬁcant leakage with 1 × 10

traces. This leakage occurs because the initial state of

} contain {P

P,2P

P} in some random order. In

the ﬁrst loop of the scalar multiplication {R

} is

overwritten with {2P

P,3P

P} or {3P

P,4P

P}, in some ran-

dom order, depending on whether the second most-

signiﬁcant bit of κ is set to 0 or 1, respectively. When

P overwrites 2P

P the side-channel leakage will be

signiﬁcantly different to any other possible combina-

tion, since the Hamming distance will be zero.

A fully secure implementation can be achieved by

randomizing the point produced by the doubling op-

eration, by multiplying the x and z-coordinate of the

resulting point by a random value. In implementing

Algorithm 8, this was achieved by randomizing R

and R

before the main loop of the scalar multipli-

cation. The resulting TVLA trace is shown in the

bottom-right of Figure 4, where we observe that there

is no signiﬁcant leakage with 1 ×10

traces. An alter-

native would be to set the coordinates of R

to zero

before setting R

to R

. Algorithm 9 shows the same

arguments applied to Algorithm 7. However there is

no need to randomize any points during the loops of

scalar multiplication. If the redundant representation

of the point assigned to R

and R

is randomized sep-

arately to that applied toU

an overwrite with a Ham-

ming distance of zero cannot occur.

Algorithm 8: Montgomery Ladder with XOR-Split

Scalar on EC.

Input: E, F

, P

P ∈ E , n-bit integers

A =

∑

n−1

i=0

, B =

∑

n−1

i=0

Output: Q

Q = [κ]P

P where κ = A ⊕ B

Uses: C =

∑

n−1

i=0

1 R

← P

P ; R

← P

P ; R

← P

P ;

2 C ← B ⊕





;

3 b

← b

n−1

;

4 R

¬b

← 2P

P ;

5 for i = n − 2 down to 0 do

6 R

← R

¬a

;

7 R

← 2R

⊕c

;

8 R

¬a

← R

;

9 end

10 return R

Algorithm 9: Montg. Ladder with XOR-Split

Scalar II on EC.

Input: E, F

, P

P ∈ E , n-bit integers

A =

∑

n−1

i=0

, B =

∑

n−1

i=0

Output: Q

Q = [κ]P

P where κ = A ⊕ B

Uses: C =

∑

n−1

i=0

and D =

∑

n−1

i=0

1 R

← P

P ; R

← P

P ;

2 U

← P

P ; U

← −P

P ;

3 C ← B ⊕





; D ← C ⊕ A;

4 b

← b

n−1

, R

¬b

← 2P

P ;

5 for i = n − 2 down to 0 do

6 R

← R

;

7 R

← R

;

8 b

← b

;

9 end

10 return R

6 CONCLUSIONS

In this paper, we show how an exponent can be split

into two shares, where the exponent is the XOR sum

of the two shares and the cost is typically an extra reg-

ister and some register copies per bit. A signiﬁcant

advantage over previously proposed exponent split-

ting methods, which can have a prohibitive impact on

performance (Clavier and Joye, 2001). Our method

can also be applied to groups whose order contains

long runs of bits set to 0 or 1 without any penalty on

performance or security. Indeed, one does not need

to know the order of the group; a signiﬁcant advan-

tage if, for example, one wished to implement RSA

SECRYPT 2021 - 18th International Conference on Security and Cryptography

330

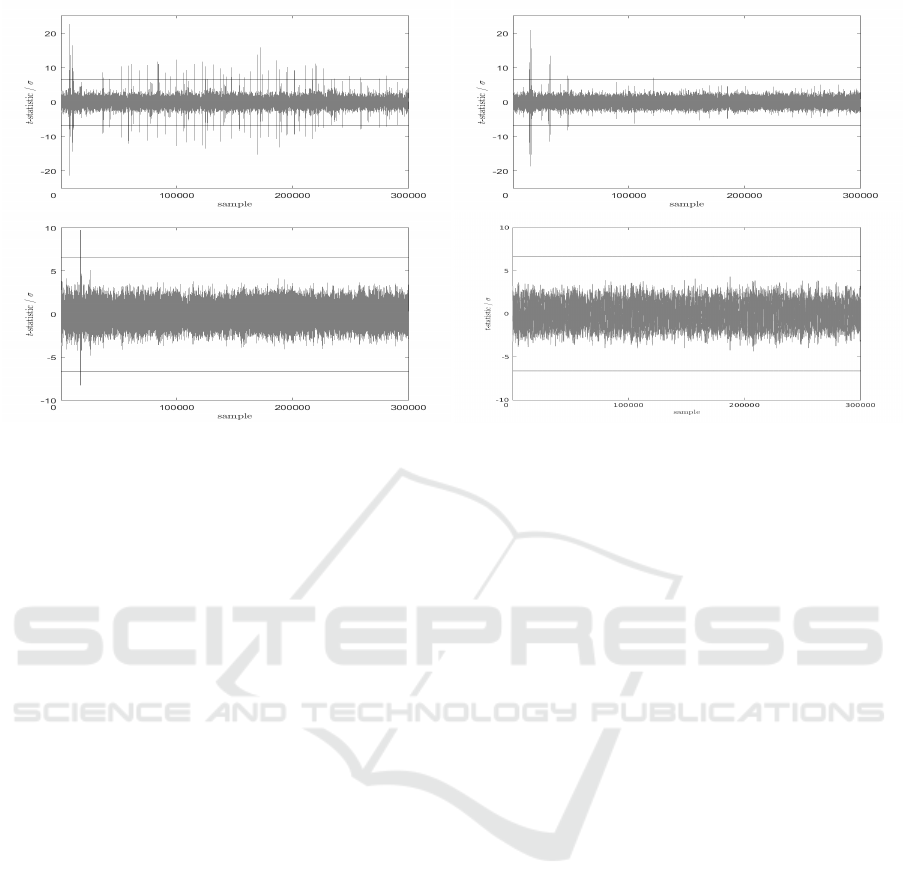
Figure 4: From top left to bottom right we show: an unmasked implementation showing leakage after 1 × 10

traces, a na

ıve

implementation of Algorithm 6 and a more secure variant both showing leakage after 1 × 10

traces, and an implementation

of Algorithm 8 that does not show leakage after 1 × 10

traces.

without using the Chinese remainder theorem.

We show that our algorithms are secure using for-

mal methods, MI-based evaluation and TVLA on an

implementation of Boolean exponent splitting. We

note that our method does not prevent an attacker

from using the intermediate states generated by the al-

gorithms as a means of attack. However, inexpensive

solutions such as randomizing projective points (Win

et al., 1998) or Ebeid and Lambert’s blinding method

for RSA (Ebeid and Lambert, 2010) can be com-

bined with our method to provide a high level of side-

channel resistance.

The algorithms presented above will be more ef-

ﬁcient than adding a multiple of the group order to

the exponent, since the bit length of the exponent is

not increased. Moreover, the resistance to collision

attacks is superior, since one would need to conduct

several attacks to derive each share and reconstruct

the exponent. Where one is adding a random mul-

tiple of the exponent any bits recovered directly re-

late to bits of the exponent used. It has not yet been

shown that one can derive an exponent from gaining

partial information on a series of blinded exponents,

but signiﬁcant advances have been made (Schindler

and Itoh, 2011; Joye and Lepoint, 2012; Schindler,

2014; Schindler and Wiemers, 2014).

ACKNOWLEDGEMENTS

The authors would like to thank Lauren De Meyer and

Michael Hamburg for their helpful comments.

REFERENCES

Balasch, J., Gierlichs, B., Grosso, V., Reparaz, O., and Stan-

daert, F. (2015). On the cost of lazy engineering for

masked software implementations. In CARDIS 2014,

volume 8968 of LNCS, pages 64–81. Springer.

Battistello, A., Coron, J., Prouff, E., and Zeitoun, R. (2016).

Horizontal side-channel attacks and countermeasures

on the ISW masking scheme. In CHES 2016, volume

9813 of LNCS, pages 23–39. Springer.

Bernstein, D. J. and Lange, T. (2009). A complete set of

addition laws

for incomplete edwards curves. Cryptology ePrint

Archive, Report 2009/580. https://eprint.iacr.org/

2009/580.

Brier, E., Clavier, C., and Olivier, F. (2004). Correlation

power analysis with a leakage model. In CHES 2004,

volume 3156 of LNCS, pages 16–29. Springer.

Brier, E. and Joye, M. (2002). Weierstraß elliptic curves

and side-channel attacks. In PKC 2002, volume 2274

of LNCS, pages 335–345. Springer.

Chari, S., Jutla, C. S., Rao, J. R., and Rohatgi, P. (1999). To-

wards sound approaches to counteract power-analysis

attacks. In CRYPTO ’99, volume 1666 of LNCS, pages

398–412. Springer.

Ciet, M. and Joye, M. (2003). (virtually) free randomiza-

tion techniques for elliptic curve cryptography. In

ICICS 2003, volume 2836 of LNCS, pages 348–359.

Springer.

Boolean Exponent Splitting

331

Clavier, C. and Joye, M. (2001). Universal exponentiation

algorithm. In CHES 2001, volume 2162 of LNCS,

pages 300–308. Springer.

Coron, J. (1999). Resistance against differential power anal-

ysis for elliptic curve cryptosystems. In CHES 1999,

volume 1717 of LNCS, pages 292–302. Springer.

Ebeid, N. M. and Lambert, R. (2010). A new CRT-RSA

algorithm resistant to powerful fault attacks. In WESS

2010, page 8. ACM.

Edwards, H. M. (2007). A normal form for elliptic curves.

In Bulletin of the American Mathematical Society,

volume 44, pages 393–422.

Feix, B., Roussellet, M., and Venelli, A. (2014). Side-

channel analysis on blinded regular scalar multiplica-

tions. In INDOCRYPT 2014, volume 8885 of LNCS,

pages 3–20. Springer.

Gandolﬁ, K., Mourtel, C., and Olivier, F. (2001). Electro-

magnetic analysis: Concrete results. In CHES 2001,

volume 2162 of LNCS, pages 251–261. Springer.

Goodwill, G., Jun, B., Jaffe, J., and Rohatgi, P. (2011). A

testing methodology for side channel resistance vali-

dation. NIST non-invasive attack testing workshop.

Goubin, L. (2003). A reﬁned power-analysis attack on ellip-

tic curve cryptosystems. In PKC 2003, volume 2567

of LNCS, pages 199–210. Springer.

Hanley, N., Kim, H., and Tunstall, M. (2015). Exploiting

collisions in addition chain-based exponentiation al-

gorithms using a single trace. In CT-RSA 2015, vol-

ume 9048 of LNCS, pages 431–448. Springer.

Itoh, K., Izu, T., and Takenada, M. (2002). Address-bit

differential power analysis of cryptographic schemes

OK-ECDH and OK-ECDSA. In CHES 2002, volume

2523 of LNCS, pages 129–143. Springer.

Itoh, K., Izu, T., and Takenada, M. (2003). A practical coun-

termeasure against address-bit differential power anal-

ysis. In CHES 2003, volume 2779 of LNCS, pages

382–396. Springer.

Izumi, M., Ikegami, J., Sakiyama, K., and Ohta, K. (2010).

Improved countermeasures against address-bit DPA

for ECC scalar multiplication. In DATE 2010, pages

981–984. IEEE.

Joye, M. and Lepoint, T. (2012). Partial key exposure on

RSA with private exponents larger than N. In IS-

PEC 2012, volume 7232 of LNCS, pages 369–380.

Springer.

Joye, M. and Villegas, K. (2002). A protected division al-

gorithm. In CARDIS 2002. USENIX.

Joye, M. and Yen, S.-M. (2002). The Montgomery pow-

ering ladder. In CHES 2002, volume 2523 of LNCS,

pages 291–302. Springer.

Kim, H., Kim, T. H., Yoon, J. C., and Hong, S. (2010).

Practical second-order correlation power analysis on

the message blinding method and its novel counter-

measure for RSA. ETRI Journal, 32(1):102–111.

Kocher, P. (1996). Timing attacks on implementations of

Difﬁe-Hellman, RSA, DSS, and other systems. In

CRYPTO ’96, volume 1109 of LNCS, pages 104–113.

Springer.

Kocher, P., Jaffe, J., and Jun, B. (1999). Differential power

analysis. In CRYPTO ’99, volume 1666 of LNCS,

pages 388–397. Springer.

Le, D.-P., Tan, C.-H., and Tunstall, M. (2015). Randomiz-

ing the Montgomery powering ladder. In WISTP 2015,

volume 9311 of LNCS, pages 155–170. Springer.

Messerges, T. S. and Dabbish, E. A. (1999). Investigations

of power analysis attacks on smartcards. In Smartcard

1999. USENIX Association.

Messerges, T. S., Dabbish, E. A., and Sloan, R. H. (1999).

Power analysis attacks of modular exponentiation in

smartcards. In CHES’99, volume 1717 of LNCS,

pages 144–157. Springer.

Montgomery, P. L. (1987). Speeding the Pollard and elliptic

curve methods of factorization. Mathematics of Com-

putation, 48(177):243–264.

National Institute of Standards and Technology (NIST)

(2009). Recommended elliptic curves for federal

government use. In the appendix of FIPS 186-

3, available from http://csrc.nist.gov/publications/ﬁps/

ﬁps186-3/ﬁps

186-3.pdf.

Quisquater, J.-J. and Samyde, D. (2001). Electromagnetic

analysis (EMA): Measures and counter-measures for

smart cards. In E-smart 2001, volume 2140 of LNCS,

pages 200–210. Springer.

Rivest, R., Shamir, A., and Adleman, L. M. (1978). Method

for obtaining digital signatures and public-key cryp-

tosystems. Communications of the ACM, 21(2):120–

126.

Schindler, W. (2014). Exclusive exponent blinding may not

sufﬁce to prevent timing attacks on RSA. Cryptol-

ogy ePrint Archive, Report 2014/869. http://eprint.

iacr.org/.

Schindler, W. and Itoh, K. (2011). Exponent blinding does

not always lift (partial) SPA resistance to higher-level

security. In ACNS 2011, volume 6715 of LNCS, pages

73–90. Springer.

Schindler, W. and Wiemers, A. (2014). Power attacks in

the presence of exponent blinding. J. Cryptographic

Engineering, 4(4):213–236.

Schneider, T. and Moradi, A. (2015). Leakage assessment

methodology - A clear roadmap for side-channel eval-

uations. In CHES 2015, volume 9293 of LNCS, pages

495–513. Springer.

Smart, N., Oswald, E., and Page, D. (2008). Randomised

representations. IET Proceedings on Information Se-

curity, 2(2):19–27.

Standaert, F., Malkin, T., and Yung, M. (2009). A uniﬁed

framework for the analysis of side-channel key recov-

ery attacks. In EUROCRYPT 2009, volume 5479 of

LNCS, pages 443–461. Springer.

Win, E. D., Mister, S., Preneel, B., and Wiener, M. J.

(1998). On the performance of signature schemes

based on elliptic curves. In ANTS 1998, volume 1423

of LNCS, pages 252–266. Springer.

Witteman, M. F., van Woudenberg, J. G. J., and Menarini, F.

(2011). Defeating RSA multiply-always and message

blinding countermeasures. In CT-RSA 2011, volume

6558 of LNCS, pages 77–88. Springer.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

332