Fair Mutual Authentication

Jacek Cicho

, Krzysztof Majcher

and Mirosław Kutyłowski

Wrocław University of Science and Technology, Wybrze

ze Wyspia

nskiego 27, Wrocław, Poland

Keywords:

Fair Authentication, Authentication with Errors, Privacy Protection, GDPR, Markov Chain, Absorbing State,

Rapid Mixing.

Abstract:

We consider a fair authentication process where at each moment of the protocol execution each participant

has almost the same certainty about the identity of the other participant. We combine this property with

authentication with errors: each authentication bit may be replaced to the wrong value. Thereby, an observer

attempting to derive the secret key(s) used for authentication in a cryptanalytic way has substantially harder job

due to an unknown error pattern (learning secrets with errors). We show that the presented protocol satisﬁes

subtle requirements of the GDPR Regulation of data minimization in case of failure.

1 INTRODUCTION

Assume that Alice and Bob wish to mutually authen-

ticate themselves based on the fact that they are the

only parties that know a secret K. There are many

protocols based on cryptographic algorithms that en-

able both Alice and Bob to show that they hold a se-

cret without exposing it. Some of them have zero-

knowledge property – an observer has no advantage

from listening to Alice and Bob: if there is an at-

tack using information from interactions between Al-

ice and Bob, then the adversary can run an analogous

attack of almost the same complexity without eaves-

dropping communication between Alice and Bob.

Let us consider the following classical example of

mutual authentication where Alice and Bob share a

key K (this mechanism is used for Basic Access Con-

trol protocol for biometric passports (ICAO, 2015)):

Algorithm 1.

1. Bob chooses a nonce r

at random and sends it to

Alice,

2. Alice chooses a nonce r

at random and sends the

ciphertext Enc

, r

) to Bob,

3. Bob decrypts the ciphertext obtained from Alice

and aborts if the plaintext does not contain r

the second position,

4. Bob returns Enc

, r

) to Alice,

https://orcid.org/0000-0002-7742-3031

https://orcid.org/0000-0003-2971-5571

https://orcid.org/0000-0003-3192-2430

5. Alice decrypts the ciphertext and aborts if the

plaintext is not (r

, r

If a party reaches the end of the protocol execution

without aborting, then it concerns the other party as

authenticated.

The main problem related to protocols of this kind

is as follows:

Problem 2. One of the parties (in this case Bob)

reaches the state in which he is sure about identity

of Alice, before Alice may judge whether she is inter-

acting with Bob. At this moment Bob can interrupt

the protocol prematurely or send invalid messages so

that Alice ﬁnally will have no idea if she is interacting

with Bob.

Indeed, it the above example Bob is sure about

Alice identity after step 3, while till this moment even

the shared secret has not been used by Bob. Until step

5, Alice has no proof that she is interacting with Bob.

Problem 2 occurs also at everyday situations. For

instance, if a call center of a bank is calling a bank’s

client, then both parties have to be authenticated.

Typically this is done by exchanging some data that

should be known by both parties. Whatever we do,

one party says this information ﬁrst. In electronic

interaction the situation is difﬁcult as well: ﬁrst, it

would be extremely difﬁcult to create something that

could be considered as really simultaneous exchange

of messages. Second, in many cases for various rea-

sons it is necessary to reduce the number of messages

exchanged. In this case asymmetry of knowledge dur-

ing protocol execution is inevitable.

754

Cicho

n, J., Majcher, K. and Kutyłowski, M.

Fair Mutual Authentication.

DOI: 10.5220/0010579507540759

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 754-759

ISBN: 978-989-758-524-1

However, sometimes the technical reality is differ-

ent. A prominent example are distance bounding pro-

tocols (see (Avoine et al., 2019)), where communicat-

ing parties rapidly exchange many short messages. In

such a scenario one can design the following mutual

authentication algorithm:

Algorithm 3 (Bitwise Exchange). Assume that Alice

and Bob share a secret K.

1. Alice chooses a nonce N

at random, Bob chooses

a nonce N

at random,

2. Alice and Bob exchange N

and N

(in cleartext),

3. Alice and Bob compute P

= H(K, N

, N

, A) and

= H(K, N

, N

, B) where H is a cryptographic

hash function.

4. For i = 1 to k, the following steps are executed:

• Alice sends a

equal to the ith bit of P

• Bob checks that a

is correct; if not, then he

aborts the protocol execution,

• Bob sends b

, the ith bit of P

• Alice checks that b

is correct; if not, then she

aborts the protocol execution.

If a party reaches the end of execution without abort-

ing, then its interlocutor is regarded as successfully

authenticated.

The important property of Algorithm 3 is that the

number of correct authenticating bits revealed by Al-

ice and Bob is almost the same at each step of the

protocol execution. The difference is at most one.

1.0.1 Authentication with Errors

A frequent technique used for weak devices limited

to lightweight cryptography is sending authentication

data with a certain number of errors. A good exam-

ple is the HB protocol and its variants: the underlying

algebraic mechanisms of linear algebra are too weak

from cryptographic point of view, but the messages

exchanged contain a signiﬁcant fraction of erroneous

bits (see e.g. (Boureanu et al., 2017)). Thereby, an at-

tacker is no more faced with a straightforward linear

algebra problem, but with a kind of learning secrets

with errors task. Learning with errors is one of the

paradigms that results in designs not lomited to au-

thentication – see e.g. (Bettaieb et al., 2018). This

principle is also the foundation of the whole strain

of cryptographic research based on the LPN problem

and lattices (see e.g. lectures (Chi et al., 2015)).

Once the bits exchanged during the execution of

Algorithm 3 are not necessarily correct in every case,

then one could substantially reduce the requirements

for the function H used. Like in case of HB-protocols,

it is not necessarily a cryptographically strong hash

function. This is a big advantage, since computing a

hash value might be too complex for the simplest IoT

devices.

One can propose the following version of Algo-

rithm 3 where the authentication bits are partially

false:

Algorithm 4 (Naive Algorithm). The algorithm is the

same as in case of Algorithm 3 apart from the bits

exchange steps: For i = 1 to k, the following steps are

executed:

• Alice sends a

, where a

equals the ith bit of P

with probability p and its negation with probabil-

ity 1 −p,

• Bob checks that a

is correct;

• Bob sends b

, the ith bit of P

, if a

was correct,

otherwise he sends its negation,

• Alice checks that b

is correct iff a

is correct; if

not, then she aborts the protocol execution.

Bob accepts if the number of correct bits a

exceeds

a threshold p ·k −∆ where ∆ is a parameter related to

standard deviation.

For Algorithm 4, an observer has no idea which

bits are correct and correspond to the strings P

and

. So we would like to claim that any brute force

attack will have to guess the location of incorrect bits.

Unfortunately, this is not true. Let α

and β

denote

the ith bits sent, respectively, by Alice and Bob. Then

of course α

⊕β

= a

⊕b

, where ⊕ denotes the XOR

operation. So the adversary may focus on ﬁnding a

K such that the ﬁrst k bits of P

⊕P

are the same as

⊕β

for i = 1, . . . , k.

As we see we have to combine the following goals

that to some extent are contradictory:

• a certain fraction of authentication bits sent by ei-

ther party should be wrong (to confuse an adver-

sary trying to retrieve the shared secret), while a

sufﬁcient majority must be correct (in order to en-

able reliable authentication),

• at each moment of protocol execution both au-

thenticating parties should have almost the same

level of certainty about the identity of the other

party,

• the locations of erroneous bits on the side of Alice

and on the side of Bob should be to some extent

independent.

1.1 GDPR

There are many practical issues concerning discrep-

ancy between technical reality and idealistic require-

ments of the the European GDPR regulation (The

Fair Mutual Authentication

755

European Parliament and the Council, 2016) on per-

sonal data protection. There are many cases where

this dilemma has been revealed (see e.g. (Spindler

and Schmechel, 2016), (Kutyłowski et al., 2020)), but

pragmatic solutions to these problems are still miss-

ing.

Authentication protocols should be particularly

carefully analyzed from the point of view of GDPR.

Of course, electronic authentication is not performed

directly by physical persons, but quite frequently the

devices are attributed to their owners and indirectly

provide data about them. It does not matter whether

these data have any signiﬁcance regarding informa-

tion security of the holder, as the requirements of the

GDPR regulation concern processing of personal data

regardless of their signiﬁcance.

If Alice executes a mutual authentication protocol

with a party that declares to be Bob, then the permis-

sion to process the authentication data is given im-

plicitly to Bob: executing the protocol is a form of

consent of Alice, as it is a clear afﬁrmative act. The

addressee of this consent is deﬁnitely Bob, as long as

the data sent by Alice depends on the identity of her

interlocutor Bob. If we talk about privacy-by-design,

almost no information should be delivered to a third

party.

In case of algorithms such as Algorithm 1 no prob-

lem arises from the point of view of GDPR, when

the protocol terminates in an accepting state on both

sides. However, this cannot be claimed if, as de-

scribed above, Bob interrupts the protocol execution

or pretends not to be Bob by providing a false answer

to the challenge of Alice. While Bob becomes sure

about identity of Alice, the consent given by proto-

col execution has concerned a mutual authentication

and not two one-way authentication protocols. From

the legal point of view, a mutual authentication pro-

tocol would strictly follow the ideas of GDPR if the

following properties are fulﬁlled:

Property 5 (GDPR Fully Compliant Mutual Authen-

tication). A mutual authentication protocol executed

by Alice and Bob should terminate on an accepting

state on the side of Alice iff it terminates in an accept-

ing state on the side of Bob. Moreover, if a protocol

terminates in a state where Alice and Bob have only

partial knowledge and cannot accept the interlocutor,

then their degree of certainty should be comparable.

Note that any deviation from the second require-

ment from Property 5 would lead to an asymmetry:

the party having higher knowledge could interrupt the

protocol and have an advantage over the other party.

Property 5 should cover all cases of protocol execu-

tion: each participant may deviate from the protocol,

including a malicious behavior.

1.2 Related Research

The problem discussed in this paper is closely related

to fair exchange of information: in case of such a pro-

tocol Alice and Bob exchange some data, and neither

of them should be advantaged to get the data before

the other party. Research on these issues has been ini-

tiated decades ago. Already in 1980 it has been indi-

cated (Even and Yacobi, 1980) that it is impossible to

exchange data so that no party gets advantaged. How-

ever, it does not mean that one cannot create a proto-

col where at each moment of execution one party can

be only slightly advantaged over the other party in the

protocol – say by knowledge of one more information

bit or even a fraction of it. In the protocols concerned

the participants release their data gradually. For in-

stance, the seminal paper (Blum, 1983) concerns ex-

change of private keys for two RSA numbers. The in-

formations are exchanged bit by bit, interleaving the

data sent by Alice and Bob.

While in the 80’s the interest on fair exchange pro-

tocols have been more of a theoretical nature, these is-

sues became extremely important due to the progress

in electronic trade, where one party provides an elec-

tronic payment (e.g. with means of a cryptocur-

rency) and the other party provides a digital contents.

In most practical business cases, the problem is re-

solved with a trusted arbiter. For example, an opti-

mistic fair exchange protocol has been proposed in

(Asokan et al., 1997). In this setting, once fairness

is somehow broken, then a trusted party is involved

and can resolve the issue at least pointing to the dis-

honest party. Somewhat related problems are solved

by means of smart contracts, where the payment is

unlocked by delivery of the purchased data and re-

ﬂected in a blockchain. The application case that we

are focusing on is of a different nature. Not only a

third party would be cumbersome in most of technical

settings, it would also create the problem of possible

tracing the users, thereby breaking the fundamental

principles of GDPR.

2 MARKOV FAIR MUTUAL

AUTHENTICATION

For the rest of this paper we shall consider the fol-

lowing mutual authentication protocol that will en-

sure that each party shows at most one more correct

bit than the other party at any moment of a protocol

execution.

Algorithm 6 (Markov-Fair-MA). Assume that Alice

and Bob share a secret K. We describe this distributed

SECRYPT 2021 - 18th International Conference on Security and Cryptography

756

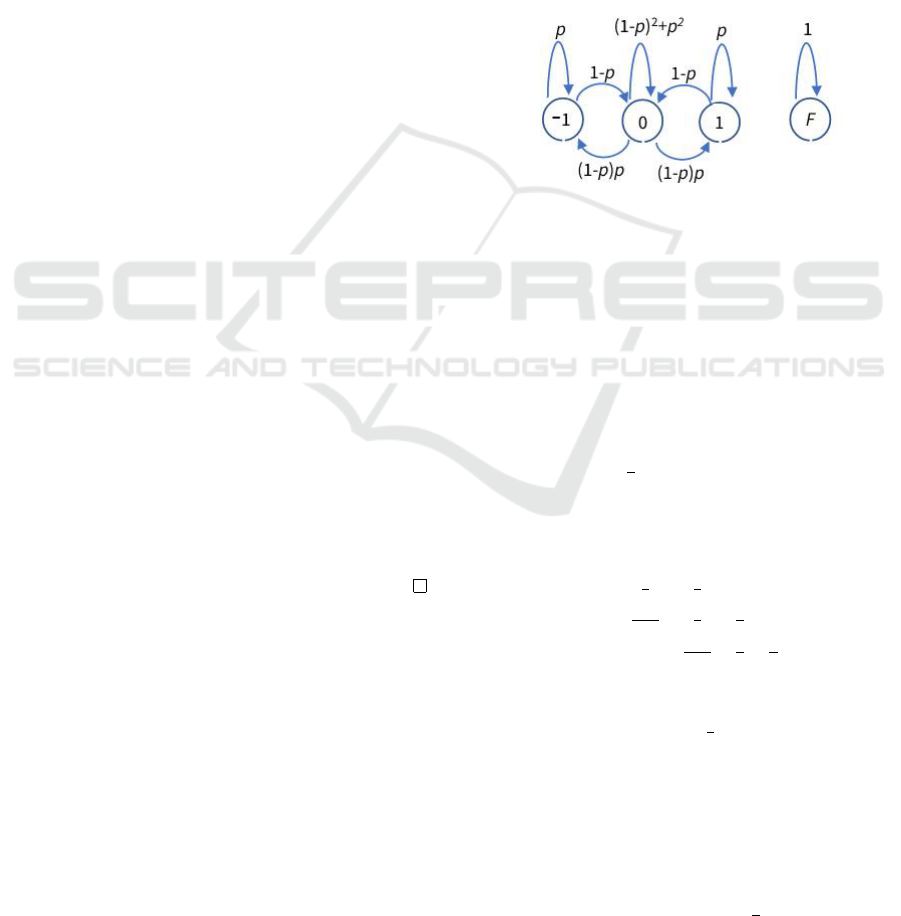
algorithm from the point of view of Alice. The inter-

locutor of Alice should follow analogous steps – how-

ever in a distributed environment Alice controls only

herself and the interlocutor – allegedly Bob – may be-

have in an arbitrary way.

Initialization:

1. Alice chooses a nonce N

at random and sends it

in cleartext to Bob,

2. Alice receives N

from Bob,

3. Alice computes P

= H(K, N, “Alice”, “Bob”)

and P

= H(K, N, “Bob”, “Alice”), where N =

and H is a cryptographic hash function.

Let a

and b

stand for, respectively, the ith bit of

and P

Main Part - Bit Exchange: There are k

rounds, at each round Alice sends one bit to Bob and

receives one bit from Bob.

Let ∆

= δ

i−1

−δ

i−1

, where δ

is the number of cor-

rect bits a

sent by Alice before step j and δ

is the

number of correct bits b

sent by Bob before step j.

Alice can be either in the normal state or in the

failure state. The initial state is normal.

In round i the following steps are executed by Alice,

if she is in the normal state:

• if ∆

= −1, then Alice sends a

• if ∆

= 0 or ∆

= 1, then Alice sends a

with prob-

ability p and ¬a

otherwise,

• if ∆

> 1, then Alice enters the failure state and

sends a random bit.

Once Alice enters the failure state, then she remains

in this state until the end of the protocol execution and

at each remaining step sends a bit chosen at random.

Decision:

If Alice terminates the execution in a normal state,

then she regards authentication as successful.

Note 7. It may not happen that Alice is in the

normal state after step i and ∆

< −1. Indeed,

note that ∆

= 0 and at each step the value of ∆

may change by at most 1. So if ∆ drops below −1,

then ∆

= −1 for step j immediately before. How-

ever, then Alice sends the correct value a

j+1

at step

j +1. If Bob at this moment sends the correct bit b

j+1

then ∆ j + 1 = −1. If Bob sends an incorrect bit, then

∆

j+1

= 0, contradiction.

Corollary 8. If Alice in a normal state after step i,

then ∆

∈ {−1, 0, 1}.

An execution of the protocol can be described by

means of a Markov chain, with states corresponding

to the value of ∆

= −1, 0, 1 and the failure state F.

If Bob honestly follows the protocol, then the com-

putation state from the point of view of Alice is de-

scribed by the Markov chain M

with the following

state transition matrix

C =







p 1 − p 0 0

(1 − p)p (1 −p)

+ p

(1 − p)p 0

0 1−p p 0

0 0 0 1







(1)

(the rows 1, 2, 3, 4 correspond to, respectively, transi-

tion from the state −1, 0, 1 and F). The initial state of

this Markov chain is 0. As long as Bob is following

the protocol, then the state F is unreachable.

Figure 1: The Markov chain M

describing the state transi-

tion when Alice is interacting with Bob honestly following

the protocol.

The situation changes, if Alice is interacting with Eve

impersonating Bob. As long as Eve does not know

the shared secret K, then Eve cannot say which bit to

be sent at round i will be regarded as correct by Alice.

We make the following assumption that describes the

situation for reasonable functions H:

Assumption 9 (forward security of H). Given the bits

, . . . , a

, and b

, . . . , b

i−1

Eve can guess the value of

with probability

+ ε, where ε ≈ 0 is negligible.

In this situation, the state of the computation from

the point of view of Alice can be described by the

Markov chain M

with the following state transition

matrix

F =







0 0

1−p

0 0 0 1







(2)

It is important that the transitions of M

are biased

towards the state F, if p >

. For example, in the

state 1 it is more likely to change to state F than to

go to the state 0. So, from the point of view of the

chain M

the value of p should be as big as possible.

On the other hand, for M

the values of p close to 1

mean that it is hard to leave any state and therefore for

the transmitted values α

, β

we have α

⊕β

= a

⊕b

with a high probability. So, the right choice for p is

somewhere in the middle between

and 1.

Fair Mutual Authentication

757

Figure 2: The Markov chain M

describing the state tran-

sition when Alice is interacting with Eve unaware of the

secret K shared by Alice and Bob.

3 BEHAVIOR OF Markov-Fair-MA

We will consider a general case of an arbitrary p ∈

(0, 1) used for the Markov-Fair-MA scheme. In Sub-

sect. 3.3, we will check its properties for p =

3.1 Correct Executions

When conﬁned to the states −1, 0, 1 the chain M

has

a stationary distribution π. Let D be transition matrix

C after deleting the 4th column and the 4th row, i.e.

D =







p 1 −p 0

(1 −p)p (1 − p)

+ p

(1 −p)p

0 1 − p p







(3)

Then π ·D = π, so one can immediately derive that

π(−1) = π(1) =

2p+1

, π(0) =

2p+1

. (4)

The stationary distribution indicates what is the ex-

pected difference of the number of correct bits a

and

correct bits b

. We see that the probabilities of the

differences −1, 0 and 1 are not substantially different

provided that neither p ≈

nor p ≈ 1. It shows that

the process is not biased to some state and therefore

the adversary should be confused about which bits

are correct. However, the problem is that the process

starts in the state 0 and the probability distribution of

the states only converges to the stationary distribution.

It is crucial to show that the distribution after round i

converges quickly to the stationary distribution.

Let π

denote the probability distribution of the

state of M

after t transitions of the chain, if the ini-

tial state is 0. A matrix D has three eigenvalues: 1, p

and p(2p −1), so using simple linear algebra we get:

Fact 10. For any t we have

( j) =

(

1+2p

−

1+2p

(p(2p −1))

for j = −1, 1

1+2p

(p(2p −1))

for j = 0

(5)

From this equations we can directly derive the total

variation distance

kπ −π

∑

j=−1,0,1

|π( j) −π

( j)| (6)

between the stationary distribution π and the distribu-

tion π

Corollary 11.

||π −π

2p+1

p(2p −1)

(7)

As |p(2p −1)| < 1 for p ∈ (0, 1), we see that the to-

tal variation distance to the stationary distribution is

decreasing exponentially. Note that the rate of con-

vergence is nevertheless slow from the practical point

of view, if p approaches 1. On the other hand, it is

very high when p approaches

3.2 Execution with a Party

Impersonating Bob

3.2.1 Convergence to the Absorbing State

The analysis of the Markov chain M

is similar to the

analysis of M

. The eigenvalues of the matrix F are

(1 −

1 −p

), and

(1 +

1 −p

) . (8)

This yields general formulas for the probability distri-

bution π

of the chain M

after step t.

Fact 12.

( j) =











1−p

√

1−p

−a

) if j = −1,

√

1−p

−a

) if j = 0,

+ a

) if j = 1,

1 −

√

1−p

t+1

−a

t+1

) if j = F,

(9)

where a =



1 −

1 − p



and b =



1 +

1 − p



Let Y be a random variable denoting the ﬁrst step

when the process M

reaches the absorbing state F.

Noting that Pr[Y = t] = Pr[Y ≤ t] −Pr[Y ≤ t −1] =

(F) −π

t−1

(F) and using equations 9 we get:

Fact 13. For t ≥ 1 we have

Pr[Y = t] = (b

a −a

b) ·

√

1−p

(10)

As a result of direct calculations we get:

Corollary 14. The expected value and variance of Y

have the following values

E[Y ] = 4p

−2

(11)

Var[Y ] = 16p

−4

−12p

−2

(12)

Corollary 14 explains why too small values of p

should be avoided. Namely, if p ≈

, then E[Y ] ≈ 16.

So it takes quite a long time until Alice will start to

send purely random bits. In the meantime Alice may

provide a partial proof of her identity.

SECRYPT 2021 - 18th International Conference on Security and Cryptography

758

3.2.2 Number of Visits in the State −1

The most critical moment from the point of informa-

tion leakage when Alice interacts with an alleged Bob

not knowing the shared key K, is the number of vis-

its in the state −1 of M

. Indeed, in this case Alice

must send the correct value of the corresponding bit

. In case of the states 0 and 1 there is only a bias

to send the correct bit: so as the number of steps until

the chain reaches the absorbing state F is small, it is

hard to derive a meaningful statistical information.

Let Z be the random variable denoting the number

of visits of the state −1 during an execution of the

chain M

. Some computations involving equations 9

yield the following formulas:

Fact 15. E[Z] =

2(1−p)

Var[Z] =

2(1 −p)



−2p + 2



(13)

Fact 13 shows that the expected number of visits in

the state −1 is quite small for any reasonable choice

of p. Also variance has relatively small values for

p ∈ (0.5, 1) (see Subsec. 3.3).

3.3 Example Choice: p =

We have already noticed that neither the values of p

close to

nor the values values of p close to 1 is the

right choice, so let us see what happens in the middle.

Honest Execution. In the case when Alice is Bob

follows honestly the protocol, then the stationary dis-

tribution is given by vector π = (

). The total

variation distance between distribution π

of M

and

its stationary distribution is

kπ −π





. (14)

So kπ−π

≈0.0003, kπ−π

≈0.00000017,

kπ −π

≈ 10

−21

Execution with Eve impersonating Bob. From

Equations 11 and 12 we get that the expected time

to reach the state F where Alice starts to send purely

random bits is E[Y ] = 9 and Var[Y ] = 54, so the stan-

dard deviation is approximately 7.35.

By Fact 15 and Equation 13 we deduce that the

number of visits of the state −1 before the process

reaches the absorbing state F we have E[Z] =

and

Var[Z] =

, and the standard deviation is ≈ 2.6.

ACKNOWLEDGEMENTS

Authors would like to thanks Łukasz Krzywiecki for

bringing attention to the problem discussed here.

REFERENCES

Asokan, N., Schunter, M., and Waidner, M. (1997). Op-

timistic protocols for fair exchange. In Graveman,

R., Janson, P. A., Neuman, C., and Gong, L., editors,

Proc. 4th ACM Conference on Computer and Commu-

nications Security, pages 7–17. ACM.

Avoine, G., Bing

ol, M. A., Boureanu, I., Capkun, S.,

Hancke, G. P., Kardas, S., Kim, C. H., Lauradoux,

C., Martin, B., Munilla, J., Peinado, A., Rasmussen,

K. B., Singel

ee, D., Tchamkerten, A., Trujillo-Rasua,

R., and Vaudenay, S. (2019). Security of distance-

bounding: A survey. ACM Comput. Surv., 51(5):94:1–

94:33.

Bettaieb, S., Bidoux, L., Connan, Y., Gaborit, P., and

Hauteville, A. (2018). The learning with rank errors

problem and an application to symmetric authentica-

tion. In 2018 IEEE International Symposium on In-

formation Theory, ISIT, pages 2629–2633. IEEE.

Blum, M. (1983). How to exchange (secret) keys (extended

abstract). In Johnson, D. S., Fagin, R., Fredman,

M. L., Harel, D., Karp, R. M., Lynch, N. A., Papadim-

itriou, C. H., Rivest, R. L., Ruzzo, W. L., and Seiferas,

J. I., editors, Proc. 15th ACM Symposium on Theory of

Computing, pages 440–447. ACM.

Boureanu, I., G

erault, D., Lafourcade, P., and Onete, C.

(2017). Breaking and ﬁxing the HB+DB protocol.

In Noubir, G., Conti, M., and Kasera, S. K., edi-

tors, Proc. of the 10th ACM Conference on Security

and Privacy in Wireless and Mobile Networks, WiSec,

pages 241–246. ACM.

Chi, D. P., Choi, J. W., Kim, J. S., and Kim, T. (2015). Lat-

tice based cryptography for beginners. IACR Cryptol.

ePrint Arch., 2015:938.

Even, S. and Yacobi, Y. (1980). Relations among public

key signature schemes. Technical Report 175, TECH-

NION.

ICAO (2015). Machine Readable Travel Documents - Part

11: Security Mechanism for MRTDs. Doc 9303.

Kutyłowski, M., Lauks-Dutka, A., and Yung, M. (2020).

GDPR - challenges for reconciling legal rules with

technical reality. In Chen, L., Li, N., Liang, K., and

Schneider, S. A., editors, Computer Security - 25th

European Symposium on Research in Computer Se-

curity, Proc., Part I, volume 12308 of LNCS, pages

736–755. Springer.

Spindler, G. and Schmechel, P. (2016). Personal data and

encryption in the European General Data Protection

Regulation. JIPITEC, 7(2):163–177.

The European Parliament and the Council (2016). Regu-

lation (EU) 2016/679 of the European Parliament and

of the Council of 27 April 2016 on the protection of

natural persons with regard to the processing of per-

sonal data and on the free movement of such data, and

repealing Directive 95/46/ec (General Data Protection

Regulation). Ofﬁcial Journal of the European Union,

119(1).

Fair Mutual Authentication

759