Robust and Hybrid Crypto-watermarking Approach for 3D
Multiresolution Meshes Security
Ikbel Sayahi
1,2
and Chokri Ben Amar
1,3
1
REsearch Groups on Intelligent Machines Laboratory (REGIM-Lab), Sfax University, Soukra Street, Sfax, Tunisia
2
Private National Engineering School of Monastir (ESPRIMS’), 5060, Monastir, Tunisia
3
College of Computers and Information Technology, Taif University, Taif, Saudi Arabia
Keywords:
3D Watermarking, Multiresolution Mesh, Wavelet Transform, RSA Algorithm, Robustness, Copyright,
Indexation.
Abstract:
Since the release of the first 3D watermarking algorithm, several approaches have grown up with a diversity
of techniques used during the embedding of information into meshes. The main objective is always to secure
data shared by remote users. The originality of the present work is issued from combining encryption and
hybrid watermarking algorithm to secure 3D multiresolution meshes. The new crypto-watermarking system
is composed of three parts: the first part is said watermark preparation and it aims to prepare data to be
inserted. During this step, the logo (which refers to copyright information) is encrypted using RSA (Rivest,
Shamir,Adleman) algorithm and then encoded by applying a convolutional encoder to the encrypted logo
already transformed into a binary sequence. As for the second part, it is called mesh preparation and it consists
on decomposing the 3D multiresolution mesh by applying wavelet transform to generate wavelet coefficient
vector. Finally, the third part of our algorithm, called hybrid watermarking, occurs to insert encrypted logo and
RSA keys into both multiresolution and spatial presentations of the mesh. In fact, the encrypted logo is inserted
into resulting wavelet coefficients after applying the transformation to spherical coordinate system, modulation
and demodulation. As for RSA key, it is inserted into the mesh resulting from the first watermarking around
by modifying geometric information of vertices. Found results prove that we are able to insert a high amount
of data without influencing the mesh quality. The application of the most popular attacks does not prevent a
correct extraction of data already inserted which is justified by the use of the RSA to encode the watermark and
the convolutional error correcting code to retrieve the corrupted information . Our algorithm is, then, robust
against these attacks.
1 INTRODUCTION
Since technology has made available speed computer
networks and remote multimedia databases, allowing
the sharing and the transmission of 3D meshes, solv-
ing security problems becomes an intellectual prop-
erty due to the fact that that digital copying does not
cause any loss of quality and the digital reproduc-
tion costs are negligible and counterfeiters can pro-
ceed anonymously without leaving a trace. All these
problems make legal protection alone is no longer suf-
ficient to ensure the peaceful management of works
transmitted to the public. Hence, the need to use
other techniques to strengthen existing legal protec-
tions seems necessary.
Digital watermarking is one of the proposed solu-
tions to ensure sharing meshes security which justify
the publication of several watermarking approaches
such as works published in (Hitendra et al., 2014),
(Yuan, 2015), (Jen-Tse et al., 2014), (Lamiaa et al.,
2015) and (Ouled Zaid et al., 2015). These algo-
rithms aim to insert data into the mesh to protect it
against any type of alterations. Unfortunately, in spite
of the variety of tools used in these approaches, 3D
watermarking domain still suffers from several defi-
ciencies.
The second solution proposed to counter to secu-
rity problems is cryptography. However the efficiency
of this later to secure shared documents mainly im-
ages, it is not yet used in the field of 3D representa-
tion. As a result, this paper aims to join cryptography
with 3D hybrid watermarking in order to guarantee
the security of 3D multiresolution meshes.
In this context, we propose a new hybrid crypto-
watermarking algorithm ensuring 3D multiresolution
meshes security. The proposed system uses encryp-
398
Sayahi, I. and Ben Amar, C.
Robust and Hybrid Crypto-watermarking Approach for 3D Multiresolution Meshes Security.
DOI: 10.5220/0010580303980407
In Proceedings of the 16th International Conference on Software Technologies (ICSOFT 2021), pages 398-407
ISBN: 978-989-758-523-4
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tion tool (RSA algorithm) and a watermarking tools
(wavelet transform, Modulation, spherical coordinate
system, convolutional error code) in order to increase
the amount of inserted data while keeping the mesh
quality and ensuring robustness against the most pop-
ular attacks. The originality of this paper is, in one
side, to work in parallel in two different fields of in-
sertion: spatial and multiresolution, hence the hybrid
notation which allow enhanced insertion rate while
keeping mesh quality. On the other side, the use of the
RSA, widely used in the field of image processing, to
encrypt the logo before inserting it will reinforce the
robustness of our algorithm.
2 STATE OF THE ART
Sharing 3D meshes between remote users poses great
security problems. Since these problems imposed
themselves, attempts to propose adequate solutions,
in the form of watermarking, encryption and stegano-
graphic algorithms, have continued to appear until to-
day.
On one side, digital watermarking is one of the
most important solutions. Indeed, to protect 3D
meshes from unauthorized actions, several 3D wa-
termarking approaches are published. The main ob-
jective is to find the best compromise between wa-
termark criteria: insertion rate (number of bits to
be inserted), invisibility (mesh quality) and robust-
ness against attacks (ability to extract correctly data
in spite of treatment applied to watermarked mesh)
through the use of multitude techniques and tools. In
order to classify these solutions, we consider the in-
serting domain as a criterion. The first category in-
cludes approaches operating in the spatial domain,
such as the approaches of Hitendra published in (Hi-
tendra et al., 2014), Tsai et al. in (Yuan, 2015) and
Wang et al. in (Jen-Tse et al., 2014). These ap-
proaches embed data either in the topological or in
the geometric information. As for the second cate-
gory, a transformed domain is used. Frequency do-
main (Lamiaa et al., 2015) and multiresolution do-
main (Ouled Zaid et al., 2015) are the most used inser-
tion areas. In this case data is inserted by modifying
frequency and multiresolutions coefficients. Notwith-
standing the significant improvements brought by al-
gorithms proposed over the last decade, the digi-
tal watermarking field still suffers from deficiencies.
This comes down, firstly, to the complexity to find
the best compromise between watermark invisibility,
high insertion rate and robustness which are contra-
dictory (the increase of capacity causes either a de-
terioration of the mesh quality or reduces the level
of robustness). Secondly, treating 3D multiresloution
meshes is not an easy mission in comparing them with
other types of meshes. This is justified by the sensi-
tivity of handling the multi-resolution appearance of
this data type.
On the other side, cryptography has proven its ef-
ficiency in securing digital data specially image. This
is justified by the abundant use of encryption algo-
rithms in the field of image processing to ensure secu-
rity ((Benyamin et al., 2014) and (Tariq and Ayesha,
2016) are examples). Despite the effectiveness and
the encouraging results of applying cryptography to
image, it has been not usd until now in the field of 3D
representation. This can be justified by the particular
presentation of 3D multiresolution meshes and to the
difficulty of manipulating these data types.
As a result, we aim, in this paper, to combine cryp-
tography and 3D watermarking in order to protect 3D
multiresolution meshes. The originality of this paper
is, in one side, to work in parallel in two different
fields of insertion: spatial and multiresolution, hence
the hybrid notation which allow enhanced insertion
rate while keeping mesh quality. On the other side,
the use of the RSA, widely used in the field of image
processing, to encrypt the logo before inserting it will
reinforce the robustness of our algorithm.
3 USED TECHNIQUES
To ensure security of 3D meshes shared between re-
mote users or saved in remote multimedia databases,
several techniques are used such as:
3.1 RSA Algorithm
RSA (Rivest–Shamir–Adleman) is the first public key
system to be invented, and the most widely used to-
day(Y. et al., 2020). RSA is based on a public key
and a private key. The public one can be known to ev-
eryone and it is used to encrypt the logo to be inserted
into the 3D multiresolution meshes. As for the second
key, it is used to decrypt the logo after being extracted
from the mesh to guarantee its authenticity. The keys
of RSA algorithm are generated by following these
steps:
• Choose two different large random prime num-
bers p and q. This should be kept secret.
• Calculate n = p × q . n is the modulus for the
public key and the private keys.
• Calculate φ(n) = (p −1) ×(q −1)
• Choose an integer e such as 1 < e < φ(n) and e
is co-prime to φ(n). e is considered as the public
Robust and Hybrid Crypto-watermarking Approach for 3D Multiresolution Meshes Security
399

key of RSA algoritm.
• Compute d to satisfy the congruence relation d ×
e ≡ 1(mod(φ(n))). d is considered as the private
key of RSA algorithm.
Key generation is the most tricky phase in the
RSA algorithm. Algorithm 1 presents the approach
to generate public and private key peers.
Algorithm 1.
INPUT: Required modulus bit length, k.
OUTPUT: An RSA key pair ((N, e), d) where N is
the modulus (N = p ×q) not exceeding k bits
in length; e is the public exponent, a number less
than and coprime to φ(n) = (p −1) ×(q −1);
and d is the private exponent such that
ed ≡ 1mod[φ(n)].
BEGIN
1. Select a value of e from 3,5,17,257,65537,...
2. repeat
/*genprime(k/2) returns a prime of exactly k/2
bits, with the (k/2)th bit set to 1*/
3. p ← genprime(k/2)
4. until (p mod[e])6= 1
5. repeat
/*genprime (k - k/2) returns a prime of
exactly (k - k/2) bits, with the (k - k/2)
th bit set to 1*/
6. q ← genprime(k - k/2)
7. until (q mod[e])neq1
8. N ← p ×q
9. φ(n) =← (p −1)(q −1)
10. d ← modinv(e, φ(n))
11. return (N,e,d)
To encrypt a message m with RSA algorithm, for-
mula 1 is used.
c = m
e
mod[n] (1)
c is the chipertext. As for decryption, it can be
done following formula 2
m = c
d
mod[n] (2)
3.2 Convolutional Error Correcting
Code
Convolutional codes (Viterbi, 1971), also known as
trellis or recursive, were discovered by Elias in 1955.
These codes are known for their simplicity, power and
efficiency, which justify their frequent use. The char-
acteristics of a convolutional code are that data, before
being inserted in a 3D mesh, is considered as a finite
series of symbols which undergo shifting operations
using memories to generate another series of encoded
symbols.
3.2.1 Convolutional Encoder
To encode data with a convolutional encoder a state
machine or a trellis presentation can be used. In the
state machine case, each state is a particular state of
the registers which are initially assumed to be zero.
Hence, each branch is the state change of the encoder
according to the arrival of a new bit from the water-
mark to be inserted. As presented in figure 1, these
branches are identified by the value of the input bit
that causes the change of state and the codeword pro-
duced at the arrival of this bit (Sayahi et al., 2017).
Figure 1: State machine representation.
As for the trellis presentation, it can be considered
as a state machine repeated numerous times (see fig-
ure 2) Thus, each vertex is the state of the encoder.
Each edge is a transition and has as label the corre-
sponding output of the encoder.
Figure 2: Trellis representation.
3.2.2 Convolutional Decoder
To decode a message, already coded with a convolu-
tional encoder, many algorithms can be used. Espe-
cially in this work, we will use a Viterbi algorithm.
This choice is justified by the ability of this algo-
rithm to correct errors which are randomly distributed
which is the case of errors generated by the applica-
tion of attacks to the host mesh (Sayahi et al., 2019).
ICSOFT 2021 - 16th International Conference on Software Technologies
400

3.3 Spherical System
To ensure the invisibility of our watermark, we chose
to transform vertex and wavelet coefficients, before
being watermarked, to the spherical system (ρ, θ, φ).
This transformation is ensured by applying the fol-
lowing formula 3:
ρ =
p
x
2
+ y
2
+ z
2
θ = arccos(
z
ρ
)
ψ =
(
arccos
x
√
x
2
+y
2
2 ×Π −arccos
x
√
x
2
+y
2
(3)
After watermarking, to reconstruct the watermark-
ing mesh, an inverse transformation should be applied
to represent again the vertex coefficients in the Carte-
sian system by applying the formula 4
x = ρ ×sin θ ×cos ψ
y = ρ ×sin θ ×sin ψ
z = ρ ×cos θ
(4)
3.4 Wavelet Transform
As shown in figure 3, wavelet transform is a step
in our crypto-watermarking algorithm allowing the
representation the host meshes in the multiresolution
field. The objective of the multiresolution analysis
is to decompose a mesh M
i
into two sets: a coarser
low resolution meshes M
i−1
and a set of details D
i−1
:
the analysis phase. This phase is applied as a pre-
processing step of the mesh to be watermarked. All
extracted details are regrouped in a wavelet coeffi-
cient vector (WCV) as it is shown in the formula 5
(Hachicha et al., 2020).
M
i
= M
i−1
⊕D
i−1
(5)
D
i−1
refers to the set of details needed to rebuild
the mesh M
i
, with higher resolution, from the mesh
M
i−1
. ⊕ is the complement orthogonal operator.
Figure 3: Wavelet transform.
The principle of the wavelet transform is to de-
compose, by filtering, the energy of a signal using
two basic functions. Thus, applying these functions
on a mesh in an analysis step, we obtain a lower res-
olution mesh and a set of wavelet coefficients needed
to reconstruct the original mesh in the synthesis step
(Sayahi et al., 2016a). All these coefficients are as-
sembled into a single vector called wavelet coefficient
vector (WCV). Especially, this vector will be modi-
fied during insertion following bits to be inserted (for-
mula 6).
WCV =



D
1
.
.
.
D
i



=



d
x
1
d
y
1
d
z
1
.
.
.
.
.
.
.
.
.
d
x
i
d
y
i
d
z
i



(6)
After the insertion step, all watermarked details
and meshes of different resolution levels are, then,
used to reconstruct the watermarked mesh: synthesis
phase.
4 PROPOSED
CRYPTO-WATERMARKING
SYSTEM
The main idea of this work is to combine a 3D hybrid
watermarking system with an RSA encryption algo-
rithm to ensure 3D multiresolution meshes security.
Our hybrid watermarking system inserts data both in
the multiresolution and spatial domain which allowed
us to enhance the insertion rate. The data inserted in
the multiresolution domain are a logo encrypted us-
ing RSA algorithm. As for the spatial domain, the
watermark is the private key used during logo encryp-
tion. The originality of this work is to join cryptogra-
phy with a 3D hybrid watermarking algorithm. This
new system is composed of an insertion and extrac-
tion step, ensure then copyright protection and index-
ation.
4.1 Insertion Step
Before sharing 3D multiresolution meshes, an inser-
tion step should be executed. The main goal is to in-
sert information related to authenticity in the form of
a logo into these objects. The logo in our case is a
grayscale image encrypted using an RSA algorithm.
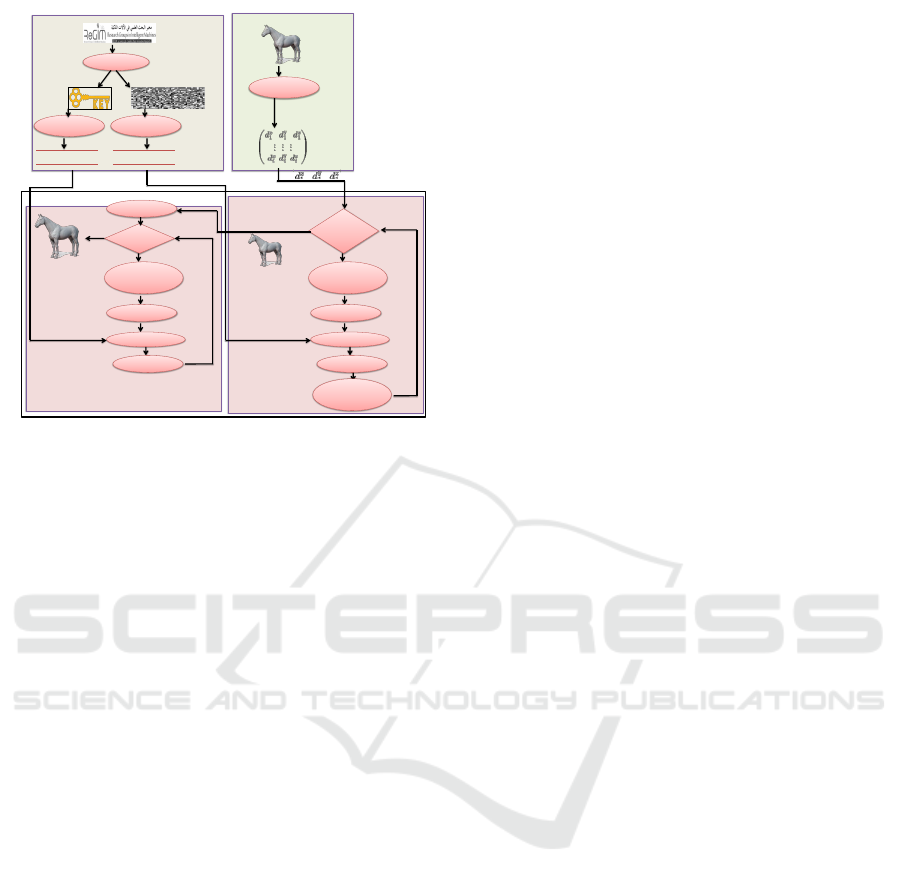
As shown in figure 4, our insertion step can be
decomposed into 3 phases such as:
4.1.1 Watermark Preparation
Before embedding data into meshes, information to
be inserted should be prepared. In fact, data in our
case is a logo, in the form of a grayscale image, re-
ferring to the author’s copyright. This logo should be
encrypted using RSA algorithm after generating pri-
vate and public RSA keys. To enhance the robustness
Robust and Hybrid Crypto-watermarking Approach for 3D Multiresolution Meshes Security
401

Logo
RSA Encoding
Convolutional
encoder
Encrypted Logo
1
0
0
1
…
1
1
Watermark 1
Watermark preparation 3D Mesh preparation
Original Mesh
Wavelet Transform
Wavelet Coefficient
vector
All Coefficients are
treated
Yes
Watermarked Mesh
Transformation to
spherical
coordinate system
Modulation
ρ
Component
No
Insertion Data
RSA Keys
Convolutional
encoder
0
1
0
1
…
1
0
Watermark 2
Watermark 1
Transformation to
spherical coordinate
system
Demodulation
All vertex are
treated
Yes
Final
Watermarked
Mesh
Transformation to
spherical
coordinate system
Modulation
ρ
Component
No
Insertion Data
Demodulation
Vertex acquisition
Watermark 2
Hybrid Watermarking
Figure 4: Insertion step.
of our crypto-watermarking system, both keys and en-
crypted logo are encoded using a convolutional error
correcting code. Results generated by this encoder are
the watermark to be inserted.
4.1.2 3D Mesh Preparation
The host mesh must be also treated before the inser-
tion phase. Therefore, a wavelet transform should be
applied to present it in the multiresolution domain to
enhance invisibility, insertion rate and the robustness
of our Algorithm. The result of this step is the WCV
which will be modified according to data to be in-
serted.
4.1.3 Hybrid Watermarking
One of the particularities of this approach is that the
3D mesh undergoes hybrid watermarking. Indeed, the
insertion iteration occurs twice. In the first one, the
multiresolution domain is adopted to insert the en-
crypted logo into the wavelet coefficients after being
modulated and transformed to the spherical coordi-
nate system. The insertion, then occurs into rho com-
ponent according to the following formula 7:
r
0
=

r + 0.7 i f bit = 1
r + 0.3 i f bit = 0
(7)
After being watermarked, all spherical coeffi-
cients should be represented again in the Cartesian
coordinate system and the watermarked mesh should
be reconstructed by applying a demodulation and a an
inverse wavelet transform.
As for the second watermarking iteration, the in-
put is the watermarked mesh resulting from the first it-
eration. The insertion in this case occurs in the spatial
domain that is to say that vertices coordinates will be
modified according to data to be inserted. The embed-
ded information at this level is RSA keys. As in the
first iteration, embedding includes modulation, trans-
formation to spherical system, insertion, demodula-
tion and transformation again in the Cartesian coordi-
nate system.
4.2 Extraction Step
After mesh sharing between remote users, verification
of authenticity and copyright should occur. To do it,
an extraction step must take place. Since our water-
marking system is hybrid, extraction should be exe-
cuted twice. In the first iteration, RSA keys are ex-
tracted. To do it, we should represent each vertex in
the spherical system; apply for it a modulation and an
extraction to obtain encoded RSA keys. These later
passes throw a convolutional decoder to correct errors
which probably took place. 3D mesh should be recon-
structed in order to start the second iteration. In this
iteration, we aim to extract the logo and decrypt it us-
ing keys resulting from the previous iteration. In fact,
the mesh should be presented in the multiresolution
domain by applying wavelet transform. The resulting
wavelet coefficients are transformed to the spherical
coordinate system before being modulated. Just after,
extraction occurs and data are collected to be decoded
using the same convolutional decoder. Once the errors
are corrected, the extracted logo will be decrypted us-
ing the RSA algorithm and a verification step should
take place (see figure 5).
5 RESULTS AND DISCUSSION
As already mentioned, the assessment of our crypto-
watermarking system is done through the following
points:
5.1 Watermarking System
Experimentation
The evaluation of the hybrid watermarking part of our
approach consists, on the one hand, of testing the im-
pact of inserting a large amount of information (en-
crypted image) on the host mesh quality. In other
words, we seek to find the best compromise between
insertion rate and invisibility which are contradictory.
On the other hand, we must also study the ability of
ICSOFT 2021 - 16th International Conference on Software Technologies
402

Watermarked Mesh
Wavelet Transform
CWV
Transformation to
spherical system
Component

Modulation
Bit Extraction
All bits are
Extracted
No
Yes
Convolutional
decoder
Encrypted Logo
RSA decryption
Extracted Logo
Extracted bits
Demodulation
Component

Transformation to
spherical system
Inverse Wavelet
Transform
Reconstructed mesh
Vertex coefficients
acquisition
Transformation to
spherical system
Component

Modulation
Bit Extraction
All bits are
Extracted
No
Yes
Convolutional
decoder
RSA Keys
Extracted bits
Figure 5: Extraction step.
our approach to maintaining the inserted image intact
despite the attacks applied to the watermarked mesh.
5.1.1 Invisibility and Insertion Rate
Insertion rate and invisibility are two contradictory
watermarking criteria. In fact, when the number of
bits to be inserted increases, there will be mesh qual-
ity deterioration. Our task is then to enhance insertion
rate while keeping mesh quality. Figure 6 shows 3D
crypto-watermarked meshes using our approach.
As it is presented in table 1, our approach has
succeeded to insert a high amount of information
(38×10
4
bits) without influencing mesh quality. This
is justified by the value of MSQE equal to 1.9 ×10
−7
.
These results are better of these recently published in
Error scale Original meshes Error Distribution Crypto-watermarked meshes
Figure 6: Crypto-watermarked meshes.
(Xiao and Qing, 2012; Ouled Zaid et al., 2015; Hiten-
dra et al., 2014; Ying et al., 2016; Yuan, 2015; Sayahi
et al., 2016b; Sayahi et al., 2017).
Table 1: Comparison with literature of our invisibility and
insertion rate results.
Approaches insertion rate MSQE
(Xiao and Qing, 2012) 765 0,007
(Ouled Zaid et al., 2015) 10650 0.2 ×10
−3
(Hitendra et al., 2014) 21022 2.7 ×10
−5
(Ying et al., 2016) 199 3.2×10
−5
(Yuan, 2015) 172974 1.2 ×10
−5
(Sayahi et al., 2016b) 250000 1, 2 ×10
−6
(Sayahi et al., 2017) 337929 2 ×10
−7
Our approach 380000 1, 9 ×10
−7
5.1.2 Robustness Against Attacks
In addition to insertion rate and invisibility, our
crypto-watermarking system must be robust against
most popular attacks such as similarity transforma-
tion, smoothing, coordinate quantization, simplifica-
tion and compression attacks (H. et al., 2018). To
evaluate the robustness of our algorithm we calculate
the correlation between the extracted watermark and
the original data to evaluate the degree of watermark
alteration. Of course, when the value of the correla-
tion is near to 1, we can say that the watermark with-
stand attacks (Tjoa et al., 2020).
• Robustness against similarity transformation
It includes translation, rotation and uniform scal-
ing are examples of this category which never alter
the form of the mesh (see Figure 7).
Applying rotation, translation and uniform scaling
on the watermarking meshes doesn’t prevent the cor-
rect extraction of the whole inserted data. Correlation
Robust and Hybrid Crypto-watermarking Approach for 3D Multiresolution Meshes Security
403

Figure 7: Similarity transformation attack.
is always equal to 1. Our crypto- watermarking sys-
tem is, then, robust against similarity transformation
attacks.
• Robustness against noise addition attack
It aims to modify the coordinates of the vertices
using a pseudo-random generator which can change
vertices position. This change will be a multiplica-
tion of these coordinates by the random factor which
reflects noise level. As a result, points describing the
mesh will be redistributed randomly in space which
threatens inserted information (see figure 8).
1
10

3
10

4
10

5
10

Noise level
Noise level Noise level Noise level
Figure 8: Noise addition attack.
In order to study the robustness of our watermark-
ing algorithm against noise addition attack, we var-
ied the noise level and calculate the correlation be-
tween the original data and information retrieved from
the watermarked and attacked mesh. Results shown
in table 2 approve that our system can extract the
whole inserted data from a noise level equal to 10
−5
.
These results are enhanced in comparison with those
in (Sayahi et al., 2015; Jen-Tse et al., 2014; Sayahi
et al., 2019; Sayahi et al., 2017).
• Robustness against smoothing attack
This attack is usually applied over building the ob-
ject to remove noise. The application of a smoothing
attack changes the positions of the vertices which may
damage the image already inserted (see Figure 9).
To evaluate the robustness of our approach against
smoothing attacks, we varied the deformation factor
Table 2: Correlation values after applying Noise addition
attack.
Noise level 10
−4
10
−5
10
−6
10
−7
In(Sayahi et al., 2015) 0.8 — — —
In(Jen-Tse et al., 2014) 0.3 — — —
In(Sayahi et al., 2019) 0.99 1 1 1
In (Sayahi et al., 2017) 0.9 1 1 1
Ours 1 1 1 1
Smoothing level Smoothing level Smoothing level Smoothing level
6
10

7
10

8
10

9
10

Figure 9: Smoothing attack.
and calculate every time the correlation between the
inserted and extracted data. Results, as exposed in ta-
ble 3, that our system can extract the whole inserted
data from a dfactor equal to 10
−8
. This result is en-
hanced in comparison with recent published results
such as (Sayahi et al., 2015; Ying et al., 2016; Sayahi
et al., 2019; Sayahi et al., 2017).
Table 3: Correlation values with applying smoothing at-
tacks.
dFactor 10
−8
10
−9
10
−10
In(Sayahi et al., 2015) 0.18 0.31 0.43
In(Ying et al., 2016) 0.5 0.8 1
In(Sayahi et al., 2019) 1 1 1
In(Sayahi et al., 2017) 0.92 1 1
Ours 1 1 1
• Robustness against coordinate quantization attack
It aims at quantifying vertex coordination using
two factors previously calculated according to the
maximum and minimum values along x, y and z co-
ordinates (Figure 10).
Quantization level: 5 Quantization level: 10 Quantization level: 12 Quantization level: 13
Figure 10: Coordinate quantization attack.
To assess the stoutness of our algorithm against
coordinate quantization attack, we changed the quan-
tization level and calculate every time the correlation
between the inserted and extracted data. All informa-
tion is correctly extracted from a quantization level
ICSOFT 2021 - 16th International Conference on Software Technologies
404

equal to 13 (see table 4). Presented results are bet-
ter than those recently published in (Ying et al., 2016;
Sayahi et al., 2016c; Sayahi et al., 2019; Sayahi et al.,
2017).
Table 4: Correlation values with applying coordinate quan-
tization attacks.
Quantization Level 10 12 13 14
In(Ying et al., 2016) 0.7 0.85 – –
In(Sayahi et al., 2016c) 0.14 0.628 0.954 1
In(Sayahi et al., 2019) 0.76 0.92 1 1
In(Sayahi et al., 2017) 0.56 0.8 0.91 1
Ours 0.8 0.95 1 1
• Robustness against Simplification attack
Simplification is one of the most popular attacks
which consists, as presented in figure 11, of reducing
the mesh resolution from one iteration to another.
Figure 11: Simplification attack.
To study the efficiency of our approach against
this attack, we calculate the correlation between orig-
inal and watermarked data in terms of iteration num-
ber. Results presented in table 5 approve that our sys-
tem is robust against simplification attack.
Table 5: Correlation values with applying simplification at-
tacks.
iteration Number 3 4 5 6
In(Hitendra et al., 2014) – 0.79 0.68 0.61
In(Dae, 2015) 0.45 0.25 0.1 0.05
In(Ying et al., 2016) 0.92 – – –
In(Sayahi et al., 2017) 1 1 1 1
In(Sayahi et al., 2019) 1 1 1 1
Ours 1 1 1 1
• Robustness against compression attack
Compression is one of the most popular treatments
applied to digital data in order to facilitate storage
and sharing of data. The compression of water-
marked data can alter and even deteriorate inserted
data. So we can say that an algorithm is robust if it
is able to extract correctly inserted data from a com-
pressed data. In particular, 3D watermarking algo-
rithm should be robust against compression attack.
Unfortunately, there are no tests on compression in
recently published articles. The evaluation of the
robustness algorithm against compression is shown
in table 6 results approve that the whole data is ex-
tracted from a rate bit/vertex equal to 2.5. These re-
sults are improved in comparison with those recently
published such as (Sayahi et al., 2016c; Sayahi et al.,
2019; Sayahi et al., 2017).
Table 6: Correlation values with applying compression at-
tack.
Bit/vertex 1 1.5 2 2.5 3
In(Sayahi et al., 2016c) 0.4 0.6 0.89 0.9 1
In(Sayahi et al., 2019) 0.79 0.83 0.9 0.56 1
In(Sayahi et al., 2017) 0.6 0.78 0.9 1 1
Ours 0.72 0.8 0.92 1 1
5.2 Encryption System Evaluation
Before insertion, the logo , to be inserted, is encrypted
using RSA algorithm. The logo is a grayscale image.
In figure 12, histograms of original and encrypted im-
ages are shown. Histograms of encrypted image are
evenly distributed and they are so distinct from those
of original images containing large spikes. As a re-
sult,it is difficult to interpret the appearance of the en-
crypted image.
Original Images Encrypted Images Histograms of encrypted Image Histograms of original Images
Figure 12: Histograms of original and encrypted images.
In order to evaluate the efficiency of RSA algo-
rithm, we calculate the entropy and the PSNR be-
tween the original and encrypted logo. Results are
presented in table 7.
Table 7: Entropy and PSNR between original and encrypted
logo.
Entropy PSNR
(Sayahi et al., 2019) 7.997 7.590
(Sayahi et al., 2017) 7.997 7.590
Our approach 7.998 7.400
Robust and Hybrid Crypto-watermarking Approach for 3D Multiresolution Meshes Security
405

6 CONCLUSION AND FUTURE
OUTLOOK
In this work, we propose a new hybrid crypto- wa-
termarking algorithm for 3D multiresolution meshes.
The particularity of this work is, on one side, the hy-
brid watermarking applied on 3D meshes. In fact, the
mesh is watermarked in the multiresolution and the
spatial domain.On the other side, the second particu-
larity is to combine cryptography with 3D watermark-
ing to secure 3D multiresolution meshes. This choice
is justified by the efficiency that cryptography and hy-
brid watermarking have proven in securing images.
Our system allows a high insertion rate (logo en-
crypted with RSA algorithm and RSA keys). The en-
crypted logo is inserted after applying wavelet trans-
form, Transformation to spherical system and mod-
ulation. After that the watermarked mesh should be
reconstructed. As for the second iteration, RSA keys
are inserted into the mesh resulting from the first iter-
ation by modifying vertices coordinates. Experimen-
tal results prove that our hybrid crypto- watermarking
approach has kept the mesh quality despite the high
insertion rate. Applying the most popular attacks to
the watermarked meshes did not prevent the correct
extraction of the logo and RSA keys.
As perspectives, we want to extend our work by
adding to it an intelligent module allowing to set au-
tomatically the coefficients to be used during insertion
using the method of quantification that are fixed em-
pirically in this work.
REFERENCES
Benyamin, N., Sattar, M., Seyed, M., S., and Mohammad,
R., M. (2014). A simple, sensitive and secure image
encryption algorithm based on hyper-chaotic system
with only one round diffusion process. Multimedia
Tools and Applications, 71(3).
Dae, J., C. (2015). Watermarking scheme of mpeg-4 laser
object for mobile device. International Journal of Se-
curity and Its Applications., 9(1):305 – 312.
H., A., K., P., W., E., and T., A. M. (2018). Current ad-
vances, trends and challenges of machine learning and
knowledge extraction: From machine learning to ex-
plainable ai. Lecture Notes in Computer Science book
series, 11015:1–8.
Hachicha, S., Sayahi, I., Elkefi, A., and Ben Amar, C.
(2020). Gpu-based blind watermarking scheme for
3d multiresolution meshes using unlifted butterfly
wavelet transformation. Circuits, Systems, and Signal
Processing, pages 1533–1560.
Hitendra, G., Krishna, Kr., K., Manish, G., and Suneeta,
A. (2014). Uniform selection of vertices for water-
mark embedding in 3-d polygon mesh using ieee754
floating point representation. In International Confer-
ence on Communication Systems and Network Tech-
nologies, pages 788 – 792.
Jen-Tse, W., Yi-Ching, C., Shyr-Shen, Y., and Chun-
Yuan, Y. (2014). Hamming code based watermark-
ing scheme for 3d model verification. In Interna-
tional Symposium on Computer, Consumer and Con-
trol, pages 1095 – 1098.
Lamiaa, B., Saleh, H., I., and Abdelhalim, M., B. (2015).
Enhanced watermarking scheme for 3d mesh models.
In International Conference on Information Technol-
ogy, pages 612 – 619.
Ouled Zaid, A., Hachani, M., and Puech, W. (2015).
Wavelet-based high-capacity watermarking of 3-d ir-
regular meshes. Multimed Tools and Applications,
74(15):5897 – 5915.
Sayahi, I., Elkefi, A., and Ben Amar, C. (2016a). Blind wa-
termarking algorithm based on spiral scanning method
and error correcting codes. International Journal of
Multimedia Tools and applications, pages 1– 24.
Sayahi, I., Elkefi, A., and Ben Amar, C. (2016b). Blind wa-
termarking algorithm for 3d multiresolution meshes
based on spiral scanning method. International Jour-
nal of Computer Science and Information Security,
14(6):331 – 342.
Sayahi, I., Elkefi, A., and Ben Amar, C. (2016c). A
multi-resolution approach for blind watermarking of
3d meshes using scanning spiral method. In Inter-
national Conference on Computational Intelligence in
Security for Information Systems, pages 526 – 537.
Sayahi, I., Elkefi, A., and Ben Amar, C. (2017). Join cryp-
tography and digital watermarking for 3d multiresolu-
tion meshes security. In International Conference on
Image Analysis and Processing, pages 637–647.
Sayahi, I., Elkefi, A., and Ben Amar, C. (2019). Crypto-
watermarking system for safe transmission of 3d mul-
tiresolution meshes. International Journal of Multi-
media Tools and applications, pages 13877–13903.
Sayahi, I., Elkefi, A., Koubaa, M., and Ben Amar, C.
(2015). Robust watermarking algorithm for 3d mul-
tiresolution meshes. In International Conference
on Computer Vision Theory and Applications, pages
150–157.
Tariq, S. and Ayesha, Q. (2016). Encrypting grayscale im-
ages using s8 sboxes chosen by logistic map. Interna-
tional Journal of Computer Science and Information
Security, 14(4):440–444.
Tjoa, S., Buttinger, C., and Holzinger, K. Kieseberg, P.
(2020). Penetration testing artificial intelligence.
ERCIM News, 123:36–37.
Viterbi, A. (1971). Convolutional codes and their perfor-
mance in communication systems. IEEE Transactions
on Communication Technology, 19(5):751 – 772.
Xiao, Z. and Qing, Z. (2012). A dct-based dual water-
marking algorithm for three-dimensional mesh mod-
els. In International Conference on Consumer Elec-
tronics, Communications and Networks, pages 1509 –
1513.
Y., G., Ji., K., W., H., P., C., and H., X. (2020). An
asymmetric image encryption algorithm based on a
ICSOFT 2021 - 16th International Conference on Software Technologies
406

fractional-order chaotic system and the rsa public-key
cryptosystem. International Journal of Bifurcation
and Chao, 30(15).
Ying, Y., Ruggero, P., Holly, R., and Ioannis, I. (2016). A 3d
steganalytic algorithm and steganalysis-resistant wa-
termarking. IEEE Transactions on visualization and
computer graphics.
Yuan, Y., T. (2015). An efficient 3d information hiding al-
gorithm based on sampling concepts. Multimed Tools
Appl, 74(34):1 – 17.
Robust and Hybrid Crypto-watermarking Approach for 3D Multiresolution Meshes Security
407