Fast Cramer-Shoup Cryptosystem

Pascal Lafourcade

1 a

, L

eo Robert

1 b

and Demba Sow

2 c

Universit

e Clermont Auvergne, LIMOS CNRS (UMR 6158), Campus des C

ezeaux, Aubi

ere, France

LACGAA, Universit

e Cheikh Anta Diop de Dakar, Senegal

Keywords:

Public Key Encryption, Cramer-Shoup, IND-CCA2.

Abstract:

Cramer-Shoup was the ﬁrst practical adaptive CCA-secure public key encryption scheme. We propose a faster

version of this encryption scheme, called Fast Cramer-Shoup. We show empirically and theoretically that

our scheme is faster than three versions proposed by Cramer-Shoup in 1998. We observe an average gain of

60% for the decryption algorithm. We prove the IND-CCA2 security of our scheme. The proof only relies on

intractability assumptions like DDH.

1 INTRODUCTION

Provable security is an important issue in modern

cryptography. It allows us to formally prove the

security of the encryption schemes by reduction to

difﬁcult problems such as discrete logarithm prob-

lem (DL), Computational Decisional Difﬁe-Hellman

problem (CDH), Decision Difﬁe-Hellman problem

(DDH) (Boneh, 1998; Joux and Guyen, 2006) or the

quadratic residuosity problem. For instance, the DDH

problem is used to prove the IND-CPA security of the

ElGamal encryption scheme (Elgamal, 1985). In or-

der to have security against adaptive chosen ciphertext

attacks (IND-CCA2), a notion introduced in 1991 by

Dolev et al. (Dolev et al., 1991), Cramer and Shoup

proposed in 1998 an encryption scheme (Cramer and

Shoup, 1998) that has a veriﬁcation mechanism in the

decryption algorithm to avoid malleability of the ci-

phertext and also uses one hash function.

Fujisaki and Okamoto in (Fujisaki and Okamoto,

1999) proposed a generic conversion from any IND-

CPA cryptosystem into an IND-CCA2 one, in the

random oracle model (ROM) (Bellare and Rogaway,

1993). However the design of an IND-CCA2 encryp-

tion scheme is not easy, as the story of Optimal Asym-

metric Encryption Padding (OAEP) (Bellare and Rog-

away, 1994; Pointcheval, 2011) can show. After a ﬁrst

try by Bellare and Rogaway (Bellare and Rogaway,

1994) in 1995, V. Shoup found a problem in (Shoup,

2001), that was ﬁxed in (Phan and Pointcheval, 2004;

https://orcid.org/0000-0002-4459-511X

https://orcid.org/0000-0002-9638-3143

https://orcid.org/0000-0002-1917-2051

Pointcheval, 2011). Finally to conclude the story of

OAEP, an computer veriﬁed proof has been made

in (Barthe et al., 2011).

Our goal is to design a faster version of Cramer-

Shoup scheme. For this, we use the approach pro-

posed in (Sow and Sow, 2011) to improve the decryp-

tion algorithm of ElGamal (Elgamal, 1985).

Contributions: Our main aim is to improve the ef-

ﬁciency of the Cramer-Shoup public key scheme:

1. We design a public key cryptosystem, called Fast

Cramer-Shoup, based on the Generalized ElGa-

mal encryption scheme (Sow and Sow, 2011).

2. We implemented all these schemes with

GMP (Granlund, 2020) to demonstrate that

Fast Cramer-Shoup is the fastest one with a gain

of 60% for decryption algorithm .

3. We prove its security against the adaptive chosen

ciphertext attack (IND-CCA2) under the (DDH)

assumption.

Related Works: Shoup and Gennaro (Shoup and

Gennaro, 1998) give two ElGamal-like practical

threshold cryptosystems that are secure against adap-

tive chosen ciphertext attack in the random oracle

model. They use H(h

) ⊕m to encrypt the message

m, unfortunately the trick of Sow et al. (Sow and Sow,

2011) cannot be applied in this case.

In (Cramer and Shoup, 2002), the authors pro-

posed a construction by considering an algebraic

primitive called universal hash proof systems. They

showed that this framework yields not only the origi-

nal DDH-based Cramer-Shoup’s scheme but also en-

766

Lafourcade, P., Robert, L. and Sow, D.

Fast Cramer-Shoup Cryptosystem.

DOI: 10.5220/0010580607660771

In Proceedings of the 18th International Conference on Security and Cryptography (SECRYPT 2021), pages 766-771

ISBN: 978-989-758-524-1

cryption schemes based on quadratic residuosity and

on Paillier’s assumption (Paillier, 1999).

In 2011, a modiﬁed variant of ElGamal’s encryp-

tion scheme was presented (Sow and Sow, 2011),

and it is called Generalized ElGamal’s encryption

scheme. This version is faster than ElGamal, encryp-

tion algorithm is the same as ElGamal’s encryption

mechanism, the key generation algorithm is slower

but the decryption process is faster. We adapt this idea

to improve Cramer and Shoup’s encryption scheme.

Outline: In Section 2, we propose our public key

cryptosystem, called Fast Cramer-Shoup. In Sec-

tion 3, we present the result of our empirically per-

formance comparison and our complexity analysis for

the key generation, encryption and decryption algo-

rithms for all versions of Cramer-Shoup.

2 Fast Cramer-Shoup’s

ENCRYPTION SCHEME

We present our Fast Cramer-Shoup’s scheme and

prove that it is IND-CCA2 secure. Let us recall some

notions and deﬁnitions like the set of non-negative in-

tegers Z

≥0

, a security parameter λ, a group descrip-

tion Γ, a computational group scheme G , a probabil-

ity distribution of group descriptions S

, hash func-

tions (HF), target collision resistant (TCR) assump-

tion for hash function (HF), some random variables

as Coins used in the following are deﬁned in (Cramer

and Shoup, 2003) (see also (Naor and Yung, 1989)).

Fast Key Generation Algorithm:

G1 : On input 1

for λ ∈Z

≥0

, select a group

G, along

with a prime-order subgroup G and choose a gen-

erator g

∈ G of order q.

G2 : Pick random elements x,y,k,t ∈ Z

with

log

(t) =

log

(q)

, and compute w

,z ∈Z

such that

kq = tw

+ z and then compute w ≡w

(mod q).

G3 : Compute g

= g

,c = g

,d = g

and h = g

G4 : Choose a hash function H

← HF.

G5 : Return (pk,sk), where pk = (Γ,H,g

,c, d,h)

and sk = (Γ, H,t,x,y,z).

Fast Encryption Algorithm:

E1 : Choose a random element r ∈ Z

and compute,

E2 : u

= g

; E3 :u

= g

;E4 :u

= h

;E5 :e = u

E6 : α = H(u

,e);

E7 : v = c

rα

and output ψ = (u

,e, v).

Fast Decryption Algorithm:

D1 : Parse ψ ← (u

,e, v) ∈ G

; output reject if ψ

is not of this form.

: Test if u

and u

belong to G; reject otherwise.

D3 : Compute α = H(u

,e).

: Test if u

= 1 and v = u

x+yα

; otherwise reject.

: Compute β = u

; D6 : Output m = βe.

Correctness: Veriﬁcation: We have βu

= u

)

= (g

)

= g

r(tw+z)

= g

rkq

= 1 since the

order of g

is q and u

x+yα

= (g

)

x+yα

= (g

)

x+yα

)

rα

= c

rα

= v.

Decryption: The decryption message is βe =

e = g

wrt

m = g

r(tw+z)

m = g

rkq

m = m, since the

order of g

is q.

2.1 Security Proof of Fast

Cramer-Shoup Scheme

As CS1’s proof in (Cramer and Shoup, 2003), to

prove that Fast Cramer-Shoup (FCS) is secure against

adaptive chosen ciphertext attack if the DDH assump-

tion holds for G and the TCR assumption holds for

HF, we need some notions.

Suppose PKE is a public-key encryption scheme

that uses a group scheme in the following natural

way: on input 1

, the key generation algorithm runs

the sampling algorithm of the group scheme on in-

put 1

, yielding a group description Γ. For a given

probabilistic, polynomial-time oracle query machine

A,λ ∈ Z

≥0

, and group description Γ, let us deﬁne

AdvCCA

PKE,A

(λ|Γ) to be A’s advantage in an adap-

tive chosen ciphertext attack where the key generation

algorithm uses the given value of Γ, instead of running

the sampling algorithm of the group scheme. For all

probabilistic, polynomial-time oracle query machines

A, for all λ ∈ Z

≥0

, let Q

(λ) be an upper bound on

the number of decryption oracle queries made by A

on input 1

. We assume that Q

(λ) is a strict bound

in the sense that it holds regardless of the probabilis-

tic choices of A, and regardless of the responses to its

oracle queries from its environment.

Theorem 2.1. The Fast Cramer-Shoup is secure

against adaptive chosen ciphertext attack if:

1. the DDH assumption holds for G;

2. and the target collision resistance (TCR) assump-

tion holds for HF.

In particular, for all probabilistic, polynomial-

time oracle query machines A, for all

λ ∈ Z

≥0

, and all Γ[

G,G, g

,q] ∈ [S

], we have



AdvCCA

FCS,A

(λ|Γ) −AdvCCA

CS1,A

(λ|Γ)



≤

(λ)/q

Fast Cramer-Shoup Cryptosystem

767

Description of Games: Suppose that

pk = (Γ, H, g

,c, d,h) and sk = (Γ,H,t, x,y,z).

Let w = log

, and deﬁne x, y, z ∈ Z

as follows:

x = x

+ x

w, y = y

+ y

w and z = z

+ z

w. We

have x = log

c, y = log

d, and z = log

As a notation convention, whenever a particular

ciphertext is under consideration in some context, the

following values are also implicitly deﬁned in that

context: u

,e, v ∈G where ψ = (u

,e, v) and

= u

; the random r ∈ Z

, where r = log

For the target ciphertext ψ

∗

, we also denote by

∗

∈ G and r

∗

∈ Z

the corresponding

values. The probability space deﬁning the attack

game is then determined by the following, mutually

independent, random variables: the coin tosses Coins

of A; the values H, w,x

generated by

the key generation algorithm; the values σ ∈ {0,1}

and r

∗

∈ Z

generated by the encryption oracle.

: Original attack game, let

σ ∈ {0,1} be

the output of A and T

the event σ =

σ, so

AdvCCA

FCS,A

(λ|Γ) = |Pr[T

] −1/2|

: We now modify game G

to obtain game G

These two games are identical, except that instead of

using the encryption algorithm as given to compute

the target ciphertext ψ

∗

, we use a modiﬁed encryption

algorithm, in which steps E4 and E7 are replaced by

= u

and E7

:v = u

x+yα

. The change we have

made is purely conceptual. The values of u

∗

and v

∗

are exactly the same in game G

as they were in G

so Pr[T

] = Pr[T

]

: We modify the encryption oracle, replacing

step E3 by E3

: ˆr

← Z

\{r}; u

← g

ˆr

Lemma 2.2. There exists a probabilistic algorithm

, whose running time is essentially the same as that

of A, such that

|Pr[T

] −Pr[T

]| ≤ AdvDDH

G,A

(λ|Γ) + 3/q. (1)

: We modify the decryption algorithm, replac-

ing steps D4 and D5 with D4

: Test if u

= u

and

v = u

x+yα

; output reject and halt if this is not the

case. D5

= u

. Note that the decryption ora-

cle now make use of w, but does not make use of

, except indirectly through the val-

ues x,y,z. Now, let R

be the event that in game G

some ciphertext ψ is submitted to the decryption or-

acle that is rejected in step D4

but that would have

passed the test in step D4. Note that if a ciphertext

passes the test in D4

, it would also have passed the

test in D4. It is clear that games G

and G

proceed

identically until the event R

occurs. In particular, the

events T

∧¬R

and T

∧¬R

are identical. So by

difference lemma |Pr[T

] −Pr[T

]| ≤ Pr[R

], and so

it sufﬁces to bound Pr[R

]. We introduce auxiliary

games G

and G

below to do this.

: We replace step E5 by E5

: r

← Z

;e ← g

so Pr[T

] = 1/2, since in game G

, the variable σ is

never used. Deﬁne the event R

to be the event in

game G

analogous to the event R

in game G

; that

is, R

is the event that in game G

, some ciphertext ψ

is submitted to the decryption oracle that is rejected

in step D4

but that would have passed the test in step

D4. We show that this modiﬁcation has no effect;

more precisely: Pr[T

] = Pr[T

], and pr[r

] = pr[r

]

. We modify the decryption oracle with a spe-

cial rejection rule: if the adversary submits a ci-

phertext ψ for decryption at a point in time after

the encryption oracle has been invoked, such that

,e) 6= (u

∗

) but α = α

∗

, then the decryp-

tion oracle immediately outputs reject and halts (be-

fore executing step D4

). to analyze this game, we

deﬁne two events. ﬁrst, we deﬁne the event C

to be

the event that the decryption oracle in game G

re-

jects a ciphertext using the special rejection rule. We

deﬁne the event R

to be the event in game G

that

some ciphertext ψ is submitted to the decryption or-

acle that is rejected in step D4

but that would have

passed the test in step D4. note that such a cipher-

text is not rejected by the special rejection rule, since

that rule is applied before step D4

is executed. Now,

it is clear that games G

and G

proceed identically

until event C

occurs. By difference lemma, we have

|Pr[R

] −Pr[R

]| ≤ Pr[C

]. Now, if event C

occurs

with non-negligible probability, we immediately get

an algorithm that contradicts the target collision re-

sistance assumption;

Lemma 2.3. There exists a probabilistic algorithm

, whose running time is essentially the same as that

of A, such that:

Pr[C

] ≤ AdvTCR

HF,A

(λ|Γ) + 1/q. (2)

Finally, we show that R

occurs with negligible

probability, based on information theoretic consider-

ations: we have Pr[R

] ≤ Q

(λ)/q.

Theorem 2.1. To prove this theorem, let us ﬁx A, λ,

and Γ[

G,G, g

,q]. Consider the attack game G

deﬁned above (or see §6.2 in (Cramer and Shoup,

2003)). This is the game that attacker A plays against

the scheme FCS for the given values of λ and Γ. We

adopt all the notations conventions established at the

beginning of §6.2 in (Cramer and Shoup, 2003). We

now modify game G

to obtain a new game G

FCS

Game

FCS

. In this game, we modify the decryp-

tion oracle so that in place of steps D4 and D5 in

CS1, we execute steps D4

and D5

as in the scheme

FCS. (Note that in the FCS encryption algorithm the

random parameter generated is r instead of u in CS1

scheme. So the parameter u

∗

in CS1 corresponds

SECRYPT 2021 - 18th International Conference on Security and Cryptography

768

to r

∗

here). We emphasize that in game G

FCS

, we

have x = x

+ x

w,y = y

+ y

w, and z = z

+ z

where w,x

, and z

are generated by the

key generation algorithm of CS1.

Let T

FCS

be the event that σ = σ

in game G

FCS

We remind the reader that games G

and G

FCS

all op-

erate on the same underlying probability space: all

of the variables Coins,H,w,x

,σ, r

∗

that ultimately determine the events T

, and T

FCS

have the same values in games G

and G

FCS

; all

that changes is the functional behavior of the de-

cryption oracle. It is straightforward to verify that

AdvCCA

FCS,A

(λ|Γ) =

Pr[T

FCS

] −1/2

Let us deﬁne the event R

FCS

to be the event that

some ciphertext is rejected in game G

FCS

in step D4

that would have passed the test in D4 in CS1 scheme

in (Cramer and Shoup, 2003). It is clear that games

and G

FCS

all proceed identically until event R

FCS

occurs. In particular, we have the events T

∧¬R

FCS

and T

FCS

∧¬R

FCS

are identical. So by difference

lemma, we have |Pr[T

]−Pr[T

FCS

]|≤Pr[R

FCS

]. So it

sufﬁces to show that Pr[R

FCS

] ≤Q

(λ)/q. To do this,

for 1 ≤ i ≤ Q

(λ), let R

(i)

FCS

be the event that there is

an i

ciphertext submitted to the decryption oracle in

game G

FCS

, and that this ciphertext is rejected in step

, but would have passed the test in step D4 in CS1

scheme in (Cramer and Shoup, 2003). The bound will

follow immediately from the following lemma.

Lemma 2.4. For all 1 ≤ i ≤ Q

(λ), we have

Pr[R

(i)

FCS

] ≤ 1/q.

Proof. The proof of this lemma is almost identical to

Lemma 10 in (Cramer and Shoup, 2003). Note that

in game G

FCS

, the encryption oracle uses the ”real”

encryption algorithm, and so itself does not leak any

additional information about (x

). This is in

contrast to game G

, where the encryption oracle does

leak additional information.

Fix 1 ≤i ≤ Q

(λ). Consider the quantities: X :=

(Coins,H,w, z,σ,r

∗

) and X

:= (x,y). The values of X

and X

completely determine the adversary’s entire

behavior in game G

, and hence determine if there

is an i

decryption oracle query, and if so, the value

of the corresponding ciphertext. Let us call X and

relevant if for these values of X and X

, there is

an i

decryption oracle query, and the correspond-

ing ciphertext passes steps D1 and D2 in CS1 scheme

in (Cramer and Shoup, 2003).

It will sufﬁce to prove that conditioned on any

ﬁxed, relevant values of X and X

, the probability that

(i)

FCS

occurs is bounded by 1/q. The remainder of the

argument is exactly as in Lemma 10 in (Cramer and

Shoup, 2003), except using X, X

, and the notion of

relevant as deﬁned here.

2 ·10

−2

4 ·10

−2

6 ·10

−2

8 ·10

−2

0.1

Size parameter

Time in seconds

Key Generation Algorithms

Original

Standard

Efﬁcient

Fast

Figure 1: Average execution time for key generation algo-

rithms depending of the security parameter size.

Table 1: Comparison of Original, Standard, Efﬁcient and

Fast Cramer-Shoup (minimum in bold).

Key Generation

Number of Original Standard Efﬁcient Fast

Generator 2 2 1

1 1

Random 6 5 4

4 4

Multiplication 3 2 0

0 3

Exponentiation 6 5 4

4 4

3 PERFORMANCES

EVALUATION

We study the complexity and the performance of Fast

Cramer-Shoup encryption scheme with the following

variants of Cramer-Shoup encryption scheme: Orig-

inal CS, Standard CS, Efﬁcient CS, Fast Cramer-

Shoup protocols. We study the number of operations

performed for key generation, encryption and decryp-

tion. We present complexity results in Table 1 to Ta-

ble 3. We also implemented those with the library

GMP (Granlund, 2020).

The tests are performed with security parameters

of size 512, 1024, 2048 and 4096 bits. The average

execution time of all schemes is carried out under the

same conditions in terms of generation of the values

and sizes of the security parameters. Indeed, given

the size of a security parameter, we perform 1000 tri-

als with new parameters: a prime number and some

random plaintexts that are generated for each trial.

Then, we measure the execution time during one ex-

ecution of each algorithm. Finally, we compute the

mean value for each algorithm (we do not present the

corresponding standard deviations since they are very

low).

Key Generation Algorithms: By studying the

complexity of the key generation algorithm of Ta-

ble 1, we notice that Fast CS and Efﬁcient CS are the

fastest in terms of number of operations. The differ-

ence lies in the multiplication where Fast CS has three

of them while Efﬁcient CS has none. One would ex-

Fast Cramer-Shoup Cryptosystem

769

·10

−2

Size parameter

Time in seconds

Full Decryption algorithms

Original

Standard

Efﬁcient

Fast

(a) Full decryption.

·10

−2

Size parameter

Time in seconds

Veriﬁcation algorithms

Original

Standard

Efﬁcient

Fast

(b) Veriﬁcation phases.

·10

−2

Size parameter

Time in seconds

Actual Decryption computations

Original

Standard

Efﬁcient

Fast

Figure 2: Average execution time for decryption algorithms.

Table 2: Comparison for key parameters.

Public Key Parameters

Number of Original Standard Efﬁcient Fast

Elements 5

5 5

Secret Key Parameters

Elements 6 5 4

4 4

Table 3: Comparison for decryption algorithms.

Veriﬁcation

Number of Original Standard Efﬁcient Fast

Sum 2 2 1

1 1

Multiplication 3 3 1

1 2

Exponentiation 2

2 2

2 3

Decryption

Number of Original Standard Efﬁcient Fast

Inverse 2 1 1 0

Multiplication 2 1

1 1

Exponentiation 2 1 1 0

pect a longer execution time for Fast CS but this is

not the case (Figure 1). It can be explained by the fact

that the Fast CS key generation algorithm computes

an Euclidean division leading to kq = wt +z where k

is generated in Z

. Hence its size is the same as q but t

is generated in Z

∗

√

and its size is half of q. Since z is

the remainder of the euclidean division, its order size

is the same as t. Thus the cost for computing h = g

half of the cost for computing h = g

where z has an

order size equal to the size of q. This gain seems to

be compensated with the three additional multiplica-

tions. To conclude for key generation, the two fastest

algorithms are Efﬁcient CS and Fast CS, while the two

slowest are Original CS and Standard CS. Moreover,

the number of secret parameters are also in favour of

Efﬁcient CS and Fast CS as depicted in Table 2.

Encryption Algorithms: We can see that all

schemes have the same number of exponents, multi-

plication and generation of random number in the en-

cryption algorithm. Thus the average execution time

is the same. We observe empirically that timings are

equal for all protocols since the number of computa-

tions are equals. In all protocols, the ciphertexts are

mainly computed with parameters of the same order

size. We do not give the curve results since the aver-

age execution time is the same in all cases.

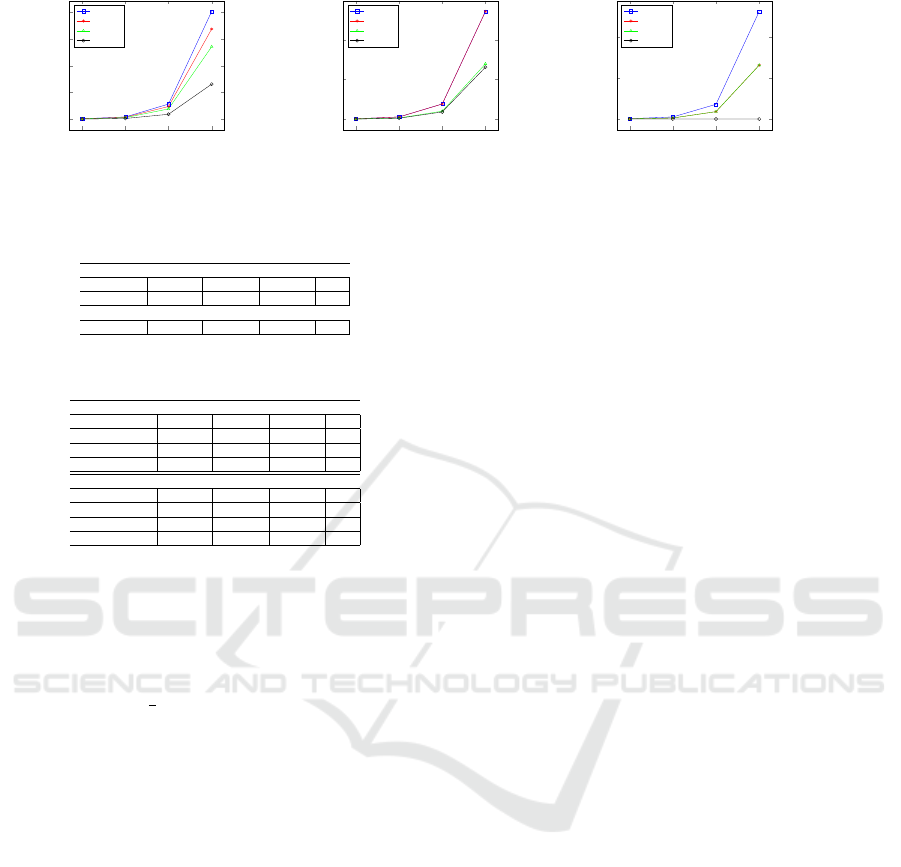
Decryption Algorithms: We observe in Figure 2a

that the fastest is Fast Cramer-Shoup followed by Ef-

ﬁcient CS which is not obvious when we are looking

at the number of total computations.

Indeed there are two components in this algo-

rithm, the veriﬁcation phase and the actual decryp-

tion. The veriﬁcation is used for checking the in-

tegrity of messages if the outputs are valid and the de-

cryption computation is executed leading to retrieve

the plaintext. In Figure 2a, we observe that Fast

Cramer-Shoup has a faster execution time. For veriﬁ-

cation phase, we observe in Figure 2b that the average

execution time of the Fast CS and Efﬁcient CS proto-

cols have the same average execution time. In both

cases the second veriﬁcation is the same. The differ-

ence is then on the ﬁrst veriﬁcation. The Efﬁcient CS

protocol uses one modular exponent, u

= u

; while

ours uses two modular exponents, βu

= u

= 1.

Despite the result given in Table 3, there is actually no

difference between those two computations in terms

of execution time since elements t and z of Fast CS

have their size equal to half the size of w in the Ef-

ﬁcient CS. Hence, the overall execution time for the

veriﬁcation of our protocol Fast CS is the same as Ef-

ﬁcient CS protocol. For the decryption phase, it is

clear that Fast CS protocol is faster than Original for

decryption since the number of exponents is reduced.

We can also say from Table 3 that Fast CS is faster

than Standard CS and Efﬁcient CS at decryption. We

observe in Figure 2c that Standard CS and Efﬁcient

CS have the same execution time. This result is ex-

pected since they both use the same computation with

the same elements size, i.e., eu

−z

= m. The latter

computation uses one exponentiation and one inver-

sion to end with a multiplication. The Fast Cramer-

Shoup decryption algorithm requires to recover m as

follows βe = m where β has been computed in the ver-

iﬁcation phase. Thus, the decryption consists of only

one multiplication. The gain comes from the fact that

we have one inverse less to compute, and also one

exponentiation less to compute. The gain of the over-

all execution time of decryption phase for our proto-

col is more than 60%. Note that the curve related to

SECRYPT 2021 - 18th International Conference on Security and Cryptography

770

Fast Cramer-Shoup is not zero but since this curve is

composed of only one multiplication, the comparison

with a modular exponent, an inversion and a multipli-

cation, is in favor of the stand alone multiplication.

4 CONCLUSION

We propose an IND-CCA2 Public Key cryptosystem

called Fast Cramer-Shoup. It is an improvement of

Cramer-Shoup scheme. We prove the IND-CCA2 se-

curity of this new scheme. We also implement in

GMP (Granlund, 2020) our scheme to compare it to

Cramer-Shoup schemes. In the future, we aim at ap-

plying our technique to other schemes that are based

on Cramer-Shoup like for instance (Kurosawa and

Trieu Phong, 2014; Abdalla et al., 2015).

REFERENCES

Abdalla, M., Benhamouda, F., and Pointcheval, D.

(2015). Public-key encryption indistinguishable un-

der plaintext-checkable attacks. In Katz, J., editor,

Public-Key Cryptography – PKC 2015, pages 332–

352, Berlin, Heidelberg. Springer Berlin Heidelberg.

Barthe, G., Gr

egoire, B., Lakhnech, Y., and Zanella

eguelin, S. (2011). Beyond provable security. Veriﬁ-

able IND-CCA security of OAEP. In Topics in Cryp-

tology – CT-RSA 2011, volume 6558 of Lecture Notes

in Computer Science, pages 180–196. Springer.

Bellare, M. and Rogaway, P. (1993). Random oracles are

practical: A paradigm for designing efﬁcient proto-

cols. In Proceedings of the 1st ACM Conference on

Computer and Communications Security, CCS ’93,

page 62–73, New York, NY, USA. Association for

Computing Machinery.

Bellare, M. and Rogaway, P. (1994). Optimal asymmetric

encryption. In Santis, A. D., editor, Advances in Cryp-

tology - EUROCRYPT ’94, Workshop on the Theory

and Application of Cryptographic Techniques, Peru-

gia, Italy, May 9-12, 1994, Proceedings, volume 950

of Lecture Notes in Computer Science, pages 92–111.

Springer.

Boneh, D. (1998). The decision difﬁe-hellman problem.

In In Proceedings of the Third Algorithmic Number

Theory Symposium, volume 1423, pages 48–63.

Cramer, R. and Shoup, V. (1998). A practical public key

cryptosystem provably secure against adaptive chosen

ciphertext attack. In Proc. of the 18th Annual Interna-

tional Cryptology Conference on Advances in Cryp-

tology, crypto’98, pages 13–25.

Cramer, R. and Shoup, V. (2003). Design and analy-

sis of practical public-key encryption schemes secure

against adaptive chosen ciphertext attack. SIAM Jour-

nal on Computing, 33(1):167–226.

Cramer, R. and Shoup, V. (May 2002). Universal hash

proofs and a paradigm for adaptive chosen ciphertext

secure public-key encryption. In In L. Knudsen, ed-

itor, Proceedings of Eurocrypt 2002, volume 2332 of

LNCS, pages 45–64.

Dolev, D., Dwork, C., and Naor, M. (1991). Non-malleable

cryptography. In Proceedings of the Twenty-Third

Annual ACM Symposium on Theory of Computing,

STOC ’91, page 542–552, New York, NY, USA. As-

sociation for Computing Machinery.

Elgamal, T. (1985). A public key cryptosystem and a

signature scheme based on discrete logarithms. In

CRYPTO, IT-31(4), volume 4, pages 469–472.

Fujisaki, E. and Okamoto, T. (1999). How to enhance the

security of public-key encryption at minimum cost. In

Public Key Cryptography, pages 53–68, Berlin, Hei-

delberg. Springer Berlin Heidelberg.

Granlund, T. (2020). GNU MP: The GNU Multiple Preci-

sion Arithmetic Library, 6.2.0 edition.

Joux, A. and Guyen, K. (2006). Separating decision difﬁe-

hellman to difﬁe-hellman in cryptographic groups.

Kurosawa, K. and Trieu Phong, L. (2014). Kurosawa-

desmedt key encapsulation mechanism, revisited. In

Pointcheval, D. and Vergnaud, D., editors, Progress

in Cryptology – AFRICACRYPT 2014, pages 51–68,

Cham. Springer International Publishing.

Naor, M. and Yung, M. (1989). Universal one-way hash

functions and their cryptographic applications. In In

21st Annual ACM Symposium on Theory of Comput-

ing.

Paillier, P. (May 1999). Public-key cryptosystems based on

composite degree residuosity classes. In In J. Stern,

editor, Proceedings of Eurocrypt 1999, volume 1592

of LNCS, pages 223–38.

Phan, D. H. and Pointcheval, D. (2004). Oaep 3-round: A

generic and secure asymmetric encryption padding. In

Advances in Cryptology - ASIACRYPT 2004, 10th In-

ternational Conference on the Theory and Application

of Cryptology and Information Security, Jeju Island,

Korea, December 5-9, 2004, Proceedings, volume

3329 of Lecture Notes in Computer Science, pages

63–77. Springer.

Pointcheval, D. (2011). OAEP: Optimal Asymmetric En-

cryption Padding, pages 882–884. Springer US,

Boston, MA.

Shoup, V. (2001). Oaep reconsidered. In Proceedings

of the 21st Annual International Cryptology Confer-

ence on Advances in Cryptology, CRYPTO ’01, page

239–259, Berlin, Heidelberg. Springer-Verlag.

Shoup, V. and Gennaro, R. (1998). Securing threshold cryp-

tosystems against chosen ciphertext attack. In In Ad-

vances in Cryptology-Eurocrypt ’98.

Sow, D. and Sow, D. (2011). A new variant of el gamal’s en-

cryption and signatures schemes. JP Journal of Alge-

bra, Number Theory and Applications, 20(1):21–39.

Fast Cramer-Shoup Cryptosystem

771