Mixed Discrete-Continuous Simulation for Digital Twins

Neha Karanjkar

1 a

and Subodh M. Joshi

2 b

Indian Institute of Technology Goa, India

Department of Computational and Data Sciences, Indian Institute of Science, Bangalore, India

Keywords:

Digital Twins, Mixed Discrete-Continuous Simulation, Python, SimPy.

Abstract:

The advent of Digital Twins has precipitated the need for an open and ﬂexible simulation framework with

unique design considerations. A key requirement of such a framework is the ability to simulate systems con-

taining a mix of discrete and continuous processes that may interact with each other. In this paper, we propose

a framework for mixed discrete-continuous simulations particularly targeted for Digital Twin applications.

The framework is based on SimPy, a popular discrete-event simulation library in Python. We ﬁrst present

a systematic approach by which continuous process simulations can be integrated within the event-stepped

engine of SimPy. We illustrate the approach using an example. We then discuss the features of the proposed

framework and the roadmap for its implementation.

1 INTRODUCTION

The emergence of Digital Twins is set to transform

manufacturing, healthcare, urban planning, trans-

portation and many other sectors by aiding monitor-

ing and real-time decision making using Internet of

Things (IoT) technology and real-time analytics. A

Digital Twin refers to a digital representation (com-

puter model) of the real system that is continuously

kept in sync with the real system using periodic sens-

ing of its health parameters and incorporates analyt-

ics for prediction, optimization and control of the real

system. It is to be noted that the term ‘Digital Twin’

implies a two-way ﬂow of information between the

real entity and its digital representation (viz. sensing

and control) and is distinct from a ‘digital model’ or

a ‘digital shadow’ which generally imply a one-way

information ﬂow from the real system to its model. A

taxonomy of Digital Twins and a detailed discussion

of their engineering aspects are presented in (Fuller

et al., 2020).

Simulation is a key aspect of Digital Twins. A

summary of challenges and desired capabilities as-

sociated with the simulation of Digital Twins is pre-

sented in (Shao et al., 2019). The design of a sim-

ulation framework for Digital Twins is driven by the

characteristics of the system to be modeled. While

https://orcid.org/0000-0003-3111-1435

https://orcid.org/0000-0002-9239-8866

some system models may necessitate a continuous

simulation framework (Aversano et al., 2020; Moli-

naro et al., 2021), a discrete-event simulation might

sufﬁce for other kinds of Digital Twins (Agalianos

et al., 2020).

The focus of this paper is on open simulation

frameworks for creating Digital Twins in applica-

tion areas such as manufacturing and process con-

trol. In these applications, the phenomena to be mod-

eled are often a mix of discrete and continuous pro-

cesses. Thus the ability to perform mixed discrete-

continuous (MDC) simulations is a key requirement

for the framework. The other requirements for such a

simulation framework are as follows:

1. The ability to model heterogeneous systems con-

taining different kinds of continuous processes,

each possibly requiring a different numerical

method for its solution and/or different character-

istic time-step sizes.

2. Support for capturing the effect of periodic sensor

updates from the real system on the model’s state.

3. The ability to perform real-time simulation.

4. The framework should be open-source and ﬂexi-

ble. It should be easy to integrate existing libraries

for enabling analytics and visualization (e.g. op-

timization, machine learning, data handling, sci-

entiﬁc computing and plotting libraries) into the

framework.

5. The language used by the framework should sup-

422

Karanjkar, N. and Joshi, S.

Mixed Discrete-Continuous Simulation for Digital Twins.

DOI: 10.5220/0010580804220429

In Proceedings of the 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2021), pages 422-429

ISBN: 978-989-758-528-9

port modular descriptions and the use of object

oriented features for modeling complex systems

with many interconnected components.

While there exist a number of frameworks that are

targeted separately for either continuous simulation

or discrete-event simulations, the requirement of sim-

ulating both discrete and continuous processes to-

gether, possibly interacting with each other, intro-

duces some challenges. Section 2 presents a brief re-

view of approaches and existing frameworks for con-

tinuous, discrete and hybrid simulation. A majority of

the existing frameworks for MDC simulations are ei-

ther commercial or domain-speciﬁc. OpenModelica

is a notable exception which offers an open simula-

tion environment based on a declarative modeling lan-

guage (Modelica) and a library of component models

for multi-domain simulation (Fritzson et al., 2020).

However, there still exists the need for a mixed

simulation framework that is written in a general-

purpose, object-oriented language which allows in-

tegration with existing continuous simulation frame-

works. Python is an attractive choice for implement-

ing such a framework because of its wide user base,

ease of use and the availability of a number of li-

braries for analytics and visualization. In this paper,

we present the outline for an open-source, Python-

based mixed simulation framework motivated by the

requirements listed above.

The proposed framework is based on SimPy,

a process-based discrete-event simulation library in

Python (SimPy-Team, 2020). Processes in SimPy are

implemented using Python’s generator functions and

can be used to model active components. The pro-

cesses are managed by an environment class, which

performs time advancement in an event-stepped man-

ner using a global event queue. The system to be mod-

eled can be described in Python using a few SimPy

constructs and does not require the user to learn a new

modeling language. SimPy also supports real-time

simulation. However, SimPy is designed for discrete-

event simulation and currently offers no features for

modeling continuous systems (SimPy-Team, 2020).

In this paper we present a systematic approach

for integrating continuous models into the event-

stepped simulation engine of SimPy for MDC sim-

ulations. The framework is particularly suited for

systems where the continuous entities are few and

loosely coupled and their interactions can be modeled

via events. We present the framework, illustrating its

key ideas using a simple example, and describe the

roadmap for its implementation.

The rest of the paper is organized as follows: in

the next section, we present a detailed review of ex-

isting approaches to continuous, discrete-event and

mixed simulations. In Section 3 we present some de-

sign considerations for simulation of MDC systems

and describe the proposed framework. The roadmap

for implementation is presented in Section 4.

2 A REVIEW OF SIMULATION

APPROACHES AND

FRAMEWORKS

Depending on the type of the system to be modeled,

simulation approaches can be broadly classiﬁed into

the following categories:

A. Continuous System Simulation.

Continuous systems are characterized by continuous

evolution of the state variables. A few examples

of such systems include transient heat conduction in

solids, ﬂuid ﬂows, acoustic wave propagation etc.

Under certain conditions, fundamentally discrete sys-

tems such as highway vehicle trafﬁc can be mod-

eled as continuous processes, e.g. evolution of vehi-

cle density over time (Lighthill and Whitham, 1955;

Sreekumar et al., 2019). The mathematical models

used for describing the dynamics of such systems of-

ten take the form of ordinary/partial differential equa-

tions (O/PDE) or mixed differential-algebraic equa-

tions (DAE). Simulating continuous systems thus in-

volves solving the differential equations using suit-

able numerical schemes (such as the ﬁnite element

spatial discretization method) as well as the appro-

priate numerical time integrators. Time is advanced

in a regular manner using a step-size that is either

ﬁxed, or adjusted dynamically over the course of a

simulation. A detailed description of continuous pro-

cesses and their simulation aspects can be found in

(LeVeque, 1990; Cellier and Kofman, 2006) and the

references therein. In practice, frameworks such as

FEniCS (Logg and Wells, 2010), Deal II (Bangerth

et al., 2016), OpenFOAM (Weller et al., 1998) are

used for continuous multiphysics simulations of com-

plex systems. Numerical techniques such as reduced

order models (ROM) (Chinesta et al., 2011; Feng,

2005) and Machine-Learning (ML) based metamod-

els (Simpson et al., 2001) may be used instead of the

high ﬁdelity models to reduce the overall computing

cost.

B. Discrete-Event Simulation.

Discrete processes are characterized by changes in the

state of the system occurring only at discrete (count-

able) instants of time, referred to as events. Discrete-

event simulation is broadly divided into event-stepped

and cycle-stepped approaches. A detailed description

Mixed Discrete-Continuous Simulation for Digital Twins

423

of discrete-event simulation approaches can be found

in (Hill, 2007). Formalisms such as Discrete Event

System Speciﬁcation (DEVS) and a subsequent gen-

eralization (GDEVS) have been proposed for speciﬁ-

cation and simulation of discrete-event systems (Zei-

gler, 1989; Giambiasi et al., 2001). Agalianos et.

al. present an overview of issues and challenges

for discrete-event simulation in the context of Digi-

tal Twins (Agalianos et al., 2020). There exist sev-

eral proprietary as well as open source libraries and

softwares for discrete-event simulations. A review

of open source discrete simulation softwares is pre-

sented in (Dagkakis and Heavey, 2016).

C. Mixed Discrete-Continuous (MDC) Simulation.

Systems containing both discrete-event and contin-

uous processes require a hybrid simulation frame-

work. Kofman proposes a quantization based in-

tegration method for simulation of hybrid systems

(Kofman, 2004). Nutaro et. al. propose a split

system approach in which a-priori knowledge about

the discrete-continuous structural split in the model

can be used for performing efﬁcient simulation (Nu-

taro et al., 2012). An approach called Discrete Rate

Simulation has been proposed for simulating linear

continuous models (such as constant-rate ﬂuid ﬂows)

within a discrete-event framework and implemented

in a commercial software (Damiron and Nastasi,

2008; Bechard and Cote, 2013). A detailed review

of various methodologies used for hybrid discrete-

continuous simulation frameworks is presented in (El-

dabi et al., 2019). In the following section, we present

some design considerations and implementation ap-

proaches for MDC simulation, and describe our pro-

posed framework.

3 FRAMEWORK

The system to be modeled can be thought of as a mix

of continuous and discrete entities that interact with

each other. An entity in this context is a collection

of state variables, methods and processes represent-

ing a particular object to be modeled in the system.

A discrete entity refers to a process whose state can

change only at discrete time instants (events). A con-

tinuous entity is an entity whose state may be consid-

ered to change continuously with time and may re-

quire continuous simulation/monitoring. The design

of a framework for simulation of such discrete and

continuous entities interacting with each other is es-

sentially driven by the following questions:

• How do we advance time?

• How do we simulate interactions between the dis-

crete and continuous entities?

These questions have been addressed by formal ap-

proaches proposed for hybrid simulations, for e.g.

(Nutaro et al., 2012). From an implementation per-

spective, the simulation approaches can be broadly

classiﬁed into two categories as summarized below

and illustrated in Figure 1.

(A) In the ﬁrst approach, the advancement of time

is controlled by a single continuous simulation

framework. The events to be modeled are embed-

ded into the continuous simulation framework as

updates to the state variables or boundary condi-

tions during simulation. These updates may oc-

cur at pre-deﬁned time-steps or whenever a certain

condition on the state variables is met (for exam-

ple, when the value of the state variable crosses

a particular threshold). The step-size for advanc-

ing time is determined by the stability considera-

tions of the numerical scheme used for continuous

simulation. If the required step-size differs across

multiple continuous entities in the system, the

smallest of the step-sizes needs to be used. Such

an approach is well suited for systems mainly con-

sisting of tightly coupled continuous entities.

(B) In the second approach, time advancement is han-

dled by an event-stepped discrete-event simula-

tion framework. Continuous solvers are embed-

ded into this framework for simulation of individ-

ual continuous entities. Interactions of a contin-

uous entity with other entities in the system are

modeled via events. This approach is well-suited

when the continuous entities in the system are few

and loosely coupled.

Approach A

Continuous Simulation

Framework

Embedded Discrete events

Approach B

Discrete-Event Framework

Continuous Entities

Continuous Simulation

Framework

Embedded Discrete Events

Global

Event queue

trigger

state-update

schedule wakeup

Figure 1: Two approaches to implementation of a MDC

simulation framework.

Approach (B) is particularly suited for simulation

of Digital Twins in manufacturing and process engi-

neering domains since the systems to be modeled are

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

424

heterogeneous, typically consisting of a larger num-

ber of discrete entities and a few continuous entities

that are loosely coupled and interact in well-deﬁned

ways. We propose a MDC simulation framework

based on this approach and describe how the ques-

tions of time advancement and capturing interactions

between entities are addressed by our framework.

3.1 Proposed Framework

In the proposed framework for MDC simulation, the

advancement of time is performed using the event-

stepped engine of SimPy. A continuous entity is char-

acterized by its state variables, a state-update function

and a deﬁnition of events that serve as an interface be-

tween the continuous entity and the external world as

summarized in Figure 2. The state update function in

the continuous entity can serve as a wrapper for per-

forming updates via an external continuous solver.

●

state variables

●

state_update_function( t ){...}

●

events declaration

- perturbation events

- probe events

- output events

- wakeup events

●

behavior_process()

{

initialization

...

while True

{

wait for a perturbation/probe

or wakeup event to occur

---------------

●

update state

●

check if any output events

need to be triggered

●

schedule a wakeup event

}

Figure 2: Components of a continuous entity model.

The interactions between a continuous entity and the

rest of the system can be implemented via events that

serve as the entity’s interface. These events are of four

types:

1. Perturbation Event: An external event that may

affect the state/trajectory of the continuous entity.

2. Probe Event: An external event which involves

querying the state of the continuous entity and

thus necessitates updating its state upto a given

time.

3. Output Event: An event triggered by the con-

tinuous entity itself as a consequence of its state

update which may affect other entities in the sys-

tem.

4. Wakeup Event: An event scheduled by the con-

tinuous entity itself for performing state updates

after a ﬁxed time step or for creating output events

whose time of occurrence can be predicted in ad-

vance.

The behaviour of the continuous entity is modeled as

a SimPy process. This process is activated whenever

a perturbation, probe or a wakeup event for the entity

occurs. When activated,

1. The state updates for the entity upto the current

time are computed.

2. If any condition for triggering output events is

met, the output events are triggered

3. The continuous entity schedules a wakeup event

for itself after a particular time interval. This time

interval is determined as follows:

• (a) If the current trajectory of the state values

in the entitity is known, and if all of the output

events can be predicted ahead of time based on

this trajectory, the wakeup can simply be sched-

uled at the time the earliest output event is pre-

dicted to occur.

• (b) If all of the output events cannot be pre-

dicted ahead of time, the state needs to be up-

dated after ﬁxed number of time steps (possi-

bly on each time step) by scheduling a wakeup

event periodically.

At each iteration of the event-stepped algorithm of

SimPy, the simulation time is advanced to the times-

tamp of the earliest scheduled event in the global

event list. All events scheduled to occur at this time

are executed and the processes waiting on this event

are triggered using callbacks.

3.1.1 An Improved Scheme for Time

Advancement

One issue with the presented approach is that if the

time step size for the continuous simulation is very

small relative to the typical time between events in

the rest of the system, the cost of adding a wakeup

event to the global event list after every time-step can

be prohibitive. To address this, we propose a modiﬁ-

cation as follows:

At each iteration (K) of the event-stepped algo-

rithm, the tentative time-step (∆

) is taken to be the

difference between the scheduled time of the next

event in the global event list (t

next event

) and the simu-

lation time for the current iteration(t

). Each contin-

uous entity is then asked to peek-ahead in time by a

total period of ∆

by executing its state-update equa-

tions. This can be done either using a single step of

size ∆

or by dividing this period into ﬁner time-steps

Mixed Discrete-Continuous Simulation for Digital Twins

425

as as dictated by the time marching scheme. The com-

putation of state updates for multiple continuous en-

tities can potentially be executed in parallel. If no

output events of interest are predicted to be gener-

ated by any of the continuous entities in this period,

the time can be advanced by ∆

and the computed

state-updates in each of the continuous entities can be

applied before proceeding to the next iteration. How-

ever, if it is found that for a continuous entity i, an

event of interest is generated at time t

< t

next event

then it may be possible that this event could affect the

state or trajectories of the other entities in the system.

Thus the actual time-step taken must be the one that

advances time to the earliest predicted event across

all of the continuous entities. That is, the simulation

time should be advanced to t

K+1

= min

) in the next

iteration.

The earliest event predicted to occur at time t

K+1

can then be inserted into the global event-list, so that

its effect on other entities can be propagated as usual

in a discrete-event framework, and the state updates

in all of the continuous entities computed up to time

K+1

can be applied before advancing simulation time

to t

K+1

. A further optimization is to adaptively adjust

the tentative time step ∆

for improved performance.

A proof-of-concept implementation of this frame-

work has been completed and validated using exam-

ples. Here, we illustrate the key ideas of the frame-

work using a simple example and present the results

generated via simulation.

3.2 An Example

The essential idea of the proposed framework can be

illustrated using an example as follows: Suppose the

system to be modeled contains multiple ﬂuid tanks

whose level is to be simulated and monitored con-

tinuously with respect to time. Each tank has an in-

let and an outlet valve that can be opened or closed

based on external triggers. The ﬂow rate through the

inlet/outlet valves can be speciﬁed in units of length

per time and deﬁned as the maximum change in tank

level per unit time when the corresponding valve is

open. The ﬂow rates and the maximum level cor-

responding to the tank capacity can be assumed to

be ﬁxed parameters for the tank. The interaction be-

tween the tank and other entities in the system can be

of two kinds: (a) The opening/closing of the valves

can be triggered by external processes and can affect

the time-trajectory of the tank level. (b) There are as-

sumed to be external processes in the system that are

affected whenever the level of the tank crosses a par-

ticular threshold (for example, whenever the tank be-

comes empty or full). These external processes need

to be notiﬁed whenever the empty/full conditions oc-

cur.

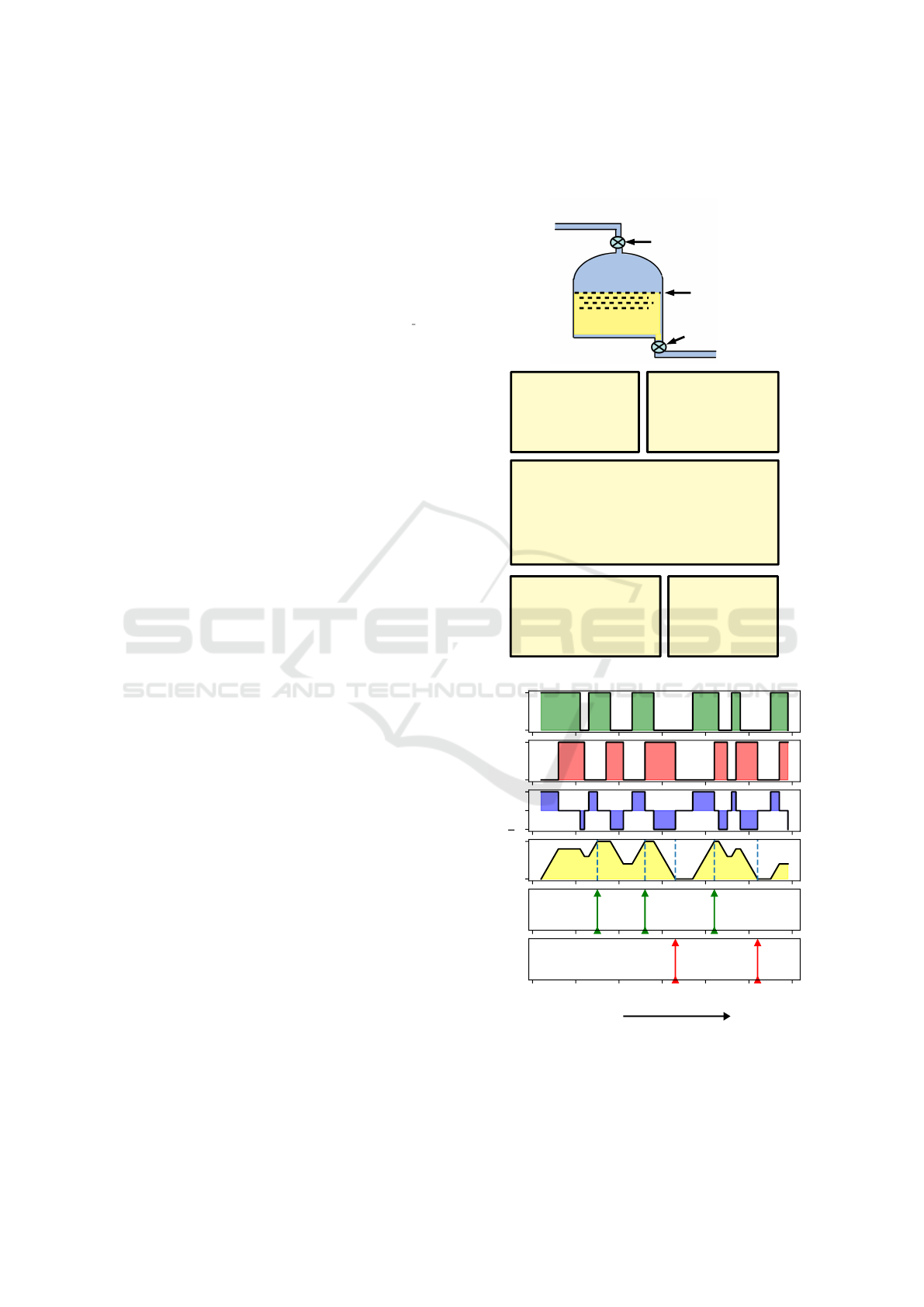
Inlet

valve

Outlet valve

level

●

net_inflow = (inlet_on * inflow_rate)

- (outlet_on * outflow_rate)

●

level (t + Δt) = level (t) + Δt * net_inflow

STATE EQUATIONS

●

max_level

●

inflow_rate

●

outflow_rate

PARAMETERS

●

level

●

inlet_on

●

outlet_on

STATE VARIABLES

TANK

●

tank_empty

●

tank_full

OUTPUT EVENTS

●

inlet_toggled

●

outlet_toggled

PERTURBATION EVENTS

Figure 3: Model of a ﬂuid tank.

OFF

inlet

OFF

outlet

inow

level

FULL

0 10 20 30 40 50 60

EMPTY

TIME

Figure 4: Plots of the time evolution of the tank’s state

showing the empty/full events generated using the MDC

simulation framework.

To model this example in the proposed frame-

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

426

work, the tank can be considered a continuous en-

tity and described as a Python class. Objects of this

class can be instantiated to create multiple tank in-

stances in the system. The tank entity is characterized

by state variables, parameters, and state-update equa-

tions as summarized in Figure 3. The opening/closing

of valves correspond to perturbation events for the

tank and are triggered by an external process. When-

ever the tank becomes full/empty a corresponding

full/empty output event is triggered by the tank en-

tity. External processes that should be affected by

the full/empty events can be automatically notiﬁed

(by using the yield <event> construct of SimPy).

The entity also speciﬁes a probe event which can be

triggered by external processes. When triggered, it

causes the tank state to be updated upto the current

time. The behavior of the tank is described as a SimPy

process as illustrated in Figure 2. Figure 4 presents

the time evolution of the tank’s states observed from

a simulation run of this example implemented using

our framework.

In this particular example, the state update equa-

tion is a simple linear algebraic equation and there-

fore an iterative time marching method is not neces-

sary for continuous state update. Implementing the

updates via plain Python code inside the state up-

date method in the tank class sufﬁces and there is no

need for invoking an external solver. Further, the ex-

act time instants at which the empty/full events occur

can be predicted if the trajectory is not affected by ex-

ternal events. In such a case, the state updates need

to be computed only at wakeup events scheduled at

time instants when the output events are predicted to

occur. Between these time instants, the state trajec-

tory is completely known. In practice, many contin-

uous processes can in fact be replaced by a reduced

order surrogate models making the state trajectories

known ahead of time. Thus, a simple event-stepped

approach can lead to fast and efﬁcient simulation. On

the other hand, if the state update equations require

iterative time integrators for their solution, it may not

be possible to predict the time instants at which out-

put events must occur. Thus, the wakeup events need

to be scheduled and the state updates applied periodi-

cally (after a ﬁxed number of time-steps).

This example serves to describe the essential com-

ponents of the proposed framework. The implemen-

tation would consist of abstract classes to model con-

tinuous entities with an interface provided by the per-

turbation, probe and wakeup events, and modules for

integration with existing continuous solvers.

3.3 Strengths of the Proposed

Framework

Some reasons that make this approach particularly

suited for application to Digital Twins are as follows:

• The event-stepped approach can result in a more

efﬁcient simulation for scenarios where only a few

kinds of events affect the trajectory of continuous

entities in the system.

• In this approach, it is possible for different contin-

uous entities in the system to use different contin-

uous solvers and internal time step-size values.

• The loose coupling between the continuous enti-

ties enables their parallel execution within a single

time-step for real-time simulation.

• For modeling entities where a high level of accu-

racy may not be necessary, coarse surrogate mod-

els can be used to predict the trajectory and time

of output events and schedule a wakeup ahead of

time.

• Sensor value updates from the real system can be

easily incorporated into the simulation as pertur-

bation events affecting the state.

4 ROADMAP

We discuss the features of the proposed framework

and a roadmap for its implementation along the fol-

lowing aspects:

1. Integration with Existing Continuous Simula-

tion Frameworks.

For fast simulation of continuous processes, in-

tegration with established continuous simulation

frameworks is necessary. We plan to use Dolﬁn

(Logg and Wells, 2010), a Python based ﬁnite-

element library for multiphysics modeling and

simulation to carry out continuous process sim-

ulations within our framework.

2. Incorporating Analytics.

For Digital Twin applications, analytics modules

need to be incorporated into the framework for

parameter extraction from sensor data, prediction,

optimization and for building surrogate models in

run-time.

3. Acceleration for Real-time Simulations.

The requirement for real-time simulation creates

a need for simulation acceleration that is possible

using hardware platforms such as GPGPUs, FP-

GAs or parallel execution on multi-core systems.

Mixed Discrete-Continuous Simulation for Digital Twins

427

We plan to explore architectures that can take ad-

vantage of these technologies for simulations.

4. Support for Sensing and Control.

Sensing and control are integral aspects of a Digi-

tal Twin. Features that support these aspects need

to be explored in detail and integrated into the

framework.

5 CONCLUSIONS

We propose a Python based framework for mixed

discrete-continuous simulations speciﬁcally targeted

for Digital Twins applications. The proposed frame-

work uses SimPy, a Python based discrete-event sim-

ulation framework for controlling time-advancement

and offers support for integrating existing libraries for

continuous process simulation. We present a system-

atic approach by which the continuous processes can

be embedded into the event-stepped discrete simula-

tion engine of SimPy and illustrate the structure of the

framework using an example. The ongoing work fo-

cuses on further development of the simulation frame-

work on several fronts including, but not limited to:

integration with existing continuous solvers, incorpo-

rating analytics, real-time simulation and an interface

for sensing and control.

REFERENCES

Agalianos, K., Ponis, S. T., Aretoulaki, E., Plakas, G., and

Efthymiou, O. (2020). Discrete Event Simulation and

Digital Twins: Review and Challenges for Logistics.

Procedia Manufacturing, 51(2019):1636–1641.

Aversano, G., Ferrarotti, M., and Parente, A. (2020). Digital

Twin of a Combustion Furnace Operating in Flame-

less Conditions: Reduced-Order Model Development

from CFD Simulations. Proceedings of the Combus-

tion Institute, 000:1–9.

Bangerth, W., Davydov, D., Heister, T., Heltai, L., Kan-

schat, G., Kronbichler, M., Maier, M., Turcksin, B.,

and Wells, D. (2016). The deal.II Library, Version

8.4. J. Numer. Math., 24:135–141.

Bechard, V. and Cote, N. (2013). Simulation of Mixed Dis-

crete and Continuous Systems: An Iron Ore Termi-

nal Example. In 2013 Winter Simulations Conference

(WSC), pages 1167–1178.

Cellier, F. E. and Kofman, E. (2006). Continuous System

Simulation. Springer-Verlag, US.

Chinesta, F., Ladeveze, P., and Cueto, E. (2011). A Short

Review on Model Order Reduction Based on Proper

Generalized Decomposition. Archives of computa-

tional methods in engineering, 18:395–404.

Dagkakis, G. and Heavey, C. (2016). A Review of Open

Source Discrete Event Simulation Software for Oper-

ations Research. Journal of Simulation, 10(3):193–

206.

Damiron, C. and Nastasi, A. (2008). Discrete Rate Simula-

tion Using Linear Programming. In Winter Simulation

Conference Proceedings, pages 740–749.

Eldabi, T., Tako, A. A., Bell, D., and Tolk, A. (2019). Tu-

torial on Means of Hybrid Simulation. Proceedings of

the 2019 Winter Simulation Conference, pages 273–

284.

Feng, L. (2005). Review of Model Order Reduction Meth-

ods for Numerical Simulation of Nonlinear Circuits.

Applied Mathematics and Computation, 167:576–

591.

Fritzson, P., Pop, A., Abdelhak, K., Ashgar, A., Bachmann,

B., Braun, W., Bouskela, D., Braun, R., Buffoni, L.,

Casella, F., Castro, R., Franke, R., Fritzson, D., Ge-

bremedhin, M., Heuermann, A., Lie, B., Mengist, A.,

Mikelsons, L., Moudgalya, K., Ochel, L., Palanisamy,

A., Ruge, V., Schamai, W., Sj

olund, M., Thiele, B.,

Tinnerholm, J., and

Ostlund, P. (2020). The Open-

Modelica Integrated Environment for Modeling, Sim-

ulation, and Model-Based Development. Modeling,

Identiﬁcation and Control, 41(4):241–295.

Fuller, A., Fan, Z., Day, C., and Barlow, C. (2020). Digital

Twin: Enabling Technologies, Challenges and Open

Research. IEEE Access, 8:108952–108971.

Giambiasi, N., Escude, B., and Ghosh, S. (2001). GDEVS:

A Generalized Discrete Event Speciﬁcation for Accu-

rate Modeling of Dynamic Systems. Proceedings -

5th International Symposium on Autonomous Decen-

tralized Systems, ISADS 2001, pages 464–469.

Hill, R. (2007). Discrete-Event Simulation: A First Course.

Journal of Simulation, 1(2):147–148.

Kofman, E. (2004). Discrete Event Simulation of Hy-

brid Systems. SIAM Journal on Scientiﬁc Computing,

25(5):1771–1797.

LeVeque, R. J. (1990). Numerical Methods for Conserva-

tion Laws. Birkhauser-Verlag, Basel.

Lighthill, M. J. and Whitham, G. B. (1955). On Kine-

matic Waves II. A Theory of Trafﬁc Flows on Long

Crowded Roads. Proceedings of The Royal Society A,

229:317–345.

Logg, A. and Wells, G. N. (2010). DOLFIN: Automated

Finite Element Computing. ACM Trans. Math. Softw.,

37(2).

Molinaro, R., Singh, J. S., Catsoulis, S., Narayanan, C., and

Lakehal, D. (2021). Embedding Data Analytics and

CFD into the Digital Twin Concept. Computers and

Fluids, 214:104759.

Nutaro, J., Kuruganti, P. T., Protopopescu, V., and Shankar,

M. (2012). The Split System Approach to Managing

Time in Simulations of Hybrid Systems Having Con-

tinuous and Discrete Event Components. Simulation,

88(3):281–298.

Shao, G., Jain, S., Laroque, C., Lee, L. H., Lendermann, P.,

and Rose, O. (2019). Digital Twin for Smart Man-

ufacturing: The Simulation Aspect. Proceedings -

Winter Simulation Conference, 2019-Decem(Bolton

2016):2085–2098.

SIMULTECH 2021 - 11th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

428

Simpson, T. W., Peplinski, J. D., Koch, P. N., and Allen,

J. K. (2001). Metamodels for Computer-based Engi-

neering Design: Survey and Recommendations. En-

gineering with Computers, 17:129–150.

SimPy-Team (2020). Simpy: Discrete-

event simulation for python {Online

https://simpy.readthedocs.io/en/latest/}.

Sreekumar, M., Joshi, S. M., Chatterjee, A., and Mathew,

T. V. (2019). Analyses and Implications of Higher

Order Finite Volume Methods on First-Order Macro-

scopic Trafﬁc Flow Models. Transportation Letters,

11:542–557.

Weller, H. G., Tabor, G., Jasak, H., and Fureby, C. (1998).

A Tensorial Approach to Computational Continuum

Mechanics Using Object-Oriented Techniques. Com-

puters in Physics, 12(6):620–631.

Zeigler, B. P. (1989). Devs Representation of Dynamical

Systems: Event-Based Intelligent Control. Proceed-

ings of the IEEE, 77(1):72–80.

Mixed Discrete-Continuous Simulation for Digital Twins

429