Formal Security Verification of the Station-to-Station based
Cell-attachment Procedure of LDACS
Nils M
¨
aurer
1 a
, Christoph Gentsch
2 b
, Thomas Gr
¨
aupl
1 c
and Corinna Schmitt
3 d
1
Institute of Communication and Navigation, German Aerospace Center (DLR), Wessling, Germany
2
Institute of Data Science, German Aerospace Center (DLR), Jena, Germany
3
Research Institute CODE, Universit
¨
at der Bundeswehr, M
¨
unchen, Germany
Keywords:
Cybersecurity, Authentication, Key Establishment, Symbolic Model, LDACS, Tamarin.
Abstract:
Aeronautical communications systems are currently undergoing a modernization process. Analogue legacy
systems shall be replaced with modern digital alternatives, offering higher bandwidth, increasing capacity and
paving the way for Unmanned Aeronautical Vehicles (UAVs). One modern candidate technology is the L-band
Digital Aeronautical Communications System (LDACS), enabling long-range safety-critical digital communi-
cations between aircraft and ground. As with any modern wireless communications system, LDACS is prone
to cyber-attacks. These issues were addressed in former research, where a secure cell-attachment procedure for
LDACS, based on a modified Station to Station (STS) Mutual Authentication and Key Establishment (MAKE)
protocol, was proposed. However, as of now, its security has not been proven. The contribution of this paper
is the formal verification of the executability and security of the LDACS cell-attachment procedure using the
symbolic model checker Tamarin. The achieved results proved that the suggested cell-attachment procedure
for LDACS is workable and enables secure communication between aircraft and ground.
1 INTRODUCTION
One of the main pillars of the modern Air Traffic
Management (ATM) system is a communication in-
frastructure that enables efficient aircraft control and
safe separation in all phases of flight. Current com-
munication systems are technically mature but suffer-
ing from the Very High Frequency (VHF) band’s in-
creasing saturation in high-density areas and the lim-
itations posed by analogue radio communications. To
overcome the capacity constraints of the legacy ana-
logue systems, digitalization of aeronautical commu-
nications is necessary and currently underway (Mah-
moud et al., 2014).
One of the candidate data link technologies
for long-range terrestrial aeronautical communica-
tions is the L-band Digital Aeronautical Commu-
nications System (LDACS) (Schnell et al., 2014),
which is a ground-based cellular digital aeronauti-
cal communications system for flight guidance and
a
https://orcid.org/0000-0003-1324-7574
b
https://orcid.org/0000-0001-7189-3465
c
https://orcid.org/0000-0002-7864-774X
d
https://orcid.org/0000-0002-4118-1878
AS
GS
ATN
Attacker
Figure 1: LDACS network architecture.
communications related to the safety and regular-
ity of flight. It is currently under standardiza-
tion in the International Civil Aviation Organiza-
tion (ICAO) (International Civil Aviation Organiza-
tion (ICAO), 2018a) and has been tested in experi-
mental flight trials (M
¨
aurer et al., 2021a). Figure 1
illustrates the assumed network architecture. An Air-
craft Station (AS) connects to a LDACS Ground Sta-
tion (GS), the transmission site, which can serve
several hundred ASs. The GS connects via the se-
cure LDACS sub-network to the global Aeronautical
Telecommunications Network (ATN). Without an au-
thenticated key establishment, an active attacker can
send arbitrary messages to both, AS and GS.
LDACS is foreseen to support a multitude of Air
Traffic Services (ATS) and Aeronautical Operational
Mäurer, N., Gentsch, C., Gräupl, T. and Schmitt, C.
Formal Security Verification of the Station-to-Station based Cell-attachment Procedure of LDACS.
DOI: 10.5220/0010580906030610
In Proceedings of the 18th International Conference on Secur ity and Cryptography (SECRYPT 2021), pages 603-610
ISBN: 978-989-758-524-1
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
603

Control (AOC) services, all related to the safety and
regularity of flight (Gr
¨
aupl et al., 2020). To guar-
antee this, cybersecurity is one of the key require-
ments of LDACS and a cybersecurity architecture
has been proposed in (M
¨
aurer, N. and Bilzhause, A.,
2018). Core of this architecture is the LDACS cell-
attachment procedure, consisting of a cell entry pro-
cedure, where LDACS radios aboard the aircraft, es-
tablish contact with the ground counterpart, enabling
basic communication. The second step of the cell-
attachment procedure is the Mutual Authentication
and Key Establishment (MAKE) protocol, establish-
ing trust and a shared secret between AS and GS
(M
¨
aurer, N. and Bilzhause, A., 2018). The MAKE
protocol assumes an existing Public Key Infrastruc-
ture (PKI) with certificates set up on all authorized
AS and GS, similar to the deployed airport communi-
cations system Aeronautical Mobile Airport Commu-
nication System (AeroMACS) (Crowe, 2016).
A comparison of scientific literature with official
aeronautical standards of systems (Aeronautical Ra-
dio, Incorporated (ARINC), 2007; Blanchet, 2017)
reveals, that after an aeronautical system is specified
and deployed, necessary changes due to newly found
security vulnerabilities are rarely applied. For ex-
ample (Blanchet, 2017) analyzes the ACARS Secure
Message (AMS) secure session initiation scheme us-
ing ProVerif, which is a symbolic model checker, and
reveals a possible replay attack not addressed in the
standard, yet. This is why a formal proof of security
of the cell-attachment procedure is paramount, before
the LDACS specification is finalized.
The objective of this paper is to provide a formal
prove of the security of the cell-attachment procedure
of LDACS by applying the symbolic model checker
Tamarin (Meier et al., 2013).
2 THE LDACS
CELL-ATTACHMENT
PROCEDURE
We focus on the cell-attachment procedure, combin-
ing the cell entry procedure and certificate based Sta-
tion to Station (STS)-MAKE protocol for LDACS as
defined in (M
¨
aurer, N. and Bilzhause, A., 2018) and
updated in (M
¨
aurer et al., 2021b).
2.1 High Level Security Objectives
In (Bilzhause et al., 2017) the authors originally iden-
tified five objectives for LDACS, which were later
extended to nine in the LDACS Standards and Rec-
ommended Practises (SARPS) endorsed by ICAO
(International Civil Aviation Organization (ICAO),
2018b). These objectives originated from previous
threats- and risk analysis (M
¨
aurer and Schmitt, 2019)
of threats to ground- or aircraft stations. Within
these works, concrete attack examples were given
as, e.g., transmission of forged Automatic Depen-
dent Surveillance-Contract (ADS-C) messages from
aircraft to ground, hence falsifying the direction, po-
sition or velocity of an aircraft or the transmission of
forged ATS or AOC messages, resulting in possibly
dangerous flight instructions in digital voice or Con-
troller–Pilot Data Link Communications (CPDLC)
messages.
Attacks accomplishing these tasks are either to
(a) falsify genuine messages, e.g., change the mes-
sage content, sender or recipient, (b) to completely
forge messages or to (c) repeat genuine messages un-
changed, but at a point in time, they are not valid any-
more. To combat such attacks, security controls such
as authentication and integrity checks of messages via
Message Authentication Codes (MAC) and sequence
numbers and timestamps in messages must be put in
place. However, to enable these message integrity-
and authenticity checks, trust has to be established
between communication partners and the establish-
ment of a shared session key between authenticated
stations is required. Finally, the cell-attachment pro-
cedure needs to be executable, which is formulated as
a provable lemma in Section 4.2.
2.2 Security Objectives
The radio link technology is the first point of contact
between aircraft and ground (International Civil Avi-
ation Organization (ICAO), 2015). Hence, the objec-
tive of the LDACS cell-attachment procedure is to es-
tablish mutual trust between any two parties AS and
GS and a shared session key K between any two par-
ties AS and GS, in which they can have “mutual be-
lief”. Following the hierarchy of authentication and
key establishment goals of Boyd et al. (Boyd et al.,
2020), this mutual belief goal can be split up into the
sub-goals entity authentication, key confirmation and
good key, which we model via the lemmata Mutual
Authentication, Secure Key Establishment and Perfect
Forward Secrecy. Table 1 summarizes the attacks on
the cell-attachment procedure, security controls de-
fending against these attacks and the corresponding
lemmata.
The objectives of the cell-attachment procedure
can be summarized in the form of objectives and lem-
mata as follows:
O1* - Mutual Authentication: Both parties can be
SECRYPT 2021 - 18th International Conference on Security and Cryptography
604

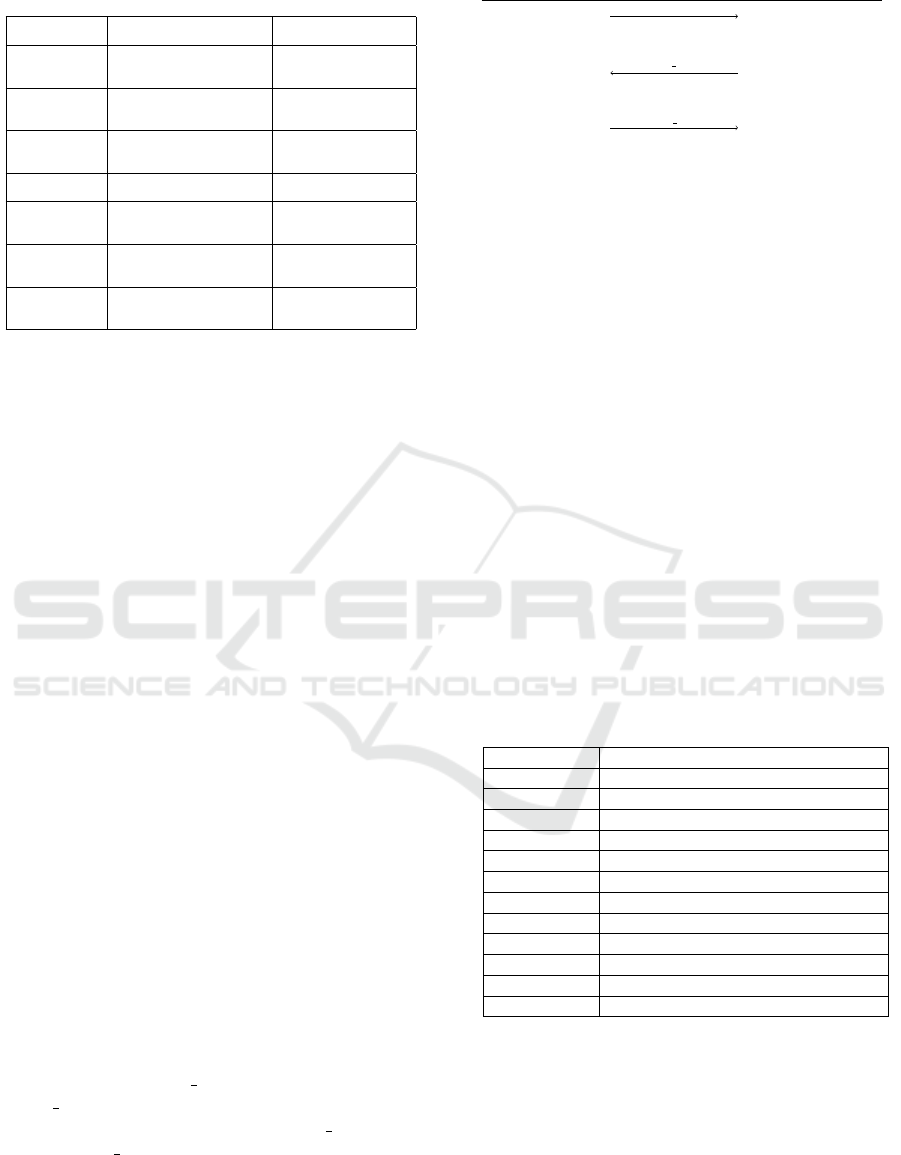
Table 1: LDACS MAKE protocol - Attacks & Controls.
Attack Security
Requirement
Proof Lemma
Unknown key
share
Each party shares the key
with the party it intended to
Secure Key
Establishment, (Mutual)
Authentication
Man in the
middle
Each party shares the key
with the party it intended to
Secure Key
Establishment, (Mutual)
Authentication
Eavesdropping The key is secret between
the two parties
Secure Key
Establishment, (Perfect
Forward) Secrecy
Replay Key freshness Secure Key
Establishment
Long-term key
compromise
Attacker can only authen-
ticate as the station, whose
keys were stolen
(Mutual)
Authentication
Long-term key
compromise
Old session keys of the
station must not be recon-
structable by the attacker
Perfect Forward Secrecy
Session key
leakage
No other session keys (from
other stations or future
sessions) are affected
Perfect Forward Secrecy
sure of the identity of the other and that both actually
participated in this interaction.
O2* - Secure Key Establishment: Both parties have
established a shared session key, which means both
parties know this key and know that they can use it
for a secure communication with the other party for
the duration of this session. The key must have never
been used before in a session and only the two parties
can know it.
O3* - Perfect Forward Secrecy: The established
session key remains secret, even when the private
signing keys of the involved parties have been com-
promised after this session, or other sessions keys
have been leaked before.
In Section 4.2 these definitions are transformed
into Tamarin provable symbolic lemmata.
2.3 The LDACS Cell Entry Procedure
The LDACS cell-attachment procedure begins with
the cell entry procedure as depicted in Figure 2. It
uses the logical Broadcast Control Channel (BCCH),
Random Access Channel (RACH), Common Control
Channel (CCCH), and Data Channel (DCH) defined
in (Gr
¨
aupl et al., 2020).
Once a GS is securely connected to the aeronauti-
cal ground network, it starts sending a broadcast mes-
sage called SIB, containing relevant information such
as network identification, physical parameters such as
channel frequencies and more. When an AS enters the
cell served by that GS, it receives the broadcast mes-
sage and sends a CELL RQST message in reply. The
CELL RQST message contains a LDACS radio ad-
dress. When the GS receives the CELL RQST mes-
sage, a CELL RESP message is sent back to the AS,
informing the AS about its local temporary address in
the cell. After this exchange of control channel mes-
sages, both communication parties are connected and
Ground Station (GS) Aircraft Station (AS)
SIB
BCCH
Store claimed ID
GS
of GS
CELL RQST
RACH
Store claimed ID
AS
of AS
CELL RESP
CCCH
. . . . . . . . . . . . . . . . . . . . . . . . . . DCH open for authentication . . . . . . . . . . . . . . . . . . . . . . . . . .
Figure 2: LDACS Cell Entry Procedure.
can start transmitting data in the DCH.
Note, that no cryptographic information has been
exchanged, yet. This is because of the sizes of
LDACS control channels: The BCCH allows for
1000 bits, the RACH 53 bits and the CCCH only
for 728 bits maximum (Gr
¨
aupl et al., 2020). How-
ever, since LDACS relevant parameters need to be ex-
changed here, the actual space to add cryptographic
parameters is reduced even further. Hence, the
MAKE protocol begins after the cell entry procedure
using the user data channel DCH, allowing for differ-
ent Diffie-Hellman key sizes and overall higher flexi-
bility in transporting authentication data than over to
the fixed-sized control channels.
2.4 The LDACS MAKE Protocol
After the cell entry procedure, the LDACS MAKE
protocol is performed over the DCH. Table 2 defines
the used notation and Figure 3 illustrates the five steps
of the realized protocol.
Table 2: Notations used in the MAKE protocol.
Notation Definition
msg1 | msg2 Concatenation msg1 with msg2
ID
A
Identifier of A
PrivKey
A
Private key in PKI of A
PubKey
A
Public key in PKI of A
Sig
A
(data) Signature of A with input data
x, y Ephemeral private key of entity A, B
t
A
Ephemeral public key of entity A
g Public Diffie-Hellman parameters
S
A,B
Shared Diffie-Hellman key of A, B
KDF Key Derivation Function
K
A,B
Session key of A, B
N
A
Nonce of entity A
In (M
¨
aurer et al., 2021b) sets of cryptographic algo-
rithms for the tasks of signing, encrypting or authenti-
cating messages were proposed. However, since this
work focuses on the symbolic model of the MAKE
protocol, specific cryptographic algorithms are not as-
signed here.
Formal Security Verification of the Station-to-Station based Cell-attachment Procedure of LDACS
605

Ground Station (GS) Aircraft Station (AS)
Has: ID
AS
, ID
GS
, PrivKey
GS
, PubKey
GS
, PubKey
AS
Has: ID
AS
, ID
GS
, PrivKey
AS
, PubKey
AS
, PubKey
GS
Agreed upon: g, KDF, Sig
A
(data), {data}
key
Agreed upon: g, KDF, Sig
A
(data), {data}
key
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . DCH open for authentication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Step 1 :
Start STS
Choose secret x
Calculate t
GS
= g
x
mod p
Step 2 :
ServerHelloKeyExchange
|t
GS
|
Choose secret y
Calculate t
AS
= g
y
mod p
Calculate S
AS,GS
with y and t
GS
= g
x
S
AS,GS
= (g
x
)
y
mod p
Generate K
AS,GS
= KDF(S
AS,GS
)
Build Sig
AS
(t
AS
, t
GS
, ID
AS
, ID
GS
)
Step 3 :
ClientHelloKeyExchange
|t
AS
|Sig
AS
(t
AS
, t
GS
, ID
AS
, ID
GS
)|
Verify Sig
AS
(t
AS
, t
GS
, ID
AS
, ID
GS
)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . AS authenticated to GS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
If correct: Finish STS
Calculate S
AS,GS
with x and t
AS
= g
y
S
AS,GS
= (g
y
)
x
mod p
Generate K
AS,GS
= KDF(S
AS,GS
), N
GS
Build Sig
GS
(N
GS
, t
GS
, t
AS
, ID
GS
, ID
AS
)
Step 4 :
ServerKeyExchangeFinished
|N
GS
|Sig
GS
(N
GS
, t
GS
, t
AS
, ID
GS
, ID
AS
)|
Verify Sig
GS
(N
GS
, t
GS
, t
AS
, ID
GS
, ID
AS
)
. . . . . . . . . . . . . . . . . . . . . . GS authenticated to AS → AS and GS mutually authenticated and sharing a master secret K
AS,GS
. . . . . . . . . . . . . . . . . . . . . .
Step 5 :
Encrypt N
GS
: {N
GS
}
K
AS,GS
ClientKeyExchangeFinished
{N
GS
}
K
AS,GS
Decrypt N
GS
: {N
GS
}
K
AS,GS
Verify N
GS
. . . . . . . . . . . . . . . . . . . . . . . . . . . . Key confirmation done, Secure communication AS-GS with K
AS,GS
can commence . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Figure 3: LDACS STS-MAKE Protocol.
3 TAMARIN MODEL OF THE
LDACS CELL-ATTACHMENT
PROCEDURE
Mechanized protocol verification tools rely either on
the (1) symbolic or the (2) computational model.
In the first case, the Dolev-Yao model (Dolev and
Yao, 1981), cryptographic primitives are black boxes,
which are ”unbreakable” as long as the attacker has
no possession of the right key. Messages are terms
of these primitives and the adversary can only apply
these primitives. This is in contrast to the compu-
tational model (Yao, 1982), where messages are re-
garded as bitstrings and cryptographic primitives are
modeled as functions on these bitstrings. The adver-
sary is regarded as a probabilistic Turing machine.
”Although in some restricted cases a proof in the
Dolev–Yao model can imply a computational proof
[...], this is in general not the case” (Boyd et al.,
2020). Therefore, only the symbolic model is con-
sidered applying Tamarin (Meier et al., 2013) in the
performed analysis.
3.1 Modeling Notes
The standards from the Tamarin documentation
(Basin et al., 2021) are followed while modeling
SECRYPT 2021 - 18th International Conference on Security and Cryptography
606

the cell-attachment procedure. As there is no built-
in role type in Tamarin, only rules and facts, roles
must be modeled using state facts, linking multi-
ple rules together by carrying the state of a role
from rule to rule. This way, the roles of AS
and GS are modeled.
Roles, Instances and Sessions: In the present model
of the roles ’AS’ and ’GS’, it is distinguished between
two levels of ’identity’: Each role can be instantiated
infinitely, identified by the public instance-variables
$AS and $GS. This reflects the fact, that in the real
world there can be many aircraft and ground-stations.
Each instance of an aircraft or a ground-station needs
a public-key pair to participate in a protocol run. In
the presented model, the existence of a global PKI is
assumed, where every principal has exactly one such
public-key pair. This is reflected in the developed and
applied Tamarin model by the first rule (cf. Listing
1), which enables any $X to register a key-pair only
once.
This is modeled via the persistent fact !Ltk($X
, ltkX), which stores the private long-term key ltkX in
the global key-store; and the fact !Pk($X, pk( ltkX)),
that stores the corresponding public key of $X respec-
tively. Finally the public key of $X is also sent to the
attacker by Out(pk( ltkX)).
1 rule R e g i s t e r p k :
2 [ F r ( ˜ l t kX ) ]
3 −−[ OnlyOnceV ( $X ) ]−>
4 [ ! Ltk ($X , ˜ l tkX )
5 , ! Pk ($X , pk ( ˜ l tk X ) )
6 , Out ( pk ( ˜ l tk X ) )
7 ]
Listing 1: Tamarin ”Register pk” rule
In the applied model, each role can participate in
an unlimited number of protocol runs. This is called
”sessions”, and they are modeled by creating a fresh
session-ID at the beginning of each instance, which
will be used by the instance until the end of the pro-
tocol run and helps to distinguish multiple sessions of
one instance in the performed proof. Both roles start
with the minimal knowledge of their own ID and their
own long-term key. They get to know each other the
first time, when the AS receives the broadcast mes-
sage of the GS, advertising its own ID - answered by
the AS with a ”CellEntryRequest”, accompanied with
its ID.
3.2 Security Assumptions
In the model presented in this paper, the following as-
sumptions about the building blocks in the LDACS
cell-attachment procedure are made: The modeled
cryptosystems are treated as black boxes meaning that
(1) signature and (2) encryption mechanisms are as-
sumed secure as long as the appropriate keys are un-
known to the adversary. That way, it is assumed, (3)
that the adversary cannot learn anything from mes-
sages he or she cannot decrypt. Also, (4) a guaranteed
freshness is assumed for all generated values like ses-
sion IDs or nonces. Physical properties of the com-
munication – e.g. timing-issues of the message ex-
change – are not modeled and therefore (5) side chan-
nel attacks are not captured. A feature of Tamarin is
(6) the unbound number of stations and therefore par-
allel or interleaved protocol runs by default, which al-
lows to identify the most complex attacks on the pro-
tocol.
Certificates: It is foreseen, that AS and GS have
certificates (handled by an LDACS PKI), signed
by a trusted Certificate Authority (CA) proving
their identity claim. AS and GS have all neces-
sary public keys of respective communication part-
ners pre-installed, to verify signatures and iden-
tity claims. Furthermore the signatures used in
certificates are unforgeable under chosen-plaintext
attacks (Goldwasser et al., 1988).
Signatures: Long term key pairs of AS and GS are
used for signatures only and signatures are assumed
to be strongly unforgeable under chosen-plaintext at-
tacks (Goldwasser et al., 1988).
Diffie-Hellman: Shared Diffie-Hellman parameters
and the choice of Diffie-Hellman Key Exchange
(DHKE) variation were agreed upon, prior to the
MAKE protocol. AS and GS generate a fresh pub-
lic Diffie-Hellman key for each protocol run (i.e., t
AS
,
t
GS
). Hence, t
AS
, t
GS
can also serve as nonces, assum-
ing enough entropy in the underlying random number
generator for secret x and y. Finally, independent of
the choice of chosen DHKE procedure for LDACS
(M
¨
aurer et al., 2021b), the underlying Diffie-Hellman
assumption is assumed to hold.
Key Derivation: It is assumed that the Key Deriva-
tion Function (KDF) is able to derive an arbitrary
amount of strong cryptographic keys from a usu-
ally not uniformly distributed input source and de-
fine ”strong cryptographic keys” as ”indistinguishable
from a random uniform string of the same length”
(Krawczyk, 2010).
4 SYMBOLIC SECURITY PROOF
The defined security objectives for the cell-
attachment procedure in Section 2.2 are proven
with the Tamarin model presented in section 3.
Formal Security Verification of the Station-to-Station based Cell-attachment Procedure of LDACS
607

4.1 Attacker Model
Tamarin follows the approach of Dolev-Yao (Dolev
and Yao, 1981), where an ideal, powerful attacker
is assumed. Additionally, the possibility is as-
sumed that the adversary can corrupt any station
and obtain their long-term secret (certificate), or
their session keys used in different runs of the
protocol. As the standard Dolev-Yao-Attacker is al-
ready built-in to Tamarin, only the Tamarin rules for
the key compromise of long-term and session-keys
have to be added.
1 rule R e v e a l l t k :
2 [ ! L tk ( $X , l t kX ) ]
3 −−[ R eve al ( $X ) ]−>
4 [ Out ( l tk X ) ]
5 . . .
6 rule L e a k s e s s i o n :
7 [ ! S e ss k ( k ) ]
8 −−[ Le ake d ( k ) ]−>
9 [ Out ( k ) ]
Listing 2: Tamarin rules for key compromise of long-term
and session-keys.
These are given in Listing 2 and enable the attacker to
corrupt any agent in the model by default.
4.2 Tamarin Lemmata
In addition to the executability of the LDACS cell-
attachment procedure, the security objectives O1* to
O3* of Section 2.2 have to be proven, as well. All
these objectives are formalized by their appropriate
Tamarin lemma in the following.
Lemma 1: ”Executable” (cf. Listing 3): There ex-
ists a trace where instance A in role AS participates
in session i
a
and instance B in role GS participates in
session i
b
, A is requesting B for cell entry, both are
starting the protocol by exchanging t
AS
and t
GS
, and
finally both commit by having the same shared data.
Lemma 2: ”Mutual Authentication Via Injective
Agreement” (cf. Listing 4): If A finishes a run with
B by exchanging y, it can be sure, B also ran the pro-
tocol with A and y has not been exchanged before in
any other run. Only exception: the private key of an
honest agent has been compromised before.
Lemma 3: ”Secure Key Establishment”
(cf. Listing 5): If A finishes a run with B, it
can be sure, that it has a fresh key P and that B also
has this key for use with A, and this key has not been
established before, implicating that also no other
agent knows it. Only exception: the private key of an
honest agent has been corrupted before.
Lemma 4: ”Perfect Forward Secrecy” (cf. List-
ing 6): The exchanged session key (K
AS,GS
) cannot be
known by the attacker, even when he acquires the pri-
vate key of one or both parties later on. The case, the
session key was leaked to the attacker, is excluded.
1 lemma e x e c u t a b l e :
2 exists-trace
3 ”Ex A B i a i b x y
4 # i # j #k # l #m # n # o .
5 C rea te AS (A, i a ) @i &
6 C rea te GS (B , i b ) @j &
7 A t t a c h i n g (A , B, i a )@k &
8 Ru nni ng (A, B , i a , x )@l &
9 Ru nni ng (B , A, ib , y )@m &
10 Commit ( B, A, ib ,<y , x>)@n &
11 Commit (A , B, i a ,<x , y>)@o”
Listing 3: Lemma 1.
1 lemma m u t u a l a u t h e n t i c a t i o n :
2 ”All A B x y i a # i .
3 Commit (A, B , i a ,<x , y>)@i ==>
4 ( Ex i b # j .
5 Runn ing ( B, A, ib , y ) @j
6 & j<i
7 & not
8 ( Ex A2 B2 i a 2 # i2 .
9 Commit ( A2 , B2 , i a2 ,<x , y>)@i2
10 & not (# i2 =# i )
11 )
12 )
13 | ( Ex C # r . Re v ea l (C )@r
14 & H on es t (C)@i & # r<#i ) ”
Listing 4: Lemma 2.
1 lemma s e c u r e k e y e s t a b l i s h m e n t :
2 ”All A B i a x # i .
3 Commit (A , B, i a , x ) @i ==>
4 ( Ex P i b # j #m.
5 Knows (A, i a , P , B )@m &
6 Knows (B , i b , P , A) @j &
7 not
8 ( Ex D E i d #k .
9 Knows (D, i d , P , E )@k &
10 not (#m=#k ) &
11 not (# j =# k )
12 )
13 )
14 | ( Ex C # r . Re v ea l (C )@r
15 & H on es t (C)@i & # r<#i ) ”
Listing 5: Lemma 3.
1 lemma s e c r e c y :
2 ”All x # i .
3 S e c r e t ( x ) @i ==>
4 not ( Ex # j . K( x ) @j)
5 | ( Ex # u . Leake d ( x )@u)
6 | ( Ex B # r . Re v ea l (B )@r
7 & H on es t (B)@i & # r<#i ) ”
Listing 6: Lemma 4.
4.3 Result
For evaluation purposes the Tamarin prover version
1.6.0 in automatic mode was used to prove the four
lemmata presented in Section 4.2. The verification
took 36.159s on a Ubuntu 18.04 Laptop with an In-
tel(R) Core(TM) i7-8650U CPU and 16GB of RAM.
All four lemmata could be verified without interac-
tion. The source code of the Tamarin model is avail-
able for download at GitHub
1
. In Table 3 the Tamarin
1
https://github.com/kr4ck-com/LDACS-MAKE,
accessed May 18, 2021.
SECRYPT 2021 - 18th International Conference on Security and Cryptography
608

output for each lemma is presented. The scope col-
umn states which type of proof has been done: ’exists-
trace’-proofs verify, that the given property or lemma
holds at least for one trace of the protocol; ’all-traces’-
proofs respectively verify that the property holds for
all traces. The last column gives the number of veri-
fication steps that were executed by Tamarin to verify
the lemma.
Table 3: Tamarin verification results.
Lemma Scope Result Steps
Executable Exists-trace 4
Verified
20
Mutual Authen- All-traces 4
Verified
29
tication (O1*)
Secure Key All-traces 4
Verified
1158
Exchange (O2*)
Perfect Forward All-traces 4
Verified
43
Secrecy (O3*)
As all lemmata have been proven to hold, all required
security controls of the LDACS cell-attachment pro-
cedure defined in Table 3 also hold.
5 DISCUSSION AND
CONCLUSIONS
The achieved results show that the LDACS attach-
ment procedure, consisting of cell entry procedure
and modified STS MAKE protocol is secure in fulfill-
ing (1) mutual authentication, (2) secure key agree-
ment (3) perfect forward secrecy for subsequent key
material, (4) consistency, and (5) executability.
The presented proof is valid only under the as-
sumptions of Section 3.2 and there are limitations
originating from the method of symbolic model
checking.
As indicated in Section 3.2 there is no guarantee
for computational soundness of the underlying cryp-
tographic algorithms of the protocol. E.g., in the sym-
bolic model, the ”Diffie-Hellman-assumption” cannot
be verified or falsified, hence in the context of the
prove it is assumed to hold. The same holds true for
the other used cryptographic primitives as signatures
or encryption schemes. Also, any assertions regarding
possible vulnerabilities of an actual software imple-
mentation of the protocol, e.g., because of buffer over-
flows, cannot be made. Also, side-channel attacks be-
cause of e.g. timing issues cannot be found in this
way, since they are also implementation-specific. An-
other point is that the current LDACS cell-attachment
procedure, in the way it is presented in this paper, has
no denial of service protection, which is solved on
protocol level for e.g., fail–stop protocols with cook-
ies. This needs to be investigated further.
Many of the assumptions from Section 3.2 rely
on the secure setup and operation of the underly-
ing LDACS PKI. For instance, the assumed im-
possibility of unauthorized key registration with a
spoofed ID, the privacy of private signing keys,
storage limits and an autonomous registration of
station public keys are all dependent on the way
the PKI is set up and how keys are transported.
In addition, similarities between the LDACS PKI and
AeroMACS PKI (Crowe, 2016) are assumed. As
this is a requirement for the proposed LDACS cell-
attachment procedure to work as intended, due to the
corroboration of identity and public keys and trust
established within the chain-of-trust model that the
PKI uses, it is reasonable to assume such a PKI
to be built for LDACS. However, already the sec-
ond assumption of a trustworthy CA, proves difficult
in practice, with many examples where intermediate
sub-CAs were compromised in the past (Roosa and
Schultze, 2013). As there is no such incident reported
for the AeroMACS PKI as of yet and with ICAO’s ef-
forts to establish their own aviation PKI (Patel, 2016),
the underlying PKI infrastructure will likely become
more robust in the future.
The contribution of this paper is the formal proof
of the security of the LDACS cell-attachement pro-
cedure. Using the symbolic model checker Tamarin,
a mathematical, formal model of this procedure was
built, focusing on the cryptographic aspects of the
MAKE protocol. Tamarin proved that the cell-
attachment is secure in the symbolic model and is
proven to have no design flaws in its architecture.
This constitutes an important step for the develop-
ment of the general LDACS cybersecurity architec-
ture since authentication and key establishment are
the most crucial steps in establishing secure wireless
communication. For future research, the investiga-
tion of the agreement procedure for Diffie-Hellman
parameters, as well as control channel security for
the control channels of LDACS, are interesting, open
tasks.
REFERENCES
Aeronautical Radio, Incorporated (ARINC) (2007).
DATALINK SECURITY PART 1 – ACARS MES-
SAGE SECURITY. Technical report, Aeronautical
Radio, Incorporated (ARINC).
Basin, D., Cremers, C., Dreier, J., Meier, S., Sasse, R., and
Schmidt, B. (2020 (accessed May 18, 2021)). Tamarin
Prover Manual.
Bilzhause, A., Belgacem, B., Mostafa, M., and Gr
¨
aupl, T.
(2017). Datalink Security In The L-band Digital Aero-
nautical Communications System (LDACS) For Air
Formal Security Verification of the Station-to-Station based Cell-attachment Procedure of LDACS
609

Traffic Management. Aerospace and Electronic Sys-
tems Magazine, 32(11):22–33.
Blanchet, B. (2017). Symbolic And Computational Mecha-
nized Verification Of The ARINC823 Avionic Proto-
cols. In 30th Computer Security Foundations Sympo-
sium (CSF), pages 68–82. IEEE.
Boyd, C., Mathuria, A., and Stebila, D. (2020). Protocols
For Authentication And Key Establishment. Springer.
Crowe, B. (2016). Proposed AeroMACS PKI Specifica-
tion Is A Model For Global And National Aeronauti-
cal PKI Deployments. In WiMAX Forum at 16th Inte-
grated Communications, Navigation and Surveillance
Conference (ICNS), pages 1–19. IEEE.
Dolev, D. and Yao, A. (1981). On The Security Of Pub-
lic Key Protocols (Extended Abstract). In 22nd An-
nual Symposium on Foundations of Computer Sci-
ence, pages 350–357. IEEE Computer Society.
Goldwasser, S., Micali, S., and Rivest, R. (1988). A
Digital Signature Scheme Secure Against Adaptive
Chosen-Message Attacks. SIAM Journal on comput-
ing, 17(2):281–308.
Gr
¨
aupl, T., Rihacek, C., and Haindl, B. (2020).
LDACS A/G Specification. SESAR2020 PJ14-02-01
D3.3.030, German Aerospace Center (DLR).
International Civil Aviation Organization (ICAO) (2015).
Doc 9896 — Manual On The Aeronautical Telecom-
munication Network (ATN) Using Internet Proto-
col Suite (IPS) Standards And Protocols. Techni-
cal report, International Civil Aviation Organization
(ICAO).
International Civil Aviation Organization (ICAO) (2018a).
Finalization of LDACS Draft SARPs - Working Paper
WP05 including Appendix. Technical report, Interna-
tional Civil Aviation Organization (ICAO), Montreal,
Canada.
International Civil Aviation Organization (ICAO) (2018b).
Finalization Of LDACS Draft SARPs - Working Paper
WP05 Including Appendix. Technical report, Interna-
tional Civil Aviation Organization (ICAO).
Krawczyk, H. (2010). Cryptographic Extraction And Key
Derivation: The HKDF Scheme. In Annual Cryptol-
ogy Conference, pages 631–648. Springer.
Mahmoud, M. S. B., Pirovano, A., and Larrieu, N. (2014).
Aeronautical Communication Transition From Ana-
log To Digital Data: A Network Security Survey.
Computer Science Review, 11-12:1–29.
M
¨
aurer, N., Gr
¨
aupl, T., Bellido-Manganell, M., Mielke, D.,
Filip-Dhaubhadel, A., Heirich, O., Gerbeth, D., Felux,
M., Schalk, L., Becker, D., Schneckenburger, N., and
Schnell, M. (2021a). Flight Trial Demonstration of
Secure GBAS via the L-band Digital Aeronautical
Communications System (LDACS). IEEE Aerospace
and Electronic Systems Magazine, pages 8–17.
M
¨
aurer, N., Gr
¨
aupl, T., and Schmitt, C. (2021b). Cyberse-
curity For The L-band Digital Aeronautical Commu-
nications System (LDACS). In Song, H., Hopkinson,
K., Cola, T. d., Alexandrovich, T., and D., L., editors,
Aviation Cybersecurity: Foundations, Principles, and
Applications, pages 1–38. Institution of Engineering
and Technology (IET).
M
¨
aurer, N. and Schmitt, C. (2019). Towards Successful Re-
alization Of The LDACS Cybersecurity Architecture:
An Updated Datalink Security Threat- and Risk Anal-
ysis. In 19th Integrated Communications, Navigation
and Surveillance Conference (ICNS), pages 1A2/1–
1A2–13. IEEE.
M
¨
aurer, N. and Bilzhause, A. (2018). A Cybersecurity Ar-
chitecture For The L-band Digital Aeronautical Com-
munications System (LDACS). In 37th Digital Avion-
ics Systems Conference (DASC), pages 1–10. IEEE.
Meier, S., Schmidt, B., Cremers, C., and Basin, D. (2013).
The TAMARIN Prover For The Symbolic Analysis Of
Security Protocols. In 25th International Conference
on Computer Aided Verification (CAV), page 696–701.
Springer.
Patel, V. (2016). ICAO Air-Ground Security Standards Sta-
tus ICNS Conference 2016. In Integrated Commu-
nications Navigation and Surveillance (ICNS), pages
1–31. IEEE.
Roosa, S. and Schultze, S. (2013). Trust Darknet: Control
And Compromise In The Internet’s Certificate Au-
thority Model. IEEE Internet Computing, 17(3):18–
25.
Schnell, M., Epple, U., Shutin, D., and Schneckenburger,
N. (2014). LDACS: Future Aeronautical Communi-
cations For Air-Traffic Management. IEEE Commu-
nications Magazine, 52(5):104–110.
Yao, A. (1982). Theory And Application Of Trapdoor Func-
tions. In 23rd Annual Symposium on Foundations of
Computer Science (SFCS), pages 80–91. IEEE.
APPENDIX
AeroMACS Aeronautical Mobile Airport
Communication System
AOC Aeronautical Operational Control
AS Aircraft Station
ATN Aeronautical Telecommunications
Network
ATS Air Traffic Services
BCCH Broadcast Control Channel
CCCH Common Control Channel
CPDLC Controller–Pilot Data Link
Communications
DCH Data Channel
DHKE Diffie-Hellman Key Exchange
GS Ground Station
ICAO International Civil Aviation
Organization
KDF Key Derivation Function
LDACS L-band Digital Aeronautical
Communications System
MAKE Mutual Authentication and Key
Establishment
PKI Public Key Infrastructure
RACH Random Access Channel
STS Station to Station
SECRYPT 2021 - 18th International Conference on Security and Cryptography
610