Automated Lane Change Decision Making in Highway using a Hybrid

Approach

Ozan C¸ aldıran

, Engin Baglayici

, Morteza Dousti

, Eren Mungan

, Enes Emre Bulut

M. Damla Demir

and Furkan Koc¸yi

git

AVL Research and Engineering, Istanbul, Turkey

Keywords:

Autonomous Driving, Automated Lane Change, Decision-making, Utility Functions, Gap Selection, Highway

Autopilot.

Abstract:

This study proposes a decision-making model for lane changing and lane keeping decisions in highway au-

tonomous driving. In order to perform a safe and efﬁcient lane change, it is crucial to decide whether a lane

change is needed, the desired lane is more suitable, and making a lane change maneuver is safe. In this work,

we propose a model that is capable of assessing these considerations and suggest appropriate lane-change

maneuvers. The model uses probabilistic utility functions and a deterministic but conservative gap selection

method that considers not only the gaps in the target lane but also the vehicles in the driving lane. In addition

to simulation tests, we integrated our model into a SUV vehicle that has 360-degree perception and motion

control capabilities and performed autonomous highway driving to test real-life performance.

1 INTRODUCTION

According to the EGM’s (General Directorate of Se-

curity of Turkey) most recent report, 87.7 percent of

the trafﬁc accidents in Turkey are caused by driver

faults (EGM, 2020). Driving requires a constant fo-

cus on the environment and even a little focus loss

can cause accidents. Nevertheless, Advanced Driv-

ing Assist Systems (ADAS) and Autonomous Driv-

ing Modules take over the tasks of driving and re-

duces the accidents signiﬁcantly. Moreover, they pro-

vide comfortable and efﬁcient driving while guaran-

teeing safety. Therefore, autonomous driving has at-

tracted researchers and automotive companies in re-

cent years.

Recently, automobile manufacturers started offer-

ing ADAS features such as Adaptive Cruise Control

(ACC) and Lane Keeping Assist (LKA) that can as-

sist drivers in longitudinal and lateral maneuvers. Al-

though these features provide additional safety and

https://orcid.org/0000-0001-6544-0419

https://orcid.org/0000-0003-3901-4752

https://orcid.org/0000-0003-2528-6730

https://orcid.org/0000-0001-9637-5293

https://orcid.org/0000-0003-2022-2359

https://orcid.org/0000-0001-5816-7610

https://orcid.org/0000-0002-8743-3241

comfort for the passengers, more complex situations

and driving actions are either not addressed or ad-

dressed in a limited sense like lane-change maneuver.

To achieve automated lane change, a better under-

standing of the scene, decision-making, trajectory and

movement planning is required compared to simple

ADAS features already available such as lane change

warning systems.

Another challenge with the automated lane change

is the diverse trafﬁc settings such as city-roads dur-

ing rush hour trafﬁc, intersections, roundabouts, high-

ways, all of which pose different challenges and re-

quirements. It is hard to fulﬁll all lane change de-

cision requirements with one base model, therefore

researchers generally focus on a single trafﬁc set-

ting to have smooth circumstances. Moreover, lane

change maneuvers are performed for different rea-

sons. Lane changes can be classiﬁed as mandatory,

discretionary, and anticipatory based on their reasons

to occur (Toledo, 2003). Mandatory lane changes de-

ﬁne the situations where drivers must perform a lane

change due to strict road rules and situations, such as

lane endings or lane blockages. Discretionary lane

changes are performed by drivers when the observa-

tion indicates that, there is another lane with better

driving conditions for the host vehicle. Finally, an-

ticipatory lane changes are performed to improve the

Çaldıran, O., Baglayici, E., Dousti, M., Mungan, E., Bulut, E., Demir, M. and Koçyi

git, F.

Automated Lane Change Decision Making in Highway using a Hybrid Approach.

DOI: 10.5220/0010581304770484

In Proceedings of the 18th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 477-484

ISBN: 978-989-758-522-7

477

road conditions for other road actors, such as allowing

a faster vehicle to pass (Nilsson et al., 2016)

In this paper, an autonomous lane-change

decision-making model is presented for discretionary

lane changes in highway driving scenarios. The

model aims to determine when and how to execute a

lane-change under efﬁciency, safety, and comfort cri-

teria. The utility functions that are designed to meet

those criteria are provided in Section 3. The utility

functions and their effects on the decisions have been

evaluated and tuned based on simulations. After the

model have been ﬁnalized in the simulations, we de-

ployed the model on our development vehicle. We

also performed a highway autonomous driving test.

In the highway tests, we performed several trafﬁc sce-

narios to observe model decisions. The simulation

and test results are presented in Section 4.2. The main

contributions of this paper: 1) establish an automated

lane change decision-making model based on deter-

mining feasible maneuvers; 2) propose a model that

selects the most appropriate maneuver using a multi-

variate utility function.

2 LITERATURE REVIEW

Different types of decision-making models have been

utilized for the autonomous lane change maneuvers,

and we will consider the following three categories of

models: (1) Microscopic trafﬁc models and decision

trees, (2) Markov Decision Processes (MDPs), and (3)

Reinforcement learning. In this section, we will intro-

duce various implementations of these methods.

Gipps (1986) introduced a decision-making model

that covers various urban driving situations. The

model considers the necessity, desirability, and safety

of lane changes. Driver’s behavior is governed by two

basic considerations: maintaining the desired speed

and being in the correct lane for an intended turn-

ing maneuver. Ahmed (1999) proposed lane change

decision-making models based on utility functions to

model microscopic highway trafﬁc scenarios. The

utility functions are linear combinations of certain

factors that evaluate a certain lane based on the safety,

comfort, and goal of the driver. The probability of

lane change was calculated based on the output of a

softmax function and the decisions of the drivers to

make lane changes were modeled using a decision

tree. Later, Toledo (2003) used the same modeling

approach to extend and improve Ahmed’s model.

Utility-based models have been used for decision-

making algorithms for lane changes on highways

(Ardelt et al., 2012; Nilsson et al., 2016). Ardelt

et al. (2012) integrated the ideas from Ahmed (1999)

and Toledo (2003), and implemented a decision tree-

based framework based on utilities of adjacent lanes,

on an actual car. In the ﬁrst phase, utilities of the

lanes are computed with a decision tree mechanism.

If the utilities indicate that a lane-change maneuver is

proﬁtable, the feasibility of this lane change is then

controlled. If the lane change maneuver is not fea-

sible, a lane change gap approach protocol, whose

details were not provided, is activated. The authors

use this decision-making model to drive from Munich

to Ingolstadt on highway A9 in German Autobahn.

Two major contributions of Ardelt et al. (2012)’s work

are the inclusion of the uncertainties in the utilities

based on sensor uncertainties and the inclusion of the

past and future values of the expected utilities in the

decision-making process.

Similarly, Nilsson et al. (2016) computed three

types of utilities of adjacent lanes and assessed the

quality of gaps for a lane change. The proposed

method does not consider cooperation between traf-

ﬁc participants. However, the low complexity of the

method makes it traceable. Besides, the authors pro-

vided all the necessary deﬁnitions for the utilities and

gap assessment procedures. They also veriﬁed their

approach using both simulations and a real car on a

test track.

A drawback of these utility-based methods is their

limited capacity regarding the incorporation of the

other trafﬁc participants actions and their possible ef-

fects on the decisions. In this regard, the Markov

Decision Process (MDP) and Partially Observable

Markov Decision Processes (PO-MDP) offer princi-

pled solutions to modeling and decision-making pro-

cesses. However, the implementation of MDPs or PO-

MDPs poses practical problems due to their computa-

tional complexity for real-time bound systems such as

autonomous cars.

For example, Brechtel (2015) outlines highway

driving scenarios as a generic Markov Decision Pro-

cess with continuous states and action spaces based

on the dynamics and inputs of a car. Nevertheless, the

authors devised a novel discretization method to ﬁt

the states and actions into a solvable MDP formula-

tion. They used the MDP approach to solve highway

driving situations where partial observability is not as

critical (Brechtel et al., 2011). Later in Brechtel et al.

(2014), the authors proposed to use Partially Observ-

able MDPs (PO-MDPs) to account for the states that

cannot be directly observed during driving such as ve-

hicles that are occluded at intersections. Furthermore,

they used continuous observation space representa-

tions. The additional complexities from the contin-

uous observation space representation and partial ob-

servability are handled by limiting the relevant trafﬁc

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

478

participants to two.

On the other hand, Ulbrich and Maurer (2013) in-

troduced a two-step algorithm to decrease the com-

plexity of POMDP for real-time decision-making.

The authors deﬁned the state space of a POMDP

decision-maker in terms of three binary state variables

deﬁning whether changing lanes is possible, beneﬁ-

cial, and in progress. This approach, while reducing

the complexity of the problem, might result in over-

simpliﬁcation of the problem. However, the authors

integrated their decision-making model on a car and

tested the system on Braunschewig’s inner-city ring

road.

With the advancements in learning-based ap-

proaches, researchers started to use machine learn-

ing and deep learning for situation assessment and

decision-making optimization. Researchers have

used these models to either tune parametric models

(utility functions, MDP, etc.) or used them directly as

decision-making mechanisms as in the case of rein-

forcement learning.

Even though the trial-error nature of reinforce-

ment learning seems infeasible in the case of real-

driving scenarios, training deep reinforcement learn-

ing agents through realistic driving simulators has

the potential to solve the decision-making problem

in autonomous driving. However, building a realis-

tic driving simulator is a challenge in itself. Nev-

ertheless, numerous research groups recently uti-

lized deep reinforcement learning: Mirchevska et al.

(2018); Alizadeh et al. (2019); Yavas et al. (2020)

all trained Deep Q-Network (DQN) agents for de-

ciding to perform lane-changes or keeping the lane;

Shi et al. (2019) proposed a hierarchical reinforce-

ment learning-based architecture to decide when to

change lanes and how to change lanes; Wang et al.

(2018) trained a Q-network agent that selects appro-

priate yaw rate from a continuous action space, thus

acting as a decision-maker coupled with a high-level

lateral controller.

All the presented approaches consider plans for

differing time horizons and detail. Therefore, the

choice of a suitable decision-maker should heavily

depend on the task in question and the properties of

the rest of the system at hand, i.e., the whole system

comprising an autonomous vehicle. In this work, we

consider normal highway driving where escape ma-

neuvers are not required. Hence, the task expected

from a decision-making module is to increase safety

and comfort while maintaining the desired speed.

Normal road driving conditions do not usually require

complex long-term planning, thus a lane change or

an overtaking maneuver can be considered separately

for escape maneuvers. Therefore, we chose to use a

utility-based method rather than more complex mod-

els like (PO)MDP. The ﬁrst reason is the intuitive ap-

proach of utility functions regarding the assessment

of the driving conditions. On the other hand, it was

understood that the utility-based methods are quite

similar to the MDP-based methods regarding the sit-

uation assessment. The simpliﬁcation of the MDP-

based methods due to their computational complex-

ity leads to this result. The major difference of the

utility-based method from (PO)MDP methods is that

the constant acceleration model is used to predict the

state of the highway actors over a time interval, which

means that future situations do not have an impact on

the current state. Despite this downside, the computa-

tional complexity of the autonomous driving problem

pushes researchers to simplify the state action domain

complexity, which ultimately weakens the robustness

of (PO)MDP solvers.

3 METHOD

3.1 Utility Functions

Highway driving requires continuous observation of

lane properties to decide which lane to keep driv-

ing on. Linear utility functions are utilized to as-

sess each driving lane according to its lane properties,

thus we can select the most appropriate lane among

them. Many factors are taken into account to evalu-

ate the lane properties include object velocities, rel-

ative positions, size of the objects, and many other

variables that affect the circumstances of the driving.

The considered driving factors form different combi-

nations of linear functions that specify different road

conditions. These road conditions can be the aver-

age time gap between objects, average longitudinal

velocity in a lane, lane line quality, presence of heavy

vehicles, and so on. These linear functions are then

weighted according to their effects on the trafﬁc and

combined to calculate the utility value of a lane in a

speciﬁc time interval. By assigning weights to func-

tions, we prioritize some functions which have more

effects on driving than others. On the other hand, we

consider not only the present variables of the trafﬁc

scene but also past and possible future states. We

discretize the time from past the future and calculate

the utilities of lanes that belong to speciﬁc time inter-

vals. We created a utility table to keep utility values

from past to future, and we update the table at each

time step with the incoming utilities. Instead of cal-

culating past lane utilities continuously, we keep past

utility values in memory. We also calculate future

utility values based on predicted environment vari-

Automated Lane Change Decision Making in Highway using a Hybrid Approach

479

Figure 1: Decision Maker Model Architecture.

ables at every time step. For future state prediction,

we use linear future state estimator functions that cal-

culate possible future velocities and positions of dy-

namic objects. For this aim, any future state predic-

tion method can be used. When using past utility

values, resetting those values is essential if the road

situation suddenly changes Ardelt et al. (2012). We

also assign weights to each time interval according

to their effects on comfort and safety criteria. It is

important to note that the negative inﬂuence of the

past increases over time with the bad driving con-

ditions, which decreases the overall utility. Either

utility function weights or time interval weights are

determined empirically. Road properties have uncer-

tainties that arise from different sensor measurements.

To fully understand the driving situation, Ardelt et al.

(2012) includes uncertainty measures into utility cal-

culations by introducing road variables as probability

distributed stochastic variables. We also follow this

procedure to have a realistic observation of the driv-

ing scene. Among the mandatory, discretionary, and

anticipatory lane changes, we only consider discre-

tionary and anticipatory lane changes, for our utility

function model. Anticipating mandatory lane changes

requires local map information, and even though we

do not include it, for now, it can easily be integrated

later on. Hereby, we present the road factors which

are considered while building the utility function.

Longitudinal Velocity: The longitudinal velocity util-

ity represents the difference between the desired ve-

locity of ego and the actual velocity of ego. This fac-

tor includes a penalty effect with the right proportion

of the difference between the desired speed and the

actual speed of the ego.

Ulv = −

des

−V

ego

des

(1)

In the formula, V

des

and V

ego

denotes the desired

longitudinal velocity and the current longitudinal ve-

locity, respectively. The formula indicates that the

minimum penalty effect is achieved by the equality

of V

des

and V

ego

Average Time Gap: The average time gap of a lane

represents the average of the time gaps between ve-

hicles in the corresponding lane. For the calculation,

the time gaps between longitudinally adjacent cars are

calculated and the average of these time gaps are used

as a utility factor.

Average Longitudinal/Lateral Velocity: These factors

denotes the average longitudinal and lateral velocities

in a speciﬁc lane. Based on the desired velocity of

ego, these factors can be used as hints to determine

which lane to keep.

Relative Leader Velocity: This factor denotes the

highest relative velocities in each lane. Even though it

is similar to the other velocity-related factors, know-

ing the fastest objects in lanes may help the driver

with the decision of keeping the current lane or not.

Presence of Heavy Vehicles: Presence of heavy ve-

hicles is an indicator of the inconvenient of a lane.

Lanes with heavy vehicles tend to be ﬂowing slower,

which should not be preferred in a highway scenario.

Safety is another regard in this condition.

Lane Line Quality: Lane line quality is another im-

portant factor to determine about a lane. With the help

of a vision algorithm, having the information of line

quality gives us a hint about how healthy to keep a

lane.

Required Number of Lane Changes: Required num-

ber of lane changes to reach a lane is an impor-

tant factor regarding driving safety and comfort. We

should avoid targeting far lanes as much as possible

and choose adjacent lanes to be sure about safety and

comfort.

Presence of Tailgating: Tailgating is an undesirable

situation that can easily cause accidents. If a behind

vehicle is driving too closely, especially in the left-

most lane, the ego vehicle should make a lane change

to allow the vehicle to pass. By using the time gap in-

formation between ego and car from the behind, tail-

gating makes an inverse proportion effect to the utility

function. While ego drives in a tailgating situation,

the overall utility of the ego lane decreases over time.

Left/Right Most Lane Check: In highway, keeping the

left-most lane and right-most lane for a long time is

generally inhibited. Thus, keeping these lanes for de-

creases the utility of that lane over time.

The above utility factors are weighted by W ∈ [0, 1],

based on their importance level and summed up to

ﬁnd total utility of a lane at a speciﬁc time.

lane

∑

n=1

(2)

For the overall utility calculation, we follow the

formulation in Ardelt et al. (2012). For each discrete

timestamp, we calculate the utilities of a lane from

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

480

past to future and get an overall utility value. Even

though past utilities are useful for a better assessment

of a trafﬁc situation, they can imply wrong predictions

and slow down the utility process. Thus, resetting the

past utilities in case of signiﬁcant changes in trafﬁc

may lead to better assessment Ardelt et al. (2012). On

the other hand, in case of a constant unsatisﬁed trafﬁc

situation on a lane, we expect the utility value of that

lane to decrease over time. By integrating the δ ∈ [-

1,0] parameter to the equation, we can manipulate the

past utilities by either resetting them to zero or give

a negative value. We ﬁnally plug the weights of each

timestamp β ∈ [0, 1] into the equation and calculate

the overall utility value of a lane between a time inter-

val. Each utility factor is calculated by the normally

distributed parameters (vehicle velocities, positions,

etc.) which also makes the factors a normally dis-

tributed variable U N(µ

,σ

). By using the overall

utility equation, we get a ﬁnal normally distributed

lane utility value. We compare lane utilities based

on cumulative distribution functions. The difference

probability of two lanes (U

−U

) is a joint density

function, and integrating the joint density over the set

of points where U

> U

gives the probability that

contains greater utility than U

P(U

> U

) =

Udi f f

√

2π

−∞

−(x−µ)

2σ

Ud i f f

)du

(3)

Finally, the host vehicle makes a lane change re-

quest if that probability exceeds a minimum thresh-

old value, which can also be determined empirically

according to comfort and safety criteria. The lane

change request is then examined by the Gap Selection

module.

3.2 Gap Selection

When a lane change decision is made, our gap se-

lection algorithm searches for inter-vehicular gaps

that comply with certain safety and comfort crite-

ria. To ﬁnd the best gap, the decision-making mod-

ule requires the kinematic information of the vehicles

around the ego vehicle for the whole 360

◦

from the

environment perception modules.

The sensor fusion module, which is the core com-

ponent of the environment perception modules, uses

Kalman Filters to track the surrounding vehicles and

hence assumes a normal distribution for the uncer-

tainty in the estimated states of these vehicles. Our

gap selection algorithm considers both the estimated

kinematic states and their uncertainties for a feasi-

ble lane change as in Ardelt et al. (2012), i.e., the

rear/front bumper of a lead/follow vehicle is consid-

ered to be 3 standard deviations away from its es-

timated mean. Moreover, we considered clearances

∆

des

based on desired time gaps between the ego ve-

hicle and the surrounding vehicles. Adding these un-

certainties and the clearances, we deﬁned safety re-

gions around each surrounding vehicle (see Fig. 2b).

When we refer to the distance between vehicles and

their closeness to one another, we consider the safety

margins instead of the actual vehicle positions.

Unlike Ardelt et al. (2012), our algorithm inspects

not only the vehicles in the target lane but also the

vehicles that are in front and back of the ego vehi-

cle Toledo (2003). In this regard, an inter-vehicular

gap is deﬁned in terms of the longitudinally closest

lead and follow vehicles either in the target or ego

lane. For example, in Fig. 2 the longitudinal dis-

tance between the lead vehicle in the ego lane and

the lead vehicle in the left lane constitutes a gap. Our

approach saves us from checking collisions with the

vehicles in the ego lane which might occupy regions

through where a lane-change maneuver is planned to

take place. Hence, we only consider gaps that are

reachable.

Furthermore, we estimate the future positions of

the surrounding vehicles using a constant acceleration

model to predict the future states of the inter-vehicular

gaps. Therefore, we can anticipate feasible but un-

reachable gaps to be reachable in a certain time hori-

zon and plan accordingly.

Nevertheless, gaps that are expected to be reach-

able in the future are not guaranteed to be reachable

or feasible in the expected time horizon (see Fig. 2a

and 2b). Therefore, gaps that are temporally closer to

the current time frame are more desirable. Moreover,

aligning with a feasible gap might require a deviation

from the desired velocity, thus rendering the gap to

be less desirable. These criteria lead to another multi-

criteria selection problem among gaps. Similar to the

lane utility functions, we deﬁned the following crite-

ria:

• U

: Time for the gap opening

• U

dur

: Duration of the gap feasibility

• U

: Time to reach the gap

• U

ddv

: Difference to desired velocity,

and compared the weighted summation of these cri-

teria for all reachable and feasible gaps. Unlike the

lane utility functions case, gap utilities are not prob-

ability distributions since we opted for a conservative

assessment of the gaps and considered the state un-

certainties of the surrounding vehicles for worst-case

scenarios as in Ardelt et al. (2012).

Automated Lane Change Decision Making in Highway using a Hybrid Approach

481

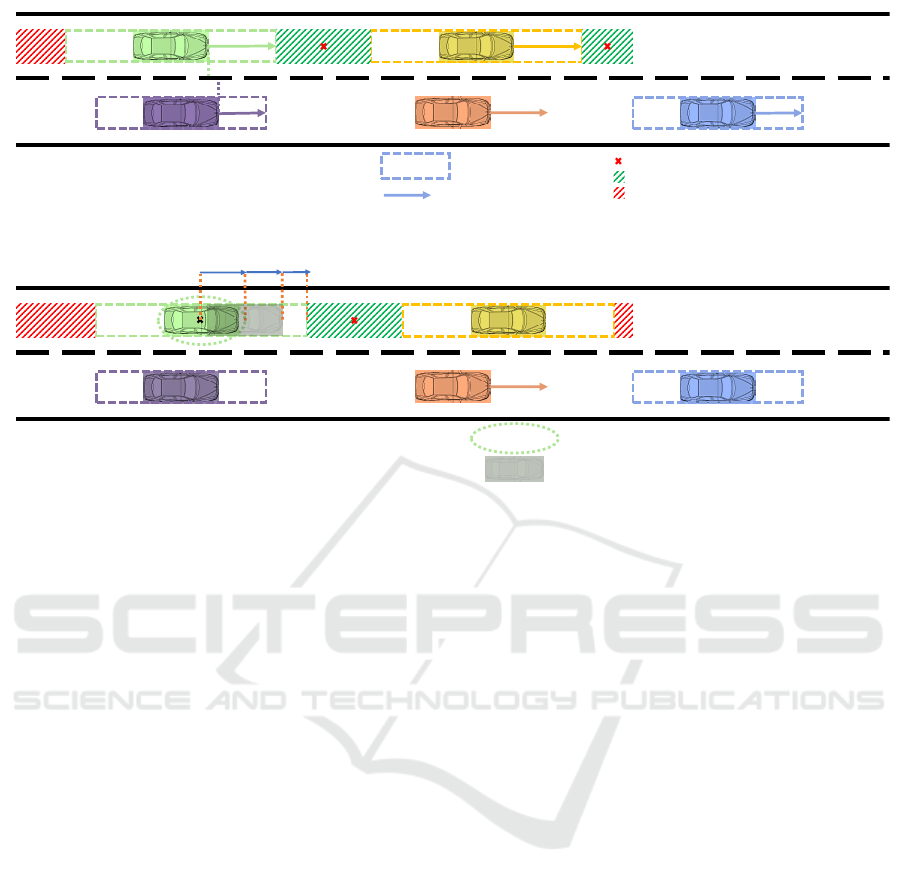
Center of gap

Currently open gap

Currently closed/unreachable gap

Safety margin

Velocity vector

(a)

3  



Uncertainty boundary of 3

Virtual car at the uncertainty boundary

(b)

Figure 2: Example scene showing the inter-vehicular gaps and safety margins around surrounding vehicles. Safety margins

are depicted with dashed-rectangles around the surrounding vehicles. (The orange-colored vehicle denotes the ego vehicle,

hence does not have a safety margin around it.) In 2a, the gap in front of the adjacent left lane is deﬁned by the lead vehicle

in the left and ego lanes. In 2b, this gap is closed, and the safety margin around the following vehicle in the left lane is broken

down into its parts: i.e., the vehicle dimensions d, the uncertainty of the perceived state of the vehicles (3σ), and desired time

gaps ∆

des

4 EXPERIMENTS

The experiments are conducted with an SUV class

vehicle that has a hybrid power-train system. The

test vehicle is surrounded by 8 mid-range radars, a

front-rear camera, MobilEye, GPS, and IMU. These

sensors are connected to the vehicle CAN network

and read by the corresponding ROS nodes for decod-

ing and data conversion purposes. The vehicle has

2 NVIDIA TX2 computers for sensor data collection

and processing as slave units and a workstation for

decision-making and high-level processing as the pri-

mary computer.

The data collected from each sensor is processed

by ﬁltering and tracking modules. The object asso-

ciation module uses the output of these modules and

creates an object list. The same approach also applies

to road lanes. Finally, at the output of the perception

package, object information and lane information are

combined to get 360

◦

environment information.

The test vehicle has Adaptive Cruise Control

(ACC), Lane Keeping Assistant (LKA) and Lane

Change Assistant (LCA) modules. These ADAS

functions use the output of the perception module and

vehicle states directly from the CAN network. Our

decision-making model governs these ADAS mod-

ules to perform maneuvers.

4.1 Model Tuning

Tuning the model directly on the test vehicle would

potentially result in hazardous situations. A common

approach is to use simulations to ensure safety during

testing newly developed functions. However, generat-

ing high-ﬁdelity simulations is costly, and it still does

not guarantee success when the model is transferred

to the real-world. Instead, we virtually tested and

tuned our model using estimations of the perception

module based on real-world sensor data.

The raw sensor data and state estimations of the

perception module are recorded synchronously in the

highway environment. To test the model under vari-

ous conditions, several trafﬁc scenarios are performed

during data collection. The collected data is replayed

in the Robotic Operation System (ROS) environment,

and the decision-making model is run standalone as

a ROS package. We also used RViz, a native vi-

sualization tool in ROS, to visualize the output of

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

482

the perception module. RViz helps us visualize what

the decision-making model is aware of about its sur-

rounding, and observe the corresponding system be-

havior.

Figure 3: Rviz visualization.

4.2 Vehicle Tests

A twelve-minute autonomous drive with no driver

intervention has been achieved on the North Mar-

mara Highway in Istanbul. During the trip, the user-

controlled desired speed of the vehicle has been set

to 90 km/h, and three more vehicles accompanied the

autonomous car: two vehicles around the autonomous

vehicle and a lead vehicle to test different scenarios

that are expected to result in different behaviors (left-

lane change, right-lane change, lane keeping).

The statistics of the lane change decisions (LC)

and gap acceptance (LCGA) occurrences have been

provided in Figure 5. The number of lane changes

are higher than expected for a twelve-minute drive

as the vehicles accompanying the autonomous vehi-

cle intentionally behaved in a way that would lead the

decision maker to decide for lane changes.

In Figure 4, signals belonging to a two-minute ex-

cerpt of the autonomous drive are presented: the de-

cision signal indicating a desire for lane change and a

start signal triggering a safe lane change (upper plot);

the ego vehicle speed (middle plot); and lane utili-

ties (lower plot). Here, the start signal is a Boolean

signal whereas the decisions are encoded as follows:

−1 for left lane, 0 for lane keeping, and 1 for right

lane. As a result of the calculated utilities (lower

plot), the decision-maker opted for three lane changes

to achieve and maintain its desired speed in this two-

minute excerpt. However, before a lane change takes

place, the gap selection algorithm should ﬁnd a suit-

able gap that the ego vehicle can align with. There-

fore, decision signals and start signals are not syn-

chronous in the upper plot.

The number of lane change, lane keep and lane

change abort decisions are shown in the Figure 5. It is

seen that due to the conservative nature of the model,

Figure 4: Lane change decisions, Lane utilities and vehicle

speed during a part of autonomous driving.

Figure 5: Lane change decisions during the vehicle test.

lane keeping decision is mostly made. In addition, the

fact that the lane change abort decision is taken from

time to time emphasizes the importance of having a

gap selection method before the lane change decision.

5 CONCLUSION AND FUTURE

WORK

In this study, we design, implement and test a

decision-making model for highway autonomous

driving with a special focus on discretionary lane-

change maneuvers. Highway driving is gener-

Automated Lane Change Decision Making in Highway using a Hybrid Approach

483

ally straightforward and does not require complex

decision-making situations like intersection handling,

pedestrian interventions, distorted roads, and so on.

The most important aspects of highway driving are

longitudinal control to keep a safe distance from other

objects, and lateral control to make lane changes

when it is necessary. Therefore, one of the required

aspects of highway autonomous driving is evaluating

the trafﬁc condition to decide whether a lane change

is needed and does it suit safety and comfort criteria.

In this regard, we design a two-step model that in-

cludes a probabilistic assessment of road lanes and a

deterministic assessment of the inter-vehicular gaps.

For the probabilistic assessment, utility functions that

are combinations of road factors are used. Highway

lanes are constantly evaluated concerning the utility

functions. Then, if a lane change is desired, the gap

selection algorithm starts evaluating inter-vehicular

gaps in the lanes to perform a safe and comfortable

lane change.

In addition to the virtual tests performed with the

sensor data collected during driving on highway, our

model was also integrated into a vehicle and tested

in real world conditions. The vehicle tests on the

highway drive indicate that our model is capable of

assessing the road conditions and reacting to the en-

vironmental changes conservatively. The test vehi-

cle avoided any dangerous maneuvers while driving,

and it generally tended to continue in the lane it was

in. Nevertheless, one limitation of our model is the

lack of assessing the future states of the environment

with a robust prediction model. Instead, we utilize a

constant-acceleration model that does not assume any

lateral maneuvers.

ACKNOWLEDGMENT

This work is supported by the Scientiﬁc and Techno-

logical Research Council of Turkey (TUBITAK) un-

der Grant No. 5169901.

REFERENCES

Ahmed, K. I. (1999). Modeling Drivers’ Acceleration and

Lane Changing Behavior. PhD thesis, MIT.

Alizadeh, A., Moghadam, M., Bicer, Y., Ure, N. K., Yavas,

U., and Kurtulus, C. (2019). Automated lane change

decision making using deep reinforcement learning in

dynamic and uncertain highway environment. In 2019

IEEE Intelligent Transportation Systems Conference

(ITSC), pages 1399–1404.

Ardelt, M., Coester, C., and Kaempchen, N. (2012). Highly

automated driving on freeways in real trafﬁc using a

probabilistic framework. IEEE Transactions on Intel-

ligent Transportation Systems, 13(4):1576–1585.

Brechtel, S. (2015). Dynamic Decision-making in Contin-

uous Partially Observable Domains: A Novel Method

and its Application for Autonomous Driving. PhD the-

sis, Karlsruher Instituts f

ur Technologie (KIT).

Brechtel, S., Gindele, T., and Dillmann, R. (2011). Prob-

abilistic MDP-Behavior Planning for Cars. In 2011

IEEE 14th International Conference on Intelligent

Transportation Systems, pages 1537–1542, Washing-

ton.

Brechtel, S., Gindele, T., and Dillmann, R. (2014). Prob-

abilistic Decision-Making under Uncertainty for Au-

tonomous Driving using Continuous POMDPs. In

17th International IEEE Conference on Intelligent

Transportation Systems (ITSC), pages 392–399, Qing-

dao.

EGM, T. (2020). Traﬁk

Istatistik b

ulteni Trafﬁc statistics

bulletin].

Gipps, P. G. (1986). A model for the structure of lane-

changing decisions. Transportation Research Part B:

Methodological, 20(5):403–414.

Mirchevska, B., Pek, C., Werling, M., Althoff, M., and

Boedecker, J. (2018). High-level decision making for

safe and reasonable autonomous lane changing using

reinforcement learning.

Nilsson, J., Silvlin, J., Brannstrom, M., Coelingh, E., and

Fredriksson, J. (2016). If, When, and How to Perform

Lane Change Maneuvers on Highways. IEEE Intelli-

gent Transportation Systems Magazine, 8(4):68–78.

Shi, T., Wang, P., Cheng, X., Cha, C.-Y., and Huang, D.

(2019). Driving decision and control for autonomous

lane change based on deep reinforcement learning.

Toledo, T. (2003). Integrated Driving Behavior Modeling.

PhD thesis, MIT.

Ulbrich, S. and Maurer, M. (2013). Probabilistic Online

POMDP Decision Making for Lane Changes in Fully

Automated Driving. In 16th International IEEE Con-

ference on Intelligent Transportation Systems (ITSC

2013), pages 2063–2067.

Wang, P., Chan, C.-Y., and de La Fortelle, A. (2018). A

reinforcement learning based approach for automated

lane change maneuvers. In 2018 IEEE Intelligent Ve-

hicles Symposium (IV), pages 1379–1384.

Yavas, U., Kumbasar, T., and Ure, N. K. (2020). A new

approach for tactical decision making in lane chang-

ing: Sample efﬁcient deep q learning with a safety

feedback reward. In 2020 IEEE Intelligent Vehicles

Symposium (IV), pages 1156–1161.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

484