Learning-based Optimal Control of Constrained Switched Linear

Systems using Neural Networks

Lukas Markolf

and Olaf Stursberg

Control and System Theory, Dept. of Electrical Engineering and Computer Science, University of Kassel,

Wilhelmsh

oher Allee 73, 34121 Kassel, Germany

Keywords:

Neural Networks, Intelligent Control, Hybrid Systems, Approximate Dynamic Programming.

Abstract:

This work considers (deep) artiﬁcial feed-forward neural networks as parametric approximators in optimal

control of discrete-time switched linear systems with controlled switching. The proposed approach is based on

approximate dynamic programming and allows the fast computation of (sub-)optimal discrete and continuous

control inputs, either by approximating the optimal cost-to-go functions or by approximating the optimal

discrete and continuous input policies. An important property of the approach is the satisfaction of polytopic

state and input constraints, which is crucial for ensuring safety, as required in many control applications. A

numeric example is provided for illustration and evaluation of the approaches.

1 INTRODUCTION

In many applications, continuous and discrete con-

trols coexist as, e.g., in all production or processing

systems which are equipped with continuous feed-

back controllers and supervisory controllers. Typi-

cally, the two types of controllers are considered and

designed separately, not only to split the correspond-

ing functions, but also to simplify the design task. The

separate design, however, may lead to degraded per-

formance if the two parts lead to opposing effects on

the plant at the same time. This motivates to investi-

gate techniques that optimize continuous and discrete

controls simultaneously. This paper considers the de-

sign of optimizing feedback controllers for discrete-

time switched linear systems (SLS). Such systems,

which constitute a special class of hybrid systems

(Branicky et al., 1998), allow to switch between lin-

ear dynamics by use of the discrete controls. Note

that this externally triggered switching is different

from the class of discrete-time piecewise afﬁne sys-

tems (Sontag, 1981), in which switching occurs au-

tonomously and is bound to the fact that the continu-

ous state enters a new (polytopic) state region.

If optimization-based computation of control

strategies for SLS is considered, typically mixed-

integer programming problems are encountered,

which are known to be NP hard problems, see e.g.

https://orcid.org/0000-0003-4910-8218

https://orcid.org/0000-0002-9600-457X

(Bussieck and Pruessner, 2003). Nevertheless, for the

optimal open-loop control of discrete-time SLS with

quadratic performance measure and without state and

input constraints relatively efﬁcient techniques have

been proposed, see e.g. in (G

orges et al., 2011). The

complexity there is reduced via pruning of the search

tree and accepting sub-optimal solutions. An on-line

open-loop control approach for the case with state

and input constraints is described in (Liu and Sturs-

berg, 2018), where a trade-off between performance

and applicability is obtained by tree search with cost

bounds and search heuristics.

In contrast, the present paper aims at determining

optimal closed-loop control laws to select the con-

tinuous and discrete inputs for any state of the SLS.

In principle, this task can be solved by dynamic pro-

gramming (Bellman, 2010), but the complexity pre-

vents the use for most systems. The concept of ap-

proximate dynamic programming (ADP) (Bertsekas,

2019) is more promising in this respect, but has not

yet been used for controller synthesis of SLS with

consideration of constraints – this is the very objec-

tive of this paper. The approach is to learn the control

law from a dataset, which may originate from off-line

solution of mixed-integer programming problems for

selected initial states, or from approximate dynamic

programming over short horizons. The use of (deep)

neural networks (NN) are proposed as parametric ar-

chitectures for either approximating cost-to-go func-

tions, or the continuous-discrete control laws. NN as

Markolf, L. and Stursberg, O.

Learning-based Optimal Control of Constrained Switched Linear Systems using Neural Networks.

DOI: 10.5220/0010581600900098

In Proceedings of the 18th Inter national Conference on Informatics in Control, Automation and Robotics (ICINCO 2021), pages 90-98

ISBN: 978-989-758-522-7

parametric approximators are appealing due to their

property of universal approximation (Cybenko, 1989;

Hornik et al., 1989) and the recent success of deep

learning (Goodfellow et al., 2016). For the different

task of model predictive control of purely continuous-

valued systems, recent work has shown that the use

of NN (determined off-line) can lead to solutions of

problems in which full on-line computation takes pro-

hibitively long, see e.g. (Chen et al., 2018; Hertneck

et al., 2018; Karg and Lucia, 2020; Paulson and Mes-

bah, 2020; Markolf and Stursberg, 2021). This mo-

tivates for the present paper to train NN also for op-

timal control of SLS, despite the complexity arising

from the mixed inputs. While the analysis of neu-

ral networks is known to be challenging due to their

nonlinear and often large-scale structure, this paper

makes use of the methods developed in (Chen et al.,

2018) and (Markolf and Stursberg, 2021) to ensure

the satisfaction of state and input constraints in addi-

tion.

The considered problem is stated in Sec. 2, while

Sec. 3 shows how an ADP approach can be formu-

lated for SLS in principle. The speciﬁc choice of NN

as function approximators and solutions for consider-

ing the constraints, as well as the main algorithms are

detailed in Sec. 4. A numerical example is provided

in Sec. 5, before the paper is concluded in Sec. 6.

2 PROBLEM STATEMENT

This paper considers discrete-time and constrained

switched systems of the form:

k+1

= f

), k ∈ {0,..., N − 1}, (1)

where k is the time index, N a ﬁnite time horizon,

∈ R

the continuous state vector, u

∈ R

the

vector of continuous control inputs, and v

∈ V =

[1]

,.. .,v

]

} the discrete control input determining

the subsystem f

: R

× R

→ R

selected at time

k. The focus in this paper is on switched linear sys-

tems with matrices A

and B

of appropriate dimen-

sions:

) = A

+ B

, k ∈ {0,. ..,N − 1}.

(2)

The states and inputs are constrained to polytopes X

and U:

∈ X =



x ∈ R

x ≤ h



, (3)

∈ U =



u ∈ R

u ≤ h



, (4)

with matrices H

, and vectors h

. For a

given state x

, k ∈ {0,. .., N − 1} and input sequences

over a time span {k,. .., N − 1}:

:= {u

,.. .,u

N−1

}, (5)

:= {v

,.. .,v

N−1

}, (6)

the corresponding unique state sequence is denoted

by:

:= {x

,.. .,x

} (7)

and obtained from (1).

Let X

⊆ X be a target set speciﬁed as polytope:



x ∈ R

x ≤ h



⊆ X. (8)

Furthermore, let a sequence of state sets

,.. .,X

N−1

} be deﬁned, satisfying:

= {x ∈ X |for each v ∈ V : ∃u ∈ U such that

(x,u) ∈ X

k+1

}, k ∈ {0,. ..,N − 1},

(9)

i.e., for any state x

∈ X

, k ∈ {0,. .., N − 1} and

an arbitrary choice of the discrete input v

∈ V , at

least one admissible continuous input u

∈ U exists

such that f

) ∈ X

k+1

. The actual computation

of these sets will be addressed later in Sec. 4.

The following fact then obviously holds:

Proposition 1. If X

is nonempty, then for each ini-

tialization x

∈ X

and each discrete input sequence

at least one admissible continuous input sequence

exists that transfers x

into the target set X

while satisfying x

∈ X

, i ∈ {0,... ,N} and u

∈ U,

i ∈ {0, ... ,N − 1}.

For introducing costs, assume that φ

has been de-

termined for a given state x

at time k ∈ {0, ..., N −

1}, and for given input sequences φ

and φ

. Then let

(φ

,φ

) denote the total cost associated with this

evolution:

(φ

,φ

) = g

) +

N−1

∑

i=k

i,v

(10)

where g

: X → R

≥0

denotes a terminal cost, and

k,v

: X × U → R

≥0

, k ∈ {0,.. .,N − 1} a stage cost

for v

∈ V at stage k. Furthermore, let J

∗

(x) be

the optimal cost-to-go for steering a state x at time

k ∈ {0,. . .,N − 1} into the target set X

within N − k

steps, while satisfying x

∈ X

, i ∈ {k,... ,N} and

∈ U, i ∈ {k,..., N − 1}, i.e.:

∗

(x) = min

,φ

(φ

,φ

) (11a)

subject to:

= x, (11b)

i+1

= A

+ B

, i ∈ {k,... ,N − 1}, (11c)

∈ U, i ∈ {k, ... ,N − 1}, (11d)

∈ X

, i ∈ {k,... ,N}. (11e)

Learning-based Optimal Control of Constrained Switched Linear Systems using Neural Networks

By convention, J

∗

is set to inﬁnity for the case that

(11) is infeasible for a speciﬁc state x ∈ R

. Subse-

quently, the constraints (11d) and (11e) are replaced

by u

∈ U

), i ∈ {k , ... ,N − 1}. Here, U

k ∈ {0,. .., N − 1} denotes a set that depends on

the state x

∈ X and the discrete input v

∈ V , and

contains all the continuous inputs u

∈ U for which

) ∈ X

k+1

(x,v) = {u ∈ U | f

(x,u) ∈ X

k+1

}. (12)

Again, the actual computation of these sets will be

addressed later in Sec. 4

The following problem is considered in this work:

Problem 1 (Finite-Horizon Control Problem). Find

an optimal control law which assigns to each state

∈ X

at time instant k ∈ {0,.. .,N − 1} a pair of

optimal admissible inputs v

∗

∈ V and u

∗

∈ U

∗

such that for any x

∈ X

, the cost J



∗

,φ

∗

,φ

∗



obtained for the resulting sequences φ

∗

, φ

∗

, φ

∗

optimal, i.e.: J



∗

,φ

∗

,φ

∗



= J

∗

In order to allow for the use of gradient methods

to tackle this problem, as proposed in (Markolf and

Stursberg, 2021), the following assumption is made,

which is not practically restrictive.

Assumption 1. Suppose that the functions g

k,v

(x,u),

k ∈ {0,. .., N − 1}, v ∈ V in (10) are continuously dif-

ferentiable with respect to u ∈ U.

3 APPROXIMATE DYNAMIC

PROGRAMMING FOR SLS

In theory, dynamic programming (DP) provides a

scheme to solve the Problem 1: Starting from:

∗

) := g

), (13)

the DP algorithm proceeds backward in time from

N − 1 to 0 to compute the optimal cost-to-go func-

tions:

∗

) = min

∈V

∈U

)

k,v

) + J

∗

k+1

( f

))

(14)

Such a version of the DP-algorithm is similar to the

standard one without discrete inputs, as can be found

e.g. in (Bertsekas, 2005). Provided that the opti-

mal cost-to-go values J

∗

are known for all relevant

and k, the optimal discrete and continuous input

sequences φ

∗

and φ

∗

for x

∈ X

can be constructed

in a forward manner by:

∗

) ∈arg min

∈V

∈U

∗

)

k,v

∗

) + J

∗

k+1



∗

)



(15)

with x

∗

= x

and x

∗

k+1

= f

∗

For the general setup considered in this work, the

DP algorithm does not lead to closed-form expres-

sions for J

∗

and for the respective optimal policies

denoted by:

∗

:= {µ

∗

(·),.. .,µ

∗

N−1

(·)}, µ

∗

: X → U, (16)

∗

:= {µ

∗

(·),.. .,µ

∗

N−1

(·)}, µ

∗

: X → V. (17)

Hence, numeric solution is necessary, but is known

to suffer from the curse of dimensions, thus limiting

practical applicability.

However, the optimal cost-to-go functions J

∗

can

be approximated by parametric functions

with real-

valued parameter vectors r

, constituting a so-called

approximation in value space (Bertsekas, 2019). The

prediction of the optimal cost-to-go J

∗

given

some state x

is a typical regression task. Suppose for

a moment that a parametric function

and a data set

consisting of state-cost pairs (x

), s ∈ {1, ... ,q

}

are available, where each J

is a regression target pro-

viding the desired value for the corresponding exam-

ple state x

. On this basis, the parameter vector r

of the parametric function

can be adapted with the

objective to improve the performance on the consid-

ered regression task by learning from the data set.

The mean squared error is here (as usual) consid-

ered as performance measure. Such an adaption pro-

cedure for r

, typically called training, is an exam-

ple for supervised learning. A challenge hereby is to

perform also well on previously not explored states

, which distinguishes the training procedure from

pure optimization. For a more detailed treatment, see

e.g. (Goodfellow et al., 2016).

The following Algorithm 1, which extends the se-

quential DP procedure from (Bertsekas, 2019) to SLS,

provides an approach for training the parametric ap-

proximators

in a recursive manner (similar to the

typical DP procedure). Once the parametric approx-

imators

are trained, approximations of the optimal

discrete and continuous input sequences, denoted as

˜v

and φ

˜u

, can be constructed for x

∈ X

in a forward

manner, similar to (15):

( ˜v

, ˜u

) ∈arg min

∈V

∈U

( ˜x

)

k,v

( ˜x

) +

k+1



( ˜x

),r

k+1



(18)

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

with ˜x

= x

and ˜x

k+1

= f

˜v

( ˜x

, ˜u

Another way to obtain approximations of the op-

timal discrete and continuous input sequences is the

approximation of the optimal policies π

∗

and π

∗

so-called parametric policies:

˜v

= {µ

˜v

(·,r

),.. .,µ

˜v

N−1

(·,r

N−1

)},

with µ

˜v

(·,r

) : X → V, (19)

˜u

= {µ

˜u

(·,r

),.. .,µ

˜u

N−1

(·,r

N−1

)},

with µ

˜u

(·,r

) : X → U

(·,µ

˜v

(·,r

)). (20)

This approach is an example of an approximation in

policy space (Bertsekas, 2019). Again, the parame-

ter vectors r

and r

can be adapted by standard su-

pervised learning techniques on the basis of avail-

able data sets (x

), s ∈ {1,. .., q

} and (x

s ∈ {1,.. .,q

}, respectively. The data may originate

from solutions of (18), constituting an example of ap-

proximation in policy space on top of approximation

in value space.

4 OPTIMAL CONTROL OF SLS

WITH CONSTRAINTS USING

Based on the rather conceptual derivations in the pre-

ceding chapter, the speciﬁc approach for synthesiz-

ing optimal control laws based on NN for SLS with

input and state constraints is now described. Two

procedures of using (deep) neural networks as para-

metric architectures for the approximation of the op-

timal continuous and discrete input sequences are pro-

posed, one by approximation in value space, and the

other by approximation in policy space. In both cases,

Algorithm 1: Sequential Dynamic Programming.

) := g

)

2: for k = N − 1 to 0 do

3: Generate a large number of states x

, s ∈

{1,.. .,q

} by sampling the state space X

4: for s = 1 to q

= min

v∈V

u∈U

(

)

k,v

,u) +

k+1



,u), r

k+1



6: end for

7: Determine r

by training with (x

), s ∈

{1,.. .,q

}

8: end for

neural networks ˆv

, k ∈ {0, ... ,N − 1} with softmax

output units and parameter vectors r

are employed

to obtain for each x

∈ X

an n

-dimensional output

vector with ˆv

k,i

) = P(v

∗

= v

[i]

). Thus, the

outputs of the neural network ˆv

determine for x

probability distribution over the discrete control in-

puts, where ˆv

k,i

) denotes the probability that the

discrete control input v

[i]

is optimal for x

at stage k.

4.1 Approximation in Value Space

Neural networks with continuous and continuously

differentiable activation functions are proposed as

parametric approximators

for the optimal cost-to-

go functions J

∗

, k ∈ {0, ..., N −1}. Furthermore, a set

priority

( ˆv

priority

) ⊆ V is introduced, which is used

in approximating the optimal discrete and optimal in-

put sequences in a forward manner for given x

∈ X

and n

priority

∈ {1,. .., n

( ˜v

, ˜u

) ∈arg min

∈V

priority

(

ˆv

(

˜x

)

priority

)

∈U

( ˜x

)

k,v

( ˜x

) +

k+1



( ˜x

),r

k+1



(21)

with ˜x

= x

and ˜x

k+1

= f

˜v

( ˜x

, ˜u

). Here, n

priority

∈

{1,.. .,n

} is a user-deﬁned number used to specify

the number of elements in V

priority

( ˆv

priority

), where

these elements are selected to be the discrete inputs

with the highest probabilities according to ˆv

. This

allows to establish a trade-off in (21) between the

consideration of only a single discrete input (with the

highest probability to be the optimal one) or all dis-

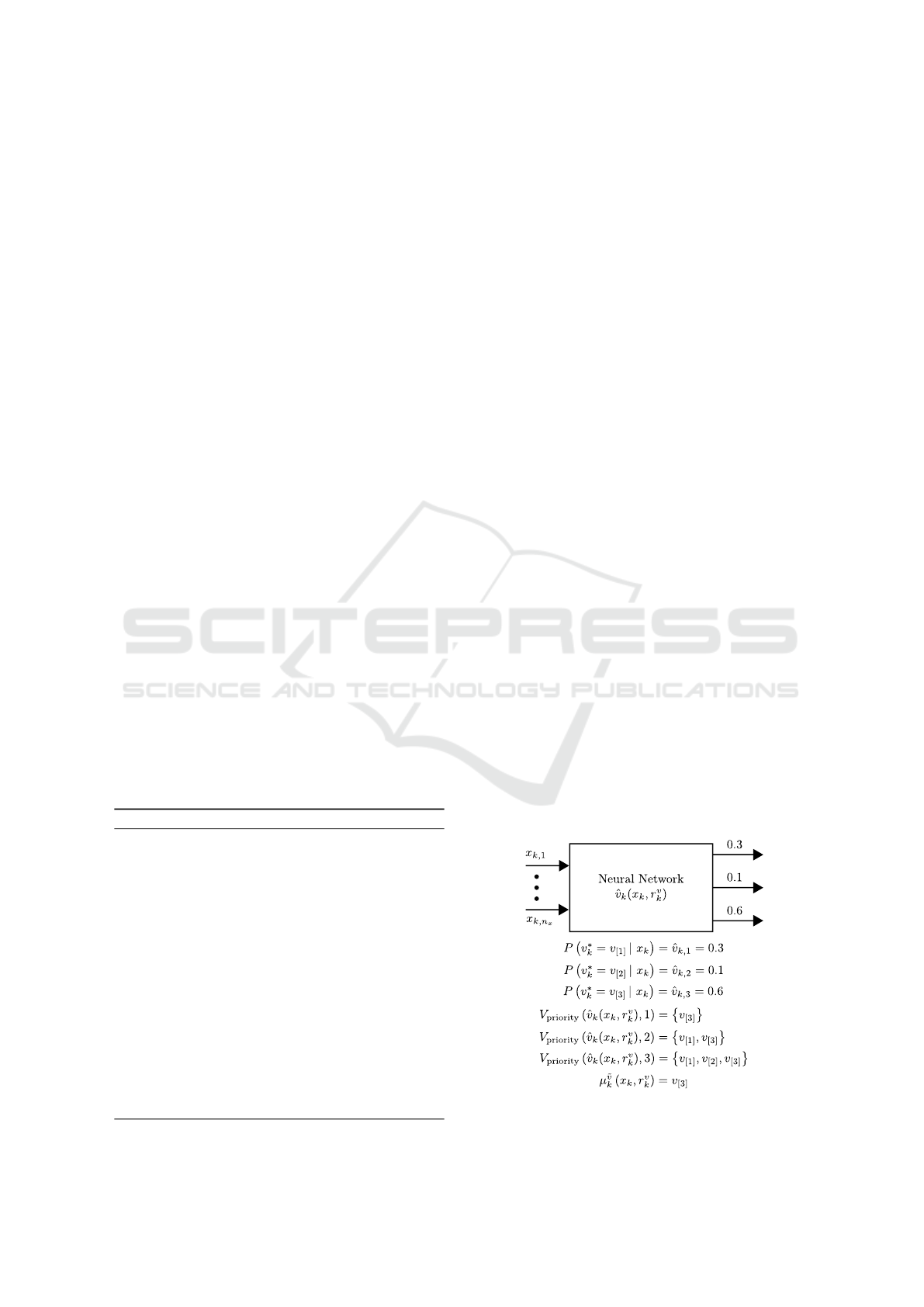
crete inputs contained in V . Fig. 1 provides an exam-

ple of the concept.

It will be addressed in detail in Sec. 4.3 how to

compute U

(x,v), k ∈ {0,.. .,N − 1}, and to show that

Figure 1: Example for illustrating the use of the neural net-

work ˆv

Learning-based Optimal Control of Constrained Switched Linear Systems using Neural Networks

(x,v) in (12) is a polytope for all x ∈ X

and v ∈ V .

The architecture of the neural networks and a closed-

form expression for the partial derivative of

(x,r

)

with respect to x will be described in Sec. 4.4. The

property that U

(x,v), k ∈ {0,. ..,N − 1} is a polytope

and the availability of closed-form expressions for

[∂

/∂x](x,r

) open the door for addressing the min-

imization problems in (18), (21), and Algorithm 1 by

applying well-established gradient methods for each

considered discrete input v ∈ V . The satisfaction of

the convex constraints u ∈ U

(x,v) in state-of-the-art

methods of this type is not a problem. Hence, the sat-

isfaction of the considered state and input constraints

in (11) is guaranteed, even in case of imperfect ap-

proximations of the optimal cost-to-go functions, or

if the iterative procedure of the gradient method is

stopped before ﬁnding a local minimum. This ap-

proach can be based on existing work on gradient-

methods for systems without switching (Markolf and

Stursberg, 2021).

4.2 Approximation in Policy Space

Alternatively, NN can be used directly as parametric

approximators µ

˜u

of the optimal continuous policies

∗

, k ∈ {0,.. .,N − 1}. The optimal discrete input

policies µ

∗

are approximated by:

˜v

) ∈



[i]

∈ V |for all j ∈ {1, ... ,n

} :



∗

= v

[i]



≥ P



∗

= v

[ j]



(22)

For a given initial state x

∈ X

, the scheme is then

to approximate the optimal continuous and discrete

input sequences in forward manner by computing:

˜v

= µ

˜v

( ˜x

) ∈ V, (23)

˜u

= µ

˜u

( ˜x

, ˜v

) ∈ U

( ˜x

, ˜v

), (24)

with ˜x

= x

and ˜x

k+1

= f

˜v

( ˜x

, ˜u

Provided that µ

˜u

) ∈ U

) for each

∈ X

and v

∈ V , the satisfaction of the state and in-

put constraints considered in (11) is guaranteed. This

can be achieved by projecting the output of the neural

network onto the polytope U

). An approach to

projecting the output of a neural network onto a poly-

tope can be found in (Chen et al., 2018).

4.3 Controllable Sets

For a given v ∈ V , let Pre

(X ) be the set of state pre-

decessors to X , i.e. containing all the states x ∈ R

for which at least one input u ∈ U exists such that

(x,u) ∈ X :

Pre

(X ) = {x ∈ R

|∃u ∈ U such that f

(x,u) ∈ X }.

(25)

If X is a polytope, then Pre

(X ) results from a linear

transformation of X , and is thus also a polytope. De-

tails about the computation of Pre

(X ) for a polytope

X can be found e.g. in (Borrelli et al., 2017).

Starting from a target set X

⊆ X, the sequence of

state sets {X

,.. .,X

N−1

} can be computed recursively

as shown in Algorithm 2. Since X

is speciﬁed in (8)

as polytope, each X

, k ∈ {0, ... , N − 1} deﬁned in (9)

is again a polytope:



x ∈ R

x ≤ h



. (26)

For polytopic sets X

, k ∈ {0, ... ,N − 1}, also the

sets U

(x,v) deﬁned by (12) are polytopes for all x ∈

and v ∈ V , and given by:

(x,v) = {u ∈ R

(v)u ≤ h

(x,v)}, (27)

with:

(v) =



k+1



, (28)

(x,v) =



k+1

− H

k+1



. (29)

4.4 Neural Networks

Feed-forward NN characterized by a chain structure:

h(x) = (h

(L)

◦ ·· · ◦ h

(2)

◦ h

(1)

)(x) (30)

are considered, with ﬁnal layer h

(L)

and hidden layers

(`)

, ` ∈ {1,. .., L−1}. Such structures are commonly

used and detailed information can be found in several

textbooks, see e.g. (Goodfellow et al., 2016). The

output of layer ` is denoted as η

(`)

in the following,

while η

(0)

is deﬁned to be the input of the overall net-

work:

(0)

(x) = x, (31)

(`)

(x) = (h

(`)

◦ ·· · ◦ h

(1)

)(x). (32)

Here, the hidden layers are (as usual) considered to be

vector-to-vector functions of the form:

(`)

(η

(`−1)

) = (φ

(`)

◦ ψ

(`)

)(η

(`−1)

), (33)

with afﬁne and nonlinear transformations ψ

(`)

and

(`)

, respectively. The afﬁne transformation can be

Algorithm 2: Controllable Set Computation.

Input: n

, N, X, X

Output: X

,.. .,X

N−1

1: for k = N − 1 to 0 do

2: X

= X

3: for i = 1 to n

4: X

← Pre

v[i]

k+1

) ∩ X

5: end for

6: end for

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

affected by the choice of the weight matrix W

(`)

and

the bias vector b

(`)

(η

(`−1)

) = W

(`)

(`−1)

+ b

(`)

. (34)

Each layer can be interpreted to consist of parallel act-

ing units, where a positive integer S

(`)

is used here to

describe the number of units in layer `. Each unit i

in layer ` deﬁnes a vector-to-scalar function, which is

the i-th component of h

(`)

. In the case of hidden lay-

ers, h

(`)

(η

(`−1)

) = φ

(`)

(`−1)

+ b

(`)

), where φ

(`)

is known as activation function and often chosen as

a rectiﬁed linear unit or a sigmoid function. For the

purposes of this work, linear and softmax output units

are considered. For a neural network with linear out-

put units, the function h

(L)

is an afﬁne transformation:

(L)

(η

(L−1)

) = W

(L)

(L−1)

+ b

(L)

. (35)

Such an afﬁne transformation arises also in softmax

output units, in which h

(L)

is set to:

softmax



(L)



(L−1)



exp



(L)



(L−1)



∑

(L)

j=1

exp



(`)



(L−1)





(36)

The neural network (30) belongs to the family of para-

metric functions, whose shape is formed by the pa-

rameter vector consisting of the weights and biases:

r =

(1)

1,1

... W

(L)

(L−1)

(1)

... b

(L)

(37)

4.4.1 Approximating the Optimal Cost-to-Go

Functions

For approximating the optimal cost-to-go functions

∗

, k ∈ {0,. .., N − 1}, the NN structure (30) is

used with continuous and continuously differentiable

activation functions (such as sigmoid functions) and

linear output units. This allows for deriving closed-

form expressions (Markolf and Stursberg, 2021) for

the partial derivatives of h with respect to its argu-

ments:

∂h(x)

∂x

L−1

∏

i=0

∂h

(L−i)

(η

(L−(i+1))

(x))

∂η

(L−(i+1))

, (38)

with:

∂h

(`)

(η

(`−1)

(x))

∂η

(`−1)

∂φ

(`)

(ψ

(`)

(η

(`−1)

(x)))

∂ψ

(`)

·W

(`)

(39)

for ` ∈ {1, ... ,L − 1}, and:

∂h

(L)

(η

(L−1)

(x))

∂η

(L−1)

= W

(L)

. (40)

4.4.2 Approximating the Optimal Discrete Input

Policies

As described above, the optimal discrete policies µ

∗

can be approximated by parametric policies µ

˜v

based

on the probability distributions deﬁned by the neu-

ral networks ˆv

, k ∈ {0, ... ,N − 1}. For this, the

NN structure (30) with softmax output units (36) is

used as architecture for ˆv

. Softmax units as output

units are common, e.g. in classiﬁcation tasks (Good-

fellow et al., 2016), to represent probability distribu-

tions over different classes. According to (36), each

output of the NN with softmax output units is in be-

tween 0 and 1, and all outputs sum up to 1, leading to

a valid probability distribution.

4.4.3 Approximating the Optimal Continuous

Input Policies

For the approximation of the optimal continuous in-

put policies µ

∗

by µ

˜u

, k ∈ {0,... ,N − 1}, the use of

the NN structure (30) with common activation func-

tions and linear output units is proposed, following

(Chen et al., 2018), where Dykstra’s projection algo-

rithm is used to project a potentially infeasible output

onto the admissible polytope. This is exploited here

to ensure that each ˜u

, as computed for x

∈ X

and

∈ V by (24), is an element of the polytope (27).

4.5 Main Algorithms

In order to summarize and combine the concepts in-

troduced above, this subsection contains the overall

algorithms to compute approximations of the optimal

discrete and continuous input sequences as solution to

Problem 1. While Algorithm 3 contains the procedure

for approximation in value space, Algorithm 4 estab-

lishes the solution by approximation in policy space.

Algorithm 3: Finite-Horizon Control by Approximation in

Value Space.

Input: ˜x

∈ X

, n

priority

∈ {1,. .., n

}

Output: φ

˜x

= { ˜x

,.. ., ˜x

}, φ

˜u

= { ˜u

,.. ., ˜u

N−1

˜v

= { ˜v

,.. ., ˜v

N−1

}

1: for k = 0 to N − 1 do

2: determine V

priority

( ˆv

( ˜x

),n

priority

)

3: obtain ( ˜v

, ˜u

) from (21) for ˜x

4: compute ˜x

k+1

= f

˜v

( ˜x

, ˜u

)

5: end for

Learning-based Optimal Control of Constrained Switched Linear Systems using Neural Networks

Algorithm 4: Finite-Horizon Control by Approximation in

Policy Space.

Input: ˜x

∈ X

Output: φ

˜x

= { ˜x

,.. ., ˜x

}, φ

˜u

= { ˜u

,.. ., ˜u

N−1

˜v

= { ˜v

,.. ., ˜v

N−1

}

1: for k = 0 to N − 1 do

2: determine ˜v

= µ

˜v



˜x



3: compute ˜u

= µ

˜u



˜x

, ˜v



4: evaluate ˜x

k+1

= f

˜v

( ˜x

, ˜u

)

5: end for

5 NUMERICAL EXAMPLE

This section provides a numerical example for the il-

lustration and evaluation of the proposed approaches.

Hereto, a switched system (2) with matrices:



0 1

−0.8 2.4



, A



0 1

−1.8 3.6





0 1

−0.56 1.8



, A



0 1

−8 6



= B





(41)

is considered. This simple example, which is taken

from (G

orges, 2012), is chosen with the intention to

ease the illustration of the procedures (not to demon-

strate computational efﬁciency). The polytopes X =

{x ∈ R

||x

| ≤ 1} and U = {u ∈ R | |u| ≤ 4} are speci-

ﬁed as state and input constraints, and a quadratic cost

function (10) is chosen:

(x) = x

x, (42)

k,v

(x,u) = x

x + u

for all

k ∈ {0,. .., N − 1},v ∈ V.

(43)

The target set is speciﬁed to be identical to the origin

of the state space X

= {0}. If for this simple system,

a low number N = 6 is chosen, the optimal solution of

the corresponding instance of Problem 1 can be com-

puted by enumerating over the 4

possible discrete

input sequences and solving one quadratic program

(QP) each – this optimal solution serves to compare

it with the approximating solutions obtained from the

two proposed approaches based on approximation in

value space, or in policy space respectively.

For all NN required in the proposed approaches,

structures with one hidden layer and 50 units have

been chosen. In each hidden unit, the hyperbolic tan-

gent has been selected as activation function. The

neural networks

used for approximating the opti-

mal cost-to-go values have been trained with state-

cost pairs (x

), s ∈ {1,.. .,q

} generated on the

0 1 2 3 4

Optimal Costs

Figure 2: Box plot diagram with showing the distribution of

the optimal costs J

∗

) for 1000 initial states x

obtained

by gridding X

basis of the sequential dynamic programming proce-

dure described in Algorithm 1, where q

= 1000 states

have been obtained for each k ∈ {0,. .., N − 1}

by gridding the state space X

obtained from Algo-

rithm 2.

For the same states x

, the NN for approximat-

ing the optimal discrete and continuous input policies

have been trained with state-input pairs (x

) and

), respectively, generated by addressing a mini-

mization problem of type (18) with the previously de-

termined

k+1

Let φ

˜u

and φ

˜v

denote approximated input se-

quences obtained for a speciﬁc initial state ˜x

∈ X

either applying Algorithm 3 or Algorithm 4. More-

over, let φ

˜x

be the resulting state sequence, and

( ˜x

)

the cost obtained for φ

˜x

, φ

˜u

, and φ

˜v

according to (10).

For the evaluation of the approximation quality, 1000

initial states x

, p ∈ {1,. .., n

= 1000} have been de-

termined by gridding the set X

, which is the back-

ward reachable set from X

for the selected N. The

distribution of the optimal costs J

∗

) for the ini-

tial states x

, p ∈ {1, ... , n

} is illustrated in the box

plot shown in Fig. 2. The average computation time

for the determination of the optimal costs was 19.8 s

on a common notebook (Intel



Core

i5 − 7200U

Processor), where the CPLEXQP solver from the

IBM



ILOG



CPLEX



Optimization Studio has

been used for the solution of the quadratic programs.

On the other hand, the costs

) for the initial states

, p ∈ {1,.. . ,n

} were determined for the approxi-

mated solutions obtained from the approaches for ap-

proximation in value space, or approximation in pol-

icy space, where for the former all possible values

for n

Priority

∈ {1,.. .,4} were considered. The cor-

responding mean-squared errors can be found in the

third column of Table 1, using:

MSE =

∑

p=1



∗

) −

)



. (44)

The average computation times are listed in the fourth

column of the same table.

As documented in Table 1, the average computa-

tion time for the optimal results is signiﬁcantly higher

than those for the approximated results. Moreover,

the average computation time for the approach based

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics

−1 0 1

−1

Finite-Horizon Control Problem

Optimal Solution

−1 0 1

−1

Finite-Horizon Control Problem

Approx. in Value Sp.

−1 0 1

−1

Finite-Horizon Control Problem

Approx. in Policy Sp.

Figure 3: Solutions for the initial state x



1 1



: optimal one, and for the two proposed techniques. The shaded polytope

marks X

Table 1: Mean squared errors according to (44) and aver-

age computation times to determine

) for 1000 initial

states x

obtained by gridding X

Type of n

Priority

MSE Average

Approx. Comp. Time

Value 4 3.51 × 10

−4

1.73 s

Space 3 3.51 × 10

−4

1.38 s

2 3.50 × 10

−4

1.03 s

1 6.56 × 10

−4

0.61 s

Policy − 5.27 × 10

−2

0.27 s

Space

on approximation in policy space was smaller than

those for the approximating in value space. For the

latter, the average computation times obviously grow

with increasing n

Priority

. Not surprisingly, the rela-

tively high computation time for the optimal solutions

are due to the large number of possible discrete input

sequences. The use of an NN, as required for approxi-

mation in policy space, is in general faster than apply-

ing the gradient method n

Priority

-times in the approach

based on approximation in value space. Interestingly,

the MSE for n

Priority

= 2 to n

Priority

= 4 are almost the

same and very small. The observation that the MSE

for the approximation in policy space is the largest de-

pends (among other factors) on the fact that the train-

ing data for the NN ˜µ

has been generated on top of

approximation in value space.

The state trajectories obtained from the optimal

and approximated solutions of Problem 1 for the ini-

tial state x



1 1



, as well as the polytope X

are

illustrated in Fig. 3. The optimal state trajectory and

the one approximated in value space are almost iden-

tical. For the state trajectory obtained from approxi-

mation in policy space, a slight difference is visible.

It is worth to stress that also for the approximated

solutions, the sets deﬁned in (27) ensure the satisfac-

tion of the state and input constraints in (11).

6 CONCLUSION

This paper has proposed two solution techniques to

synthesize optimal closed-loop controllers in form

of NN for ﬁnite-horizon optimal control problems

for discrete-time and constrained switched linear sys-

tems. Two general types of ADP, namely approxima-

tion in value space and approximation in policy space,

were considered for fast approximation of the opti-

mal solutions. For both ADP types, (deep) neural net-

works were chosen as parametric approximators. Es-

tablished methods for projection or for constraint han-

dling in nonlinear programming have been exploited

to ensure the satisfaction of polytopic state and input

constraints.

Properties of the optimal cost-to-go functions and

optimal policies for the considered problem class

have not been investigated in this work. Gaining a

deeper insight by future work may help to specify the

architectures of the neural networks. An approach to

ensure the satisfaction of polytopic (continuous) input

constraints by a policy based on neural networks with-

out a subsequent projection has been recently pro-

posed in (Markolf and Stursberg, 2021). A point of

work future is to investigate if also that approach can

be extended to guarantee the satisfaction of the con-

sidered state constraints.

REFERENCES

Bellman, R. (2010). Dynamic Programming. Princeton

University Press.

Learning-based Optimal Control of Constrained Switched Linear Systems using Neural Networks

Bertsekas, D. P. (2005). Dynamic programming and optimal

control. Athena Scientiﬁc.

Bertsekas, D. P. (2019). Reinforcement learning and opti-

mal control. Athena Scientiﬁc.

Borrelli, F., Bemporad, A., and Morari, M. (2017). Predic-

tive control for linear and hybrid systems. Cambridge

University Press.

Branicky, M. S., Borkar, V. S., and Mitter, S. K. (1998). A

uniﬁed framework for hybrid control: model and op-

timal control theory. IEEE Transactions on Automatic

Control, 43(1):31–45.

Bussieck, M. and Pruessner, A. (2003). Mixed-integer non-

linear programming. SIAG/OPT Newsletter: Views &

News, 14(1):19–22.

Chen, S., Saulnier, K., Atanasov, N., Lee, D. D., Kumar,

V., Pappas, G. J., and Morari, M. (2018). Approx-

imating explicit model predictive control using con-

strained neural networks. In Proc. American Control

Conference, pages 1520–1527.

Cybenko, G. (1989). Approximation by superpositions of a

sigmoidal function. Mathematics of Control, Signals,

and Systems, 2(4):303–314.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press.

orges, D. (2012). Optimal control of switched systems:

With application to networked embedded control sys-

tems. Logos-Verlag.

orges, D., Izak, M., and Liu, S. (2011). Optimal control

and scheduling of switched systems. IEEE Transac-

tions on Automatic Control, 56(1):135–140.

Hertneck, M., Kohler, J., Trimpe, S., and Allgower, F.

(2018). Learning an approximate model predictive

controller with guarantees. IEEE Control Systems Let-

ters, 2(3):543–548.

Hornik, K., Stinchcombe, M., and White, H. (1989). Multi-

layer feedforward networks are universal approxima-

tors. Neural Networks, 2(5):359–366.

Karg, B. and Lucia, S. (2020). Efﬁcient representation

and approximation of model predictive control laws

via deep learning. IEEE transactions on cybernetics,

50(9):3866–3878.

Liu, Z. and Stursberg, O. (2018). Optimizing online control

of constrained systems with switched dynamics. In

Proc. European Control Conference, pages 788–794.

Markolf, L. and Stursberg, O. (2021). Polytopic input con-

straints in learning-based optimal control using neural

networks. arXiv e-print:2105.03376.

Paulson, J. A. and Mesbah, A. (2020). Approximate closed-

loop robust model predictive control with guaranteed

stability and constraint satisfaction. IEEE Control Sys-

tems Letters, 4(3):719–724.

Sontag, E. (1981). Nonlinear regulation: The piecewise lin-

ear approach. IEEE Transactions on Automatic Con-

trol, 26(2):346–358.

ICINCO 2021 - 18th International Conference on Informatics in Control, Automation and Robotics