Data Driven Hybrid Approach for Health Monitoring and Fault

Detection in Military Ground Vehicles

Indu Shukla, Antoinette Silas, Haley Dozier, Brandon E. Hansen and W. Glenn Bond

US Army ERDC, Information Technology Laboratory, Vicksburg, MS, 39180, U.S.A.

Keywords: Long Short-Term Memory (LSTM), Vector Auto Regression (VAR), Prognostics and Health Management

(PHM).

Abstract: This paper presents a data driven hybrid approach for Prognostics and Health Management (PHM) of military

ground vehicles to mitigate a number of the unexpected failures, enabling intelligent decision-making for

improved performance, safety, reliability, and maintainability. For military ground vehicles, the Controller

Area Network (CAN) bus provides sensor data for collection and analysis. In this study we used collected

operational time-series data for generating future operational time series data for military ground vehicles.

Our sensor data share stochastic trends with more than one-time dependent variable to develop Vector Auto-

Regression (VAR) models suitable to forecast operational data. We have developed Long Short-Term

Memory (LSTM) fault detection models which ingest VAR forecasted data to identify fault detection. Our

experimental results show our hybrid approach provides promising fault diagnosis performance. Root mean

squared error, mean absolute percentage error and mean absolute error have been used as the evaluation

criteria.

1 INTRODUCTION

Excessive wear conditions occur when Army ground

vehicles are operated under extreme stress, with

heavy loads in a harsh environment. These conditions

reduce the usable lifetime of mechanical components.

This may cause unpredictable situations when a

component is nearing the end of service life. It can be

replaced instead of risking potential failure during the

mission. Rather than relying on traditional preventive

and reactive maintenance, data collected from the

Collective Area Network (CAN) bus on-board

sensors can be used for Prognostics and Health

Management (PHM) to assess diagnostic and

prognostics health state of the vehicle, moving

maintenance into the predictive and preemptive roles.

The main benefits of predictive health maintenance

are increased safety due to the reduction of

unexpected failures, reduced operation and

sustainment costs, and increased reliability,

availability and maintainability of army vehicles.

U.S. Army ground vehicle operational sensor data

has been collected for several years from some

platforms. Monitoring the vehicle data trends and

deviations with statistical and machine learning

models can lead to insight that will allow the

maintainer in the field to schedule maintenance

before failure occurs. As a

result, maintenance plans

can be optimized, avoiding many potential break

downs. Another main advantage of data-driven

approaches is that machine learning models are

scalable to entire fleets or families of vehicles.

Generic models have the potential to be used for other

vehicle models.

To evaluate the health of the system, various

techniques are used in data driven models (Lee et al.,

2014). For our study, we focus on data collected from

the vehicle at one second intervals (1Hz data) coupled

with system fault codes to design a supervised

learning fault detection model for enhanced fault

prediction. A Vector Autoregression (VAR) model

using historical 1Hz data and a multivariate Long

Short-Term Memory (LSTM) neural network for

operational data forecasting was implemented.

Comparing the forecast to real sensor output provides

diagnosis and fault detection capability. The output

from the LSTM model identifies whether the system

is operating under normal operating conditions,

represented with a value of zero. A nonzero value

LSTM model can be further evaluated to determine

the system fault code that the vehicle encounters. A

fault code is a pre-defined list of numerical

300

Shukla, I., Silas, A., Dozier, H., Hansen, B. and Bond, W.

Data Driven Hybrid Approach for Health Monitoring and Fault Detection in Military Ground Vehicles.

DOI: 10.5220/0010582603000307

In Proceedings of the 10th International Conference on Data Science, Technology and Applications (DATA 2021), pages 300-307

ISBN: 978-989-758-521-0

 2021 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

identifiers, which correlate to a particular failure or

error message for a component within the vehicle

system.

The applications of this study are twofold: (1) the

forecasted data can be used to predict whether a

vehicle is projected to continue operating within

normal bounds using the LSTM fault detection

model, and (2) the forecasted data can be used to

predict the remaining useful life (RUL) of the vehicle.

In this work, we focused on the first application by

introducing an approach to predict the future

operational health of a ground vehicle (section 2),

demonstrated the preliminary results from this

methodology (section 3), and discussed the future

direction of this work (section 4). By predicting

abnormal behavior potential field failure of a vehicle

can be prevented.

2 MATERIALS AND

METHODOLOGY

Hybrid autoregressive and LSTM models have been

used to forecast anomalous events, such as stock

market volatility (Ha and Chang, 2018). This paper

particularly focuses on implementing a hybrid VAR-

LSTM forecast model as a novel approach to fault

detection in military ground vehicles.

This research effort explores the VAR model for

forecasting. The VAR model uses historical 1 Hz

operational data to forecast vehicle operational data.

Then, LSTM model learns from the vehicle’s

historical fault and operational data to develop a

custom fault detection model. Once the model is built,

it ingests the forecasted data and provides a fault

detection and diagnosis based on what has been

predicted.

Figure 1: VAR-LSTM Hybrid model workflow.

Figure 1 shows the hybrid workflow to provide an

enhanced model for future fault detection. The

motivation behind the hybrid model is to speed up the

fault prediction modeling and forecasting process.

For building the VAR model Statmodels python

API is used, which provide classes and functions to

explore data, estimate statistical models, and perform

statistical tests (Seabold and Perktold, 2010).

2.1 Ground Vehicle Data Description

The ground vehicle data are collected from the

vehicle’s CAN Bus, during all operational intervals,

by a Dynamic Stability Controller box. This time

series data consists of sensor readings, such as oil

pressure, RPM, accelerator position, vehicle speed,

position, and other data points. Analysis of this data

details the performance of vehicles and different

components with respect to the driving status of those

vehicles. For the demonstrated predictive model, we

are using 1 Hz data from 25 vehicles. The entire 1 Hz

operational dataset was collected from roughly 4500

vehicles over seven years. Each 1 Hz vehicle history

dataset contains approximately 20+ million rows and

70+ columns. Figure 2 shows our data collection

workflow. For training purposes, only clean data was

selected and made stationary but outlier adjustments

were not considered.

Figure 2: Data Collection from CAN bus.

2.2 Time Series Visualization

Plotting the time series data will help visualize

patterns, unusual observations, changes over time and

relationships between the variables. Line plot, box

plot and autocorrelation plot are used to learn about

the statistical properties and the features present in the

time series.

2.3 Data Preparation

Preparing and pre-processing the data is a multistep

process involving missing value replacement and

filtering columns and entries by specific criteria. This

enhances the utility of the data in training and testing

models and ensures that confounding attributes of the

data don’t negatively impact the model’s

performance. Specific data cleaning and imputation

methods are discussed in Section 3.

Vehicle

DSC connected to

vehicle CAN bus

Vehicle data

files (.cdf)

HPC data

ingestion,

processing

and analysis

Algorithm

development and

implementation

Data

visualization and

prediction

Data Driven Hybrid Approach for Health Monitoring and Fault Detection in Military Ground Vehicles

301

2.4 Operational Data Forecasting

Forecasting often presents a complex problem for

data scientists and statisticians. This is due to many

factors, including

• Disappearance of correlation between variables in

future states

• Unexpected events can shift the data in ways the

model cannot predict

• The complexity of most multivariate time series

datasets

Selecting a suitable forecasting method for a dataset

is also often a large task on its own. Choosing a

method depends on the

• Availability of historical data

• Time interval that needs to be forecasted

• Desired degree of accuracy

• Computational power available for the model to

run and train.

Here we will discuss the Vector Auto Regression

model for operation data forecasting

We chose the VAR model to forecast this 1 Hz

operational data because it is one of the most

successful, flexible, and easy to use models for the

analysis of multivariate time series data (Zivot and

Wang 2006). These models are used to estimate

future values of time series variables that influence

each other. Besides forecasting economics and

financial time series data, VAR models are also used

for other disciplines such as medical research (Seth et

al., 2015) and signal processing (Basu et al., 2019).

VAR models are stochastic processes which are

natural extensions of univariate autoregressive

models as applied to dynamic multivariate time

series. Univariate time series models, such as

ARIMA, contain only one time-dependent variable

while multivariate time series models consist of

multiple time-dependent variables. Multivariate

models leverage complex dependencies between

variables to provide more reliable and accurate

forecasts for specific data. All variables in the VAR

model are treated as endogenous. There is one

equation for each endogenous variable in its reduced

form, and the right-hand side of each equation

includes lagged values of all dependent variables in

the system (Zivot and Wang, 2006).

For to the VAR model, we can write a 𝑝



order

model as the linear combination of previous vector

values,

𝒗



 𝛼𝛽



𝒗



𝛽



𝒗



⋯𝛽



𝒗



𝜀



Where 𝒗



represents the predicted future values of

each component in the past value vectors 𝒗

𝒕𝒊

where

𝑖∈



1, 𝑝



and 𝑖 represents the lag of the vector. The

variable 𝛼 is the intercept of the model and 𝜀



is an

error or noise term. The procedure to build VAR

models involves several steps. Figure 3 demonstrates

the procedure of building VAR model.

Figure 3: VAR model flowchart.

2.4.1 Testing for Stationarity

Time series data exhibits trend and seasonal residuals.

Checking for stationarity was therefore important in

our analysis because statistical forecasting models

cannot forecast on non-stationary data. For a time-

series dataset to be stationary, its mean, variance, and

autocovariance (at various lags) remain constant over

time; that is, they are time invariant. The study used

the two methods for testing stationarity of the

variables, because these tests can provide

contradictory results due to differences in type of

stationarity.

The Augmented Dickey–Fuller (ADF) test

(Dickey and Fuller, 1979) is a statistical significance

test to identify the presence of unit root in the time

series. There are several possible unit root tests but

the ADF test is a reliable option for time series with a

large number of observations. The presence of a unit

root in the ADF test means the time series difference

is stationary. If the ADF test statistic is greater than a

critical value based on alpha levels of 1%, 5% and

10% then the null hypotheses is rejected and the series

is non-stationary. The ADF significance level

assesses the statistical significance of data for a null

hypothesis.

The Kwiatkowski–Phillips–Schmidt–Shin

(KPSS) approach is another test for checking the

stationarity nature of time series data (Kwiatkowski

et al., 1992). It differs from the ADF tests in the sense

that the series is assumed to be stationary under null

hypothesis. According to the KPSS test, the null

hypothesis tells us the process trends stationary and

the alternate hypothesis identifies the unit root, which

DATA 2021 - 10th International Conference on Data Science, Technology and Applications

302

denotes the presence of stationarity. Both approaches

were applied to ensure that the series used in the

present investigation is stationary.

2.4.2 Testing for Causality

Once stationarity is established, we applied Granger’s

causality test on our time series data. Granger’s

causality test (Granger, 1969) is a statistical

hypothesis test to investigate whether one time series

is useful for forecasting another, which is the basis of

the VAR model. It determines if systems influence

each other. If the p-value obtained from the test is

less than the significance level, the hypothesis is

rejected and we can conclude that one time series is

causing the other. Significance level assess the

statistical significance of data for a null hypothesis.

For our test we used popular 1%, 5% and 10% of

significance level. We must make the time series

stationary before running Granger’s Causality test to

eliminate the possibility of auto correlation. To

accomplish this, our study employs chi-square

distribution because we are testing with a large

number of lags and variables.

2.4.3 Selection of Model Order

Model order selection for reliable forecast is an

important step in statistical analysis when using the

VAR model. The most common approach for model

order selection involves choosing a model order that

minimizes one or more information criteria evaluated

over a range of model orders. Choosing optimal lag

reduces residual correlation. To select the right order

of the VAR model we iteratively fit the model which

requires the maximum number of lags. The command

returns a statistical information criterion to use for

order selection which are Akaike Information

Criterion (AIC) (Akaike, 1985), Schwarz-Bayes

Criterion (SBC) (Schwarz, 1978) – also known as the

Bayesian Information Criterion (BIC) – Akaike’s

Final Prediction Error Criterion (FPE), and Hannan-

Quinn Criterion (HQ) (Hannan and Quinn, 1979). We

have selected the order that produces the lowest AIC,

BIC, FPE and HQIC scores.

2.4.4 Residual Checking

After choosing the lag order, the selected model is

trained and check for serial correlation of residuals.

For our study, we are using Durbin Watson Statistics

(Durbin and Watson, 1951), which is a standard tool

for checking residual autocorrelation in VAR models.

The null hypothesis is that there is no residual

autocorrelation; the alternative is that residual

autocorrelation exists. The Durbin Watson test

reports a test statistic with a value from 0 to 4 where

a value close to 2 has no autocorrelation, closer to 0

indicates positive autocorrelation, and closer to 4

implies negative autocorrelation.

2.4.5 Forecasting and Model Diagnostic

Based on the best fit of the VAR(p) model we obtain

the forecast for each variable where p indicates the

model order. After training the model on training

data, we use the model to make predictions on test

data. Based on test data predictions, we can determine

how the model performed. If we are detrending or

differencing our time series, the differenced or

detrend forecasts must be reversed into the original

forecast values. We use descriptive statistics mean,

minimum, maximum, standard deviation to observe

how the statistical distribution of test values differ

from forecasted values. Root Mean Square Error

(RMSE) is used to evaluate model accuracy.

2.5 Supervised Fault Detection Model

This section discusses a supervised learning model

that provides a novel approach to fault detection (Dai

and Zhao, 2013). Preliminary results indicate that

artificial neural network models, namely LSTM

models, provide promising fault detection capabilities

for highly dimensional data observed over millions of

samples.

The vehicle’s operational behaviors, as presented

in the 1Hz dataset, coupled with the observed fault

data for that particular vehicle over the same

timeframe, provided the framework to design a

supervised learning model for enhanced fault

prediction. We hope to identify a significantly greater

number of fault conditions and component failures

than are identifiable using physics-based models

before they occur, increasing mission capability and

cost savings. Logistics, sustainment, and operational

decisions and policies will also benefit from insights

provided by these models.

2.5.1 Long-Short Term Memory Model

Artificial neural networks (ANNs) lie within the

realm of supervised machine learning and can process

operational data and produce fault detection and

prediction values (Helbing and Ritter, 2018).

Univariate regression models use input data and,

under an assumed linear relationship, generate

coefficients representing their functional values (Park

et al., 1991). However, ANNs utilize both linear and

Data Driven Hybrid Approach for Health Monitoring and Fault Detection in Military Ground Vehicles

303

non-linear functional capabilities to detect the

correlation of input and output values.

Our method deploys a LSTM model as a data-

driven approach for fault detection. LSTMs are an

ANN that utilize deep-learning, artificial recurrent

neural network methods (Fu, Huang, Qin, Liang, &

Yang, 2018). Deployed on the historical 1 Hz vehicle

data, the LSTM model observed multiple columns of

sensor data and provided fault detection and

diagnosis. The detection levels identify operating

conditions that could be classified as normal,

representing them with a value of 0. The LSTM

model further identified the type of numerical fault

code encountered by the system. A fault code is an

integer value that correlates to a unique failure

indicator or error status for a component within the

vehicle system.

The LSTM model, with network layers shown in

Figure 4, provided the capability to distinguish

normal operational behavior from a fault interval.

Though, the original dataset contained over 28

columns of data, the input layer only received 5

columns of data needed to detect a fault. The LSTM

model received the 5 input neurons and through a

hidden layer, transcribed it to 1 output neuron which

corresponds to a fault code. The LSTM model was

trained over 15 epochs.

Figure 4: LSTM network layer based on operational data.

The two available datasets used to train the LSTM

model were the multivariate 1Hz operational data,

spanning over one year, and the vehicle’s fault data

for the same timeframe. The raw historical data

contained mostly normal operational data. The

sample size of the historical data was filtered,

reducing the occurrence of normal event data, to

prevent overfitting of the LSTM model. To filter the

historical data, an anomaly detection model was built

using Independent Component Analysis (ICA) to

identify a low-dimensional subspace of the dataset in

which normal and abnormal operation could be

identified using statistical methods along with K-

means clustering. Abnormal operational data was

determined to be data that resided in clusters that

related timewise with known fault indicators.

Analysis from the unsupervised anomaly

detection model identified areas within the data where

a fault was likely to occur. The training batch size and

epochs were reset, reflecting a more constricted time

frame. The separate multivariate fault dataset

correlated time-wise to the operational dataset

columns. The fault data’s sample size pre-processing

techniques included applying a fault code toward the

operational data.

The independent datasets, coupled as a supervised

learning problem, enhance fault detection. Input data

for LSTM is filtered 1Hz operational data with

reduced columns that mirror the layout VAR dataset.

Column reduction decreases dimensionality and

mitigates model overfitting. The columns that were

used to train the model were filtered according to the

columns identified by the VAR methodology. As a

stand-alone model, the LSTM detects faults based on

the historical data upon which it was trained.

Including the VAR model in the workflow increases

model effectiveness while lowering computational

complexity by reducing input dimensionality.

Column alignment allows the independently

developed LSTM and VAR models to seamlessly

transition the VAR output data as input data for the

LSTM model. VAR-LSTM can function as one

hybrid model. Once the projected data is ingested into

the LSTM model, the LSTM model analyzes and

classifies which data represent specific fault

conditions. The LSTM model evaluation used a

Binary cross-entropy loss function.

3 RESULTS AND DISCUSSION

This study evaluated an expansive 1Hz operational

time series dataset and corresponding fault data. We

estimated and validated our model on the data from

several vehicles. We have used one-year operational

data generated from 25 vehicles, we found that results

from our best performing models are identical.

Therefore, results and analysis presented here focused

on a one-year operational interval for one vehicle.

3.1 VAR Results

For data preparation, we removed columns with

outlier percentages greater than 80% and with

variance less than 0.05. These columns don’t

meaningfully contribute to the model’s predictive

capability because the data they contain is either

unreliable or approximately constant. We used scatter

plot and IQR (Interquartile range) for multivariate

outlier analysis.

DATA 2021 - 10th International Conference on Data Science, Technology and Applications

304

Analyzing the line plot of time series in Figure 5,

we see that all of the time series data follow a

stochastic trend, showing stronger intertemporal

variations with larger drops. All of the series seem to

be related in some way and none look stationary in

their levels. They all appear to have common trends,

an indication that they may be co-integrated.

Figure 5: Time Series line plot.

The series was differenced to make it stationary.

Results from KPSS and ADF tests verified that the

series was difference stationary. The differenced

series was then checked for stationarity. Granger’s

causality test was performed on the first order of the

differenced time series, then tested with 20, 30 and 40

lags applied at 1% and 5% significance levels. P-

values less than the significance levels were found

consistently, confirming the relationships of multiple

variables in the time series and justifying the VAR

modelling approach to forecast the 1Hz operational

dataset.

To determine optimal lag order we have used the

python library model.select_order(maxlags) method

with different values for our max lag. BIC statistics

from running the command suggest the optimal lag

order is 44 and FPE statistics suggest 45. We ran this

command for other VIN numbers and other years, and

the resultant lag order suggestion stayed

approximately the same for all of the data we

considered. Durbin-Watson residual tests indicated

no autocorrelation between the residuals.

We experimented with model VAR model orders

between 42 and 49 for different VIN numbers. In this

paper, we are presenting results from best performing

model. Most models performed best between the lag

length 44-48 and had the lowest number of outliers as

suggested during multivariate outlier analysis. The

worst performing models had RMSE in the range of

40-50% and were discarded.

Before forecasting we de-differenced the

forecasted data once to bring it back to original scale.

Figure 6 shows the plot of forecasted data against

the actual test data for Transmission Oil Temperature,

Engine Coolant Temperature and Engine Oil

Pressure. Forecasting for 8 days was generated using

fitted VAR (44) model in blue. Red represents the

actual value. Forecasted and actual data demonstrate

similar pattern throughout the forecasted days. For

Engine Oil Pressure, forecasted data is close to actual

data but except near transition points. The

Transmission Oil Temperature data pattern is also

very close but predicted values are overestimated.

The Forecast plot for Engine Coolant Temperature

shows a similar pattern, but predicted values were

underestimated for the last two days. In general, we

observed phases of high forecasting accuracy

alternating with phases of low forecasting accuracy.

Identifying structural breaks (Allaro, 2018) in the

data and training the model with segments of time

series is expected to improve forecast accuracy. Table

1 shows the evaluation of VAR model to measure the

average forecast accuracy. RMSE value indicate that

VAR model was not able to successfully forecast

large variation in data therefore it suffered from

accuracy issue.

Figure 6: VAR model forecast data vs. test data.

Table 1: VAR model forecast accuracy.

Variable RMSE

EngCoolantTemp 20.2

EngineOilPressure 17.3

TransOilTem

32.3

Data Driven Hybrid Approach for Health Monitoring and Fault Detection in Military Ground Vehicles

305

3.2 LSTM Results

Fault detection accuracy varied between the vehicle

models. The entire research effort implemented the

model across several vehicles, but this paper presents

results from building a hybrid VAR-LSTM model for

a single vehicle. The LSTM model that was built

using only historical data provided 65% - 90%

accuracy across multiple vehicles. Once the LSTM

model was built, LSTM model was given the

forecasted VAR data to see if it could detect any fault.

The combined LSTM-VAR model, as a preliminary

finding for a single vehicle, provided at most a 64%

detection accuracy as shown in Figure 7. Therefore,

the LSTM model lost accuracy when detecting faults

as a hybrid model than it did as a stand-alone model.

The loss function in Figure 7 showed a loss of 57%

for this particular vehicle. The LSTM model proved

successful in learning the correlation between normal

operational data and fault data. The LSTM model can

be further expanded to observe data across the entire

vehicle fleet and for an increased period of time. An

increase of time-series data observations and may

contribute to increased model accuracy.

Figure 7: LSTM model training and validation

accuracy/loss.

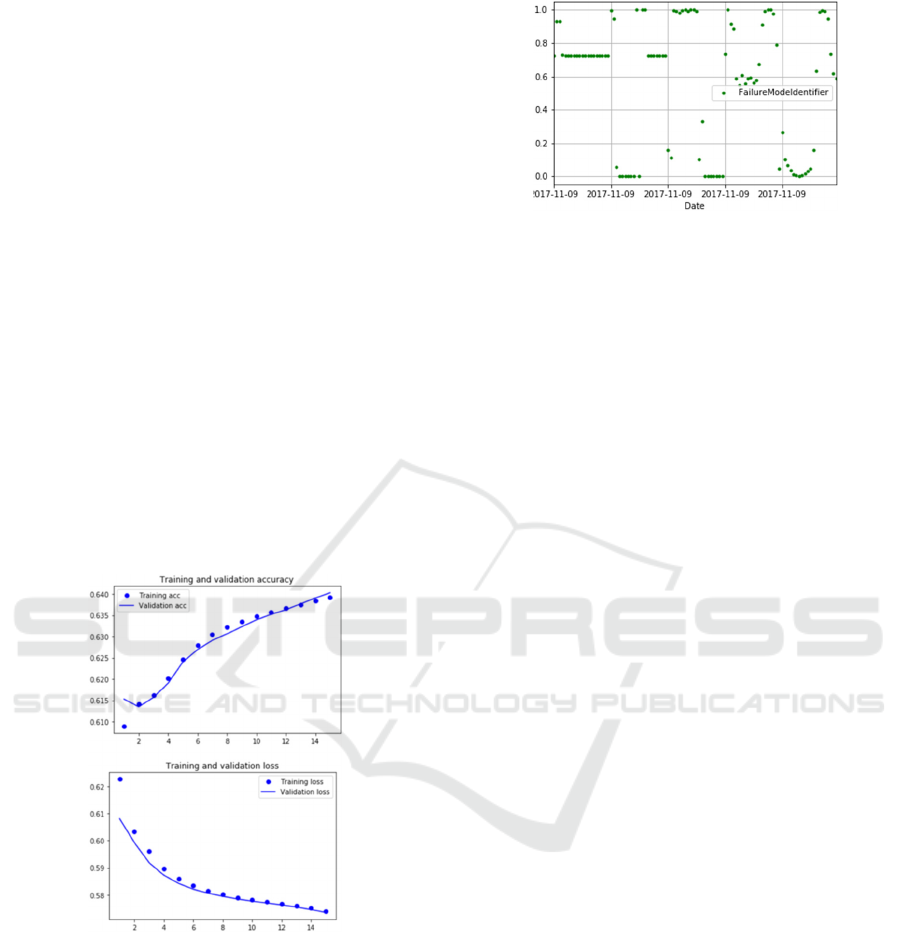
The hybrid VAR-LSTM model output, produced

scaled fault detection values, labeled as

FailureModeIdentifier, as shown in Figure 8. The

corresponding plot corresponds to the fault values are

indicated as a failure mode value as a function of

time, as shown along the x-axis. These values can be

descaled and traced directly back to the fault code

status log to determine the projected fault status of the

vehicle

Figure 8: Hybrid VAR-LSTM model output for fault

detection.

4 CONCLUSIONS AND FUTURE

WORK

The VAR model captured the temporal dynamics of

our time series data but was not able to improve the

accuracy. Experimentation with different VIN

numbers, selection of variable and lag order shows no

signs of improving the VAR model forecast. The

VAR model is a popular tool in time series

forecasting but its parameters are estimated by the

least square technique which is very sensitive to the

presence of outliers. We did not smooth or filter the

outliers from our data because removing the outliers

may disturb the information content hence the series

was only differenced to make it stationary which is a

prerequisite for inferring Granger’s Causality test.

We couldn’t scale the VAR model across the fleet

because this model is computationally expensive to

run and adding more data complicates the learning

ability of the model. We only experimented with a

few variables at a time because adding more variables

to a VAR model creates complications. Predictions

become more unreliable. Another challenge with the

VAR model is that predictions quickly deteriorate.

Very short-term forecasting was found to be slightly

more accurate than long term forecasting, suggesting

some gain is possible by iteratively running the model

over short intervals. In terms of forecast stability, the

model does not constantly yield accurate results

mainly due to structural breaks in the data which can

occur due to periods of inactivity or major

maintenance related change in the vehicle.

Though the LSTM model provided low accuracy

levels using forecasted data, we have succeeded in

building a hybrid workflow for a fault detection

model. However, it can be improved upon with

expanding the model to learn across additional

vehicles and increase the size of the dataset. The

VAR-LSTM hybrid model is very promising for fault

prediction. However, further comparisons of LSTM

DATA 2021 - 10th International Conference on Data Science, Technology and Applications

306

hybrid models should also be evaluated to potentially

increase model accuracy. We will explore other deep

learning models such as CNN-LSTM model (Livieris

et al., 2020), which has been proven successful in

forecasting time series data.

In next phase of the project, in addition to

increasing model sample size, we will be using

corresponding maintenance data for more accurate

forecasting. We will expand our model further using

the fault detection codes to identify data-driven

Remaining Useful Life (RUL) estimation for systems

with abrupt failures. The patterns and trends of

forecasted data our analysis reveals will be used for

condition monitoring and identifying abnormal

operating conditions.

REFERENCES

Allaro HB (2018) A Time Series Analysis of Structural

Break Time in Ethiopian GDP, Export and Import. J

Glob Econ 6: 303. doi: 10.4172/2375-4389.1000303

Akaike, H. (1985), "Prediction and entropy", in Atkinson,

A. C.; Fienberg, S. E. (eds.), A Celebration of Statistics,

Springer, pp. 1–24

Basu, S., Li, X. Q. & Michailidis, G. (2019), ‘Low rank and

structured modeling of high-dimensional vector

autoregressions’, IEEE Transactions on Signal

Processing 67(5), 1207–1222

Dai, X. and Gao, Z. (2013). From Model, Signal to

Knowledge: A Data-Driven Perspective of Fault

Detection and Diagnosis, IEEE Transactions on

Industrial Informatics, vol. 9, (no. 4).

Dickey, D. A.; Fuller, W. A. (1979). "Distribution of the

Estimators for Autoregressive Time Series with a Unit

Root". Journal of the American Statistical Association.

74 (366): 427–431. doi:10.1080/01621459.1979.

10482531

Durbin, J.; Watson, G. S. (1951). "Testing for Serial

Correlation in Least Squares Regression, II".

Biometrika. 38 (1–2): 159–179. doi:10.1093/biomet/

38.1-2.159

Granger, C.W.J. (1980). "Testing for causality: A personal

viewpoint". Journal of Economic Dynamics and

Control. 2: 329–352. doi:10.1016/0165-1889(80)

90069-X

Fu, Y., Huang, D., Qin, N., Liang, K. and Yang, Y. (2018).

High-Speed Railway Bogie Fault Diagnosis Using

LSTM Neural Network, 37th Chinese Control

Conference.

Ha, Y., Chang H. (2018). Forecasting the volatility of stock

price index: A hybrid model integrating LSTM with

multiple GARCH-type models, Expert Systems with

Applications, vol 103.

Hannan, E. J., and B. G. Quinn (1979), "The Determination

of the order of an autoregression", Journal of the Royal

Statistical Society, Series B, 41: 190–195Park, D.C., El-

Sharkawi, M.A., Marks, R.J., Atlas, L.E. and Damborg,

M.J. (1991). Electric load forecasting using an artificial

neural network, IEEE Transactions on Power Systems,

vol. 6, no. 2.

Helbing, G. & Ritter, M. (2018). Deep Learning for fault

detection in wind turbines, Renewable and Sustainable

Energy Reviews, vol 98.

Kwiatkowski, D.; Phillips, P. C. B.; Schmidt, P.; Shin, Y.

(1992). "Testing the null hypothesis of stationarity

against the alternative of a unit root". Journal of

Econometrics. 54 (1–3): 159–178. doi:10.1016/0304-

4076(92)90104-Y

Lee J., Wu F., Zhao W., Ghaffari M., Liao L., Siegel D.

Prognostics and health management design for rotary

machinery systems—Reviews, methodology and

applications Mech Syst Signal Process, 42 (1–2)

(2014), pp. 314-334

Livieris, I.E., Pintelas, E. & Pintelas, P. A CNN–LSTM

model for gold price time-series forecasting. Neural

Comput & Applic. 32, 17351–17360 (2020).

Seabold, S., & Perktold, J. (2010). Statsmodels:

Econometric and Statistical Modeling with Python.

Seth, A. K., Barrett, A. B., & Barnett, L. (2015). Granger

causality analysis in neuroscience and neuroimaging.

The Journal of neuroscience: the official journal of the

Society for Neuroscience, 35(8), 3293–3297.

https://doi.org/10.1523/JNEUROSCI.4399-14.2015

Schwarz, Gideon E. (1978), "Estimating the dimension of a

model", Annals of Statistics, 6 (2): 461–464,

doi:10.1214/aos/1176344136

Zivot, E. and Wang, J. (2006) Vector Autoregressive

Models for Multivariate Time Series. Modeling

Financial Time Series with S-PLUS®. Springer, New

York, NY doi: 10.1007/978-0-387-32348-0_11.

Data Driven Hybrid Approach for Health Monitoring and Fault Detection in Military Ground Vehicles

307